TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(e)

I.
Question 1.
prove that sin 50° – sin 70° + sin 10° = 0
Answer:
sin 50° – sin 70° + sin 10°
= 2 cos \(\left(\frac{50^{\circ}+70^{\circ}}{2}\right)\) sin \(\left(\frac{50^{\circ}-70^{\circ}}{2}\right)\) + sin 10°
= 2 cos 60° sin (- 10°) + sin 10°
= 2\(\left(\frac{1}{2}\right)\) (- sin 10°) + sin 10°
= – sin 10° + sin 10° = 0

Question 2.
Prove that \(\frac{\sin 70^{\circ}-\cos 40^{\circ}}{\cos 50^{\circ}-\sin 20^{\circ}}\) = \(\frac{1}{\sqrt{3}}\)
Answer:

Question 3.
Prove that cos55° + cos 65° + cos 175° = 0
Answer:
cos 55° + cos 65° + cos 175°
= 2 cos \(\left(\frac{55+65}{2}\right)\) cos \(\left(\frac{55-65}{2}\right)\)
= 2 cos 60° cos (- 5°) – cos 5°
= 2 \(\left(\frac{1}{2}\right)\) cos 5° cos 5° = cos 5° – cos 5° = 0

Question 4.
Prove that
4 (cos 66° + sin 84°) = √3 + √15
Answer:
4 (cos 66° + sin 84°)
= 4 [cos 66° + sin (90 – 6°)]
= 4 [cos 66° + cos 6°]

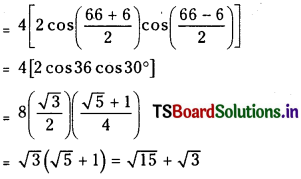
Question 5.
Prove that cos 20° cos 40° – sin 5° sin 25° = \(\frac{\sqrt{3}+1}{4}\)
Answer:
cos 20° cos 40° – sin 5° sin 25°
= \(\frac{1}{2}\) [2 c0s 20° c0s 40° – 2 sin 5° sin 25°]
= \(\frac{1}{2}\) [(cos 60 + cos 20) – (cos 20 – cos 30°)]
= \(\frac{1}{2}\) [cos 60° + cos 30°] = \(\frac{1}{2}\left[\frac{1}{2}+\frac{\sqrt{3}}{2}\right]\) = \(\frac{\sqrt{3}+1}{4}\)

Question 6.
Prove that cos 48° cos 12° = \(\frac{3+\sqrt{5}}{8}\)
Answer:
cos 48° cos 12°
= \(\frac{1}{2}\) [2 cos 48° cos 12°]
= \(\frac{1}{2}\) [cos 60° + cos 36°]

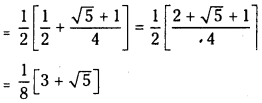
Short Answer Questions

II.
Question 1.
Prove that
cos θ + cos \(\left(\frac{2 \pi}{3}+\theta\right)\) + cos \(\left(\frac{4 \pi}{3}+\theta\right)\) = 0
Answer:
cos θ + cos (120 + θ) + cos (240 + θ)

Question 2.
Prove that sin² \(\left(\alpha-\frac{\pi}{4}\right)\) + sin² – sin² \(\left(\alpha+\frac{\pi}{12}\right)\) \(\left(\alpha-\frac{\pi}{12}\right)\) = \(\frac{1}{2}\)
Answer:
sin² (α – 45°) + sin² (α + 15°) – sin² (α – 15°)
= sin² (α – 45°) + sin (α + 15 + α – 15) sin (α + 15 – α + 15)
= sin² (α – 45°) + sin 2α sin 30°

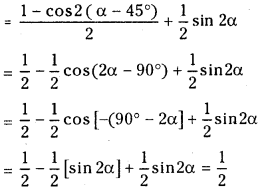
Question 3.
If sin x + sin y = \(\frac{1}{4}\) and cos x + cos y = \(\frac{1}{3}\) then show that
(i) tan \(\left(\frac{x+y}{2}\right)\) = \(\frac{3}{4}\)
Answer:

(ii) cot (x + y) = \(\frac{7}{24}\)
Answer:

Question 4.
If neither [A – \(\frac{\pi}{12}\)] nor [A – \(\frac{5 \pi}{12}\)] is an integral multiple of π.
Prove that cot [\(\frac{\pi}{12}\) – A] + tan [\(\frac{\pi}{12}\) + A] = \(\frac{4 \cos 2 A}{1-2 \sin 2 A}\)
Answer:

Question 5.
Prove that 4 cos 12° cos 48° cos 72° = cos 36°
Answer:
4 cos 12° cos 48° cos 72°
= 2 cos 12° [2 cos 48° cos 72°]
= 2 cos 12° [cos (48° + 72°) + cos (48° – 72°)]
= 2 cos 12° [cos 120° + cos 24°]
= 2 cos 12° [- \(\frac{1}{2}\) + cos 24°]
= – cos 12° + 2 cos 12° cos 24°
= – cos 12° + cos (12° + 24°) + cos (12° – 24°)
= – cos 12° + cos 36° + cos 12°
= – cos 36°

Question 6.
Prove that
sin 10° + sin 20° + sin 40° + sin 50° = sin 70° + sin 80°
Answer:
sin 10° + sin 500 + sin 20° + sin 40°
= 2 sin \(\frac{\left(10^{\circ}+50^{\circ}\right)}{2}\) cos \(\frac{\left(10^{\circ}-50^{\circ}\right)}{2}\) + 2 sin \(\left(\frac{20^{\circ}+40^{\circ}}{2}\right)\) cos \(\left(\frac{20^{\circ}-40^{\circ}}{2}\right)\)
= 2 sin 30° cos 20° + 2 sin 30° cos 10°
= 2 \(\left(\frac{1}{2}\right)\) cos 20° + 2 \(\left(\frac{1}{2}\right)\) cos 10°
= cos 20° + cos 10°
= cos (90° – 70°) + cos (90° – 80°)
= sin 70° + sin 80°

III.
Question 1.
If cos x + cos y = \(\frac{4}{5}\) and cos x – cos y = \(\frac{2}{7}\).
find the value of 14 tan \(\left(\frac{x-y}{2}\right)\) + 5 cot \(\left(\frac{x+y}{2}\right)\)
Answer:
Given cos x + cos y = and cos x – cos y = \(\frac{2}{7}\)

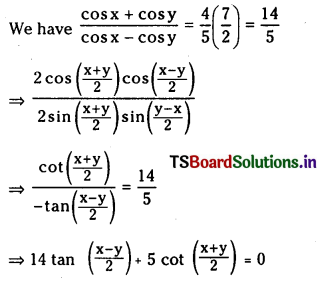
Question 2.
If none of the denominators is zero, prove that

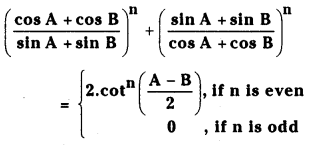
Answer:

If n is odd, since (- 1)ⁿ = 1
we have LHS = O
If n is even and (- 1)ⁿ = 1
L.H.S = 2 cot²\(\left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)\)

Question 3.
If sin A = sin B and cos A = cos B, then prove that A = 2nπ + B for some integer n.
Answer:
sin A = sin B and cos A = cos B
⇒ sin A – sin B = 0 and cos A – cos B = 0
⇒ 2 cos \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{A-B}{2}\right)\) = 0 ……………. (1)
and cos A – cos B = 0
⇒ 2 sin \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{B-A}{2}\right)\) = 0 ……………… (2)
From (1) and (2),
sin \(\left(\frac{A-B}{2}\right)\) = o ⇒ \(\left(\frac{A-B}{2}\right)\) = nπ
⇒ A = 2nπ + B for some n ∈ Z

Question 4.
If cos nα ≠ 0 and cos \(\frac{\alpha}{2}\) ≠ 0 then show that
\(\frac{\sin (n+1) \alpha-\sin (n-1) \alpha}{\cos (n+1) \alpha+2 \cos n \alpha+\cos (n-1) \alpha}\) = tan \(\frac{\alpha}{2}\)
Answer:
L.H.S

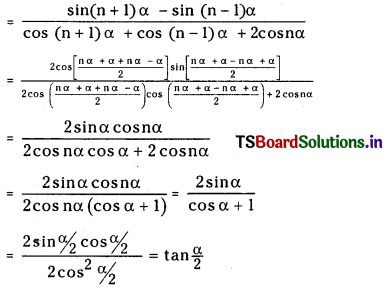
Question 5.
If sec (θ + α) + sec (θ – α) = 2 sec θ and cos α ≠ 1, then show that cos θ = ± √2 cos \(\frac{\alpha}{2}\).
Answer:
Given(θ + α) + sec (θ – α) = 2 sec θ

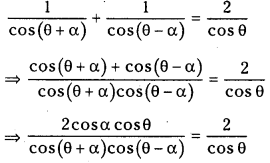
⇒ cos α cos²θ = cos²θ – sin²α
⇒ cos² θ (1 – cos α) = sin²α
⇒ cos² θ (1 – cos α) = 1 – cos²α
⇒ cos² θ = 1 – cos α = [∵ cos α ≠ 1]
⇒ cos² θ = 2 cos² \(\frac{\alpha}{2}\)
⇒ cos θ = ±√2 cos \(\left(\frac{\alpha}{2}\right)\)

Question 6.
If none of x, y, z is an odd multiple of \(\frac{\pi}{2}\) and if sin (y + z – x), sin (z + x – y), sin (x + y – z) are In AP then prove that tan x, tan y, tan z are also in AP.
Answer:
sin (y + z – x), sin(z + x – y), sin(x + y – z) are in A.P
⇒ sin(z + x – y) – sin (y + z – x) = sin (x + y – z) – sin (z + x – y)
⇒ z cos z sin(x – y) 2 cos x sin(y – z)
⇒ cos z [sin x cos y – cos x sin y] = cos x [ sin y cos z – cos y sin z]
Dividing by cos x cos y cos z. We get,
\(\frac{\sin x}{\cos x}-\frac{\sin y}{\cos y}=\frac{\sin y}{\cos y}-\frac{\sin z}{\cos z}\)
⇒ tan x – tan y = tan y – tan z
⇒ tan x + tan z = 2 tan y
⇒ tan x, tan y, tan z are in A.P

Question 7.
If x, y, z are non zero real numbers and if x cos θ = y cos\(\left(\theta+\frac{2 \pi}{3}\right)\) = z c0s\(\left(\theta+\frac{4 \pi}{3}\right)\) for some θ ∈ R, then show that xy + yz + zx = 0
Answer:
x ≠ 0, y ≠ 0, z ≠ 0

Question 8.
If neither A nor A + B Is an odd multiple of \(\frac{\pi}{2}\) and if m sin B = n sin (2A + B), then prove that (m +n) tanA =(m – n) tan(A + B).
Answer:
Given, m sin B = n sin (2A + B)

Question 9.
If tan(A + B) = λ tan(A – B) show that (λ + 1) sin 2B = (λ – 1) sin 2A
Answer:
Given tan (A + B) = λ tan (A – B)