TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(d)

I.
Question 1.
Simplify
(i) \(\frac{\sin 2 \theta}{1+\cos 2 \theta}\)
Answer:

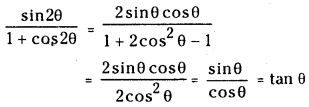
(ii) \(\frac{3 \cos \theta+\cos 3 \theta}{3 \sin \theta-\sin 3 \theta}\)
Answer:

Question 2.
Evaluate the following
(i) 6sin 20° – 8 sin³ 20°
Answer:
2(3 sin 20° – 4sin³ 20°) (Formula)
= 2.sin (3 × 20°) = 2 sin 60°
= \(\frac{2 \sqrt{3}}{-2}\) = √3

(ii) cos²72° – sin²54°
Answer:
cos²72° – sin²54°
= sin²18° – cos²36°

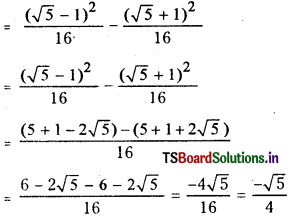
(iii) sin²42° – sin²12°
Answer:
sin²42° – sin²12° (Formula)
sin (42° + 12°) sin (42° – 12°)
= sin 54° sin 30°
= \(\left(\frac{\sqrt{5}+1}{4}\right) \frac{1}{2}=\frac{\sqrt{5}+1}{8}\)

Question 3.
(i) Express \(\frac{\sin 4 \theta}{\sin \theta}\) in terms of cos3 θ and cos θ.
Answer:
sin4θ = sin (3θ + θ) = sin 3θ cos θ +cos 3θ sin θ
= (3 sin θ – i sin 3θ) cos θ + (4 cos 3θ – 3 cos θ) sin θ
= 3 sin θ cos θ – 4 sin 3θ cos θ + 4 cos 3θ sin θ – 3 cos θ sin θ
= 4 cos 3θ sin θ – 4 sin 3θ cos θ
= sin θ(1 cos 3θ – 4 sin 2θ cos θ)
= sin θ [4 cos 3θ – 4 sin 2θ cos θ]
∴ \(\frac{\sin 4 \theta}{\sin \theta}=\frac{\sin \theta\left(4 \cos ^3 \theta-4 \sin ^2 \theta \cos \theta\right)}{\sin \theta}\)
= 4 cos 3θ – 4 sin 2θ cos θ
= 4 cos 3θ – 4 (1- cos 2θ) cos θ
= 8 cos 3θ – 4 cos θ

(ii) Express cos⁶ A + sin⁶ A in terms of sin 2A.
Answer:
cos⁶A + sin⁶A = (cos²A + sin²A)³
= (cos²A + sin²A)³ – 3 cos²A sin²A (cos²A + sin² A)
= 1 – 3 cos²A sin²A ……………(1)
= 1 – \(\frac{3}{4}\) (4 cos² A sin² A)
= 1 – \(\frac{3}{4}\)sin²2A

(iii) Express \(\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}\) in terms of tan \(\frac{\theta}{2}\)
Answer:

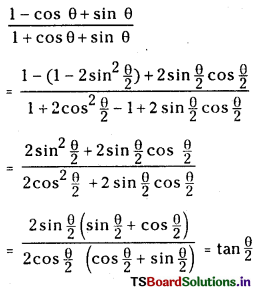
Question 4.
(i) If sin α = \(\frac{3}{5}\), where \(\frac{\pi}{2}\) < α < π, evaluate cos 3α and tan 2α. (March 2015-T.S)
Answer:
since \(\frac{\pi}{2}\) < α < π, a lies in second quadrant and given sin α = \(\frac{3}{5}\) we have cos α = –\(\frac{4}{5}\)
cos 3α = 4 cos³ α – 3 cos α

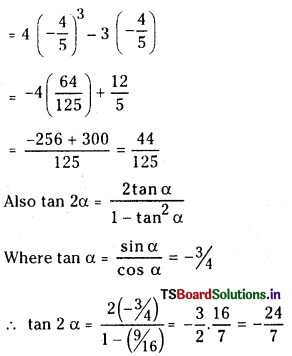
(ii) If cos A = \(\frac{7}{25}\) and \(\frac{3 \pi}{2}\) < A < 2π, then find the value of cot \(\frac{A}{2}\).
Answer:

(iii) If 0 < θ < \(\frac{\pi}{8}\), show that \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 4 \theta}}}\) = 2cos(θ/2)
Answer:

Question 5.
Find the extreme values of
(i) cos 2x + cos2x
Answer:
cos 2x + cos2x = 2 cos² x – 1 + cos² x
= 3 cos² x – 1
and 0 ≤ cos² x ≤ 1
⇒ 0 ≤ 3 cos² x ≤ 3
⇒ -1 ≤ 3 cos² x – 1 ≤ 2
Maximum value = 2
and minimum value = -1
(or) cos 2x + cos² x = cos 2x + \(\left(\frac{1+\cos 2 x}{2}\right)\)
We have -1 < cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3
⇒ -2 ≤ 3 cos 2x + 1 ≤ 4
⇒ -1 ≤ \(\frac{3 \cos 2 x+1}{2}\) ≤ 2
Maximum value = 2
Minimum value = -1

(ii) 3sin²x + 5 cos²x
Answer:
3sin²x + 5 cos²x

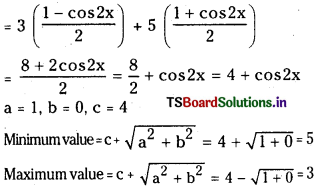
Question 7.
Find the periods for the following functions
(i) cos⁴x
Answer:

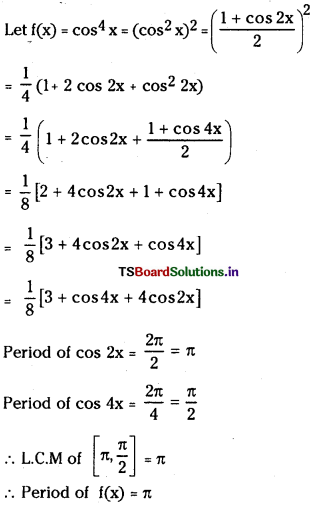
(ii) 2sin\(\left(\frac{\pi \mathbf{x}}{\mathrm{4}}\right)\) + 3cos\(\left(\frac{\pi x}{3}\right)\)
Answer:

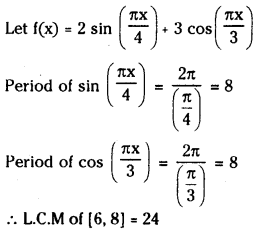
(iii) sin²x + 2 cos²x
Answer:
Let f(x) = sin²x + 2cos²x

(iv) 2sin(\(\frac{\pi}{4}\) + x)cos x
Answer:

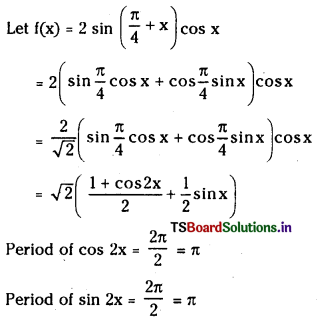
Period of f(x) is LCM of [π, π] = π

(v) \(\frac{5 \sin x+3 \cos x}{4 \sin 2 x+5 \cos x}\)
Answer:

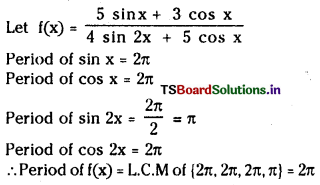
II.
Question 1.
(i) If 0 < A < \(\left(\frac{\pi}{4}\right)\), and cos A = \(\frac{4}{5}\), find the values of sin 2A and cos 2A.
Answer:

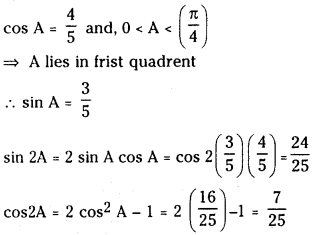
(ii) For what values of A in the first quadrant, the expression \(\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\) is positive?
Answer:
\(\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\) > 0
⇒ cot³A – 3 cot A > 0
⇒ cot A (cot² A – 3) > 0
⇒ cot A > 0 or cot² A > 3
⇒ cot A > √3

(iii) Prove that \(\frac{\cos 3 A+\sin 3 A}{\cos A-\sin A}\) = 1 + 2 sin 2A
Answer:

Question 2.
(i) Prove that cot(\(\frac{\pi}{4}\) – θ) = \(\frac{\cos 2 \theta}{1-\sin 2 \theta}\) and hence find the value of cot 15°.
Answer:

(ii) If θ lies in third quadrant and sin θ = –\(\frac{4}{5}\), find the values of cosec\(\left(\frac{\theta}{2}\right)\) and tan\(\left(\frac{\theta}{2}\right)\).
Answer:
Given θ lies in third quadrant.

(iii) If 450° < θ < 540° and sin θ = \(\frac{12}{13}\), then calculate sin\(\left(\frac{\theta}{2}\right)\) and cos\(\left(\frac{\theta}{2}\right)\).
Answer:

(iv) Prove that \(\frac{1}{\cos 290^{\circ}}+\frac{1}{\sqrt{3} \sin 250^{\circ}}=\frac{4}{\sqrt{3}}\)
Answer:

Question 3.
Prove that
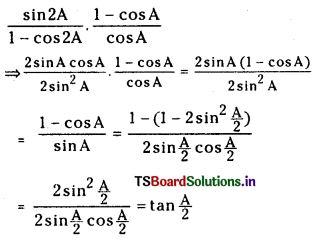
(i) \(\frac{\sin 2 A}{(1-\cos 2 A)} \cdot \frac{(1-\cos A)}{\cos A}\) = tan\(\frac{\mathrm{A}}{2}\)
Answer:

(ii) \(\frac{\sin 2 x}{(\sec x+1)} \cdot \frac{\sec 2 x}{(\sec 2 x+1)}\) = tan\(\left(\frac{x}{2}\right)\)
Answer:

(iii) \(\frac{\left(\cos ^3 \theta-\cos 3 \theta\right)}{\cos \theta}+\frac{\sin ^3 \theta+\sin 3 \theta}{\sin \theta}\) = 3.
Answer:

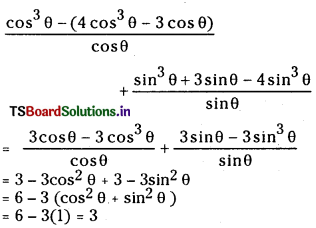
Question 4.
(i) Show that cos A = \(\frac{\cos 3 A}{2 \cos 2 A-1}\). Hence find the value of cos 15°.
Answer:

(ii) Show that sin A = \(\frac{\sin 3 A}{1+2 \cos 2 A}\). Hence find the value of sin 15°.
Answer:

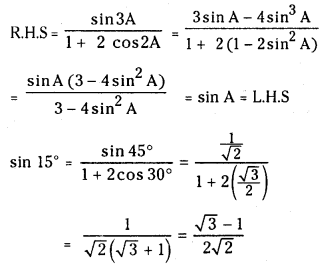
(iii) Prove that tan α = \(\frac{\sin 2 \alpha}{1+\cos 2 \alpha}\) and hence deduce the values of tan 15° and tan 22\(\frac{1}{2}\).
Answer:

Question 5.
Prove that \(\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}\) = 4
(i) \(\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}\) = 4 (Mar’ 2003, Jun 2004)
Answer:

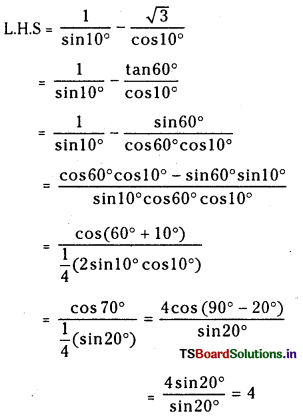
(ii) √3 cosec 20° – sec 20° = 4.
Answer:

(iii) tan 9° – tan 27° – cot 27° + cot 9° = 4
Answer:
We have that tan A + cot A = \(\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}=\frac{1}{\sin A \cos A}\) = 2 cosec 2A
Put A = 9°, we have tan 9° + cot 9° = 2 cosec 18°
Put A = 27°, we have tan 27°+ cot 27° = 2 cosec 54°
∴ L.H.S
∴ tan 9° – tan 27° + cot 9° – cot 27° = 2 (cosec 17° – cosec 54°)

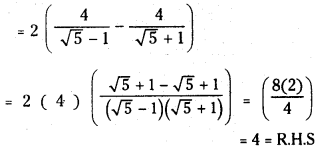
(iv) If \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\), then prove that a sin 2α + b cos 2α = b.
Answer:
Given that \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\)
⇒ b sin α + a cos α
L.H.S = a sin 2α + b cos 2α
= a (2 sin α cos α) + b ( 1 – 2 sin²α)
= 2 sin α (a cos α) + b – 2 b sin²α
= 2 sin α (b sin α) + b – 2b sin²α
= 2b sin²α + b – 2b sin²α = b

Question 6.
(i) In a ΔABC; if tan \(\frac{A}{2}=\frac{5}{6}\), and tan \(\frac{B}{2}=\frac{20}{37}\) then show that tan(C/2) = \(\frac{2}{5}\)
Answer:
In ΔABC, A + B + C = 180°

(ii) If cos θ = \(\frac{5}{13}\) and 270° < θ < 360°, evaluate sin \(\left(\frac{\theta}{2}\right)\) and cos \(\left(\frac{\theta}{2}\right)\).
Answer:
Given cos θ = \(\frac{5}{13}\), where 270° < θ < 360°,
⇒ 135° < \(\frac{\theta}{2}\) < 180°
⇒ \(\frac{\theta}{2}\) lies in second quadrant
since cos θ = \(\frac{5}{13}\)

(iii) If 180° < θ < 270° and sin θ = –\(\frac{4}{5}\) calculate sin\(\left(\frac{\theta}{2}\right)\) and cos\(\left(\frac{\theta}{2}\right)\)
Answer:

Question 7.
(i) Prove that cos²\(\frac{\pi}{8}\) + cos²\(\frac{3 \pi}{8}\) + cos²\(\frac{5 \pi}{8}\) + cos²\(\frac{7 \pi}{8}\) = 2
Answer:

(ii) Show that cos⁴\(\left(\frac{\pi}{8}\right)\) + cos⁴\(\left(\frac{3 \pi}{8}\right)\) + cos⁴\(\left(\frac{5 \pi}{8}\right)\) + cos⁴\(\left(\frac{7 \pi}{8}\right)=\frac{3}{2}\)
Answer:

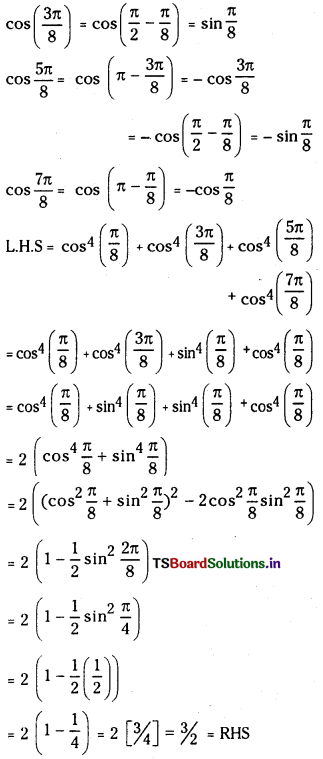
III.
Question 1.
(i) If tan x + tan (x + \(\frac{\pi}{3}\)) + tan(x + \(\frac{2 \pi}{3}\)) = 3, show that tan 3x = 1
Answer:

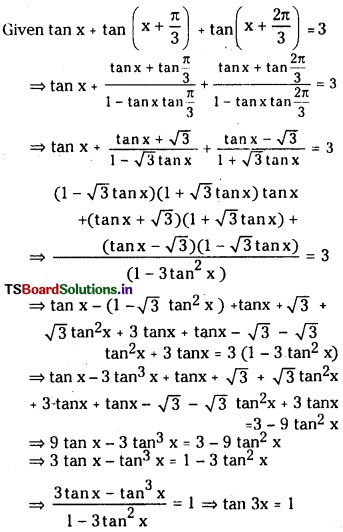
(ii) Prove that (March 2013)
sin\(\frac{\pi}{5}\) sin\(\frac{2 \pi}{5}\).sin\(\frac{3 \pi}{5}\).sin\(\frac{4 \pi}{5}=\frac{5}{16}\)
Answer:
L.H.S = sin\(\frac{\pi}{5}\) sin\(\frac{2 \pi}{5}\).sin\(\frac{3 \pi}{5}\).sin\(\frac{4 \pi}{5}\)
= sin 36° . sin 72° . sin 108° . sin 144°
= sin 36° . sin 72°. sin (90° + 18°) sin (180° – 36°)
= sin 36° . sin (90° – 18°) . sin (90° + 18°). sin (180° – 36°)
= sin 36° . cos 18° . cos 18° . sin 36°
= sin236° . cos218°
= \(\left(\frac{10-2 \sqrt{5}}{16}\right)\left(\frac{10+2 \sqrt{5}}{16}\right)\)
= \(\frac{100-20}{256}=\frac{80}{256}=\frac{5}{16}\)

(iii) Show that cos²\(\left(\frac{\pi}{10}\right)\) + cos²\(\left(\frac{2 \pi}{5}\right)\) + cos²\(\left(\frac{3 \pi}{5}\right)\) + cos²\(\left(\frac{9 \pi}{5}\right)\) = 2
Answer:
cos²18° + cos² 72°+ cos² 108° + cos² 162°
= cos²18° + cos² 72°+ cos2 (90 + 18) + cos²(108° – 18°)
= cos² 18° + sin² 18° + sin² 18° + cos² 18°
= 1 + 1 = 2

Question 2.
Prove that
(i) \(\frac{1-\sec 8 \alpha}{1-\sec 4 \alpha}=\frac{\tan 8 \alpha}{\tan 2 \alpha}\)
Answer:

(ii) (1 + cos \(\frac{\pi}{10}\))(1 + cos \(\frac{3 \pi}{10}\))(1 + cos \(\frac{7 \pi}{10}\))(1 + cos \(\frac{9 \pi}{10}\)) = \(\frac{1}{16}\). (March 2015-A.P)
Answer:
(1 + cos 18) (1 + cos 54) (1 + cos 126) (1 + cos 162)
= (1 + cos 18) (1 + sin 36) (1 – sin 36) (1 – cos 18)
= (1 + cos 18) (1 – cos 18) (1 + sin 36) (1 – sin 36)
= sin² 18° cos² 36°
= \(\left(\frac{\sqrt{5}-1}{4}\right)^2\left(\frac{\sqrt{5}+1}{4}\right)^2\)
= \(\frac{(5-1)^2}{256}=\frac{16}{256}=\frac{1}{16}\)

Question 3.
Prove that
(i) cos \(\frac{2 \pi}{7}\) cos\(\frac{4 \pi}{7}\) cos \(\frac{8 \pi}{7}=\frac{1}{8}\)
Answer:
Let \(\frac{2 \pi}{7}\) = α
and x = cos α cos2 α cos 4 α
and y = sin α sin2 α sin4 α (suppose)

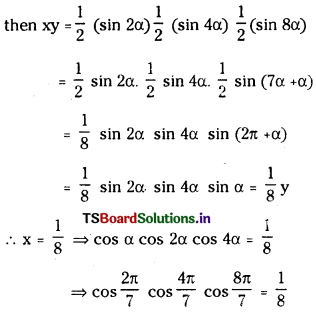
(ii) cos \(\frac{\pi}{11}\) cos\(\frac{2 \pi}{11}\) cos\(\frac{3 \pi}{11}\)cos\(\frac{5 \pi}{11}\)cos\(\frac{4 \pi}{11}=\frac{1}{32}\)
Answer:
Let \(\frac{\pi}{11}\) = α
and x = cos α cos 2α cos 3α cos 4α cos 5α
and y = sin α sin 2α sin 3α sin 4α sin 5α
xy =

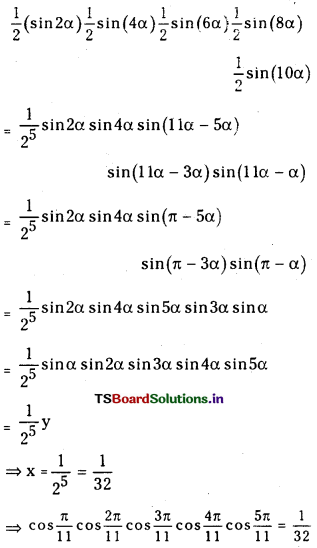
Question 4.
(i) If cos α = \(\frac{3}{5}\) and cos β = \(\frac{5}{13}\) and α, β are acute angles, then prove that
(a) sin²\(\left(\frac{\alpha-\beta}{2}\right)=\frac{1}{65}\) and
(b) cos²\(\left(\frac{\alpha+\beta}{2}\right)=\frac{16}{65}\)
Answer:
α, β are acute angles and cos α = \(\frac{3}{5}\) and cos β = \(\frac{5}{13}\)

(ii) If A is not an integral multiple of π, prove that cos A . cos 2A . cos 4A . cos 8A = \(\frac{\sin 16 A}{16 \sin A}\) and hence deduce that cos A. cos 2A . cos 4A .cos 8A = \(\frac{\sin 16 A}{16 \sin A}\) and hence deduce that
cos \(\frac{2 \pi}{15}\).cos\(\frac{4 \pi}{15}\).cos\(\frac{8 \pi}{15}=\frac{16 \pi}{15}=\frac{1}{16}\) (Mar 2012, May 2012)
Answer:
We have to prove that
16 sin A cos A cos 2A cos 4A cos 8A = sin 16A
L.H.S = 8(2 sinA cos A) cos2A cos 4A cos 8A = sin 16A
= 8 sin 2A cos 2A cos 4A cos 8A
= 4 (2 sin 2A cos 2A ) cos 4A cos 8A
= 4 sin 4A cos 4A cos 8A = 2 (2 sin 4A cos 4A) cos 8A
= 2 (sin 8A) (cos 8A)
= cos 16A
= R.H.S