TS Inter 2nd Year

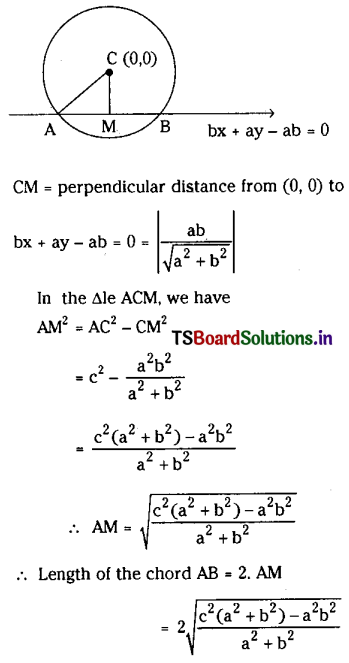
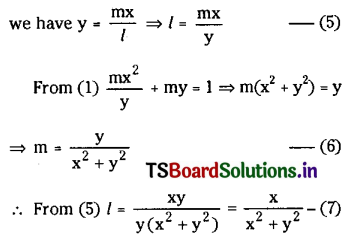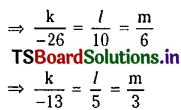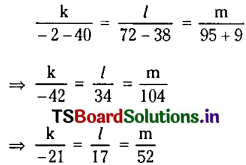Students must practice this TS Intermediate Maths 2B Solutions Chapter 3 Parabola Ex 3(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Exercise 3(b)

I.

Question 1.
Find the equations of the tangent and normal to the parabola y² = 6x at the positive end of the latus rectum.
Solution:
Given equation of parabola is y² = 6x ……..(1)
Comparing with y² = 4ax we get 4a = 6
⇒ a = \(\frac{3}{2}\)
Let L be the positive end of the latus rectum of the parabola y² = 6x
∴ L = (a, 2a) = (\(\frac{3}{2}\), 3)
The equation of tangent to the parabola (1) at (\(\frac{3}{2}\), 3) is yy₁ – 2a(x + x₁) = 0
y(3) = 3(x + \(\frac{3}{2}\))
⇒ 3y = 3x + \(\frac{9}{2}\)
⇒ 6y = 6x + 9
⇒ 2x – 2y + 3 = 0 ……(2)
The equation of normal to the parabola (1) at (\(\frac{3}{2}\), 3) is

Question 2.
Find the equation of tangent and normal to the parabola x² – 4x – 8y + 12 = 0 at (4, \(\frac{3}{2}\)).
Solution:
Given equation of parabola is x² – 4x – 8y + 12 = 0 ……..(1)
Let P(x₁, y₁) = P(4, \(\frac{3}{2}\)) be the given point.
Differentiating (1) w.r.t x we get
2x – 4 – 8 \(\frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}=\frac{x-2}{4}\)
∴ The slope of the tangent at (4, \(\frac{3}{2}\)) is m = \(\frac{4-2}{4}=\frac{2}{4}=\frac{1}{2}\)
and slope of the normal at (4, \(\frac{3}{2}\)) is -2
The equation of a tangent to the parabola (1) at (4, \(\frac{3}{2}\)) is y – y₁ = m(x – x₁)
⇒ y – \(\frac{3}{2}\) = \(\frac{1}{2}\) (x – 4)
⇒ 2y – 3 = x – 4
⇒ x – 2y – 1 = 0 ………(2)
The equation of normal to the parabola (1) at (4, \(\frac{3}{2}\)) is y – y₁ = \(-\frac{1}{m}\)(x – x₁)
⇒ y – \(\frac{3}{2}\) = -2(x – 4)
⇒ 2y – 3 = -4(x – 4)
⇒ 4x + 2y – 19 = 0

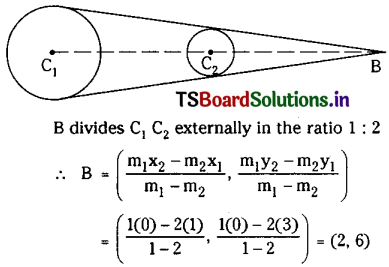
Question 3.
Find the value of k if the line 2y = 5x + k is a tangent to the parabola y² = 6x.
Solution:
Given the equation of the line is 2y = 5x + k.
⇒ y = \(\frac{5}{2} x+\frac{k}{2}\) which is of the form y = mx + c where m = \(\frac{5}{2}\) and c = \(\frac{k}{2}\)
Comparing y² = 6x with y² = 4ax we get
4a = 6 ⇒ a = \(\frac{3}{2}\)
The condition for the line y = mx + c to be a tangent to the parabola y² = 4ax is y = mx + \(\frac{a}{m}\)
Where c = \(\frac{a}{m}\)
∴ \(\frac{k}{2}=\frac{3 / 2}{5 / 2}=\frac{3}{5}\)
⇒ k = \(\frac{6}{5}\)

Question 4.
Find the equation of normal to the parabola y² = 4x which is parallel to y – 2x + 5 = 0.
Solution:
Given equation of parabola is y² = 4x ………(1)
Comparing with y² = 4ax we get a = 1
Given y – 2x + 5 = 0, the slope, m = 2
∴ The slope of the line parallel to the above line is ‘2’.
The equation of normal to the parabola which is parallel to the line is having slope m = 2 is
y = mx – 2am – am³
= 2x – 4 – 8
= 2x – 12
⇒ 2x – y – 12 = 0
∴ The equation of the required normal is 2x – y – 12 = 0.

Question 5.
Show that the line 2x – y + 2 = 0 is a tangent to the parabola y² = 16x. Find also the point of contact.
Solution:
Given line is 2x – y + 2 = 0
and slope m = 2, and c = 2.
Comparing y² = 16x with y² = 4ax
we have a = 4
Condition for a line y = mx + c to be a tangent to the parabola y² = 4ax is c = \(\frac{a}{m}\)
∴ c = 2 and \(\frac{\mathrm{a}}{\mathrm{m}}=\frac{4}{2}\) = 2
∴ c = \(\frac{a}{m}\)
The point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\) = (1, 4)

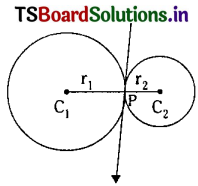
Question 6.
Find the equation of a tangent to the parabola y² = 16x inclined at an angle of 60° with its axis and also find the point of contact.
Solution:
Given parabola is y² = 16x ……..(1)
Comparing with y² = 4ax we get 4a = 16
⇒ a = 4
Given that inclination of the tangent line is 60°.
∴ Slope of the tangent is m = tan 60° = √3
∴ The equation of the tangent to the parabola (1) having slope √3 is y = mx + \(\frac{a}{m}\)
⇒ y = √3x + \(\frac{4}{\sqrt{3}}=\frac{3 x+4}{\sqrt{3}}\)
⇒ √3y = 3x + 5
⇒ 3x – √3y + 4 = 0
∴ Point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=\left(\frac{4}{3}, \frac{8}{\sqrt{3}}\right)\)

II.

Question 1.
Find the equations of tangents to the parabola y² = 16x which are parallel and perpendicular respectively to the line 2x – y + 5 = 0, also find the coordinates of their points of contact.
Solution:
Given equation of parabola y² = 16x …….(1)
and comparing with y² = 4ax we have 4a = 16
⇒ a = 4
Equation of any line parallel to the given line 2x – y + 5 = 0 is 2x – y + k = 0 …….(1)
⇒ y = 2x + k
∴ m = 2 and c = k
if (1) is a tangent to the parabola, then c = \(\frac{a}{m}\)
⇒ k = 2
∴ The equation of the required tangent is y = 2x + 2
⇒ 2x – y + 2 = 0
Point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\) = (1, 4)
Equation of any line perpendicular at 2x – y + 5 = 0 is x + 2y + k = 0
⇒ 2y = -x – k ………(2)
⇒ y = \(-\frac{\mathrm{x}}{2}-\frac{\mathrm{k}}{2}\)
Here c = \(\frac{k}{2}\) and m = \(-\frac{1}{2}\)
If (2) is a tangent to the parabola then c = \(\frac{a}{m}\)
⇒ \(-\frac{k}{2}=\frac{4}{-1 / 2}=-8\)
⇒ k = 16
∴ The equation of the required tangent is x + 2y + 16 = 0 ……..(3)
Point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)
= \(\left(\frac{4}{(1 / 4)}, \frac{8}{-1 / 2}\right)\)
= (16, -16)

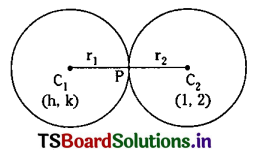
Question 2.
If lx + my + n = 0 is a normal to the parabola y² = 4ax, then show that al³ + 2alm² + nm² = 0.
Solution:
Given equation of parabola is y² = 4ax ……..(1) and given lx + my + n = 0 is a normal to the parabola y² = 4ax ……(2)
Equation of normal at a point P(t) on the parabola y² = 4ax is y + xt = 2at + at³
⇒ xt + y = 2at + at³ …….(3)
Equations (2) and (3) represent the same line.
Eliminating ‘t’ from (2) and (3) we get,

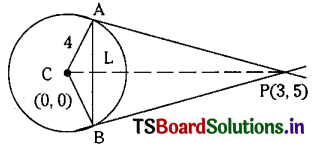
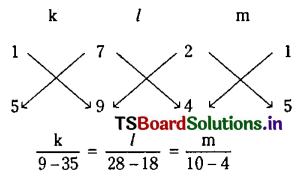
Question 3.
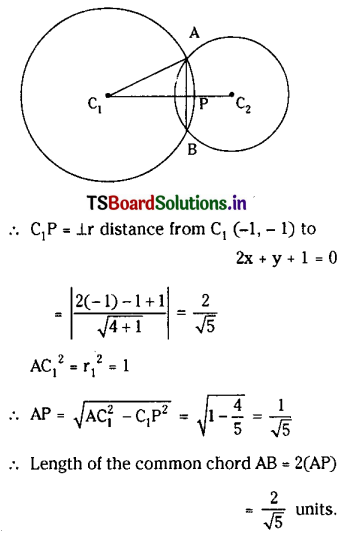
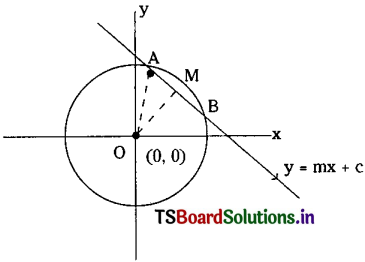
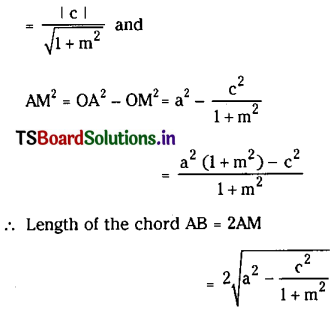
Show that the equation of the common tangents to the circle x² + y² = 2a² and the parabola y² = 8ax are y = ±(x + 2a). (Mar. ’10, ’09)
Solution:
Given equation of parabola is y² = 8ax …….(1) and circle is x² + y² = 2a² ……..(2)
The Centre of the circle is C = (0, 0) and the radius of the circle is r = √2a
Equation of the tangent to the parabola (1) having slope ‘m’ is y = mx + \(\frac{2a}{m}\)
⇒ my = m²x + 2a (∵ y² = 8ax is the parabola)
⇒ m²x – my + 2a = 0 ………(3)
Line (3) is also a tangent to circle (2).
∴ The perpendicular distance from C(0, 0) to line (3) is equal to radius √2a.
∴ \(\left|\frac{2 a}{\sqrt{m^4+m^2}}\right|=\sqrt{2 a}\)
⇒ \(\frac{4 a^2}{m^4+m^2}\) = 2a²
⇒ m⁴ + m² – 2 = 0
⇒ m⁴ + 2m² – m² – 2 = 0
⇒ (m² – 1) (m² + 2) = 0
⇒ m² = 1 or m² = -2
⇒ m² = 1 (∵ m² ≠ -2)
⇒ m = ±1
∴ The equations of the required tangents are y = \(\pm x+\frac{2 a}{\pm 1}\)
⇒ y = ±(x + 2a)

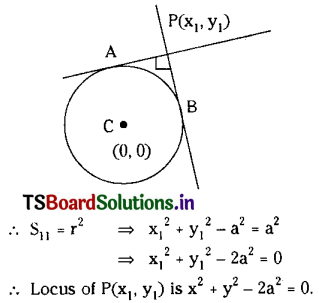
Question 4.
Prove that the tangents at the extremities of a focal chord of a parabola intersect at right angles on the directrix.
Solution:

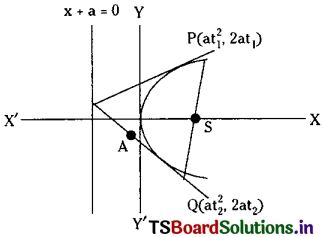
Let y² = 4ax be the equation of a parabola and
Let P\(\left(a t_1^2, 2 a t_1\right)\), Q\(\left(a t_2^2, 2 a t_2\right)\) be two extremeties of the focal chord.
Since \(\overline{\mathrm{PQ}}\) is the focal chord we have t₁t₂ = -1 (standard result)
The equation of tangent to the parabola y² = 4ax at P(t₁) is x = \(\mathrm{yt}_1+\mathrm{at}{ }_1^2\) ………(1)
Slope of the tangent (m₁) = \(\frac{1}{t_1}\)
The equation of the tangent Q(t₂) to the parabola y² = 4ax is x = \(\mathrm{yt}_2+\mathrm{at}_2^2\) ……..(2)
Slope of the tangent (m₂) = \(\frac{1}{t_2}\)
Now m₁m₂ = \(\frac{1}{t_1 t_2}\) = -1 (∵ t₁t₂ = -1)
∴ The tangents drawn at P, Q are perpendicular to each other.
The point of intersection of tangents (1) and (2) = [at₁t₂, a(t₁ + t₂)]
= [-a, a(t₁ + t₂)]
Substituting this point of intersection on the directrix of the parabola y² = 4ax i.e., x + a = 0.
We have -a + a = 0 and hence the point of intersection of tangents lie on the directrix.
∴ The tangents drawn at the extremities of the focal chord of a parabola intersect at right angles on the directrix.

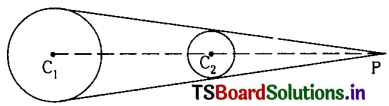
Question 5.
Find the condition for the line y = mx + c to be a tangent to the parabola x² = 4ay. (Mar. ’12)
Solution:
Given equation of parabola as x² = 4ay …….(1)
and given line is mx – y + c = 0 ……..(2)
Suppose (2) is a tangent to the parabola (1).
Let P(x₁, y₁) be the point of contact.
Then the equation of the tangent to the parabola (1) at (x₁, y₁) is xx₁ – 2a(y + y₁) = 0
⇒ xx₁ – 2ay – 2ay₁ = 0 ………(3)
Since equations (2) and (3) represent the same line, the corresponding coefficients are proportional.
∴ \(\frac{x_1}{m}=\frac{-2 a}{-1}=\frac{-2 a y_1}{c}\)
⇒ x₁ = 2am, y₁ = -c
Since P(x₁, y₁) is a point on x² = 4ay we have \(\mathbf{x}_1^2\) = 4ay₁
⇒ (2am)² = 4a(-c)
⇒ am² = -c
⇒ c = -am²
∴ The condition for the line y = mx + c to be a tangent to the parabola x² = 4ay is am² + c = 0.

Question 6.
Three normals are drawn from (k, 0) to the parabola y² = 8x one of the normal is the axis and the remaining two normals are perpendicular to each other, then find the value of k.
Solution:
Given equation of parabola is y² = 8x ………(1)
Comparing with y² = 4ax we have 4a = 8
⇒ a = 2
The equation of normal to the parabola (1) having slope ‘m’ is
y = mx – 2am – am²
⇒ y = mx – 4m – 2m³
Given that the normal passes through (k, 0).
Then 0 = mk – 4m – 2m³
⇒ m(2m² + 4 – k) = 0
⇒ m = 0 or 2m² – k + 4 = 0 ……(2)
Let m₁, m₂ be the roots of a quadratic equation (2) then
m₁ + m₂ = 0, m₁m₂ = \(\frac{4-k}{2}\)
Given that the two normals are perpendicular, we have m₁m₂ = -1
⇒ \(\frac{4-k}{2}\) = -1
⇒ k = 6

Question 7.
Show that the locus of the point of intersection of the perpendicular tangents to the parabola y² = 4ax is the directrix x + a = 0.
Solution:
Given y² = 4ay ………(1) and Let P(x₁, y₁) be the point of intersection of perpendicular tangents.
Any tangent to the parabola will be of the form y = mx + \(\frac{a}{m}\) of this passes through (x₁, y₁) then y₁ = mx₁ + \(\frac{a}{m}\)
⇒ m²x₁ – my₁ + a = 0 …….(2)
Let m₁, m₂ be the slopes of tangents drawn from P(x₁, y₁) to the parabola (1) which corresponds to the roots of a quadratic equation (2).
Then m₁ + m₂ = \(\frac{y_1}{x_1}\) and m₁m₂ = \(\frac{a}{x_1}\) …….(3)
Since the tangents are perpendicular we have m₁m₂ = -1 and hence from (3),
-1 = \(\frac{a}{x_1}\)
⇒ x₁ + a = 0
∴ The Locus of (x₁, y₁) is x + a = 0 which is the equation of the directrix of the parabola (1).

Question 8.
Two parabolas have the same vertex and equal length of latus rectum such that their axes are at the right angle. Prove that the common tangents touch each at the end of the latus rectum.
Solution:

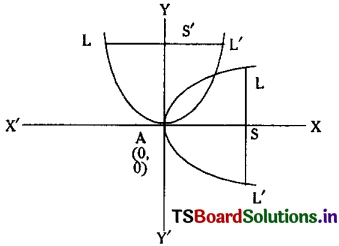
Let the equations of parabolas having the same vertex and equal length of latus rectum be
y² = 4ax …….(1)
x² = 4ay …….(2)
Let the equation of the tangent to the parabola (1) having slope ‘m’ is
y = mx + \(\frac{a}{m}\) …….(3)
But this is also a tangent to x² = 4ay
∴ c = -am²
∴ \(\frac{a}{m}\) = -am²
⇒ m³ = -1
⇒ m = 1
∴ From (3), we have y = -x – a
⇒ x + y + a = 0 ………(4)
L'(a, -2a) is the end of latus rectum of parabola (1).
∴ From (4), x + y + a = a – 2a + a = 0
∴ The common tangents to the parabolas y² = 4ax, x² = 4ay will touch the parabola at the end of the latus rectum.

Question 9.
Show that the foot of the perpendicular from focus to the tangent of parabola y² = 4ax lies on the tangent at the vertex.
Solution:
Given parabola is y² = 4ax ……….(1)
Equation of any tangent to (1) is of the form y = mx + \(\frac{a}{m}\)
⇒ my = m²x + a
⇒ m²x – my + a = 0 ……..(2)
Equation of the line perpendicular to the line (2) and passing through S(a, 0) is -m(x – a) + m²(y – 0) = 0
⇒ x + my – a = 0 ……..(3)
From (2) and (3)
(m² + 1)x = 0
⇒ x = 0
From (3), my – a = 0
⇒ y = \(\frac{a}{m}\)
∴ The point of intersection of (2) and (3) is (0, \(\frac{a}{m}\))
∴ The point (0, \(\frac{a}{m}\)) lies on the y-axis which is a tangent at the vertex.

Question 10.
Show that the tangent at one extremity of a focal chord of a parabola is parallel to the normal at the other extremity.
Solution:
Let y² = 4ax be the given parabola.
Let P = \(\left(a t_1{ }^2, 2 a t_1\right)\) and Q = \(\left(a t_2{ }^2, 2 a t_2\right)\) be the two extremities of a focal chord. then t₁t₂ = -1
The equation of the tangent to the parabola at P(t₁) is x – yt₁ + \(\mathrm{at}_1{ }^2\) = 0 …….(1)
then m₁ = \(\frac{1}{t_1}\)
The equation of the normal at Q(t₂) is xt₂ + y – 2at₂ – \(\mathrm{at}_2^3\) = 0 ……..(2)
The slope of the normal (m₂) = -t₂
= \(-\left(\frac{-1}{t_1}\right)=\frac{1}{t_1}\) (∵ t₁t₂ = -1)
∴ m₁ = m₂ and the tangent at P(t₁) is parallel to the normal at Q(t₂) to the parabola y² = 4ax.
∴ The tangent at one extremity of a focal chord is parallel to the normal at other extremities.

III.

Question 1.
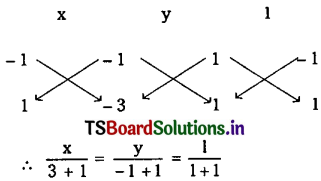
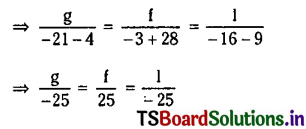
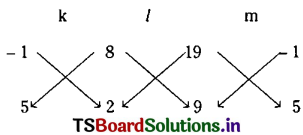
The normal at a point t₁ on y² = 4ax meets the parabola again at the point t₂. Then prove that t₁t₂ + \(t_1{ }^2\) + 2 = 0.
Solution:
Given equation of parabola is y² = 4ax ……..(1)
Let P = \(\left(a t_1^2, 2 a t_1\right)\) = P(t₁) be any point on (1).
The equation of normal at P(t₁) on the parabola (1) is y + xt₁ = 2at₁ + \(\mathrm{at}_1{ }^3\)
⇒ t₁x + y = 2at₁ + \(\mathrm{at}_1{ }^3\) ……..(2)
The normal drawn at P(t₁) meets the parabola at Q(t₂).
∴ PQ is the chord of the parabola.
The equation of chord \(\overline{\mathrm{PQ}}\) of the parabola y² = 4ax is y(t₁ + t₂) = 2x + 2at₁t₂
⇒ 2x = y(t₁ + t₂) + 2at₁t₂ = 0 ……….(3)
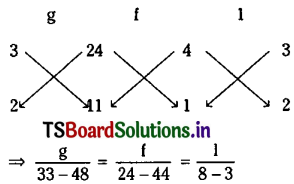
Since equations (2) and (3) represent the same line, the coefficients of line turns are proportional.

Question 2.
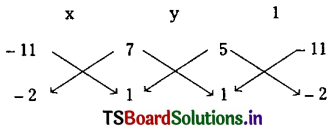
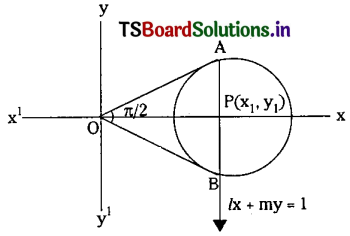
From an external point, P tangents are drawn to the parabola y² = 4ax and these tangents make angles θ₁, θ₂ with its axis, such that cot θ₁ + cot θ₂ is a constant ‘d’. Then show that all such P lies on a horizontal line.
Solution:

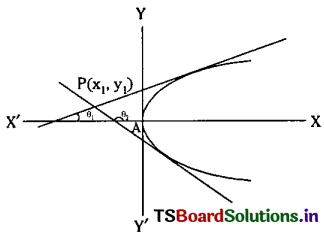
Given y² = 4ax ………(1) and Let P(x₁, y₁) be an external point.
Let the equation of a tangent to the parabola (1) having slope ‘m’ is y = mx + \(\frac{a}{m}\) …….(2)
if (2) passes through P(x₁, y₁) then y₁ = mx₁ + \(\frac{a}{m}\)
⇒ my₁ = m²x₁ + a
⇒ m²x₁ – my₁ + a = 0 …….(3)
Since this is a quadratic equation in ‘m’.
Let m₁ and m₂ be the roots. Then
m₁ + m₂ = \(\frac{y_1}{x_1}\) and m₁m₂ = \(\frac{\mathrm{a}}{\mathrm{x}_1}\)
Given that the tangents are making angles θ₁, θ₂ with its axis we have m₁ = tan θ₁ and m₂ = tan θ₂.
Also given that cot θ₁ + cot θ₂ = d

∴ The Locus of P(x₁, y₁) is y = ad which is a line parallel to X-axis.
∴ P(x₁, y₁) lies on a horizontal line.

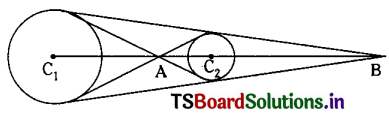
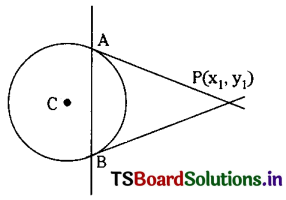
Question 3.
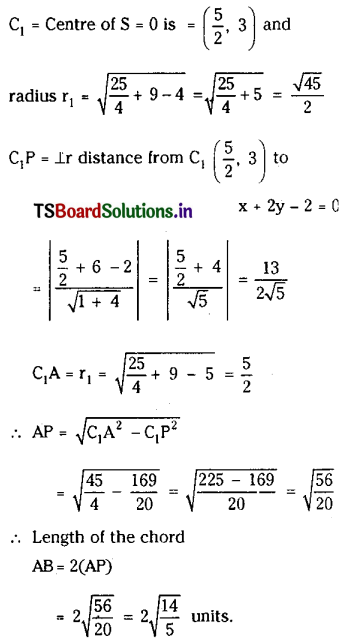
Show that the common tangents to the circle 2x² + 2y² = a² and the parabola y² = 4ax intersect at the focus of the parabola y² = -4ax.
Solution:
Given equation of circle is x² + y² = \(\frac{a^2}{2}\) ……..(1)
and the given equation of parabola is y² = 4 ax ……..(2)
Let y = mx + c be a common tangent to (1) and (2).
If y = mx + c is a tangent to (1) then by the condition of tangency
c² = \(\frac{a^2}{2}\) (1 + m2) ………(3)
Also if y = mx + c is a tangent to the parabola y² = 4ax then
c = \(\frac{a}{m}\) …….(4)
∴ From (3) and (4) we have \(\frac{a^2}{m^2}=\frac{a^2}{2}\left(1+m^2\right)\)
⇒ m⁴ + m² = 2
⇒ m⁴ + m² – 2 = 0
⇒ m⁴ + 2m² – m² – 2 = 0
⇒ (m² + 2) (m² – 1) = 0
⇒ m² + 2 = 0 or m² – 1 = 0
m² + 2 = 0 is not admissible.
∴ m² – 1 = 0
⇒ m = ±1
From y = mx + c we have
= mx + \(\frac{a}{m}\)
= \(\pm x+\frac{a}{\pm 1}\)
= ± x ± a
Also y = ± x ± a satisfy the focus (-a, 0) of the parabola y² = -4ax.
Hence the common tangents to the circle (1) and parabola (2) intersect at the focus of the parabola y² = -4ax.

Question 4.
The sum of the ordinates of two points on y² = 4ax is equal to the sum of the ordinates of two other points on the same curve. Show that the chord joining the first two points is parallel to the chord joining the other two points.
Solution:
Given equation of parabola is y² = 4ax …..(1)
Let A = \(\left(\mathrm{at}_1{ }^2, 2 \mathrm{at}_1\right)\), B = \(\left(\mathrm{at}_2{ }^2, 2 \mathrm{at}_2\right)\), C = \(\left(\mathrm{at}_3{ }^2, 2 \mathrm{at}_3\right)\) and D = \(\left(\mathrm{at}_4{ }^2, 2 \mathrm{at}_4\right)\) be the four points on the parabola (1).
Given that 2at₁ + 2at₂ = 2at₃ + 2at₄
⇒ t₁ + t₂ = t₃ + t₄ ………(2)
The equation of the chord \(\overline{\mathrm{AB}}\) of the parabola y² = 4ax is y(t₁ + t₂) = 2x + 2at₁t₂
⇒ 2x – (t₁ + t₂) y + 2at₁t₂ = 0 ………(3)
Let m₁ be the slope of line (3) then m₁ = \(\frac{2}{t_1+t_2}\)
The equation of the chord \(\overline{\mathrm{CD}}\) of the parabola (1) is y(t₃ + t₄) = 2x + 2at₃t₄ and slope of this chord m₂ = \(\frac{2}{t_3+t_4}\)
∴ From (2) we have t₁ + t₂ = t₃ + t₄
Hence m₁ = m₂
∴ Chord \(\overline{\mathrm{AB}}\) is parallel to the chord \(\overline{\mathrm{CD}}\).

Question 5.
If a normal chord at a point ‘t’ on the parabola y² = 4ax subtends a right angle at the vertex then prove that t = ±√2.
Solution:
Given equation of parabola is y² = 4ax ……(1)
The equation of normal at a point P(t) on (1) is xt + y = (2at + at³) …….(2)
Let the normal at P(t) meet (1) again at Q(t₁) then PQ is the chord of the parabola (1)

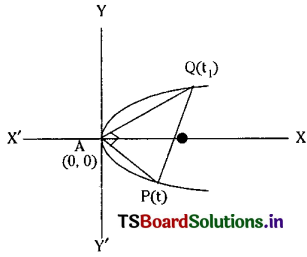
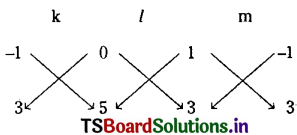
Equation of chord \(\overline{\mathrm{PQ}}\) is y(t₁ + t) – 2x – 2at₁t = 0
⇒ -2x + (t₁ + t)y – 2at₁t = 0 ………(3)
Equations (2) and (3) represent the same straight line.
∴ Coefficients of like terms are proportional

Telangana TSBIE TS Inter 2nd Year English Study Material Revision Test-IV Exercise Questions and Answers.

TS Inter 2nd Year English Study Material Revision Test-IV

Time : 1 1/2 Hrs
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words.  [1 × 4 = 4]

a) The ideal of perfection preached by the forest-dwellers of ancient India runs through the heart of our classical literature and still dominates our mind.
Answer:
Reference :
These lines are extracted from the essay The Religion of the “Forest Written by Rabindranath Tagore.

Context:
Indian civilization has been distinctive in locating its source of regeneration, material and intellectial, in the forest, not the city. India’s best ideas have come where man was in communion with trees and rivers and lakes, away from the crowds. The peace of the forest has helped the intellectual evolution of man.

Meaning :
The ideal of perfection preached by the forest dwellers of ancient India run through the heart of our classical literature and still dominates our mind”. The forests are sources of life and they are the storehouse of biodiversity.

b) Nature stands on her own right, proving that she has her great function, to impart the peace of the eternal to human emotions.
Answer:
Reference :
These lines are extracted from the essay “The Religion of the “Forest written by Rabindranath Tagore

Context:
Harmony and unity in diversity is the nature of the forest, whereas being monotonous is the nature of industrialism based on a mechanical world view.

Meaning : The forest also teaches us enormousness as the principle of ‘equity, enjoying the gifts of Nature without exploitatiÒn and accumulation. In The Religion of the Forest Tagore quotes from the ancient texts written in the forest. Know all that moves in this moving world as enveloped by God; and find enjoyment through renunciation, not through greed of possession.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) Awaken and sever the woes that enthral us
Answer:
Introduction :
This patriotic line is taken from the patriotic lyric, “Awake” Written by Sarojini Naidu, the nightingale of India. This is the last poem of “The broken wings: Songs of Love”.

Context and meaning :
It is a soul stirring plea foraction and zenity. The woes of bondage are to be cut. Mother India should gain its glory gain and grow and glow. Hence, the children implore the mother to rouse them from their slumber and to cut off the ties of bondage in which they are bound at present their hands are to be purified by her so that they might be prompted to undertake more and more deeds of victory and triumph.

Critical Comment :
The poem expresses strong nationalistic feelings. It was written more than a century ago. Yet, it is very relevant today.

b) ……………… Hearken,
0 queen and 0 goddess, we hail thee!
Answer:
Introduction :
These are the concluding lines of the patriotic lyric, “Awake” written by sarojini Naidu, the Nightingale of India. This is the last poem of “The Broken wing! Songs of Love”.

Context and meaning :
Here, people of all Indian religions assure her chat they would serve her with devotion to the best of their ability. They call upon their great mother, their queen and their goddess to listen to their prayer and awake from her present slumber. Their fearless united and devoted efforts shall certainly be sufficient to free her from her present bondage.

Critical Comment :
This lyric is a soul stirring call for unity and action. It expresses strong nationalistic feelings.

Question 3.
Answer ANY ONE of the following questions in about 100 words [1 × 4 = 4]

a) This aspect of truth cannot be ignored; it has to be known and mastered. What is that aspect of truth, according to Tagore? Who has mastered it?
Answer:
Rabindranath Tagore (1861-1941) was a psychologist and social realist. He wrote a number of essays in both English and Bengali. “The Religion of the Forest” is one of his most famous essays. It represents the author’s perspective on an individual’s relationship with the forest and nature.

The truth of our life depends upon our attitude of mind towards it- -an attitude which is formed by our habit of dealing with it according to the special circumstance of our surroundings and our temperaments. It guides our attempts to establish relations with the universe either by conquest or by union, either through the cultivation of power or through that of sympathy. And thus, in our realisation of the truth of existence, we put our emphasis either upon the. principle of dualism or upon the principle of unity.

b) Explain how the bid simplicity of Hindu life had broken up in Kalidas’s time.
Answer:
Rabindranath Tagore (1861-1941) was a psychologist and social realist. He wrote a number of essays in both English and Bengali. “The Religion of the Forest” is one of his most famous essays. It represents the author’s perspective on an individual’s relationship with the forest and nature. When Vikramaditya became king, Ujjayini a great capital, and Kalidasa its poet, the age of India’s forest retreats had passed.

Then we had taken our stand in the midst of the great concourse of humanity. The Chinese and the Hun, the Scythian and the Persian, the Greek and the Roman, had crowded round us. But, even in that age of pomp and prosperity, the love and reverence with which its poet sang about the hermitage shows what was the dominant ideal that occupied the mind of India; what was the one current of memory that continually flowed through her life.

In Kalidasa’s drama, Shakuntala, the hermitage, which dominates the play, overshadowing the king’s palace, has the same idea running through it the recognition of the kinship of man with conscious and unconscious creation.

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Substantiate the critical comment that the poem Awake is a patriotic lyric.
Answer:
Yes, Sarojini Naidu’s song”Awake’ has been acclaimed as a patriotic lyric. A lyric is poem. A single speaker expresses emotions and thoughts in it. It is noteworthy for its musical quality and rhythm. And its theme is losty. According to it, the poem, “Awake”, has all these qualities in abundance. It is rich in musical element. If expresses strong nationalistic feelings.

Thus, the content is patriotic and hence noble. With its preformed theme and artistic and lyrical form the poem is very much entitled to be applauded as patriotic lyric. It is a touching call to all Indians for unity and action. People of all religions pledge to come together to guard their mother, queen and goddess. Hence, this is a patriotic lyric.

b) How do Indians plan to set their mother again in the forefront of glory?
Answer:
The patriotic lyric, “Awake” is written by Sarojini Naidu, The nightingale of India. According to the poetess, the children of the motherland are invoking her to rise from her sound and long sleep and bless them so that they succeed in their holy object of setting her free from the chain of slavery under, the British rule. The poetess says that her children love her very much.

They have a great devotion for their motherland. They are her true children. They have inherited her pride, moral and spiritual strength they want to preserve these qualities. They will never fail to protect her. They will never desert her, Their hearts are the home of the mother. They are moreover her shield and her alfar. It is with her help that they will be set again in the forefront of glory. All medians should forget their mutual differences for the attainment of freedom and rise against British tyranny.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Narrate the incident that led to the agreement between the lady and the Baron.
Answer:
Guy De Maupassant was a fantastic French author. He was one of the world’s best short story writers.

The current short Lost deals with the complex issues that women face from men. When the licentious baron was prepared to go to any length to obtain her, she suggested that if he was willing to accept 25 whippings, she would listen to him. “Are you telling the truth?” she inquired.

After the ghetto man finished his response, he grabbed her hand and passionately pressed it to his lips. When he asked when she could come, she said tomorrow at eight o’clock. When he asked if I could bring the sable close and whip, she said no, I’d handle it myself.

b) What was the Baron’s wish? Was it fulfilled? Explain.
Answer:
Guy De Maupassant was a fantastic French author. He was one of the world’s best short story writers. The current short Lost deals with the complex issues that women face from men A gorgeous, married woman caught the eye of a ghetto baron, who developed an enduring crush on her. Baron wished that she would provide to him because of her limited salary.

His wish was not granted because she said that if he was willing to take twenty-five lashes, she would listen to him.

But on the appointed day, she whipped him 24 times in a ruthless manner. He would have reached her one more time, but the shrewd little lady purposefully avoided handing him the twenty-five cut. She mockingly laughed at him and insisted that she would only give in to him after giving him 25 lashes.

Section – B

Question 6.
Read the following passage and answer ANV FIVE questions given below: [5 × 1 = 5]

“Do look at that lovely ‘fur, the baroness said, while her dark eyes express d h r p east:e, “I must have it.”

But she looked at the white ticket on which the price was market.
“Four thousand rubles,” she said ¡n despair; “that is about six tho .isand florins.”
“Certainly,” he replied, “but what of that? It is a sum not worth mentioning in the presence of such a charming lady.’

i) What attracted the attention of the baroness?
Answer:
the beautiful fur coat

ii) What was there on the white ticket?
Answer:
the price of that coat

iii) What is the price of the fur?
Answer:
4000 rubles

iv) “I must have it.” Who does the word I refer to?
Answer:
the baroness

v) The lady could afford the lovely fur. Write Yes or No.
Answer:
No

vi) Write the antonym from the passage of the word hope.
Answer:
Despair

vii) Write the word which means a state of being happy.
Answer:
Pleasure

viii) “Certainly,” he replied. Who does the word he refer to?
Answer:
The Baron from the Ghetto

Question 7.
Read the following passage and answer ANY FIVE questions given below: [5 × 1 = 5]

Bird Lover of a Rare Kind
Penumaka Malakshmi (a man, please) of Kadium in East Godavari district is a daily wage earner from a downtrodden community. Yet, he has been feeding thousands of birds regularly for over six decades. He is now seventy- two and his service continues. He collects sheafs of paddy from farmers during the harvest time. He stores those paddy bundles in a nearby temple. Every evening, he picks up some ears of paddy and weaves them into ornamental tassels and hangs them from buildings. Birds in flocks feed on them joyously.

On New Year Days, he erects an arch near the temple and hangs some beautifully-woven tassels from it. Thousands of chirping birds picking grains from that ornamental arch is a sight to behold! This rare act of real charity has seen the light of day as a national best teacher awardee, Mr Chilukuri Srinivasa Rao (himself a lover of dogs and plants – feeds hundreds of stray dogs every day and planted over one lakh saplings so far!) has written about Malakshmi in Prajasakthi (January, 2021).

i) How does Penumaka Malakshmi make his living?
Answer:
As a daily wage labour

ii) How does Malakshmi find means to feed hundreds of birds every day?
Answer:
Collect sheats of paddy from farmaers doring the harvest

iii) What is his art that attracts people’s attention towards his charity?
Answer:
Weaving ears of paddy in to ornamental tessels .

iv) How has Malakshmi’s rare act of charity come to light?
Answer:
As mister chilukuri srinivasarao

v) Write the idiom used in the passage to mean become publicly known.
Answer:
Seen the light of day

vi) Write the word used in the passage that forms a set of homophones with site / cite.
Answer:
sight

vii) Find out the synonym from the passage of see.
Answer:
Be hold

viii) Put stress mark on the right syllable of the word community.
Answer:
Community

Question 8.
Study the following advertisement and answer ANY FIVE questions that follow. [5 × 1 = 5]

i) When is the World Water Day celebrated?
Answer:
on march 22 every year

ii) Who declared 22 March as the World Water Day?
Answer:
United National General Assignment

iii) World Water Day serves to raise awareness in ___________. (Fill in the blank.)
Answer:
Water issues such as water storage

iv) “You ain’t gonna miss your water until your well runs dry.” Who said this?
Answer:
Bob Marley

v) Make a conscious effort to use __________ on World Water Day and other days. (Fill in the blank)
Answer:
Less Watr

vi) When there is a lack of safe and clean water, what happens to our lives?
Answer:
Lake of safe and clean water impacts the economy, health of the population and the well being of women and children world wide.

vii) In which year was the World Water Day proposed?
Answer:
In 1992 -1993

viii) Pick the synonym of the word effect from the advertisement.
Answer:
impact

Question 9.
Study the tree diagram below and answer ANY FIVE questions given after it. [5 × 1 = 5]

i) What does the tree diagram describe?
Answer:
Values

ii) What are the two kinds of values?
Answer:
Material and spiritual

iii) Which value do hard work and discipline belong to?
Answer:
Material

iv) Truth is a ____________ value. (Fill in the blank.)
Answer:
Spiritual

v) From which source can one acquire the trait of Simple Observation?
Answer:
Family

vi) Generosity is a material value. Write true or false.
Answer:
False

vii) Children do get some values by self experience. Write true or false.
Answer:
True

viii) Formal teaching consists of ___________. (Fill in the blank.)
Answer:
Books and Syllabus

Question 10.
You are Ch. Krishna. Your Account number is 56218561932. Deposit an of Rs. 9,300/ into your Savings Bank Account with the SBI, Punjagutta Branch. Your mobile number is 8374373612. The amount is in the denomination of Rs. 500 notes 18 and the remaining are Rs. 100 notes. [10 × 1/2 = 5]

Answer:

1. Panjagutta
2. 14.06.2022
3. 56218561932
4. Ch. Krishna
5. 8374373612
6. 9300/-
7. Nine thousand and three hundred only
8. 500 × 18; 100 × 3
9. 9300
10. Ch. Krishna

Question 12.
Prepare a curriculum vitae in response to the following advertisement published in a local newspaper. [5 × 1 = 5]

Answer:
MANOJA KSSP

ADDRESS: Flat no. 402, Nagarjuna Apartments, Ramalayam Road,
Ramgiri, Nalgonda. Telangana- 508001
New Nallakunta, Hyderabad – 500044

E-mail: manojak04yahoo.com
Ph: 9XXXXXXXX8

CAREER OBJECTIVE

To be a professional who can make a qualitative difference with an esteemed organization, where high competence and skill is rewarded.

EDUCATION:

TECHNICAl SKILLS

Telugu Typing, Computer skills
Communication Skills – Fluency in English and Telugu.

WORK EXPERIENCE:

• Worked as News presenter for City Cable Nalgonda, Summer 2021
• Covered Covid hit areas and interviewed officials and did live coverage

HOBBLES:

• Singing – Won awards in singing competition during schooling
• Making short films – on mobile

LANGUAGES KNOWN : Telugu, Hindi and English

PERSONAL PROFILE : Will be provided on request

REFERENCES :

1. Dr. Ghanshyam, Principal, GDC(W) Nalgonda
2. Venu Madhavi, Program Executive, City Cable, Nalgonda.

KSSP Manoja
Place : HYDERABAD

Telangana TSBIE TS Inter 2nd Year English Study Material Revision Test-III Exercise Questions and Answers.

TS Inter 2nd Year English Study Material Revision Test-III

Time: 1 1/2 Hrs
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) One day your test will become the convention.
Answer:
Reference :
These lines are taken from the internet-based article “Solution to Plastic Pollution”. Written by Dr R. Vasudevan’s.

Context :
This crushed plastic waste is sprayed on stones that has been heated to 170°C. The plastic melts and forms a coat on the soft sand during this process. There are no harmful gases released during the process, and it also solves two major problems filling gaps in retired roads and reducing plastic sculpting bolection.

Meaning:
He advocates that people sell their domestic plastic waste to junk dealers, as they do with their old newspapers, and not throw it in the bins. Segregation has to be carried out at various levels. Plastic waste ought to be collected from every private and public place and the SHGs could be involved in collecting, shredding and selling it to companies that lay roads.

b) The plastic instantly melts and coats the gravel without releasing toxic gases into the atmosphere.
Answer:
Reference :
These lines are taken from the internet-based article “Solution to Plastic Pollution”. Written by Dr R. Vasudevan’s.

Context:
Plastic is a big problem in our country and world. But plastic is the only material which very uses full for the daily use purpose of every person.

Meaning :
The implementation of plastics inroads also opens a new option for recycling post-consumer plastics. Australia, Indonesia, India, the United Kingdom, the United States, and many other countries have used technology that can incorporate plastic waste into an asphalt mix. The plastic waste items that can be used for road construction are various items like plastic carry bags, plastic cup’s, plastic packaging for potato chips, biscuits, chocolates, etc.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) I knock and yet remain unseen
Answer:
Introduction :
This line is taken from the poem,”Hiroshima Child”, written by Nazim Hikmet. He is a turkish poet, play wright and novelist. He is recognised as one of the greatest poets of the twentieth century. Most of his writings are about war.

Content and Meaning:
Here, the speaker is a seven-year old. Hiroshima girl. She died when an atom bomb was dropped on Hiroshima during the world war II. The soul of the girl knocks on every door to warn them about the adverse effects of war. But nobody pays attention to her as she invisible.

Critical comment:
The speaker begs people to fight for peace and to let children grow happily. The war against war touches our hearts.

b) All that I need is that for peace You fight today you fight today
Answer:
Introduction:
These heart touching lines are taken from the poem.”Hiroshima child”, written by Naziin Hikmet. He is a turkish poet, playwright and novelist. He is recognised as one of the greatest poets of the twentieth century.

Content & Meaning :
The child is the speaker in the poem. She lost her life at seven in the Hiroshima bomb blast. Since then, she has felt neither growth nor hunger. She continues to be in the same state, she visits every home, seek, neither food nor things. She warns us, about the evils of war. As she doesn’t want anything, she begs us to fight for peace. Her desire is to promote peace. She urges us to let every child grow, play and laugh. The only thing she want is peace: Fight for peace.

Critical comment:
The poet uses the repetition to demonstrate that we must fight for peace and nothing else, or else innocent people and children would die for our unnecessary injustices.

Question 3.
Answer ANY ONE of the following questions in about 100 words [1 × 4 = 4]

a) Describe the deportment of Dr. Vasudevan as the Professor of TCE.
Answer:
Dr. Rajagopalan Vasudevan is an Indian scientist working mainly in waste management. Currently a professor in Thiagarajar College of Engineering, Dr. Vasudevan has developed an innovative method to reuse plastic waste to construct better, more durable and very cost-effective roads. This shredded plastic waste is sprayed on the gravel heated up to 170°C. at this process the plastic melts and form a coat on the gravel.

In the process no harmful gasses are released and it also solves two major problems like filling the gaps a tad retired roads and reduces plastic molding bolection.He finds a solution in the Bhagavad Gita to any problem in the world. And he readily offers them to his students. He quotes liberally from the Gita. That gives one the impression that he is a Sanskrit scholar.

b) How did APJ Kalam encourage Dr. Vasudevan and what has been the outcome?
Answer:
Dr. Rajagopalan Vasudevan is an Indian scientist working mainly in waste management. Currently a professor in Thiagarajar College of Engineering, Dr. Vasudevan has developed an innovative method to reuse plastic waste to construct better, more durable and very cost-effective roads. Vasudevan’s patented process involves drying and shredding discarded plastic packaging, thinner than 80 microns-made essentially of polyethylene, polypropylene and polystyrene-into 2 mm to 4 mm pieces. When sprinkled over gravel heated to 170°C, shredded plastic melts instantaneously.

It coats the gravel, after which, bitumen is added and the mixture is ready for road laying. For construction of a kilometer of road, the mixture uses a tonne of plastic, equivalent to 100,000 plastic carry bags. Plastic replaces a fraction of the costly bitumen in the road-laying mixture, cutting costs. “The cost of road laying is reduced to one-sixth as opposed to a conventional bitumen road,” Vasudevan says. “Waste plastic becomes an important resource again,” he emphasises.

“It happened due to the blessings of Dr. APJ Abdul Kalam,” he recalls, referring to the late Indian scientist who served as president from 2002 to 2007. When Kalam visited Vasudevan’s college as a chief guest for a function in 2001, he was fascinated by Vasudevan’s idea and encouraged him to lay out the first stretch of road within college premises. With support from the college management, the job was done swiftly. “It’s been almost 20 years and that road still doesn’t have cracks or potholes,” Vasudevan says. “Dr. Kalam promoted the idea and became the biggest ambassador for my work.

Question 4.
Answer ANY ONE of the following questions in about 100 words [1 × 4 = 4]

a) Why does the poet appeal for peace through a dead child?
Answer:
Nazim Hikmet is recognised as one of the greatest poets of the 20th century. Most of his writings are about war. His present poem,”Hirosliima Child” is about a seven year old girl who died in the Hiroshima bomb blast during the World War II. The little girl is the speaker in the poem. The soul of the girl knocks on every door to warn them about to let children grow happily.

The poet to fight for peace and to let children grow happily. The poet appeals for peace through the mouth of the little girl, a dead child. It is because the poet wants to press upon our guilty conscience. The child no longer needs food or water to survive because we have taken away her life with our unnecessary injustices. We have taken away everything from her. Thus, the poet uses a dead child to touch our hearts to promote peace.

b) Describe the feelings of the child when she knew that she was dead at the age of seven.
Answer:
Nazim Hikmet is recognised as one of the greatest poets of the 20th century. Most of his writings are about war. His present poem,”Hiroshima Child” is about a seven year old girl who died in the Hiroshima bomb blast during the World War II. The little girl is the speaker in the poem. The girl knocks on every door.

She says that she doesn’t want anything. It is because she has already died. She no longer needs food or water to survive. She continues to be in the same state. She visits every home and begs them to fight for peace and to let children grow happily. Her feelings touch our hearts and awake us plunge into thought first and action next through her mouth, the poet emphasizes the need for peace.

Question 5.
Answer ANY ONE of the following questions in about 100 words; [1 × 4 = 4]

a) Sketch the character of Dr. Raman.
Answer:
R K Narayan wrote The Doctor’s Word, which was his next connector in Malgudi Days. He is a well-known Indian author as well as the founder of Indian Thought Publications. Among his numerous works are The Painter of Signs, The Guide, and The Bachelor of Arts. The story is set in the well-known Malgudi Village.

The poet describes about Dr Raman individual personality of the behavior in the society. First of all he was an intelligent doctor. He speak less and work hard. He never believes white washing and comforting lies. He is a straight forward person. he always try to fulfillment his patients with courage. His main aim was to saved his patients from the clusters death. He mingled with every one in a friendly manner and he always loves his profession. He is an honorable and admirable person in the society.

b) Describe Gopal’s health condition and his anxiety about the will.
Answer:
The Doctor’s Word was R K Narayan’s next wire in Malgudi Days. He is a well-known Indian author and the creator of Indian Thought Publications. By many’ is writings are The Painter of Signs, The Guide, and The Bachelor of Arts. The story takes ace in the well-known Malgudi Village.

Dr. Raman and Gopal’s wife were conversing. According to the latter, Gopal’s condition is critical. Gopal’s wife began to cry as she heard this. Gopal heard her cry and thought he was going to die. He asked the doctor for confirmation-Doctor! Is it possible that I will die? He was worried about his death. Gopal asked to the doctor to give him a piece of paper.

He wants to leave his property to his children that is his will. Dr. Raman reasoned that by signing the will, he declared his intention to die. In this case, his chances of dying would be increased. Subbiah and his gang would occupy his property if he did not give the will. He went against his nature and told a lie in order to keep Gopal happy so that he could be psychologically cured.

Section – B

Question 6.
Read the following passage and answer ANV FIVE questions given below: [5 × 1 = 5]

The lady felt giddy and sank down on the floor, unable to bear the strain. The nurse attended to her and led her out. At about eight in the evening the patient opened his eyes and stirred slightly in bed. The assistant was overjoyed. He exclaimed enthusiastically, “Sir, he will pull through.” The doctor looked at him coldly and whispered: “I would give anything to see him through but, but the heart… “

i) Who does the phrase the lady refer to in the passage?
Answer:
Gopal’s wife

ii) Why did she sink down on the floor?
Answer:
Unable to bear the strain

iii) When did the patient open his eyes?
Answer:
At about eight in the evening

iv) Why was the assistant overjoyed?
Answer:
As the patient opened his eyes and moved a little

v) Analyse the word enthusiastically into its root and suffixes.
Here is a model: slight (root) + ly (suffix) = slightly.
Answer:
enthuse(root) + iast(sufflx) + ic(suffix) + (al)ly(suffix)

vi) Write the phrasal verb from the passage that means get better after a serious illness.
Answer:
Pull through

vii) Write the antonym, from the passage, of the word indifferently.
Answer:
enthusiastically

viii) Write the part of speech of the word giddy.
Answer:
adjective

Question 7.
Read the following passage and answer ANV FIVE questions given below: [5 × 1 = 5]

UBUNTU
Ready… steady… go! The referee announced the beginning of the race. A basket of sweets was placed near a tree and the participating African Tribal Children were made to stand 100 meters away. The winner of the race would get all the sweets in the basket. Everyone there was anxious to see the winner.

To their, surprise, all the participants held one another’s hand, ran together towards the tree and divided the sweets equally among themselves. When the amazed referee asked why they did so, all of them cried in one voice, UBUNTU meant How can one be happy when the others are sad? Ubuntu in their language means, I am, because we are. It’s a strong message for all generations. Let’s all have this attitude and spread happiness wherever we go.

i) What was the target in the race?
Answer:
a basket of sweets

ii) To which continent did the participants belong?
Answer:
Africa

iii) The referee was amazed because no one tried to run the race. Write true or false.
Answer:
falls

iv) What does the word UBUNTU mean in their native language?
Answer:
I am, because we are

v) Pick the word from the passage that means a person who takes part in something.
Answer:
participant

vi) Sharing increases happiness. Support the statement with a sentence in the passage.
Answer:
_______ and divided sweets among themselves equally

vii) What message is advocated in the passage?
Answer:
share, care and stay united and be happy

viii) Write the part of speech of the word race as used in the first sentence.
Answer:
noun

Question 8.
Read the following advertisement and answer ANY FIVE questions that follow. [5 × 1 = 5]

i) What is the advertisement about?
Answer:
About National Voter awareness contest

ii) What is the theme of NVAC?
Answer:
My vote is my future, power of one vote

iii) Name any two areas in which the contest takes place.
Answer:
Quiz, songs, video making

iv) Who has issued this advertisement?
Answer:
Election commission of India

v) How many categories of participants can contest the competition?
Answer:
3

vi) Write the antonym, from the advertisement, of the word amateur.
Answer:
Professional

vii) When is the contest scheduled?
Answer:
25-1-2022 to 15-3-2022

viii) Pick the synonym of the word consciousness from the passage.
Answer:
awareness

Question 9.
Study the table below and answer ANY FIVE questions given after it. [5 × 1 = 5]

i) What does the table show?
Answer:
India’s Medal tally at Tokyo Olympics

ii) Who won the gold medal for India?
Answer:
Neeraj Chopra

iii) Who won a bronze medal in boxing?
Answer:
Lovlina Borgohain

iv) How many medals did India win at the Olympics?
Answer:
Seven

v) Bhajarang Puniya won the bronze medal. Write true or false.
Answer:
True

vi) Meerabhai Chanu won the silver in. (Fill in the blank.)
Answer:
Weight Lifting

vii) India won 5 bronze medals at the Tokyo Olympics. Write true or false.
Answer:
False

viii) Who won the bronze medal in badminton?
Answer:
PV. Sindhu

Section – C

Question 10.
Write a letter to your uncle describing your feelings about monotonous academic work. [1 × 5 = 5]
Answer:
Letter to Uncle – Monotonous Academic Work:

10, Tagore Hostel
Ideal College
Ravindra Nagar
13.05.2022

Dear uncle

How are you all there? I’m fine here.

I write this to relieve myself of the stress resulting from our monotonous academic activity. Right from 5 in the morning to 10 in the evening, work, work and nothing else. And that too all mechanical mugging up tasks. No scope for thinking. No room for creativity. Play, exercise, entertainment are strangers in the campus. I am fed up totally.

I crave for a change. I pray for wisdom to dawn on the administrators. I know you understand me well. I felt like unburdening myself.
Hope to see you this weekend.

Lovingly yours
Praveen Kumar

Vivek K
12 Bhagyanagar Towers
Vallabh Nagar
Vaisali

OR

Write a letter of complaint to the Sub-Inspector of Police of your area about the theft of your mobile in your hostel.
Answer:
Letter of Complaint:

Room 12
Godavari Hostel
New Wings Jr. College
Peddapalli

16.09.2021

Sub-Inspector
Peddapalli Police Station

Dear Sir

I am Madhavi of second MPC. I stay in Room 10. This morning while going to classes I kept my mobile in my cupboard as usual. But, to my shock and surprise, I found it missing this evening.

I request you to look into the issue and see that my phone is restored to me at the earliest.

Thank you Sir,
Yours sincerely
Sai Kumar P

Question 11.
Rewrite the following passage using FIVE punctuation marks wherever necessary. [5 × 1 = 5]

after a decades hard work and persistent efforts his simple invention of a technology to use – plastic waste to lay roads patented by TCE finally got a shot in the arm last month with the centre approving its wider application.
Answer:
After a decade’s hard work and persistent efforts, his invention of a simple technology to use plastic waste to lay roads, patented by TCE, finally got a shot in the arm with the Centre approving its wider application.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Exercise 2(b)

I.

Question 1.
Find the equation of the radical axis of the following circles.
(i) x² + y² – 3x – 4y + 5 = 0, 3(x² + y²) – 7x + 8y – 11 = 0
Solution:
Let S ≡ x² + y² – 3x – 4y + 5 = 0 and S’ ≡ \(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}=0\) be the given circles.
The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ (x² + y² – 3x – 4y + 5) – (\(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}\)) = 0
⇒ -3x – 4y + 5 + \(\frac{7}{3} x-\frac{8}{3} y+\frac{11}{3}\) = 0
⇒ -9x – 12y + 15 + 7x – 8y + 11 = 0
⇒ -2x – 20y + 26 = 0
⇒ x + 10y – 13 = 0

(ii) x² + y² + 2x + 4y + 1 = 0, x² + y² + 4x + y = 0
Solution:
Let S ≡ x² + y² + 2x + 4y + 1 = 0 and S’ ≡ x² + y² + 4x + y = 0 be the given circles.
Then the radical axis of circles S = 0, S’ = 0 is S – S’ = 0.
⇒ (x² + y² + 2x + 4y + 1) – (x² + y² + 4x + y) = 0
⇒ -2x + 3y + 1 = 0
⇒ 2x – 3y – 1 = 0
∴ The equation of the radical axis of circles is 2x – 3y – 1 = 0.

(iii) x² + y² + 4x + 6y – 7 = 0, 4(x² + y²) + 8x + 12y – 9 = 0.
Solution:
Let S ≡ x² + y² + 4x + 6y – 7 = 0 and S’ ≡ x² + y² + 2x + 3y – \(\frac{9}{4}\) = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 2x + 3y – \(\frac{19}{4}\) = 0
⇒ 8x + 12y – 19 = 0

(iv) x² + y² – 2x – 4y – 1 = 0, x² + y² – 4x – 6y + 5 = 0
Solution:
Let S ≡ x² + y² – 2x – 4y – 1 = 0 and S’ ≡ x² + y² – 4x – 6y + 5 = 0
∴ The equation of radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ 2x + 2y – 6 = 0
⇒ x + y – 3 = 0

Question 2.
Find the equation of the common chord of the following pair of circles.
(i) x² + y² – 4x – 4y + 3 = 0, x² + y² – 5x – 6y + 4 = 0
Solution:
Let S ≡ x² + y² – 4x – 4y + 3 = 0 and S’ = x² + y² – 5x – 6y + 4 = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ x + 2y – 1 = 0

(ii) x² + y² + 2x + 3y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
Solution:
Denote S ≡ x² + y² + 2x + 3y + 1 = 0 and S’ ≡ x² + y² + 4x + 3y + 2 = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ -2x – 1 = 0
⇒ 2x + 1 = 0

(iii) (x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b)
Solution:
Denote S ≡ (x – a)² + (y – b)² = c²
⇒ x² + y² – 2ax – 2by + a² + b² – c² = 0 …….(1)
and S’ ≡ (x – b)² + (y – a)² = c²
⇒ x² + y² – 2bx – 2ay + b² + a² – c² = 0 ……..(2)
Radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 2bx – 2ax + 2ay – 2by = 0
⇒ 2x(b – a) + 2y(a – b) = 0
⇒ x – y = 0 (∵ a ≠ b)

II.

Question 1.
Find the equation of the common tangent of the following circles at their point of contact.
(i) x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0
Solution:
Denote S ≡ x² + y² + 10x – 2y + 22 = 0 and S’ ≡ x² + y² + 2x – 8y + 8 = 0.
The equation of the common tangent of the circles at their point of contact is the equation of the radical axis of S = 0 and S’ = 0 given by S – S’ = 0.
⇒ 8x + 6y + 14 = 0
⇒ 4x + 3y + 7 = 0

(ii) x² + y² – 8y – 4 = 0, x² + y² – 2x – 4y = 0
Solution:
Let S ≡ x² + y² – 8y – 4 = 0 and S’ ≡ x² + y² – 2x – 4y = 0
The equation of the common tangent at the point of contact of circles is the equation of the radical axis of the circles S = 0, S’ = 0 given by S – S’ = 0.
⇒ x² + y² – 8y – 4 – x² – y² + 2x + 4y = 0
⇒ 2x – 4y – 4 = 0
⇒ x – 2y – 2 = 0

Question 2.
Show that the circles x² + y² – 8x – 2y + 8 = 0 and x² + y² – 2x + 6y + 6 = 0 touch each other and find the point of contact.
Solution:
Let the equations of the given circles be denoted by S ≡ x² + y² – 8x – 2y + 8 = 0 and S’ = x² + y² – 2x + 6y + 6 = 0
Centres are C₁ = (4, 1) and C₂ = (1, -3)
and radii of circles are r₁ = \(\sqrt{16+1-8}\) = 3 and r₂ = \(\sqrt{1+9-6}\) = 2
∴ C₁C₂ = \(\sqrt{(4-1)^2+(1+3)^2}=\sqrt{9+16}\) = 5
Also r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the circles touch each other externally.

The point of contact P divides C₁C₂ internally in the ratio of their radii i.e., 3 : 2.
∴ The point of contact

Question 3.
If the two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other, then show that fg’ = f’g.
Solution:
Let S = x² + y² + 2gx + 2fy = 0 and S’ = x² + y² + 2g’x + 2f’y = 0 be the given circles.
Centres of the circles are C₁ = (-g, -f) and C₂ = (-g, -f’)
Also r₁ = \(\sqrt{g^2+f^2}\) and r₂ = \(\sqrt{g^{\prime 2}+f^{\prime 2}}\)
Given that the two circles touch each other we have C₁C₂ = |r₁ ± r₂|
⇒ \(\sqrt{\left(g-g^{\prime}\right)^2+\left(f-f^{\prime}\right)^2}\) = \(\left|\sqrt{g^2+f^2} \pm \sqrt{g^{+2}+f^2}\right|\)

Question 4.
Find the radical centre of the following circles.
(i) x² + y² – 4x – 6y + 5 = 0, x² + y² – 2x – 4y – 1 = 0, x² + y² – 6x – 2y = 0
Solution:
Let S = x² + y² – 4x – 6y + 5 = 0, S₁ = x² + y² – 2x – 4y – 1 = 0 and S₂ = x² + y² – 6x – 2y = 0 be the given circles.
Radical axis of S = 0, S₁ = 0 is S – S₁ = 0
⇒ -2x – 2y + 6 = 0
⇒ x + y – 3 = 0 ……….(1)
Radical axis of S₁ = 0, S₂ = 0 is 4x – 2y – 1 = 0 ……….(2)
Solving (1) and (2), we get the coordinates 0f Radical centre of the circles S = 0, S₁ = 0, and S₂ = 0

(ii) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0
Solution:
Denote S = x² + y² + 4x – 7 = 0
S₁ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
and S₂ = x² + y² + y = 0
Radical axis of S = 0, S₁ = 0 is S – S₁ = 0.
⇒ \(\frac{5}{2} x-\frac{5}{2} y+\frac{5}{2}=0\)
⇒ x – y + 1 = 0 ………(1)
Radical axis of S₁ = 0, S₂ = 0 is S₁ – S₂ = 0.
⇒ \(\frac{3}{2} x+\frac{3}{2} y-\frac{9}{2}=0\)
⇒ x + y – 3 = 0 ……..(2)
Solving 2x – 2 = 0 ⇒ x = 1
and From (2), y = 2
∴ Radical centre = (1, 2)

III.

Question 1.
Show that the common chord of the circles x² + y² – 6x – 4y + 9 = 0 and x² + y² – 8x – 6y + 23 = 0 is the diameter of the second circle and also find its length.
Solution:

Let S = x² + y² – 6x – 4y + 9 = 0 and S’ = x² + y² – 8x – 6y + 23 = 0
Then the equation of the common chord of circles is S – S’ = 0 is 2x + 2y – 14 = 0
⇒ x + y – 7 = 0
The Centre of S’ = 0 is (4, 3)
∴ x + y – 7 = 4 + 3 – 7 = 0 and common chord of circles S = 0, S’ = 0 is the diameter of the second circle.
The length of the common chord = 2(the radius of the circle S’ = 0) = 2√2 units.
(or) C₁P = ⊥ distance from C₁(3, 2) to the common chord x + y – 7 = 0.
∴ C₁P = \(\left|\frac{3+2-7}{\sqrt{2}}\right|\) = √2
AC₁ = radius of S = 0
= \(\sqrt{9+4-9}\)
= 2
∴ AP = \(\sqrt{\mathrm{AC}_1^2-\mathrm{C}_1 \mathrm{P}^2}=\sqrt{4-2}=\sqrt{2}\)
∴ Length of the common chord AB = 2(AP) = 2√2.

Question 2.
Find the equation and length of the common chord of the following circles.
(i) x² + y² + 2x + 2y + 1 = 0, x² + y² + 4x + 3y + 2 = 0
Solution:
Let S = x² + y² + 2x + 2y + 1 = 0 and S₁ = x² + y² + 4x + 3y + 2 = 0
Then the equation of the common chord of S = 0, S₁ = 0 is S – S₁ = 0.
⇒ -2x – y – 1 = 0
⇒ 2x + y + 1 = 0
C₁ = Centre of S = 0 is (-1, 1) and r₁ = \(\sqrt{1+1-1}\) = 1

(ii) x² + y² – 5x – 6y + 4 = 0, x² + y² – 2x – 2 = 0
Solution:
Denote S = x² + y² – 5x – 6y + 4 = 0 and S₁ = x² + y² – 2x – 2 = 0
Equation of common chord of S = 0, S₁ = 0 is S – S₂ = 0.
⇒ -3x – 6y + 6 = 0
⇒ x + 2y – 2 = 0

Question 3.
Prove that the radical axis of the circle x² + y² + 2gx + 2fy + c = 0 and x² + y² + 2g’x + 2f’y + c’ = 0 is the diameter of the latter circle (or the former bisector the circumference of the latter) if 2g'(g – g’) + 2f(f – f’) = c – c’.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 and S’ ≡ x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.
Centre of the circle S’ = 0 is C2 = (-g’, -f’)
The equation of the Radical axis of S = 0 and S’ = 0 is S – S’ = 0.
⇒ 2(g – g’)x + 2(f – f’)y + c – c’ = 0 …….(1)
Substituting the centre (-g’, -f’) of S’ = 0, we get
2(g – g’) (-g’) + 2(f – f’) (-f’) + c – c’ = 0
⇒ 2g'(g – g’) + 2f'(f – f’) = c – c’
The radical axis of the circles S = 0, S’ = 0 is the diameter of the circle S’ = 0 if 2g'(g – g’) + 2f(f – f’) = c – c’

Question 4.
Show that the circles x² + y² + 2ax + c = 0 and x² + y² + 2by + c = 0 touch each other if \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c}\)
Solution:
Let S = x² + y² + 2ax + c = 0 and S’ = x² + y² + 2by + c = 0 be the given circles.
Centre of S = 0 is C₁ (-a, 0) and radius of the circle S = 0 is \(\sqrt{a^2-c}\).
The equation of common tangent of circles S = 0, S’ = 0 is S – S’ = 0
⇒ 2ax – 2by = 0
⇒ ax – by = 0
Let L = ax – by = 0
The two circles S = 0 and S’ = 0 touch each other if the perpendicular distance from C₁ (-a, 0) to the common tangent L = 0 is equal to the radius of the circle S = 0.
∴ The perpendicular distance from C₁ (-a, 0)

Question 5.
Show that the circles x² + y² – 2x = 0 and x² + y² + 6x + 6y + 2 = 0 touch each other. Find the coordinates of the point of contact. Is the point of contact external or Internal?
Solution:
Let S = x² + y² – 2x = 0 and S’ = x² + y² + 6x – 6y + 2 = 0 be the given circles.
Centre of S = 0 is C₁ = (1, 0),
and radius of S₁ = 0 is r₁ = √1 = 1.
Centre of S’ = 0 is C₂ = (-3, 3)
and radius of S’ = 0 is r₂ = \(\sqrt{9+9-2}\) = 4.
Distance between centres C₁C₂ = \(\sqrt{(1+3)^2+(0-3)^2}=\sqrt{16+9}\) = 5
and r₁ + r₂ = 1 + 4 = 5.
Since C₁C₂ = r₁ + r₂, the two circles touch externally at a point and the point of contact divides C₁C₂ internally in the ratio 1 : 4.
∴ Point of contact

∴ The point of contact is \(\left(\frac{1}{5}, \frac{3}{5}\right)\) and the two circles touch each other externally.

Question 6.
Find the equation of the circle which cuts the following circles orthogonally.
(i) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0
Solution:
Let S = x² + y² + 4x – 7 = 0
S’ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
and S” = x² + y² + y = 0 be the equations of the given circles.
Radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 5x – 5y – 5 = 0
⇒ x – y – 1 = 0 ………(1)
The radical axis of S’ = 0, S” = 0 is S’ – S” = 0.
⇒ \(\frac{3}{2} x+\frac{3}{2} y-\frac{9}{2}=0\)
⇒ x + y – 3 = 0 ………(2)
Solving (1) and (2), we get
the Radical centre of circles S = 0, S’ = 0 and S” = 0

⇒ x = 2 and y = 1
∴ The radical centre of the given circles is (2, 1).
The length of the tangent drawn from (2, 1) to S = 0 is \(\sqrt{4+1+8-7}\) = √6
So by the property that a circle having radical centre as centre and length of the tangent to S = 0 as radius cuts every given circle orthogonally.
So the equation of a required circle with C(2, 1) as a radical centre and √6 as the radius is given by
(x – 2)² + (y + 1)² = (√6)²
⇒ x² + y² – 4x – 2y – 1 = 0

(ii) x² + y² + 2x + 4y + 1 = 0, 2x² + 2y² + 6x + 8y – 3 = 0, x² + y² – 2x + 6y – 3 = 0. (May ’12)
Solution:
Let S = x² + y² + 2x + 4y + 1 = 0
S’ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
and S” = x² + y² – 2x + 6y – 3 = 0 be the equations of the given circles.
Radical axis of centre S = 0, S’ = 0 is S – S’ = 0.
⇒ -x + \(\frac{5}{2}\) = 0
⇒ x = \(\frac{5}{2}\) ……..(1)
Radical axis of centre S’ = 0, S” = 0 is S’ – S” = 0
⇒ 5x – 2y + \(\frac{3}{2}\) = 0
⇒ 10x – 4y + 3 = 0 ………(2)
By solving (1) and (2), we get the Radical centre of the given circles.
Since x = \(\frac{5}{2}\) and from(2),
25 – 4y + 3 = 0
⇒ y = 7
∴ Radical centre = (\(\frac{5}{2}\), 7)
Length of the tangent from (\(\frac{5}{2}\), 7) to S = 0 is

Hence the circle with centre (\(\frac{5}{2}\), 7) and \(\sqrt{\frac{357}{4}}\) as radius cuts every circle of the given system orthogonally.
∴ The equation of required circle with centre (\(\frac{5}{2}\), 7) and \(\sqrt{\frac{357}{4}}\) as radius is

(iii) x² + y² + 2x + 17y + 4 = 0, x² + y² + 7x + 6y + 11 = 0, x² + y² – x + 22y + 3 = 0
Solution:
Denote the given circles by
S = x² + y² + 2x + 17y + 4 = 0
S’ = x² + y² + 7x + 6y + 11 = 0
S” = x² + y² – x + 22y + 3 = 0
Radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ -5x + 11y – 7 = 0
⇒ 5x – 11y + 7 = 0 ………(1)
Radical axis of S’ = 0, S” = 0 is S’ – S” = 0
⇒ 8x – 16y + 8 = 0
⇒ x – 2y + 1 = 0 ……..(2)
Solving (1) and (2), we get the coordinates of the Radical centre of circles.

∴ \(\frac{x}{-11+14}=\frac{y}{7-5}=\frac{1}{-10+11}\)
⇒ x = 3, y = 2
∴ Radical centre = (3, 2)
Length of the tangent from (3, 2) to the circle S = 0 is \(\sqrt{9+4+6+34+4}=\sqrt{57}\).
Since the circle with centre (3, 2) and radius √57 cuts every circle of the given system orthogonally,
the equation of the required circle is (x – 3)² + (y – 2)² = 57
⇒ x² + y² – 6x – 4y – 44 = 0.

(iv) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0.
Solution:
Denote the given circles by S = x² + y² + 4x + 2y + 1 = 0, S’ = x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0, and S” = x² + y² + 6x – 2y – 3 = 0
Radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ -y + \(\frac{5}{2}\) = 0
⇒ y = \(\frac{5}{2}\) ……..(1)
The radical axis of S’ = 0, S” = 0 is S’ – S” = 0.
⇒ -2x + 5y + \(\frac{3}{2}\) = 0
⇒ -4x + 10y + 3 = 0
⇒ 4x – 10y – 3 = 0 ………(2)
Solving (1) and (2), we get the Radical centre of circles.
∴ From (2), 4x – 25 – 3 = 0
⇒ x = 7
∴ Radical centre = (7, \(\frac{5}{2}\))
Length of the tangent from (7, \(\frac{5}{2}\)) to S = 0 is = \(\sqrt{49+\frac{25}{4}+28+5+1}=\sqrt{\frac{357}{4}}\)
∴ The equation of the required circle with centre (7, \(\frac{5}{2}\)) and as radius which cuts every circle of the system orthogonally is given by
(x – 7)² + \(\left(y-\frac{5}{2}\right)^2=\frac{357}{4}\)
⇒ x² + y² – 14x – 5y + 49 + \(\frac{25}{4}-\frac{357}{4}\) = 0
⇒ x² + y² – 14x – 5y – 34 = 0.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(e) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(e)

I.

Question 1.
Discuss the relative position of the following pair of circles.
(i) x² + y² – 4x – 6y – 12 = 0, x² + y² + 6x + 18y + 26 = 0
Solution:
Let S ≡ x² + y² – 4x – 6y – 12 = 0 ……..(1) and S’ ≡ x² + y² + 6x + 18y + 26 = 0 ……..(2) be the given circles.
The Centre of the circle (1) is C₁ = (2, 3)
Centre of circle (2) is C₂ = (-3, -9)
Radius of circle (1) is \(\sqrt{4+9+12}\) = 5 = r₁
Radius of circle (2) is \(\sqrt{9+81-26}\) = 8 = r₂
Now C₁C₂ = \(\sqrt{(2+3)^2+(3+9)^2}\) = 13
and r₁ + r₂ = 5 + 8 = 13
Since C₁C₂ = r₁ + r₂, the two circles touched each other externally.

(ii) x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0
Solution:
Taking S ≡ x² + y² + 6x + 6y + 14 = 0 ……….(1) and S’ ≡ x² + y² – 2x – 4y – 4 = 0 ………(2)
The Centre of the circle (1) is C₁1 = (-3, -3)
and the Centre of the circle (2) is C₂ = (1, 2)
Radius of circle (1) is r₁ = \(\sqrt{9+9-14}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{1+4+4}\) = 3
Now C₁C₂ = \(\sqrt{(1+3)^2+(2+3)^2}\) = √41
r₁ + r₂ = 5
Since C₁C₂ > r₁ + r₂, each circle lies on the exterior of the other circle.

(iii) (x – 2)² + (y + 1)² = 9, (x + 1)² + (y – 3)² = 4
Solution:
The equation of the given circles are
(x – 2)² + (y + 1)² = 9 ………(1)
(x + 1)² + (y – 3)² = 4 ……….(2)
Centre of circle (1) is C₁ = (2, -1)
The Centre of the circle (2) is C₂ = (-1, 3)
The radius of the circle (1) is r₁ = 3
The radius of the circle (2) is r₂ = 2
C₁C₂ = \(\sqrt{(2+1)^2+(-1-3)^2}\) = 5
and r₁ + r₂ = 3 + 2 = 5
∴ Since C₁C₂ = r₁ + r₂, the two circles touch each other externally.

(iv) x² + y² – 2x + 4y – 4 = 0, x² + y² + 4x – 6y – 3 = 0
Solution:
Given equations of circles are
x² + y² – 2x + 4y – 4 = 0 ……….(1)
x² + y² + 4x – 6y – 3 = 0 ……….(2)
Centre of circle (1) is C₁ = (1, -2)
The Centre of the circle (2) is C₂ = (-2, 3)
Radius of circle (1) is r₁ = \(\sqrt{1+4+4}\) = 3
Radius of circle (2) is r₂ = \(\sqrt{4+9+3}\) = 4
Distance between centres C₁C₂ = \(\sqrt{(1+2)^2+(-2-3)^2}=\sqrt{9+25}=\sqrt{34}\)
r₁ + r₂ = 3 + 4 = 7 and |r₁ – r₂| = |3 – 4| = 1
∴ |r₁ – r₂| < C₁C₂ < r₁ + r₂
∴ The two given circles (1) and (2) intersect each other in two points.

Question 2.
Find the number of possible common tangents that exist for the following pairs of circles.
(i) x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0
Solution:
The given equations of circles are
x² + y² + 6x + 6y + 14 = 0 ………(1)
and x² + y² – 2x – 4y – 4 = 0 ……..(2)
Centre of circle (1) is C₁ = (-3, -3)
The Centre of the circle (2) is C₂ = (1, 2)
Radius of circle (1) is r₁ = \(\sqrt{9+9-14}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{1+4+4}\) = 3
C₁C₂ = \(\sqrt{(-3-1)^2+(-3-2)^2}=\sqrt{16+25}\) = √41
and r₁ + r₂ = 2 + 3 = 5
Since C₁C₂ > r₁ + r₂ the given circles do not intersect each other.
The number of possible common tangents that can be drawn to the above circles is ‘4’.

(ii) x² + y² – 4x – 2y + 1 = 0, x² + y² – 6x – 4y + 4 = 0
Solution:
The given equations of circles are
x² + y² – 4x – 2y + 1 = 0 ………(1)
and x² + y² – 6x – 4y + 4 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (2, 1)
The Centre of the circle (2) is C₂ = (3, 2)
Radius of circle (1) is r₁ = \(\sqrt{4+1-1}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{9+4-4}\) = 3
C₁C₂ = \(\sqrt{(2-3)^2+(1-2)^2}=\sqrt{1+1}=\sqrt{2}\)
and r₁ + r₂ = 2 + 3 = 5
∴ |r₁ – r₂| = |2 – 3| = 1
∴ |r₁ – r₂| < C₁C₂ < r₁ + r₂
∴ The two given circles intersect each other in two points.
The number of possible common tangents that can be drawn to the circles is ‘2’.

(iii) x² + y² – 4x + 2y – 4 = 0, x² + y² + 2x – 6y + 6 = 0
Solution:
The given equations of circles are
x² + y² – 4x + 2y – 4 = 0 ……….(1)
and x² + y² + 2x – 6y + 6 = 0 …………(2)
Centre of circle (1) is C₁ = (2, -1)
The Centre of the circle (2) is C₂ = (-1, 3)
Radius of circle (1) is r₁ = \(\sqrt{4+1+4}\) = 3
Radius of circle (2) is r₂ = \(\sqrt{1+9-6}\) = 2
C₁C₂ = \(\sqrt{(2+1)^2+(-1-3)^2}=\sqrt{9+16}\) = 5
and r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the two circles touch externally and the number of possible common tangents is ‘3’.

(iv) x² + y² = 4, x² + y² – 6x – 8y + 16 = 0
Solution:
The equations of given circles are x² + y² = 4 ………(1) and x² + y² – 6x – 8y + 16 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (0, 0)
The Centre of the circle (2) is C₂ = (3, 4)
The radius of the circle (1) is r₁ = 2
Radius of circle (2) is r₂ = \(\sqrt{9+16-16}\) = 3
C₁C₂ = \(\sqrt{9+16}\) = 5 = r₁ + r₂
Hence the two circles touch externally and the number of possible common tangents is ‘3’.’

(v) x² + y² + 4x – 6y – 3 = 0, x² + y² + 4x – 2y + 4 = 0
Solution:
The equations of circles are
x² + y² + 4x – 6y – 3 = 0 ……….(1)
and x² + y² + 4x – 2y + 4 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (-2, 3)
The Centre of the circle (2) is C₂ = (-2, 1)
Also radius of circle are r1 = \(\sqrt{4+9+3}\) = 4
Radius of circle (2) are r2 = \(\sqrt{4+1-4}\) = 1
Now C₁C₂ = \(\sqrt{(-2+2)^2+(3-1)^2}\) = 4
and |r₁ – r₂| = |4 – 1| = 3
∴ C₁C₂ < |r₁ + r₂|, one circle lies completely inside the other circle.
∴ The number of common tangents that can be drawn to the circles S = 0 and S’ = 0 is zero.

Question 3.
Find the internal centre of similitude of the circles x² + y² + 6x – 2y + 1 = 0 and x² + y² – 2x – 6y + 9 = 0.
Solution:
Equations of given circles are
x² + y² + 6x – 2y + 1 = 0 ……….(1)
x² + y² – 2x – 6y + 9 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (-3, 1)
The Centre of the circle (2) is C₂ = (1, 3)
Also radius of circle (1) is r₁ = \(\sqrt{9+1-1}\) = 3
radius of circle (2) is r₂ = \(\sqrt{1+9-9}\) = 1
Now C₁C₂ = \(\sqrt{(-3-1)^2+(1-3)^2}=\sqrt{16+4}\) = √20
and r₁ + r₂ = 3 + 1 = 4
Since C₁C₂ > r₁ + r₂, the two circles do not touch or do not intersect each other but each circle lies in the exterior of the other.
∴ Number of common tangents = 4
Both internal and external centres of similitude exist.

Let A be the internal centre of similitude and r₁ : r₂ = 3 : 1.
∴ A divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio 3 : 1 internally.

∴ The internal centre of similitude is (0, \(\frac{5}{2}\))

Question 4.
Find the external centre of similitude for the circles x² + y² – 2x – 6y + 9 = 0, x² + y² = 4.
Solution:
The equations of given circles are x² + y² – 2x – 6y + 9 = 0 ……..(1) and x² + y² = 4 ……..(2)
Centre of circles are C₁ = (1, 3) and C₂ = (0, 0)
Radius of circles are r₁ = \(\sqrt{1+9-9}\) = 1 and r₂ = √4 = 2
Now C₁C₂ = \(\sqrt{1+9}=\sqrt{10}\) and r₁ + r₂ = 1 + 2 = 3
Since C₁C₂ > r₁ + r₂, each circle lies in the exterior of the other circle, and the number of common tangents = 4
∴ Both internal and external centres of similitudes do exist in this case.
C₁ = (1, 3) = (x₁, y₁) and C₂ = (0, 0) = (x₂, y₂)

∴ The external centre of the similitude of the circle is (2, 6).

II.

Question 1.
(i) Show that the circles x² + y² – 6x – 2y + 1 = 0, x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. (Mar. ’11, ’10, ’09)
Solution:
Let S = x² + y² – 6x – 2y + 1 = 0 and S’ = -x² + y² + 2x – 8y + 13 = 0 be the given circles.
The centre of circles are C₁ = (3, 1) and C₂ = (-1, 4)
Radius of circles are r₁ = \(\sqrt{9+1-1}\) = 3 and r₂ = \(\sqrt{1+16-13}\) = 2
Distance between centres C₁C₂ = \(\sqrt{(3+1)^2+(1-4)^2}=\sqrt{16+9}\) = 5 and r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the two circles touch externally at a point.

Let P be the point of contact of circles such that r₁ : r₂ = 3 : 2.
Since P divides C₁, C₂ internally in the ratio 3 : 2,
the coordinates of the point of contact

The equation of common tangent is S – S’ = 0
⇒ x² + y² – 6x – 2y + 1 – x² – y² – 2x + 8y + 13 = 0
⇒ -8x + 6y – 12 = 0
⇒ 4x – 3y + 6 = 0
∴ The equation of the common tangent at the point of contact is 4x – 3y + 6 = 0.

(ii) Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact.
Solution:
Given equations of circles are S = x² + y² – 6x – 9y + 13 = 0 and S’ = x² + y² – 2x – 16y = 0
Centre of circles are C₁ = (3, \(\frac{9}{2}\)) and C₂ = (1, 8)

The point P divides C₁C₂ externally in the ratio of their radius \(\frac{\sqrt{65}}{2}\) : √65 = 1 : 2

The equation of the common tangent at P(5, 1) to the circles S = 0 and S’ = 0 is S – S’ = 0.
⇒ x² + y² – 6x – 9y + 13 – x² – y² + 2x + 16y = 0
⇒ -4x + 7y – 13 = 0
⇒ 4x – 7y + 13 = 0
∴ The equation of the required common tangent is 4x – 7y + 13 = 0.

Question 2.
Find the equation of the circle which touches the circle x² + y² – 2x – 4y – 20 = 0 externally at (5, 5) with radius ‘5’.
Solution:

Let C₁ = (h, k) be the centre and r1 be the radius of the required circle.
Given r₁ = 5
Equation of the given circle is x² + y² – 2x – 4y – 20 = 0 ……….(1)
Centre of the circle C₂ = (1, 2) and radius r₂ = \(\sqrt{1+4+20}\) = 5
∴ r₁ : r₂ = 5 : 5 = 1 : 1
Point P(5, 5) divides C₁C₂ in the ratio 1 : 1 internally.
∴ \(\left(\frac{\mathrm{h}+1}{2}, \frac{\mathrm{k}+2}{2}\right)\) = (5, 5)
⇒ \(\frac{\mathrm{h}+1}{2}\) = 5 and \(\frac{\mathrm{k}+2}{2}\) = 5
⇒ h = 9 and k = 18
∴ C1 = (h, k) = (9, 8)
∴ The equation of a required circle with centre (9, 8) and radius ‘5’ is (x – 9)² + (y – 8)² = 25
⇒ x² + y² – 18x – 16y + 120 = 0

Question 3.
Find the direct common tangents of the circles x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0. (New Model Paper)
Solution:
Let S = x² + y² + 22x – 4y – 100 = 0 ……….(1) and S’ = x² + y² – 22x + 4y + 100 = 0 …….(2) be the given circles.
Then centres of the circles are C₁ = (-11, +2) and C₂ = (11, -2)
The radius of the circles are

and r₁ + r₂ = 15 + 5 = 20
Since C₁C₂ > r₁ + r₂, the two circles are such that each lies on the exterior of the other.
Hence both internal and external centre of similitude exists.

Now r₁ : r₂ = 15 : 5 = 3 : 1
Point P divides C₁, C₂ externally in the ratio of radii 3 : 1.

The equation of direct common tangent passing through (22, -4) having slope ‘m’ is y + 4 = m(x – 22)
⇒ mx – y – 4 – 22m = 0 …….(1)
Since the line is tangent to S’ = 0.
Perpendicular distance from C₂ = (11, -2) to the line (1) = radius of the circle S’ = 0
∴ \(\left|\frac{m(11)+2-4-22 m}{\sqrt{m^2+1}}\right|\) = 5
⇒ \(\left|\frac{-(11 m+2)}{\sqrt{m^2+1}}\right|\) = 5
⇒ (11m + 2)² = 25(m² + 1)
⇒ 121m² + 44m + 4 = 25m² + 25
⇒ 96m² + 44m – 21 = 0
⇒ 96m² + 72m – 28 m – 21 = 0
⇒ 24m(4m + 3) – 7(4m + 3) = 0
⇒ (24m – 7) (4m + 3) = 0
⇒ m = \(\frac{-3}{4}\) or m = \(\frac{7}{24}\)
∴ Equations of direct common tangents from (1) are y + 4 = \(\frac{-3}{4}\)(x – 22)
⇒ 4y + 16 = -3x + 66
⇒ 3x + 4y – 50 = 0
and y + 4 = \(\frac{7}{24}\)(x – 22)
⇒ 24y + 96 = 7x – 154
⇒ 7x – 24y – 250 = 0
∴ The equations of direct common tangents are given by 3x + 4y – 50 = 0 and 7x – 24y – 250 = 0.

Question 4.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x – 6y + 4 = 0.
Solution:
Let S = x² + y2 – 4x – 10y + 28 = 0 ………(1)
S’ = x² + y2 + 4x – 6y + 4 = 0 ……….(2)
be the given circles.
Centres of the circles are C₁ = (2, 5) and C₂ = (-2, 3)
Also, the radius of circles are r₁ = \(\sqrt{4+25-28}\) = 1 and r₂ = \(\sqrt{4+9-4}\) = 3
Also C₁C₂ = \(\sqrt{(2+2)^2+(5-3)^2}\) = √20 = 2√5 and r₁ + r₂ = 4
Since C₁C₂ > r₁ + r₂, we have each circle lying in the exterior of other circles.
Hence we get 2 direct common tangents and 2 transverse common tangents that can be drawn.

Point P divides C₁C₂ internally in the ratio r₁ : r₂ = 1 : 3.
Let P be the internal centre of similitude.

Let the equation of transverse common tangent be y – \(\frac{9}{2}\) = m(x – 1) ……(1)
⇒ 2y – 9 = 2mx – 2m
⇒ 2mx – 2y + (9 – 2m) = 0 ……….(2)
Since line (2) is a tangent to the circle S = 0, the perpendicular distance from C₁ (2, 5) to line (2) is equal to the radius of the circle S = 0.
∴ \(\left|\frac{2 m(2)-2(5)+9-2 m}{\sqrt{4 m^2+4}}\right|\) = 1
⇒ |2m – 1| = \(2 \sqrt{m^2+1}\)
⇒ 4m² – 4m + 1 = 4(m² + 1)
⇒ 4m² – 4m + 1 – 4m² – 4 = 0
⇒ -4m – 3 = 0
⇒ m = \(\frac{-3}{4}\)
∴ Equation of tangent is y – \(\frac{9}{2}\) = \(\frac{-3}{4}\)(x – 1)
⇒ \(\frac{2 y-9}{2}=-\frac{3}{4}(x-1)\)
⇒ 2(2y – 9) = -3(x – 1)
⇒ 4y – 18 = -3x + 3
⇒ 3x + 4y – 21 = 0
Since the m² term is canceled, the slope of one of the transverse common tangents is not defined.
One transverse common tangent is passing through P(1, \(\frac{9}{2}\)) and parallel to y-axis.
∴ The equation of other transverse common tangents is x = 1.
∴ The equations of transverse common tangents are x = 1 and 3x + 4y – 21 = 0.

Question 5.
Find the pair of tangents from (4, 10) to the circle x² + y² = 25.
Solution:
Let P(x₁, y₁) be the given point.
The equation to the pair of tangents drawn from P(4, 10) to S = 0 is \(\mathrm{S}_1^2=\mathrm{SS}_{11}\).
Given S = x² + y² – 25 = 0
(xx₁ + yy₁ – 25)² = (x² + y² – 25) (\(x_1^2+y_1^2\) – 25)
⇒ (4x + 10y – 25)² = (x² + y² – 25) (16 + 100 – 25)
⇒ (4x + 10y – 25)² = (x² + y² – 25) (91)
⇒ 16x² + 100y² + 625 + 80xy – 500y – 200x = 91x² + 91y² – 2275
⇒ 75x² – 9y² – 80xy + 200x + 500y – 2900 = 0

Question 6.
Find the pair of tangents drawn from (0, 0) to x² + y² + 10x + 10y + 40 = 0.
Solution:
Let P(x₁, y₁) be the given point.
The equation to the pair of tangents drawn from P(0, 0) to S = 0 is \(\mathrm{S}_1^2=\mathrm{SS}_{11}\).
Given S = x² + y² + 10x + 10y + 40 = 0
∴ The equation to the pair of tangents from (0, 0) to S = 0 is [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]² = (x² + y² + 2gx + 2fy + c) (\(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c)
⇒ (5x + 5y + 40)² = (x² + y² + 10x + 10y + 40) (40)
⇒ 25x² + 25y² + 1600 + 50xy + 400xy + 400x = 40(x² + y² + 10x + 10y + 40)
⇒ 15x² + 15y² – 50xy = 0
⇒ 3x² + 3y² – 10xy = 0

III.

Question 1.
Find the equation of the circle which touches x² + y² – 4x + 6y – 12 = 0 at (-1, 1) internally with a radius of ‘2’.
Solution:
The given circle is x² + y² – 4x + 6y – 12 = 0
The centre of the circle is (2, -3) and radius = \(\sqrt{4+9+12}\) = 5
Let the centre of the required circle be (h, k), and given that 2 is the radius with the point of contact of circles internally as (-1, 1).
Suppose (x₁, y₁) = (2, -3), (x₂, y₂) = (h, k), r₁ = 5, r₂ = 2
point of contact (x, y) = (-1, 1)
using the formula for the external division since two circles touch internally.

⇒ (5x – 1)² + (5y – 3)² = 100
⇒ 25x² + 25y² – 10x – 30y – 90 = 0
⇒ 5x² + 5y² – 2x – 6y – 18 = 0

Question 2.
Find all common tangents of the following pairs of circles.
(i) x² + y² = 9 and x² + y² – 16x + 2y + 49 = 0
Solution:
Let S = x² + y² – 9 = 0 and S’ = x² + y² – 16x + 2y + 49 = 0 be the given circles.
Centre of the circle S = 0 is C₁ (0, 0) and radius = 3
Centre of the circle S’ = 0 is C₂ (8, -1) and radius r2 = \(\sqrt{64+1-49}\) = 4
r₁ + r₂ = 3 + 4 = 7 and C₁C₂ = \(\sqrt{64+1}=\sqrt{65}\) > 7
Since C₁C₂ > r₁ + r₂ we get each circle lies completely in the exterior of the other.
∴ Two direct and two transverse common tangents can be drawn to S = 0 and S’ = 0.
r₁ : r₂ = 3 : 4
Let A be the internal centre of similitude and A divides C₁C₂ in the ratio 3 : 4 internally

⇒ 64x² + y² + 441 – 16xy + 42y – 336x = 16(x² + y² – 9)
⇒ 48x² – I6xy – 15y² + 42y – 336x + 585 = 0
⇒ 48x² – 36xy + 20xy – 15y² + 42y – 336x + 585 = 0
⇒ 12x(4x – 3y) + 5y(4x – 3y) + 42y – 336x + 585 = 0
⇒ (12x + 5y)(4x – 3y) – 336x + 42y + 585 = 0
Let 48x² – 16xy – 15y² + 42y – 336x + 585 = (12x + 5y + l) (4x – 3y + m)
= 48x² – 36xy + 12mx + 20xy – 15y² + 5ym + 4lx + 3ly + lm
= 48x² – 16xy – 15y² + (4l + 12m)x + (-3l + 5m)y + lm
Equating coefficients of x, y, and the constant term
4l + 12m = -336
⇒ l + 3m = -84 ………(1)
-3l + 5m = 42
⇒ 3l – 5m = -42 ……..(2)
and lm = 585 …….(3)
From (1), 5l + 15m = -420
From (2), 9l – 15m = -126
∴ 14l = -546
⇒ l = -39
From (1), -39 + 3m = -84
⇒ 3m = -45
⇒ m = -15
∴ 48x² – 16xy – 15y² + 42y – 336x + 585 = (12x + 5y – 39) (4x – 3y – 15)
∴ The transverse common tangents are 12x + 5y – 39 = 0 and 4x – 3y – 15 = 0
Let B be the external centre of the similitude of circles.
∴ B divides C1C2 in the ratio 3 : 4 externally
∴ B = \(\left(\frac{3(8)-4(0)}{3-4}, \frac{3(-1)-4(0)}{3-4}\right)\) = (-24, 3)
The equation is the pair of direct common tangents to the circle S = 0 from (-24, 3) is \(S_1^2=S S_{11}\)
⇒ [x(-24) + y(3) – 9]² = (x² + y² – 9) (576 + 9 – 9)
⇒ (-24x + 3y – 9)² = (576) (x² + y2 – 9)
⇒ 9(-8x + y – 3)² = 9 × 64 (x² + y2 – 9)
⇒ (-8x + y – 3)² = 64(x² + y2 – 9)
⇒ 64x² + y² + 9 – 16xy – 6y + 48x = 64x² + 64y² – 576
⇒ 63y² + 16xy – 48x + 6y – 585 = 0
⇒ y(63y + 16x) – 48x + 6y – 585 = 0
∴ 63y² + 16xy – 48x + 6y – 585 = (y + l) (63y + 16x + m)
Equating coefficients of x, y, and constants
16l = 48 ……..(4)
63l + m = 6 ………(5)
lm = -585 ……….(6)
∴ l = -3 and from (6), m = 195
∴ 63y² + 16xy – 48x + 6y – 585 = (y – 3) (63y + 16x + 195)
∴ The equations of direct common tangents to the circles S = 0, S’ = 0 are y – 3 = 0, 63y + 16x + 195 = 0.
Hence equations of all common tangents to the circles S = 0 and S’ = 0 are 4x – 3y – 15 = 0, 12x + 5y – 39 = 0 and y – 3 = 0, 16x + 63y + 195 = 0.

(ii) x² + y² + 4x + 2y – 4 = 0 and x² + y² – 4x – 2y + 4 = 0
Solution:
Let S = x² + y² + 4x + 2y – 4 = 0 and S’ = x² + y² – 4x – 2y + 4 = 0
Centre of S = 0 is C₁ (-2, 1) and the radius is r₁ = \(\sqrt{4+1+4}\) = 3
Centre of S’ = 0 is C₂ (2, 1) and the radius r₂ = \(\sqrt{4+1-4}\) = 1
Also C₁C₂ = \(\sqrt{(2+2)^2+(1+1)^2}=\sqrt{16+4}\) = √20 = 2√5 and r₁ + r₂ = 3 + 1 = 4
Since C₁C₂ > r₁ + r₂, each circle lies in the exterior of the other circle.
∴ Two direct and two transverse common tangents can be drawn to the circles S = 0 and S’ = 0.
Let A, B be the internal and external centres of similitudes of circles S = 0 and S’ = 0
A divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ = 3 : 1 internally
∴ A = \(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)\)


⇒ -(2x + y – 1)² = (x² + y² + 4x + 2y – 4)
⇒ (2x + y – 1)² = (x² + y² + 4x + 2y – 4)
⇒ 4x² + y² + 1 + 4xy – 2y – 4x = x² + y² + 4x + 2y – 4
⇒ 3x² + 4xy – 8x – 4y + 5 = 0
⇒ x(3x + 4y) – 8x – 4y + 5 = 0
⇒ 3x² + 4xy – 8x – 4y + 5 = (x + l) (3x + 4y + m)
Comparing the coefficients of x, y, and constants
3l + m = -8 ………(1)
4l = -4 ……….(2)
lm = 5 ……….(3)
∴ From (2), l = -1 and From (3), m = -5
∴ 3x² + 4xy – 8x – 4y + 5 = (x – 1) (3x + 4y – 5)
The equations of transverse common tangents are x – 1 = 0, 3x + 4y – 5 = 0.
The equation of pair of direct common tangents to the circle S = 0 is \(\mathrm{s}_1^2=\mathrm{S} \mathrm{S}_{11}\).
⇒ [x(4) + y(2) + 2(x + 4) + 1(y + 2) – 4]² = (x² + y² + 4x + – 2y – 4) (16 + 4 + 16 + 4 – 4)
⇒ (6x + 3y + 6)² = (x² + y² + 4x + 2y – 4)(36)
⇒ 9(2x + y + 2)² = 36(x² + y² + 4x + 2y – 4)
⇒ (2x + y + 2)² = 4(x² + y² + 4x + 2y – 4)
⇒ 4x² + y² + 4 + 4xy + 4y + 4x = 4x² + 4y² + 16x + 8y – 16
⇒ 3y² – 4xy + 8x + 4y – 20 = 0
⇒ y(3y – 4x) + 8x + 4y – 20 = 0
∴ 3y² – 4xy + 8x + 4y – 20 = (y + l) (3y – 4x + m)
Comparing coefficients of x, y, and constants we get
-4l = 8 ………(4)
3l + m = 4 ………(5)
lm = -20 ………(6)
From (4), l = -2 and from (6), m = 10
∴ 3y² – 4xy + 8x + 4y – 20 = (y – 2) (3y – 4x + 10)
Hence the equations of direct common tangents are y – 2 = 0, 3y – 4x + 10 = 0.
∴ The equations of all common tangents to the circles S = 0, S’ = 0 are x – 1 = 0, 3x + 4y – 5 = 0 and y – 2 = 0, 4x – 3y – 10 = 0

Question 3.
Find the pair of tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0.
Solution:
Let S ≡ x² + y² – 6x + 4y – 2 = 0 be the given circle.
The equation of pair of tangents drawn from (3, 2) to the circle S = 0 is \(S_1^2=S . S_{11}\)
⇒ [x(3) + y(2) – 3(x + 3) + 2(y + 2) – 2]² = (x² + y² – 6x + 4y – 2) (3² + 2² – 18 + 8 – 2)
⇒ (4y – 7)² = 1 . (x² + y² – 6x + 4y – 2)
⇒ 16y² – 56y + 49 = x² + y² – 6x + 4y – 2
⇒ x² – 15y² – 6x + 60y – 51 = 0

Question 4.
Find the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 and also find the angle between them.
Solution:
Denote S ≡ x² + y² – 2x + 4y – 11 = 0
The equation of pair of tangents from (1, 3) to the circle S = 0 is by the formula \(S_1^2=S . S_{11}\)
⇒ [x(1) + y(3) – (x + 1) + 2(y + 3) – 11]² = (x² + y² – 2x + 4y – 11) (1² + 3² – 2 + 12 – 11)
⇒ (5y – 6)² = (x² + y² – 2x + 4y – 11) (9)
⇒ 25y² – 60y + 36 = 9x² + 9y² – 18x + 36y – 99
⇒ 9x² – 16y² – 18x + 96y – 135 = 0
If θ is the angle between the above pair of tangents to S = 0, then

(or) θ = \(\cos ^{-1}\left(\frac{7}{25}\right)\) is the angle between pair of tangents to S = 0.

Question 5.
Find the pair of tangents from the origin to the circle x² + y² + 2gx + 2fy + c = 0 and hence deduce a condition for these tangents to the perpendicular.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 be the given circle.
Then the equation of the pair of tangents drawn from (0, 0) to S = 0 is by the formula \(S_1^2=S . S_{11}\)
⇒ [x(0) + y(0) + g(x + 0) + f(y + 0) + c]² = (x² + y² + 2gx + 2fy + c) (c)
⇒ (gx + fy + c)² = cx² + cy² + 2gcx + 2fcy + c²
⇒ (g²x² + f²y² + c² + 2fgxy + 2fcy + 2cgx) = cx² + cy² + 2gcx + 2fcy + c²
⇒ x²(g² – c) + y²(f² – c) + 2fgxy = 0
Given that pair of tangents represented by this equation are perpendicular we have
coefficient of x² + coefficient of y² = 0
⇒ g² – c + f² – c = 0
⇒ g² + f² = 2c

Question 6.
From a point on the circle x² + y² + 2gx + 2fy + c = 0 two tangents are drawn to the circle x² + y² + 2gx + 2fy + c sin²α + (g² + f²) cos²α = 0 (0 < α < π/2). Prove that the angle between them is 2α.
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0 and S’ = x² + y² + 2gx + 2fy + c sin²α + (g² + f²) cos²α = 0 be the given circles.
Let P(x₁, y₁) be any point on S = 0 then

Let θ be the angle between the tangents drawn from P(x₁, y₁) to S’ = 0 then

= \(\frac{\left(g^2+f^2-c\right)\left(\cos ^2 \alpha-\sin ^2 \alpha\right)}{\left(g^2+f^2-c\right)\left(\cos ^2 \alpha+\sin ^2 \alpha\right)}\)
= cos 2α
∴ cos θ = cos 2α ⇒ θ = 2α
∴ The angle between the tangents drawn from P(x1, y1) to the circle S’ = 0 is 2α.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(d)

I.

Question 1.
Find the condition that the tangents are drawn from (0, 0) to S ≡ x² + y² + 2gx + 2fy + c = 0 be perpendicular to each other.
Solution:
If the angle between the tangents drawn from P(x₁, y₁) to S = 0 is θ then

Question 2.
Find the chord of contact of (0, 5) with respect to the circle x² + y² – 5x + 4y – 2 = 0.
Solution:
Comparing with x² + y² + 2gx + 2fy + c = 0,
we get g = \(-\frac{5}{2}\), f = 2, c = -2
∴ Equation of chord of contact of (x1, y1) w.r.t S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
∴ The equation of chord of contact of (0, 5) w.r.t. x² + y² – 5x + 4y – 2 = 0 is x(0) + y(5) + \(\left(\frac{-5}{2}\right)\) (x + 0) + 2(y + 5) – 2 = 0
⇒ 5y – \(\frac{5 x}{2}\) + 2y + 10 – 2 = 0
⇒ 5y – \(\frac{5 x}{2}\) + 2y + 8 = 0
⇒ 10y – 5x + 4y + 16 = 0
⇒ -5x + 14y + 16 = 0
⇒ 5x – 14y – 16 = 0

Question 3.
Find the chord of contact of (1, 1) to the circle x² + y² = 9.
Solution:
Equation of chord of contact of (x₁, y₁) w.r.t x² + y² = a² is xx₁ + yy₁ – a² = 0.
∴ The equation of chord of contact of (1, 1) w.r.t x² + y² = 9 is x(1) + y(1) – 9 = 0
⇒ x + y – 9 = 0

Question 4.
Find the polar of (1, 2) with respect to x² + y² = 7.
Solution:
Equation of polar of (x₁, y₁) with respect to x² + y² = a² is xx₁ + yy₁ – 9 = 0.
∴ The equation of polar of (1, 2) with respect to x² + y² = 7 is x(1) + y(2) – 7 = 0
⇒ x + 2y – 7 = 0

Question 5.
Find the polar of (3, -1) with respect to the circle 2x² + 2y² = 11.
Solution:
Given equation of circle is x² + y² = \(\frac{11}{2}\)
∴ Equation of polar of (x₁, y₁) w.r.t x² + y² = a² is xx₁ + yy₁ – a² = 0.
⇒ x(3) + y(-1) – \(\frac{11}{2}\) = 0
⇒ 6x – 2y – 11 = 0

Question 6.
Find the polar of (1, -2) with respect to x² + y² – 10x – 10y + 25 = 0.
Solution:
Polar of (x₁, y₁) w.r.t x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
⇒ -4x – 7y + 30 = 0
⇒ 4x + 7y – 30 = 0

Question 7.
Find the pole of ax + by + c = 0 (c ≠ 0) w.r.t x² + y² = r²
Solution:
Let (x₁, y₁) be the pole of ax + by + c = 0 ……(1) w.r.t. x² + y² = r²; then the equation of polar is xx₁ + yy₁ – r² = 0 ……….(2)
∴ From (1) and (2)

Question 8.
Find the pole of 3x + 4y – 45 = 0 w.r.t x² + y² – 6x – 8y + 5 = 0
Solution:
Let (x₁, y₁) be the pole of 3x + 4y – 45 = 0 ………(1)
Then the equation of polar of (x₁, y₁) w.r.t the circle x² + y² – 6x – 8y + 5 = 0 is xx₁ + yy₁ – 3(x + x1) – 4(y + y1) + 5 = 0
⇒ x(x₁ – 3) + y(y₁ – 4) – (3x₁ + 4y₁ – 5) = 0 ……….(2)
∴ From (1) and (2)
\(\frac{x_1-3}{3}=\frac{y_1-4}{4}=\frac{-\left(3 x_1+4 y_1-5\right)}{-45}\)
⇒ \(\frac{x_1-3}{3}=\frac{y_1-4}{4}\)
⇒ 4x₁ – 12 = 3y₁ – 12
⇒ 4x₁ – 3y₁ = 0 ……….(3)
\(\frac{y_1-4}{4}=\frac{3 x_1+4 y_1-5}{45}\)
⇒ 45y₁ – 180 = 12x₁ + 16y₁ – 20
⇒ 12x₁ – 29y₁ + 160 = 0 ………(4)
Solving (3) and (4) we get
12x₁ – 9y₁ = 0
12x₁ – 29y₁ = -160
∴ 20y₁ = 160
⇒ y₁ = 8
and from (3)
4x₁ = 24
⇒ x₁ = 6
∴ Pole of 3x + 4y – 45 = 0 w.r.t x² + y² – 6x – 8y + 5 = 0 is (6, 8).

Question 9.
Find the pole of x – 2y + 22 = 0 w.r.t x² + y² – 5x + 8y + 6 = 0.
Solution:
Let (x₁, y₁) be the pole of the line x – 2y + 22 = 0 ………(1)
Then the equation of polar of (x₁, y₁) w.r.t circle x² + y² – 5x + 8y + 6 = 0 ………(2) is

⇒ 22y₁ + 88 = 5x₁ – 8y₁ – 12
⇒ 5x₁ – 30y₁ – 100 = 0
⇒ x₁ – 6y₁ – 20 = 0 ………(5)
∴ 2x₁ – 12y₁ – 40 = 0 and 2x₁ + y₁ – 1 = 0
solving -13y₁ – 39 = 0 ⇒ y₁ = -3
and from (4), 2x₁ – 3 – 1 = 0 ⇒ x₁ = 2
pole of x – 2y + 22 = 0 w.r.t. x² + y² – 5x + 8y + 6 = 0 is (2, -3).

Question 10.
Show that the points (-6, 1) and (2, 3) are conjugate points w.r.t the circle x² + y² – 2x + 2y + 1 = 0.
Solution:
Let P(-6, 1) and Q(2, 3) be the given points.
Two points P(x₁, y₁) and Q(x₂, y₂) one said to be conjugate
⇔ S₁₂ = 0
⇔ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
∴ S₁₂ = (-6)(2) + (1)(3) – 1(-6 + 2) + 1(1 + 3) + 1
= -12 + 3 + 4 + 4 + 1
= 0
∴ Hence the points P and Q are conjugate w.r.t. the given circle.

Question 11.
Show that the points (4, 2) and (3, -5) are conjugate points w.r.t the circle x² + y² – 3x – 5y + 1 = 0.
Solution:
Let P(x₁, y₁) = (4, 2) and Q(x₂, y₂) = (3, -5)
Now S₁₂ = x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
= (4)(3) + (2)(-5) – \(\frac{3}{2}\)(4 + 3) – \(\frac{5}{2}\)(2 – 5) + 1
= 12 – 10 – \(\frac{21}{2}+\frac{15}{2}\) + 1 = 0
= 24 – 20 – 21 + 15 + 2
= 0
Hence the points P and Q are conjugate w.r.t. the given circle.

Question 12.
Find the value of k if kx + 3y – 1 = 0, 2x + y + 5 = 0 are conjugate lines w.r.t the x² + y² – 2x – 4y – 4 = 0.
Solution:
Two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 are said to be conjugate w.r.t. x² + y² + 2gx + 2fy + c = 0.
If r²(l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
Here g = -1, f = -2,
r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{1+4+4}\) = 3
l₁ = k, m₁ = 3, n₁ = -1, l₂ = 2, m₂2 = 1, n₂ = 5
∴ r²(l₁l₂ + m₁m₂) = 9(2k + 3)
and (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = (-k – 6 + 1) (-2 – 2 – 5) = (-k – 5) (-9)
∴ 9(2k + 3) = 9(k + 5)
⇒ 2k + 3 = k + 5
⇒ k – 2 = 0
⇒ k = 2

Question 13.
Find the value of k if x + y – 5 = 0, 2x + ky – 8 = 0 are conjugate w.r.t the circle x² + y² – 2x – 2y – 1 = 0.
Solution:
Comparing the given equation of circle with x² + y² + 2gx + 2fy + c = 0,
we have g = -1, f = -1, c = -1 and
radius = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{1+1+1}=\sqrt{3}\)
Condition for two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 to be conjugate w.r.t. S = 0
r² (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
Given that the equations of lines are x + y – 5 = 0 and 2x + ky – 8 = 0
l₁ = 1, m₁ = 1, n₁ = -5, l₂ = 2, m₂ = k, n₂ = -8
∴ r²(l₁l₂ + m₁m₂) = 3(2 + k) and (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = (-1 – 1 + 5) (-2 – k + 8)
∴ 3(2 + k) = 3(6 – k) = 18 – 3k
⇒ 6 + 3k = 18 – 3k
⇒ 6k = 12
⇒ k = 2

Question 14.
Find the value of k if the points (1, 3) and (2, k) are conjugate w.r.t the circle x² + y² = 35.
Solution:
The condition for two points P(x₁, y₁) and Q(x₂, y₂) to be conjugate w.r.t x² + y² = a² is x₁x₂ + y₁y₂ – a² = 0
Given P(x₁, y₁) = (1, 3) and Q(x₂, y₂) = (2, k) and a² = 35.
∴ x₁x₂ + y₁y₂ – a² = 2 + 3k – 35
⇒ 3k – 33 = 0
⇒ k = 11

Question 15.
Find the value of k if the points (4, 2), (k, -3) are conjugate points w.r.t the circle x² + y² – 5x + 8y + 6 = 0.
Solution:
Two points P(x₁, y₁) and Q(x₂, y₂) are said to be conjugate w.r.t the circle S = 0 if S₁₂ = 0.
i.e., x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
Given P(x₁, y₁) = (4, 2) and Q(x₂, y₂) = (k, -3)
Then S₁₂ = 4k – 6 – \(\frac{5}{2}\)(4 + k) + 4(2 – 3) + 6 = 0
⇒ 4k – 6 – \(\frac{5}{2}\)(4 + k) – 4 + 6 = 0
⇒ 4k – \(\frac{5}{2}\)(4 + k) – 4 = 0
⇒ 4k – 10 – \(\frac{5k}{2}\) – 4 = 0
⇒ 8k – 20 – 5k – 8 = 0
⇒ 3k – 28 = 0
⇒ k = \(\frac{28}{3}\)

II.

Question 1.
Find the angle between the tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0. (Mar. ’12)
Solution:
If θ is the acute angle between the tangents drawn from P(3, 2) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\) where r is the radius of the circle.
Where S₁₁ = \(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c
= 9 + 4 – 6(3) + 4(2) – 2
= 1
and r = radius of the given circle = \(\sqrt{9+4+2}=\sqrt{15}\)
∴ cos θ = \(\left|\frac{1-15}{1+15}\right|=\left|\frac{-14}{16}\right|=\frac{7}{8}\)
∴ θ = \({Cos}^{-1} \cdot\left(\frac{7}{8}\right)\)
∴ The angle between tangents drawn from (3, 2) to the given circle is \({Cos}^{-1} \cdot\left(\frac{7}{8}\right)\).

Question 2.
Find the angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0.
Solution:
If θ is the acute angle between the tangents drawn from P(3, 2) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\) where r is the radius of the circle.
S₁₁ = \(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c
= 1 + 9 – 2 + 12 – 11
= 9
and r = radius of the given circle (r) = \(\sqrt{1+4+11}\) = 4
∴ cos θ = \(\left|\frac{9-16}{9+16}\right|=\left|\frac{7}{25}\right|\)
∴ θ = \({Cos}^{-1}\left(\frac{7}{25}\right)\)
∴ The angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 is \({Cos}^{-1}\left(\frac{7}{25}\right)\)

Question 3.
Find the angle between the pair of tangents drawn from (0, 0) to the circle x² + y² – 14x + 2y + 25 = 0.
Solution:
If θ is the angle between the tangents drawn from O(0, 0) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\)
where S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2\) + 2gx₁ + 2fy₁ + c
= 0 + 0 + 0 + 0 + 25
= 25
and r = \(\sqrt{49+1-25}\) = 5
∴ cos θ = \(\left|\frac{25-25}{25+5}\right|\) = 0
∴ θ = \(\frac{\pi}{2}\)
∴ The angle between the pair of tangents drawn from (0, 0) to the given circle is \(\frac{\pi}{2}\).

Question 4.
Find the locus of P if the tangents drawn from P to x² + y² = a² include an angle α.
Solution:
The centre of the circle x² + y² = a² is C = (0, 0) and radius = a

Question 5.
Find the locus of P if the tangents drawn from P to x² + y² = a² are perpendicular to each other.
Solution:
Equation of the given circle is x² + y² = a² and radius = a
Let P(x₁, y₁) be any point on the locus.
Since the tangents drawn from P(x₁, y₁) to the circle are perpendicular to each other,
the angle between tangents is \(\frac{\pi}{2}\)

Question 6.
Find the slope of the polar of (1, 3) with respect to the circle x² + y² – 4x – 4y – 4 = 0. Also, find the distance from the centre to it.
Solution:
Equation of polar of the point P(x₁, y₁) w.r.t circle S ≡ x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
∴ Polar of (1, 3) w.r.t. circle x² + y² – 4x – 4y – 4 = 0 is x(1) + y(3) – 2(x + 1) – 2(y + 3) – 4 = 0
⇒ -x + y – 12 = 0
⇒ x – y + 12 = 0
∴ The slope of the polar is ‘1’
Also, the distance from the centre (2, 2) to the polar of (1, 3) i.e., x – y + 12 = 0 is \(\left|\frac{2-2+12}{\sqrt{1+1}}\right|=\frac{12}{\sqrt{2}}=6 \sqrt{2}\)

Question 7.
If ax + by + c = 0 is a polar of (1, 1) w.r.t the circle x² + y² – 2x + 2y + 1 = 0 and H.C.F of a, b, c is equal to one then find a² + b² + c².
Solution:
Equation of polar of (1, 1) w.r.t the circle x² + y² – 2x + 2y + 1 = 0 is x(1) + y(1) – 1(x + 1) + 1(y + 1) + 1 = 0
⇒ 2y + 1 = 0 ……….(1)
Given that polar of P(1, 1) is ax + by + c = 0 ………(2)
since (1) and (2) represent the same line
\(\frac{\mathrm{a}}{0}=\frac{\mathrm{b}}{2}=\frac{\mathrm{c}}{1}=\mathrm{k}\)
⇒ a = 0, b = 2k, c = k
Given that H.C.F of a, b, c is ‘1’ we have k = 1
∴ a = 0, b = 2, c = 1
∴ a² + b² + c² = 0 + 4 + 1 = 5

III.

Question 1.
Find the coordinates of the point of intersection of tangents at the points where x + 4y – 14 = 0 meets the circle x² + y² – 2x + 3y – 5 = 0.
Solution:

Let P(x₁, y₁) be the point of intersection of tangents drawn to the circle x² + y² – 2x + 3y – 5 = 0 …………(1) and given that x + 4y – 14 = 0 ………..(2) meets the circle at points A, B.
∴ Equation of chord of contact of (x₁, y₁) w.r.t circle (1) is xx₁ + yy₁ – (x + x₁) + \(\frac{3}{2}\)(y + y₁) – 5 = 0
⇒ \(x\left(x_1-1\right)+y\left(y_1+\frac{3}{2}\right)-\left(x_1-\frac{3}{2} y_1+5\right)=0\) …….(3)
Since (2) and (3) represent the same chord of contact

Question 2.
If the polar of the points on the circle x² + y² = a² w.r.t the circle x² + y² = b2 touches the circle x² + y² = c² then prove that a, b, c are in geometrical progression.
Solution:
Given equations of circles
x² + y² = a² …….(1)
x² + y² = b² …….(2)
x² + y² = c² ……(3)
Let P(x₁, y₁) be any point on (1) then
\(x_1^2+y_1^2\) = a² ………(4)
The equation of polar of P(x₁, y₁) w.r.t circle (2) is xx₁ + yy₁ – b² = 0 ……..(5)
The Centre of (3) is (0, 0), and the radius = c.
Given that line (5) is polar of P w.r.t the circle (2) which touches the circle (3).
∴ The perpendicular distance from C(0, 0) of circle (3) to the line (5) = radius of circle (3)
∴ \(\frac{1-b^2 \text { । }}{\sqrt{x_1^2+y_1^2}}\) = c
⇒ \(\frac{\mathrm{b}^2}{\sqrt{\mathrm{a}^2}}\) = c
⇒ b² = ac
⇒ a, b, c are in geometric progression.

Question 3.
Tangents are drawn to the circle x² + y² = 16 from the point P(3, 5). Find the area of the triangle formed by these tangents and the chord of contact of P.
Solution:

The given equation of a circle is x² + y² = 16
Centre C = (0, 0) and radius = 4
The equation of chord of contact of (3, 5) w.r.t. circle x² + y² = 16 is xx₁ + yy₁ – 16 = 0
⇒ 3x + 5y – 16 = 0
PL is the perpendicular distance from the point P(3, 5) to the chord AB.


∴ Area of the triangle formed by the tangents and the chord of P = \(\frac{108 \sqrt{2}}{17}\) square units.

Question 4.
Find the locus of the point whose polar with respect to the circles x² + y² – 4x – 4y – 8 = 0 and x² + y² – 2x + 6y – 2 = 0 are mutually perpendicular.
Solution:
Let P(x₁, y₁) be the locus of the point whose polars w.r.t the given circles x² + y² – 4x – 4y – 8 = 0 ……(1) and x² + y² – 2x + 6y – 2 = 0 ……(2) are mutually perpendicular.
Polar of P(x₁, y₁) w.r.t circle (2) is xx₁ + yy₁ – (x + x₁) + 3(y + y₁) – 2 = 0
⇒ x(x₁ – 1) + y(y₁ – 3) – (x₁ – 3y₁ + 2) = 0 ………(3)
Polar of P(x₁, y₁) w.r.t circle (1) is xx₁ + yy₁ – 2(x + x₁) – 2(y + y₁) – 8 = 0
⇒ x(x₁ – 2) + y(y₁ – 2) – (2x₁ + 2y₁ + 8) = 0 ………(4)
Slope of (3) is \(-\left(\frac{x_1-1}{y_1+3}\right)\)
and slope of (4) is \(\left(\frac{x_1-2}{y_1-2}\right)\)
If (3) and (4) are mutually perpendicular then
\(\left(\frac{x_1-1}{y_1+3}\right)\left(\frac{x_1-2}{y_1-2}\right)\) = -1
⇒ \(\left(x_1^2-3 x_1+2\right)=-\left(y_1^2+y_1-6\right)\)
⇒ \(x_1^2+y_1^2-3 x_1+y_1-4=0\)
∴ Locus of P(x₁, y₁) is x² + y² – 3x + y – 4 = 0.

Question 5.
Find the locus of the foot of the perpendicular drawn from the origin to any chord of the circle S ≡ x² + y² + 2gx + 2fy + c = 0 which subtends a right angle at the origin.
Solution:

Any chord of the circle may be taken as lx + my = 1 ………(1)
Given equation of circle is x² + y² + 2gx + 2fy + c = 0 ………(2)
Chord (1) subtends a right angle at the origin.
Hence the lines joining the origin to the points of intersection of (1) and (2) are obtained by homogenizing equation (2) with equation (1).
From (1), lx + my = 1
and from (2), x² + y² + (2gx + 2fy)(1) + c(1)² = 0
⇒ x² + y² + (2gx + 2fy) (lx + my) + c(lx + my)² = 0
⇒ x² + y² + (2glx² + 2fy²m + 2flm + 2gmxy) + c(l²x² + 2lmxy + m²y²) = 0
⇒ (1 + 2gl + cl²) x² + (1 + 2fm + cm²)y² + xy(2fl + 2gm + 2lmc) = 0
This is a homogenizing second-degree equation that represents pair of lines OA and OB passing through the origin. If these lines are perpendicular then
the coefficient of x² + coefficient of y² = 0.
⇒ 1 + 2gl + 1 + cl² + 2fm + cm² = 0
⇒ c(l² + m²) + 2(gl + fm) + 2 = 0 ……….(3)
From (1), the equation of the line perpendicular to the chord is mx – ly = 0 ………..(4)
Solving lx + my = 1 …..(1) and mx – ly = 0 ………(4)

To find the locus of the foot of the perpendiculars we have to eliminate ‘l’ and ‘m’.
Substituting these values of l and m in (3), we get

⇒ c + 2(gx + fy) + 2(x2 + y2) = 0
⇒ 2(x² + y²) + 2(gx + fy) + c = 0
∴ Locus of the foot of the perpendiculars drawn from the origin to any chord of circle S ≡ x² + y² + 2gx + 2fy + c = 0 which subtends a right angle at the origin is 2(x² + y²) + 2(gx + fy) + c = 0.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Exercise 2(a)

I.

Question 1.
Find k if the following pairs of circles are orthogonal.
(i) x² + y² + 2by – k = 0, x² + y² + 2ax + 8 = 0.
Solution:
The given equations of circles are x² + y² + 2by – k = 0 ……….(1) and x² + y² + 2ax + 8 = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 0, f = b, c = -k, g’ = a, f’ = 0, c’ = 8
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 0 + 0 = 8 – k
⇒ k = 8

(ii) x² + y² – 6x – 8y + 12 = 0, x² + y² – 4x + 6y + k = 0
Solution:
The given equations of circles are x² + y² – 6x – 8y + 12 = 0 …….(1) and x² + y² – 4x + 6y + k = 0 ……….(2)
Comparing with S = 0 and S’ = 0
We get g = -3, f = -4, c = 12 and g’ = -2, f’ = 3, c’ = k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 2(6 – 12) = 12 + k
⇒ -12 = 12 + k
⇒ k = -24

(iii) x² + y² – 5x – 14y – 34 = 0, x² + y² + 2x + 4y + k = 0
Solution:
The given equations of circles are x² + y² – 5x – 14y – 34 = 0 ……..(1) and x² + y² + 2x + 4y + k = 0 ……….(2)
Comparing with S = 0 and S’ = 0
We get g = \(\frac{-5}{2}\), f = -7, c = -34 and g’ = 1, f = 3, c’ = k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 2[\(\frac{-5}{2}\)(1) + (-7)(2)] = k – 34
⇒ -5 – 28 = k – 34
⇒ k = 1

(iv) x² + y² + 4x + 8 = 0, x² + y² – 16y + k = 0
Solution:
The given equations of circles are x² + y² + 4x + 8 = 0 ………(1) and x² + y² – 16y + k = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 2, f = 0, c = + 8 and g’ = 0, f’ = -8, c’ = +k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 0 = 8 + k
⇒ k = -8

Question 2.
Find the angle between the circles given by the equations
(i) x² + y² – 12x – 6y + 41 = 0, x² + y² + 4x + 6y – 59 = 0
Solution:
The given equations of circles are
x² + y² – 12x – 6y + 41 = 0 ………(i)
and x² + y² + 4x + 6y – 59 = 0 ……..(ii)
Comparing with S = 0 and S’ = 0 We get
g = -6, f = -3, c = 41
g’ = 2, f’ = 3, c’ = -59
Also, centres of circles (1) and (2) are C₁ = (6, 3) and C₂ = (-2, -3)

(ii) x² + y² + 6x – 10y – 135 = 0, x² + y² – 4x + 14y – 116 = 0
Solution:
The given equations of circles are
x² + y² + 6x – 10y – 135 = 0 ………(1)
and x² + y² – 4x + 14y – 116 = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 3, f = -5, c = -135 and g’ = -2, f’ = 7, c’ = -116
Also, centres of circles (1) and (2) are C₁ = (-3, 5) and C₂ = (2, -7)

Question 3.
Show that the angle between the circles x² + y² = a², x² + y² = ax + ay is \(\frac{3 \pi}{4}\).
Solution:
Let S = x² + y² – a² = 0 and S’ = x² + y² – ax + ay = 0 be the given of circles.
C₁ = (0, 0) and C₂ = \(\left(\frac{\mathrm{a}}{2}, \frac{\mathrm{a}}{2}\right)\) are the centres of circles.

Question 4.
Show that the circles given by the following equations intersect each other orthogonally.
(i) x² + y² – 2x – 2y – 7 = 0, 3x² + 3y² – 8x + 29y = 0
Solution:
Equations of given circles are
x² + y² – 2x – 2y – 7 = 0 ………(1)
and \(x^2+y^2-\frac{8}{3} x+\frac{29}{3} y=0\) ……….(2)

c + c’ = -7 + 0 = 7
∴ 2(gg’ + ff’) = c + c’, hence circles (1) and (2) intersect orthogonally.

(ii) x² + y² + 4x – 2y – 11 = 0, x² + y² – 4x – 8y + 11 = 0
Solution:
Equations of given circles are
x² + y² + 4x – 2y – 11 = 0 ………(1)
and x² + y² – 4x – 8y + 11 = 0 ………(2)
g = 2, f = -1, c = -11 and g’ = -2, f’ = -4, c = 11
∴ 2(gg’ + ff’) = 2(-4 + 4) = 0 and c + c’ = -11 + 11 = 0
Since 2(gg’ + ff’) = c + c’, the two circles intersect orthogonally.

(iii) x² + y² – 2x + 4y + 4 = 0, x² + y² + 3x + 4y + 1 = 0
Solution:
Equations of given circles are
x² + y² – 2x + 4y + 4 = 0 ………(1)
and x² + y² + 3x + 4y + 1 = 0 ……….(2)
Centres of circles are C₁ = (1, -2) and C₂ = (\(\frac{-3}{2}\), -2)
Also g = -1, f = 2, c = 4
g’ = \(\frac{3}{2}\), f’ = 2, c’ = 1
∴ 2(gg’ + ff’) = 2(\(\frac{-3}{2}\) + 4) = 5
c + c’ = 4 + 1 = 5
Since 2(gg’ + ff’) = c + c’, we have the two circles intersect orthogonally with each other.

(iv) x² + y² – 2lx + g = 0, x² + y² + 2my – g = 0
Solution:
Equations of given circles are
x² + y² – 2lx + g = 0 ……..(1)
and x² + y² + 2my – g = 0 ……….(2)
g = -l, f = 0, c = g and g’ = -0, f’ = m, c’ = -g
∴ 2(gg’ + ff’) = 2[(0) + (0)] = 0
c + c’ = g – g = 0
Since 2(gg’ + ff’) = c + c’, the two circles intersect each other orthogonally.

II.

Question 1.
Find the equation of the circle which passes through the origin and intersects the circle given below orthogonally.
(i) x² + y² – 4x – 6y + 10 = 0, x² + y² + 12y + 6 = 0.
Solution:
Equations of given circles are
x² + y² – 4x – 6y + 10 = 0 ……..(1)
and x² + y² + 12y + 6 = 0 ………(2)
Let the equation of the circle passing through the origin be
x² + y² + 2gx + 2fy = 0 ………(3)
If (1) intersects (3) orthogonally then
2(-2) (g) + 2(3)(f) = 10
⇒ -4g + 6f = 10
⇒ 2g – 3f = -5 ……….(4)
If (2) intersects (3) orthogonally then
2g(0) + 2f(6) = 6
⇒ 12f = 6
⇒ f = \(\frac{1}{2}\) …….(5)
∴ From (4),

(ii) x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0
Solution:
Equations of given circles are
x² + y² – 4x – 6y – 3 = 0 ……..(1)
and x² + y² – 8y + 12 = 0 ……(2)
Let the equation of the required circle passing through the origin be
x² + y² + 2gx + 2fy = 0 ……..(3)
If (1) and (3) are orthogonal then
2g(-2) – 2f (- 3) = -3
⇒ 4g + 6f = 3
If (2) and (3) are orthogonal then
2g(0) + 2f(- 4) = 12
⇒ -8f = 12
⇒ f = \(\frac{-12}{8}=\frac{-3}{2}\) ………(5)
∴ From (4),
4g + 6(\(\frac{-3}{2}\)) = -3
⇒ 4g – 9 = -3
⇒ 4g = 6
⇒ g = \(\frac{3}{2}\) …….(6)
∴ From (3), the Equation of the required circle is x² + y² + 6x – 3y = 0.

Question 2.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally.
Solution:
Equations of given circles are
x² + y² – 6x + 3y + 5 = 0 ……..(1)
and x² + y² – x – 7y = 0 …….(2)
Let S ≡ x² + y² + 2gx + 2fy + c = 0 ………(3) be the required circle.
Let S’ = 0 …….(1) and S” = 0 ……..(2) be the given circles.
Given that (3) passes through (0, -3) we have
0 + 9 – 6f + c = 0
⇒ 9 – 6f + c = 0 ……(4)
If (1) and (3) are orthogonal then
2g(-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f = c + 5 ……..(5)
If (2) and (3) are orthogonal then
\(2 g\left(-\frac{1}{2}\right)+2 f\left(-\frac{7}{2}\right)=c\)
⇒ -g – 7f = c
⇒ g + 7f + c = 0
From (5)
6g – 3f + c = -5
⇒ -5g + 10f = 5
⇒ g – 2f = -1 ………(7)
Also from (4), 9 – 6f + c = 0
and from (5), 6g – 3f + c = -5
∴ -6g – 3f + 9 = 5
⇒ -6g – 3f + 4 = 0
⇒ 6g + 3f – 4 = 0
From (7) and (8),
6g – 12f = -6
⇒ 15f – 10 = 0
⇒ f = \(\frac{10}{15}\)

Question 3.
Find the equation of the circle passing through the origin and having its center on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let the equation of the circle passing through the origin be x² + y² + 2gx + 2fy = 0 ……..(1)
Given that the centre (-g, -f) lies on the line x + y = 4
⇒ -g – f = 4
⇒ g + f = -4 ……….(2)
If (1) intersects x² + y² – 4x + 2y + 4 = 0 orthogonally then
2g (-2) + 2f(1) = 4
⇒ -2g + f = 2
⇒ 2g – f = -2 ………(3)
From (2) and (3)
3g = -6
⇒ g = -2
2(-2) – f = -2
⇒ -f = 2
⇒ f = -2
∴ The equation of the required circle from (1) is x² + y² – 4x – 4y = 0.

Question 4.
Find the equation of the circle which passes through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ……..(1)
If this passes through the points (2, 0) and (0, 2) then
4 + 4g + c = 0 ………(2)
and 4 + 4f + c = 0 ………(3)
From (2) and (3),
g = f …….(4)
Also (1) intersects the given circle x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 orthogonally then
\(2 g\left(\frac{5}{4}\right)+2 f\left(\frac{-3}{2}\right)\) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = c + 2
⇒ 5g – 6f = 2c + 4
Since g = f, we have
5f – 6f = 2c + 4
⇒ -f = 2c + 4
⇒ f + 2c + 4 = 0
From (3)
4f + c + 4 = 0
-3f + c = 0
⇒ c = 3f
From (5)
f + 6f + 4 = 0
⇒ 7f + 4 = 0
⇒ f = \(\frac{-4}{7}\)
and c = 3f = \(\frac{-12}{7}\), Also g = \(\frac{-4}{7}\)
∴ The equation of the required circle from (1) is \(x^2+y^2-\frac{8}{7} x-\frac{8}{7} y-\frac{12}{7}=0\)
⇒ 7(x² + y²) – 8x – 8y – 12 = 0.

Question 5.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having centre at (2, 3).
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ………(1)
Since the centre is given to be (2, 3) we have
-g = 2 and -f = 3
⇒ g = -2 and f = -3
Since (1) cuts x² + y² – 4x + 2y – 7 = 0 orthogonally we have
2g(-2) + 2f(1) = c – 7
⇒ -4(-2) – 6 = c – 7
⇒ 2 = c – 7
⇒ c = 9
∴ The equation of the required circle from (1) is x² + y² – 4x – 6y + 9 = 0.

III.

Question 1.
Find the equation of the circle which intersects the circle x² + y² – 6x + 4y – 3 = 0 orthogonally and passes through the point (3, 0) and touches Y-axis.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since this passes through point (3, 0) we have
9 + 6g + c = 0 ……..(2)
If (1) touches Y-axis then \(\sqrt{\mathfrak{f}^2-c}\) = 0
⇒ c = f² ……..(3)
If (1) intersects x² + y² – 6x + 4y – 3 = 0 orthogonally then
2g(-3) + 2f(2) = c – 3
⇒ -6g + 4f = c – 3 ………(3)
Also from (2), 6g = -c – 9
Solving, 4f = -12
⇒ f = -3
From (3)
c = f²
⇒ c = 9
From (2)
9 + 6g + 9 = 0
⇒ g = -3
∴ The equation of the required circle from (1) is x² + y² – 6x – 6y + 9 = 0.

Question 2.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 = 0 and x² + y² – 10x – 4y + 21 = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7.
Solution:
Equations are given circles are
x² + y² – 4x – 6y + 11 = 0 ……..(1)
and x² + y² – 10x – 4y + 21 = 0 ………(2)
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……..(3)
If this cuts (1) and (2) orthogonally then
2g(-2) + 2f(-3) = c + 11
⇒ 4g + 6g = – c – 11 …….(3)
and if (1) and (3) are orthogonal then
2g(-5) + 2f(-2) = c + 21
⇒ -10g – 4f = c + 21
⇒ 10g + 4f = -c – 21 ………..(4)
From (3) and (4)
-6g + 2f = 10
⇒ 6g – 2f = -10
⇒ 3g – f = -5 ………(5)
Since the centre of circle (1) (-g, -f) lies on the diameter 2x + 3y = 7, we have
2(-g) + 3(-f) = 7
⇒ 2g + 3f = -7 ……..(6)
Solving (5) and (6)

∴ From (3)
(-8) – 6 = -c – 11
⇒ -14 = -c – 11
⇒ c = 3
∴ The equation of a required circle is x² + y² – 4x – 2y + 3 = 0.

Question 3.
If P, Q are conjugate points w.r.t. a circle S ≡ x² + y² + 2gx + 2fy + c = 0 then prove that the circle on PQ as diameter cuts the circle S = 0 orthogonally.
Solution:
Given S ≡ x² + y² + 2gx + 2fy + c = 0 ………(1)
Let P(x₁, y₁) and Q(x₂, y₂) be the given points.
The polar of P(x₁, y₁) w.r.t. a circle S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0.
Since P, Q are conjugate points w.r.t. S = 0
⇒ x₁x₂ + y₁y₂ + g(x₂ + x₁) + f(y₂ + y₁) + c = 0
∴ -g(x₁ + x₂) – f(y₁ + y₂) = x₁x₂ + y₁y₂ + c ……(2)
The equation of the circle having \(\overline{\mathrm{PQ}}\) as diameter is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ x² – x(x₁ + x₂) + y² – y(y₁ + y₂) + (x₁x₂ + y₁y₂) = 0 …….(3)
Using conditions between (1) and (3) orthogonally
2gg’ + 2ff’ = \(2 \mathrm{~g}\left[\left(\frac{-\mathrm{x}_1+\mathrm{x}_2}{2}\right)\right]+2 \mathrm{f}\left[\left(\frac{-\mathrm{y}_1+\mathrm{y}_2}{2}\right)\right]\)
= -g(x₁ + x₂) – f(y₁ + y₂)
= x₁x₂ + y₁y₂ + c [∵ From (2)]
= c’ + c When c’ = x₁x₂ + y₁y₂ from (3)
∴ The circle (3) cuts the circle S = 0 orthogonally.

Question 4.
If the equation of two circles whose radii are a, a’ are S = 0 and S’ = 0, then show that the circles \(\frac{\mathbf{S}}{\mathbf{a}}+\frac{\mathbf{S}^{\prime}}{\mathbf{a}^{\prime}}=0\) and \(\frac{S}{a}-\frac{S^{\prime}}{a^{\prime}}=0\) intersect orthogonally.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 and S’ ≡ x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.

Question 5.
Find the equation of the circle which intersects each of the following circles orthogonally.
(i) x² + y² + 2x + 4y + 1 = 0, x² + y² – 2x + 6y – 3 = 0, 2(x² + y²) + 6x + 8y – 3 = 0 (May ’12)
Solution:
Let the circle x² + y² + 2gx + 2fy + c = 0 …….(1) cuts each of the circles
x² + y² + 2x + 4y + 1 = 0 …….(2)
x² + y² – 2x + 6y – 3 = 0 ………(3)
and x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0 ………(4) orthogonally.
Then (1) and (2) are orthogonal.
⇒ 2g(1) + 2f(2) = c + 1 …….(4)
(1) and (3) are orthogonal
⇒ 2g(-1) + 2f(3) = c – 3 ……..(5)
(1) and (4) are orthogonal
⇒ 2g(\(\frac{3}{2}\)) + 2f(2) = c – \(\frac{3}{2}\) …….(6)
From (4) and (5),
2g + 4f = c + 1 and -2g + 6f = c – 3
4g – 2f = 4
⇒ 2g – f = 2 ………(7)
From (5) and (6)
-2g + 6f = c – 3
and 3g + 4f = c – \(\frac{3}{2}\)
⇒ -5g + 2f = \(-\frac{3}{2}\) …….(8)
From (7),
2g – f = 2 and -10g + 4f = -3 from (8)
Solving

From (4),
2g + 4f = c + 1
⇒ -5 – 28 = c + 1
⇒ c = -34
∴ The equation of required circle (1) cutting each of the circles (2), (3), and (4) is x² + y² – 5x – 14y – 34 = 0.

(ii) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0
Solution:
Equations of given circles are
x² + y² + 4x + 2y + 1 = 0 ………(1)
x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ……..(2)
and x² + y² + 6x – 2y – 3 = 0 ………(3)
Let the equation of the circle that cuts (1), (2), and (3) orthogonally be
x² + y² + 2gx + 2fy + c = 0 ……..(4)
Since (1) and (4) are orthogonal
2g(2) + 2f(1) = c + 1 ……(4)
⇒ 4g + 2f = c + 1 ………(5)
Since (2) and (4) are orthogonal
and from (2), x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0
2g(2) + 2f(\(\frac{3}{2}\)) = c – \(\frac{3}{2}\)
⇒ 4g + 3f = c – \(\frac{3}{2}\) …….(6)
Since (3) and (4) are orthogonal
2g(3) + 2f(-1) = c – 3 ………(6)
⇒ 6g – 2f = c – 3 …….(7)
From (5) and (6),
-f = \(\frac{5}{2}\)
⇒ f = \(\frac{-5}{2}\)
From (6) and (7),
-2g + 5f = \(\frac{3}{2}\)
⇒ 2g – \(\frac{25}{2}\) = \(\frac{3}{2}\)
⇒ -2g = 14
⇒ g = -7
∴ From (5),
4g + 2f = c + 1
⇒ -28 – 5 = c + 1
⇒ c = -34
∴ The equation of the required circle from (4) which cuts (1), (2), and (3) orthogonally is given by x² + y² – 14x – 5y – 34 = 0.

Question 6.
If the straight line 2x + 3y = 1 intersects the circle x² + y² = 4 at points A and B, then find the equation of the circle having AB as diameter.
Solution:
Given that the line 2x + 3y – 1 = 0 intersects the circle x² + y² – 4 = 0 at points A and B then
the equation of the circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0
⇒ x² + y² – 4 + λ(2x + 3y – 1) = 0
⇒ x² + y² + 2λx + 3λy – (4 + λ) = 0 ………(1)
Centre of the circle C’ = \(\left(-\lambda-\frac{3 \lambda}{2}\right)\)
Given that the circle x² + y² – 4 = 0 has the line 2x + 3y – 1 = 0 as the diameter, the centre C’ lies on line 2x + 3y = 1.
∴ 2(-λ) + 3\(\left(-\frac{3}{2} \lambda\right)\) – 1 = 0
⇒ -4λ – 9λ – 2 = 0
⇒ λ = \(\frac{-2}{13}\)
∴ From (1), Equation of required circle is x² + y² – 4 – \(\frac{2}{13}\)(2x + 3y – 1) = 0
⇒ 13(x² + y²) – 52 – 4x – 6y + 2 = 0
⇒ 13(x² + y²) – 4x – 6y – 50 = 0

Question 7.
If x + y = 3 is the equation of chord AB of the circle x² + y² – 2x + 4y – 8 = 0, find the equation of the circle having AB as diameter.
Solution:
Let S ≡ x² + y² – 2x + 4y – 8 = 0 be the circle.
Let L ≡ x + y – 3 = 0 be the given line.
Given that L = 0 intersects the circle S = 0 at A, B.
The equation of the circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0 where λ is a constant.
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0
⇒ x² + y² + (λ – 2)x + y(λ + 4) – (8 + 3λ) = 0 …….(1)
Centre of the circle = \(\left[-\left(\frac{\lambda-2}{2}\right),-\left(\frac{\lambda+4}{2}\right)\right]\)
Given that the line L = 0 is the diameter of the circle (1).
Centre \(\left(\frac{2-\lambda}{2},-\frac{\lambda-4}{2}\right)\) lies on the line x + y – 3 = 0.
∴ \(\frac{2-\lambda}{2}+\left[-\left(\frac{\lambda+4}{2}\right)\right]-3=0\)
⇒ -λ + 2 – λ – 4 – 6 = 0
⇒ – 2λ – 8 = 0
⇒ 2λ = -8
⇒ λ = -4
∴ The equation of the required circle from (1) is x² + y² + (-4 – 2)x + (-4 + 4)y – 8 – 3(-4) = 0
⇒ x² + y² – 6x + 4 = 0

Question 8.
Find the equation of the circle passing through the intersection of the circles x² + y² = 2ax and x² + y² = 2by and having its centre on the line \(\frac{x}{a}-\frac{y}{b}=2\).
Solution:
Let S = x² + y² – 2ax = 0 and S’ = x² + y² – 2by be the given circles.
Given line is \(\frac{x}{a}-\frac{y}{b}=2\)
⇒ bx – ay = 2ab
⇒ bx – ay – 2ab = 0 …….(1)
The equation of the radical axis of circles S = 0 and S’ = 0 is S – S’ = 0.
⇒ x² + y² – 2ax – (x² + y² – 2by) = 0
⇒ ax – by = 0
Let L = ax – by = 0 ……….(2)
The equation of the circle passing through the points of intersection of S = 0 and L = 0 is S + λL = 0.
⇒ x² + y² – 2ax + λ(ax – by) = 0 — (3)
⇒ x² + y² + x(λa – 2a) – λby = 0
Centre of the circle (3) is \(\left(\frac{2 a-\lambda a}{2}, \frac{\lambda b}{2}\right)\)
Given that centre lies on (1)
∴ \(\mathrm{b}\left(\frac{2 \mathrm{a}-\lambda \mathrm{a}}{2}\right)-\mathrm{a} \frac{\lambda \mathrm{b}}{2}-2 \mathrm{ab}=0\)
⇒ 2ab – abλ – abλ – 4ab = 0
⇒ -2abλ – 2ab = 0
⇒ λ = -1
∴ From (3), the equation of the required circle is x² + y² – 3ax + by = 0.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(c)

I.

Question 1.
Find the equation of the tangent at P of the circle S = 0 where P and S are given by
(i) P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Solution:
P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Comparing the equation x² + y² – 6x + 4y – 12 =0 with the general equation we have
2g = -6, 2f = 4 and c = -12
g = -3, f = 2, c = -12
∴Equation of tangent at P(x₁, y₁) to the circle S = 0 is given by xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(7) + y(-5) – 3(x + 7) + 2(y – 5) – 12 = 0
⇒ 4x – 3y – 43 = 0

(ii) P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Solution:
P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Comparing the equation x² + y² – 6x + 4y – 12 = 0 with the general equation S = 0, we get
2g = -6, 2f = 4 and c = -12
g = -3, f = 2, c = -12
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-1) + y(1) – 3(x – 1) + 2(y + 1) – 12 = 0
⇒ -4x + 3y – 7 = 0
⇒ 4x – 3y + 7 = 0

(iii) P = (-6, -9), S ≡ x² + y² + 4x + 6y – 39
Solution:
Given P = (-6, -9) = (x₁, y₁) and S ≡ x² + y² + 4x + 6y – 39 = 0
Also 2g = 4, 2f = 6 and c = -39
g = 2, f = 3, c = -39
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-6) + y(-9) + 2(x – 6) + 3(y – 9) – 39 = 0
⇒ -4x – 6y – 78 = 0
⇒ 2x + 3y + 39 = 0

(iv) P = (3, 4), S ≡ x² + y² – 4x – 6y + 11
Solution:
Given P = (3, 4) = (x₁, y₁) and S ≡ x² + y² – 4x – 6y + 11 = 0
2g = -4, 2f = -6 and c = 11
g = -2, f = -3, c = 11
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ 3x + 4y – 2(x + 3) – 3(y + 4) + 11 = 0
⇒ x + y – 7 = 0

Question 2.
Find the equation of normal at P of the circle S = 0 where P and S are given by
(i) P = (3, -4), S ≡ x² + y² + x + y – 24
Solution:
P = (3, -4) = (x₁, y₁) and S ≡ x² + y² + x + y – 24 = 0
we have g = \(\frac{1}{2}\), f = \(\frac{1}{2}\), c = -24
∴ Equation of normal at (x₁, y₁) is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 3) (-4 + \(\frac{1}{2}\)) – (y + 4) (3 + \(\frac{1}{2}\)) = 0
⇒ (x – 3) + (-7) – (y + 4) (7) = 0
⇒ -7x – 7y – 7 = 0
⇒ x + y + 1 = 0

(ii) P = (3, 5), S ≡ x² + y² – 10x – 2y + 6
Solution:
P = (3, 5) = (x₁, y₁) and S ≡ x² + y² – 10x – 2y + 6 = 0
2g = -10, 2f = -2, c = 6
g = -5, f = -1
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 3) (5 – 1) – (y – 5) (3 – 5) = 0
⇒ 4(x – 3) + 2(y – 5) = 0
⇒ 4x + 2y – 22 = 0
⇒ 2x + y – 11 = 0

(iii) P = (1, 3), S ≡ 3(x² + y²) – 19x – 29y + 76
Solution:
P = (1, 3) = (x₁, y₁) and S ≡ \(x^2+y^2-\frac{19}{3} x-\frac{29}{3} y+\frac{76}{3}=0\)
\(2 g=-\frac{19}{3}, 2 f=-\frac{29}{3}, c=\frac{76}{3}\)
\(g=-\frac{19}{6}, f=-\frac{29}{3}\)
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 1) (3 – \(\frac{29}{6}\)) – (y – 3) (1 – \(\frac{19}{6}\)) = 0
⇒ (x – 1) (\(\frac{-11}{6}\)) – (y – 3) (\(\frac{-13}{6}\)) = 0
⇒ -11(x – 1) + 13(y – 3) = 0
⇒ -11x + 13y – 28 = 0
⇒ 11x – 13y + 28 = 0

(iv) P = (1, 2), S ≡ x² + y² – 22x – 4y + 25
Solution:
P = (1, 2) = (x₁, y₁) and S ≡ x² + y² – 22x – 4y + 25 = 0
2g = -22, 2f = -4 and c = 25
g = -11, f = -2
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 1) (2 – 2) – (y – 2) (1 – 11) = 0
⇒ -(y – 2) (-10) = 0
⇒ y – 2 = 0
⇒ y = 2

II.

Question 1.
Find the length of the chord intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3. (May. ’11)
Solution:
Given equation of circle is x² + y² – x + 3y – 22 = 0
comparing with general equation S = 0, we get
2g = -1, 2f = 3 and c = -22
g = \(-\frac{1}{2}\), f = \(\frac{3}{2}\)

Given line is y = x – 3 and L = x – y – 3 = 0.
AB is the chord intercepted by the line L = 0 on the circle.
CM = Perpendicular distance from C\(\left(\frac{1}{2},-\frac{3}{2}\right)\) to x – y – 3 = 0.

∴ AM = √24
and the length of the chord AB = 2 AM
= 2√24
= 4√6 units

Question 2.
Find the length of the chord intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0.
Solution:
The Centre of the given circle is C(4, 1)
and radius = \(\sqrt{16+1+8}\) = 5

AB is the chord intercepted by the line x + y + 1 = 0 on the circle.
CM = Perpendicular distance from C(4, 1) to x + y + 1 = 0.
∴ CM = \(\left|\frac{4+1+1}{\sqrt{1^2+1^2}}\right|=\frac{6}{\sqrt{2}}\) = 3√2
In the ∆ACM, we have AM² = AC² – CM²
= 25 – 18
= 7
∴ AM = √7
∴ Length of the chord AB = 2 AM = 2√7 units.

Question 3.
Find the length of the chord formed by x² + y² = a² on the line x cos α + y sin α = p.
Solution:
Centre of the circle x² + y² = a² is C(0, 0) and radius = ‘a’

CM = Perpendicular distance from the centre C(0, 0) to the line x cos α + y sin α = p.
∴ CM = \(\left|\frac{0(\cos \alpha)+0(\sin \alpha)-p}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\right|\) = p
In the ∆ACM, we have AM² = AC² – CM² = a² – p²
∴ AM = \(\sqrt{a^2-p^2}\)
and length of the chord AB = 2.AM = 2\(\sqrt{a^2-p^2}\)

Question 4.
Find the equation of the circle with centre (2, 3) and touch the line 3x – 4y + 1 = 0.
Solution:

If a given line touches the circle, then the perpendicular distance from the centre to the line is equal to the radius of the circle.
∴ Radius = perpendicular distance from C(2, 3) to the line 3x – 4y + 1 = 0.
∴ Radius = \(\left|\frac{3(2)-4(3)+1}{\sqrt{9+16}}\right|=\left|\frac{-5}{5}\right|\) = 1
∴ The equation of a circle with radius ‘1’ and centre (2, 3) is given by (x – 2)² + (y – 3)² = 12
∴ x² + y² – 4x – 6y + 12 = 0

Question 5.
Find the equation of the circle with centre (-3, 4) and touching y-axis.
Solution:

Equation of y-axis is x = 0 and given that the centre C = (-3, 4)
CM = perpendicular distance from C to y = axis
i.e., x = 0,
= |-3|
= 3
∴ The equation of a circle with centre (-3, 4) and radius ‘3’ is given by (x + 3)² + (y – 4)² = 9
x² + y² + 6x – 8y + 16 = 0

Question 6.
Find the equations of tangents to the circle x² + y² – 8x – 2y + 12 = 0 at the points whose ordinates are 1.
Solution:
Let P(x₁, y₁) be a point on the circle x² + y² – 8x – 2y + 12 = 0
given that ordinates of points is ‘1’ i.e., y₁ = 1
∴ \(x_1^2\) + 1 – 8x₁ – 2 + 12 – 0
\(x_1^2\) – 8x₁ + 11 = 0 which is a quadratic equation.

∴ Points on the circle are P = (4 + √5, 1) and Q = (4 – √5, 1)
Equation of tangent at P(4 + √5, 1) is by the formula xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(4 + √5) + y – 4(x + 4 + √5) – 1(y + 1) + 12 = 0
⇒ 4x + √5x + y – 4x – 16 – 4√5 – y – 1 + 12 = 0
⇒ √5x – 4√5 – 5 = 0
⇒ x – 4 – √5 = 0
⇒ x = 4 + √5
Similarly the equation of tangent at Q(4 – √5, 1) is
x(4 – √5) + y – 4(x + 4 – √5) – 1(y + 1) + 12 = 0
⇒ 4x – √5x + y – 4x – 16 + 4√5 – y – 1 + 12 = 0
⇒ -√5x + 4√5 – 5 = 0
⇒ x – 4 + √5 = 0
⇒ x = 4 – √5
∴ The equation of tangents of the given circle at the points when ordinates are ‘1’ are given by x = 4 + √5, x = 4 – √5

Question 7.
Find the equations of the tangents of the circle x² + y² – 10 = 0 at the points whose abscissae are 1.
Solution:
Let P(x1, y1) be a point on the circle x² + y² – 10 = 0
given that abscissae are ‘1’
i.e., x₁ = 1
1 + \(y_1^2\) – 10 = 0
y₁ = ±3
Hence the points on the circle are P(1, 3), Q(1, -3).
Equation of tangent at the point P(1, 3) on the circle x² + y² – 10 = 0 is xx₁ + yy₁ – 10 = 0
x + 3y – 10 = 0
Similarly equation of tangent at the point Q(1, -3) on the circle x² + y² – 10 = 0 is xx₁ + yy₁ – 10 = 0
x – 3y – 10 = 0

III.

Question 1.
If x² + y² = c² and \(\frac{x}{a}+\frac{y}{b}=1\) intersect at A and B then find \(\overline{\mathbf{A B}}\). Hence deduce the condition that the line touches the circle.
Solution:
Given x² + y² = c² ……..(1)
and \(\frac{x}{a}+\frac{y}{b}=1\)
⇒ bx + ay – ab = 0 ……….(2)
Centre of the circle C = (0, 0) and the radius of the circle CA = ‘c’.

If the line touches the circle that is if the line becomes a tangent to the circle, then the perpendicular distance from (0, 0) to the given line is equal to the radius of the circle.

Question 2.
The line y = mx + c and the circle x² + y² = a² intersect at A and B and if AB = 2λ then show that c² = (1 + m²) (a² – λ²).
Solution:

Centre of the circle C = (0, 0).
The line y = mx + c intersects the circle at A and B.
OM = Perpendicular distance from (0, 0) to mx – y + c = 0

Question 3.
Find the equation of the circle with centre (-2, 3) cutting a chord of length 2 units on 3x + 4y + 4 = 0. (Mar. ’11)
Solution:

Given the length of the chord AB = 2 units
∴ AM = 1 unit
CM = Perpendicular distance from the centre (-2, 3) to the line 3x + 4y + 4 = 0.
= \(\left|\frac{3(-2)+4(3)+4}{\sqrt{3^2+4^2}}\right|=\left|\frac{-6+12+4}{5}\right|=\frac{10}{5}=2\)
In the ΔACM, we have
AC² = AM² + CM²
= 1 + 4
= 5
∴ The equation of a circle with centre (-2, 3) and radius √5 units is (x + 2)² + (y – 3)² = 5
⇒ x² + 4x + 4 + y² – 6y + 9 = 5
⇒ x² + y² + 4x – 6y + 8 = 0

Question 4.
Find the equation of the tangent and normal at (3, 2) of the circle x² + y² – x – 3y – 4 = 0.
Solution:
Let S = x² + y² – x – 3y – 4 = 0 be the given circle, comparing with the general equation.
2g = -1, 2f = 3 and c = -4
∴ Equation of tangent at (x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 3x + 2y – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 6x + 4y – x – 3 – 3y – 6 – 8 = 0
⇒ 5x + y – 17 = 0
Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁)(x₁ + g) = 0
⇒ (x – 3) (2 – \(\frac{3}{2}\)) – (y – 2) (3 – \(\frac{1}{2}\)) = 0
⇒ (x – 3) (\(\frac{1}{2}\)) – (y – 2) (\(\frac{5}{2}\)) = 0
⇒ x – 3 – 5y + 10 = 0
⇒ x – 5y + 7 = 0

Question 5.
Find the equation of the tangent and normal at (1, 1) of the circle 2x² + 2y² – 2x – 5y + 3 = 0.
Solution:
Given equation of circle is x² + y² – x – \(\frac{5}{2}\)y + \(\frac{3}{2}\) = 0
2g = -1, 2f = \(-\frac{5}{2}\) and c = \(\frac{3}{2}\)
The point (1, 1) = (x₁, y₁)
The equation of the tangent at (x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0

Question 6.
Prove that the tangent at (3, -2) of the circle x² + y² = 13 touches the circle x² + y² + 2x – 10y – 26 = 0 and find its point of contact
Solution:
The equation of tangent at (3, -2) to the circle x² + y² = 13 is x(3) + y(-2) – 13 = 0
3x – 2y – 13 = 0 ………..(1) [∵ By the formula, xx₁ + yy₁ – a2 = 0]
To show that (1) touches the circle x² + y² + 2x – 10y – 26 = 0.
We have to show that the perpendicular distance from the centre of the circle (-1, 5) to the line 3x- 2y – 13 = 0 is equal to the radius of the circle which is \(\sqrt{1+25+26}=\sqrt{52}\).
∴ The perpendicular distance from (-1, 5) to the line 3x – 2y – 13 = 0 is \(\left|\frac{3(-1)-2(5)-13}{\sqrt{9+4}}\right|\)
= \(\left|\frac{-26}{\sqrt{13}}\right|\)
= 2√13
= √52
Hence the tangent 3x – 2y – 13 = 0 touches the circle x² + y² + 2x – 10y – 26 = 0
Let P(h, k) be the point of contact between the tangent and the circle.

Then P(h, k) will be the foot of the perpendicular drawn from C(-1, 5) to 3x – 2y – 13 = 0.
So by the formula

∴ The point of contact of the line (1) to the circle x² + y² + 2x – 10y – 26 = 0 is (5, 1).

Question 7.
Show that the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0 and also finds its point of contact. (New Model Paper and June ’10)
Solution:
Let S = x² + y² – 4x – 8y + 7 = 0 and S’ = x² + y² + 4x + 6y = 0,
comparing S = 0 with x² + y² + 2gx + 2fy + c = 0
we have 2g = -4, 2f = -8, c = 7
g = -2, f = -4, c = 7
Equation of tangent at (-1, 2) to the circle S = 0 is xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
⇒ x(-1) + y(2) + (-2)(x – 1) – 4(y + 2) + 7 = 0
⇒ -x + 2y – 2x + 2 – 4y – 8 + 7 = 0
⇒ -3x – 2y + 1 = 0
⇒ 3x + 2y – 1 = 0 ……….(1)
Centre of the circle S’ = x² + y² + 4x + 6y = 0 is (-2, -3)
If (1) touches S’ = 0, then the perpendicular distance from (-2, -3) to the line 3x + 2y -1 = 0 is equal to the radius of the circle.
Radius = \(\sqrt{4+9}=\sqrt{13}\)
Perpendicular distance from (-2, -3) to 3x + 2y – 1 = 0 is equal to \(\left|\frac{3(-2)+2(-3)-1}{\sqrt{9+4}}\right|=\left|\frac{-6-6-1}{\sqrt{13}}\right|=\sqrt{13}\)
Hence tangent at (-1, 2) to the circle S = 0 touches the circle S’ = 0.
Let P(h, k) be the point of contact of (1) and S’ = 0.
Then P(h, k) will be the foot of the perpendicular drawn from the centre (-2, -3) to the line 3x + 2y – 1 = 0.
By the formula

∴ The point of contact = (1, -1)

Question 8.
Find the equations of tangents to the circle x² + y² – 4x + 6y – 12 = 0 which are parallel to x + y – 8 = 0.
Solution:
Let S = x² + y² – 4x + 6y – 12 = 0 and comparing with x² + y² + 2gx + 2fy + c = 0 we get
g = -2, f = 3, c = -12
Centre of the circle = (2, -3)
and radius = \(\sqrt{4+9+12}\) = 5
The equation of any line parallel to x + y – 8 = 0 is of the form x + y + k = 0.
So the perpendicular distance from (2, -3) to x + y + k = 0 is equal to the radius.
∴ \(\left|\frac{2-3+k}{\sqrt{2}}\right|\) = 5
⇒ \(\left|\frac{k-1}{\sqrt{2}}\right|\) = 5
⇒ k – 1 = ±5√2
⇒ k = 1 ± 5√2
The equations of tangents to the circle S = 0 which are parallel to the line x + y – 8 = 0 are x + y + (1 ± 5√2) = 0.

Question 9.
Find the equations of the circle x² + y² + 2x – 2y – 3 = 0 which are perpendicular to 3x – y + 4 = 0.
Solution:
Centre of the circle x² + y² + 2x – 2y – 3 = 0 is (-1, 1) and radius = \(\sqrt{1+1+3}=\sqrt{5}\)
Equation of any line perpendicular to 3x – y + 4 = 0 is x + 3y + k = 0
If this is a tangent to the above circle then the perpendicular distance from (-1, 1) to the line x + 3y + k = 0 is equal to radius √5.
∴ \(\left|\frac{-1+3+\mathbf{k}}{\sqrt{1+9}}\right|\) = √5
⇒ \(\left|\frac{k+2}{\sqrt{10}}\right|\) = √5
⇒ k + 2 = ±5√2
⇒ k = -2 ± 5√2
∴ Equations of required tangents is x + 3y – 2 ± 5√2 = 0.

Question 10.
Find the equation of the tangents to the circle x² + y² – 4x – 6y + 3 = 0 which makes an angle of 45° with the X-axis.
Solution:
Centre of the circle x² + y² – 4x – 6y + 3 = 0 is (2, 3)
and radius = \(\sqrt{4+9-3}=\sqrt{10}\)
Since the tangents make an angle of 45° with X-axis we have
m = tan 45° = 1.
∴ The equation of tangent will be y = x + c
x – y + c = 0 ……….(1)
The perpendicular distance from (2, 3) to x – y + c = 0is equal to the radius of circle
∴ \(\left|\frac{2-3+c}{\sqrt{1+1}}\right|\) = √10
⇒ \(\left|\frac{c-1}{\sqrt{2}}\right|\) = √10
⇒ c – 1 = ±2√5
⇒ c = 1 ± 2√5
∴ Equations of required tangents are x – y + (1 ± 2√5) = 0

Question 11.
Find the equation of the circle passing through (-1, 0) and touching the line x + y – 7 = 0 at (3, 4).
Solution:

Let the circle passes through P(-1, 0) and touching the line x + y – 7 = 0 …….(1)
at Q(3, 4), suppose centre of the circle be C = (h, k)
Then PC = PQ
⇒ PC² = PQ²
⇒ (h + 1)² + k² = (h – 3)² + (k – 4)²
⇒ h² + 2h + 1 + k² = h² – 6h + 9 + k² – 8k + 16
⇒ 8h + 8k – 24 = 0
⇒ h + k – 3 = 0 ……..(2)
Slope of the line x + y – 7 = 0 is -1
and slope of CQ is = \(\frac{\mathrm{k}-4}{\mathrm{~h}-3}\)
Since CQ is perpendicular to the line x + y – 7 = 0
we have a product of slopes = -1
∴ (\(\frac{\mathrm{k}-4}{\mathrm{~h}-3}\)) (-1) = (-1)
⇒ k – 4 = h – 3
⇒ h – k + 1 = 0 ……….(3)
Solving (2) and (3)
2h – 2 = 0
⇒ h = 1
and -k + 2 = 0
⇒ k = 2
∴ Centre of the circle C(h, k) = C(1, 2)
and radius PC = \(\sqrt{(1+1)^2+(2-0)^2}\) = √8
Hence equation of a circle with centre (1, 2) and radius √8 is given by (x – 1)² + (y – 2)² = 8
⇒ x² – 2x + 1 + y² – 4y + 4 = 8
⇒ x² + y² – 2x – 4y – 3 = 0

Question 12.
Find the equation of the circle passing through (1, -1) touching the lines 4x + 3y + 5 = 0 and 3x – 4y – 10 = 0.
Solution:
Given lines are
4x + 3y + 5 = 0 ……..(1)
3x – 4y – 10 = 0 ………(2)
Since the circle touches the given lines which are perpendicular, centre of the circle lies on the bisectors of angles between the given lines.
The bisectors of angles between the given lines are
\(\frac{4 x+3 y+5}{\sqrt{16+9}} \pm \frac{3 x-4 y-10}{\sqrt{16+9}}=0\)
⇒ (4x + 3y + 5) ± (3x – 4y – 10) = 0
⇒ 4x + 3y + 5 + 3x – 4y – 10 = 0
⇒ 7x – y – 5 = 0 ……….(3)
or
4x + 3y + 5 – 3x + 4y + 10 = 0
⇒ x + 7y + 15 = 0 ………(4)
From (3) we have y = 7x – 5
and from (4), x = -(7y + 15)
If the centre lies on y = 7x – 5 then the centre will be of the form (k, 7k – 5).
∴ The perpendicular distance from (k, 7k – 5) to the line (1) is equal to the radius of the circle.
∴ \(\left|\frac{4 k+3(7 k-5)+5}{\sqrt{16+9}}\right|=\sqrt{(k-1)^2+(7 k-5+1)^2}\)
⇒ \(\frac{|4 k+21 \mathrm{k}-10|}{5}=\sqrt{(\mathrm{k}-1)^2+(7 \mathrm{k}-4)^2}\)
⇒ \(\frac{|25 k-10|}{5}=\sqrt{k^2-2 k+1+49 k^2-56 k+16}\)
⇒ |5k – 2| = \(\sqrt{50 k^2-58 k+17}\)
⇒ (5k – 2)² = 50k² – 58k + 17
⇒ 25k² – 20k + 4 = 50k² – 58k + 17
⇒ 25k² – 38k + 13 = 0
⇒ 25k² – 25k – 13k + 13 = 0
⇒ 25k(k – 1) – 13(k – 1) = 0
⇒ k = 1 or k = \(\frac{13}{25}\)
when k = 1, centre of the circle is [1, 7(1) – 5] = (1, 2)
and radius of the centre = \(\sqrt{(1-1)^2+(2+1)^2}\) = 3
∴ Equation of required circle is (x – 1)² + (y – 2)² = 3²
⇒ x² + y² – 2x – 4y – 4 = 0

Question 13.
Show that x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0 and find its point of contact. (May ’09)
Solution:
The equation of the given circle is x² + y² – 3x + 7y + 14 = 0 ………(1)
If the line x + y + 1 = 0 ……..(2) touches the circle (1)
then the perpendicular distance from the centre of the circle C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0 is equal to the radius of the circle.
Radius of the given circle = \(\sqrt{\frac{9}{4}+\frac{49}{4}-14}=\sqrt{\frac{2}{4}}=\frac{1}{\sqrt{2}}\)
Perpendicular distance from C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0 is \(\left|\frac{\frac{3}{2}-\frac{7}{2}+1}{\sqrt{1^2+1^2}}\right|=\left|-\frac{1}{\sqrt{2}}\right|=\frac{1}{\sqrt{2}}\)
Hence circle (1) touches line (2).
Let P(h, k) be the point of contact between the circle (1) and line (2).
Then P(h, k) will be the foot of the perpendicular drawn from C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0.
∴ By the formula

∴ The point of contact of the given line with the circle (1) is (2, -3).

Telangana TSBIE TS Inter 2nd Year Hindi Study Material Grammar महावरे और लोकोक्तियाँ Questions and Answers.

TS Inter 2nd Year Hindi Grammar महावरे और लोकोक्तियाँ

भाषा की सुंदर रचना हेतु मुहावरों एवं लोकोक्तियों का प्रयोग आवश्यक माना जाता है । ये दोनों भाषा को सजीव, प्रवाहपूर्ण एवं आकर्षक बनाने में सहायक होते हैं । यही कारण है कि हिन्दी भाषा में विभिन्न महावरों एवं लोकोक्तियों का अक्सर प्रयोग होते हुए देखा गया है।

‘मुहावरा’ शब्द अरबी भाषा से लिया गया है, जिसका अर्थ है- अभ्यास । मुहावरा अतिसंक्षिप्त रूप में होते हुए भी बड़े भाव या विचार को प्रकट करता है जबकि ‘लोकोक्तियों को ‘कहावतो’ के नाम से भी जाना जाता है ।

साधारणतया लोक में प्रचलित उक्ति को लोकोक्दि नाम दिया जाता है। कुछ लोकोक्तियाँ अंतर्कथाओं से भी संबंध रखती हैं, जैसे भगीरथ प्रयास अर्थात जितना परिश्रम राजा भगीरथ को गंगा के अवतरण के लिए करना पड़ा, उतना ही कठिन परिश्रम करने से सफलता मिलती है । संक्षेप में कहा जाए तो मुहावरे वाक्यांश होते हैं, जिनका प्रयोग क्रिया के रूप में वाक्य के बीच में किया जाता है, जबकि लोकोक्तियाँ स्वतंत्र वाक्य होती हैं, जिनमें एक पूरा भाव छिपा रहता है ।

मुहावरा :
विशेष अर्थ को प्रकट करने वाले वाक्यांश को मुहावरा कहते है । मुहावरा पूर्ण वाक्य नहीं होता, इसीलिए इसका स्वतंत्र रूप से प्रयोग नहीं किया जा सकता। मुहावरे का प्रयोग करना और ठीक ठीक अर्थ समझना बड़ा कठिन है, यह अभ्यास से ही सीखा जा सकता है ।

लोकोक्ति :
बहु अधिक प्रचलित और लोगों के मुँहचढ़े वाक्य लोकोक्तियाँ कहलाती हैं । इन वाक्यों में जनता के अनुभवों का निचोड़ या सार होता है । इनकी उत्पत्ति एवं रचनाकार ज्ञात नहीं होते ।

लोकोक्तियाँ आम जनमानस द्वारा स्थानीय बोलियों में हर दिन की परिस्थितियों एवं संदर्भों से उपजे वैसे पद एवं वाक्य होते हैं जिनका किसी रवास समूह, उम्र वर्ग या क्षेत्रीय दायरे में प्रयोग किया जाता है। इसमें स्थान विशेष के भूगोल, संस्कृति, भाषाओं का मिश्रण इत्यादि की झलक मिलती है। लोकोक्तियाँ वाक्यांश न होकर स्वतंत्र वाक्य होती हैं ।

मुहावरों और लोकोक्तियों में अंतर :
लोकोक्ति का वाक्य में ज्यों का त्यों उपयोग होता है । मुहावरे का उपयोग क्रिया के अनुसार बदल जाता है लेकिन लोकोक्ति का प्रयोग करते समय इसे बिना बदलाव के रखा जाता है । कभी – कभी काल के अनुसार परिवर्तन सम्भव है ।

कुछ लोकप्रिय मुहावरे :

कुछ लोकप्रिय लोकोक्तियाँ

निम्नलिखित मुहावरों के अर्थ लिखिए:

1. अंगूठा छाप होना = अनपढ़ होना
2. अपने पाँव पर आप कुल्हाड़ी मारना = अपना नुकसान करना
3. पेट में चूहे कूदना = बहुत भूख लगना
4. तारे तोड़ लाना = मुश्किल काम करना
5. आग में घी डालना = क्रोध को और भड़काना
6. ईद का चाँद होना = बहुत दिनों के बाद दिखाई देना
7. कुएँ का मेंढ़क होना = अल्पज्ञ
8. अंधे की लाठी = एक मात्र सहारा
9. खाल खींचना = दंड देना
10. आँखों में धूल झोंकना = धोखा देना

निम्नलिखित लोकोक्तियों के अर्थ लिखिए :

1. आ बैल मुझे मार = स्वयं मुसीबत मोल लेना
2. उल्टा चोर कोतवाल को डाँटे = अपराधी निरपराध को डाँटे
3. एक पंथ दो काज = एक काम से दूसरा काम हो जाना
4. एक हाथ से ताली नहीं बजती = झगडा एक ओर से नही होता
5. काला अक्षर भैंस बराबर = अनपढ़ व्यक्ति
6. खोदा पहाड़ निकली चुहिया = बहुत कंठिन परिश्रम का थोडा लाभ
7. यथा राजा तथा प्रजा = जैसा स्वामी वैसाः ही सेवक
8. पाँचों उँगलियाँ घी में होना = ‘हर’ तरफ से लाभ होना
9. आग में घी डालना = पहले से हो रहे झगडे को भड़काने की क्रिया
10. कंगाली में आटा गीला होना = परेशानी पर पेरशानी आना

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(b)

I.

Question 1.
Locate the position of the point P with respect to the circle S = 0 when
(i) P(3, 4) and S ≡ x² + y² – 4x – 6y – 12 = 0
Solution:
Let S ≡ x² + y² – 4x – 6y – 12 = 0
and given P = (3, 4) = (x₁, y₁), g = -2, f = -3.
Then S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= 3² + 4² + 2g(3) + 2f(4) – 12
= 9 + 16 + 6(-2) + 8(-3) – 12
= 25 – 12 – 24 – 12 < 0 and S₁₁ < 0
∴ Point P(3, 4) lies in the interior of the circle S = 0.

(ii) P(1, 5) and S ≡ x² + y² – 2x – 4y + 3 = 0
Solution:
Let S ≡ x² + y² – 2x – 4y + 3 = 0
we have 2g = -2 and 2f = -4
g = -1 and f = -2
Given P(1, 5) = (x₁, y₁) and S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= 1² + 5² + 2(-1)(1) + 2(-2)(5) + 3
= 1 + 25 – 2 – 20 + 3
= 7 > 0
∴ Point P(1, 5) lies in the exterior of the circle S = 0.

(iii) P(4, 2) and S ≡ 2x² + 2y² – 5x – 4y – 3 = 0
Solution:
P(4, 2) = (x₁, y₁), S ≡ x² + y² – \(\frac{5}{2}\)x – 2y – \(\frac{3}{2}\) = 0
2g = \(-\frac{5}{2}\) ⇒ g = \(-\frac{5}{4}\)
and 2f = -2 ⇒ f = -1
∴ S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= 16 + 4 + (\(-\frac{5}{2}\))(4) + 2(-1)(2) – \(\frac{3}{2}\)
= 20 – 10 – 4 – \(\frac{3}{2}\)
= 6 – \(\frac{3}{2}\)
= \(\frac{9}{2}\) > 0
S₁₁ > 0
∴ P(4, 2) lies in the exterior of the circle S = 0.

(iv) P(2, -1) and S ≡ x² + y² – 2x – 4y + 3 = 0
Solution:
P(2, -1) = (x₁, y₁), 2g = -2; 2f = -4, c = 3
S₁₁ ≡ \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= 4 + 1 + (-2)(2) + (-4)(-1) + 3
= 5 – 4 + 4 + 3
= 8 > 0
∴ Since S₁₁ > 0, the point P lies in the exterior of the circle S = 0.

Question 2.
Find the power of the point P with respect to the circle S = 0 when
(i) P = (5, -6) and S ≡ x² + y² + 8x+ 12y + 15
Solution:
Given P = (5, -6) = (x₁, y₁) and S ≡ x² + y² + 8x + 12y + 15
we have 2g = 8, 2f = 12, c = 15
The power of the point P (5, -6) w.r.t. circle S = 0 is
S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= 25 + 36 + 8(5) + 12(-6) + 15
= 61 + 40 – 72 + 15
= 44
∴ The power of the point P w.r.t. the given circle is 44.

(ii) P = (-1, 1) and S ≡ x² + y² – 6x + 4y – 12
Solution:
Given P = (-1, 1) = (x₁, y₁) and S ≡ x² + y² – 6x + 4y – 12 = 0
S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= 1 + 1 – 6(-1) + 4(1) – 12
= 2 + 6 + 4 – 12
= 0
∴ Power of the point P(-1, 1) w.r.t. the given circle is ‘0’.

(iii) P = (2, 3) and S ≡ x² + y² – 2x + 8y – 23
Solution:
Given P = (2, 3) = (x₁, y₁) and S ≡ x² + y² – 2x + 8y – 23
S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= \(x_1^2+y_1^2-2 x_1+8 y_1-23\)
= 4 + 9 – 2(2) + 8(3) – 23
= 13 – 4 + 24 – 23
= 10
∴ Power of the point P(2, 3) w.r.t. S = 0 is 10.

(iv) P = (2, 4) and S ≡ x² + y² – 4x – 6y – 12
Solution:
Given P = (2, 4) = (x₁, y₁) and S ≡ x² + y² – 4x – 6y – 12 = 0
S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx_{1 }}+2 f \mathrm{y}_1+\mathrm{c}\)
= \(x_1^2+y_1^2-4 x_1-6 y_1-12\)
= 4 + 16 – 4(2) – 6(4) – 12
= 20 – 8 – 24 – 12
= -24
∴ Power of the point P(2, 4) w.r.t. S = 0 is -24.

Question 3.
Find the length of the tangent from P to the circle S = 0 when
(i) P = (-2, 5) and S ≡ x² + y² – 25
Solution:
Length of the tangent from a point P(x₁, y₁) to the given circle S = 0 is \(\sqrt{S_{11}}\)
given P(x₁, y₁) = (-2, 5)
∴ \(\sqrt{S_{11}}\) = \(\sqrt{x_1^2+y_1^2-25}\)
= \(\sqrt{4+25-25}\)
= 2 units

(ii) P = (0, 0) and S ≡ x² + y² – 14x + 2y + 25
Solution:
Given P = (0, 0) = (x₁, y₁) and S ≡ x² + y² – 14x + 2y + 25 = 0
∴ The length of the tangent from P to S = 0 is
\(\sqrt{\mathrm{S}_{11}}=\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2-14 \mathrm{x}_1+2 \mathrm{y}_1+25}\)
= \(\sqrt{0+0-0+0+25}\)
= 5 units

(iii) P = (2, 5) and S ≡ x² + y² – 5x + 4y – 5
Solution:
Given P = (2, 5) = (x₁, y₁) and S ≡ x² + y² – 5x + 4y – 5 = 0
∴ The length of the tangent from P to S = 0 is
\(\sqrt{S_{11}}=\sqrt{x_1^2+y_1^2-5 x_1+4 y_1-5}\)
= \(\sqrt{4+25-5(2)+4(5)-5}\)
= \(\sqrt{29-10+20-5}\)
= √34 units

II.

Question 1.
If the length of the tangent from (5, 4) to the circle x² + y² + 2ky = 0 is 1 then find ‘k’.
Solution:
Given P = (5, 4) = (x₁, y₁) and S ≡ x² + y² + 2ky = 0 is the given circle.
Given that the length of the tangent from P(5, 4) to S = 0 is ‘1’.
∴ \(\sqrt{S_{11}}\) = 1
⇒ \(\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{ky}_1}\) = 1
⇒ \(\sqrt{25+16+8 k}\) = 1
⇒ \(\sqrt{41+8 k}\) = 1
⇒ 41 + 8k = 1
⇒ 8k = -40
⇒ k = -5

Question 2.
If the length of the tangent from (2, 5) to the circle x² + y² – 5x + 4y + k = 0 is √37 then find k.
Solution:
Given P = (2, 5) = (x₁, y₁) and S ≡ x² + y² – 5x + 4y + k = 0
Given \(\sqrt{S_{11}}=\sqrt{37}\)
⇒ \(\sqrt{x_1^2+y_1^2-5 x_1+4 y_1+k}=\sqrt{37}\)
⇒ \(\sqrt{4+25-10+20+k}=\sqrt{37}\)
⇒ \(\sqrt{k+39}=\sqrt{37}\)
⇒ k + 39 = 37
⇒ k = -2

III.

Question 1.
If a point P is moving such that the lengths of tangents drawn from P to the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 are in the ratio 2 : 3, then find the equation of the locus of P. (Mar. ’09)
Solution:
The given equations of circles are
x² + y² – 4x – 6y – 12 = 0 ………(1)
x² + y² + 6x + 18y + 26 = 0 ……….(2)
Let P (x1, y1) be any point on the locus and \(\overline{\mathrm{PT}_1}, \overline{\mathrm{PT}_2}\) are the lengths of tangents drawn from P to the circles (1) and (2) then we have \(\frac{\overline{\mathrm{PT}_1}}{{\overline{\mathrm{PT}_2}}}=\frac{2}{3}\)
⇒ \(\text { 3. } \overline{\mathrm{PT}_1}=2 \overline{\mathrm{PT}_2}\)
⇒ \(9 \mathrm{PT}_1^2=4 \mathrm{PT}_2^2\)
⇒ 9[\(x_1^2+y_1^2\) – 4x₁ – 6y₁ – 12] = 4[\(x_1^2+y_1^2\) + 6x₁ + 18y₁ + 26]
⇒ \(5 x_1^2+5 y_1^2\) – 60x₁ – 126y₁ – 212 = 0
∴ The equation of locus of P is 5(x² + y²) – 60x – 126y – 212 = 0

Question 2.
If a point P is moving such that the lengths of tangents drawn from P to the circles x² + y² + 8x + 12y + 15 = 0 and x² + y² – 4x – 6y – 12 = 0 are equal then find the equation of the locus of P.
Solution:
The given equations of circles are
x² + y² + 8x + 12y + 15 = 0 ……….(1)
and x² + y² – 4x – 6y – 12 = 0 ……….(2)
Let P (x1, y1) be any point on the locus such that the lengths of tangents \(\overline{\mathrm{PT}_1}\) and \(\overline{\mathrm{PT}_2}\) are equal.
∴ \(\overline{\mathrm{PT}_1}=\overline{\mathrm{PT}_2}\)
⇒ \(\mathrm{PT}_1{ }^2=\mathrm{PT}_2{ }^2\)
⇒ \(x_1^2+y_1^2\) + 8x₁ + 12y₁ + 15 = \(x_1^2+y_1^2\) – 4x₁ – 6y₁ – 12
⇒ 12x₁ + 18y₁ + 27 = 0
⇒ 4x₁ + 6y₁ + 9 = 0
∴ The equation to the locus of P is 4x + 6y + 9 = 0.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(a)

I.

Question 1.
Find the equations of circles with centre C and radius r where
(i) C = (2, -3), r = 4
Solution:
Given C = (2, -3) = (h, k) and r = 4,
we have equation of circle as (x – h)² + (y – k)² = r²
(x – 2)² + (y + 3)² = 4²
x² + 4 – 4x + y² + 9 + 6y = 16
x² + y² – 4x + 6y – 3 = 0

(ii) C = (-1, 2), r = 5
Solution:
Given C = (-1, 2) = (h, k) and r = 5, then
the equation of circle is (x – h)² + (y – k)² = r²
(x + 1)² + (y – 2)² = 5²
x² + y² + 2x – 4y + 1 + 4 = 25
x² + y² + 2x – 4y – 20 = 0

(iii) C = (a, -b), r = a + b
Solution:
Given C = (a, -b) = (h, k) and r = a + b
we have the equation of circle as (x – h)² + (y – k)² = r²
(x – a)² + (y + b)² = (a + b)²
x² + y² – 2ax + 2by + a² + b² – (a + b)² = 0
x² + y² – 2ax + 2by – 2ab = 0

(iv) C = (-a, -b), r = \(\sqrt{a^2-b^2}\) (|a| > |b|)
Solution:
Given C = (h, k) = (-a, -b) and r = \(\sqrt{a^2-b^2}\)
then the equation of circle is (x + a)² + (y + b)² = a² – b²
x² + y² + 2ax + 2by + a² + b² – a² + b² = 0
x² + y² + 2ax + 2by + 2b² = 0

(v) C = (cos α, sin α), r = 1
Solution:
Given C = (cos α, sin α) = (h, k) and r = 1
we have the equation of the circle as
(x – cos α)² + (y – sin α)² = 1²
x² + y² – 2x cos α – 2y sin α + cos²α + sin²α – 1 = 0
x² + y² – 2x cos α – 2y sin α + 1 – sin²α + sin²α – 1 = 0
x² + y² – 2x cos α – 2y sin α = 0

(vi) C = (-7, -3), r = 4
Solution:
Given C = (-7, -3) = (h, k) and r = 4,
we have the equation of the circle as (x + y)² + (y + 3)² = 4²
x² + y² + 14x + 6y + 49 + 9 – 16 = 0
x² + y² + 14x + 6y + 42 = 0

(vii) C = (\(\frac{-1}{2}\), -9), r = 5
Solution:
Given C = (\(\frac{-1}{2}\), -9) = (h, k) and r = 5,
the equation of the circle is (x – h)² + (y – k)² = r²
(x + \(\frac{1}{2}\))² + (y + 9)² = 0
x² + y² + x + 18y + \(\frac{1}{4}\) + 81 – 25 = 0
x² + y² + x + 18y + \(\frac{1}{4}\) + 56 = 0
4x² + 4y² + 4x + 72y + 225 = 0

(viii) C = \(\left(\frac{5}{2},-\frac{4}{3}\right)\), r = 6
Solution:
Given C = \(\left(\frac{5}{2},-\frac{4}{3}\right)\) = (h, k) and r = 6,
the equation of the circle is (x – h)² + (y – k)² = r²
\(\left(x-\frac{5}{2}\right)^2+\left(y+\frac{4}{3}\right)^2=6^2\)
x² + y² – 5x + \(\frac{8}{3} y+\frac{25}{4}+\frac{16}{9}\) – 36 = 0
36(x² + y²) – 180x + 96y – 1007 = 0
∴ Equation of circle is 36(x² + y²) – 180x + 96y – 1007 = 0

(ix) C = (1, 7), r = \(\frac{5}{2}\)
Solution:
The equation of the circle is (x – h)² + (y – k)² = r²
where C = (h, k) = (1, 7) and r = \(\frac{5}{2}\)
(x – 1)² + (y – 7)² = \(\frac{25}{4}\)
x² + y² – 2x – 14y + 50 = \(\frac{25}{4}\)
4(x² + y²) – 8x – 56y + 200 – 25 = 0
4(x² + y²) – 8x – 56y + 175 = 0

(x) C = (0, 0), r = 9
Solution:
Given C = (0, 0) = (h, k) and r = 9,
the equation of the circle is (x – h)² + (y – k)² = r²
x² + y² = 81

Question 2.
Find the equation of the circle passing through the origin and having the centre at (-4, -3).
Solution:
Let C = (-4, -3) and O(0, 0) be any point on the circumference of the circle.
Then OC = r will be the radius
∴ r = \(\sqrt{(0+4)^2+(0+3)^2}=\sqrt{16+9}\) = 5
The equation of a circle with centre (-4, -3) and radius ‘5’ is
(x + 4)² + (y + 3)² = 25
x² + y² + 8x + 6y + 16 + 9 – 25 = 0
x² + y² + 8x + 6y = 0

Question 3.
Find the equation of the circle passing through (2, -1) having the centre at (2, 3).
Solution:
Given C = (2, 3) and P = (2, -1)
∴ Radius of the circle PC = \(\sqrt{(2-2)^2+(3+1)^2}\) = 4
∴ The equation of the circle with centre (2, 3) and radius ‘4’ is
(x – 2)² + (y – 3)² = 4²
x² + y² – 4x – 6y + 4 + 9 = 16
x² + y² – 4x – 6y – 3 = 0

Question 4.
Find the equation of the circle passing through (-2, 3) and having the centre at (0, 0).
Solution:
Given C = (0, 0) and P = (-2, 3)
We have radius PC = \(\sqrt{4+9}=\sqrt{13}\) = r
∴ Equation of circle with C(0, 0) and radius √13 is x² + y² = 13.

Question 5.
Find the equation of the circle passing through (3, 4) and having the centre at (-3, 4). (Mar. ’12)
Solution:
Given C = (-3, 4) and P = (3, 4)
The radius of the circle PC = \(\sqrt{(3+3)^2+(4-4)^2}\) = 6
∴ The equation of the circle with C = (-3, 4) and radius 6 is
(x + 3)² + (y – 4)² = 6²
x² + y² + 6x – 8y + 9 + 16 – 36 = 0
x² + y² + 6x – 8y – 11 = 0

Question 6.
Find the value of ‘a’ if 2x² + ay² – 3x + 2y – 1 = 0 represents a circle and also find its radius. (Mar. ’13)
Solution:
If the given equation 2x² + ay² – 3x + 2y – 1 = 0 represents a circle then
coefficient of x² = coefficient of y²
and the coefficient of the xy term is ‘0’.
2 = a
∴ a = 2
and the equation of circle is 2x² + 2y² – 3x + 2y – 1 = 0

Question 7.
Find the values of a and b if ax² + bxy + 3y² – 5x + 2y – 3 = 0 represents a circle. Also, find the radius and centre of the circle. (New Model Paper)
Solution:
Given ax² + bxy + 3y² – 5x + 2y – 3 = 0 represents a circle,
we have coefficient of x² = coefficient of y²
and coefficient of xy term = 0
∴ a = 3 and b = 0
∴ Equation of circle is 3x² + 3y² – 5x + 2y – 3 = 0

Question 8.
If x² + y² + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3) find g, f, and its radius. (May ’11)
Solution:
Given x² + y² + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3) we have
(-g, -f) = (2, 3)
g = -2, f = -3
∴ Radius of the circle = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9+12}\)
= 5

Question 9.
If x2 + y2 + 2gx + 2fy = 0 represents a circle with centre (-4, -3) then find g, f, and the radius of the circle.
Solution:
Centre = (-g, -f) = (-4, -3) (given)
g = 4 and f = 3
∴ Radius of the circle = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{16+9}\)
= 5

Question 10.
If x² + y² – 4x + 6y + c = 0 represents a circle with radius 6 then find the value of c. (Mar. ’09)
Solution:
Centre of the given circle = (2, -3)
and radius = 6 (given)
\(\sqrt{g^2+f^2-c}\) = 6
\(\sqrt{4+9-c}\) = 6
13 – c = 36
c = -23

Question 11.
Find the centre and radius of each of the circles whose equations are given below:
(i) x² + y² – 4x – 8y – 41 = 0
Solution:
x² + y² – 4x – 8y – 41 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we have
2g = -4 and 2f = -8
∴ Centre = (-g, -f) = (2, 4)
Radius = \(\sqrt{g^2+f^2-c}=\sqrt{4+16+41}=\sqrt{61}\)

(ii) 3x² + 3y² – 5x – 6y + 4 = 0
Solution:
3x² + 3y² – 5x – 6y + 4 = 0
Writing the given equation in the standard form
\(x^2+y^2-\frac{5}{3} x-2 y+\frac{4}{3}=0\)
Compared with the standard equation, we get

(iii) 3x² + 3y² + 6x – 12y – 1 = 0
Solution:
3x² + 3y² + 6x – 12y – 1 = 0
Writing the given equation in the standard form, x² + y² + 2x – 4y – \(\frac{1}{3}\) = 0
∴ Centre = (-1, 2) and
radius = \(\sqrt{1+4+\frac{1}{3}}=\sqrt{\frac{16}{3}}=\frac{4}{\sqrt{3}}\)

(iv) x² + y² + 6x + 8y – 96 = 0
Solution:
x² + y² + 6x + 8y – 96 = 0
Centre = (-g, -f) = (-3, -4),
since 2g = 6, 2f = 8
and radius = \(\sqrt{9+16+96}=\sqrt{121}\) = 11

(v) 2x² + 2y² – 4x + 6y – 3 = 0
Solution:
2x² + 2y² – 4x + 6y – 3 = 0
Writing the given equation in the standard form,
x² + y² – 2x + 3y – \(\frac{3}{2}\) = 0
2g = -2, 2f = 3
g = -1, f = \(\frac{3}{2}\)
Centre = (-g, -f) = (1, \(-\frac{3}{2}\))
Radius = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{1+\frac{9}{4}+\frac{3}{2}}=\sqrt{\frac{19}{4}}=\frac{\sqrt{19}}{2}\)

(vi) 2x² + 2y² – 3x + 2y – 1 = 0
Solution:
2x² + 2y² – 3x + 2y – 1 = 0
Writing the given equation in the standard form \(x^2+y^2-\frac{3}{2} x+y-\frac{1}{2}=0\), we get

(vii) \(\sqrt{1+m^2}\) (x² + y²) – 2cx – 2mcy = 0 (June ’10)
Solution:
Writing the given equation in the standard

(viii) x² + y² + 2ax – 2by + b² = 0
Solution:
x² + y² + 2ax – 2by + b² = 0
Compared with the general equation we get
2g = 2a and 2f = -2b
g = a and f = -b
∴ Centre = (-g, -f) = (-a, b)
radius = \(\sqrt{g^2+f^2-c}=\sqrt{a^2+b^2-b^2}\) = a

Question 12.
Find the equations of circles for which the points given below are the endpoints of a diameter.
(i) (1, 2), (4, 6)
Solution:
Equation of circle having A(x₁, y₁) and B(x₂, y₂) as extremities (endpoints) of the diameter is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
∴ Taking A(x₁, y₁) = (1, 2) and B(x₂, y₂) = (4, 6)
We have the equation of a circle having A, B as extremities of the diameter is (x – 1) (x – 4) + (y – 2) (y – 6) = 0
x² – 5x + 4 + y² – 8y + 12 = 0
x² + y² – 5x – 8y + 16 = 0

(ii) (-4, 3), (3, -4)
Solution:
Take A(x₁, y₁) = (-4, 3) and B(x₂, y₂) = (3, -4)
We have equation of required circle as (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x + 4) (x – 3) + (y – 3) (y + 4) = 0
x² + x – 12 + y² + y – 12 = 0
x² + y² + x + y – 24 = 0

(iii) (1, 2), (8, 6)
Solution:
Take A = (1, 2) and B = (8, 6),
we have the equation of circle in the form (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 1) (x – 8) + (y – 2) (y – 6) = 0
x² – 9x + 8 + y² – 8y + 12 = 0
x² + y² – 9x – 8y + 20 = 0

(iv) (4, 2), (1, 5)
Solution:
Taking A = (4, 2) and B = (1, 5),
we have the equation of circle in the required form (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 4) (x – 1) + (y – 2) (y – 5) = 0
x² – 5x + 4 + y² – 7y + 10 = 0
x² + y² – 5x – 7y + 14 = 0

(v) (7, -3), (3, 5)
Solution:
Taking A = (7, -3) and B = (3, 5),
we have the equation of circle in the required form (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 7) (x – 3) + (y + 3) (y – 5) = 0
x² – 10x + 21 + y² – 2y – 15 = 0
x² + y² – 10x – 2y + 6 = 0

(vi) (1, 1), (2, -1)
Solution:
Taking A = (1, 1) and B = (2, -1),
we get the equation of circle in the required form (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 1) (x – 2) + (y – 1) (y + 1) = 0
x² – 3x + 2 + y² – 1 = 0
x² + y² – 3x + 1 = 0

(vii) (0, 0), (8, 5)
Solution:
Taking A = (0, 0) and B = (8, 5),
we get the equation of circle in the required form (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 0) (x – 8) + (y – 0) (y – 5) = 0
x² – 8x + y² – 5y = 0
x² + y² – 8x – 5y = 0

(viii) (3, 1), (2, 7)
Solution:
Taking A = (3, 1) and B = (2, 7),
the equation of circle in the required form is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 3) (x – 2) + (y – 1) (y – 7) = 0
x² – 5x + 6 + y² – 8y + 7 = 0
x² + y² – 5x – 8y + 13 = 0

Question 13.
Obtain the parametric equation of each of the following circles.
(i) x² + y² = 4
Solution:
Given equation is in the form x² + y² = r²
centre C(h, k) = (0. 0), and the radius of the circle is r = 2
The parametric equations of the given circle are x = h + r cos θ, y = k + r sin θ
x = 2 cos θ, y = 2 sin θ, (0 ≤ θ ≤ 2π)

(ii) 4(x² + y²) = 9
Solution:
The given equation can be written as x² + y² = \(\frac{9}{4}\)
Centre of the circle C(h, k) = (0, 0) and radius = \(\frac{3}{2}\)
∴ The parametric equations of the given circle are x = h + r cos θ, y = k + r sin θ
x = \(\frac{3}{2}\) cos θ, y = \(\frac{3}{2}\) sin θ, (0 ≤ θ ≤ 2π)

(iii) 2x² + 2y² = 7
Solution:
The given equation can be written as x² + y² = \(\frac{7}{2}\)
Centre of the circle C(h, k) = (0, 0) and radius = \(\sqrt{\frac{7}{2}}\)
∴ The parametric equations of the given circle are x = h + r cos θ, y = k + r sin θ
x = \(\sqrt{\frac{7}{2}}\) cos θ, y = \(\sqrt{\frac{7}{2}}\) sin θ, (0 ≤ θ ≤ 2π)

(iv) (x – 3)² + (y – 4)² = 8²
Solution:
From the given equation,
centre C(h, k) = (3, 4) and radius r = 8
∴ Parametric equations are x = h + r cos θ, y = k + r sin θ
x = 3 + 8 cos θ, y = 4 + 8 sin θ, (0 ≤ θ ≤ 2π)

(v) x² + y² – 4x – 6y – 12 = 0 (Mar. ’11)
Solution:
Centre of the given circle C(h, k) = (2, 3)
and radius = \(\sqrt{4+9+12}\) = 5
∴ Parametric equations are x = h + r cos θ, y = k + r sin θ
x = 2 + 5 cos θ, y = 3 + 5 sin θ, (0 ≤ θ ≤ 2π)

(vi) x² + y² – 6x + 4y – 12 = 0 (Mar. ’10)
Solution:
Centre of the given circle C(h, k) = (3, -2)
and radius = \(\sqrt{4+9+12}\) = 5
∴ Parametric equations are x = h + r cos θ, y = k + r sin θ
x = 3 + 5 cos θ, y = -2 + 5 sin θ, (0 ≤ θ ≤ 2π)

II.

Question 1.
If the abscissae of points A, B are the roots of the equation x² + 2ax – b² = 0 and ordinates of A, B are the roots of y² + 2py – q² = 0 then find the equation of circle for which \(\overline{\mathrm{AB}}\) is a diameter.
Solution:
Let A(x₁, y₁) and B(x₂, y₂) be the extremities of diameter \(\overline{\mathrm{AB}}\) of a circle.
Abscissae of points A, B are x₁, x₂ which are the roots of x² + 2ax – b² = 0.
∴ x₁ + x₂ = -2a, and x₁x₂ = -b²
Similarly given that ordinates of A, B are y₁, y₂ which are the roots of y² + 2py – q² = 0, then
y₁ + y₂ = -2p and y₁y₂ = -q²
∴ The equation of a circle with A, B as the extremities of diameter is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
x² – x(x₁ + x₂) + x₁x₂ + y² – y(y₁ + y₂) + y₁y₂ = 0
x² – x(-2a) – b² + y² – y(-2p) – q² = 0
x² + 2ax – b² + y² + 2py – q² = 0
x² + y² + 2ax + 2py – (b² + q²) = 0

Question 2.
(i) Show that A(3, -1) lies on the circle x² + y² – 2x + 4y = 0. Also, find the other end of the diameter through A.
Solution:
Substituting x = 3, y = -1 in LHS of the equation of circle we have
3² + (-1)² – 2(3) + 4(-1)
= 9 + 1 – 6 – 4
= 0
and A(3, -1) lies on the circle x² + y² – 2x + 4y = 0
Centre of the circle is, C = (1, -2)
Let the other end of the diameter be B(h, k).
Then C is the midpoint of AB.
∴ \(\frac{\mathrm{h}+3}{2}\) = 1 and \(\frac{\mathrm{k}-1}{2}\) = -2
h = -1 and k = -3
∴ The other end of the diameter through A is B = (-1, -3).

(ii) Show that A(-3, 0) lies on x² + y² + 8x + 12y + 15 = 0 and find the other end of the diameter through A.
Solution:
Substituting x = -3, y = 0 in LHS of the given equation of circle we have
(-3)² + 0² + 8(-3) + 12(0) + 15
= 9 – 24 + 15
= 0
Hence the point A(-3, 0) lies on x² + y² + 8x + 12y + 15 = 0
Let B (h, k) be the end of the diameter \(\overline{\mathrm{AB}}\).
The centre ‘C’ of the given circle is C = (-4, -6)
Since c is the midpoint of the diameter \(\overline{\mathrm{AB}}\).
we have \(\frac{\mathrm{h}-3}{2}\) = -4 and \(\frac{\mathrm{k}+0}{2}\) = -6.
h = -5 and k = -12
∴ The other end of the diameter is (-5, -12).

Question 3.
Find the equation of the circle which passes through (2, -3) and (-4, 5) and has the centre on 4x + 3y + 1 = 0.
Solution:
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……….(1)
Since (1) passes through (2, -3) we have
2² + (-3)² + 2g(2) + 2f(-3) + c = 0
4g – 6f + c = -13 ……….(2)
Similarly (1) passes through (-4, 5) we have
(-4)² + 5² + 2g(-4) + 2f(5) + c = 0
16 + 25 – 8g + 10f + c = 0
8g – 10f – c = 41 ………..(3)
Also given that the centre of the circle (1)
i.e., (-5, -f) lies on the line 4x + 3y + 1 = 0, we have
-4g – 3f + 1 = 0
4g + 3f – 1 = 0 ……….(4)
From equations (2) and (3)
4g – 6f + c = -13 and 8g – 10f – c = 41
12g – 16f = 28
3g – 4f = 7 ………(5)
Solving equations (4) and (5) we get


g = 1, f = -1
∴ From equation (3)
8(1) – 10(-1) – c = 41
-c = 41 – 18 = 23
c = -23
Hence from (1), the equation of the required circle is x² + y² + 2(1)x + 2(-1)y – 23 = 0
x² + y² + 2x – 2y – 23 = 0

Question 4.
Find the equation of a circle that passes through (4, 1), (6, 5) and has the centre on 4x + 3y – 24 = 0. (Mar. ’12)
Solution:
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ………(1)
The centre of the circle is (-g, -f)
Since (1) passes through (4, 1) we have
4² + 1² + 2g(4) + 2f(1) + c = 0
8g + 2f + c = -17 ………(2)
Also since (1) passes through the point (6, 5) we have
6² + 5² + 2g(6) + 2f(5) + c = 0
12g + 10f + c = -61 ……….(3)
Given that the centre (-g, -f) lies on the line 4x + 3y – 24 = 0, we have
-4g – 3f – 24 – 0
4g + 3f = -24 ……….(4)
From (2) and (3)
8g + 2f + c = – 17 and 12g + 10f + c = -61
We have -4g – 8f – 44 = 0
g + 2f + 11 = 0 ……….(5)
Solving (4) and (5)

g = -3, f = -4
Substituting in (2) we get
8(-3) + 2(-4) – c = -17
-24 – 8 + c = -17
c = – 17 + 32 = 15
∴ From (1), the equation of the required circle is x² + y² + 2(-3)x + 2(-4)y + 15 = 0
x² + y² – 6x – 8y + 15 = 0

Question 5.
Find the equation of the circle which is concentric with x² + y² – 6x – 4y – 12 = 0 and passing through (-2, 14).
Solution:
The equation of the given circle is
x² + y² – 6x – 4y – 12 = 0 ………(1)
The equation of the circle which is concentric with the given circle (1) is
x² + y² – 6x – 4y + λ = 0 ……….(2)
where λ is a constant.
Circle (2) is passing through (-2, 14), and hence
4 + 196 + 12 – 56 + λ = 0
λ + 156 = 0
λ = -156
∴ The equation of a circle that is concentric with a circle (1) is x² + y² – 6x – 4y – 156 = 0.

Question 6.
Find the equation of the circle whose centre the lies on X-axis and passes through (-2, 3) and (4, 5). (Mar. ’10)
Solution:
Let the equation of a circle whose centre lies on the X-axis be
x² + y² + 2gx + c = 0 ………(1)
Since the circle passes through (-2, 3) we have
4 + 9 – 4g + c = 0
4g – c – 13 = 0 ……….(2)
Also, circle (1) passes through (4, 5) we have
16 + 25 + 8g + c = 0
8g + c + 41 = 0 ………(3)
Solving (2) and (3) we get

∴ From (1) we have the equation of the circle is
\(x^2+y^2+2\left(-\frac{7}{3}\right) x-\frac{67}{3}=0\)
3(x² + y²) – 14x – 67 = 0

Question 7.
If ABCD is a square then show that the points A, B, C, and D are concyclic. (May ’09)
Solution:
Given that ABCD is a square
and Let AB = BC = CD = DA = a.

The two adjacent sides \(\overline{\mathrm{AB}}, \overline{\mathrm{AD}}\) are taken as coordinate axes.
∴ A = (0, 0), B = (a, 0), C = (a, a), D = (0, a).
Let the equation of the circle passing through A, B, D be
x² + y² + 2gx + 2fy + c = 0 ……….(1)
since (1) passes through (0, 0) we have c = 0
since (1) passes through B(a, 0), we have
a² + 0 + 2g(a) + 2f(0) + c = 0
a² + 2ga = 0 (∵ c = 0)
g = \(\frac{-a^2}{2 a}=\frac{-a}{2}\)
since (1) passes through C(0, a) we have
0 + a² + 2g(0) + 2f(a) + c = 0
a² + 2fa = 0 (∵ c = 0)
∴ The equation of the circle passing through points A, B, and D is
\(\mathrm{x}^2+\mathrm{y}^2-2\left(\frac{\mathrm{a}}{2}\right) \mathrm{x}-2\left(\frac{\mathrm{a}}{2}\right) \mathrm{y}=0\) …….(1)
Substituting the point C(a, a) in LHS of (2)
a² + a² – a² – a² = 0
equation (2) is satisfied.
Hence points A, B, C, D are concyclic.

III.

Question 1.
Find the equation of the circle passing through each of the following three points.
(i) (3, 4), (3, 2), (1, 4)
Solution:
Here (x₁, y₁) = (3, 4), (x₂, y₂) = (3, 2), (x₃, y₃) = (1, 4)
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(9 + 16)
= -25
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(9 + 4)
= -13
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(1 + 16)
= -17
The equation of a circle passing through the given three points is

-4(-51 + 13) – 25(12 – 2)
= 3(18) – 4(-38) – 250
= 54 + 142 – 250
= -44
∴ Equation of required circle is -4(x² + y²) + 16x + 24y – 44 = 0
x² + y² – 4x – 6y + 11 = 0

(ii) (1, 2), (3, -1), (5, -6)
Solution:
Let (x₁, y₁) = (1, 2), (x₂, y₂) = (3, -4), (x₃, y₃) = (5, -6)
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(1 + 4)
= -5
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(9 + 16)
= -25
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(24 + 36)
= -61
The equation of a circle passing through the given three points is


= 1(244 – 150) – 2(-183 + 125) – 5(-18 + 20)
= 94 – 2(-58) – 10
= 94 + 116 – 10
= 200
∴ Equation of required circle is 8(x² + y²) – 176x – 32y + 200 = 0
x² + y² – 22x – 4y + 25 = 0.

(iii) (2, 1), (5, 5), (-6, 7)
Solution:
(x₁, y₁) = (2, 1), (x₂, y₂) = (5, 5), (x₃, y₃) = (-6, 7)
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(4 + 1)
= -5
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(25 + 25)
= -50
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(36 + 49)
= -85
The equation of the circle passing through the above three non-collinear points is given by


= -150 + 725 – 325
= 725 – 475
= 250
∴ Equation of required circle is 50(x² + y²) + 50x – 600y + 250 = 0
x² + y² + x – 12y + 5 = 0.

(iv) (5, 7), (8, 1), (1, 3) (June ’10)
Solution:
(x₁, y₁) = (5, 7), (x₂, y₂) = (8, 1), (x₃, y₃) = (1, 3)
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(25 + 49)
= -74
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(64 + 1)
= -65
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(1 + 9)
= -10
The equation of the required circle passing through the above points is


= 5(-10 + 195) – 7(-80 + 65) – 74(24 – 1)
= 5(185) – 7(-15) – 74(23)
= 925 + 105 – 1702
= -672
Equation of required circle is -36(x² + y²) + 348x + 228y – 672 = 0
3(x² + y²) – 29x – 19y + 56 = 0.

Question 2.
(i) Find the equation of the circle passing through (0, 0) and making intercepts 4, 3 on the X-axis and Y-axis respectively.
Solution:
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……….(1)
Since the circle passes through the origin, c = 0
Given that the X-intercept = 4

∴ The equation of the required circle is x² + y² + 2(±2)x + 2(±\(\frac{3}{2}\))y = 0
x² + y² ± 4x ± 3y = 0.

(ii) Find the equation of the circle passing through (0, 0) and making 6 units on the X-axis and intercepting 4 units on the Y-axis.
Solution:
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……….(1)
If this passes through (0, 0) then c = 0.
Given that the X-intercept = 6
\(2 \sqrt{g^2-c}\) = 6
4g² = 36
g = ±3
and Y-intercept = 4
\(2 \sqrt{\mathrm{f}^2-\mathrm{c}}\) = 4
4f² = 16
f² = 4
f = ±2
∴ Equation of the required circle is x² + y² + 2(±3)x + 2(±2)y = 0
x² + y² ± 6x ± 4y = 0.

Question 3.
Show that the following four points in each of the following are concyclic and find the equation of the circle on which they lie.
(i) (1, 1) (-6, 0), (-2, 2), (-2, -8) (New Model Paper)
Solution:
To show that the given four points are concyclic, we have first to find the equation of the circle passing through the points
A(1, 1) = (x₁, y₁), B(-6, 0) = (x₂, y₂) and C(-2, +2) = (x₃, y₃) and verify whether the fourth point D(-2, -8) lies on the circle.
c₁ = \(-\left(\mathrm{x}_1^2+\mathrm{y}_1^2\right)\)
= -(1 + 1)
= -2
c₂ = \(-\left(\mathrm{x}_2^2+\mathrm{y}_2^2\right)\)
= -(36 + 0)
= -36
c₃ = \(-\left(\mathrm{x}_3^2+\mathrm{y}_3^2\right)\)
= -(4 + 4)
= -8
The equation of the circle passing through points A, B, C is given by

= 1(0 + 72) – 1(48 – 72) – 2(-12 + 0)
= +72 + 24 + 24
= 120
∴ The equation of the circle passing through the points A, B, C is -10(x² + y²) – 40x – 60y + 120 = 0
(x² + y²) + 4x + 6y – 12 = 0
Substituting D(-2, -8) in LHS of above equation we get
4 + 64 – 8 – 48 – 12 = 0
Hence the given points A, B, C, D are concyclic.

(ii) (1, 2) (3, -4), (5, -6), (19, 8) (May ’11)
Solution:
Let A(1, 2) = (x₁, y₁), B = (3, -4) = (x₂, y₂), C = (5, -6) = (x₃, y₃) and D (19, 8).
To show that A, B, C, D are concyclic we have to find the equation of the circle passing through A, B, and C and verify whether D satisfies the resulting equation.
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(1 + 4)
= -5
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(9 + 16)
= -25
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(25 + 36)
= -61
The equation of the circle passing through points A, B, C is given by

= 1(244 – 150) – 2(-183 + 125) – 5(-18 + 20)
= 94 + 116 – 10
= 200
∴ The equation of the circle passing through A, B, C is 8(x² + y²) – 176x – 32y + 200 = 0
x² + y² – 22x – 4y + 25 = 0.
Substituting (19, 8) in LHS of the above equation
(19)² + 64 – 22(19) – 4(8) + 25 = 0
361 + 64 – 418 – 32 + 25 = 0
Hence points A, B, C, D are concyclic.

(iii) (1, -6) (5, 2), (7, 0), (-1, -4)
Solution:
Let A(1, -6) = (x₁, y₁), B = (5, 2) = (x₂, y₂), C = (5, -6) = (x₃, y₃) and D(-1, -4)
We first find the equation passing through points A, B, C.
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(1 + 36)
= -37
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(25 + 4)
= -29
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(49 + 0)
= -49
The equation of the circle passing through points A, B, C is

\(\left|\begin{array}{lll}
\mathbf{x}_1 & \mathbf{y}_1 & \mathrm{c}_1 \\
\mathbf{x}_2 & \mathbf{y}_2 & \mathrm{c}_2 \\
\mathrm{x}_3 & \mathbf{y}_3 & \mathrm{c}_3
\end{array}\right|=\left|\begin{array}{ccc}
1 & -6 & -37 \\
5 & 2 & -29 \\
7 & 0 & -49
\end{array}\right|\)
= 1(-98) + 6(-245 + 203) – 37(-14)
= -98 + 6(-42) + 518
= -98 – 252 + 518
= -350 + 518
= 168
∴ The equation of the circle passing through the points A, B, C is -24(x² + y²) + 144x – 96y + 168 = 0
(x² + y²) – 6x + 4y – 7 = 0 represents a circle.
Substituting D(-1, -4) in LHS of above equation
1 + 16 + 6 – 16 – 7 = 0, the equation is satisfied.
Hence points A, B, C, D are concyclic.

(iv) (9, 1), (7, 9), (-2, 12), (6, 10)
Solution:
Let A = (9, 1) = (x₁, y₁), B = (7, 9) = (x₂, y₂) C = (-2, 12) = (x₃, y₃) and D = (6, 10)
We first find the equation of a circle passing through points A, B, C.
To show that the four points A, B, C, D are concyclic
we verify whether point D lies on the circle or not.
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(81 + 1)
= -82
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(49 + 81)
= -130
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(4 + 144)
= -148
The equation of the circle passing through points A, B, C is


= 9(-1332 + 1560) – 1(-1036 – 260) – 82(84 + 18)
= 9(228) + 1296 – 82(102)
= 2052 + 1296 – 8364
= 3348 – 8364
= -5016
∴ The equation of the circle passing through A, B, C is 66(x² + y²) – 396y – 5016 = 0
x² + y² – 6y – 76 = 0
Substituting D(6, 10) in LHS of the above equation. We get
36 + 100 – 60 – 76 = 0
∴ Points A, B, C, D are concyclic.

Question 4.
If (2, 0), (0, 1), (4, 5), and (0, c) are concyclic then find c.
Solution:
Let A = (2, 0) = (x₁, y₁), B = (0, 1) = (x₂, y₂) and C = (4, 5) = (x₃, y₃)
We have to find the equation of a circle passing through A, B, C.
c₁ = \(-\left(x_1^2+y_1^2\right)\)
= -(4 + 0)
= -4
c₂ = \(-\left(x_2^2+y_2^2\right)\)
= -(0 + 1)
= -1
c₃ = \(-\left(x_3^2+y_3^2\right)\)
= -(16 + 25)
= -41
The equation of the circle passing through points A, B, C is given by

= 2(-41 + 5) – 4(-4)
= 2(-36) + 16
= -72 + 16
= -56
∴ The equation of the circle passing through the points A, B, C is -12(x² + y²) – 52x + 68y – 56 = 0
12(x² + y²) – 52x – 68y + 56 = 0
3(x² + y²) – 13x – 17y + 14 = 0
Given that four points A(2, 0), B(0, 1), C(4, 5), and D(0, c) are concyclic, point D must lie on the above circle.
3(c²) – 13(0) – 17(c) + 14 = 0
3c² – 17c + 14 = 0
3c² – 14c – 3c + 14 – 0
3c(c – 1) – 14(c – 1) = 0
c = 1 or c = \(\frac{14}{3}\)
c = 1 is not admissive and hence c = \(\frac{14}{3}\).

Question 5.
Find the equation of the circumcircle of the triangle formed by the straight lines given in each of the following.
(i) 2x + y = 4, x + y = 6, x + 2y = 5
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L₁ = 2x + y – 4 = 0
L₂ = x + y – 6 = 0
L₃ = x + 2y – 5 = 0
Suppose L₁, L₂; L₂, L₃; L₃, L₁ intersect at A, B and C respectively.
Consider a curve whose equation is
k(2x + y – 4) (x + y – 6) + l(x + y – 6) (x + 2y – 5) + m(x + 2y – 5) (2x + y – 4) = 0 ……….(1)
We can verify that the curve passes through A, B, C. So it represents a circle.
If equation (1) represents a circle then
coefficient of x² = coefficient of y²
2k + l + 2m = k + 2l + 2m
k – l = 0 ………..(2)
coefficient of xy = 0
3k + 3l + 5m = 0 ………(3)
solving k – l + 0m = 0 and 3k + 3l + 5m = 0, we get

\(\frac{k}{-5}=\frac{l}{-5}=\frac{m}{6}\)
So the required equation is -5(2x + y – 4)(x + y – 6) – 5(x + y – 6) (x + 2y – 5) + 6(x + 2y – 5) (2x + y – 4) = 0
-5[2x² + 2xy – 12x + xy + y² – 6y – 4x – 4y + 24] – 5[x² + 2xy – 5x + xy + 2y² – 5y – 6x – 12y + 30] + 6[2x² + xy – 4x + 4xy + 2y² – 8y – 10x – 5y + 20] = 0
-3x² – 3y² + 51x + 57y – 150 = 0
x² + y² – 17x – 19y + 50 = 0

(ii) x + 3y – 1 = 0, x + y + 1 = 0, 2x + 3y + 4 = 0
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L₁ = x + 3y – 1 = 0
L₂ = x + y + 1 = 0
L₃ = 2x + 3y + 4 = 0
Suppose L₁, L₂; L₂, L₃; L₃, L₁ intersect at A, B and C respectively.
Consider a curve whose equation is
k(x + 3y – 1) (x + y + 1) + l(x + y + 1)(2x + 3y + 4) + m(2x + 3y + 4) (x + 3y – 1) = 0 ……….(1)
We can verify that the curve passes through A, B, C. So it represents a circle.
If equation (1) represents a circle then
coefficient of x2 = coefficient of y2
k + 2l + 2m = 3k + 3l + 9m
2k + l + 7m = 0 ………(2)
coefficient of xy is zero.
4k + 5l + 9m = 0 ……….(3)
Solving (2) and (3), we get


So the required equation is
-13(x + 3y – 1) (x + y + 1) + 5(x + y + 1) (2x + 3y + 4) + 3(2x + 3y + 4) (x + 3y – 1) = 0
-13[x² + xy + x + 3xy + 3y² + 3y – x – y – 1] + 5[2x² + 3xy + 4x + 2xy + 3y² + 4y + 2x + 3y + 4] + 3[2x² + 3xy + 4x + 6xy + 9y² + 12y – 2x – 3y – 4] = 0
3x² + 3y² + 36x + 36y + 21 = 0
x² + y² + 12x + 12y + 7 = 0

(iii) 5x – 3y + 4 = 0, 2x + 3y – 5 = 0, x + y = 0
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L₁ = 5x – 3y + 4 = 0
L₂ = 2x + 3y – 5 = 0
L₃ = x + y = 0
Suppose L₁, L₂; L₂, L₃; L₃, L₁ intersect at A, B and C respectively.
Consider a curve whose equation is
k(5x – 3y + 4) (2x + 3y – 5) + l(2x + 3y – 5) (x + y) + m(x + y) (5x – 3y + 4) = 0 ………(1)
We can verify that the curve passes through A, B, C. So it represents a circle.
If equation (1) represents a circle then
coefficient of x² = coefficient of y²
10k + 2l + 5m = -9k + 3l – 3m
19k – l + 8m = 0 ……….(2)
coefficient of xy is zero.
9k + 5l + 2m = 0 ……….(3)
Solving (2) and (3) we get


So the required equation is
-21(5x – 3y + 4) (2x + 3y – 5) + 17(2x + 3y – 5) (x + y) + 52(x + y) (5x – 3y + 4) = 0
-21[10x² + 15xy – 25x – 6xy – 9y² + 15y + 8x + 12y – 20] + 17[2x² + 2xy + 3xy + 3y² – 5x – 5y] + 52[5x² – 3xy + 4x + 5xy – 3y² + 4y] = 0
84(x² + y²) + 480x – 444y + 420 = 0
7(x² + y²) + 40x – 37y + 35 = 0
49(x² + y²) + 280x – 259y + 245 = 0

(iv) x – y – 2 = 0, 2x – 3y + 4 = 0, 3x – y + 6 = 0
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L₂ = x – y – 2 = 0
L₂ = 2x – 3y + 4 = 0
L₃ = 3x – y + 6 = 0
Suppose L₁, L₂; L₂, L₃; L₃, L₁ intersect at A, B and C
consider a curve whose equation is
k(x – y – 2) (2x – 3y + 4) + l(2x – 3y + 4) (3x – y + 6) + m(3x – y + 6)(x – y – 2) = 0 ………(1)
We can verify that the curve passes through A, B, C.
So we find k, l, and m such that equation (1) represents a circle, Hence
coefficient of x² = coefficient of y²
2k + 6l + 3m = 3k + 3l + m
k – 3l – 2m = 0
coefficient of xy term = 0
-5k – 11l – 4m = 0
5k + 11l + 4m = 0 ……….(3)
Solving (2) and (3) we get

Hence from (1), the equation of a circle is
5(x – y – 2) (2x – 3y + 4) – 7(2x – 3y + 4) (3x – y + 6) + 13(3x – y + 6) (x – y – 2) = 0
5[2x² – 3xy + 4x – 2xy + 3y² – 4y – 4x + 6y – 8] – 7[6x² – 12xy + 12x – 9xy + 3y² – 18y + 12x – 4y + 24] + 13[3x² – xy + 6x – 3xy + y² – 6y – 6x + 2y – 12] = 0
7x² + 7y² – 168x + 112y – 364 = 0
x² + y² – 24x + 16y – 52 = 0

Question 6.
Show that the locus of the point of intersection of the lines x cos α + y sin α = a, x sin α – y cos α = b (α is a parameter) is a circle.
Solution:
The given lines are
x cos α + y sin α = a ………(1)
x sin α – y cos α = b ……….(2)
Let (x, y) be the point of intersection of (1) and (2).
The locus of the point (x, y) is obtained by eliminating a from equations (1) and (2).
Squaring and adding (1) and (2), we get
(x cos α + y sin α) (x sin α – y cos α) = a² + b²
x² cos²α + y² sin²α + 2xy cos α sin α + x² sin²α + y² cos²α – 2xy cos α sin α = a² + b²
x² (cos²α + sin²α) + y² (sin²α + cos²α) = a² + b²
x² + y² = a² + b²
∴ The locus of the point of intersection of the given lines is x² + y² = a² + b² is a circle.

Question 7.
Show that the locus of a point such that the ratio of the distance of it from two given points is constant k(≠ ±1) is a circle.
Solution:
Let P(x1, y1) be any point on the locus
and A = (-a, 0), B = (a, 0) be the two given points.
Given that PA : PB = k : 1