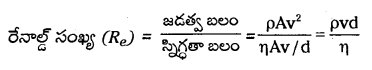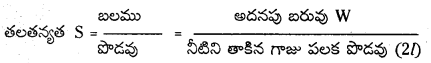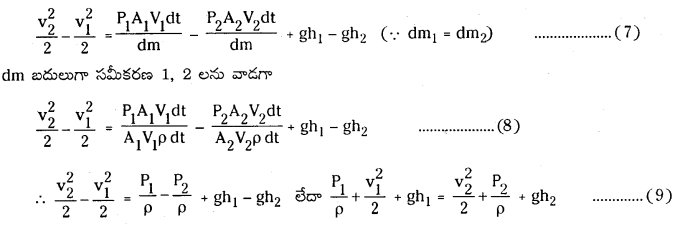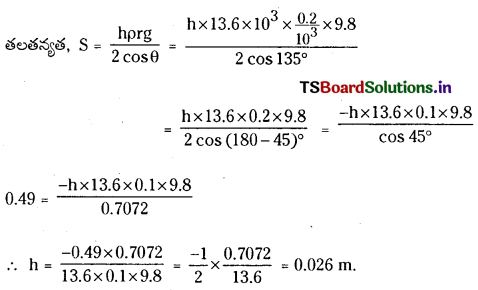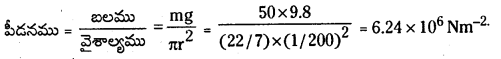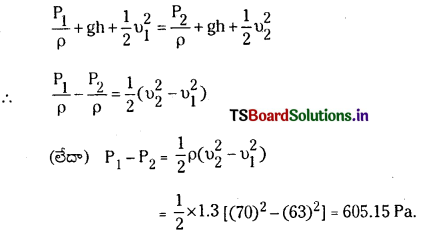TS Inter 1st Year

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(f)

Question 1.
If A, B, C are angles in a triangle, then prove that
(i) sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C
Answer:
sin 2A – sin 2K + sin 2C,
Given A + B + C = 180°
= 2 cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) sin\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + 2 sin C cos C
= 2 cos (A – B) sin (A – B) + 2 sin C cos C
= – 2 cos C sin (A – B) + 2 sin C cos C
(∵ A + B + C = 180° ⇒ cos(A + B) cos(180 – C) = – cos C and sin (A + B) = sin C)
= 2 cos C [sin C – sin (A – B)
= 2 cos C [sin(A + B) – sin(A – B)]
= 2 cos C[2 cos A sin B]
= 4 cos A sin B cos C = R. H. S

(ii) cos 2A – cos 2B + cos 2C = 1 – 4 sin A cos B sin C
Answer:
cos 2A – cos2B + cos 2C
= 2 sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) sin\(\left(\frac{2 \mathrm{~B}-2 \mathrm{~A}}{2}\right)\) + cos 2C
= 2 sin (A + B) sin (B – A) + cos 2C
= 2 sin C sin(B – A + 1 – 2 sin² C
= 1 + 2 sin C sin(B – A) – 2 sin² C
= 1 + 2sinC [sin (B – A) – sin C]
(∵ A + B + C = 180° = sin(A + B) sin C)
= 1 + 2 sin C[sin (B – A) – sin(A + B)]
= 1 – 2 sin C [sin (A – B) + sin (A + B)]
= 1 – 2 sin C[2 sin A cos B]
= 1 – 4 sin A cos B sin C = R.H.S

Question 2.
If A, B, C are angles in a triangle, then prove that
(i) sin A + sin B – sin C = 4 sin \(\frac{\mathrm{A}}{2}\) sin \(\frac{\mathrm{B}}{2}\) cos \(\frac{\mathrm{C}}{2}\)
Answer:

(ii) cos A + cos B – cos C = – 1 + 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\) (March 2006)
Answer:
LH.S = cos A + cos B – cos C

Question 3.
If A, B, C are angles in a triangle, then prove that
(i) sin²A + sin²B – sin²C = 2 sin A sin B cos C
Answer:
Given A + B+ C = 180°
We have L.H. S = sin² A + sin²B – sin² C
= sin²A+ sin (B + C) sin (B – C)
= sin² A + sin A sin (B – C)
= sin A [sin A + sin (B – C)]
= sin A[sin (B + C) + sin (B – C)]
= sin A[2 sin B cos C] = 2 sin A sin B cos C = R.H.S

(ii) cos²A + cos² B – cos² C = 1 – 2 sin A sin B cos C
Answer:
L.H.S = cos² A + cos² B – cos² C
= cos² A + 1 – sin² B – cos² C
(∵ A + B + C = 180° = cos (A + B) = – cos C)
= 1 – cos² C + cos² A – sin² B
= 1 -. cos² C + cos (A + B) cos (A – B)
= 1 – cos² C – cos C cos (A – B)
= 1 – cos C [ cos C + cos (A – B)]
= 1 – cos C ( cos (A – B) – cos (A + B)]
= 1 – cos C[2 sin A sin B]
= 1 – 2 sin A sin B cos C = R.H.S

Question 4.
If A + B + C = π, then prove that
(i) cos² \(\frac{A}{2}\) + cos² \(\frac{B}{2}\) + cos² \(\frac{C}{2}\) = 2(1 + sin \(\frac{A}{2}\) + sin \(\frac{B}{2}\) sin \(\frac{C}{2}\) ) (Mar. 2012) (March 2015-A.P&T.S)
Answer:
Given A + B + C = π
We have B + C = π – A and

(ii) cos² \(\frac{A}{2}\) + cos² \(\frac{B}{2}\) +- cos² \(\frac{C}{2}\) = 2 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\) ) (June 2010)
Answer:

Question 5.
In triangle ABC, prove that
(i) cos \(\frac{A}{2}\) + cos \(\frac{B}{2}\) + cos \(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\) (Mar 2010, Jun 2007)
Answer:
In ∆ABC, A + B + C = 180°

(ii) cos \(\frac{A}{2}\) + cos \(\frac{B}{2}\) – cos \(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi+\mathrm{A}}{4}\right)\) cos\(\left(\frac{\pi+\mathrm{B}}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\) (Mar 2005)
Answer:
In ∆ABC, A + B + C = 180°

(iii) sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) – sin\(\frac{C}{2}\) = – 1 + 4 cos\(\left(\frac{\pi+A}{4}\right)\) cos\(\left(\frac{\pi+B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\)
Answer:
In ∆ABC, A + B + C = 180° ……………………. (1)

Question 6.
If A + B + C = \(\frac{\pi}{2}\), then prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C
Answer:
LH.S = cos 2A + cos 2B cos 2C
= 2 cos \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + 1 – 2 sin² C
= 2 sin C cos (A – B) + 1 – 2 sin 2C
= 1 + 2 sin C [cos (A – B) – sin C]
(∵ A + B = \(\frac{\pi}{2}\) – C ⇒ cos (A + B) = cos (\(\frac{\pi}{2}\) – C) = sin C)
= 1 + 2 sin C[cos (A – B) – sin C]
= 1 + 2 sin C[cos (A – B) – cos(A + B)]
= 1 + 4 sin A sin B sin C = RHS.

Question 7.
If A + B + C = \(\frac{3 \pi}{2}\), then prove that
(i) cos² A + cos²B – cos² C = – 3 cos A cos B sin C
Answer:
L.H.S = cos²A + cos² B – cos² C
= cos² A + 1 – sin² B – cos² C
= (cos² A – sin² B) + (1 – cos²C)
= (cos² A – sin² B) + sin² C
= cos (A + B) cos (A – B) + sin²C
= – sin C cos (A – B) + sin² C
= sin C [sin C – cos (A – B)]
= sin C (- cos (A + B) – cos (A – B)]
= – sin C [cos (A + B) + cos (A – B)]
= – 2 cos A cos B sin C
(Given A + B + C = \(\frac{3 \pi}{2}\)
cos (A + B) = cos (270 – c) = – sin C)

(ii) sin 2A + sin 2B – sin 2C = – 4 sin A sin B cos C
Answer:
A + B + C = \(\frac{3 \pi}{2}\)
LH.S = sin 2A + sin 2B – sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) – sin 2C
= 2 sin (A + B) cos (A – B) – 2 sin C cos C
= – 2 cos C cos (A – B) – 2 sin C cos C
= – 2 cos C (cos (A – B) + sin C]
= – 2 cos C[cos (A – B) – cos(A + B)]
= – 2 cos C [ 2 sin A sin B]
= – 4 sin A sin B cos C R.H.S
(∵ A + B = 270 – C
⇒ cos(A + B) = cos(270 – C) = – sin C)

Question 8.
If A + B + C = 0 then prove that
(i) sin 2A + sin 2B – sin 2C = – 4 sin A sin B sin C
Answer:
Given A + B + C = O
∴ cos(B + C) = cos A and sin (B + C) = – sin A
L.H.S = sin 2A + sin 2B + sin 2C
= 2 sin (A+B) cos (A – B) + 2 sin C cos C
= – 2 sin C cos (A – B) + 2 sin C cosC
= 2 sin C [cos C – cos(A – B)]
= 2 sin C [cos (A + B) – cos(A – B)]
= – 4 sin C sin A sin B
= R.H.S

(ii) sin A + sin B – sin C = – 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)
Answer:
sin A + sin B – sin C

Question 9.
If A + B + C + D = 2π, then prove that
(i) sin A – sin B + sin C – sin D
= – 4 cos \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{A+C}{2}\right)\) cos \(\left(\frac{A+D}{2}\right)\)
Answer:
sin A – sin B + sin C – sin D

(ii) cos 2A + cos 2B + cos 2C + cos 2D = 4 cos (A + B) cos (A + C) cos (A +D)
Answer:
A + B + C + D = 360°
⇒ C + D = 360° – (A + B)
L.H.S = 2 cos (A + B) cos (A – B) + 2 cos (C + D) cos (C – D)
= 2 cos (A + B) cos (A – B) + 2 cos [360 – (A + B)] cos (C – D)
= 2 cos (A + B) cos (A – B) + 2 cos (A + B) cos (C – D)
= 2 cos (A + B) [cos (A – B) + cos (C – D)]
= 2 cos (A + B)

= 4 cos (A + B) cos [- 180 + (A + C)] cos [- 180 + (A + D)]
= 4 cos (A + B) cos (A + C) cos (A + D)

Question 10.
If A + B + C = 2S, then prove that
(i) sin (S – A) + sin (S – B) + sin C = 4 cos \(\left(\frac{S-A}{2}\right)\) cos \(\left(\frac{S-B}{2}\right)\) sin \(\frac{C}{2}\) (Jun 2008)
Answer:
Given A + B + C = 2S
LHS = sin(s – A) + sin (s – B) + sin C

(ii) cos (s – A) + cos (S – B) + cos C = – 1 + 4 cos \(\left(\frac{S-A}{2}\right)\) cos \(\left(\frac{S-B}{2}\right)\) cos \(\frac{C}{2}\)
Answer:
Given A + B + C = 2S
L.H.S

Telangana TSBIE TS Inter 1st Year English Study Material Revision Test-IV Exercise Questions and Answers.

TS Inter 1st Year English Study Material Revision Test-IV

Time : 1 1/2 Hrs.
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) A voice shouting ‘Relax’ penetrated into me above the noise of the crowd.
Answer:
Introduction :
This sentence is taken from Roger Bannister’s inspirational essay The First Four Minutes’. It is his personal experience.

Context & Explanation:
Bannister looked at the flag as he lined up for the start. The flag swayed gently. The race started. He understood that he was going very slow. He himself shouted ‘Faster’. His worry increased when he heard the first lap time 57.5 seconds. In that excitement his knowledge of pace had deserted him. At one and a half laps he was still worrying about the pace. Then a voice shouting “Relax” penetrated into him above the noise of the crowd. He followed it and started relaxing. There was no pain and stress. Later, he came to know that it was his coach ‘Stampfl’s advice.

Critical Comment :
Dr. Roger Bannister narrates his glorious moments and second to second experience while running for the goal of one mile race.

b) The physical overdraft came only from greater will power.
Answer:
Introduction :
This sentence is taken from Roger Bannister’s inspirational essay The First Four Minutes’. It is his personal experience.

Context & Explanation :
Here, he describes the power of will power. Now, he had turned the last bend. There were only fifty yards more. His body exhausted all its energy. But, it went on running just the same. That energy came from greater will power. At that crucial time, determination, dedication and will-power lead his legs ahead. Thus, with all his energy and will power he could succeed.

Critical Comment :
He narrates his glorious moments and second to second experience while running for completing a one mile race.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) It is not growing like a tree In bulk, doth make Man better be;
Answer:
Introduction :
These are the opening lines of the impressive poem, The Noble Nature’ written by Ben Jonson. He is regarded as the second most popular of English dramatists, after Shakespeare.

Context & Explanation :
The poet employs examples from flora to drive home his point. He straight away introduces the main idea how to become a better man. But, mere bulk doesn’t make one great. Smartness, even in small measure, impresses and impacts everyone. Neither long life nor large size can help one attain nobility. Quality counts more than quantity. Motherwords, matter matters, not the magnitude!. To explain this, the poet compares man to both an Oak tree and a Lily.

Critical Comment :
The poem seeks to explain what makes Man noble in his life.

b) It was the plant and flower of Light.
Answer:
Introduction :
This line is taken from the poem, The Noble Nature penned by Ben Jonson. He is regarded as one of the major dramatists and poets of the Seventeenth Century.

Context & Explanation :
The poem says leading a meaningful life even for a short while is worthier than leading a long life with neither charm nor value. The core meaning of the poem centres round this single idea. The lily plant has a short life. It blooms in May and is very beautiful. Although the flower has the life span of a day and falls and dies by nightfall, it spreads beauty and delight in that short period. The poet feels, that a meaningful life like lily flower though short is what makes a man noble. Even though a man’s life is short, it can be a perfect life.

Critical Comment :
The poet advises one to lead a meaningful life-of light-like that of a lily.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) How did Roger Bannister feel in the first lap of the race ?
Answer:
Bannister narrates his eventual victory of the race in the essay. During the first lap of the rase, Bannister looked at the flag as he lined up for the start. The flag fluttered gently as the sails moved gently in Bernard Shaw’s Saint Joan. He felt complete silence on the ground.

When the gun fired for the second time, Brasher went into the lead and he slipped in behind him. It seemed his legs lost control of himself. He understood that he was going very slow. He himself shouted ‘Faster’. His worry increased when he heard the first lap time 57.5 seconds. In that excitement his knowledge of pace had deserted him. However, he could succeed.

b) What gave Dr. Bannister strength in the final spurt ?
Answer:
Dr. Roger Bannister was the first man to run the race of one mile in 3 minutes 59.4 seconds. He narrates his eventual victory of race in this essay. In the final spurt, he got the strength from his will power. He had turned the last bend. There was only 50 yards more to be run. His body tired and consumed all his energy. But, it went on running. That strength came from great will power. At that juncture, determination, dedication and strong will power lead him ahead. Therefore, he could succeed with his will power.

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Bulk does not make Man better be. How does the oak support this stand ?
Answer:
Ben Jonson’s poem, The Noble Nature is one of his most popular lyrics. This short poem discusses a noble thought in simple style. That profound message is expressed clearly with the help of example and images from nature. It highlights the point that equality counts more than quantity.

Growing physically like a bulky tree or living long like a sturdy Oak does not make a man noble being. The huge, strong a and aged Oak will soon become a lifelesss, ‘dry’ and withered piece of log. So too will be the fate of a man who is only blessed with long life and physical and material well being. Therefore, mere bulk doesn’t make Man better be. Matter matters, not the magnitude.

b) Explain with the example of the lily that size matters not but beauty counts a lot.
Answer:
Ben Jonson, in the poem, The Noble Nature talks about what makes a man noble. He compares man to a sturdy Oak and to a delicate Lily in order to explain this point. The Lily plant has a short life. It blooms in May and is very beautiful.

Although, the flower has the span of a day and dies by nightfall it spreads beauty and delight in that short period the poet feels that a meaningful life like the Lily flower, though short, is what makes a man noble and even though a man’s life is short it can be perfect life. People will continue to talk good about him even after he is gone. This is what actually makes a man noble, thus, beauty counts a lot.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Is the title, Sanghala Panthulu, apt to the story ? Explain.
Answer:
Suravaram Pratapa Reddy’s thought provoking Telugu story, SANG HALA PANTHUW is a social and historical narration. It was rendered into English by Elanaaga (Dr. N. Surendra). The story pictures the struggles and sufferings of innocent and ignorant villagers.

Ramasagaram village is just a representative of any village in Nizam’s rule. Timidity and lack of unity and awareness among the masses helped a handful of people to exploit the poor. A well-informed and good-intentioned gentleman (Panthulu) came to their rescue. He explained to the villagers about their rights. He helped them pick up courage and form into associations (SANGHALU). That ultimately solved their problems. Hence, the title perfectly suits the story.

b) Describe the result of the declaration by the Mohathemeem.
Answer:
Suravaram’s social story, “Sanghala Panthulu”, presents the pathetic plight of Ramasagaram villagers. Elanaaga translated this moving Telugu story into English. The police went on exploiting the innocent villagers ruthlessly. Sandhala Panthulu came to the rescue of the poor. The police were angry with Panthulu.

When they tried to arrest Panthulu, a good number of youth revolted against the police. The police complained against them. The Mohathemeem came to enquire into the incident. He found the police were guilty. He declared the dismissal, suspension and scaling down of different police personnel. The villagers felt happy. Their joy knew no bounds. Feasts followed. Justice prevailed.

Question 6.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

The news about the arrival of the elderly man from city had spread in the village by morning. The villagers said he was a tall stout man. He helped form associations in villages. He sported a kerchief like lawyers do. He brought a leather suitcase i which was full of books. He knew all the bigwigs in the city. He would do away with all our troubles.

Questions:
i) Name the story from which this passage is taken.
Answer:
Sanghala Panthulu

ii) Who does the phrase the elderly man refer to ?
Answer:
Sanghala Panthulu

iii) How would the elderly man help the villagers ?
Answer:
He would help the villagers form associations and solve their problems.

iv) What did he bring with him ?
Answer:
a leather suitcase, full of books

v) The villagers talked about the elderly man ……….. (fill in).
1) adversely
2) appreciatively
3) accusingly
4) arrogantly
Answer:
(2) appreciatively

vi) Find the Phrasal Verb used in the passage that means put an end to; eliminate.
Answer:
do(es) away with

vii) The word sported as used in this passage means ……….. (fill in)
1) game
2) athletics
3) wore
4) played
Answer:
(3) wore

viii) Find in the passage the antonym of lean.
Answer:
stout

Question 7.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

Maitri – Indeed a Friend in Need
The world is in a word, says Wordsmith. Words packed with positive vibrations can light up the dark world of narrowminded, selfish and loveless millions, says Ms. Jalandhara, a writer, guide, mentor and most importantly, healer ! An incarnation of simplicity and modesty, Ms Jalandhara was bom into the family of Gali Bala Sundara Rao (GBS), a godlike doctor and multifaceted personality. And she was married to Mr. Chandra Mohan, a versatile, multi-lingual cine star.

Yet, she shines like a star, uneclipsed between the two mighty personalities. With innumerable creative works – stories, novels etc., – to her credit, she seeks to promote peace in minds and homes with a missionary zeal. Unconditional and universal love is her panacea. Cite your problems to Maitri, a question-answer feature both online and offline, and prompt comes the solution in the form of thought-provoking counselling. Homes flourishing with smiles following her advice are innumerable all over the globe ! The true symbol of empowering woman !

Questions:
i) How can the dark world of millions be filled up with light ?
Answer:
Words packed with positive vibrations can light up the dark world of millions.

ii) What are the two traits highlighted here in the lead character’s personality ?
Answer:
simplicity and modesty

iii) Name the two prominent personalities mentioned here associated with her.
Answer:
Gali Bala Sundara Rao, her father and Mr. Chandra Mohan, her husband.

iv) What is her mission ?
Answer:
to promote peace in minds and homes

v) How does she seek to promote peace in minds and homes ?
Answer:
through her thought provoking counselling

vi) What is her panacea ?
Answer:
unconditional and universal love

vii) What does the central character stand for as a symbol ?
Answer:
as a symbol of empowering woman

viii) Write the word used in the passage to mean cure-for-all.
Answer:
panacea

Section – B

Question 8.
Match ANY EIGHT of the following words in Column-A with their meanings in Column-B. [8 × 1/2 = 4]
Questions:

Answer:
i) – f
ii) – j
iii) – h
iv) – b
y) – j
vi) – d
vii) – a
viii) – e
ix) – c
x) – g

Question 9.
Identify the parts of speech of ANY EIGHT of the following underlined words. [8 × 1/2 = 4]

It fluttered (1) more gently (2) now, and (3) the scene (4) from (5) Shaw’s Saint Joan flashed through (6) my mind, how she, at (7) her desperate (8) moment, waited (9) for the wind (10) to change.
Answer:
1) fluttered – verb
2) gently – adverb
3) and – conjunction
4) scene – noun
5) from – preposition
6) through – preposition
7) at – preposition
8) desperate – adjective
9) waited – verb
10) wind – noun

Question 10.
Fill ANY EIGHT of the following blanks with a, an or the. [8 × 1/2 = 4]

i) There was complete silence on _________ (1) ground ___________ (2) false start …… I felt angry that precious moments during __________ (3) lull in _________ (4) wind might be slipping by.
ii) Birbal told _________ (5) interesting story.
iii) Amitabh Bachan is __________ (6) famous actor.
iv) Today there is __________ (7) lot of progress in ___________ (8) field of communication.
v) I live in ________ (9) apartment. It is _________ (10) new one.
Answer:
i) 1 – the
2 – a
3 – the
4 – the

ii) 5 – an
iii) 6 – a

iv) 7 – a
8 – the

v) 9 – an
10 – a

Question 11.
Fill in ANY SIX of the following blanks with suitable prepositions. [6 × 1/2 = 3]

i) I felt suddenly and gloriously free __________ (1) the burden ________ (2) athletic ambition that I had been carrying _________ (3) years. No words could be invented _________ (4) such supreme happiness, eclipsing all other feelings.
ii) Chataway went ________ (5) the lead.
iii) There is no point ________ (6) the argument.
iv) I have not slept properly _________ (7) two days.
v) The shop is open _________ (8) 10 am ________ (9) 8 pm.
vi) I have been reading this book ________ (10) 2014.
Answer:
i) 1) of
2) of
3) for
4) for

ii) 5) into
iii) 6) in
iv) 7) for

v) 8) from
9) to

vi) 10) since

Question 12.
Fill in ANY THREE of the following blanks with suitable forms of the verbs given in brackets. [3 × 1 = 3]

1. This ________ (be) the moment when I _________ (make) my decision.
2. I _________ (have) a moment of mixed joy and anguish. When my mind ________ (take) over.
3. My sister ________ (just, receive) a call from her office.

Answer:

1. was, made
2. had, took
3. has just received

Question 13.
Rewrite ANY FOUR of the following sentences as directed. [4 × 1 = 4]

i) Brasher did not change the pace.
(Change the Voice.)
Answer:
The pace was not changed by Brasher.

ii) Someone already cast my vote.
(Change the Voice.)
Answer:
My vote was already cast. (by someone)

iii) Mother said to me, “Come home urgently.”
(Change to Indirect speech.)
Answer:
Mother has asked me to come home urgently.

iv) She said to me, “I will go to Warangal tomorrow.”
(Change to Indirect speech.)
Answer:
She told me that she would go to Warangal the following day.

v) He is more intelligent than I.
(Change to Positive degree.)
Answer:
I am not as intelligent as he.

vi) The noise in my ears was that of the faithful Oxford crowd.
(Add a Question Tag.)
Answer:
wasn’t it?

Telangana TSBIE TS Inter 1st Year English Study Material Revision Test-III Exercise Questions and Answers.

TS Inter 1st Year English Study Material Revision Test-III

Time: 1 1/2 Hrs.
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) Though the trees grown by her are worth several crores of rupees today, her life has no respite from poverty.
Answer:
Introduction :
These touching words are extracted from the internet-based inspired write up, The Green Champion – Thimmakka. It shows the magnificent achievement of an ordinary woman with an extraordinary commitment to conserve nature.

Context & Explanation :
Born into a poor family. Thimmakka did not go to school. She worked as a labourer. As she grew up, she was married to Chikkayya, a labourer. When they came to know that they could not beget children, they were not disappointed. They came up with the idea of planting saplings and nurturing them as their own children. It became their life mission. But, she suffers from poverty. Her sole source of income is the pension of Rs. 500/- given by the government. Thus, she is an example of simple living and high thinking.

Critical Comment :
These words describe her pains and problems.

b) Her intentions are evidently good as she has planted trees rich in biodiversity.
Answer:
Introduction :
These are the concluding words taken from the internet – based article, The Green Champion-Thimmakka. It describes her magnificent achievements in preserving the environment.

Context & Explanation :
Thimmakka and her husband started planting saplings and nurturing them as their own children. Even after the death of her husband, she pursuded her mission with the same determination and courage. She is 100 plus now and still cherishes the dream of planting more trees. She continues her fight against deforestation. Her contributions are truly remarkable. She proves that age is not a big problem if we aspire to do anything. So, she is a true inspiration to us to have good intentions towards society. Please plant a sapling and make the world a better place for our children. Even thousand mile journey begins with a single step.

Critical Comment :
The words describe her passion for planting trees and expanding her mission.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) Have you sighted anyone With shadows in his dusky eyes ?
Answer:
Introduction :
These are the opening lines of the poem, ‘The Beggar” written by Dr. Ammangi Venugopal, a popular Telugu poet. He has written in Telugu as Bichchagadu. It is translated into English by Elanaaga, (Dr. Surendra).

Context & Explanation :
The poem projects the intense grief and suffering of the farmers. A farmer today is misery incarnate. His eyes speak volumes about farmers’ sorrow. The poet minces no words in highlighting their woes. He opens the poem with a question. It identifies farmers with dark eyes that are filled with the shadows of their struggles. The reader, addressed as ‘you’, is forced to understand and sympathise with farmers. Therefore the lines play an important role in initiating the thought process effectively.

Critical Comment :
The poet portrays the pathetic plight of farmers. He is questioning the reader to make him to think about the farmers.

b) His stomach is full of infinite void
Answer:
Introduction :
This heart touching line is taken from the thought provoking poem, The Beggar’, penned by Dr. Ammangi Venugopal, a famous Telugu poet. His original Telugu poem, Bichchagadu is rendered into English by Elanaaga (Dr. Surendra).

Context & Explanation :
The poet tries to draw the attention of readers to the gravity of farmers problems. it is because farmers work hard. They help others. They are the food providers to all yet the irony is that they struggle to survive. They starve. They don’t find food for themselves, even a morsel ! Their stomachs get no food. They suffer from empty stomachs. Their emptiness is infinite. Thus, the poet highlights farmers’ woes and worries in a touching way. He also compels the readers to ponder over possible solutions.

Critical Comment:
Here the poet depicts the pathetic condition of farmers in a touching way.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Why did Thimmakka and her husband decide to plant trees ? Describe how hard they tried to succeed in their mission.
Answer:
This inspiring essay describes Thimmakka’s undying passion for planting trees even at an advanced age. It also insists the need to follow her selfless service in preserving and protecting nature.

Thimmakka was a poor and uneducated woman. She was married to Chikkayya. The couple didn’t get children. However, her husband was very supportive of her. WIth nothing in life to be cherish, Thimmakka thought of ending her life. Then, wisdom dawned. They decided to plant trees and nurture them as their children. They planted 10 banyan s. lings in the first year soon it became their life mission. Year after year the number increased. They not only planted them but tended them to maturity. They also fenced and guarded them. Now there exist around 8000 other trees planted by them.

b) Why was Thimmakka named Saalumarada ?
Answer:
The present internet-based essay, the Green Champion – Thimmakka describes the magnificent achievements of an ordinary woman with an excellent commitment to conserve nature. Thimmakka, a woman mre than 100 years in age, from Karnataka has been launded globally as the green champion for her planting mission. Thimmakka along with her husband planted over 8000 other trees.

Even after her husband’s death, she continued her mission of planting frees. Her outstanding work earned her the name Saalumarada, which means a row of trees in Kannada. Thimakka is popular as Saalumarada Thimmakka due to her work. She continues her fight against deforestation. Her contributions are truly remarkable. With her achievements, she is called Saalumarada Thimmakka.

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) List the abilities a farmer is endowed with, according to the poem.
Answer:
Dr. Ammangi Venugopal is a creative genius. He is well aware of the abilities of a farmer. In his poem, The Beggar, the poet minces no words in depicting farmers’ abilities. They are the food providers to all. Their eyes are dark with shadows of their struggles and sufferings. Their backs are bent with burden. Their hands are soiled and severed. Their feet bleed. Yet, their ability to produce food and satisfy others’ hunger remains fully active. They work hard and help others. They are capable of feeding millions. They reduce and satisfy the hunger of even skies. Thus, the poem is endowed with the abilities of a farmer.

b) The poet addresses the reader as “you” and talks about the farmer as “my farmer”. Explain the. significance in a paragraph.
Answer:
Dr. Ammangi Venugopal has written the poem in Telugu as Bichchagadu. It is translated into English as the ‘The Beggar’ by Elanaga, (Dr. Surendra) the poem portrays the pitiable condition of the farmers. In the last stanza the poet describes the farmer as a beggar.

It is due to his condition at present society. The farmers are suffering from lack of food. They become beggars. They are at the thresholds for food. So, the poet tells the reader that the beggar at the threshold of the reader is none other than the farmer. The reader is addressed as ‘you’ to understand and sympathise with farmers. The poet tells about the farmer as ‘My farmer’. The reader is moved to ponder over the problem and find away out.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Is the title, The Short-sighted Brothers, apt to the story ? Explain.
Answer:
Yes. The name “The Short-sighted Brothers” and the content of the story look like made-for-each-other things. The title matches perfectly well with the theme. Three brothers are the lead characters. All the three brothers were very short-sighted. It was a physical disability. And they all suffered from the related mental disability too. They failed to see the possible result of their crooked plans. They were selfish. They were greedy. They tried to cheat one another. Finally their follies were exposed. As the entire story deals with their physical and mental short sightedness, the title is appropriate to this ancient chinese folk tale.

b) How did the three brothers try to outsmart one another ?
Answer:
‘The Short-sighted Brothers” is a famous Chiness folk story. It exposes the folly of the three brothers. All the three brothers were very short-sighted. Even their personality suffered from the same flaw. They tried to deceive themselves and one another. The youngest brother one day proposed to take charge of their family finances.

He cited his eldest brother’s short sightedness to support his claim. The second brother too joined the race. The eldest brother proposed a test to prove the power of their sight. They should read the inscription on the newly installed tablet on the door way of the nearest monastery. To outsmart one another, each met the monk secretly and learnt about the writing on it.

Question 6.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

“I have my doubts about that,” said the eldest brother. “Let’s settle this once and for all. I’ve heard the monastery is putting up a tablet inscribed with a saying, above the main doorway, tonight. Let’s go there tomorrow and test our vision. Whoever can read the inscription with the least strain will get charge of our money. Agreed ?

Questions:
i) Name the story from which this passage is taken.
Answer:
The Short-sighted Brothers.

ii) Who does “I” in the paragraph refer to ?
Answer:
“I” in the paragraph refers to the eldest brother.

iii) ’What did the speaker want to settle once and for all ?
Answer:
as to who among the three brothers had a better sight.

iv) What did the speaker come to know of ?
Answer:
of the monastery putting up a tablet inscribed with a saying, above the main doorway, that night.

v) Where should they go to get their vision tested, the following day ?
Answer:
to the monastery

vi) Who would get the charge of their money, according to the proposal ?
Answer:
the one who could read the inscription with the least strain

vii) When was the monastery putting up a tablet above their doorway ?
Answer:
on that night (when this discussion in the story was going on)

viii) Write the word that is used in the passage that means a place where monks live.
Answer:
monastery

Question 7.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

Where Shadow Stays Stable
Shadows keep changing positions and sizes, if the distance between the source of light and the object changes ! But at Chaya Someswara Temple at Panagal, near Nalgonda, the shadow (Chaya, hence the name of the temple) of pillars stays constant on the lingam at any time, despite changes in the above said distance. The pillars of ardhamandapa and open spaces near the central shrine were designed and placed in such a way by the then architects as to produce this effect of stable shadow on the lingam all through the day. A miracle one must see to believe ! Believed to have been built in the 11 century AD, the construction credits go to Kanduru Chodas. This thrikutalayam has three shrines dedicated to Lord Shiva, Vishnu and Surya. A common hall, mandapam, keeps these three shrines as one complex. Many intricately carved pillars around this mandapam depict scenes from the Ramayana, the Mahabharatha and the Pumas !

Questions:
i) Describe the nature of shadows.
Answer:
Shadows keep changing positions and sizes if the distance between the source of light and the object changes.

ii) Give an example of exception to this nature of shadows.
Answer:
the shadow of pillars at Chaya Someswara Temple at Panagal, near Nalgonda.

iii) Why is the temple called Chaya Someswara Temple ?
Answer:
‘Chaya’ in Telugu, means shadow. As he shadow here stays stable all through the day on the Lingam. the temple is called Chaya Someswara Temple.

iv) What makes the te.mple also known as thrikutalayam ?
Answer:
as there are three shrines

v) Who is believed to have built this unique temple ?
Answer:
Kanduru Chodas

vi) Where does the shadow fall all through the day ?
Answer:
on the Linga

vii) Is it the shadow of a single object ? Support your answer with a sentence from the passage.
Answer:
No. “The pillars of … produce this effect of stable shadow.”

viii) What do the pillars depict ?
Answer:
scenes from the Ramayana, the Mahabharatha and the Puranas

Section – B

Question 8.
Match ANY SIX of the following words in Column-A with their meanings in Column- B. [6 × 1/2 = 3]
Questions :

Answer:
i) – h
ii) – g
iii) – j
iv) – i
v) – a
vi) – c
vii) – e
viii) – b
ix) – f
x) – d

Question 9.
Identify the parts of speech of ANY SIX of the following underlined words. [6 × 1/2 = 3]

In spite of (1) receiving hundreds (2) of (3) awards, Saalumarada Thimmakka (4) remains (5) an innocent and (6) a modest (7) person (8).
Answer:
1) in spite of – preposition
2) hundreds – noun
3) of – preposition
4) Thimmakka – noun
5) remains – verb
6) and – conjunction
7) modest – adjective
8) person – noun

Question 10.
Fill ANY EIGHT of the following blanks with a, an or the. [8 × 1/2 = 4]

i) Thimmakka is __________ (1) individual who has brought worldwide recognition to _________ (2) state of Karnataka through her incredible and massive environmental services.
ii) Unfortunately, she is dependent on __________ (3) pension of Rs. 500/- given by ________ (4) government, which is __________ (5) sole source of her income.
iii) Would you like ________ (6) apricot ?
iv) _________ (7) Ramayana is ________ (8) epic.
v) Sarojini Naidu was not only _________ (9) poet but also ________ (10) freedom fighter.
Answer:
i) 1 – an
2 – the

ii) 3 – a
4 – the
5 – the

iii) 6 – an

iv) 7 – The
8 – an

v) 9 – a
10 – a

Question 11.
Fill in ANY SIX of the following blanks with suitable prepositions. [6 × 1/2 = 3]

i) The mission _________ (1) preserving the environment is taken forward ________ (2) Thimmakka’s foster son, Sri Umesh. B.N. Umesh has been planting and tending to trees ________ (3) the roads, schools, public places, and _________ (4) the mountain and hilltops.
ii) ________ (5) the time I reached my office, I was late _________ (6) a few minutes.
iii) He prefers coffee _________ (7) tea.
iv) He fell ________ (8) a bicycle.
v) He is good _________ (9) English, but weak _________ (10) Mathematics.
Answer:
i) 1) of
2) by
3) along
4) on

ii) 5) By
6) by

iii) 7) to

iv) 8) off

v) 9) at
10) in

Question 12.
Fill in ANY THREE of the following blanks with suitable forms of the verbs given in brackets. [3 × 1 = 3]
i) Both Thimmakka and her husband _________ (start) with 10 banyan saplings on either side of the road along a stretch of 4 km in the first year.
ii) Thimmakka and her husband _________ (take) care of the plants just like their children. Every year, the count of these trees (keep) increasing.
iii) Look ! The bird _________ (fly).
iv) Suresh ran to the station but the train _________ (leave).
v) Let us walk fast. We must reach home before it ________ (get) dark.
Answer:
i) started
ii) took, kept
iii) is flying
iv) had left
v) gets

Question 13.
Supply the missing letters to ANY SIX of the following words. [6 × 1/2 = 3]
i) hi _ _ top
ii) ba _ _ an
iii) r _ _ time
iv) su _ _ icient
v) m _ _ ntain
vi) mi _ _ ion
vii) in _ _ edible
viii) mons _ _ n
ix) ca _ _ y
x) reco _ _ ition
Answer:
i) hilltop
ii) banyan
iii) routine
iv) sufficient
v) mountain
vi) mission
vii) incrdible
viii) monsoon
ix) carry
x) recognition

Question 14.
Identify the silent consonant letters in ANY SIX of the following words. [6 × 1/2 = 3]

i) foreign
ii) what
iii) psalm
iv) high
v) would
vi) often
vii) depot
viii) pneumonia
ix) island
x) knot
Answer:
i) foreign – g
ii) what – h
iii) psalm – p, l
iv) high – g
v) would – l
vi) often – t
vii) depot – t
viii) pneumonia – p
ix) island – s
x) knot – k

Telangana TSBIE TS Inter 1st Year English Study Material Revision Test-II Exercise Questions and Answers.

TS Inter 1st Year English Study Material Revision Test-II

Time: 1 1/2 Hrs.
Marks: 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) Yes, my first rank slipped to the second.
Answer:
Introduction:
This sentence is taken from the prose piece, Father, Dear Father written by Raj Kinger. Actually this is an article published in the English daily, The Hindu.

Context & Explanation: Rahul is the class topper in his school. His first rank slips to the second. Admitting the guilt, he writes a letter to his father. His father’s advice to think before studying, before answering the papers makes him think and think. The word think makes him reflect on several issues including many pitfalls in our education system. Further, he says that the sense of life is not taught to him. He feels that the education should give a feel of life to him and should be useful in life.

Critical Comment:
Rahul, the class topper in his school, presents his anguish over the present education system through a letter to his father in this context.

b) And she was cross. She said go ask the guy who keeps gardening things.
Answer:
Introduction:
This sentence is taken from the prose piece, Father, Dear Father written by Raj Kinger. Actually this is an article published in the English daily, The Hindu.

Context & Explanation:
Rahul has an unpleasant experience with his Biology teacher. When his rose plant is attacked by pests he seeks advice of his teacher to save his plant. But, the teacher gets irritated as she thinks it a question out of their syllabus and asks him to approach a gardener for advice. The teacher serves as a warning to all those teachers who do not show any interest or reverence towards their profession. Therefore, Rahul criticizes such an education system which curbs independent thinking and encourages blind adherence to whatever the teacher teaches.

Critical Comment:
Here, Rahul narrates the incident of his biology teacher not able to help him with a practical science related problem.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) O my Luve’s like the melodie That’s sweetly play’d in tune.
Answer:
Introduction :
This couplet is taken from the poem, A Red Red Rose written by Robert Burns. It is one of the best lyrics of English poetry. It blends the eternity of love with the mortality of life.

Context & Explanation :
The poet begins by using a simile to compare his love to a rose. In other words, his love is like a flower that has just bloomed in June. His love is fresh and is bursting with life. His feelings are very profound.

Critical Comment : It is an address to the speaker’s lover to whom he swears eternal love and loyalty.

b) And fare thee weel, my only Luve And fare thee weel a while !
Answer:
Introduction :
This couplet is taken from the beautiful lyric, A Red Red Rose’ written by Robert Burns. It is one of the best lyrics of English poetry. It blends the eternity of love with the mortality of life.

Context & Explanation :
The speaker says that he will love his beloved forever. Even after the seas get dried up, all the rocks melt, and the sands of life exhaust their love stays alive. It will last forever. For the present, the speaker says good bye only to return soon, though the journey is to a far off place the poem blends the eternity of love with the mortality of life.

Critical Comment :
The poet makes several promises to love his beloved forever.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]
a) Write a paragraph on the present day education system as described in Rahul’s letter.
Answer:
Rai Kinger’s Father, Dear Father is a heart wrenching letter addressed to a father by his son, Rahul. In his letter, Rahul condemns our and define rote educational system and explains the reason for losing his first rank. If was due to his disagreement with his teacher regarding an answer in English Grammar.

Although the teacher was wrong, he was adamant that he was correct. Rahul criticizes such an education system which curbs independent thinking and encourages blind adherence to whatever the teacher teachers. Thus, he condemns the emphasis placed on examinations, marks and ranks. For him practical education matters more than theoretical.

b) What is the attitude of teachers towards learners as illustrated in Father, Dear Father ?
Answer:
Raj Kinger’s Father, Dear Father is a thought provoking commentary on the present education system. It highlights the defects in the mind sets of parents, learners, teachers and the government bodies. It sets all to a new wave of thinking. However, the attitude of teachers towards learners are rude and adamant.

When Rahul seeks adviœ of his Biology teacher to save his rose plant, she gets irritated. She thinks it a question out of their syllabus and asks him to approach a gardener for advice. Her response to Rahul reveals her crossness, irritability and rudeness. She serves as a warning to all those teachers who do not show any interest or reverence towards their profession. The letter also illustrates Rahul’s experience with his English teacher who was adamant.

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Why is love compared to a red red rose ?
Answer:
The poem, ‘A Red Red Rose’ is written by Robert Burns. He is one of the leading voices of Scotland in English literature. The present poem pictures his love for his beloved. His love is as beautiful as a fresh rose that has just bloomed in June. It is fresh and bursting with life. Here love is compared to a red rose because red rose has been an ancient symbol of love in almost all cultures. In this case, rose is newly spring in June. So, we can understand that his love is always at the starting point. Robert uses his rose with the meaning that it is very strong and passionate. It shows how strong is the speaker’s feeling.

b) What does the speaker promise in A Red Red Rose ?
Answer:
The poem, A Red Red Rose, is written by Robert Burns. It is one of the best lyrics of English poetry. The speaker shares his romantic lone for his beloved. He promises different things to his beloned.

He vones to love his beloved until the seas have dried up, the fire of the sun has melted the ice, and human life is over. He uses these examples to express his feelings. Thus, promises his eternal Love to his bonny lass and that no matter how far he might go, he will always return to her side.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]
a) Every time the youth chooses a gift, the fairy expresses her dissatisfaction with her gestures. Comment.
Answer:
Mark Twain’s story, The Five Boons of Life” offers us a valuable lesson. It highlights the need to choose right. The fairy in the story advises the youth to select a boon. She tells him that of the five boons “Fame, Love, Riches, Pleasures and Death” only one is precious. But, each time the youth makes a wrong choice.

The fairy expresses her displeasure. Once, her eyes are filled with tears. Yet again, she sighs deeply. At another time, she asks him to use his wisdom. But the youth repeats the same mistake. The fairy here represents an opportunity. Opportunities knock our doors often. It is our responsibility to use that chance aptly. Here, the youth’s failure presents a lesson to us.

b) What are the thoughts in the mind of the youth when he choose wealth ? What is the result ?
Answer:
‘The Five Boons of Life”, by Mark Twain, presents a philosophical approach to life. It shows us how foolish we are in our priorities at times. The youth stands for man’s follies. He gets a chance, from a fairy to choose from ‘Fame, Love, Riches, Pleasures and Death’. He is led by false appearances.

The fairy’s warning fails to corred him. He chooses ‘Pleasures’ first. He soon realises how painful those pleasures are ! He than opts for ‘Love’. He understands how grief follows love. Then, he goes for Fame. Again, it proves to be a wrong choice. Then he thinks Wealth’ will make him happy. He plans to spend, shine, and feed his hungry heart with his mockers envy. He thinks he can buy everything the earth can offer. He is wrong, once again.

Question 6.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

The fairy came, bringing again four of the gifts, but Death was wanting. She said: “I gave it to a mother’s pet, a little child. It was innocent, but trusted me, asking me to choose for it. You did not ask me to choose.”
“Oh, miserable me ! What is left for me ?”
“What not even you have deserved : the wanton insult of Old Age.”

Questions:
i) The fairy brought the gift, Death too. Say Yes or No.
Answer:
No

ii) What does the word I refer to ?
Answer:
The word ‘I’ refers to the fairy.

iii) What did the fairy give the little child ?
Answer:
Death

iv) What is the epithet used to describe the little child ?
Answer:
a mother’s pet

v) The man didn’t repose faith in the fairy. Write true or false.
Answer:
true

vi) What was left for the man ?
Answer:
not even what he deserved; the wanton insult of old age

vii) Write the word from the passage that means very unhappy.
Answer:
miserable

viii) Write the antonymn of the word intelligent from the passage.
Answer:
innocent

Question 7.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

Kumbh Mela
In my own city of Allahabad or in Haridwar, I would go to the great bathing festivals, the Kumbh Mela, and see hundreds of thousands of people come, as their forebears had come for thousands of years from all over India, to bathe in the Ganges. I would remember descriptions of these festivals written thirteen hundred years ago by Chinese pilgrims and others, and even then these melas were ancient and lost in unknown antiquity. What was the tremendous faith, I wondered, that had drawn our people for untold generations to this famous river of India ?
[From The Discovery on India]

Questions:
i) What is the phrase used in the passage to mean Kumbh Mela ?
Answer:
the great bathing festivals

ii) Kumbh Mela is a modem event. Say true or false.
Answer:
false

iii) When did Chinese pilgrims write about this festival ?
Answer:
thirteen hundred years ago

iv) Can we say when exactly the festival began ?
Answer:
No

v) What draws people to this famous river festival for so many years ?
Answer:
The tremendous faith

vi) Write the word used in the passage to mean festival, fair.
Answer:
‘mela’

vii) Write the synonym (from the passage) of ancestors.
Answer:
forebears

viii) Write the noun form of describe.
Answer:
description-noun

Section – B

Question 8.
Match ANY EIGHT of the following words in Column-A with their meanings in Column-B. [8 × 1/2 = 4]

Answer:
i) – g
ii) – i
iii) – e
iv) – j
v) – c
vi) – a
vii) – d
viii) – b
ix) – f
x) – h

Question 9.
Identify the parts of speech of ANY EIGHT of the following underlined words. [8 × 1/2 = 4]

i) Papa, my (1) grandmother is semi literate (2). Yet (3) she is at (4) peace with (5) her pots, pans, her flowers and (6) garden, her Bhagavad Geeta (7) and scriptures.

ii) Qh ! (8) Papa, last (9) week my rose plant almost (10) died.
Answer:
1) my – possessive pronoun/adjective
2) literate – adjective
3) yet – conjunction
4) at – preposition
5) with – preposition
6) and – conjunction
7) Geeta – noun
8) oh – interjection
9) last – adjective
10) almost – adverb

Question 10.
Fill in ANY EIGHT of the following blanks with a, an or the. [8 × 1/2 = 4]

i) Oh father, it matters not to me why __________ (1) apple does not fall upwards, nor do I care what Archimedes did. What matters to me is that my rose plants remain healthy; when there’s _________ (2) fuse in my house, I should know to do something about it; I should know to make _________ (3) desk for myself from my carpenters tools.
ii) Can you bring me all _________ (4) empty coffee cups, please ?
iii) Abdul Kalam is __________ (5) extraordinary man.
iv) Madhu is _________ (6) cleverest boy in __________ (7) class.
v) Raghu wore ________ (8) uniform which was crumpled.
vi) People usually go for _________ (9) walk in _________ (10) morning.
Answer:
i) 1 – the
2 – a
3 – a

ii) 4 – the
iii) 5 – an
iv) 6 – the
7 – the

v) 8 – the
vi) 9 – a
10 – the

Question 11.
Fill in ANY EIGHT of the following blanks with suitable prepositions. [8 × 1/2 = 4]

i) This is ___________ (1) answer to your letter _______ (2) my transgression. Yes, my first rank slipped _________ (3) the second. You advise that I should think ________ (4) studying, _______ (5) answering the papers.
ii) I congratulated her _________ (6) her success.
iii) There is some dispute _________ (7) the boundary line ________ (8) the two neighbours.
iv) He has been absent _________ (9) the classes _________ (10) Friday last.
Answer:
i) 1) in
2) about
3) to
4) before
5) before

ii) 6) on

iii) 7) about
8) between

iv) 9) for
10) since

Question 12.
Supply the missing letters to ANY SIX of the following words. [6 × 1/2 = 3]
i) childh _ _ d
ii) p _ _ ce
iii) frus _ _ ation
iv) ha _ _ en
v) gra _ _ ar
vi) col _ _r
vii) ang _ _ sh
viii) li _ _ ten
ix) obed _ _ nt
x) ye _ _ ow
Answer:
i) childhood
ii) piece/peace
iii) frustration
iv) happen
v) grammar
vi) colour
vii) anguish
viii) lighten
ix) obedient
x) yellow

Question 13.
Identify the silent consonant letters in ANY SIX of the following words. [6 × 1/2 = 3]

i) rightly
ii) should
iii) tomb
iv) Wednesday
v) knife
vi) column
vii) talk
viii) island
ix) lighten
x) receipt
Answer:
i) rightly – g,h
ii) should – l
iii) tomb – b
iv) Wednesday – d
v) knife – k
vi) column – n
vii) talk – l
viii) island – s
ix) lighten – gh
x) receipt -p

Students must practice these TS Intermediate Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(c)

I.
Question 1.
Compute [i̅ – j̅ j̅ – k̅ k̅ – i̅]
Answer:
[i̅ – j̅ j̅ – k̅ k̅ – i̅] = \(\left|\begin{array}{rrr}
1 & -1 & 0 \\
0 & 1 & -1 \\
-1 & 0 & 1
\end{array}\right|\)
= 1 (1) + 1 (- 1) = 1 – 1 = 0

Question 2.
If a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅ then compute a̅ . (b̅ × c̅)
Answer:
Given a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅ then
a̅.(b̅ × c̅) = (a̅ b̅ c̅) = \(\left|\begin{array}{ccc}
1 & -2 & -3 \\
2 & 1 & -1 \\
1 & 3 & -2
\end{array}\right|\)
= 1 (- 2 + 3) + 2 (- 4 + 1) – 3 (6 – 1)
= 1 – 6 – 15 = – 20

Question 3.
If a̅ = (1, -1, -6), b̅ = (1, -3, 4) and c̅ = (2, -5, 3), then compute the following.
(i) a̅ . (b̅ × c̅)
Answer:
a̅ × (b̅ × c̅) = (a̅ . c̅) b̅ – (a̅ . b̅) c̅
= (2 + 5 – 18) b̅ – (1 + 3 – 24) c̅
= -11b̅ + 20c̅
= — 11 (i̅ – 3j̅ + 4k̅) + 20(2i̅ – 5j̅ + 3k̅)
= 29i̅ – 67j̅ + 16k̅

(ii) a̅ × (b̅ × c̅)
Answer:
a̅ × (b̅ × c̅) = (a̅.c̅)b̅ – (a̅.b̅)c̅
= (2 + 5 – 18)b̅ – (1 + 3 – 24)c̅
= -11b̅ + 20c̅
= -11(i̅ – 3j̅ + 4k̅) + 20(2i̅ – 5j̅ + 3k̅)
= 29i̅ – 67j̅ + 16k̅

iii) (a̅ × b̅) × c̅
Answer:
(a̅ × b̅) × c̅
= (a̅ . c̅)b̅ – (b̅ . c̅)a̅
= (2 + 5 – 18) b̅ – (2 + 15 + 12) a̅
= -11 (i̅ – 3j̅ + 4k̅) – 29 (i̅ – j̅ – 6k̅)
= -40i̅ + 62j̅ + 130k̅

Question 4.
Simplify the following :
i) (i̅ – 2j̅ + 3k̅) × (2i̅ + j̅ – k̅) – (j̅ + k̅)
Answer:
(i̅ – 2j̅ + 3k̅) × (2i̅ + j̅ – k̅) – (j̅ + k̅)
= \(\left|\begin{array}{rrr}
1 & -2 & 3 \\
2 & 1 & -1 \\
0 & 1 & 1
\end{array}\right|\)
= 1 (2) + 2(2) + 3(2)
= 2 + 4 + 6
= 12

ii) (2i̅ – 3j̅ + k̅) – (i̅ – j̅ + 2k̅) × (2i̅ + j̅ + k̅)
Answer:
(2 i̅ – 3j̅ + k̅) . (i̅ – j̅ + 2k̅) × (2i̅ + j̅ + k̅)
= \(\left|\begin{array}{rrr}
2 & -3 & 1 \\
1 & -1 & 2 \\
2 & 1 & 1
\end{array}\right|\)
= 2 (- 1 – 2) + 3 (1 – 4) + 1 (1 + 2)
= – 6 – 9 + 3
= -12

Question 5.
Find the volume of the parallelopiped having coterminus edges i̅ + j̅ + k̅, i̅ – j̅ and i̅ + 2j̅ – k̅
Answer:
Let a̅ = i̅ + j̅ + k̅, b̅ = i̅ – j̅ and c̅ = i̅ + 2j̅ – k̅ then the volume of parallelopiped =
| (a̅ b̅ c̅)|
= \(\left|\begin{array}{rrr}
1 & 1 & 1 \\
1 & -1 & 0 \\
1 & 2 & -1
\end{array}\right|\)
= 1 (1) – 1 (- 1) + 1 (2 + 1)
= 1 + 1 + 3 = 5 cubic units.

Question 6.
Find ‘t’ for which the vectors 2i̅ – 3j̅ + k̅, i̅ + 2j̅ – 3k̅ and j̅ – tk̅ are coplanar.
Answer:
Denote the given vectors by a, b, c .and if the vectors are coplanar then [a̅ b̅ c̅] = 0
⇒ \(\left|\begin{array}{rrr}
2 & -3 & 1 \\
1 & 2 & -3 \\
0 & 1 & -t
\end{array}\right|\) = 0
⇒ 2 (- 2t + 3) + 3 (- t) + 1 (1) = 0
⇒ – 7t + 7 = 0
⇒ t = 17.

Question 7.
For non coplanar vectors a̅,b̅ and c̅, determine p for which the vectors a̅ + b̅ + c̅, a̅ + pb̅ + 2c̅ and -a̅ + b̅ + c̅ are coplanar.
Answer:
Given a,b,c are non coplanar vectors We have [a̅ b̅ c̅] = 0 If the vectors a̅ + b̅ + c̅, a̅ + pb̅ + 2c̅ and -a̅ + b̅ + c̅ are coplanar.
Then \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & p & 2 \\
-1 & 1 & 1
\end{array}\right|\)[a̅ b̅ c̅] = 0
⇒ \(\left|\begin{array}{rrr}
1 & 1 & 1 \\
1 & p & 2 \\
-1 & 1 & 1
\end{array}\right|\) = 0 (∵ [a̅ b̅ c̅] = 0)
⇒ 1 (p – 2) – 1 (1 + 2) + 1 (1 + p) = 0
⇒ 2p = 4 ⇒ p = 2

Question 8.
Determine λ for which the volume of the parallelopiped having coterminus edges i̅ + j̅, 3i̅ – j̅ and 3j̅ + λ.k̅ is 16 cubic units.
Answer:
Denoting the coterminus edges by a̅,b̅,c̅ the volume of the parallelopiped =
|[a̅ b̅ c̅]| = ±16
∴ \(\left|\begin{array}{rrr}
1 & 1 & 0 \\
3 & -1 & 0 \\
0 & 3 & \lambda
\end{array}\right|\) = ±16
⇒ 1(-λ) – 1(3λ) = ±16
⇒ – 4λ = ±16
⇒ λ = ±4

Question 9.
Find the volume of the tetrahedron having the edges i̅ + j̅ + k̅; i̅ – j̅ and i̅ + 2j̅ + k̅.
Answer:
Denoting the edges by a̅, b̅, c̅ of tetrahedron, then its volume is = \(\frac{1}{6}\)[a̅ b̅ c̅]

Question 10.
Let a̅, b̅ and c̅ be non coplanar vectors and α = a̅ + 2b̅ + 3c̅, β = 2a̅ + b̅ – 2c̅ and γ = 3a̅ – 7c̅, then find [α̅ β̅ γ̅].
Answer:
Given α = a̅ + 2b̅ + 3c̅
β = 2a̅ + b̅ – 2c̅
γ = 3a̅ – 7c̅
and a̅, b̅, c̅ are non coplanar ⇒ [a̅ b̅ c̅] ≠ 0
then [α̅ β̅ γ̅] = \(\left|\begin{array}{rrr}
1 & 2 & 3 \\
2 & 1 & -2 \\
3 & 0 & -7
\end{array}\right|\)[a̅ b̅ c̅]
= [ 1 (- 7) – 2 (- 14 + 6) + 3 (- 3)] [a̅ b̅ c̅]
= (- 7 + 16 – 9) [a̅ b̅ c̅] = 0

Question 11.
Let a̅, b̅ and c̅ be non coplanar vectors. If [2a̅ – b̅ + 3c̅, a̅ + b̅ – 2c̅, a̅ + b̅ – 3c̅] = λ [a̅ b̅ c̅] then find the value of λ.
Answer:
Given a,b,c as non coplanar vectors We have [a̅ b̅ c̅] ≠ 0
∴ \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
1 & 1 & -2 \\
1 & 1 & -3
\end{array}\right|\)[a̅ b̅ c̅]
= [2 (- 3 + 2) + 1 (- 3 + 2) + 3 (1 – 1)][a̅ b̅ c̅]
= [-2 – 1] [a̅ b̅ c̅]
= -3[a̅ b̅ c̅]
Given [2a̅ – b̅ + 3c̅, a̅ + b̅ – 2c̅, a̅ + b̅ – 3c̅]
= λ [a b c]
We have -3[a̅ b̅ c̅] = λ [a̅ b̅ c̅]
⇒ λ = -3

Question 12.
Let a̅, b̅ and c̅ be non coplanar vectors.
If [a̅ + 2b̅ 2b̅ + c̅ 5c̅ + a̅] = λ [a̅ b̅ c̅], then find λ.
Answer:
Given a̅, b̅ and c̅ as non coplanar vectors. We have [a̅ b̅ c̅] ≠ 0. Given that
∴ \(\left|\begin{array}{lll}
1 & 2 & 0 \\
0 & 2 & 1 \\
1 & 0 & 5
\end{array}\right|\)[a̅ b̅ c̅] = λ[a̅ b̅ c̅]
⇒ [1 (10 – 0) – 2 (0 – 1)] [a̅ b̅ c̅] = λ[a̅ b̅ c̅]
⇒ 12 [a̅ b̅ c̅] = λ [a̅ b̅ c̅]
⇒ λ = 12

Question 13.
If a̅, b̅, c̅ are non coplanar vectors, then find the value of \(\frac{(\overline{\mathrm{a}}+2 \overline{\mathrm{b}}-\overline{\mathrm{c}}) \cdot[(\overline{\mathrm{a}}-\overline{\mathrm{b}}) \times(\overline{\mathrm{a}}-\overline{\mathrm{b}}-\overline{\mathrm{c}})]}{[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]}\)
Answer:
Given a̅, b̅, c̅ are non coplanar we have [a̅ b̅ c̅] ≠ 0, then

= 1 (1) – 2 (- 1) – 1 (- 1 + 1) = 3

Question 14.
If a̅, b̅, c̅ are mutually perpendicular unit vectors, then find the value of [a̅ b̅ c̅]².
Answer:
Given a̅, b̅, c̅ are mutually perpendicular unit vectors.
We have |a̅| = |b̅| = |c̅| = 1
and taking a̅ = i̅, b̅ = j̅, c̅ = k̅
We have [a̅ b̅ c̅] = [i̅ j̅ k̅]
= i̅ . (j̅ × k̅) = i̅.i̅ = 1
∴ [a̅ b̅ c̅]² = 1

Question 15.
a̅, b̅, c̅ are non zero vectors and a̅ is perpendicular to both b̅ and c̅. If |a̅|= 2, |b̅|= 3, |c̅| = 4 and (b̅, c̅) = \(\frac{2 \pi}{3}\) then find |[a̅ b̅ c̅]|. (May 2008)
Answer:
Given a̅, b̅, c̅ are non zero vectors and a is perpendicular to both b̅ and c̅
⇒ a̅ is parallel to (b̅ × c̅)
⇒ (a̅, b̅ × c̅) = 0 (or) 180°
∴ [a̅ b̅ c̅] = [a̅ . b̅ × c̅]

Question 16.
If a̅, b̅, c̅ are unit coplanar vectors, then find [2a̅ – b̅ 2b̅ – c̅ 2c̅ – a̅].
Answer:
Given |a̅| = |b̅| = |c̅| = 1
[2a̅ – b̅ 2b̅ – c̅ 2c̅ – a̅]
= \(\left|\begin{array}{rrr}
2 & -1 & 0 \\
0 & 2 & -1 \\
-1 & 0 & 2
\end{array}\right|\)[a̅ b̅ c̅]
= [2 (4) + 1 (- 1)] [a̅ b̅ c̅]
= 7 [a̅ b̅ c̅] = 7 (0) = 0 (∵ a̅, b̅, c̅ are coplanar vectors [a̅ b̅ c̅] = 0 ]

II.
Question 1.
If [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅] = [a̅ b̅ c̅], then show that the points with position vectors a̅, b̅, c̅ and d̅ are coplanar. (May 2014)
Answer:
Given [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅]
= [a̅ b̅ c̅] ………..(1)
Let OA = a̅, OB = b̅, OC = c̅ and OD = d̅ with respect to a fixed origin ‘O’. Then
AB = b̅ – a̅,
AC = c̅ – a̅,
AD = d̅ – a̅ if the points A, B, C, D are coplanar then
[AB AC AD] = 0
⇒ [b̅ – a̅ c̅ – a̅ d̅ – a̅] = 0
⇒ (b̅ – a̅) . [(c̅ – a̅) × (d̅̅ – a̅)] = 0
⇒ (b̅ – a̅) . [c̅ × d̅ – (c̅ × a̅) – (a̅ × d̅) + (a̅ × a̅)] = 0
⇒ (b̅ – a̅) – [(c̅ × d̅) – (a̅ × d̅) – (c̅ × a̅)] = 0
⇒ [b̅ c̅ d̅] – (b̅ a̅ d̅) – [b̅ c̅ a̅] – [a̅ c̅ d̅] + [a̅ a̅ d̅] + [a̅ c̅ a̅] = 0
⇒ [b̅ c̅ d̅] – [b̅ a̅ d̅] – [b̅ c̅ a̅] – [a̅ c̅ d̅] = 0
⇒ [b̅ c̅ d̅] + [a̅ b̅ a̅] – [a̅ b̅ c̅] + [c̅ a̅ d̅] = 0
⇒ [b̅ c̅ d̅] + [a̅ b̅ d̅] + [c̅ a̅ d̅] = [a̅ b̅ c̅]

Question 2.
If a̅, b̅ and c̅ are non coplanar vectors, then prove that the four points with position vectors 2a̅ + 3b̅ – c̅, a̅ – 2b̅ + 3c̅, 3a̅ + 4b̅ – 2c̅ and a̅ – 6b̅ + 6c̅ are coplanar.
Answer:
Suppose A, B, C, D are the given points with respect to a fixed origin ‘O’ and given that
\(\overline{\mathrm{OA}}\) = 2a̅ + 3b̅ – c̅, \(\overline{\mathrm{OB}}\) = a̅ – 2b̅ + 3c̅
\(\overline{\mathrm{OC}}\) = 3a̅ + 4b̅ – 2c̅ and \(\overline{\mathrm{OD}}\) = a̅ – 6b̅ + 6c̅
∴ \(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\)
= (a̅ – 2b̅ + 3c̅) – (2a̅ + 3b̅ – c̅)
= -a̅ – 5b̅ + 4c̅

\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\)
= (3a̅ + 4b̅ – 2c̅) – (2a̅ + 3b̅ – c̅)
= a̅ + b̅ – c̅

\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\)
= (a̅ – 6b̅ + 6c̅) – (2a̅ + 3b̅ – c̅)
= -a̅ – 9b̅ + 7c̅

∴ \(\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]=\left|\begin{array}{rrr}
-1 & -5 & 4 \\
1 & 1 & -1 \\
-1 & -9 & 7
\end{array}\right|\left[\begin{array}{lll}
\overline{\mathbf{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}}
\end{array}\right]\)
= [ – 1 (7 – 9) + 5 (7 – 1) + 4 (- 9 + 1)] [a̅ b̅ c̅]
= [- 1 (- 2) + 5 (6) + 4 (- 8)] [a̅ b̅ c̅]
= (2 + 30 – 32) [a̅ b̅ c̅] = 0
Hence the given points A, B, C, D are coplanar.

Question 3.
a̅, b̅ and c̅ are non zero and non collinear vectors and θ ≠ 0, is the angle between b̅ and c̅. If (a̅ × b̅) × c̅ = \(\frac{1}{3}\)|b̅||c̅||a̅| find sin θ.
Answer:
Given |a̅| ≠ 0, |b̅| ≠ 0, |c̅| ≠ 0 and (b̅, c̅) = θ
and (a̅ × b̅) × c̅ = \(\frac{1}{3}\)|b̅||c̅|a̅
⇒ (a̅ . c̅) b̅ – (b̅ . c̅) a̅ = \(\frac{1}{3}\)|b̅||c̅|a̅
∵ a,b, c are non collinear vectors

Question 4.
Find the volume of the tatrahedron whose vertices are (1, 2, 1), (3, 2, 5), (2. – 1, 0) and (- 1, 0, 1). (Mar. 2015-T.S) [May 2007]
Answer:
Let O be the origin with A, B, C, D as vertices of tetrahedron.

Question 5.
Show that (a̅ + b̅) . (b̅ + c̅) × (c̅ + a̅) = 2 [a̅ b̅ c̅]
Answer:
(a̅ + b̅) .(b̅ + c̅) × (c̅ + a̅)
= \(\left|\begin{array}{lll}
1 & 1 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1
\end{array}\right|\)[a̅ b̅ c̅]
= [1(1) – 1(-1)][a̅ b̅ c̅] = 2[a̅ b̅ c̅]

Question 6.
Show that the equation of the plane passing through the points with position vectors 3i̅ – 5j̅ – k̅, -i̅ + 5j̅ + k̅ and parallel to the vector 3i̅ – j̅ + 7k̅ is 3x + 2y – z = 0.
Answer:
Let \(\overline{\mathrm{OA}}\) = (3i̅ – 5 j̅ – k̅), \(\overline{\mathrm{OB}}\) = – i̅ + 5j̅ + 7k̅
The given plane passes through the points A, B and parallel to the vector
\(\overline{\mathrm{OC}}\) = 3i̅ – j̅ + 7k̅,
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = -4i̅ + 10j̅ + 8k̅
∴ Equation of the plane is

= x (70 + 8) – y (- 28 – 24) + z (4 – 30)
= 78x + 52y – 26z
= 26 (3x + 2y – z)

\(\left[\begin{array}{lll}
\bar{a} & \bar{b} & \bar{c}
\end{array}\right]=\left|\begin{array}{rrr}
3 & -5 & -1 \\
-4 & 10 & 8 \\
3 & -1 & 7
\end{array}\right|\)
= 3 (70 + 8) + 5 (- 28 – 24) – 1 (4 – 30)
= 234 – 260 + 26 = 0
Equation of the required plane is
26 (3x + 2y – z) = 0
⇒ 3x + 2y – z = 0

Question 7.
Prove that a̅ × [a̅ × (a̅ × -(a̅ . a̅) (b̅ × a̅)
Answer:
L.H.S = a × [a̅ × (a̅ × b̅)]
= a̅ × [(a̅ . b̅)a – (a̅. a̅)b̅]
= (a̅. b̅) (a̅ × a̅) – (a̅. a̅) (a̅ × b̅)
= (a̅. b̅) (0) – (a̅. a̅) (a̅ × b̅)
= (a̅. a̅) (b̅ × a̅)
= R.H.S.

Question 8.
If a̅, b̅, c̅ and d̅ are coplanar vectors, then show that (a̅ × b̅) × (c̅ × d̅) = 0.
Answer:
Given a̅, b̅, c̅, d̅ are coplanar vectors
⇒ a̅ × b̅ is perpendicular to the plane S.
In the similar way c̅ × d̅ is perpendicular to the plane S.
a̅ × b̅ and c̅ × d̅
are parallel vectors.
⇒ (a̅ × b̅) × (c̅ × d̅) = 0 (or)
(a̅ × b̅) × (c̅ × d̅) = [a̅ c̅ d̅]b̅ – [b̅ c̅ d̅]a̅
= 0b̅ – 0a̅ = 0 (∵ a̅, b̅, c̅, d̅ are coplanar)

Question 9.
Show that [(a̅ × b̅) × (a̅ × c̅)] d̅ = (a̅ . d̅) [a̅ b̅ c̅]
Answer:
We have (a̅ × b̅) × (c̅ × d̅)
= [a̅ c̅ d̅]b̅ – [b̅ c̅ d̅]a̅
(a̅ × b̅) × (a̅ × c̅) = [a̅ a̅ c̅] b̅ – [b̅ a̅ c̅]a̅
= 0(b̅) – [b̅ a̅ c̅] a̅ = (a̅ b̅ c̅)a̅
[(a̅ × b̅) × (a̅ × c̅)] d̅ = [a̅ b̅ c̅](a̅.d̅)

Question 10.
Show that a̅.[(b̅ + c̅) × [a̅ + b̅ + c̅]] = 0
Answer:

Question 11.
Find λ in order that the four points A (3, 2, 1), B (4, λ, 5), C (4, 2, – 2) and D (6, 5, – 1) are coplanar.
Answer:

⇒ 1(9) – (λ – 2) (- 2 + 9) + 4 (3) = 0
⇒ 21 – (λ – 2)(7) = 0
⇒ λ – 2 = 3
⇒ λ = 5

Question 12.
Find the vector equation of the plane passing through the intersection of planes.
r̅ -(2i̅ + 2j̅ – 3k̅) = 7, r̅ = (2i̅ + 5j̅ + 3k̅) = 9 and through the point (2, 1, 3).
Answer:
The planes are of the form
r̅.n̅₁ = d₁ and r̅.n̅₂ = d₂
The vector equation of the plane passing through the intersection of above plane is of the form
r̅ . (n̅₁ + λn̅₂) = d₁ + λd₂
∴ r̅ . [(2i̅ + 2j̅ – 3k̅) + λ(2i̅ + 5j̅ + 3k̅)]
= 7 + 9λ

Denote r̅ = xi̅ + yj̅ + zk̅ ………..(1)
then (2x + 2y – 3z) + λ (2x + 5y + 3z)] = 7 + 9λ
⇒ (2x + 2y – 3z – 7) + λ (2x + 5y + 3z – 9) = 0 …..(2)
Since this plane passes through the point (2, 1, 3)
We have
(4 + 2 – 9 – 7) + λ (4 + 5 + 9 – 9) = 0
⇒ – 10 + 9λ = 0
⇒ λ = \(\frac{10}{9}\)
From (2), (2 + 2λ) x + (2 + 5λ) y + (3λ – 3) z – (7 + 9λ) = 0

Question 13.
Find the equation of the plane passing through (a̅, b̅, c̅) and parallel to the plane r̅. (i̅ + j̅ + k̅) = 2.
Answer:
Given equation of the plane is
r̅ . (i̅ + j̅ + k̅) = 2
Suppose r̅ = xi̅ + yj̅ + zk̅ then
(xi̅ + yj̅ + zk̅) . (i̅ + j̅ + k̅) = 2
⇒ x + y + z = 2
Equation of parallel plane is x + y + z = k
Since this passes through (a, b, c) we have a + b + c = k
Equation of the required plane is x + y + z = a + b + c

Question 14.
Find the shortest distance between the lines r̅ = 6i̅ + 2j̅ + 2k̅ + λ(i̅ – 2j̅ + 2k̅) and r̅ = -4i̅ – k̅ + μ(3i̅ – 2j̅ – 2k̅).
Answer:
Given lines are

Shortest distance between the lines = 9 units.

Question 15.
Find the equation of the plane passing through the line of intersection of the planes
r̅.(i̅ + j̅ + k̅) = l and r̅.(2i̅ + 3j̅ – k̅) + 4 = 0 and parallel to X – axis.
Answer:
Cartesian form of the given plane is x + y + z = 1 and 2x + 3y – z + 4 = 0
Equation of required plane will be of the form
(x + y + z – 1) + λ (2x + 3y – z + 4) = 0 …………(i)
⇒ (1 + 2λ)x + (1 + 3λ)y + (1 – λ)z – (1 – 4λ) = 0
Since this is parallel to X-axis coefficient of x = 0
⇒ 1 + 2λ = 0 ⇒ λ = \(\frac{1}{2}\)
Required plane equation from (1) is
(x + y + z – 1) –\(\frac{1}{2}\)(2x + 3y – z + 4) = 0
⇒ 2x + 2y + 2z – 2 – 2x – 3y + z – 4 = 0
⇒ y – 3z + 6 = 0

Question 16.
Prove that the four points 4i̅ + 5j̅ + k̅, -(j̅ + k̅), 3i̅ + 9j̅ + 4k̅ and -4i̅ + 4j̅ + 4k̅ are coplanar.
Answer:

= – 4 (12 + 3) + 6 (- 3 + 24) – 2(1 + 32)
= -60 + 126 – 66 = 126 – 126 = 0
Given points are coplanar.

Question 17.
If a̅, b̅, c̅ are non coplanar, then show that the vectors a̅ – b̅, b̅ + c̅, c̅ + a̅ are coplanar.
Answer:
Given that a̅, b̅, c̅ are non coplanar
we have [a̅ b̅ c̅] ^O
∴ [a̅ – b̅ b̅ + c̅ c̅ + a̅]
= \(\left|\begin{array}{ccc}
1 & -1 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1
\end{array}\right|\)[a̅ b̅ c̅]
= [1 + 1 (-1)][a̅ b̅ c̅]
= 0 [a̅ b̅ c̅] = 0
∴ Vectors a̅ – b̅, b̅ + c̅, c̅ + a̅ are coplanar.

Question 18.
If a̅, b̅, c̅ are the position vectors of the points A, B and C respectively, then prove that the vector a̅ × b̅ + b̅ × c̅ + c̅ × a̅ is perpendicular to the plane of ΔABC.
Answer:
Let O be the origin and

= (b̅ × c̅) – (b̅ × a̅) – (a̅ × c̅) + (a̅ × a̅)
= (b̅ × c̅) + (a̅ × b̅) + (c̅ × a̅) (∵ (a̅ × a̅) = 0)
= (a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)
Hence (a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅) is perpendicular to the plane of ΔABC.

III.
Question 1.
Show that
(a̅ × (b̅ × c̅)) × c̅ = (a̅ . c̅) (b̅ × c̅) and (a̅ × b̅) . (a̅ × c̅) + (a̅ . b̅) (a̅. c̅) = (a̅.a̅)(b̅.c̅)
Answer:
i) L.H.S : a̅ × (b̅ × c̅) = (a̅ . c̅)b̅ – (a̅ . b̅)c̅
∴ (a̅ × (b̅ × c̅)) × c̅
= (a̅.c̅)(b̅ × c̅) – (a̅. b̅)(c̅ × c̅)
= (a̅.c̅)(b̅ × c̅) (∵ c̅ × c̅ = 0)
= R.H.S

ii) (a̅ × b̅).(a̅ × c̅) =
= (a̅.a̅)(b̅.c̅) – (a̅.c̅)(b̅.a̅) ………..(1)
∴ L.H.S = (a̅ × b̅). (a̅ × c̅) + (a̅ . b̅)(a̅ . c̅)
= (a̅.a̅)(b̅.c̅) = R.H.S

Question 2.
If A = (1, – 2, – 1), B = (4, 0, – 3), C = (1, 2, – 1) and D = (2, – 4, – 5), find the distance between \(\overline{\mathrm{A B}}\) and \(\overline{\mathrm{C D}}\). (Mar. ’14) [Board Model Paper]
Answer:
Let ‘O’ be the origin and \(\overline{\mathrm{O A}}\) = i̅ – 2j̅ – k̅,

Question 3.
If a̅ = i̅ – 2j̅ + k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + 2j̅ – k̅, find a̅ × (b̅ × c̅) and |(a̅ × b̅) × c̅|.
Answer:
Given a̅ = i̅ – 2 j̅ + k̅
b̅ = 2i̅ + j̅ + k̅
c̅ = i̅ + 2 j̅ – k̅
Then a̅ × (b̅ × c̅) = (a̅ . c̅)b̅ – (a̅ . b̅)c̅ (formula)
= (1 – 4 – 1) (2i̅ + j̅ + k̅) – (2 – 2 + 1)(i̅ + 2j̅ – k̅)
= – 4 (2i̅ + j̅ + k̅) – (i̅ + 2j̅ – k̅)
= -9i̅ – 6j̅ – 3k̅
Also (a̅ × b̅) × c̅ = (a̅ . c̅)b̅ – (b̅ . c̅) a̅ (formula)
= – 4 (2i̅ + j̅ + k̅) – (2 + 2 – 1) (i̅ – 2j̅ + k̅)
= -4 (2i̅ + j̅ + k̅)- 3 (i̅ – 2j̅ + k̅)
= – 11i̅ + 2j̅ – 7k̅
|(a̅ × b̅) × c̅| = \(\sqrt{121+4+49}\)
= \(\sqrt{174}\)

Question 4.
If a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅ and c̅ = i̅ + 3j̅ – 2k̅, verify that a̅ × |b̅ × c̅| ≠ (a̅ × b̅) × c̅, [May ’11, March 2008, Board Model Paper]
Answer:
Given a̅ = i̅ – 2 j̅ – 3k̅
b̅ = 2i̅ + j̅ – k̅
and c̅ = i̅ + 3j̅ – 2k̅ then a̅ × (b̅ × c̅)
=(a̅. c̅) b̅ – (a̅. b̅) c̅ (formula of vector triple product)
= (1 – 6 + 6) (2i̅ + j̅ – k̅) – ( 2 – 2 + 3) (i̅ + 3j̅ – 2k̅)
= (2i̅ + j̅ – k̅) – 3(i̅ + 3j̅ – 2k̅)
= – i̅ – 8 j̅ + 5k̅
Also (a̅ × b̅) × c̅
= (a̅. c̅)b̅ – (b̅. c̅)a̅ (formula)
= 1 (2i̅ + j̅ – k̅) – (2 + 3 + 2) (i̅ – 2j̅ – 3k̅)
= (2i̅ + j̅ – k̅) – 7(i̅ – 2j̅ – 3k̅)
= -5i̅ + 15 j̅ + 20k̅
a̅ × (b̅ × c̅) ≠ (a̅ × b̅) × c̅

Question 5.
If a̅ = 2i̅ + j̅ – 3k̅, b̅ = i̅ – 2j̅ + k̅, c̅ = – i̅ + j̅ – 4k̅ and d̅ = i̅ + j̅ + k̅, then compute |(a̅ × b̅) × (c̅ × d̅)|.
Answer:
Given a̅ = 2i̅ + j̅ – 3k̅
b̅ = i̅ – 2 j̅ + k̅
c̅ = – i̅ + j̅ – 4k̅
and d̅ = i̅ + j̅ + k̅

We have (a̅ × b̅) × (c̅ × d̅)
= [a̅ c̅ d̅]b̅ – [b̅ c̅ d̅]a̅

Question 6.
If A̅ = (1, a, a²), B̅ = (1, b, b²) and C̅ = (1, c, c²) are non coplanar vectors and \(\left|\begin{array}{ccc}
a & a^2 & 1+a^3 \\
b & b^2 & 1+b^3 \\
c & c^2 & 1+c^3
\end{array}\right|\) = 0.
Answer:
A̅, B̅, C̅ are non coplanar vectors.

Question 7.
If a̅, b̅, c̅ are non zero vectors, then |a̅ × b̅ – c̅| = |a̅||b̅||c̅| o a̅ . b̅ = b̅ . c̅ = c̅ . a̅ = 0
Answer:
We have a̅ x b̅ = |a̅||b̅| sinθ n̂
= |a̅| |b̅| sin(a,b) n̂ where n̂ is a unit vector perpendicular to a̅ and b̅ and a̅, b̅, n̅ form a right handed system

⇔ a̅, b̅ are perpendicular and c is perpendicular to both a and b
⇔ a̅, b̅, c̅ form an orthogonal system
⇔ a̅ is perpendicular to b̅, b̅ is perpendicular to c̅ and c̅ is perpendicular to a
⇔ a̅ . b̅ = 0, b̅ . c̅ = 0, a̅ . c̅ = 0

Question 8.
If a̅ = i̅ – 2j̅ + 3k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + j̅ + 2k̅, then find |(a̅ × b̅) × c̅| and |a̅ × (b̅ × c̅)|.
Answer:
a̅ = i̅ – 2 j̅ + 3k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + j̅ + 2k̅
Now (a̅ × b̅) × c̅ = (a̅ . c̅)b̅ – (b̅ . c̅)a̅
= [(i̅ – 2j̅ + 3k̅).(i̅ + j̅ + 2k̅)]b̅ – [(2i̅ + j̅ + k̅). (i̅ + j̅ + 2k̅)]a̅
= (1 – 2 + 6)b̅ – (2 + 1 + 2)a̅
= 5b̅ – 5a̅
= 5[2i̅ + j̅ + k̅ – i̅ + 2j̅ – 3k̅]
= 5 [i̅ + 3j̅ – 2k̅]
|(a̅ × b̅) × c̅| = \(5 \sqrt{1+9+4}=5 \sqrt{14}\)
a̅ × (b̅ × c̅) = (a̅ . c̅)b̅ – (a̅ . b̅)c̅
= 1(i̅ – 2j̅ + 3k̅) – (i̅ + j̅ + 2k̅)b̅ – [(i̅ – 2j̅ + 3k̅) .(2i̅ + j̅ + k̅)] c̅
= (1 – 2 + 6) b̅ – (2 – 2 + 3)c̅ = 5b̅ – 3c̅
= 5(2i̅ + j̅ + k̅)- 3(i̅ + j̅ + 2k̅)
= 7i̅ + 2j̅ – k̅
Hence |a̅ × (b̅ × c̅)| = |7i̅ + 2j̅ – k̅|
= \(\sqrt{49+4+1}=\sqrt{54}=3 \sqrt{6}\)

Question 9.
If |a̅| = 1, |b̅| = 1, |c̅| = 2 and a̅ × (a̅ × c̅) + b̅ = 0, then find the angle between a̅ and c̅.
Answer:
Given |a̅| = 1, |b̅| = 1, |c̅| = 2 and a̅ × (a̅ × c̅) + b̅ = 0
⇒ (a̅. c̅) a̅ – (a̅. a̅)c̅ + b̅ = 0
⇒ [|a̅||c̅| cos θ] a̅ – |a̅| c̅ + b̅ = 0
⇒ (1) (2)cos θ a̅ – c̅ + b̅ = 0
⇒ 2 cos θ a̅ + b̅ – c̅ = 0
⇒ (2cos θ a̅ – c̅)² = |-b|² = |b̅|²
⇒ 4cos²θa̅² – 4cosθ(a̅. c̅) + c̅² = b̅²
⇒ 4cos²θ – 4cosθ|a̅| |c̅|cos θ + 4 = 1
⇒ 4cos²θ – 4cos θ (1) (2) cos θ + 4 = 1
⇒ 4(1 – cos²θ) = 1
⇒ 4cos²θ = 3
⇒ cos²θ = \(\frac{3}{4}\)
⇒ cos θ = \(\pm \frac{\sqrt{3}}{2}\)
⇒ θ = 30° (or) 150°

Question 10.
Let a̅ = i̅ – k̅, b̅ = xi̅ + j̅ + (1 – x)k̅ and c̅ = yi̅ + xj̅ + (1 + x – y)k̅. Prove that the scalar triple product [a̅ b̅ c̅] is independent of x and y.
Answer:
a̅ = i̅ – k̅
b̅ = xi̅ + j̅ + (1 – x)k̅
c̅ = yi̅ + xj̅ + (1 + x – y)k̅
∴ [a̅ b̅ c̅] = \(\left|\begin{array}{ccc}
1 & 0 & -1 \\
\mathrm{x} & 1 & (1-\mathrm{x}) \\
\mathrm{y} & \mathrm{x} & (1+\mathrm{x}-\mathrm{y})
\end{array}\right|\)
= 1 [1 + x – y – x + x²] – 1 [x² – y]
= 1 – y + x² – x² + y
= 1
∴ [a̅ b̅ c̅] is independent of x and y.

Question 11.
Let b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3k̅. If a is a unit vector then find the maximum value of [a̅ b̅ c̅].
Answer:
Let a̅ = xi̅ + yj̅ + zk̅ and x² + y² + z² = a² = 1 (∵ a̅ is a unit vector |a̅| = 1)
[a̅ b̅ c̅] = \(\left|\begin{array}{rrr}
x & y & z \\
2 & 1 & -1 \\
1 & 0 & 3
\end{array}\right|\)
= x(3) – y(6 + 1) + z(-1)
= 3x – 7y – z
∴ x² + y² + z² = 1, the maximum value of 3x – 7y – z is
\(\sqrt{3^2+(-7)^2+(-1)^2}=\sqrt{9+49+1}=\sqrt{59}\)

Question 12.
Let a̅ = i̅ – j̅, b̅ = j̅ – k̅, c̅ = k̅ – i̅. Find unit vector d̅ such that a̅. d̅ = 0 = [b̅ c̅ d̅].
Answer:
Given a̅ = i̅ – j̅, b̅ = j̅ – k̅, c̅ = k̅ – i̅ and suppose d̅ = xi̅ + yj̅ + zk̅
0 1 -1
-1 0 1
x y z
= – 1 (- z – x) – 1 (- y)
= z + x + y
Also
a̅ . d̅ = 0 ⇒ (i̅ – j̅) • (xi̅ + yj̅ +zk̅) = 0
⇒ x – y = 0
[b̅ c̅ d]̅ = 0 ⇒ x + y + z = 0
and a̅ d̅ = 0 ⇒ x = y
x + x + z = 0
⇒ z + 2x = 0 ⇒ z = -2x
x : y : z = x : x : -2x = 1: 1: -2
Let x = λ, y = λ and z = – 2λ
d = λi + λj – 2λk = λ (i + j – 2k), λ ∈ ℝ

Students must practice these TS Inter 1st Year Maths 1A Study Material Chapter 6 Trigonometric Ratios upto Transformations Ex 6(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(c)

I.
Question 1.
Simplify the following
(i) cos 100° . cos 40° + sin 100° . sin 40°
Answer:
Use cos A. cos B + sin A sin B = cos (A – B)
∴ cos 100° . cos 40° + sin 100°.sin 40°
= cos (100° – 40°)
= cos 60°
= \(\frac{1}{2}\) = R.H.S

(ii) \(\frac{\cot 55^{\circ} \cot 35^{\circ}-1}{\cot 55^{\circ}+\cot 35^{\circ}}\)
Answer:

(iii) tan [\(\frac{\pi}{4}\) + θ]. tan[\(\frac{\pi}{4}\) – θ]
Answer:

(vi) Evaluate Σ\(\frac{\cos ^2 \mathrm{~B}-\cos ^2 \mathrm{~A}}{\cos ^2 \mathrm{~A} \cos ^2 \mathrm{~B}}\) if none of sin A, sin B, sin C is zero.
Answer:
Σ\(\frac{\cos ^2 \mathrm{~B}-\cos ^2 \mathrm{~A}}{\cos ^2 \mathrm{~A} \cos ^2 \mathrm{~B}}\) = Σ\(\left(\frac{\sin C \cos A-\cos C \sin A}{\sin C \sin A}\right)\)
= Σ (cot A – cot C)
= cot A – cot C + cot B – cot A + cot C – cot B = 0

Question 4.
(i) Prove that
cos 35° + cos 85° + cos 155° = 0
Answer:
cos 35° + cos 85° + cos 155°
= cos 35° + 2cos\(\left(\frac{85+155}{2}\right)\)cos\(\left(\frac{85-155}{2}\right)\)
= cos 35° + 2 cos 120° cos (-35°)
= cos 35° – cos 35° = 0

(ii) tan 72° = tan 18° + 2 tan 54°
Answer:
We have cot A – tan A = \(\frac{1}{\tan A}\) – tan A
⇒ \(\frac{1-\tan ^2 A}{\tan A}=\frac{2\left(1-\tan ^2 A\right)}{2 \tan A}\) = 2 cot 2A
∴ cot A – tan A = 2 cot 2A
⇒ cot A = tan A + 2 cot 2A°
Take A = 18°, then cot 18° = tan 18° + 2 cot 36°
⇒ cot(90 – 72) = tan 18° + 2 cot(90 – 54)
⇒ tan 72° = tan 18° + 2 tan 54°

(iii) sin 750° cos 480° + cos 120° cos 60° = –\(\frac{1}{2}\)
Answer:
L.H.S = sin [2.(360) + 30] cos[360 + 120] + cos 120 cos 60
= sin 30 cos 120 + cos 120 cos 60
= \(\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)\left(\frac{1}{2}\right)=-\frac{1}{2}\)

(iv) cos A + cos(\(\frac{4 \pi}{3}\) – A) + cos(\(\frac{4 \pi}{3}\) + A) = 0
Answer:
Use cos(A + B) + cos(A – B) = 2cos A cos B
L.H.S = cos A + 2cos\(\frac{4 \pi}{3}\)cos A
= cos A + 2 cos 240 cos A
= cos A + 2 cos ( 180 + 60) cos A
= cos A + 2 ( – cos 60) cos A
= cos A + 2\(\left(-\frac{1}{2}\right)\)cos A = cos A – cos A = 0

(v) cos²θ + cos²(\(\frac{2 \pi}{3}\) + θ) + cos²(\(\frac{2 \pi}{3}\) – θ) = \(\frac{3}{2}\)
Answer:
cos²θ + cos²( 120 + θ) + cos²( 120 – θ)
= cos²θ + cos²(120 + θ) + 1 – sin²(120 – θ)
= 1 + cos²θ + cos [ 120 + θ + 120 – θ] cos [ 120 + θ- 120 + θ]
= 1 + cos²θ + cos (240) cos 2θ
= 1 + cos²θ + cos (180 + 60) cos 2θ
[∵ Use cos²A – sin²B = cos (A + B) cos (A – B)]
= 1 + cos²θ – cos 60 ( 2 cos2θ – 1)
= 1 + cos²θ – \(\frac{1}{2}\) ( 2 cos2θ – 1)
= 1 + cos²θ – cos² θ + \(\frac{1}{2}=\frac{3}{2}\)

Question 5.
Evaluate
(i) sin²82\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
Answer:
sin²82\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
= sin[82\(\frac{1}{2}^{\circ}\) + 22\(\frac{1}{2}^{\circ}\)]
∵ Use sin²A – sin²B = sin(A + B) sin(A – B)
= sin 105° . sin 60°
= sin 60° sin (60° + 45°)
= sin 60° [sin 60° cos 45° + cos 60° sin 45°]
= \(\frac{\sqrt{3}}{2}\left[\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}}\right]=\frac{\sqrt{3}(\sqrt{3}+1)}{4 \sqrt{2}}=\frac{3+\sqrt{3}}{4 \sqrt{2}}\)

(ii) cos² 112\(\frac{1}{2}^{\circ}\) – sin²52\(\frac{1}{2}^{\circ}\)
Answer:
Use cos² A – sin² B = cos (A + B) cos (A – B)
cos²112\(\frac{1}{2}^{\circ}\) – sin² 52\(\frac{1}{2}^{\circ}\)
= cos [112\(\frac{1}{2}^{\circ}\) + 52\(\frac{1}{2}^{\circ}\)]cos[112\(\frac{1}{2}^{\circ}\) -52\(\frac{1}{2}^{\circ}\)]
= cos 165° . cos 60
= cos 60° cos (180 – 15)
= -cos 60°. cos 15°
= \(-\frac{1}{2}\left[\frac{\sqrt{3}+1}{2 \sqrt{2}}\right]=-\frac{(\sqrt{3}+1)}{4 \sqrt{2}}\)

(iii) sin²\(\left[\frac{\pi}{8}+\frac{A}{2}\right]\) – sin²\(\left[\frac{\pi}{8}-\frac{A}{2}\right]\)
Answer:

(iv) cos²52\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\) (M’ 2010, 06 Jun 08)
Answer:
[∵ cos²A – sin²B = cos (A + B) cos (A – B)]
cos²52\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
= cos[52\(\frac{1}{2}^{\circ}\) + 22\(\frac{1}{2}^{\circ}\)]cos[52\(\frac{1}{2}^{\circ}\) – 22\(\frac{1}{2}^{\circ}\)]
= cos 75° cos 30°
= cos 30° cos(90 – 15)
= cos 30° sin 15°
= \(\frac{\sqrt{3}}{2}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)=\frac{3-\sqrt{3}}{4 \sqrt{2}}\)

Question 6.
Find the minimum and maximum values of
(i) 3 cos x + 4 sin x
Answer:
Recall for a cos x + b sin x + c

(ii) sin 2x – cos 2x
Answer:
a = 1, b = -1, c = 0

Question 7.
Find the range of
(i) 7 cos x – 24 sin x + 5
Answer:
a = -24, b = 7, c = 5

(ii) 13 cos x + 3√3 sin x – 4
Answer:
a = 3√3, b = 13, c = -4

II.
Question 1.
(i)If cos α = –\(\frac{3}{5}\) and sin β = \(\frac{7}{25}\) where \(\frac{\pi}{2}\) < α < π and 0 < β < \(\frac{\pi}{2}\), then find the values of tan(α + β) and sin(α + β).
Answer:
cos α = –\(\frac{3}{5}\), and α lies in second quadrant
sin α = \(\frac{4}{5}\) ∴ tan α = –\(\frac{4}{5}\)

(ii) If 0 < A < B < \(\frac{\pi}{4}\) and sin(A + B) = \(\frac{24}{25}\) and cos (A – B) = \(\frac{4}{5}\), then find the value of tan 2A. (March 2015-T.S)
Answer:

(iii) If A + B, A are acute angles such that sin (A + B) = \(\frac{24}{25}\) and tan A = \(\frac{3}{5}\), then find the value of cos B.
Answer:
A + B, A are acute angles ⇒ B is also acute.
Given sin (A + B) = \(\frac{24}{25}\), we have

(iv) If tan α – tan β = m, and cot α – cot β = n then prove that cot(α – β) = \(\frac{1}{\mathrm{~m}}-\frac{1}{\mathrm{n}}\).
Answer:
We have tan α – tan β = m

(v) If tan (α – β) = \(\frac{7}{24}\) and tan α = \(\frac{4}{3}\) where α and β are in the first quadrant prove that α + β = π/2.
Answer:

Question 2.
i) Find the expansion of sin (A + B – C).
Answer:
0 sin (A + B – C) = Sin [ (A + B) – C]
= sin (A + B) cos C – cos (A + B) sin C] – (sin A cos B + cos A sin B) cos C – (cos A cos B – sin A sin B] sin C
= sin A cos B cos C + cos A sin B cos C – cos A cos B sin C – sin A sin B sin C

ii) Find the expansion of cos (A – B – C).
Answer:
cos (A – B – C) = cos [(A – B) – C]
= cos (A – B) cos C + sin (A – B) sin C
= (cos A cos B + sin A sin B) cos C + (sin A cos B – cos A sin B] sin C
= cos A cos B cos C + sin A sin B cos C + sin A cos B sin C – cos A sin B sin C

iii) In a ΔABC, A is obtuse. If sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\), then show that sin C = \(\frac{16}{65}\)
Answer:
Given, A + B + C = 180°
⇒ A + B = 180° – C
∴ sin (A + B) = sin (180° – C)
= sin C ………………..(1)
∴ A is obtuse angle and A lies in II quadrant.

iv) If \(\frac{\sin (\alpha+\beta)}{\sin (\alpha-\beta)}=\frac{a+b}{a-b}\) then prove that a tan β = b tan α.
Answer:

III.
Question 1.
i) If A – B = \(\frac{3 \pi}{4}\), then show that (1 – tan A) (1 + tan B) = 2.
Answer:
A – B = \(\frac{3 \pi}{4}\)
⇒ tan(A – B) = tan\(\frac{3 \pi}{4}\)
⇒ \(\frac{\tan A-\tan B}{1+\tan A \tan B}\) = -1
⇒ tan A – tan B = – 1 – tan A tan B
⇒ tan A – tan B + tan A tan B = -1
⇒ – tan A + tan B – tan A tan B = 1
⇒ (1 – tan A) + tan B (1 – tan A) = 1 + 1 = 2
= (1 – tan A) (1 + tan B) = 2

ii) If A + B + C = \(\frac{\pi}{2}\) and if none of A, B, C is an odd multiple of \(\frac{\pi}{2}\), then prove that cot A + cot B + cot C = cot A cot B cot C
a) Given A + B + C = \(\frac{\pi}{2}\) ⇒ A + B = \(\frac{\pi}{2}\) – C
∴ cot(A + B) = cot(\(\frac{\pi}{2}\) – C)
= tan C = \(\frac{1}{\cot C}\)
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}=\frac{1}{\cot C}\)
⇒ cot A + cot B + cot C = cot A cot B cot C

b) tan A tan B + tan B tan C + tan C tan A = 1
Answer:
tan (A + B) = tan(\(\frac{\pi}{2}\) – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = cot C = \(\frac{1}{\tan C}\)
⇒ tan A tan C + tan B tan C= 1 – tan A tan B
⇒ tan A tan B + tan B tan C + tan C tan A = 1

c) Σ\(\frac{\cos (B+C)}{\cos B \cos C}\) = 2
Answer:
\(\Sigma \frac{\cos B \cos C-\sin B \sin C}{\cos B \cos C}\)
= Σ (1 – tan BtanC)
= 1 – tan B tan C + 1 – tan C tan A + 1 – tan A tan B
= 3 – (tan B tan C + tan C tan A + tan A tan B]
= 3 – 1 = 2 [∵ from (b) Σ tanA tan B = 1 ]

Question 2.
i) Prove that sin² α + cos² (α + β) + 2 sin α sin β cos (α + β) is independent of α.
Answer:
sin²α + cos² (α + β) + 2 sin α sin β cos (α + β)
= sin²α + cos (α + β) [cos (α + β) + 2sin α sin β ]
= sin²α + cos (α + β) [ cos (α + β) + cos (α – β) – cos (α + β)] (Formula)
= sin²α + cos (α + β) cos (α – β)
= 1 – sin²β = cos2β
Which is independent of α.

ii) Prove that cos² (α – β) + cos²β – 2 cos (α – β) cos α cos β is independent of β.
Answer:
cos² (α – β) + cos² β – 2 cos (α – β) cos α cos β
= cos² (α – β) – 2 cos (α – β)
= cos α cos β + cos² β = cos (α – β) [cos (α – β) – 2 cos α cosβ] + cos² β
= cos (α – β) [cos (α – β) – cos (α + β) – cos (α – β)] + cos2 β (Formula)
= – cos (α – β) cos (α + β) + cos2 β (Formula)
= – (cos²α – sin²β) + cos2 β = – cos² α + 1
= sin²α which is independent of β.

Students must practice these TS Intermediate Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Equations Solutions Exercise 7(a)

I.
Question 1.
Find the principal solutions of the angles in the equations. (V.S.A)
(i) 2 cos² θ = 1
Answer:
cos² θ = \(\frac{1}{2}\)
⇒ principal values are θ = 45°,135° (∵ cos θ = ±\(\frac{1}{\sqrt{2}}\))

(ii) √sec θ + 2 = 0
Answer:
sec θ = \(\frac{-2}{\sqrt{3}}\), cos θ = – \(\frac{\sqrt{3}}{2}\)
∴ Principal solution is θ = 150°.

(iii) √3 tan²θ = 1
Answer:
tan²θ = \(\frac{1}{3}\) ⇒ tan θ = ± \(\frac{1}{\sqrt{3}}\)
∴ θ = ± \(\frac{\pi}{6}\)

Question 2.
Solve the following equations. (VSA)
(i) cos 2θ = \(\frac{\sqrt{5}+1}{4}\), θ ∈ [0, 2π]
Answer:
cos 2θ = \(\frac{\sqrt{5}+1}{4}\) = cos 36° = cos \(\left(\frac{\pi}{5}\right)\)
and \(\frac{\pi}{5}\) ∈ [0, 2π] ∴ 2θ = \(\frac{\pi}{5}\) ⇒ θ = \(\frac{\pi}{10}\)
is the principal solution.
and 2θ = 2nπ ± \(\frac{\pi}{5}\) where n ∈ Z is the general solution
∴ θ = nπ ± \(\frac{\pi}{10}\)
Values of θ in [0, 2π] are \(\left\{\frac{\pi}{10}, \frac{9 \pi}{10}, \frac{11 \pi}{10}, \frac{19 \pi}{10}\right\}\)
for n = 0, n = 1 and n = 2.

(ii) tan²θ = 1, θ ∈ [- π, π]
Answer:
tan θ = ± 1 + tan \(\left(\pm \frac{\pi}{4}\right)\)
The principal solutions are θ = ± \(\frac{\pi}{4}\)
and general solution is θ = nπ ± \(\frac{\pi}{4}\), n ∈ Z
For n = – 1, 0, 1 we have \(\left\{-\frac{3 \pi}{4}, \frac{-\pi}{4}, \frac{\pi}{4}, \frac{3 \pi}{4}\right\}\) is
the solution set [or the given equation in [-π, π].

(iii) sin 3θ = \(\frac{\sqrt{3}}{2}\), θ ∈ [- π, π]
Answer:

(iv) cos² θ = \(\frac{3}{4}\), θ ∈ [0, π]
Answer:

For values of n = 0, 1 we have solution set for the given equation in [0, π] is \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

(v) 2 sin² θ = sin θ, θ ∈ (0, π)
Answer:
2 sin² θ = sin θ
⇒ sin θ (2 sin θ – 1) = 0
⇒ sin θ = 0 or sin θ = \(\frac{1}{2}\)
When sin θ = 0 we have θ = nπ
and sin θ = \(\frac{1}{2}\) ⇒ θ = nπ + (- 1)ⁿ \(\frac{\pi}{6}\)
Since θ ∈ (0, π), solution set is \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

Question 3.
Find general solutions of the following equations. (V.S.A)
(i) sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = – \(\frac{1}{2}\)
Answer:
sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = – \(\frac{1}{2}\)
⇒ θ has in II quadrant.
∴ The principal value of θ is π – \(\frac{\pi}{3}\) = \(\frac{2 \pi}{3}\)
∴ The general solution is
θ = 2nπ + \(\frac{2 \pi}{3}\), n ∈ Z

(ii) tan x = – \(\frac{1}{\sqrt{3}}\), sec x = \(\frac{2}{\sqrt{3}}\)
Answer:
Given tan x = – \(\frac{1}{\sqrt{3}}\) and sec x = \(\frac{2}{\sqrt{3}}\)
⇒ x lies in IV quadrant.
∴ The principal values of x are \(\frac{-\pi}{6}\) or 2π – \(\frac{\pi}{6}\) = \(\frac{11 \pi}{6}\)
n ∈ Z (or) x = 2nπ – \(\frac{\pi}{6}\), n ∈ Z

(iii) cosec θ = – 2, cot θ = – √3
Answer:
cosec θ = – 2, cot θ = – √3
⇒ θ lies in IV quadrant.
The principal value of θ is
θ = 2π – \(\frac{\pi}{6}\) = \(\frac{11\pi}{6}\) or θ = – \(\frac{\pi}{6}\)
∴ General solution of θ is θ = 2nπ + \(\frac{11\pi}{6}\)
or θ = 2nπ – \(\frac{\pi}{6}\)

Question 4.
(i) If sin (270° – x) = cos 292° then find x in (0, 360°) (V.S.A)
Answer:
sin (270° – x) = cos 292°
= sin (270° – x) = cos (270° + 22°) sin 22°
270° – x = 22° ⇒ x = 270° – 22 = 248°

(ii) If x < 90°and sin (x + 28°) = cos(3x – 78°) then find x.
Answer:
Given sin (x + 28°) = cos (3x – 78°)
= sin [90° – (3x – 78°)]
∴ x + 28° = 90 – (3x – 78°)
⇒ 3x + x = 168° – 28° = 140°
⇒ 4x = 140° ⇒ x = 35°

Question 5.
Find the general solutions of the following equations.
(i) 2 sin² θ 3 cos θ
Answer:
Given 2 sin²θ = 3 cos θ
⇒ 2(1 – cos²θ) = 3 cos θ
⇒ 2 cos² θ + 3 cos θ – 2 = 0
⇒ 2 cos² θ + 4 cos θ – cos θ – 2 = θ
⇒ 2 cos θ(cos θ + 2) – 1 (cos θ + 2) = θ
⇒ (2cos θ – 1) (cos θ + 2) = 0
⇒ cos θ = \(\frac{1}{2}\) or cos θ = – 2 (not admissible)
⇒ cos θ = \(\frac{1}{2}\) ⇒ principal solution is α = – \(\frac{\pi}{3}\)
∴ General solution is θ = 2nπ ± α
= 2nπ ± \(\frac{\pi}{3}\)

(ii) sin² θ – cos θ = \(\frac{1}{4}\)
Answer:
sin² θ – cos θ = \(\frac{1}{4}\)
⇒ 1 – cos² θ – cos θ = 1
⇒ 4 – 4 cos² θ – 4 cos θ = 1
⇒ 4 cos² θ + 4 cos θ – 3 = 0
⇒ 4cos² θ + 6 cos θ – 2 cos θ – 3 = 0
⇒ 2 cos θ(2 cos θ + 3) – 1(2 cos θ + 3) = 0
⇒ (2 cos θ – 1)(2 cos θ + 3)= 0
⇒ cos θ = \(\frac{1}{2}\) or cos θ = \(\frac{-3}{2}\) (not admissible)
If cos θ = \(\frac{1}{2}\) then the principal value α = \(\frac{\pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ z

(iii) 5 cos² θ + 7 sin² θ = 6
Sol.
Given 5 cos² θ + 7 sin² θ = 6
Dividing by cos² θ we get,
⇒ 5 + 7 tan² θ = 6 sec² θ
⇒ 5 + 7 tan² θ = 6(1 + tan² θ)
⇒ tan² θ – 1 = 0 ⇒ tan² θ = 1
= tan θ = ±1
∴ θ = nπ ± \(\frac{\pi}{4}\), n ∈ Z is the general solution.

(iv) 3 sin⁴ x + cos⁴ x = 1
Answer:
3 sin⁴ x + cos⁴ x = 1
⇒ 3(sin² x)² + cos⁴ = 1
⇒ 3(1 – cos² x)² + cos⁴ x = 1
⇒ 4 cos⁴ x – 6 cos² x + 2 = 0
⇒ 2 cos⁴ x – 3 cos² x + 1 = 0
⇒ 2 cos⁴ x – 2 cos² x – cos² x + 1 = 0
⇒ 2 cos² x (cos²x – 1) – 1(cos² x – 1) = 0
⇒ (2cos² x – 1) (cos² x – 1) = 0

Case (i): 2 cos² x – 1 = 0
⇒ cos² x = \(\frac{1}{2}\) ⇒ cos x = ± \(\frac{1}{\sqrt{2}}\)
General solution is
x = 2nπ ± \(\frac{\pi}{4}\), n ∈ Z if cos x = \(\frac{1}{\sqrt{2}}\) and
x = 2nπ ± \(\frac{3 \pi}{4}\), n ∈ Z for cos x = – \(\frac{1}{\sqrt{2}}\)

Case(ii): cos²x – 1 = 0
⇒ cos²x = 1
cos x = ±1
If cos x = 1 then x = 2nπ, n ∈ Z and
If cos x = – 1 then x = 2nπ ± π, n ∈ Z
∴ General solution is x = 2nπ ± \(\frac{3 \pi}{4}\), n ∈ Z
x = 2nπ ± π, x = 2nπ, and x = 2nπ ± π

II.
Question 1.
Solve the following equations and write general solutions. (SA)
(i) 2 sin² θ – 4 = 5 cos θ
Answer:
2 sin2 θ – 4 = 5 cos θ
⇒ 2(1 – cos² θ) – 5 cos θ – 4 = 0
⇒ 2 cos² θ + 5 cos θ + 4 – 2 = 0
⇒ 2 cos² θ + 5 cos θ + 2 = 0
⇒ 2 cos² θ + 4 cos θ + cos θ + 2 = 0
⇒ 2 cos θ (cos θ + 2) + 1(cos θ + 2) = 0
⇒ (cos θ + 2) (2 cos θ + 1) = 0
cos θ + 2 = 0 is not admissible.
Consider 2 cos θ + 1 = 0 ⇒ cos θ = –\(\frac{1}{2}\), the
principal solution is α = \(\frac{2 \pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z

(ii) 2 + √3 sec x – 4 cos x = 2√3
Answer:
2 + \(\frac{\sqrt{3}}{\cos x}\) – 4 cos x = 2√3
⇒ 2 cos x + √3 – 4 cos² x = 2√3 cos x
⇒ 4 cos² x – 2 cos x + 2√3 cos x – √3 = 0
⇒ 2 cos x(2 cos x + √3) – 1(2 cos x + √3) = 0
⇒ (2 cos x – 1) (2 cos x + √3) = 0

Case (i): If 2 cos x – 1 = 0 then cos x = \(\frac{1}{2}\) and the principal solution is α = \(\frac{\pi}{3}\)
∴ General solution is x = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z

Case (ii): 2 cos x + √3 = 0 cos x = – \(\frac{\sqrt{3}}{2}\)
∴ The principal solution is α = 150° = \(\frac{5 \pi}{6}\)
∴ The general solution is
x = 2nπ ± \(\frac{5 \pi}{6}\), n ∈ Z

(iii) 2 cos² θ + 11 sin θ = 7
Answer:
Given equation is 2 cos² θ + 11 sin θ = 7
⇒ 2 (1 – sin² θ) + 11 sin θ = 7
⇒ – 2 sin² θ + 11 sin θ = 5
⇒ 2 sin² θ – 11 sin θ + 5 = 0
⇒ 2 sin² θ – 10 sin θ – sin θ + 5 = 0
⇒ 2 sin² θ (sin θ – 5) – 1(sin θ – 5) = 0
⇒ (2 sin θ – 1) (sin θ – 5) = 0
If sin θ – 5 = 0 then sin θ = 5 is not admissible.
If 2 sin θ – 1 = 0 ⇒ Sin θ = \(\frac{1}{2}\) and the principal solution is α = \(\frac{\pi}{6}\)
∴ General solution is θ = nπ + (- 1)ⁿ \(\frac{\pi}{6}\), n ∈ z

(iv) 6 tan² x – 2 cos² x = cos 2x
Answer:
Given 6 tan² x – 2 cos² x = cos 2x
⇒ 6(sec² x – 1) – 2 cos² x = 2 cos² x – 1
⇒ 6\(\left(\frac{1}{\cos ^2 x}-1\right)\) – 2 cos² x = 2 cos² x – 1
⇒ \(\frac{6}{\cos ^2 x}\) – 4 cos² x – 5 = 0
⇒ 6 – 4 cos⁴ x – 5 cos² x = 0
⇒ 4 cos⁴ x + 5 cos² x – 6 = 0
⇒ 4 cos⁴ x + 8 cos² x – 3 cos² x – 6 = 0
⇒ 4 cos⁴ x (cos² x + 2) – 3(cos⁴ x + 2) = o
⇒ (4 cos² x – 3) (cos²x + 2) = o
If cos² x + 2 = 0 then solution is admissible
and if 4 cos² x – 3 = 0 ⇒ cos²x = \(\frac{3}{4}\)
⇒ cos x = ± \(\frac{\sqrt{3}}{2}\)
and the general solution is x = nπ ± \(\frac{\pi}{6}\), n ∈ Z

(v) 4 cos² θ + √3 = 2(√3 + 1) cos θ
Answer:
4 cos² θ – 2(√3 + 1) cos θ + √3 = 0
⇒ 4 cos² 0 – 2√3 cos θ – 2 cos θ + √3 = 0
⇒ 2 cos θ(2 cos θ – √3) – 1 (2 cos θ – √3) = 0
⇒ (2 cos θ – 1) (2 cos θ – √3) = 0
If cos θ = \(\frac{1}{2}\) then θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
If 2 cos θ – √3 = 0 then cos θ = \(\frac{\sqrt{3}}{2}\)
Hence the general solution in this case is
θ = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z

(vi) 1 + sin 2x = (sin 3x – cos 3x)²
Answer:
1 + sin 2x = sin² 3x. cos² 3x – 2 sin 3x cos 3x
= 1 – sin 6x
⇒ sin 6x + sin 2x = 0
⇒ 2 sin\(\left(\frac{6 x+2 x}{2}\right)\) cos\(\left(\frac{6 x-2 x}{2}\right)\) = 0
⇒ sin 4x cos 2x = 0
If cos 2x = 0 then 2x = (2n + 1) \(\frac{\pi}{2}\)

(vii) 2 sin² x + sin² 2x = 2
Answer:
2 sin² x + (2 sin x cos x)² = 2
⇒ sin² x + 2 sin² x cos² x – 1 = 0
⇒ 2 sin² x cos² x – (1 – sin² x) = o
⇒ 2 sin² x cos² x – cos² x = 0
⇒ cos² x (2 sin² x – 1) = o

Case (i): cos² x = 0 ⇒ cos x = 0
⇒ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z is the general solution.

Case (ii): 2 sin²x – 1 = 0 ⇒ sin²x = \(\frac{1}{2}\)

Question 2.
Solve the following equations. (S.A)
(i) √3 sin θ – cos θ = √2 (May 2014)
Answer:
Given √3 sin θ – cos θ = √2
Divide both sides by √3 + 1 = 2

(ii) cot x + cosec x = √3
Answer:
\(\frac{\cos x}{\sin x}+\frac{1}{\sin x}\) = √3
⇒ cos x + 1 = √3 sin x
⇒ √3 sin x – cos x – 1= 0
Divide both sides by √3 + 1 = 2,

(iii) sin x + √3 cos x = √2 (March 2010)
Answer:
Given sin x + √3 cos x = √2
Divide both sides by √1 + 3 = 2, we get

Question 3.
Solve the following equations. (S.A)
(i) tan θ + sec θ = √3, 0 ≤ θ ≤ 2π
Answer:
Given tan θ + sec θ = √3
⇒ \(\frac{\sin \theta}{\cos \theta}+\frac{1}{\cos \theta}\) = √3
⇒ sin θ + 1 = √3 cos θ
⇒ √3 cos θ – sin θ = 1
Divide both sides by √3 + 1 = 2, we get

We find that \(\frac{\pi}{6}\) is the only solution in (0, 2π)
Since θ = \(\frac{3 \pi}{2}\) is not admissible since tan θ is not defined for odd multiples of \(\frac{\pi}{2}\).
Also \(\frac{13 \pi}{6}\) ∉ (0, 2π)

(ii) cos 3x + cos 2x = sin \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\), 0 ≤ x ≤ 2π.
Answer:
Given cos 3x + cos 2x = sin \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\)

Case (i) cos \(\frac{x}{2}\) = 0 ⇒ \(\frac{x}{2}\) = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
x = (2n + 1)π, n ∈ Z
Put n = 0, we get {π} is the solution in [0, 2π]

Case (ii):

(iii) cot² x – (√3 + 1) cot x + √3 = 0; 0 < x < \(\frac{\pi}{2}\). (Mar. ‘14, ’12)
Answer:
Given cot² x – (√3 + 1) cot x + √3 = o
⇒ cot² x – √3 cot x – cot x + √3 = 0
⇒ cot x (cot x – √3) – 1 (cot x – √3) = 0
⇒(cot x – 1) (cot x – √3) = 0

Case (i) cot x – 1 = 0 = cot x = 1;
Principal solution is α = \(\frac{\pi}{4}\)
∴ General solution is x = nπ + \(\frac{\pi}{4}\), n ∈ Z

Case(ii): cot x – √3 = 0 ⇒ cot x = √3
Principal solution is α = \(\frac{\pi}{6}\)
∴ General solution is x = nπ + \(\frac{\pi}{6}\), n ∈ Z
For n = 0, we get x = \(\frac{\pi}{4}\) and x = \(\frac{\pi}{6}\) and they belong to \(\left(0, \frac{\pi}{2}\right)\)
∴ Solutions are \(\left\{\frac{\pi}{6}, \frac{\pi}{4}\right\}\)

(iv) sec x cos 5x + 1 = 0. 0 < x < 2π.
Answer:
Given sec x cos 5x + 1 = 0. 0 < x < 2π.

Case (i):

III.
Question 1.
(i) Solve sin x + sin 2x + sin 3x = cos x + cos 2x + cos 3x (E.Q)
Answer:
(sin 3x + sin x) + sin 2x = (cos 3x + cos x) + cos 2x
⇒ 2 sin 2x cos x + sin 2x = 2 cos 2x cos x + cos 2x
⇒ sin 2x (2 cos x + 1) = cos 2x (2cos x + 1)
⇒ (2 cos x + 1) (sin 2x – cos 2x) = 0

Case (i):2 cos x + 1 = 0 ⇒ cos x = – \(\frac{1}{2}\)
Principal solution is α = \(\frac{2 \pi}{3}\)
∴ General solution is x = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z

Case (ii): sin 2x – cos 2x = 0 ⇒ tan 2x = 1
Principal solution is α = \(\frac{\pi}{4}\);
∴ General solution is 2x = nπ ± \(\frac{\pi}{4}\)
⇒ x = \(\frac{\mathrm{n} \pi}{2}+\frac{\pi}{8}\), n ∈ Z
∴ General solution is

(ii) If x + y = \(\frac{2 \pi}{3}\), and sin x + sin y = \(\frac{3}{2}\) find x and y.
Answer:

Given x + y = 120° ………………. (2)
Solving x = 90°, y = 30°

(iii) If sin 3x + sin x + 2 cos x = sin 2x + 2 cos 2x, find the general solution.
Answer:
Given sin 3x + sin x + 2 cos x = sin 2x + 2 cos 2x
⇒ 2 sin 2x cos x + 2 cos x = 2 sin x cos x + 2 cos² x
⇒ 2 cos x(sin 2x + 1) = 2 cos x(sin x + cos x)
⇒ 2 cos x[sin 2x + 1 – sin x – cos x] = 0
⇒ cos x = 0 or sin 2x + 1 – sin x – cos x = 0
⇒ cos x = 0 or (sin 2x – sin x) + (1 – cos x) = 0
⇒ cos x = 0 (or) 2 cos \(\frac{3 x}{2}\) sin \(\frac{x}{2}\) + 2 sin²\(\frac{x}{2}\) = 0
⇒ cos x = 0 or 2 sin \(\frac{x}{2}\) (cos \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\)) = 0
⇒ cos x = 0 or sin \(\frac{x}{2}\) = 0 or cos \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\) = 0

Case (i): cos x = 0 ⇒ x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z

Case (ii): sin \(\frac{x}{2}\) = 0 ⇒ \(\frac{x}{2}\) = nπ ⇒ 2nπ, n ∈ Z

Case (iii):

(iv) Solve cos 3x – cos 4x = cos 5x – cos 6x
Answer:
Given cos 3x – cos 4x = cos 5x – cos 6x

Question 2.
Solve the following equations. (E.Q)
(i) cos 2θ + cos 8θ = cos 5θ
Answer:
Given cos 2θ + cos 8θ = cos 5θ
⇒ 2 cos 5θ cos 3θ = cos 5θ
⇒ cos 5θ (2 cos 3θ – 1) = 0

Case (i): cos 5θ = 0 ⇒ 5θ = (2n + 1)\(\frac{\pi}{2}\)
⇒ θ = (2n + 1)\(\frac{\pi}{10}\), n ∈ Z

Case (ii): 2 cos 3θ – 1 = 0
⇒ cos 3θ = \(\frac{1}{2}\)
Principal solution is α = \(\frac{\pi}{3}\)
∴ General solution is 3θ = 2nπ ± \(\frac{\pi}{3}\)
⇒ θ = \(\frac{2 n \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z
∴ General solutions are

(ii) cos θ – cos 7θ = sin 4θ
Answer:
2 sin\(\left(\frac{\theta+7 \theta}{2}\right)\) sin\(\left(\frac{7 \theta-\theta}{2}\right)\) = sin 4θ
⇒ 2sin 4θ sin 3θ = sin 4θ
⇒ sin 4θ (2 sin 3θ – 1) = θ

Case (i): sin 4θ = 0 ⇒ 4θ = nπθ ⇒ \(\frac{\mathrm{n} \pi}{4}\), n ∈ Z

Case (ii): 2 sin 3θ – 1 = 0

(iii) sin θ + sin 5θ = sin 3θ, 0 < θ < π
Answer:
Given sin θ + sin 5θ = sin 3θ
⇒ 2 sin \(\left(\frac{\theta+5 \theta}{2}\right)\) cos \(\left(\frac{\theta-5 \theta}{2}\right)\) = sin 3θ
⇒ 2 sin 3θ cos 2θ = sin 3θ
⇒ sin 3θ (2 cos 2θ – 1) = 0
⇒ sin 3θ = 0 or 2 cos 2θ – 1 = 0

Case (i): sin 3θ = 0 and the general solution is given by 3θ = nπ ⇒ θ = \(\frac{\mathrm{n} \pi}{3}\), n ∈ Z

Case (ii): 2 cos 2θ – 1 = 0
⇒ cos 2θ = \(\frac{1}{2}\) and the principal solution is α = \(\frac{\pi}{3}\)

Question 3.
(i) If tan pθ = cot qθ and p ≠ – q, show that the solutions are in A.P. with common difference \(\frac{\pi}{\mathbf{p}+\mathbf{q}}\). (E.Q)
Answer:

The solutions form an arithmetical progression with \(\frac{2 \pi}{2(p+q)}=\frac{\pi}{p+q}\) as common difference.

(ii) Show that the solutions of cos pθ = sin qθ form two series each of which is an A.P.
Find also the common difference of each A.P. (p ≠ ±q)
Answer:
cos pθ = sin qθ ⇒ cos pθ – sin qθ = 0

(iii) Find the number of solutions of the equation tan x + sec x = 2 cos x; cos x ≠ 0, lying in the interval (0, π).
Answer:
Given tan x + sec x = 2 cos x
⇒ \(\frac{\sin x}{\cos x}+\frac{1}{\cos x}\) = 2 cos x
⇒ 1 + sin x = 2 cos 2x
⇒ 1 + sin x = 2 (1 – sin² x)
⇒ 2 sin² x + sin x – 1 = 0
⇒ 2 sin² x + 2 sin x – sin x – 1 = 0
⇒ 2 sin x(sin x + 1) – 1 (sin x + 1) = 0
⇒ (2 sin x – 1) (sin x + 1) = 0

Case (i): 2 sin x – 1 = 0 ⇒ sin x = \(\frac{1}{2}\),
Principal solution is α = \(\frac{\pi}{6}\); and
general solution is x = nπ + (- 1)ⁿ \(\frac{\pi}{6}\)
solutions in (0, π) are \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

Case (ii) sin x + 1 ⇒ sin x = – 1
⇒ x = – \(\frac{\pi}{2}\) (or) \(\frac{3 \pi}{2}\)
∴ Number of solutions in (0, π) for the given equation is two.

(iv) Solve sin 3α = 4 sin α sin(x + α) sin(x – α) where α ≠ nπ, n ∈ Z.
Answer:
Given
sin 3α = 4 sin α sin(x + α)sin(x – α)
= 4 sin α(sin² x – sin² α)
= 3 sin α – 4 sin³ α
= 4 sin α (sin²x – sin²α)
⇒ 3 sin α = 4 sin α sin² x
⇒ sin α (3 – 4 sin² x) = 0
⇒ 3 – 4 sin² x = 0 ⇒ sin²x = \(\frac{3}{4}\)
⇒ sin x = ±\(\frac{\sqrt{3}}{2}\)
∴ General solution is
x = nπ + (- 1)ⁿ (±\(\frac{\pi}{3}\)), n ∈ Z.
Since the principal solution is α = ±\(\frac{\pi}{3}\)

Question 4.
(i) If tan (π cos θ) = cot (π sin θ), then prove that cos \(\left(\theta-\frac{\pi}{4}\right)\) = ± \(\frac{1}{2 \sqrt{2}}\) (E.Q.)
Answer:
Given that tan (π cos θ) = cot (π sin θ) = tan (\(\frac{\pi}{2}\) – π sin θ)

(ii) Find the average of θ if cos θ + sin θ is positive.
Answer:

Question 5.
If α, β are the solutions of the equation a cos θ + b sin θ = c, where a, b, c ∈ R and If a² + b² >0, cos α ≠ cos β and sin α ≠ sin β then show that (E.Q)
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α . cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Answer:
Given a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ a² cos² θ = c² – 2bc sin θ + b² sin² θ
⇒ a² (1 – sin²θ) = c² – 2bc sin θ + b² sin² θ
⇒ (a² + b²)sin²θ – 2bc sin θ + (c² – a²) = 0
This is a quadratic in sin θ and let the roots be sin α and sin β. Then
sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Also b sin θ = c – a cos θ
⇒ b² sin² θ = c² – 2ac cos θ + a² cos² θ
⇒ b² (1 – cos² θ) = c² – 2ac cos θ + a² cos² θ
⇒ (b² + a²)cos² θ – 2ac cos θ + (c² – b²) = 0
This is a quadratic in cos θ and let cos α, cos β be the roots. Then

Question 6.
(i) Find the common roots of the equations cos 2x + sin 2x cot x and 2 cos² x + cos² 2x = 1. (E.Q)
Answer:
Let tan x = A and given that
cos 2x + sin 2x = cot x

⇒ (1 – A² + 2A)A = (1 + A²)
⇒ A – A³ + 2A² = A² + 1
⇒ A³ – A² – A + 1 = 0
∴ A = 1 satisfy the equation.
By synthetic division

∴ A³ – A² – A + 1 = 0
⇒ (A – 1)(A³ – 1) = 0
⇒ A = 1, A = – 1
When A = ±1 then tan x = ±1.
⇒ x = nπ ± \(\frac{\pi}{4}\) ……………….. (1)
Also given 2 cos² x + cos² 2x = 1
⇒ (2 cos² x – 1) + cos² 2x = 0
⇒ cos 2x(1 + cos 2x) = 0
⇒ cos 2x = 0 (or) cos 2x = – 1

Case (i): When cos 2x = 0 then
2x = (2n + 1) \(\frac{\pi}{2}\)
⇒ x = (2n + 1)\(\frac{\pi}{4}\), n ∈ Z ……………….. (2)
From (1) and (2) we have
(2n + 1)\(\frac{\pi}{4}\), n ∈ Z is the common root for the given two trigonometric equations.

(ii) Solve the equation
\(\sqrt{6-\cos x+7 \sin ^2 x}\) + cos x = 0
Answer:
Given
\(\sqrt{6-\cos x+7 \sin ^2 x}\) + cos x = 0
∴ 6 – cos x + 7 sin² x = cos²x
⇒ 7(1 – cos²x – cos x + 6 = cos²x
⇒ 8 cos x + cos x – 13 = 0
∴ cos x = \(\frac{-1 \pm \sqrt{1+4(8)(13)}}{16}\)
= \(\frac{-1 \pm \sqrt{417}}{16}\)
The solution is not possible since – 1 ≤ cos x ≤ 1

(iiii) It |tan x| = tan x + \(\frac{1}{\cos x}\) and x ∈ [0, 2π], find the value of x.
Answer:
|tan x| = tan x if x lies either in 1 or in III quadrants.
∴ tan x = tan sec x
⇒ sec x = 0 since sec x ∉ (- 1, 1)
Also |tan x| = – tan x If x lies in either II or IV quadrants.
∴ – tan x = tan x + sec x
⇒ – 2 tan x = sec x

Telangana TSBIE TS Inter 1st Year English Study Material Revision Test-V Exercise Questions and Answers.

TS Inter 1st Year English Study Material Revision Test-V

Time : 1 1/2Hrs
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) It was a capital idea of mine – that it was !
Answer:
Introduction :
This line is taken from the one-act play, Box and Cox written by John Maddison Morton. This play is regarded as the best farce of the nineteenth century.

Context & Explanation :
Mrs. Bouncer is by nature covetous lady. It is this trait of personality that makes her let out a single room to two different persons simultaneously, taking unadvantage of their different professions and callings. By this, she is able to earn double income from the same room. She takes the opportunity thinking it as a capital idea. Practically, nobody can imagine such a thing. As soon as Cox leaves the room, she gets busy in the room to put his things out of Mr. Box’s way.

Critical Comment :
Here, Mrs Bouncer feels proud of herself to have got an idea to rent out the room to two different people at the same time.

b) It’s quite extraordinary the trouble I always have to get rid of that venerable female.
Answer:
Introduction :
This line is taken from the one-act play, Box and Cox written by John Maddison Morton. This play is regarded as the best farce of the nineteenth century.

Context & Explanation :
Mrs. Bouncer is a greedy landlady. She lets out her lodge room to two persons separately. She manages to keep it unknown to both of them. The drama emanates from this fact. Mrs. Bouncer meets both Mr. Box and Mr. Cox almost every day. She cautiously guards her secret plan. But Mr. Box finds is very difficult to put up with this woman. He works all night very hard. Becomes to the room in the morning very tired. He longs to rest at once. But, to get rid of this woman turns out to be difficult.

Critical Comment :
Mr. Box expresses his problem here in his strange style.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) Rest if you must – but don’t you quit.
Answer:
Introduction :
This wonderful line of valuable advice is taken from the poem, keep going penned by Edgar Albert Guest. He is very popular as people’s poet. This poem is universally acknowledged as one of the best inspirational poems.

Context & Explanation :
This simple sounding poem speaks volumes about the need to keep going, despite hurdles in life. Troubles may come and stay. But, one shouldn’t lose the fighting spirit. Samples of types of problems are presented first. They could be money-related, health-related or of some other kind. 1f the pressure over weighs, one may take rest. But, one should never quit.

Critical Comment :
The poet keeps on advising the reader never give up.

b) Often the goal is nearer than It seems to a faint and faltering man.
Answer:
introduction :
These lines are taken from the inspirational poem, ‘Keep Going’ written by Edgar Albert Guest. He is regarded as a people’s poet. The poem keeps on advising the reader never to quit.

Context & Explanation :
The poem announces the idea that your goals are just around the corner. At a time when you are uncertain and you lack strength, you may perceive the aspired goal to be so far away yet it could be nearer than what you think. Therefore, you don’t let your current state of weakness or miserable situation cloud your judgement. You may be so near to where you want to be. Keep going.

Critical Comment :
The poem rekindles the self-confidence in the readers to achieve their goals that may appear beyond any common reasoning and normal logic.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Box and Cox is regarded as the best farce of the nineteenth centuary. Support the statement with illustrations from the play.
Answer:
Box and Cox, crafted by John Maddison Morton is a one act play. It is hilarious. It drives readers into one continuous rear of laughter. A farce is a play with a style of humour marked by improbabilities. Th play Box and Cox is remarkable for its stark improbabilities. Mrs. Bouncer, the greedy landlady, renting out the same room to two gentlemen separately is the most unimaginable improbability.

The tenants, Mr. Box and Mr. Cox, do not know this. Mr. Box, a printer stays in the room only during the day. Mr. Cox, a hatter, occupies the room only at nights. Mrs. Bouncer somehow manages to ensure that they do not meet each other in the room. Yet, they suspect that something is wrong. Her explanations to their complaints add to the fun. The language Mr. Box and Mr. Cox use is so verbose that it evokes lots of laughter. Thus, the play proves itself to be a farce of rare quality.

b) “………… So that I’m getting double rent for my room, and neither of my lodgers is any the wiser for it”, says Mrs Bouncer. Is she right in her estimate of her lodgers ? Support your answer with details.
Answer:
John Maddison is an English playwright. His play Box and Cox is a one-act farce. It is hilarious. It has just three characters. Mrs. Bouncer is a greedy landlady. She rents out her room to two persons at the same time. The tenants, Box and Cox do not know it. It shows her greediness. She boasts of her capital idea. She feels that neither of her lodgers
finds it.

Even though she feels like that she is always in tremble of fear. Initially, she may succeed in deceiving them for a while we can observe it when she gives various excuses when they suspect something is wrong. In order to escape from their doubts, she gets busy to put things out of their notice. That is why they fail to know her deceptive nature. Later, they come to know her deceitful dealings. Thus, her estimate of her lodgers is not completely right.

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) It may be near when it seems afar; What seems afar and why” ?
Answer:
Edgar Albert Guest is very popular as a people’s poet. His poem, Keep Going, keeps on advising the reader never to quit. It encourages the reader to keep on the struggle till the goal is attained. Sometimes, a goal ‘situated near may appear far often when eyes are tired because of exhaustion. You may think that you are not going to succeed, yet you are close to success.

Therefore, you must continue with your efforts till success greets you. Life is a fight. It will often present you with pain or hardships. You may be hit with many challenges. You should not lose the fighting spirit. Don’t quit and go through your hardships. Success is yours. Sure! thus, the poem inspires us to acheive our goals.

b) An easy-to-read poem, Keep Going is rich both in its content and form’. Explain the above statement with examples.
Answer:
Edgar Albert Guest’s poem ‘Keep Going’ is truly an inspirational poem. It undoubtedly rich both in its context and form. It is very well written with simple words and free flowing rhymes and with an extremely powerful message that applies to anyone and every one.

It is all about perserverence, tenacity, determination and will power to not to give up especially when things are going wrong the poem reminds us that there are seeds of success in every failure. That is why we mustn’t quit. It rekindles the self-confidence to believe in our abilities to achieve the goals that may appear beyond our reach this self-confidence empowers us to bring our dreams into action. Thus, the context is motivational. The form is acceptable.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Describe the scene of the dinner party.
Answer:
‘The Dinner Party”, by Mona Gardner, is a gripping narration of an interesting incident. A colonial officer and his wife host a large dinner party. It is in their spacious dining hail. The hail has a bare marble floor. The rafters are open and glass doors are wide.

Government, army and embassy officials with their wives are the guests. A visiting American naturalist is the special invitee there. Twenty guests take part in that party. There is a spirited discussion about the nerve control a woman has. A snake is there. The American naturalist takes control of the situation. He succeeds in making everyone stay calm till the snake crawls out.

b) Describe the role of the American naturalist in the story, The Dinner Party.
Answer:
Mona Gardner’s short story “The Dinner Party” offers us an interesting reading. It highlights women’s nerve control. The American naturalist is a special guest at the dinner party. All others are government officials or military personnel. Others are involved in a discussion. He alone stays silent and observes others keenly.

He notices strange changes in the features on the face of the hostess. He watches a servant placing a bowl of milk in the veranda. He understands there is a snake. He thinks fast. He plans a strategy. It works out. He manages to make all the guests stay cool and calm till the snake creeps out. When the host appreciates his nerve control, he proves that it is the hostess who has real nerve control.

Question 6.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

The country is India. A colonial official and his wife are giving a large dinner party. They are seated with their guests – army officers and government attaches and their wives, and a visiting American naturalist – in their spacious dining room, which has a bare marble floor, open rafters and wide glass doors opening onto a veranda.

Questions:
i) In which country is this story set ?
Answer:
in India

ii) Who is the host of the party ?
Answer:
a colonial official and his wife

iii) Where is the party arranged ?
Answer:
in the spacious dining room of the hosts

iv) What is the synonym for the word porch in the passage ?
Answer:
veranda

v) Who is the special guest in the party ?
Answer:
a visiting American naturalist

vi) Describe the place where the dinner is hosted.
Answer:
a spacious dining room with a bare marble floor, open rafters and wide glass doors opening onto a veranda

vii) Write the antonym of narrow from the passage.
Answer:
spacious

viii) Identify the word from the passage that means touring.
Answer:
visiting

Question 7.
Read the following passage carefully and answer ANY FOUR questions given below in a word or a sentence each. [4 × 1 = 4]

Innocence Unbeatable
Do you think you can confuse innocent kids easily ? Find out for yourself. Once a currious boy asked his mother, Mommy, why is your hair turning grey ? The mother tried to use this occasion to teach her child a lesson in behaviour. So, she said, “It is because of you, dear. Every bad action of yours will turn one hair grey”. Instantly came the retort from the innocent boy, “Now I know why grandmother has only grey hair on her head”. Can you see who taught whom a lesson in manners ?

Questions:
i) What is the message given in the passage ?
Answer:
One cannot confuse innocent kids easily.

ii) What quality of the boy made him ask his mother a question ?
Answer:
his curiosity

iii) How did the mother want to use this occasion ?
Answer:
to teach her child a lesson in behaviour

iv) Why would her hair turn grey, according to the mother ?
Answer:
Every bad action of her son would turn one of her hairs grey.

v) Was the mother true in saying that reason for her grey hair ?
Answer:
No, she wasn’t true.

vi) Did the boy take time to answer his mother ? Support your answer with a phrase from the passage.
Answer:
No, instantly came the innocent retort from the boy.

vii) Write the word used in the passage to mean a witty, sharp reply.
Answer:
‘retort’

viii) Find the antonym in the passage of experienced.
Answer:
‘innocent’

Section – B

Question 8.
Match ANY EIGHT of the following words in Column-A with their meanings in Column-B. [8 × 1/2 = 4]

Answer:
i) – i
ii) – e
iii) – f
iv) – g
v) – h
vi) – j
vii) – a
viii) – d
ix) – c
x) – b

Question 9.
Identify the parts of speech of ANY EIGHT of the following underlined words. [8 × 1/2 = 4]

Cox : Your apartment (1) ? Ha ! (2) ha ! Come, I like (3) that! Look here (4), sir [Produces a paper (5) out of (6) his pocket.] Mrs. Bouncer’s receipt (7) for (8) the last (9) week’s rent, sir ! (10)
Answer:
1) apartment – noun
2) Ha – interjection
3) like – verb
4) here – adverb
5) paper – noun
6) of – preposition
7) receipt – noun
8) for – preposition
9) last – adjective
10) sir – noun

Question 10.
Fill in ANY SIX of the following blanks with a, an or the. [6 × 1/2 = 3]

i) In ________ (1) first place, _________ (2) candle is ________ (3) article that I don’t require, because I’m only at home in (4) day time – and I bought this candle on _________ (5) first of May calculating that it would last me three months, and here’s one week not half over, and __________ (6) candle three parts gone !
ii) Corona is spreading like _________ (7) wild fire. It’s ________ (8) fatal virus.
Answer:
i) 1 – the
2 – a
3 – an
4 – the
5 – the
6 – the

ii) 7 – a
8 – a

Question 11.
Fill in ANY SIX of the following blanks with suitable prepositions. [6 × 1/2 = 3]

i) I can’t say I did, Mrs. Bouncer. I should feel obliged __________ (1) you, if you could accommodate me with a monoprotuberant bolster, Mrs. Bouncer. This one I’ve got now seems to me to have __________ (2) a handful and a half _________ (3) .feathers _________ (4) each, and nothing whatever _______ (5) the middle.
ii) Hamlet was written ___________ (6) Shakespeare.
iii) I like that picture hanging ___________ (7) the wall ________ (8) the kitchen.
Answer:
i) 1) to
2) about
3) of
4) at
5) in

ii) 6) by

iii) 7) on
8) in

Question 12.
Fill ANY TWO of the following blanks with suitable forms of the verbs given in brackets. [2 × 1 = 2]

Eight o’clock! I ___________ (declare) I _________ (have, not) a moment to Jose. Fate _________ (place) me with the most punctual and particular of hatters, and I _________ (fulfill) my destiny.
Answer:
declare;
haven’t;
has placed;
must fulfill

Question 13.
Rewrite ANY THREE of the following sentences as directed. [3 × 1 = 3]

i) Open the window.
(Change the Voice.)
Answer:
Let the window be opened.

ii) Mrs. Bouncer said : “Is there anything else you’ve got to grumble about, sir (Cox)”?
(Change the above into the Indirect Speech.)
Answer:
Mrs. Bouncer asked Cox if there was anything else he had got to grumble about.

iii) It belongs to both of you.
(Add a Question Tag.)
Answer:
doesn’t it’

iv) Jagan is the tallest boy in the class.
(Change the adjective into Comparative degree.)
Answer:
Jagan is tallet than any other boy in the class. (C.D)
No other boy in the class is as tall as Jagan. (P.D)

v) Savitha is more intelligent than Vinitha.
(Change the adjective into Positive degree.)
Answer:
Vinitha is not so intelligent as Savitha.

Question 14.
Rewrite ANY THREE of the following sentences correcting the underlined errors. [3 × 1 = 3]

1. I have a good news for you.
2. Overeating is more worse than any other habit.
3. My idea is different than yours.
4. We are listening Shaw’s speech.
5. As Ranga was busy so he could not attend the party.

Answer:

1. I have good news for you.
2. Overeating is worse than any other habit.
3. My idea is different from yours.
4. We are listening to Shaw’s speech.
5. As Ranga was busy he could not attend the party.

Telangana TSBIE TS Inter 1st Year Physics Study Material 14th Lesson అణుచలన సిద్ధాంతం Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 14th Lesson అణుచలన సిద్ధాంతం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
స్వేచ్ఛా పథమధ్యమాన్ని నిర్వచించండి.
జవాబు:
స్వేచ్ఛా పథమధ్యమము : ఒక వాయు అణువు లేక పరమాణువు అభిఘాతం చెందకుండా ప్రయాణించే సగటు దూరాన్ని స్వేచ్ఛా పథమథ్యమం అంటారు.
(లేక)
ఒక వాయు అణువు రెండు వరుస అభిఘాతాల మధ్య ప్రయాణించే దూరాన్ని స్వేచ్ఛా పథమధ్యమం అంటారు.

ప్రశ్న 2.
అణుచలన సిద్ధాంతం అవొగాడ్రో పరికల్పనను ఏ విధంగా సమర్థిస్తుంది ? వివిధ వాయువులకు ఉండే అవొగాడ్రో సంఖ్య ఒకటే అయి ఉంటుందని చూపండి.
జవాబు:
అవొగాడ్రో నియమము లేక అవొగాడ్రో పరికల్పన :
“సమాన ఉష్ణోగ్రత, పీడనాల వద్ద సమాన ఘనపరిమాణం ఉన్న అన్ని వాయువులలో అణువుల సంఖ్య సమానం”. వాయు సమీకరణం ప్రకారం PV = KT
ఇందులో వాయు అణువుల సంఖ్య N ను లెక్కలోనికి తీసుకుంటే స్థిరాంకము K = NK_B అని రాయగా
\(\frac{\mathrm{PV}}{\mathrm{NT}}\) = K_B లేదా \(\frac{\mathrm{P}_1 \mathrm{~V}_1}{\mathrm{~N}_1 \mathrm{~T}_1}=\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~N}_2 \mathrm{~T}_2}\)
= K_B
K_B బోల్ట్స్మన్ స్థిరాంకము అన్ని వాయువులకు సమానము. కావున P, V, T లు సమానంగా ఉంటే అవాయువులలో గల అణువుల సంఖ్య N కూడా సమానంగా ఉంటుంది.

ప్రశ్న 3.
నిజ వాయువు ఆదర్శ వాయువు లాగా ఎప్పుడు ప్రవర్తిస్తుంది ?
జవాబు:
ఆదర్శ వాయువు అనేది ఒక వాయువుకు సరళ, సైద్ధాంతిక నమూనా. ఏ నిజ వాయువైనా యధార్థంగా ఆదర్శ వాయువు కాదు. అల్ప పీడనాలు, అధిక ఉష్ణోగ్రతల వద్ద కొన్ని నిజ వాయువులు (H₂, O₂, N₂, He వంటివి) ఆదర్శ వాయువులుగా ప్రవర్తిస్తాయి. వాయువులోని అణువుల మధ్య అన్యోన్య చర్యలు లేనప్పుడు వాయువు ఆదర్శ వాయువు వలె ప్రవర్తిస్తుంది.

ప్రశ్న 4.
బాయిల్, ఛార్లెస్ నియమాలను పేర్కొనండి.
జవాబు:
బాయిల్ నియమం : ఉష్ణోగ్రత స్థిరంగా ఉన్నప్పుడు, ఇచ్చిన ద్రవ్యరాశి కలిగిన వాయు పీడనం (P), దాని ఘనపరిమాణానికి (V) విలోమానుపాతంలో మారుతూ ఉంటుంది.
∴ V ∝ \(\frac{1}{\mathrm{P}}\) లేక PV = స్థిరాంకం = K.
ఛార్లెస్ నియమం : స్థిర పీడనం వద్ద వాయువు ఘనపరిమాణము (V), దాని పరమ ఉష్ణోగ్రతకు (T) అనులోమానుపాతంలో ఉంటుంది.
∴ V ∝ T లేక = \(\frac{\mathrm{V}}{\mathrm{T}}\) = K (స్థిరాంకము)

ప్రశ్న 5.
డాల్టన్ పాక్షిక పీడనాల నియమాన్ని తెలపండి.
జవాబు:
డాల్టన్ పాక్షిక పీడనాల నియమము : స్థిర ఉష్ణోగ్రత వద్ద, వాయువుల మిశ్రమం మొత్తం పీడనం ఆ మిశ్రమంలోని వివిధ వాయువులు కలుగజేసే పాక్షిక పీడనాల మొత్తానికి సమానము.
మొత్తం పీడనం, P = P₂ + P₂ + P₃
ఇక్కడ P₁, P₂, P₃……………………..మిశ్రమంలోని వివిధ వాయువులు కలుగచేసే పాక్షిక పీడనాలు.

ప్రశ్న 6.
పాత్రలోని ఆదర్శ వాయువు పీడనం పాత్ర ఆకారంపై ఆధారపడదు – వివరించండి.
జవాబు:
నిర్వచనం ప్రకారముగా, వాయు పీడనము ఆ వాయు అణువులు పాత్ర గోడలపై జరిపే వరుస అభిఘాతాల ఫలితము అని తెలియుచున్నది. ఇటువంటి ప్రతి అభిఘాతములో కొంత ద్రవ్యవేగము అణువుల నుండి పాత్ర ‘గోడలకు అందుతుంది. ఈ మార్పు పాత్ర యొక్క ఆకారంపై ఆధారపడదు ఎందుకనగా తుది ఫలితంలో పాత్ర వైశాల్యం A, అభిఘాతం సమయం ∆t లు ఉండవు. కావున, పాత్రలోని ఆదర్శ వాయువు పీడనం పాత్ర ఆకారంపై ఆధారపడదు.

ప్రశ్న 7.
వాయువులోని అణువుల స్వతంత్ర పరిమితులనే భావనను వివరించండి.
జవాబు:
అంతరాళంలో స్వేచ్ఛగా చలిస్తున్న అణువు యొక్క స్థానాన్ని నిర్దేశించడానికి కావలసిన నిరూపకాల సంఖ్యను స్వతంత్ర పరిమితులు అని చెప్పవచ్చును.

ప్రశ్న 8.
వాయు అణువు గతిజశక్తికీ, వాయు పీడనానికి మధ్య సంబంధాన్ని తెలిపే సమాసం ఏమిటి ?
జవాబు:
ఆదర్శ వాయువు యొక్క పీడనము ఆ వాయు అణువుల యొక్క సగటు గతిజశక్తికి \(\frac{2}{3}\) వ వంతు ఉంటుంది.
P = \(\frac{2}{3}\) E

ప్రశ్న 9.
వాయువు పరమ ఉష్ణోగ్రతను 3 రెట్లు పెంచితే, ఆ వాయు అణువు rms వేగంలో పెరుగుదల ఎంత ఉంటుంది ?
జవాబు:
వాయువు పరమ ఉష్ణోగ్రత మరియు వాయు అణువు rms వేగముల మధ్య సంబంధం
C ∝ \(\sqrt{\mathrm{T}}\).
కావున, పరమ ఉష్ణోగ్రతను 3 రెట్లు పెంచితే rms వేగం \(\sqrt{3}\) C అవుతుంది.
∴ rms వేగం పెరుగుదల = \(\sqrt{3}\) C – C = 0.732C = 73.2%

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణోగ్రతకు గతిక అర్థ వివరణను వివరించండి.
జవాబు:
వాయు అణుచలన సిద్ధాంతం ప్రకారం, ఒక మోల్ వాయువు కలిగించే పీడనం P కి సమీకరణము
P = \(\frac{1}{3}\) ρC²
⇒ P = \(\frac{1}{3}\) \(\frac{\mathrm{M}}{\mathrm{V}}\) C² (∵ సాంద్రత, ρ = \(\frac{\mathrm{M}}{\mathrm{V}}\))
⇒ PV = \(\frac{1}{3}\) MC²
⇒ \(\frac{1}{3}\) MC² = RT ………………… (1)
(∵ PV = RT (1 మోల్ వాయువునకు))
⇒ C² = \(\frac{3 \mathrm{RT}}{\mathrm{M}}\) లేక C² ∝ T
⇒ C ∝ \(\sqrt{\mathrm{T}}\) లేక \(\sqrt{\mathrm{T}}\) ∝ C …………………. (2)
కావున, ఒక ఆదర్శ వాయువు యొక్క పరమ ఉష్ణోగ్రత వర్గమూలం దాని అణువుల యొక్క rms వేగానికి అనులోమానుపాతంలో ఉంటుంది.
మరియు సమీకరణం (1) నుండి
\(\frac{1}{3} \frac{\mathrm{M}}{\mathrm{N}_{\mathrm{A}}}\)C² = \(\frac{\mathrm{R}}{\mathrm{N}_{\mathrm{A}}}\) T = K_BT (లేక) = \(\frac{1}{2}\) mc² = \(\frac{3}{2}\) k_BT
⇒ \(\frac{1}{2}\) mc² ∝ T (∵ \(\frac{3}{2}\) k_B ఒక స్థిరాంకం)
కాని \(\frac{1}{2}\) mc² అనునది వాయువులోని అణువుల సగటు స్థానాంతరణ గతిజశక్తి.
కాబట్టి, వాయు అణువుల సగటు స్థానాంతరణ గతిజశక్తి ఆ వాయువు యొక్క పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.

ప్రశ్న 2.
ఏకపరమాణుక, ద్విపరమాణుక, బహు పరమాణుక వాయువుల విశిష్టోష్ణ సామర్థ్యాన్ని శక్తి సమవిభాజన నియమం ఆధారంగా ఏ విధంగా వివరించవచ్చు ?
జవాబు:
శక్తి సమవిభజన నియమం ప్రకారం ఒక్కొక్క స్వేచ్ఛా కంపన స్థితికి గల వక్తి = \(\frac{1}{2}\)K_BT
ఏకపరమాణుక వాయువులకు మూడు స్వతంత్ర పరిమితులు ఉంటాయి. ఒక మోల్ వాయువుకు శక్తి
U = \(\frac{3}{2}\) K_BT × N_A = \(\frac{3}{2}\) RT
∴ స్థిర ఘనపరిమాణ విశిష్టోష్ణ సామర్థ్యము \(\frac{\mathrm{dU}}{\mathrm{dT}}\) = \(\frac{3}{2}\) R
స్థిర పీడన విశిష్టోష్ణ సామర్థ్యము C_p = C_v + R = (\(\frac{3}{2}\) + 1) = \(\frac{5}{2}\) R
ద్విపరమాణుక వాయువుకు మూడు స్థానాంతరణ, 2 భ్రమణ స్వతంత్ర పరిమితులు కలవు. మొత్తం స్వతంత్ర పరిమితుల సంఖ్య 5.
∴ ఒక మోల్ వాయువుకు శక్తి U = 5 × \(\frac{1}{2}\) k_B× N_A = \(\frac{5}{2}\) RT
స్థిర ఘనపరిమాణ విశిష్టోష్టము C_v = \(\frac{\mathrm{dU}}{\mathrm{dT}}\) = \(\frac{5}{2}\) R
స్థిర పీడన విశిష్టోష్ణ సామర్థ్యము C_p = C_v + R = (\(\frac{5}{2}\) + 1) R = \(\frac{7}{2}\) R
బహుపరమాణుక వాయువులకు మూడు స్థానాంతరణ, మూడు భ్రమణ మరియు కనీసం ఒక కంపన స్వతంత్ర రీతులు ఉంటాయి.
∴ 1 మోల్ వాయువు శక్తి U = (\(\frac{3}{2}\) k_BT + \(\frac{3}{2}\) k_BT + \(\frac{3}{2}\) k_BT) N_A
∴ U = (3 + f) K_BTN_A = (3 + f) R
∴ C_v = \(\frac{\mathrm{dU}}{\mathrm{dT}}\) = (3 + f) R; C_p = C_v + R = (4 + f) R

ప్రశ్న 3.
అణుచలన సిద్ధాంతం ఆధారంగా పరమ శూన్య ఉష్ణోగ్రత భావనను వివరించండి.
జవాబు:
వాయు అణుచలన సిద్ధాంతం ప్రకారంగా, ఒక మోల్ ఆదర్శ వాయువు కలుగజేసే పీడనము,
P = \(\frac{1}{3}\) ρC² ⇒ P = \(\frac{1}{3}\) \(\frac{\mathrm{M}}{\mathrm{V}}\) C²
⇒ P = \(\frac{1}{3}\) MC²
⇒ \(\frac{1}{3}\) MC² = RT …………… (1) (∵ PV = RT)
పరమ శూన్య ఉష్ణోగ్రత :
ఉష్ణోగ్రత, T = 0 అయిన సమీకరణం (1) నుండి, C = 0 కాబట్టి, పరమశూన్య ఉష్ణోగ్రత అనగా వాయు అణువుల యొక్క rms వేగము శూన్యముగా మారు ఉష్ణోగ్రత. అనగా, పరమ శూన్య ఉష్ణోగ్రత వద్ద వాయు అణువులలో ఎటువంటి కదలికా లేక నిశ్చల స్థితిలో ఉండును.

ఈ నిర్వచనము కేవలము ఆదర్శ వాయువులకు మాత్రమే వర్తిస్తుంది. కానీ, వాడుకలో ఉన్న నిజ వాయువులు ఆదర్శ వాయువులుగా అతి తక్కువ ఉష్ణోగ్రతల వద్ద వ్యవహరించవు.

ప్రశ్న 4.
ఆదర్శ వాయువులోని అణువు సగటు గతిజశక్తి, వాయువు పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుందని రుజువు చేయండి.
జవాబు:
వాయు అణుచలన సిద్ధాంతం ప్రకారంగా, ఒక మోల్ ఆదర్శ వాయువు కలుగజేసే పీడనము,
P = \(\frac{1}{3}\) ρC² ఇచ్చట ρ = వాయుసాంద్రత
∴ P = \(\frac{1}{3}\) \(\frac{\mathrm{M}}{\mathrm{V}}\) C²
⇒ PV = \(\frac{1}{3}\) MC²
కాని PV = RT (ఆదర్శ వాయు సమీకరణము నుండి)
∴ \(\frac{1}{3}\) MC² = RT
⇒ \(\frac{1}{3} \frac{\mathrm{m}}{\mathrm{N}_{\mathrm{A}}}\) C² = \(\frac{\mathrm{R}}{\mathrm{N}_{\mathrm{A}}}\) T = k_BT (∵ K_B = \(\frac{\mathrm{R}}{\mathrm{N}_{\mathrm{A}}}\))
⇒ \(\frac{1}{2}\) mc² = \(\frac{3}{2}\) k_BT (లేదా)
⇒ \(\frac{1}{2}\) mc² ∝ T
\(\frac{1}{2}\) mc² అనగా వాయువులోని అణువు సగటు గతిజశక్తి.
కాబట్టి, ఆదర్శ వాయువులోని అణువు సగటు గతిజశక్తి, వాయువు పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.

ప్రశ్న 5.
V₁, V₂ ఘనపరిమాణాలు కలిగిన రెండు ఉష్ణ బంధక పాత్రలు 1, 2 లను ఒక వాల్వుతో కలిపి వాటిలో ఉష్ణోగ్రతలు (T₁, T₂) పీడనాలు (P₁, P₂) వరుసగా ఉండేటట్లుగా గాలిని నింపారు. ఈ రెండు పాత్రలను కలిపే ఆ వాల్వ్ ను ఇప్పుడు తెరిస్తే, సమతాస్థితి వద్ద ఆ పాత్రల్లో ఉష్ణోగ్రత ఎంత ఉంటుంది ?
జవాబు:
ఆదర్శ వాయు సమీకరణము నుండి
\(\frac{\mathrm{P}_1 \mathrm{~V}_1}{\mathrm{~T}_1}\) = μ₁ R; మరియు \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\) = μ₂R
వాయు పాత్రలు ఉష్ణబంధక పాత్రలు గనుక, ఎటువంటి బాహ్యపని జరుగదు, కనుక మొత్తం శక్తి స్థిరముగా ఉండును.
కాబట్టి, \(\frac{3}{2}\) (P₁V₁ + P₂V₂) = \(\frac{3}{2}\) P(V₁ +V₂)
∴ మిశ్రమ పీడనము P = \(\frac{P_1 V_1+P_2 V_2}{V_1+V_2}\) …………… (2)
రెండు వాయువుల మిశ్రమంలో,
(μ₁ + μ₂) RT = P(V₁ + V₂)
ఇందులో T = మిశ్రమ ఉష్ణోగ్రత
సమీకరణాలు (1), (2) లను పై సమీకరణంలో ప్రతిక్షేపించగా,

ఇదే సమతాస్థితి వద్ద ఆ పాత్రల్లో ఉన్న గాలి యొక్క ఉష్ణోగ్రత.

ప్రశ్న 6.
ఒకే ఉష్ణోగ్రత వద్ద ఉన్న ఆక్సిజన్, హైడ్రోజన్ అణువుల rms వడుల నిష్పత్తి ఎంత ? (మే 2014)
జవాబు:
T ఉష్ణోగ్రత వద్ద ఉన్న ఆక్సిజన్ వాయువులోని అణువుల rms వడి,
C_{ఆక్సి} = \(\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}_0}}\) = \(\sqrt{\frac{3 \mathrm{RT}}{32}}\)
అదే ఉష్ణోగ్రత (T) వద్ద ఉన్న హైడ్రోజన్ వాయు అణువుల rms వడి,
C_హై = \(\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}_{\mathrm{H}}}}=\sqrt{\frac{3 \mathrm{RT}}{1}}=\sqrt{3 \mathrm{RT}}\)
ఆక్సిజన్, హైడ్రోజన్ అణువుల rms వడుల నిష్పత్తి

∴ C_{ఆక్సి} : C_హై = 1 : 5.656

ప్రశ్న 7.
ఒక వాయువులోని నాలుగు అణువులు 1, 2, 3, 4km/s ల వడులు కలిగి ఉన్నాయి. ఆ వాయు అణువు rms వడిని కనుక్కోండి.
జవాబు:
ఇక్కడ, C₁ = 1 km/s; C₂ = 2 km/s; C₃ = 3 km/s; C₄ = 4km/s
వాయు అణువుల rms వడి,
C_rms = \(\sqrt{\frac{\mathrm{c}_1^2+\mathrm{C}_2^2+\mathrm{C}_3^2+\mathrm{C}_4^2}{4}}\) = \(\sqrt{\frac{1^2+2^2+3^2+4^2}{4}}\)
= \(\sqrt{\frac{1+4+9+16}{4}}\) = \(\sqrt{7.5}\)
∴ C_rms = 2.75 km/s

ప్రశ్న 8.
ఒక వాయువుకు f స్వతంత్ర పరిమితులు ఉంటే, C_p, C_v ల నిష్పత్తిని కనుక్కోండి.
జవాబు:
ఒక బహుపరమాణుక వాయువుకు ‘f’ స్వతంత్ర పరిమితులు ఉన్నాయి అని అనుకొనుము.
కాబట్టి, ఒక గ్రాము మోల్ వాయువు యొక్క అంతర్గత శక్తి,

ప్రశ్న 9.
127°C వద్ద ఉన్న 1 గ్రాము హీలియం (అణుభారం 4) కు అణు గతిజశక్తిని లెక్కించండి. R = 8.31 J mol^-1 K^-1.
జవాబు:
n = హీలియం వాయువులోని మోలుల సంఖ్య = \(\frac{1 \mathrm{gm}}{4 \mathrm{gm} \mathrm{mol}^{-1}}\) = 0.25 మోల్
R = 8.314 J mol^-1 K^-1,
T = 127°C = 127 + 273 = 400K
∴ అణు గతిజశక్తి = \(\frac{3}{2}\) nRT = \(\frac{3}{2}\) × 0.25 mol × 8.314 J mol^-1 K^-1 × 400K = 1247.1 J

ప్రశ్న 10.
ఒక వాయువుకు పీడనం 2% పెరిగితే, దాని ఘనపరిమాణంలో తగ్గుదల శాతం ఎంత వుంటుంది ? వాయువు బాయిల్ నియమం పాటిస్తుందని ఊహించండి.
జవాబు:
ఒక వాయువు యొక్క తొలిపీడనం ‘P’ మరియు ఘనపరిమాణం ‘V’ అని అనుకొనుము.
ఆ వాయు పీడనం 2% పెరిగితే, కొత్త పీడనం,
P’ = P + \(\frac{2}{100}\) P
⇒ P¹ = \(\frac{102}{100}\) P
బాయిల్ నియమం ప్రకారం, PV = స్థిరాంకం ⇒ PV = P¹V¹
⇒ PV = \(\frac{102}{100}\) P × V¹
⇒ V¹ = \(\frac{100}{102}\) V
వాయు ఘనపరిమాణంలో తగ్గుదల శాతం = \(\frac{\mathrm{V}-\mathrm{V}^{\prime}}{\mathrm{V}}\) × 100 = \(\frac{\left(\mathrm{V}-\frac{100}{102} \mathrm{~V}\right)}{\mathrm{V}}\) × 100 = \(\frac{2}{102}\) × 100 = 1.96%
కావున వాయుపీడనం 2% పెరిగితే వాయు ఘనపరిమాణం 1.96% తగ్గుతుంది.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
అణుచలన సిద్ధాంతం నుంచి ఒక పాత్రలోని ఆదర్శ వాయువు పీడనానికి సమాసం రాబట్టి, తద్వారా ఉష్ణోగ్రతకు గతిక అర్ధ వివరణను ఇవ్వండి.
జవాబు:
భుజము పొడవు ‘ ఉన్న ఒక ఘనాన్ని తీసుకోండి. దాని భుజముల వెంబడి నిరూపకాక్షాలు x, y మరియు Z అనుకోండి. ఈ దిశలలో వాయు అణువు వేగ అంశాలు v_x, v_y మరియు v_z అనుకోండి. y – z తలానికి లంబంగా X – అక్షం వెంబడి చలించే అణువు వేగము v_x. ఇది y – z తలంతో స్థితిస్థాపక అభిఘాతం జరపడం వల్ల వచ్చిన దిశలో వెనుకకు మరలుతుంది కావున వేగాలు v_y, v_z లు ప్రభావితం కావు.

x – దిశలో వాయు అణువు ద్రవ్యవేగంలో మార్పు తుది ద్రవ్య వేగము (-mv_x) – తొలి ద్రవ్య వేగము (mv_x) = -mv_x – (mv_x) = -2mv_x …………… (1)

పాత్ర గోడ వైశాల్యము A అనుకుంటే ∆t కాలంలో పాత్ర గోడ నుండి v_x ∆t దూరంలో గల అణువులు మాత్రమే గోడను ఢీకొంటాయి. కావున Av_x. ∆t ఘనపరిమాణంలో ఏకాంక ఘనపరిమాణానికి గల అణువుల సంఖ్య ‘n’ అనుకుంటే వీటిలో సగం పాత్రవైపు మిగిలినవి పాత్ర గోడ నుండి దూరంగా చలిస్తాయి. కావున ∆t కాలంలో గోడకు బదిలీ ఐన ద్రవ్యవేగము

Q = 2mv_x × గోడను తాకిన అణువుల సంఖ్య
∴ Q = 2mv_x (\(\frac{1}{2}\)n . Av_x∆t)
పాత్ర గోడ y, z తలంపై పీడనము

పాస్కల్ నియమం ప్రకారం పాత్ర అంతటా ఒకే పీడనం ఉంటుంది. కాబట్టి x, y, z దిశలో ఏ దిశ వెంబడి అయినా పీడనం విలువ ఒక్కటే.

పై సమీకరణలో పాత్ర ఆకారానికి సంబంధించిన పదం లేకపోవడం వల్ల ఈ సమీకరణ ఎటువంటి ఆకారం గల పాత్రకైనా వర్తిస్తుంది.

ఉష్ణోగ్రతకు గతిక వివరణ :
వాయు సమీకరణం నుండి PV = \(\frac{1}{3} \mathrm{nvm} \overline{v^2}\) = \(\frac{2}{3} \mathrm{~N}\left(\frac{1}{2} \mathrm{~m} \overline{\mathrm{v}^2}\right)\)
ఇందులో N = nv మరియు \(\frac{1}{2} m \overline{v^2}\) = గతిజశక్తి
ఆదర్శ వాయువు అంతర్గత శక్తి శుద్ధంగా గతిజశక్తి కావున E = N.\(\frac{1}{2}\)mv²
∴ PV = \(\frac{3}{2}\) E = \(\frac{3}{2}\) K_BNT పై సమీకరణాల నుండి
\(\frac{E}{N}=\frac{1}{2} m \overline{v^2}\) ; మరియు \(\frac{\mathrm{B}}{\mathrm{N}}=\frac{3}{2}\)K_BT ⇒ \(\frac{\mathrm{B}}{\mathrm{N}}\) ∝ T
అనగా ఒక అణువు సగటు గతిజశక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. ఇది వాయువు పీడనం, పాత్ర ఘనపరిమాణం మీద ఆధారపడని ఉష్ణ గతిక చలరాశి.

లెక్కలు

ప్రశ్న 1.
STP వద్ద ఆక్సిజన్ వాయువు ఆక్రమించే ఘనపరిమాణంలో, ఆక్సిజన్ అణు ఘనపరిమాణ భాగాన్ని అంచనావేయండి. ఆక్సిజన్ అణువు వ్యాసాన్ని 3 Å గా తీసుకోండి.
సాధన:
ఇచ్చట అణువు వ్యాసము, d = 3 ,
అణువు వ్యాసార్ధము, r = \(\frac{\mathrm{d}}{\mathrm{2}}\) = \(\frac{3}{2}\) Å = \(\frac{3}{2}\) × 10^-8 cm.
అణు ఘనపరిమాణము, V = \(\frac{4}{3}\) πr³ . N,
ఇచ్చట N అనునది అవొగాడ్రో సంఖ్య
= \(\frac{4}{3}\) × \(\frac{22}{7}\) (1.5 × 10)³ × (6.023 × 10²³) = 8.52 cc.
STP వద్ద 1 మోల్ వాయువు ఆక్రమించు నిజ ఘనపరిమాణము, V’ = 22400 cc
∴ \(\frac{\mathrm{V}}{\mathrm{V}^{\prime}}\) = \(\frac{8.52}{22400}\) = 3.8 × 10^-4 ≈ 4 × 10^-4

ప్రశ్న 2.
ప్రామాణిక ఉష్ణోగ్రతా పీడనాల వద్ద (STP : 1 వాతావరణ పీడనం, 0°C) ఏదైనా ఒక మోల్ (ఆదర్శ) వాయువు ఆక్రమించే ఘనపరిమాణాన్ని మోలార్ ఘనపరిమాణం అంటారు. ఇది 22.4 లీటర్లు అని చూపండి.
సాధన:
1 మోల్ ఆదర్శ వాయువుకు, PV = RT ∴ V = \(\frac{\mathrm{RT}}{\mathrm{P}}\)
R = 8.31 J mole^-1 K^-1, T = 273 K, మరియు P = 1 వాతావరణ పీడనం = 1.013 × 10⁵ Nm^-2 విలువలను పై సమీకరణములో ప్రయోగించగా,
V = \(\frac{8.31 \times 273}{1.013 \times 10^5}\) = 0.0224 m³ = 0.0224 × 10⁶ cc = 22400 cc = 22.4 లీటర్లు.

ప్రశ్న 3.
రెండు వేరు వేరు ఉష్ణోగ్రతల వద్ద 1.00 × 10^-3 kg ఆక్సిజన్ వాయువుకు PV/Tకి P కీ మధ్య గ్రాఫ్ వక్రాన్ని పటం సూచిస్తుంది.
a) చుక్కల గీత వక్రం ఏ ప్రాధాన్యతను సూచిస్తుంది ?
b) వీటిలో ఏది నిజం : T₁ >T₂ (లేదా) T₁ < T₂?
c) Y-అక్షంపై వక్రాలు కలిసిన చోట PV/T విలువ ఎంత ?
d) 1.00 × 10^-3 kg హైడ్రోజనక్కు ఇటువంటి వక్రాలే వస్తే, Y-అక్షంపై వక్రాలు కలిసిన చోట PV/T కి ఇదే విలువ వస్తుందా ? ఒకవేళ రాకుంటే, ఎంత ద్రవ్యరాశి ఉన్న హైడ్రోజన్, అదే PV/T విలువను ఇస్తుంది. (గ్రాఫ్లో అల్పపీడనం, అధిక ఉష్ణోగ్రత ఉన్న ప్రాంతానికి) ? (H₂ అణు ద్రవ్యరాశి = 2.02 u, O₂ అణు ద్రవ్యరాశి = 32.0 u, R = 8.31 Jmol^-1 K^-1.)

సాధన:
a) చుక్కల గీత \(\frac{\mathrm{PV}}{\mathrm{T}}\) (= μR) అనునది స్థిరరాశి అని సూచిస్తుంది. ఇది పీడనంపై ఆధారపడదు. చుక్కల గీత వక్రం ఆదర్శ వాయు ప్రవర్తనను సూచిస్తుంది.

b) T₁ ఉష్ణోగ్రతా వక్రం, T₂ ఉష్ణోగ్రతా వక్రం కన్నా చుక్కల గీతకు సమీపంలో ఉంది. ఉష్ణోగ్రతను పెంచినపుడు నిజవాయువు ప్రవర్తన ఆదర్శ వాయు ప్రవర్తనకు దగ్గరగా ఉంటుంది. అందువల్ల T₁ > T₂.

c) Y-అక్షంపై వక్రాలు కలిసిన చోట \(\frac{\mathrm{PV}}{\mathrm{T}}\) విలువ μ R కు సమానం.
∴ \(\frac{\mathrm{PV}}{\mathrm{T}}\) = μR = \(\left(\frac{1}{32}\right)\) × 8.31 JK^-1 = 0.26 JK^-1

d) Y-అక్షంపై వక్రాలు కలిసిన చోట \(\frac{\mathrm{PV}}{\mathrm{T}}\) కి ఇదే విలువ రాదు. Y-అక్షంపై వక్రాలు కలిసిన చోట ఇదే విలువ రాదు. ఎందువలన అనగా ఆక్సిజన్ అణు ద్రవ్యరాశి, హైడ్రోజన్ అణు ద్రవ్యరాశికి మధ్య తేడా ఉంటుంది. \(\frac{\mathrm{PV}}{\mathrm{T}}\) విలువ పైన ఉదహరించినట్లుగా రావలెనంటే, కావలసిన హైడ్రోజన్ ద్రవ్యరాశి
\(\frac{\mathrm{PV}}{\mathrm{T}}\) = μR = \(\frac{\mathrm{m}}{2.02}\) × 8.31 = 0.26
m = \(\frac{2.02 \times 0.26}{8.31}\) gram = 6.32 ×10^-2 gram.

ప్రశ్న 4.
30 లీటర్ల ఘనపరిమాణం ఉన్న ఆక్సిజన్ సిలిండర్ తొలి గేజ్ పీడనం 15 atm, ఉష్ణోగ్రత 27°C. ఆ సిలిండర్ నుంచి కొంత ఆక్సిజన్ వాయువును తొలగించిన తరువాత గేజ్ పీడనం 11atm కు, ఉష్ణోగ్రత 17°Cకు పడిపోయాయి. అయితే, సిలిండరు నుంచి తొలగించిన ఆక్సిజన్ వాయువు ద్రవ్యరాశిని అంచనా కట్టండి.
(R = 8.31 J mole^-1 K^-1, O₂ అణు ద్రవ్యరాశి = 32 u).
సాధన:
ప్రారంభమున ఆక్సిజన్ సిలిండరు నందు, V₁ = 30 litres = 30 × 10^-3m³
P₁ = 15 atm. = 15 × 1.01 × 10° Pa; T₁ = 27 + 273 = 300 K.
సిలిండర్ n₁ మోల్ల ఆక్సిజన్ కల్గియున్న P₁V₁ = n₁ RT₁
(లేదా) n₁ = \(\frac{\left(15 \times 1.01 \times 10^5\right) \times\left(30 \times 10^{-3}\right)}{8.3 \times 300}\) = 18.253
ఆక్సిజన్ అణువు భారం M = 32 g
సిలిండర్లో ఆక్సిజన్ అణువు తొలి ద్రవ్యరాశి = m₁ = n₁ M = 18.253 × 32 = 584.1 g.
చివరగా ఆక్సిజన్ సిలిండర్ నందు n₂ మోల్ల ఆక్సిజన్ మిగిలినది.
ఇచ్చట V₂ = 30 × 10^-3m³; P₂ = 11 × 1.01 × 10⁵ Pa; T₂ = 17 + 273 = 290 K
ఇపుడు n₂ = \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{RT}_2}=\frac{\left(11 \times 1.01 \times 10^5\right) \times\left(30 \times 10^{-3}\right)}{8.3 \times 290}\) = 13.847
∴ సిలిండర్లో ఆక్సిజన్ వాయువు తుది ద్రవ్యరాశి, m₂ = 13.847 × 32 = 453.1 g
∴ సిలిండర్ నుంచి తొలగించిన ఆక్సిజన్ వాయువు ద్రవ్యరాశి = m₁ – m₂ = 584.1 – 453.1 = 131.0 g

ప్రశ్న 5.
40 m లోతు, 12°C ఉష్ణోగ్రత ఉన్న సరస్సు అడుగు నుంచి 1.0 cm³ ఘనపరిమాణం ఉన్న గాలి బుడగ పైకి లేస్తుంది. ఉష్ణోగ్రత 35°C ఉన్న సరస్సు ఉపరితలాన్ని చేరుకోగానే అది ఎంత ఘనపరిమాణానికి పెరుగుతుంది ?
సాధన:
V₁ = 1.0 cm³ = 1.0 × 10^-6 m³; T₁ = 12°C = 12 + 273 = 285 K;
P₁ = 1 atm. + h₁ ρg = 1.01 × 10⁵ + 40 × 10³ × 9.8 = 493000 Pa.
గాలి బుడగ సరస్సు ఉపరితలాన్ని చేరినపుడు
V₂ = ? ; T₂ = 35°C = 35 + 273 = 308 K; P₂ = 1 atm. = 1.01 × 10⁵ Pa
ఇప్పుడు \(\frac{\mathrm{P}_1 \mathrm{~V}_1}{\mathrm{~T}_1}=\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\) or V₂ = \(\frac{\mathrm{P}_1 \mathrm{~V}_1 \mathrm{~T}_2}{\mathrm{~T}_1 \mathrm{P}_2}\)
∴ V₂ = \(\frac{(493000) \times\left(1.0 \times 10^{-6}\right) \times 308}{285 \times 1.01 \times 10^5}\) = 5.275 × 10^-6 m³

ప్రశ్న 6.
27°C ఉష్ణోగ్రత 1 atm పీడనం వద్ద 25.0 m³ ఘనపరిమాణం ఉన్న గదిలోని మొత్తం గాలి (ఆక్సిజన్, నైట్రోజన్, నీటి ఆవిరి, ఇతర అంతర్భాగాలను కలుపుకొని) అణువుల సంఖ్యను అంచనా కట్టండి.
సాధన:ద
త్తాంశము ప్రకారము V = 25.0m³; T = 27 + 273 = 300 K; k = 1.38 × 10^-23 JK^-1;
ఇప్పుడు, PV = nRT = n(Nk)T = (nN) kT = N’ kT
nN = N’ = గదిలోని మొత్తం గాలిలో గల అణువుల సంఖ్య.
∴ N’ = \(\frac{\mathrm{PV}}{\mathrm{kT}}=\frac{\left(1.01 \times 10^5\right) \times 25}{\left(1.38 \times 10^{-23}\right) \times 300}\) = 6.10 × 10²⁶

ప్రశ్న 7.
హీలియం పరమాణువు సగటు ఉష్ణశక్తిని,
(i) గది ఉష్ణోగ్రత (27°C),
(ii) సూర్యుని ఉపరితల ఉష్ణోగ్రత (6000 K),
(iii) 10 మిలియన్ కెల్విన్ ఉష్ణోగ్రత (ఒక నక్షత్రం యొక్క మాదిరి అంతర్భాగ ఉష్ణోగ్రత) ల వద్ద అంచనా కట్టండి.
సాధన:
i) దత్తాంశము ప్రకారము T = 27°C = 27 + 273 = 300 K
సగటు ఉష్ణశక్తి = \(\frac{3}{2}\) kT = \(\frac{3}{2}\) × 1.38 × 10^-23 × 300 = 6.2 × 10^-21 J.

ii) T = 6000 K, సగటు ఉష్ణశక్తి = \(\frac{3}{2}\) kT = \(\frac{3}{2}\) × 1.38 × 10^-23 × 6000 = 1.24 × 10^-19 J.

iii) T = 10 మిలియన్ కెల్విన్ K = 10⁷ K వద్ద
సగటు ఉష్ణశక్తి = \(\frac{3}{2}\) kT = \(\frac{3}{2}\) × 1.38 × 10^-23 × 10 7 = 2.1 × 10^-16 J.

ప్రశ్న 8.
సమాన ఘనపరిమాణాలు ఉన్న మూడు పాత్రలలోని వాయువులు ఒకే ఉష్ణోగ్రతా పీడనాల వద్ద ఉన్నాయి. మొదటి పాత్రలో నియాన్ (ఏకపరమాణుక), రెండో దానిలో క్లోరిన్ (ద్విపరమాణుక), మూడో దానిలో యురేనియం హెక్సాఫ్లోరైడ్ (బహుపరమాణుక) వాయువులు ఉన్నాయి. ఈ పాత్రలలో ఉన్న సంబంధిత వాయు అణువుల సంఖ్యలు సమానంగా ఉంటాయా ? ఈ అణువుల rms (వడి వర్గమధ్యమ వర్గమూల) వడి మూడు సందర్భాల్లో సమానంగా ఉంటుందా ? అలా ఉండకపోతే, ఏ సందర్భానికి V_rms అత్యధికమై ఉంటుంది ?
సాధన:
మూడు పాత్రలు (ఒకే ఉష్ణోగ్రత మరియు పీడనం వద్ద) సమాన ఘనపరిమాణాన్ని కలిగి ఉన్నాయి. అవొగాడ్రో నియమం ప్రకాకరము మూడు పాత్రలు సమాన సంఖ్యలో అణువులను కలిగి ఉంటాయి. ఇది అవొగాడ్రో సంఖ్యకు
సమానము.
అనగా N = 6.023 × 10²³.
నిర్ణీత ఉష్ణోగ్రత వద్ద V_rms = \(\sqrt{\frac{3 \mathrm{kT}}{\mathrm{m}}}\) i.e., V_rms ∝ \(\frac{1}{\sqrt{m}}\)
అణువుల rms వేగము మూడు సందర్భాలలో సమానము కాదు. నియాన్కు అతి తక్కువ ద్రవ్యరాశీ వుంటుంది. కావున rms వేగం చాలా ఎక్కువ.

ప్రశ్న 9.
ఏ ఉష్ణోగ్రత వద్ద ఆర్గాన్ వాయువు సిలిండర్లోని ఒక పరమాణువు rms వడి -20°C వద్ద ఉన్న హీలియం పరమాణువు rms వడికి సమానంగా ఉంటుంది (Ar పరమాణు ద్రవ్యరాశి = 39.9 u, He పరమాణు ద్రవ్యరాశి = 4.0u).
సాధన:
TK మరియు T’ K ఉష్ణోగ్రతల వద్ద వరుసగా ఆర్గాన్ మరియు హీలియం వాయు పరమాణువులు. rms వేగము C మరియు C’ అని అనుకొనుము.
ఇచ్చట, M = 39.9 ; M’ = 4.0; T= ? T’ = -20 + 273 = 253K

ప్రశ్న 10.
ఒక సిలిండర్లో 2.0 atm పీడనం, 17°C ఉష్ణోగ్రత వద్ద ఉన్న నైట్రోజన్ వాయు అణువు స్వేచ్ఛా పథమధ్యమాన్ని, అభిఘాత పౌనఃపున్యాన్ని లెక్కించండి. నైట్రోజన్ అణువు వ్యాసార్ధాన్ని సుమారు 1.0Å గా తీసుకోండి. దాని అభిఘాత కాలాన్ని రెండు వరుస అభిఘాతాల మధ్య అణువు స్వేచ్ఛగా తిరగడానికి పట్టే కాలంతో పోల్చండి. N₂ అణువు ద్రవ్యరాశి = 28.0 u),
సాధన:
λ = ?, f = ? ; p = 2 atm = 2 × 1.013 × 10⁵ Nm^-2; T = 17°C = (17 + 273) K = 290 K
σ = 2 × 1 = 2 Å = 2 × 10^-10 m; k = 1.38 × 10^-23 J molecule^-1 K^-1‚ M = 28 × 10^-3 kg

అభిఘాత పౌనఃపున్యము = ఒక సెకనులో జరిగే అభిఘాతాల సంఖ్య = \(\frac{\mathrm{v}_{\mathrm{rms}}}{\lambda}=\frac{508.24}{1.11 \times 10^{-7}}\) = 4.58 × 10⁹.

ప్రశ్న 11.
ఒక మీటరు పొడవు కలిగి, ఇరుకైన బోలు రంధ్రం (bore) ఉన్న (ఒకవైపు మూసిన) గొట్టాన్ని క్షితిజ సమాంతరంగా ఉంచినప్పుడు, అందులో 76 cm పొడవైన పాదరస దారం (thread) ఉంటే, అది 15 cm (పొడవైన) ల గాలి స్తంభాన్ని పట్టుకోగలుగుతుంది. ఇప్పుడు గొట్టాన్ని, తెరిచిన కొన కిందివైపు ఉండేటట్లు నిలువుగా ఉంచితే ఏం జరుగుతుంది?
సాధన:
గాజు గొట్టమును క్షితిజ సమాంతరంగా వుంచిన, 76 cm పొడవుగా గల పాదరసం 15 cm పొడవు గల గాలిని బంధించును. తెరిచి ఉన్న వైపు 9 cm పొడవు గల గొట్టం మిగిలి ఉంటుంది.
గొట్టంలో గల గాలిపై వాతావరణ పీడనం వుండును.
గొట్టం అడ్డుకోత వైశాల్యంను 1sq.cm. అని అనుకొనుము.
∴ P₁ = 76 cm మరియు V₁ = 15 cm³.
అదే గొట్టమును నిట్టనిలువుగా వుంచిన, 15cm పొడవు గల గాలి అదనముగా 9 cm పెరుగును. మరియు పాదరసం, వాతావరణ పీడనమును సమము చేయుటకు h cm దూరం బయటకి ప్రవహించును. దీనిని పటం (b)లో చూపితిమి. అందువలన గాలి ఎత్తు మరియు పాదరసం ఎత్తు వరుసగా (24 + h) cm మరియు (76 – h) cm.
గాలి పీడనము = 76 – (76 – b) = h cm పాదరసం

∴ V₂ = (24 + b) cm³ మరియు P₂ = h cm
ఉష్ణోగ్రత స్థిరం అని ఊహించిన
P₁V₁ = P₂V₂
(లేదా) 76 × 15 = h × (24 + b)
(లేదా) h² + 24h – 1140 = 0
(లేదా) h = \(\frac{-24 \pm \sqrt{(24)^2+4 \times 1140}}{2}\)
= 23.8 cm (లేదా) 47.8 cm
h అనునది ఋణాత్మకము కాదు. కావున
(ఎందువలన అనగా ఎక్కువ పాదరసం గొట్టంలో ప్రవహించదు)
h = 23.8 cm అందువల్ల, గొట్టం నిట్టనిలువు స్థితిలో 23.8 cm పాదరసం బయటికి వచ్చును.

ప్రశ్న 12.
ఒక నిర్దిష్టమైన పరికరం నుంచి హైడ్రోజన్ సగటు విసరణ రేటు విలువ 28.7 cm³s^-1 గా ఉంది. అదే పరిస్థితులలో ఉన్న మరొక వాయువు సగటు విసరణ రేటు 7.2 cm³s^-1 గా కొలవడమైంది. ఆ వాయువు ఏదో గుర్తించండి. సూచన : గ్రాహమ్ విసరణ నియమాన్ని ఉపయోగించండి. R₁/R₂ = (M₂/ M₁)^1/2 ఇందులో R₁, R₂ లు వరుసగా 1, 2 వాయువుల విసరణ రేట్లు, M₁, M₂లు వాటి (అనురూప) అణు ద్రవ్యరాశులు. అణుచలన సిద్ధాంతం యొక్క సరళమైన పర్యవసానమే ఈ నియమం.]
సాధన:
గ్రాహమ్ విసరణ వాయు నియమము ప్రకారము \(\frac{r_1}{r_2}=\sqrt{\frac{M_2}{M_1}}\)
హైడ్రోజన్ వాయువు విసరణ రేటు r₁ = 28.7 cm³ s^-1
వేరొక వాయువు విసరణ రేటు r₂ = 7.2 cm³ s^-1
M₁ = హైడ్రోజన్ అణు ద్రవ్యరాశి = 2 u
M₂ = ?
∴ \(\frac{28.7}{7.2}=\sqrt{\frac{\mathrm{M}_2}{2}}\) (లేదా) M₂ = \(\left(\frac{28.7}{7.2}\right)^2\) × 2 = 31.78 ≈ 32.
ఇది ఆక్సిజన్ వాయువు యొక్క అణు ద్రవ్యరాశి.

ప్రశ్న 13.
సమతాస్థితిలో ఉన్న వాయువు, దాని ఘనపరిమాణమంతటా ఏకరీతి సాంద్రత, పీడనాలను కలిగి ఉంది. ఇది తప్పనిసరిగా బాహ్య ప్రభావాలు లేనపుడే యదార్థం. ఉదాహరణకు, గురుత్వ ప్రభావంలో ఉన్న ఒక వాయు స్తంభం ఏకరీతి సాంద్రత (పీడనం) కలిగి ఉండదు. ఎత్తుతో దాని సాంద్రత తగ్గుతుందని మీరు ఊహించవచ్చు. ఎత్తుపై వాయు సాంద్రత కచ్చితంగా ఎలా ఆధారపడుతుందో మనం చెప్పుకొనే వాతావరణాల నియమం ఇవ్వగలుగుతుంది.
అది,
n₂ = n₁ exp [-mg (h₂ – h₁) / k_B T]
దీనిలోని ng, n, లు ఎత్తులు h, h, వద్ద గల సంఖ్య సాంద్రతను వరుసగా సూచిస్తాయి. ద్రవ స్తంభంలోని వ్యాక్షేపం (suspension) యొక్క అపసారం (మద్ది) (sedimentation)కు ఉండే కింది సమీకరణాన్ని ఉత్పాదించటానికి పై సంబంధాన్ని ఉపయోగించండి.
n₂ = n₁ exp (-mg N_A (ρ – ρ’) (h₂ – h₁)/(ρRT)
ఇందులో p ద్రవంలో వేలాడే కణం సాంద్రత, p’ అనేది ఆ కణం చుట్టూ ఉన్న యానకం సాంద్రత (NA అవొగాడ్రో సంఖ్య. R సార్వత్రిక వాయు స్థిరాంకం) (సూచన : వేలాడే కణం దృశ్య భారాన్ని కనుక్కోవడానికి ఆర్కిమెడిస్ సూత్రాన్ని ఉపయోగించండి.)
సాధన:
వాతావరణాల నియమం ప్రకారము n₂ = n₁ exp.[-\(\frac{\mathrm{mg}}{\mathrm{k}_{\mathrm{B}} \mathrm{T}}\) (h₂ – h₁] ………….. (i)
ఇచ్చట n₁, n₂ లు వరుసగా h₁, h₂ ఎత్తుల వద్ద కణాల సంఖ్యా సాంద్రతలు.

ద్రవ స్తంభంలోని వ్యాక్షేపం యొక్క అపసారంను పరిగణించినపుడు mg స్థానంలోని వ్యాక్షేపం చెందిన కణాల దృశ్యాభారంను తీసుకొనవలెను.

వ్రేలాడే కణం ఘనపరిమాణము V అని దాని సాంద్రతను ρ అని మరియు కణం చుట్టూ ఉన్న యానకం సాంద్రతను ρ’ అని, వ్రేలాడే ఒక కణం ద్రవ్యరాశి m అని, కణం వలన స్థానభ్రంశం చెందిన ద్రవం ద్రవ్యరాశిని m’ అని అనుకొనుము.

ఆర్కిమెడీస్ సూత్రమును అనుసరించి వ్రేలాడే ఒక్క కణం దృశ్యాభారం = నిజభారం – స్థానభ్రంశం చెందిన ద్రవభారం.
= mg – m’ g
= mg – V ρ’g – mg – \(\left(\frac{m}{\rho}\right)\) ρ’g = mg\(\left(1-\frac{\rho^{\prime}}{\rho}\right)\)
బోల్ట్ స్థిరాంకము ప్రకారము k_B = \(\frac{\mathrm{R}}{\mathrm{N}_{\mathrm{A}}}\)
R = సార్వత్రిక వాయు స్థిరాంకము మరియు N_A = అవొగాడ్రో
mg స్థానంలో mg \(\left(1-\frac{\rho^{\prime}}{\rho}\right)\) ను మరియు k_B విలువను సమీకరణం (1) లో ప్రతిక్షేపించగా
n₂ = n₁ exp. [\(\frac{\mathrm{mg} \mathrm{N}_{\mathrm{A}}}{\mathrm{RT}}\left(1-\frac{\rho^{\prime}}{\rho}\right)\) (h₂ – h₁)]
ఇదే మనకు అవసరమయిన సంబంధం.

ప్రశ్న 14.
కొన్ని ఘనపదార్థాలకు, ద్రవాలకు సాంద్రతలను కింద ఇచ్చాం. వాటి పరమాణువుల పరిమాణా (size) లకు ఉజ్జాయింపు అంచనాలను ఇవ్వండి.

(సూచన : ఘన (పదార్థం) రూప, ద్రవరూప ప్రావస్థలో అణువులు దగ్గర దగ్గరగా బంధితమై ఉంటాయని ఊహించుకొంటూ మీకు తెలిసిన అవొగాడ్రో సంఖ్య విలువను ఉపయోగించండి. అయితే, వివిధ పరమాణు పరిమాణాలకు, ఈ విధంగా మీరు పొందే వాస్తవిక విలువలను నిజంగానే వాటికుంటాయని మాత్రం భావించకండి. దగ్గర దగ్గరగా అణువులు బంధితమై ఉంటాయనే ఉజ్జాయింపుకుండే ముడితత్వ భావన (Crudeness of the tight packing approximation) వల్ల, ఈ ఫలితాలు కొన్ని Åల వ్యాప్తిలో పరమాణు పరిమాణాలు ఉంటాయని మాత్రమే సూచిస్తాయి).
సాధన:
పరమాణు వ్యాసార్ధం r అయిన, పరమాణు ఘనపరిమాణం = \(\frac{4}{3}\) πr³
ఒక మోల్ పదార్థంలో B అన్ని పరమాణువుల ఘనపరిమాణం = \(\frac{4}{3}\) πr³ × N = \(\frac{\mathrm{M}}{\rho}\)
∴ r = \(\left[\frac{3 M}{4 \pi \rho N}\right]^{1 / 3}\)
కార్బన్కు M = 12.01 × 10^-3 kg, ρ = 2.22 × 10³ kg m^-3
కావున r = \(\frac{3 \times 12.01 \times 10^{-3}}{4 \times \frac{22}{7} \times\left(2.22 \times 10^3\right) \times\left(6.023 \times 10^{23}\right)}\) = 1.29 × 10^-10 m = 1.29 Å
ఇదే విధంగా బంగారం, r = 1.59 Å
ద్రవ నైట్రోజన్క r = 1.77 Å
లిథియమ్కు r = 1.73 Å
మరియు ద్రవ ఫ్లోరిన్్కు r = 1.88 Å

Telangana TSBIE TS Inter 1st Year Physics Study Material 13th Lesson ఉష్ణోగతిక శాస్త్రం Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 13th Lesson ఉష్ణోగతిక శాస్త్రం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణ సమతాస్థితిని నిర్వచించండి. ఇది ఉష్ణగతిక శాస్త్ర శూన్యాంక నియమానికి ఎలా దారితీసిందో తెలపండి.
జవాబు:
ఉష్ణ సమతాస్థితి : ఒక వ్యవస్థలోని స్థూలచరరాశులైన పీడనం, ఘనపరిమాణం, ఉష్ణోగ్రత, ద్రవ్యరాశి, వాటి సంఘటన కాలంతోపాటు మారకుండా ఉంటే ఆ వ్యవస్థ ఉష్ణ సమతాస్థితిలో ఉంది అంటారు.

రెండు వ్యవస్థలు ఉష్ణ సమతాస్థితిలో ఉండాలంటే ఆ రెండు వ్యవస్థల ఉష్ణోగ్రతలు సమానంగా ఉండాలి. ఈ భావన ఆధారంగా ఉష్ణ గతిక శాస్త్ర శూన్యాంక నియమం రూపుదిద్దుకుంది.

ప్రశ్న 2.
కెలోరిని నిర్వచించండి. కెలోరి, ఉష్ణయాంత్రిక తుల్యాంకాల మధ్య గల సంబంధం ఏమిటి ?
జవాబు:
కెలోరి : ఒక గ్రాము నీటి ఉష్ణోగ్రతను 1°C మేరకు పెంచడానికి కావలసిన ఉష్ణరాశిని కెలోరిగా నిర్వచించారు.

ప్రామాణిక కెలోరి లేదా సగటు 15°C కెలోరి : ఒక గ్రాము నీటి ఉష్ణోగ్రతను 14.5°C నుండి 15.5°C వరకు పెంచడానికి కావలసిన ఉష్ణరాశిని సగటు 15°C కెలోరిగా నిర్వచించారు.

ఉష్ణయాంత్రిక తుల్యాంకము (1) నిర్వచనం ప్రకారము J అనగా 1 కెలోరి ఉష్ణాన్ని జనింపచేయడానికి కావలసిన పని J = 4.186 J/g – k

ప్రశ్న 3.
a) శూన్యాంక నియమం
b) మొదటి నియమాల వల్ల ఏ ఉష్ణగతిక చరరాశులు నిర్వచించడమైంది ?
జవాబు:
a) ఉష్ణగతిక శాస్త్ర శూన్యాంక నియమం నుండి ఉష్ణోగ్రత మరియు ఉష్ణ సమతాస్థితి అన్న భావనలు రూపొందుకున్నాయి. ఫలితంగా ఉష్ణోగ్రతను కొలవడం అన్న భావన రూపుదిద్దుకుంది.

b) ఉష్ణగతిక శాస్త్ర మొదటి నియమం నుండి అంతరికశక్తి ∆U = ∆Q – ∆W వ్యవస్థ పని జరిగే మార్గంపై ఆధారపడక కేవలం వ్యవస్థ తొలిస్థితి (i) మరియు తుది స్థితి (f) పైనే ఆధారపడుతుంది అని స్పష్టం చేసింది.

ప్రశ్న 4.
పదార్థ విశిష్టోష్ణ సామర్థ్యాన్ని నిర్వచించండి. అది వేటి మీద ఆధారపడి ఉంటుంది ?
జవాబు:
విశిష్టోష్ణ సామర్ధ్యం (S) : ప్రమాణ ద్రవ్యరాశిగల పదార్థంలో ఏకాంక ఉష్ణోగ్రతా మార్పు కోసం అందజేసిన ఉష్ణరాశిని లేదా కోల్పోయిన ఉష్ణరాశిని విశిష్టోష్ణ సామర్థ్యము అంటారు.

విశిష్టోష్ణ సామర్థ్యం S = \(\frac{1}{\mathrm{~m}} \frac{\Delta \mathrm{Q}}{\Delta \mathrm{T}}\) ప్రమాణము J/kg-k

విశిష్టోష్ణ సామర్థ్యము ఒక వస్తువుకు సంబంధించిన భౌతిక స్థిరరాశి. ఇది పదార్థపు రసాయన సంఘటనముపై ఆధారపడును.

ప్రశ్న 5.
మోలార్ విశిష్టోష్ణ సామర్థ్యాన్ని నిర్వచించండి.
జవాబు:
మోలార్ విశిష్టోష్ణ సామర్థ్యం : 1 గ్రామ్ మోల్ ద్రవ్యరాశిగల పదార్థానికి అందజేసిన ఉష్ణరాశి ∆Q మరియు దాని ఉష్ణోగ్రతలోని మార్పు ∆T కి గల నిష్పత్తిని మోలార్ విశిష్టోష్ణ సామర్థ్యము అంటారు.
మోలార్ విశిష్టోష్ణ సామర్థ్యము C = \(\frac{1}{\mu} \frac{\Delta \mathrm{Q}}{\Delta \mathrm{T}}\) J/g-mol-k

ప్రశ్న 6.
ఒక ఘనపదార్థంలో ఒక డోలకం మొత్తం శక్తి ఎంత ?
జవాబు:
ఘనపదార్థంలో డోలకం మొత్తం శక్తి Eని దానికి గల స్థితిజ శక్తి PE మరియు గతిజశక్తి KE ల మొత్తంగా భావిస్తాము. డోలకం మొత్తం శక్తి E = PE + KE

ప్రశ్న 7.
నీటి విశిష్టోష్ఠం ఉష్ణోగ్రతతో పాటు మారడాన్ని తెలియచేసే గ్రాఫ్ను సూచించండి. ఇది దేనిని తెలియచేస్తుంది ?
జవాబు:
నీటి విశిష్టోష్ణ సామర్థ్యం నీటి ఉష్ణోగ్రతతో పాటు మారుతుంది. పటం నుండి 15°C వద్ద నీటి విశిష్టోష్ణ ధారణ సామర్థ్యాన్ని కెలోరీగా నిర్వచిస్తే 0°C నుండి 15°C వరకు కెలోరి పరిమాణం ఎక్కువ. 40°C వద్ద విశిష్టోష్ట సామర్థ్యం అతి తక్కువ. 40°C నుండి ‘s’ విలువ క్రమంగా పెరుగుతూ సుమారు 60°C ప్రాంతంలో ‘S’ విలువ ఒక కెలోరిగా
ఉంటుంది.

60°C నుండి 100°C అవధిలో ‘s’ విలువ కెలోరికన్నా ఎక్కువ.

ప్రశ్న 8.
స్థితి చరరాశులను, స్థితి సమీకరణాన్ని నిర్వచించండి.
జవాబు:
స్థితి చరరాశులు : ఉష్ణయాంత్రిక శాస్త్రంలో ఒక వ్యవస్థ సమతాస్థితిని సూచించే పీడనము, ఘనపరిమాణము, ఉష్ణోగ్రత, ద్రవ్యరాశి వంటి చరరాశులను స్థితి చరరాశులు అంటారు.
స్థితి చరరాశుల మధ్య సంబంధాన్ని సూచించే సమీకరణం PV = μ RT

ప్రశ్న 9.
100% దక్షతతో పనిచేసే ఉష్ణయంత్రాన్ని తయారుచేయడం సాధ్యం కాదు. ఎందుకు ?
జవాబు:
ఉష్ణయంత్రం సామర్ధ్యము η = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\) ఇందులో పరిసరాలకు ఇచ్చిన ఉష్ణం Q₂ = 0 అయితే ఆ ఉష్ణయంత్రం 100% దక్షత కలిగి ఉంటుంది లేదా కొలిమి ఉష్ణోగ్రత, (Q₁ = ∞) అనంతము కావాలి. ఉష్ణగతిక శాస్త్ర రెండవ నియమం నుండి ఇటువంటి పరిస్థితులు సాధ్యపడవు అని తెలుస్తుంది.
కాబట్టి ఉష్ణ యంత్రాలను 100% దక్షతతో తయారుచేయలేము.

ప్రశ్న 10.
వేసవికాలంలో సైకిల్ ట్యూబ్ నుంచి గాలిని తొలగిస్తున్నప్పుడు ఆ గాలి చల్లగా అనిపించడానికి కారణం ఏమిటి ?
జవాబు:
సైకిల్ ట్యూబ్ నుండి వేగంగా గాలి తొలగించేటపుడు అది స్థిరోష్ణక వ్యాకోచం చెందుతుంది. కాబట్టి వాయువు కొంత పనిచేస్తుంది. W = \(\frac{\mu \mathrm{R}\left(\mathrm{T}_1-\mathrm{T}_2\right)}{\gamma-1}\) ఈ పనికి కావలసిన శక్తి వ్యవస్థ నుండే పొందటం వల్ల తుది ఉష్ణోగ్రత T₂ తగ్గుతుంది.

ప్రశ్న 11.
ఒక మోటారు వాహనాన్ని ఏటవాలు రోడ్డుపై దిగువకు స్థిరవడితో ప్రయాణం చేసేటట్లు బ్రేకులను ఉపయోగిస్తే బ్రేక్ డ్రమ్ములు ఎందుకు వేడెక్కుతాయి ?
జవాబు:
ఏటవాలు మార్గంలో స్థిర వడితో కిందికి ప్రయాణం చేయడానికి గురుత్వ త్వరణ అంశ (g Sin θ కి) సమానమైన మంద త్వరణాన్ని ప్రయోగించాలి. ఇందుకోసం కారు చలనదిశకు వ్యతిరేకంగా కొంత మందబలము F = mg sinθ ను బ్రేకులు ప్రయోగిస్తాయి. ఈ బలం పనిగా మారి బ్రేకు డ్రమ్ములను వేడి చేస్తుంది లేదా వాహనం కిందికి దిగేటప్పుడు స్థితిశక్తిలో మార్పు (mg h₁ – mgh₂) పనిగా మారటం వల్ల బ్రేకు డ్రమ్ములు వేడెక్కుతాయి.

ప్రశ్న 12.
విద్యుత్ శీతలీకరణ యంత్రాన్ని (రిఫ్రిజిరేటర్) తెరచి ఉంచి గదిని చల్లబరచడం సాధ్యమవుతుందా ?
జవాబు:
సాధ్యపడదు. శీతలీకరణ యంత్రం రెండు వేరువేరు వ్యవస్థలు (ఉష్ణాశయం, శీతలాశయం)ల మధ్య మాత్రమే పనిచేస్తుంది. రిఫ్రిజిరేటరు తలుపు తెరిస్తే గది మరియు రిఫ్రిజిరేటరు ఒకే వ్యవస్థగా వ్యవహరిస్తాయి. కావున శీతలీకరణ యంత్రం పనిచేయదు.

ప్రశ్న 13.
వ్యవస్థ ఘనపరిమాణాన్ని 50%కి తగ్గించినప్పుడు, స్థిరోష్ణక లేదా సమ ఉష్ణోగ్రతా ప్రక్రియలలో దేనిలో పీడనం అధికంగా పెరుగుతుంది ?
జవాబు:
స్థిరోష్ణక ప్రక్రియలో వ్యవస్థ నుండి శక్తి బయటకు పోవడం లేదా లోపలికి రావడం జరగదు. ఘనపరిమాణాన్ని 50% తగ్గించడానికి బాహ్యపని అవసరము. ఇది వ్యవస్థ ఉష్ణోగ్రతను పెంచుతుంది. కాబట్టి పీడనం ఎక్కువ ఉంటుంది.
సమఉష్ణోగ్రతా ప్రక్రియలో వ్యవస్థ ఉష్ణోగ్రత T స్థిరం కావున V లో తగ్గుదల వల్ల పీడనంలో పెరుగుదల స్థిరోష్ణక ప్రక్రియ కన్నా తక్కువ.

ప్రశ్న 14.
ఒక థర్మాస్ ఫ్లాస్క్ లో ఉన్న ద్రవాన్ని బాగా కుదిపితే, దాని ఉష్ణోగ్రత ఏమవుతుంది ?
జవాబు:
థర్మాస్ ఫ్లాస్క్ లో ద్రవాన్ని బాగా కుదిపితే దానిలోని ద్రవం ఉష్ణోగ్రత పెరుగుతుంది.
కారణం థర్మాస్ ఫ్లాస్క్ ఉష్ణ బంధక వ్యవస్థ. అంటే స్థిరోష్ణక మార్పులు జరుగుతాయి. కాబట్టి కుదుపులకు వాడిన పని ఉష్ణంగా మారి లోపలి ద్రవాన్ని వేడెక్కిస్తాయి.

ప్రశ్న 15.
వాయువుతో నిండి ఉన్న గొట్టంలోకి ఒక ధ్వని తరంగాన్ని పంపితే దాని అంతరిక శక్తి మారుతుందా ?
జవాబు:
మారుతుంది. ధ్వని తరంగం కొంత శక్తిని కలిగి ఉంటుంది. దీనిని గొట్టంలోకి పంపితే వ్యవస్థ అంతరికశక్తి పెరుగుతుంది.

ప్రశ్న 16.
i) సమ ఉష్ణోగ్రతా ప్రక్రియ
ii) స్థిరోష్ణక ప్రక్రియలలో అంతరిక శక్తిలోని మార్పు ఎంత ?
జవాబు:
i) సమ ఉష్ణోగ్రతా ప్రక్రియలో, ఉష్ణోగ్రత (T) స్థిరము ∴ dT = 0 కావున అంతరికశక్తిలో మార్పు dU = 0
స్థిరోష్ణక ప్రక్రియలో dQ = dU + dw కాని dQ = 0 కావున du = -dW.
అనగా స్థిరోష్ణక ప్రక్రియలో అంతరికశక్తిలో మార్పు వ్యవస్థ జరిపిన పనికి సమానము.

ప్రశ్న 17.
రసాయనిక లేదా అణుకేంద్రాలలో వాడే శీతలీకరణి అధిక విశిష్టోష్టతను కలిగి ఉంటుంది. ఎందుకు ?
జవాబు:
ఒకే ద్రవ్యరాశి గల శీతలీకరణులలో అవి ఉష్ణాన్ని గ్రహించి బయటకు తేగల సామర్థ్యం విశిష్టోష్ణ సామర్థ్యంకు అనులోమానుపాతంలో ఉంటుంది. (Q = mc T కావున Q ∝ C) అందువల్ల శీతలీకరణిగావాడే ద్రవానికి వీలైనంత ఎక్కువ విశిష్టోష్ణ సామర్థ్యం ఉండాలి.

ప్రశ్న 18.
i) సమ ఘనపరిమాణ ప్రక్రియ,
ii) సమ పీడన ప్రక్రియలను గురించి వివరించండి.
జవాబు:
i) సమ ఘనపరిమాణ ప్రక్రియ : సమఘనపరిమాణ ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు వ్యవస్థ ఘనపరిమాణంను స్థిరంగా ఉంచుతూ జరుగుతాయి. ఈ ప్రక్రియలో dV = 0.

ii) సమపీడన ప్రక్రియ : సమపీడన ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు వ్యవస్థ స్థిరంగా ఉంచుతూ జరుగుతాయి. అనగా dP = 0

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణగతికశాస్త్ర మొదటి నియమాన్ని నిర్వచించి, వివరించండి.
జవాబు:
ఒక వ్యవస్థ ఒక స్థితి నుండి మరియొక స్థితికి మారినపుడు ఆ వ్యవస్థకు సరఫరా చేసిన ఉష్ణరాశి dQ ఆ వ్యవస్థ అంతర్గత శక్తి పెరుగుదల (dU) మరియు వ్యవస్థ చేయు బాహ్య పని (dW) ల మొత్తమునకు సమానమని మొదటి నియమం తెల్పుతుంది.
∴ dQ = dU + dW కాని dW = PdV, కనుక dQ = dU + PdV.
ఉష్ణ సరఫరా లేకుండా వ్యవస్థ పనిచేస్తే
dQ = 0 కనుక dU + PdV = 0; ∴ PdV = – dU
అంటే దాని అంతర్గత శక్తి ఎంత తగ్గుతుందో, అదంతా బాహ్యపని చేయడానికి ఉపయోగపడుతుంది.
ఉష్ణగతికశాస్త్ర మొదటి నియమానికి అవధులు : ఉష్ణగతికశాస్త్ర ప్రథమ నియమానికి రెండు అవధులు ఉన్నాయి. అవి

1. ఈ నియమం ఉష్ణప్రవాహ దిశను తెలియజేయదు మరియు ఏ పరిస్థితులలో పని జరపడానికి లేదా ఉత్పన్నం చేయడానికి వస్తువు ఉష్ణశక్తిని వినియోగించుకుంటుందో తెలియజేయదు.
2. ఈ నియమం వ్యవస్థ ఎంత దక్షతతో ఉష్ణశక్తిని యాంత్రికశక్తిగా మార్చగలదో తెలియజేయదు.

ప్రశ్న 2.
వాయువుల రెండు ప్రధాన విశిష్టోష్టాలను నిర్వచించండి. ఆ రెండింటిలో ఏది ఎక్కువ ? ఎందుకు ?
జవాబు:
స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C_v): స్థిరఘనపరిమాణము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల ‘ వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్థ్యము C_v గా నిర్వచించినారు.
C_v = \(\frac{1}{\mu} \frac{\mathrm{dQ}}{\mathrm{dT}}\)
μ = వాయువులోని మోల్ ల సంఖ్య

స్థిరపీడన మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C_p) : స్థిరపీడనము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ మేరకు పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరపీడన మోలార్ విశిష్టోష్ణ సామర్థ్యము C_p గా నిర్వచించినారు.
C_p = \(\frac{1}{\mu} \frac{\mathrm{dQ}}{\mathrm{dT}}\)
μ = వాయువులోని గ్రామ్ మోల్ సంఖ్య

వాయువులలో C_p > C_v వివరణ : వాయువును స్థిర ఘనపరిమాణం వద్ద వేడిచేస్తే వాయువుకు అందజేసిన మొత్తం ఉష్ణరాశి వాయువు ఉష్ణోగ్రతను పెంచడానికి ఉపయోగపడును. అనగా దాని అంతర్గత శక్తి పెరుగును.
∴ dQ = dU = C_vdT

స్థిర పీడనం వద్ద వాయువుకు అందజేసిన ఉష్ణరాశి (dQ) వాయువు అంతర్గతశక్తిని పెంచడంతో పాటు వాయువును వ్యాకోచింపచేయడానికి కొంత పని (dW = PdV) కూడా చేస్తుంది. కావున ఈ స్థిరపీడనం వద్ద dQ = dU + PdV.

వాయువులలో స్థిరపీడన విశిష్టోష్ణము, స్థిరఘనపరిమాణ విశిష్టోష్టము కన్నా ఎక్కువ. స్థిరపీడనం వద్ద వాయువును వేడిచేయటానికి ఇచ్చిన ఉష్ణశక్తి 1) వాయువును వేడిచేయటానికి 2) వాయువు పీడనానికి వ్యతిరేకంగా వ్యాకోచించడానికి కూడా ఉపయోగపడుతుంది. అనగా ఉష్ణశక్తి కొంత పని (dW = PdV) అదనంగా చేయడం వలన C_p > C_v అవుతుంది.

ప్రశ్న 3.
ఉష్ణ గతిక శాస్త్ర మొదటి నియమం ఆధారంగా, వాయువు రెండు విశిష్టోష్ణ సామర్థ్యాల మధ్య ఉన్న సంబంధాన్ని ఉత్పాదించండి.
జవాబు:
స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C_p) : స్థిరఘనపరిమాణము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్ధ్యము Cగా నిర్వచించినారు.
C_v = \(\frac{1}{\mu} \frac{\mathrm{dQ}}{\mathrm{dT}}\)
μ = వాయువులోని మోత్ల సంఖ్య

స్థిరపీడన మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C_v) : స్థిరపీడనము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ మేరకు పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరపీడన మోలార్ విశిష్టోష్ణ సామర్థ్యము C_p గా నిర్వచించినారు.
C_p = \(\frac{1}{\mu} \frac{\mathrm{dQ}}{\mathrm{dT}}\)
μ = వాయువులోని గ్రామ్ మోల్ల సంఖ్య
గమనిక : విశిష్టోష్ణము మరియు విశిష్టోష్ణసామర్థ్యములను ఒకే అర్థంలో వాడతారు.

ఉష్ణ గతిక శాస్త్ర మొదటి నియమం నుండి C_p – C_v = R ఉత్పాదన.
ఉష్ణ గతిక శాస్త్ర మొదటి నియమం నుండి dQ = dU + dW = ∆U = P∆V………….. (1)
ఒక మోల్ వాయువును స్థిర ఘనపరిమాణం వద్ద వేడి చేస్తే అది శోషించుకున్న ఉష్ణం dQ = dU (∵ dV = 0 కావున)
∴ C_v = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{T}}=\frac{\Delta \mathrm{U}}{\Delta \mathrm{T}}\) ……………. (2)
ఒక మోల్ వాయువును స్థిరపీడనం వద్ద వేడిచేస్తే అది శోషించుకున్న ఉష్ణరాశి = C_p = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{T}}=\frac{\Delta \mathrm{U}}{\Delta \mathrm{T}}+\mathrm{P} \frac{\Delta \mathrm{V}}{\Delta \mathrm{T}}\) ……………….. (3)
వాయు సమీకరణం PV = RT అవకలనం చేయగా
P ∆ V + V ∆ P = R ∆ T కాని C_p వద్ద ∆P = 0
∴ P \(\frac{\Delta \mathrm{V}}{\Delta \mathrm{T}}\) = R ……………… (4)
సమీకరణ 2, 4 లను 3 లో ప్రతిక్షేపించగా C_p = C_v + R లేదా C_p – C_v = R

ప్రశ్న 4.
సమఉష్ణోగ్రతా ప్రక్రియలో ఒక వాయువు చేసిన పనికి సమాసాన్ని సాధించండి.
జవాబు:
సమ ఉష్ణోగ్రతా ప్రక్రియ : సమ ఉష్ణోగ్రతా ప్రక్రియలో వ్యవస్థ ఉష్ణోగ్రత T స్థిరము. ఇది PV = μ RT ని పాటిస్తుంది. వ్యవస్థ పీడనం P, ఘనపరిమాణం V₁ నుండి V₂ మారడం వల్ల జరిగిన పని dW = PdV ……….. (1) కాని P = \(\frac{\mu \mathrm{RT}}{\mathrm{V}}\)
ఇందులో μ = వాయువులోని మోత్ల సంఖ్య
ఈ ప్రక్రియలో జరిగిన మొత్తం పని W = \(\int\) dW = \(\int\) P dV
= \(\int_{\mathrm{v}_1}^{\mathrm{v}_2} \frac{\mu \mathrm{RT}}{\mathrm{V}} \mathrm{dV}=\mu \mathrm{RT} \int_{\mathrm{v}_1}^{\mathrm{v}_2} \frac{\mathrm{dV}}{\mathrm{V}}=\mu \mathrm{RT}\left[\log _{\mathrm{e}} \mathrm{V}\right]_{\mathrm{v}_1}^{\mathrm{v}_2}\) = μ RT [log_e V₂ = log_e V₁]
∴ సమ ఉష్ణోగ్రతా ప్రక్రియలో జరిగిన పని W = μ RT log_e \(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\)

ప్రశ్న 5.
స్థిరోష్ణక ప్రక్రియలో ఒక వాయువు చేసిన పనికి సమాసాన్ని సాధించి, వివరించండి.
జవాబు:
స్థిరోష్ణక ప్రక్రియ : స్థిరోష్ణక ప్రక్రియలో వ్యవస్థకు గల శక్తి Q స్థిరము. ఈ ప్రక్రియలో PV^γ = K స్థిరము. …..(1) μ మోల్ల ఒక ఆదర్శ వాయువును స్థిరోష్ణక ప్రక్రియలో వ్యాకోచింపచేయడంవల్ల దాని పీడనము P₁ నుండి P₂ కు ఘనపరిమాణం V₁ నుండి V₂కు మారినదనుకోండి. ఆదర్శ వాయువు వ్యాకోచించడంలో జరిగిన పని
W = \(\int_{\mathrm{V}_1}^{\mathrm{v}_2} \mathrm{PdV}\) కాని స్థిరోష్ణక ప్రక్రియలో PV^γ = K లేదా P = \(\frac{\mathrm{K}}{\mathrm{V}^\gamma}\)
∴ మొత్తం పని W = \(\int_{v_1}^{v_2} \frac{K}{v^\gamma}\) dV. దీనిని సమాకలనం చేయగా

ప్రశ్న 6.
సమఉష్ణోగ్రత, స్థిరోష్ణక ప్రక్రియలను పోల్చండి.
జవాబు:
సమఉష్ణోగ్రతా ప్రక్రియ

1. ఈ ప్రక్రియలో వ్యవస్థ ఉష్ణోగ్రత (T) స్థిరము.
   ∴ ∆T = 0
2. వ్యవస్థను ఉత్తమ ఉష్ణ వాహకంతో చేయవలెను.
3. వాయుసమీకరణ PV = RTని పాటిస్తాయి.
4. వ్యవస్థకు పరిసరాలకు మధ్య ఉష్ణ వినిమయం ఉంటుంది.
5. ఈ చర్యలు నెమ్మదిగా జరుగును.
6. అంతర్గత శక్తిలో మార్పు ∆U = 0
7. విశిష్టోష్ణము అనంతము
8. సమ ఉష్ణోగ్రతా ప్రక్రియ వక్రాల వాలు \(\frac{\mathrm{dP}}{\mathrm{dV}}\) = -P / V కి సమానము.

స్థిరోష్ణక ప్రక్రియ

1. ఈ ప్రక్రియలో వ్యవస్థ మొత్తం శక్తి ‘Q’ స్థిరము.
   ∴ ∆Q = 0
2. వ్యవస్థను అధమ ఉష్ణ వాహకంతో చేయవలెను.
3. PV^γ = స్థిరరాశి అన్న నియమం పాటిస్తాయి.
4. వ్యవస్థకు పరిసరాలకు మధ్య ఉష్ణ వినిమయం ఉండదు.
5. ఇవి వేగంగా జరుగుతాయి.
6. అంతర్గత శక్తి మారుతుంది. ∆U ≠ 0
7. విశిష్టోష్ణము ‘0’
8. ఈ వక్రాల వాలు \(\frac{\mathrm{dP}}{\mathrm{dV}}\) = -r \(\frac{\mathrm{P}}{\mathrm{V}}\) కి సమానము.

ప్రశ్న 7.
కింది ప్రక్రియలను ఉదాహరణతో వివరించండి.
i) చక్రీయ ప్రక్రియ
ii) చక్రీయం కానటువంటి ప్రక్రియ
జవాబు:
i) చక్రీయ ప్రక్రియ (Cyclic Process) : ఏదైనా ఉష్ణయాంత్రిక వ్యవస్థ దాని పీడనం, ఉష్ణోగ్రత వంటి చలరాశులలో వేరువేరు దశలలో మార్పులు పొందినప్పటికి చివరకు తొలిస్థితికి తిరిగివస్తే అటువంటి ప్రక్రియను చక్రీయ ప్రక్రియ అంటారు.
చక్రీయ ప్రక్రియ తొలిపీడనం, ఉష్ణోగ్రతలకు తిరిగి వస్తుంది కాబట్టి దీని అంతర్గత శక్తిలోని మార్పు dU = 0.
చక్రీయ ప్రక్రియలో జరిగిన పని ఆ వ్యవస్థ శోషణం చేసుకున్న ఉష్ణశక్తికి సమానము. అనగా dW = dQ.
చక్రీయ ప్రక్రియలో అంతర్గత శక్తిలోని మార్పు dU = 0 మరియు వ్యవస్థ జరిపిన పని dW = dQ. కావున సాధారణంగా అన్నిరకాల ఉష్ణయంత్రాలు మరియు శీతలీకరణ యంత్రాలు చక్రీయ ప్రక్రియ ఆధారంగా పనిచేస్తాయి.

ii) చక్రీయం కానటువంటి ప్రక్రియ : ఏదైనా ఉష్ణయాంత్రిక వ్యవస్థలో పీడనము, ఘనపరిమాణము, ఉష్ణోగ్రత వంటి చలరాశులు వివిధ దశలలో మార్పులు పొందినప్పటికి చివరి దశలో తొలి విలువలను పొందలేకపోతే అటువంటి ప్రక్రియను అచక్రీయ ప్రక్రియ అంటారు.

ప్రశ్న 8.
అర్ధస్థితిక ప్రక్రియ మీద లఘుటీక రాయండి.
జవాబు:
అర్ధస్టైతిక ప్రక్రియ (Quasi static process) : అర్ధస్థితిక ప్రక్రియలో ఉష్ణయాంత్రిక వ్యవస్థలోని మార్పులు అత్యంత నిదానంగా జరుగుతూ ప్రతిదశలోను వ్యవస్థకు చెందిన ఉష్ణగతిక స్థిరరాశులు పరిసరాలతో దాదాపు సమతాస్థితిలో ఉన్నట్లు భావిస్తాము.

వివరణ : సమతాస్థితిలో లేని ఏదైనా ఉష్ణయాంత్రిక వ్యవస్థను గురించి వివరించడానికి ఆ వ్యవస్థ ప్రతిస్థితిలోను పరిసరాలతో సమతాస్థితిలో ఉండే ఆదర్శవంతమైన ప్రక్రియగా ఊహిస్తారు.

ఇటువంటి ఉష్ణయాంత్రిక వ్యవస్థలో ముషలకాన్ని వేగంగా, లేదా అకస్మాత్తుగా జరిపే బదులుగా అతి నెమ్మదిగా ముషలకాన్ని జరిపినట్లు భావిస్తారు. అందువల్ల వ్యవస్థలోపలి పీడనం P + ∆P మరియు ఉష్ణోగ్రత T + ∆T లు పరిసరాల పీడనము P మరియు ఉష్ణోగ్రత T లకు దాదాపు సమానము.

ఈ ప్రక్రియ అత్యంత నెమ్మదిగా జరగడం వల్ల పీడనంలో మార్పు ∆P మరియు ఉష్ణోగ్రతలో మార్పు ∆T లు అతిచిన్నవి కావడం వల్ల P + ∆P = P మరియు T + ∆T = T అని భావిస్తారు. ఇటువంటి ప్రక్రియలను అర్ధస్థితిక ప్రక్రియలు అంటారు.

ప్రశ్న 9.
ఉష్ణయంత్రం పనిచేసే విధానాన్ని వివరించండి.
జవాబు:
ఉష్ణయంత్రాలు : ఉష్ణశక్తిని పని లేక యాంత్రికశక్తిగా మార్చే పరికరాన్ని ఉష్ణయంత్రం అంటారు.
ఉష్ణయంత్రాలు అన్నీ చక్రీయ ప్రక్రియలపై ఆధారపడతాయి. వీటిలో మూడు ముఖ్యమైన భాగాలు ఉంటాయి.
1) జనకం : ఇది అధిక ఉష్ణోగ్రత వద్ద ఉండే వస్తువు. ఉష్ణయంత్రం దీని నుండి ఉష్ణశక్తి (Q₁) ని గ్రహిస్తుంది.

2) పనిచేసే పదార్థము : ఇది యంత్రం పనిచేయడానికి అవసరమైన పదార్థాన్ని కలిగి ఉంటుంది. సాధారణంగా ఈ పనిచేసే పదార్థం ఎక్కువ పీడనం కలిగిన నీటి ఆవిరి లేదా ఇంధన మిశ్రితమైన గాలి రూపంలో ఉంటాయి.

3) సింక్ లేదా రిజర్వాయర్ : ఇది తక్కువ ఉష్ణోగ్రత వద్ద గల వస్తువు లేదా పదార్థం. ఉష్ణయంత్రంలోని పనిచేసే పదార్థం పని పూర్తి ఐన తరువాత తనలో మిగిలి ఉన్న ఉష్ణశక్తిని సింక్ లేదా రిజర్వాయర్లోకి విసర్జిస్తుంది. ప్రతి ఉష్ణ యంత్రం జనకం నుండి Q₁ అన్నే ఉష్ణశక్తిని తీసుకొని కొంత పనిచేసిన తరువాత మిగిలిన ఉష్ణరాశి Q₂ ని సింక్లోనికి విసర్జిస్తుంది.
ఉష్ణయంత్రం జరిపిన పని W = Q₁ – Q₂

ఉష్ణయంత్రపు సామర్ధ్యము : ఏదైనా యంత్రము జరిపిన పనికి, దానికి అందజేసిన శక్తికి గల నిష్పత్తిని ఆ ఉష్ణ యంత్రపు సామర్థ్యంగా నిర్వచించినారు.

ఇందులో Q₁ = యంత్రానికి అందజేసిన శక్తి, Q₂ = యంత్రం సింక్కి అందజేసిన శక్తి.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఏకగత, ద్విగత ప్రక్రియలను వివరించండి. కార్నో యంత్రం పనిచేసే విధానాన్ని వివరించి, దాని దక్షతకు సమాసాన్ని రాబట్టండి. (మార్చి 2014)
జవాబు:
ఏకగత ప్రక్రియ లేదా ఉత్రమణీయ ప్రక్రియ : విశ్వంలో ఎక్కడా ఏ విధమైన మార్పులూ లేకుండా, వ్యవస్థ మరియు పరిసరాలు తొలిదశకు చేరుకునేటట్లుగా ఒక ప్రక్రియను అదే ప్రక్రియ సూటి పద్ధతిలో ఏయే దశల గుండా ప్రయాణం చేసిందో అదే దశల గుండా దానిని వెనుకకు తీసుకొనిరాగలిగితే ఆ ప్రక్రియను ఉత్రమణీయ ప్రక్రియ అంటారు. ఉత్రమణీయ ప్రక్రియ కేవలం ఆదర్శభావన మాత్రమే.
ఉత్రమణీయ ప్రక్రియ పాటించవలసిన నిబంధనలు :

1. వ్యవస్థ జరిపే మార్పులు అత్యంత నెమ్మదిగా ఉండాలి.
2. వ్యవస్థ ఎప్పుడూ పరిసరాలతో ఉష్ణ మరియు యాంత్రిక సమతాస్థితిలో ఉండాలి.
3. ఉష్ణవహనం, సంవహనం, ఘర్షణ మరియు నిరోధం వంటి ఏ విధమైన పద్ధతుల ద్వారా వ్యవస్థ ఉష్ణశక్తిని నష్టపోరాదు.
4. ఉష్ణశక్తి ఏ విధమైన ఇతర శక్తులలోనికి (విద్యుత్తు లేదా అయస్కాంత శక్తి వంటివి) రూపాంతరం చెందరాదు.

ద్విగత ప్రక్రియ లేదా అనుత్ప్ర్కమణీయ ప్రక్రియ : ఏదైనా ఉష్ణయాంత్రిక ప్రక్రియను సూటి పద్ధతి ప్రక్రియకు వ్యతిరేకదిశలో వెనుకకు మరలించి తీసుకొని రాలేకపోతే అటువంటి ప్రక్రియను అనుత్రమణీయ ప్రక్రియ అంటారు.
ఉదా :

1. ఘర్షణ బలాలకు వ్యతిరేకంగా పని జరుపుట.
2. వాహకం గుండా విద్యుత్ పంపినపుడు అది వేడెక్కుట. దీనిని జౌల్ ఉష్ణ ప్రభావం అంటారు.

కార్నో యంత్రం : కార్నో యంత్రం T₁ మరియు T₂ ఉష్ణోగ్రతల మధ్య పనిచేసే ఉత్రమణీయ ఉష్ణయంత్రము. దానిలోని నాలుగు వరుస ప్రక్రియలను కలిపి కార్నో చక్రము (cornot cycle) అంటారు.
1వ దశలో వాయువు సమఉష్ణోగ్రత వ్యాకోచం చెందటం వల్ల స్థిరము కావున ఈ దశను

ఈ దశలో జరిగిన పని W_3-4 = Q₂ = μ RT log_e \(\left(\frac{V_3}{V_4}\right)\)
నాల్గవ దశలో వాయువు స్థిరోష్ణక సంపీడనం చెంది తిరిగి మొదటి స్థితికి వస్తుంది.

ఈ దశలో జరిగిన పని W_4-1 = \(\left(\mu \mathrm{R} \frac{\mathrm{T}_1-\mathrm{T}_2}{\mathrm{r}-1}\right)\)
పూర్తి చక్రంలో జరిపిన పని W = W_1,2 + W_2,3 + W_3,4 + W_4,1
ఈ మొత్తం పని Q₁ – Q₂ కి సమానము. అనగా రిజర్వాయరు నుండి గ్రహించిన ఉష్ణరాశి Q₁ మరియు సింక్కు ఇచ్చిన ఉష్ణరాశి Q₂ ల భేదానికి సమానము.

కార్నో యంత్రం దక్షత η = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\) = 1 – \(\frac{\mathrm{T}_2}{\mathrm{T}_1}\)

ప్రశ్న 2.
ఉష్ణగతికశాస్త్ర రెండవ నియమాన్ని నిర్వచించండి. ఉష్ణ యంత్రం శీతలీకరణ యంత్రం కంటె ఏ విధంగా భిన్నమయిందో తెలపండి. (మే 2014)
జవాబు:
ఉష్ణగతిక శాస్త్ర రెండవ నియమము :
a) కెల్విన్ – ప్లాంక్ ప్రవచనము : ఒక ఉష్ణాశయం నుంచి ఉష్ణశక్తిని గ్రహించి ఏ ఇతర ఫలితాలు కలుగజేయకుండా మొత్తం శక్తిని పనిగా మార్చే చక్రీయ ప్రక్రియ సాధ్యం కాదు.

b) క్లాసియస్ ప్రవచనము : తక్కువ ఉష్ణోగ్రత గల ఒక వస్తువు నుంచి ఎక్కువ ఉష్ణోగ్రత గల మరొక వస్తువుకు తనంతట తాను ఉష్ణరూపంలో శక్తిని బదిలీ చేసే ఏ ప్రక్రియ సాధ్యం కాదు.
ఉష్ణ గతిక శాస్త్ర రెండవ నియమం ఉష్ణ ప్రసార దిశను తెలుపుతుంది.
ఉష్ణగతిక శాస్త్ర రెండవ నియమం ప్రకారము ఏ ఉష్ణ యంత్రం దక్షత η విలువ 1కి సమానం కాదని మరియు శీతలీకరణ యంత్రం క్రియాశీలతా గుణకం (∝) విలువ అనంతం కాదని చెపుతుంది.

I. ఉష్ణయంత్రాలు : ఉష్ణశక్తిని పని లేక యాంత్రికశక్తిగా మార్చే పరికరాన్ని ఉష్ణయంత్రం అంటారు.
సాధారణంగా ఉష్ణయంత్రాలు అన్నీ చక్రీయ ప్రక్రియలపై ఆధారపడతాయి. ప్రతి ఉష్ణ యంత్రంలోను మూడు ముఖ్యమైన భాగాలు ఉంటాయి.
1) జనకం : ఇది అధిక ఉష్ణోగ్రత వద్ద ఉండే వస్తువు. ఉష్ణయంత్రం దీని నుండి ఉష్ణశక్తి (Q) ని గ్రహిస్తుంది.

2) పనిచేసే పదార్థము : ఇది యంత్రం పనిచేయడానికి అవసరమైన పదార్థాన్ని కలిగి ఉంటుంది. సాధారణంగా ఈ పనిచేసే పదార్థం ఎక్కువ పీడనం కలిగిన నీటి ఆవిరి లేదా ఇంధన మిశ్రితమైన గాలి రూపంలో ఉంటాయి.

3) సింక్ లేదా రిజర్వాయర్ : ఇది తక్కువ ఉష్ణోగ్రత వద్ద గల వస్తువు లేదా పదార్థం. ఉష్ణయంత్రంలోని పనిచేసే పదార్థం పని పూర్తి అయిన తరువాత తనలో మిగిలి ఉన్న ఉష్ణశక్తిని సింక్ లేదా రిజర్వాయర్లోకి విసర్జిస్తుంది. ప్రతి ఉష్ణయంత్రం జనకం నుండి Q₁ అనే ఉష్ణశక్తిని తీసుకొని కొంత పనిచేసిన తరువాత మిగిలిన ఉష్ణరాశి Q₂ని సింక్లోనికి విసర్జిస్తుంది.
ఉష్ణయంత్రం జరిపిన పని W = Q₁ – Q₂

ఉష్ణయంత్రపు సామర్థ్యము : ఏదైనా యంత్రము జరిపిన పనికి, దానికి అందజేసిన శక్తికి గల నిష్పత్తిని ఆ ఉష్ణ యంత్రపు సామర్థ్యంగా నిర్వచించినారు.

కాని పని W = Q₁ – Q₂ కావున η = \(\frac{\mathrm{Q}_1-\mathrm{Q}_2}{\mathrm{Q}_1}\) = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\)
ఇందులో Q₁ = యంత్రానికి అందజేసిన శక్తి, Q₂ = యంత్రం సింక్లోనికి వదిలివేసిన శక్తి.

II. శీతలీకరణ యంత్రము : శీతలీకరణ యంత్రం, ఉష్ణయంత్రం యొక్క విలోమ ప్రక్రియ ద్వారా పనిచేస్తుంది. ఇది తక్కువ ఉష్ణోగ్రత వద్ద గల వస్తువు సింక్ నుండి ఉష్ణశక్తి Q₂ని గ్రహించి దానికి కొంతపనిని జోడించి (బాహ్య పని Wని) ఉష్ణరాశి Q₁ ని అధిక ఉష్ణోగ్రత గల వస్తువు (Source) కు అందజేస్తుంది.

శీతలీకరణ యంత్రం జరిపిన బాహ్య పని W = Q₁ – Q₂ శీతలీకరణ యంత్రం పనిచేసే పదార్థానికి బాహ్య పనిని జోడిస్తుంది.

ఉష్ణయంత్రము, శీతలీకరణ యంత్రాల మధ్య భేదము.
ఉష్ణయంత్రం జనకం నుండి ఉష్ణశక్తి ‘Q₁‘ గ్రహించి దానిలో కొంత భాగాన్ని పనిగా మార్చి (W) మిగిలిన ఉష్ణశక్తిని (Q₂) రిజర్వాయర్ లేదా సింక్కు ఇస్తుంది. ఈ యంత్రంలో Q₂ < Q₁

శీతలీకరణ యంత్రము రిజర్వాయర్ లేదా తక్కువ ఉష్ణోగ్రత గల పదార్థం నుండి ఉష్ణశక్తిని గ్రహించి దానికి కొంత బాహ్య పనిని జోడించి మొత్తాన్ని ఎక్కువ ఉష్ణోగ్రత గల పదార్థానికి అందజేస్తుంది. అనగా శీతలీకరణ యంత్రం చల్లని వస్తువు నుండి గ్రహించిన ఉష్ణరాశి Q₂ కన్న పరిసరాలకు అందజేసిన ఉష్ణరాశి Q₁ ఎక్కువ.

లెక్కలు

ప్రశ్న 1.
N.T.P. వద్ద 1 లీటరు ఘనపరిమాణం ఉన్న ఒక ఏక పరమాణుక ఆదర్శ వాయువును సంపీడనం చేశారు. (i) సంపీడనం స్థిరోష్ణకమై, ఘనపరిమాణం సగం అయితే వాయువు మీద జరిగిన పనిని, (ii) సంపీడనం సమ ఉష్ణోగ్రతమైతే జరిగిన పనిని లెక్కించండి. (y=5/3)
సాధన:

మోల్లల సంఖ్య, n = \(\frac{1}{22.4}\) ; T = 273 K; R = 8.314 J mol^-1K^-1
∴ W = \(\frac{2.3026 \times 8.314 \times 273 \log _{10}(0.5)}{22.4}\) = – 70J.

ప్రశ్న 2.
5 మోల్ల హైడ్రోజన్ను స్థిర పీడనం 10⁵ N/m⁵ వద్ద ఉష్ణోగ్రతలో పెరుగుదల 20 K ఉండేటట్లు వేడిచేస్తే అది 8.3 × 10^-3m³ ల వ్యాకోచం చెందింది. C_v = 20 J/mole K, అయితే C^p ని కనుక్కోండి.
సాధన:
వాయువులలో C_p – C_v = R.
ఇరువైపులా n ∆T చే గుణించగా
nC_p ∆T- nC_v ∆T = nR ∆ T లేదా n ∆ T(C_p – C_v) = P ∆ V
5 × 20 (C_p – 20) = 105 ×‍ 8.3 × 10 – 3 (∵ nR∆T = P∆V)
C_p – 20 = 8.3 ⇒ C_p = 28.3 J/mole K.
( ∵ n = 5, ∆T = 20 K, P = 1 × 10⁵N/m² & C_v = 20 J/mole K and ∆V = 8.3 × 10³ m³)

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
ఒక గీజరు నిముషానికి 3.0 లీటర్ల ప్రవాహ రేటు కలిగిన నీటిని 27°C నుంచి 77°C వరకు వేడిచేస్తుంది. గీజరులో 4.0 × 10⁴ J/g దహనోష్ణం గల సహజ వాయువు ఇంధనంగా పనిచేస్తే, ఇంధనం ఖర్చయ్యే రేటును కనుక్కోండి.
సాధన:
వేడి చేయబడిన నీటి ఘనపరిమాణము = 3.0 లీ./ ని.
వేడెక్కిన నీటి ద్రవ్యరాశి, = m = 3000 గ్రా./ని.
ఉష్ణోగ్రతలో పెరుగుదల, ∆T = 77 – 27 = 50°C
నీటి విశిష్టోష్ణం c = 4.2 J g^-1°C^-1
వాడిన ఉష్ణశక్తి, ∆Q = mc ∆T = 3000 × 4.2 × 50 = 63 × 10⁴ J/min.
దహనం వల్ల విడుదలైన ఉష్ణశక్తి = 4 × 10⁴ J/g
ఇంధనం దహనం చెందిన రేటు = \(\frac{63 \times 10^4}{4 \times 10^4}\) = 15.75 g/min.

ప్రశ్న 2.
స్థిర పీడనం వద్ద, గది ఉష్ణోగ్రత వద్ద ఉన్న 2.0 × 10^-2 kg ల నైట్రోజన్ ఉష్ణోగ్రతను 45°C కు పెంచడానికి ‘ అందచేయాల్సిన ఉష్ణం ఎంత ? (N₂ అణు ద్రవ్యరాశి = 28; R = 8.3 Jmol^-1K^-1)
సాధన:
వాయువు ద్రవ్యరాశి, m = 2 × 10^-2 kg = 20g; ఉష్ణోగ్రతలో పెరుగుదల, ∆T = 45°C
కావలసిన ఉష్ణశక్తి, ∆Q = ?;
అణుభారము, M = 28
గ్రామ్ మోల్ల సంఖ్య, n = \(\frac{\mathrm{m}}{\mathrm{M}}=\frac{20}{28}\) = 0.714 నైట్రోజన్ ద్విపరమాణుక వాయువు కావున
C_p = \(\frac{7}{2}\) R = \(\frac{7}{2}\) × 8.3 J mol^-1 K^-1, కావున ∆Q = n C_p ∆T
∴ ∆Q = 0.714 × \(\frac{7}{2}\) × 8.3 × 45 J = 933.4 J

ప్రశ్న 3.
కింద ఇచ్చిన వాటిని వివరించండి.
a) T₁, T₂ ఉష్ణోగ్రతల వద్ద ఉన్న రెండు వస్తువులను ఒకదానితో ఒకటి తాకుతున్నట్లు ఉంచినప్పుడు వాటి సగటు ఉష్ణోగ్రత (T₁ + T₂) /2 కు చేగాల్సిన అవసరం లేదు.
b) ఒక రసాయనిక లేదా న్యూక్లియర్ ప్లాంట్లో ఉపయోగించే శీతలీకరణి (ప్లాంట్ లోని వివిధ భాగాలు అత్యధిక ఉష్ణోగ్రతలు పొందకుండా చల్లబరిచే ద్రవం) తప్పకుండా అధిక విశిష్టోష్ణ సామర్థ్యాన్ని కలిగి ఉండాలి.
c) మోటారు వాహనం చలనంలో ఉన్నప్పుడు, దాని టైరులోని గాలి పీడనం పెరుగుతుంది.
d) ఒకే అక్షాంశంపై ఉన్న సముద్రతీర పట్టణ వాతావరణం ఎడారి ప్రాంత పట్టణ వాతావరణం కంటే అధిక సమశీతోష్ణత కలిగి ఉంటుంది.
సాధన:
a) వస్తువులు ఒకదానితో ఒకటి తాకి ఉన్నపుడు ఎక్కువ ఉష్ణోగ్రత గల వస్తువుల నుంచి తక్కువ ఉష్ణోగ్రత గల వస్తువుకు ఉష్ణం ప్రసరిస్తుంది. తుది ఉష్ణోగ్రత సగటు ఉష్ణోగ్రత \(\frac{\mathrm{T}_1+\mathrm{T}_2}{2}\)కి సమానము. ఇది వాటి విశిష్టోష్ణ సామర్థ్యాలు సమానమైతేనే సాధ్యపడును.

b) ఒక వస్తువు గ్రహించిన ఉష్ణరాశి దాని విశిష్టోష్ణ సామర్థ్యానికి అనులోమానుపాతంలో ఉండును.

c) డ్రైవింగ్లో ఉన్నపుడు చక్రాలు చలనంలో ఉండటంవల్ల చక్రాలలోని గాలి ఉష్ణోగ్రత పెరుగును. ఉష్ణోగ్రత పెరిగితే పీడనం ‘P’ పెరుగును. ఛార్లెస్ నియమం నుండి P∝ T కావున

d) ఎడారి పట్టణాల కంటే నౌకాశ్రయ పట్టణాలలోని గాలిలో తేమ ఎక్కువ. కావున సముద్ర పట్టణ ప్రాంతాలలో అధిక సమశీతోష్ణస్థితి ఉంటుంది.

ప్రశ్న 4.
కదలగలిగే ముషలకం ఉన్న ఒక స్థూపాకార పాత్రలో, సాధారణ ఉష్ణోగ్రతా పీడనాల వద్ద 3 మోల్ల హైడ్రోజన్ వాయువు ఉంది. పాత్ర గోడలు, ముషలకాలు ఉష్ణబంధక పదార్థంతో చేయడమైంది. ముషలకంపైన కొంత ఇసుక ఉన్నది. వాయువును, దాని తొలి ఘనపరిమాణంలో సగానికి తగ్గేటట్లుగా సంపీడనం చెందిస్తే వాయు పీడనం ఎన్ని రెట్లు పెరుగుతుంది ?
సాధన:
వ్యవస్థ నుండి ఉష్ణ వినిమయం లేకపోవడం వల్ల ఇది స్థిరోష్ణక ప్రక్రియ
∴ P₂V₁^γ లేదా \(\frac{\mathrm{P}_2}{\mathrm{P}_1}=\left(\frac{\mathrm{V}_1}{\mathrm{~V}_2}\right)^\gamma\)
దత్తాంశం నుండి V₂ = \(\frac{1}{2}\) V₁
∴ \(\frac{\mathrm{P}_2}{\mathrm{P}_1}=\left(\frac{\mathrm{V}_1}{\frac{1}{2} \mathrm{~V}_1}\right)^{1.4}\) = 2^1.4 = 2.64

ప్రశ్న 5.
ఒక వాయువును స్థిరోష్ణక ప్రక్రియ ద్వారా సమతాస్థితి A నుంచి మరొక సమతాస్థితి B కి మార్చడానికి, దానిపై 22.3Jల పని జరపడమైంది. వాయువు 9.35 cal నికర ఉష్ణాన్ని గ్రహించేటట్లుగా ఒక ప్రక్రియ ద్వారా వాయు స్థితిని A నుంచి B కి చేర్చితే ఈ ప్రక్రియలో వాయువుపై జరిగిన నికర పని ఎంత ? (1 cal = 4.19 J గా తీసుకోండి)
సాధన:
స్థిరోష్ణక మార్పులో ∆Q = 0, ∆W = – 22.3 J
అంతర్గత శక్తిలో మార్పు du అయితే ∆Q = ∆U + ∆W
0 = ∆U – 22.3 (లేదా) ∆U = 22.3 J
రెండవ సందర్భంలో, ∆ = 9.35 cal. = 9.35 × 4.2 J = 39.3 J ; ∆W = ?
కాని ∆U + ∆W = ∆Q
∴ ∆W = ∆Q – ∆U = 39.3 – 22.3 = 17.0 J

ప్రశ్న 6.
సమాన ఘనపరిమాణాలున్న A, B రెండు స్థూపాకార పాత్రలను ఒక స్టాప్ కాక్ (ప్రవాహ నియంత్రణ మర) తో కలపడమైంది. పాత్ర A లో సాధారణ ఉష్ణోగ్రతా పీడనాల వద్ద ఒక వాయువు ఉన్నది. B పూర్తిగా శూన్యం చేయడమైంది. ఈ మొత్తం వ్యవస్థ అంతా ఉష్ణబంధకం చేయడమైంది. స్టాప్కక్ను ఒక్కసారిగా తెరిచారు. కింది ప్రశ్నలకు సమాధానాలు తెలపండి.
a) A, B లలో వాయువు తుది పీడనం ఎంత ?
b) వాయువు అంతరిక శక్తిలో మార్పు ఎంత ?
c) వాయువు ఉష్ణోగ్రతలో మార్పు ఎంత ?
d) వ్యవస్థ యొక్క మధ్యస్థ స్థితులు (తుది సమతాస్థితిని చేరడానికి పూర్వం) P-V-T గ్రాఫ్ తలంపై ఉంటాయా ?
సాధన:
a) స్థూపములు A, B ల మధ్య గల స్టాపిక్ను తెరిస్తే Aలోని వాయువు B లోకి పీడనం సమానమయ్యే దాకా వ్యాపిస్తుంది. ఇప్పుడు ఘనపరిమాణం V₁ = V_A + V_B = 2V. కాని PV స్థిరరాశి
∴ P₁V₁ = PV + 0 ⇒ P₁ = P . \(\frac{V}{2 V}=\frac{P}{2}\)
అనగా కొత్త పీడనం P = \(\frac{P}{2}\) తొలి పీడనంలో సగము

b) వాయువు ఉష్ణోగ్రతలో మార్పు లేకపోవడం వల్ల, PV స్థిరంగా ఉండటం వల్ల అంతరిక శక్తిలో మార్పు ఉండదు.

c) ఈ ప్రక్రియలో వాయువు పని చేయలేదు. కావున దాని ఉష్ణోగ్రతలో మార్పులేదు.

d) ఉండవు. ఎందుకనగా వాయువులు స్వేచ్ఛగా శూన్యంలోకి వ్యాపించాయి. ఇది వేగవంతమైన ప్రక్రియ దీనిని అదుపులో ఉంచలేము. అందువల్ల మధ్యస్థ దశ సమతాస్థితిలో ఉండదు. కావున వాయు సమీకరణాన్ని తృప్తిపరచదు. ఇది అనుత్రమణీయ చర్య.

ప్రశ్న 7.
ఒక ఆవిరి యంత్రం నిమిషానికి 5.4 × 10⁸ Jల పని జరిపి, నిమిషానికి 3.6 × 10⁹ J ల ఉష్ణాన్ని దాని బాయిలర్ ద్వారా సరఫరా చేస్తుంది. ఆ యంత్రం దక్షత ఎంత ? నిమిషానికి ఎంత ఉష్ణం వృధాగా పోతుంది ?
సాధన:
నిమిషానికి జరిగిన పని = 5.4 × 10⁸ J
నిమిషంలో వాడిన ఉష్ణశక్తి = 3.6 × 10⁹ J

= \(\frac{5.4 \times 10^8}{3.6 \times 10^9}\) = 0.15 = 0.15 × 100% = 15%
నిమిషంలో వృధా అయిన ఉష్ణం = నిమిషంలో గ్రహించిన ఉష్ణము – నిమిషంలో జరిగిన పని
= 3.6 × 10⁹ – 5.4 × 10⁸ = 109 (3.6 – 0.54) = 3.06 × 10⁹ J

ప్రశ్న 8.
ఒక ఎలక్ట్రిక్ హీటరు 100W రేటు చొప్పున ఉష్ణాన్ని ఒక వ్యవస్థకు అందచేస్తుంది. వ్యవస్థ సెకనుకు 75 J ల రేటు చొప్పున పనిచేస్తుంటే, అంతరిక శక్తి ఏ రేటుతో పెరుగుతుంది ?
సాధన:
అందజేసిన ఉష్ణరాశి, ∆Q = 100 W = 100 J/s
ఉపయోగపడిన పని, ∆W = 75 J/s
సెకనుకు అంతర్గత శక్తిలో పెరుగుదల ∆U = ?
కాని ∆Q = ∆U + ∆W
∴ ∆U = ∆Q – ∆W = 100 – 75 = 25J/s

ప్రశ్న 9.
ఒక ఉష్ణగతిక వ్యవస్థను దాని నిజ స్థితి నుంచి ఒక మధ్యస్థ స్థితికి, రేఖీయ ప్రక్రియ ద్వారా పటంలో చూపినట్లుగా తీసుకోవడమైంది.

వ్యవస్థ ఘనపరిమాణం, నిజ విలువకు E నుంచి F కు సమపీడన ప్రక్రియ ద్వారా తగ్గించడమైంది. వాయువును D నుంచి Eకు, E నుంచి F కు చేర్చడానికి జరిగిన మొత్తం పనిని లెక్కించండి.
సాధన:
పటం నుండి
పీడనంలో మార్పు, dP = DF = 5.0 – 2.0 = 3.0 atm = 3.0 × 10⁵ Nm^-2
ఘనపరిమాణంలో మార్పు, dV = EF = 600 – 300 = 300 cc = 300 × 10^-6 m³
D నుండి E నుండి F వరకు జరగటంలో వాయువు జరిపిన పని = వైశాల్యం ∆DEF
W = \(\frac{1}{2}\) × EF × DF = \(\frac{1}{2}\) × (300 × 10^-6) × (3.0 × 10⁵) = 45 J

ప్రశ్న 10.
ఒక శీతలీకరణ యంత్రంలో ఉంచిన తినే పదార్థాలను ఆ యంత్రం 9°C వద్ద ఉంచుతుంది. గది ఉష్ణోగ్రత 36°C అయితే దాని క్రియాశీలతా గుణకాన్ని లెక్కించండి.
సాధన:
దత్తాంశం నుండి, T₂ = 9°C = 9 + 273 = 282 K ;
T₁ = 36°C = 36 + 273 = 309 K
క్రియాశీలతా గుణకం నుండి = \(\frac{\mathrm{T}_2}{\mathrm{~T}_1-\mathrm{T}_2}\) = \(\frac{282}{309-282}\) = \(\frac{282}{27}\) = 10.4

Telangana TSBIE TS Inter 1st Year Physics Study Material 11th Lesson ప్రవాహుల యాంత్రిక ధర్మాలు Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 11th Lesson ప్రవాహుల యాంత్రిక ధర్మాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సగటు పీడనాన్ని నిర్వచించండి. దీని ప్రమాణం, మితీయ ఫార్ములాను తెలపండి. ఇది సదిశరాశా ? అదిశరాశా ?
జవాబు:
సగటు పీడనం : ఏకాంక వైశాల్యంపై చర్య జరిపే అభిలంబ బలాన్ని సగటు పీడనం అంటారు.
అనగా, సగటు పీడనం, P_av = \(\frac{\mathrm{F}}{\mathrm{A}}\) ; (ఇది అదిశరాశి.)
పీడనం యొక్క SI ప్రమాణం : Nm^-2 ; మితిఫార్ములా : ML^-1 T^-2

ప్రశ్న 2.
స్నిగ్ధతను నిర్వచించండి. స్నిగ్ధతా గుణకం ప్రమాణాలు, మితులు ఏమిటి ?
జవాబు:
స్నిగ్ధత : ప్రవాహి పొరల మధ్య సాపేక్ష చలనాన్ని నిరోధించే ప్రవాహి ధర్మాన్ని స్నిగ్ధత అంటారు.
స్నిగ్ధతా గుణకం SI ప్రమాణం : Nm^-2 s లేదా Pa- s ; C.G.S. ప్రమాణం : పాయిజ్
స్నిగ్ధతా గుణకం మితిఫార్ములా : ML^-1T^-1

ప్రశ్న 3.
ఒక ఆటోమొబైల్ యొక్క కార్బ్యురేటర్ పనిచేయడం వెనక ఉన్న సూత్రం ఏది ?
జవాబు:
ఆటోమొబైల్ యొక్క కార్బ్యురేటర్ బెర్నౌలీ సిద్దాంతము ఆధారంగా పనిచేస్తుంది.

ప్రశ్న 4.
మాగ్నస్ ప్రభావం అంటే ఏమిటి ?
జవాబు:
మాగ్నస్ ప్రభావం : బంతి స్పిన్ కావడం వల్ల ఏర్పడే గతిక ఉత్థాపనాన్ని మాగ్నస్ ప్రభావం అంటారు.

ప్రశ్న 5.
ద్రవ బిందువులు, బుడగలు గోళాకారంలో ఎందుకు ఉంటాయి ? (మార్చి 2014, మే 2014)
జవాబు:
తలతన్యత వలన ద్రవ బిందువు కనిష్ఠ వైశాల్యమును పొందడానికి ప్రయత్నిస్తుంది. సమాన ఘనపరిమాణం గల వివిధ రూపాలలో గోళమునకు కనిష్ఠ తలవైశాల్యం ఉంటుంది. కావున వర్ష బిందువులు, బుడగలు తలతన్యత వల్ల గోళాకారం పొందుతాయి.

ప్రశ్న 6.
ద్రవ బిందువులోని అదనపు పీడనానికి సమీకరణాన్ని తెలపండి.
జవాబు:
ద్రవ బిందువులో గల అదనపు పీడనము, P = \(\frac{2 \mathrm{~s}}{\mathrm{r}}\) ఇచ్చట ‘S’ అనునది తలతన్యత మరియు ‘r’ అనునది ద్రవ బిందువు వ్యాసార్ధము.

ప్రశ్న 7.
ద్రవంలోపల ఉండే గాలి బుడగలోని అదనపు పీడనానికి సమీకరణాన్ని తెలపండి.
జవాబు:
ద్రవం లోపల ఉండే గాలి బుడగలో అదనపు పీడనము, P = \(\frac{2 \mathrm{~S}}{\mathrm{r}}\) ఇచ్చట ‘S’ అనునది తలతన్యత మరియు ‘r’ అనునది గాలి బుడగ వ్యాసార్ధము.

ప్రశ్న 8.
గాలీలో ఉన్న సబ్బు బుడగలోని అదనపు పీడనానికి సమీకరణాన్ని తెలపండి.
జవాబు:
గాలిలో ఉన్న సబ్బు బుడగలోని అదనపు పీడనము, P = \(\frac{4 \mathrm{~S}}{\mathrm{r}}\) ‘ఇచ్చట ‘S’ అనునది తలతన్యత మరియు ‘r’ అనునది సబ్బు బుడగ వ్యాసార్ధము.

ప్రశ్న 9.
జలసంసక్తకాలు (Water wetting agents), జలఅసక్తకాలు (Water proofing agents) అంటే ఏమిటి ? అవి ఏమిచేస్తాయి ?
జవాబు:
జలసంసక్తకాలు : స్పర్శ కోణమును తగ్గించటానికి ఉపయోగించే వాటిని జలసంసక్తకాలు అని అంటారు.
ఉదా : రంగులద్దే ద్రవ్యాలు.
జల అసక్తకాలు : స్పర్శకోణంను పెంచటానికి ఉపయోగించే వాటిని జల అసక్తకాలు అంటారు.
ఉదా : సబ్బులు, డిటర్జెంట్లు,
జలరసక్తీపాలను ద్రవాలను నలిపినప్పుడుప్పు కూర పెరుగువాంచి 10. . అందమున వడిపి స్వభావం తగ్గుతుంది.

ప్రశ్న 10.
స్పర్శకోణం అంటే ఏమిటి ? (మే 2014)
జవాబు:
పాత్ర గోడలను తాకి ఉన్న ద్రవపు ఉపరితలంపై గీసిన స్పర్శరేఖకు, పాత్ర గోడలకు మధ్య ద్రవాంతర్భాగంలో కొలిచిన I కోణాన్ని స్పర్శకోణము ‘θ’ గా నిర్వచించినారు.

ప్రశ్న 11.
బెర్నౌలీ సిద్ధాంతాన్ని పాటించే వాటికి రెండు ఉదాహరణలను ఇవ్వండి. ఆయా ఉదాహరణలను సమర్ధించండి.
జవాబు:
ఎ) వస్తువులు ద్రవంలో తేలుతున్నపుడు ద్రవంలో మునిగిన వస్తువు ఘనపరిమాణ భాగము =

(బి) వస్తువు ప్రవాహిలో తేలుతున్నపుడు వస్తువు వలన తొలగింపబడిన ద్రవం భారము, ప్రవాహిలో తేలుతున్న వస్తువు భారమునకు సమానము.

ప్రశ్న 12.
ఒక గొట్టం ద్వారా నీరు ప్రవహిస్తున్నప్పుడు ఆ నీటి ప్రవాహంలో ఏ పొర అత్యధిక వేగంతో ప్రవహిస్తుంది ? ఏ పొర అత్యల్ప వేగంతో ప్రవహిస్తుంది ?
జవాబు:
గొట్టం ద్వారా నీరు ప్రవహిస్తున్నపుడు గొట్టము లోపలి వైపు ఆనుకొని ఉన్న నీటి పొరలకు వేగం తక్కువ. గొట్టం అడుగుభాగం నుండి దూరంగా ఉన్న పొరలకు వేగం ఎక్కువ. అనగా గొట్టంలోపల పై అంచుకు దగ్గరగా ఉన్న ద్రవం పొరలకు వేగం ఎక్కువ.

ప్రశ్న 13.
ఒక వస్తువు యొక్క ఉపరితల వైశాల్యం ఎక్కువైనప్పుడు దాని చరమ వేగం (Terminal Velocity)కూడా అధికంగా ఉంటుంది. మీ సమాధానాన్ని సమర్ధించే కారణాలను తెలపండి.
జవాబు:
వస్తువు ఉపరితల వైశాల్యం ఎక్కువ ఐతే ఆ వస్తువుకు అంత్య వేగము ఎక్కువ.
స్టోక్స్ సిద్ధాంతం ప్రకారము అంత్యవేగము v = \(\frac{2}{9}\) a² \(\frac{(\rho-\sigma) g}{\eta}\) మిగిలిన రాశులు స్థిరంగా ఉన్నపుడు v ∝ a²
గోళాకార వస్తువు ఉపరితల వైశాల్యం A = 4π a² అనగా A ∝ a² కావున v ∝ A అవుతుంది. అనగా ఉపరితల వైశాల్యం A పెరిగితే చరమ వేగం v పెరుగును.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాతావరణ పీడనం అంటే ఏమిటి ? భారమితి (బారో మీటర్) సహాయంతో ఎలా నిర్ధారిస్తారు ?
జవాబు:
వాతావరణ పీడనం : ఏదైనా ఒక బిందువు వద్ద వాతావరణ పీడనం, ఆ బిందువు నుంచి విస్తరిస్తూ వాతావరణపు పై అంచుదాకా కొనసాగే ఏకాంక మధ్యచ్ఛేద వైశాల్యం గల వాయుస్తంభం యొక్క బరువుకు సమానము.

భారమితి (Barometer) సహాయంతో వాతవరణ పీడనాన్ని నిర్ధారించుట :
పాదరస భారమితి : ఇది వాతావరణ పీడనాన్ని కొలిచే పరికరం సుమారు 1 మీటరు పొడవు గల గాజు గొట్టాన్ని పాదరసంతో నింపి దీనిని పాదరసపు తొట్టెలో తలక్రిందులుగా నిలబెడతారు. సముద్రమట్టం వద్ద ఈ గాజు గొట్టంలో 76 సెం.మీ. ఎత్తులో పాదరసం నిలిచి ఉంటుంది. పాదరస మట్టం పైన గల భాగంలో కేవలం పాదరస భాష్పం ఉంటుంది. పాదరసానికి భాష్పపీడనం చాలా తక్కువ కావటం వల్ల గొట్టంలో పాదరసం పై భాగాన్ని శూన్యంగా భావిస్తారు. వాతావరణ పీడనం బట్టి పాదరస మట్టము ఎత్తు ‘h’ మారుతుంది. ఈ పాదరస మట్టపు ఎత్తునే పీడనంగా వ్యవహరిస్తారు.

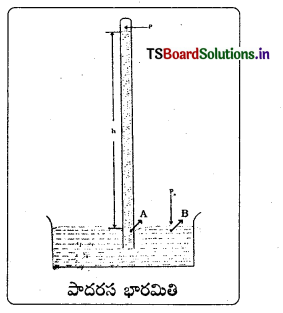
సముద్రమట్టం వద్ద వాతావరణ పీడనం P = hρg
ρ = పాదరసం సాంద్రత, g = గురుత్వ త్వరణము, h = పాదరస స్థంభం ఎత్తు = 76 c.m.
పాదరసము సాంద్రత, ρ = 13.6 × 10³ kg m^-3 g = 9.8 ms^-2.
∴ వాతావరణ పీడనము, P_a = hρg = 0.76 × (13.6 × 10³) × 9.8 = 1.013 × 10⁵ Nm^-2 or Pa

ప్రశ్న 2.
గేజ్ పీడనం అంటే ఏమిటి ? మానోమీటర్ సహాయంతో పీడన వ్యత్యాసాన్ని ఎలా కనుక్కొంటారు ?
జవాబు:
గేజ్ పీడనం : ఒక ద్రవంలోపల ‘h’ లోతులో ఉన్న ఒక బిందువు వద్ద గల పీడనం P, ద్రవ ఉపరితలంపై పనిచేసే వాతావరణ పీడనం విలువ (P_a) కన్నా ρgh ఎక్కువగా ఉంటుంది. ‘h’ లోతులో గల బిందువు వద్ద గల ఈ పీడన వ్యత్యాసాన్నే (P – P_a) ఆ బిందువు వద్ద గల గేజ్ పీడనం అని అంటారు.

మానోమీటర్ సహాయంతో పీడన వ్యత్యాసాన్ని కనుగొనుట :
మానోమీటరు పీడన భేదం కొలవడానికి వాడే పరికరం. ఇది ఒక ‘U’ గొట్టము. ఈ ‘U’ గొట్టంలో ద్రవాన్ని తీసుకొని గొట్టం ఒక కొనను పీడనం కొలవవలసిన ప్రాంతానికి కలిపి రెండవ కొనను వాతావరణ పీడనం వద్ద ఉండే విధంగా స్వేచ్ఛగా వదిలేస్తారు. ‘U’ గొట్టంలోని ద్రవమట్టములలోని ఎత్తుల భేదము పీడనాన్ని తెలియచేస్తుంది. అల్పపీడన వ్యత్యాసాలను కొలవడానికి ‘U’ గొట్టంలో తక్కువ సాంద్రత గల ద్రవాన్ని, ఎక్కువ పీడన బేధనాన్ని కొలవడానికి ‘U’ గొట్టంలో పాదరసాన్ని వాడతారు.

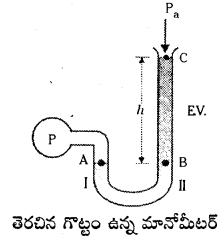
బిందువు వద్ద ఉండే పీడనం P బిందువు B వద్ద ఉన్న పీడనానికి సమానము అవుతుంది. పాత్రలోని పీడనం ‘P’, వాతావరణ పీడనము కన్నా అధికమైనచో, U-గొట్టంలోని భుజము ” లోని ద్రవ మట్టము బిందువు ‘A’ వద్దకు తగ్గుతుంది. మరియు భుజము-‘I’ లోని ద్రవ మట్టము బిందువు ‘C’ వరకు పెరుగును, అప్పుడు పాత్రలోని వాయువు యొక్క పీడనము బిందువు ‘A’ వద్ద గల పీడనమునకు సమానమగును. U- గొట్టంలోని రెండు భుజములలో గల ద్రవ మట్టముల వ్యత్యాసము ‘h’ అనుకొనుము. U- గొట్టంలోని ద్రవము యొక్క సాంద్రత ‘ρ’, మరియు వాతావరణ పీడనము ρ_a అని అనుకొనుము.
ఒకే మట్టములో గల అన్ని బిందువుల వద్ద సమాన పీడనము ఉండును.
∴ P_A = P_B = P_C + hρg
బిందువు A వద్ద పీడనము, P_A = బిందువు B వద్ద పీడనము
= బిందువు C వద్ద పీడనము (P) + ‘h’ ఎత్తు గల ద్రవస్తంభం వలన కలిగిన పీడనము
∴ P_A = P + h

ప్రశ్న 3.
పాస్కల్ నియమాన్ని తెలిపి ఒక ప్రయోగం సహాయంతో దాన్ని నిరూపించండి.
జవాబు:
పాస్కల్ నియమం :
“విరామస్థితిలో ఉన్న ఒక ప్రవాహిలో ఒకే ఎత్తులో ఉన్న అన్ని బిందువుల వద్ద పీడనం ఒకే విలువను కలిగి ఉంటుంది.”

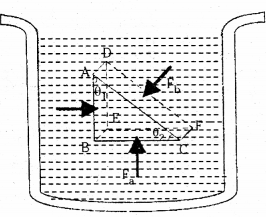
పాస్కల్ నియమానికి నిరూపణ :
ఒక విరామ స్థితిలో ప్రవాహి లోపలి స్వల్పంశ భాగాన్ని పటములో చూపిన విధముగా అనుకొనుము. ఈ స్వల్పాంశ భాగము ABC – DEF ఒక లంబకోణ పట్టకాకృతిలో ఉంది.

సూత్రప్రాయంగా, ఈ పట్టకీయ స్వల్పాంత భాగం ఎంత స్వల్పాతి స్వల్పంగా ఉంటుందంటే, దాని ప్రతి భాగం ద్రవ ఉపరితలం నుంచి ఒకే లోతులో ఉన్నట్లుగా మనం భావించవచ్చు. కాబట్టి ఈ బిందువులన్నింటి వద్ద గురుత్వ ప్రభావం ఒకే విధంగా ఉంటుంది.

ఈ స్వల్పాంశ భాగంపై ఉండే బలాలు తక్కిన ప్రవాహి దానిపై ప్రయోగించే బలాలే. ఇవి స్వల్పాంశ ఉపరితలాలకు అభిలంబంగా ఉంటాయి.

కాబట్టి పటములో చూపిన విధముగా వైశాల్యంశాలు A_a, A_b, A_c లు వరుసగా సూచించే ముఖాలు BEFC, ADFC, ADEB ల పైన అభిలంబ బలాలు F_a, F_b, F_c ల వల్ల ప్రవాహి P_a, P_b, P_c లు అనే పీడనాలను ఆయా వైశాల్యంశాల పైన కలుగచేస్తుంది.
అప్పుడు,
F_b sin θ₂ – F_c and F_b cos θ₂ = F_a (సమతాస్థితి వల్ల)
A_b sin θ₂ = A_c and A_b cos θ₂ = A_a (జ్యామితి వల్ల)
కాబట్టి,
\(\frac{F_b}{A_b}=\frac{F_c}{A_c}=\frac{F_a}{A_a}\) ⇒ P_b = P_c = P_a
కాబట్టి, ఒక విరామ స్థితిలోని ప్రవాహిలో అన్ని దిశలలో అది కలుగచేసే పీడనం ఒకే విలువను కలిగి ఉంటుంది. ఇదే పాస్కల్ నియమము.

ప్రశ్న 4.
హైడ్రాలిక్ లిఫ్ట్, హైడ్రాలిక్ బ్రేక్లను వివరించండి.
జవాబు:
హైడ్రాలిక్ (జలోత్పీడన) యంత్రాలు : పాస్కల్ పీడనం ప్రసరణ నియమం ప్రకారము ఒక పాత్రలో ఉన్న ప్రవాహి యొక్క ఏ భాగం మీద అయినా బాహ్యపీడనాన్ని ప్రయోగిస్తే ఆ పీడనం విలువ ఏ మాత్రం క్షీణించకుండా ద్రవం అన్నివైపులకు సమానంగా ప్రసరిస్తుంది. ఈ సూత్రం ఆధారంగా హైడ్రాలిక్ లిఫ్ట్ పనిచేస్తుంది.

హైడ్రాలిక్ లిఫ్ట్లో భిన్న వైశాల్యాలు గల రెండు ముషలకాలు (A₁, A₂) లు ద్రవంతో పూర్తిగా నింపబడిన ‘U’ గొట్టం వంటి పరికరం ద్వారా
కలుపబడి ఉంటాయి.

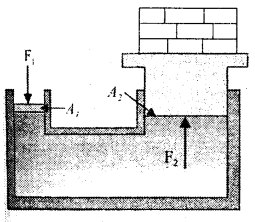
పీడనం P = F₁/A₁ ను చిన్న గొట్టంపై ప్రయోగిస్తే అదే పీడనం P = F₂/A₂ను పెద్ద ముషలకం A₂ పై ప్రయోగిస్తుంది. పాస్కల్ నియమం ప్రకారం P సమానం కావున
\(\frac{\mathrm{F}_1}{\mathrm{~A}_1}=\frac{\mathrm{F}_2}{\mathrm{~A}_2}\) లేదా F₂ = \(\frac{\mathrm{A}_2}{\mathrm{~A}_1}\) F₁ అనగా చిన్న ముషలకంపై ప్రయోగించిన F₁ బలం A₂/A₁ అన్న రెట్లు పెద్దదిగా పెద్ద ముషలకంపై పనిచేయడం వల్ల ఎక్కువ వైశాల్యం గల ముషలకం అధిక బరువును పైకి లేపుతుంది. ఇందులో A₂/A₁ ను యాంత్రిక లాభం అంటారు.

హైడ్రాలిక్ బ్రేకులు : హైడ్రాలిక్ బ్రేకులు పాస్కల్ పీడన ప్రసరణ నియమం ఆధారంగా పనిచేస్తాయి. ఇందులో మన పాదం క్రింద గల పెడల్పై స్వల్ప బలం ప్రయోగిస్తే అది మాస్టర్ స్థూపంలో గల బ్రేక్ నూనెపై పీడనాన్ని కలుగచేస్తుంది. ఈ బ్రేక్ నూనె అధిక వైశాల్యాలు గల ముషలకాలపై ఎక్కువ ప్రభావం చూపుతుంది. ఈ ముషలకాలు చక్రాలకు కలుపబడిన బ్రేక్ లైనింగులకు వ్యతిరేకంగా బ్రేక్ షూలను వ్యాకోచింపచేసి వాహనాలకు అధికమందక బలం (Retarding force) ను అందజేస్తాయి. ఈ అమరికలో ద్రవం ద్వారా పీడనం అన్ని చక్రాల ముషలకాలకు సమానంగా అందటం వల్ల అన్ని చక్రాలపై ఒకే పరిమాణం గల బలం ప్రయోగింపబడి బ్రేకింగ్ వ్యవస్థ అధిక సౌకర్యవంతంగా ఉంటుంది.

ప్రశ్న 5.
ద్రవ స్థితిక విరోధాభాసము అంటే ఏమిటి ?
జవాబు:
ద్రవస్థితిక విరోధభాసం : ఒకే క్షితిజ సమాంతర మట్టం వద్ద ఉన్న అన్ని బిందువుల వద్ద ద్రవ పీడనం సమానంగా ఉంటుంది. ఈ ఫలితాన్నే ద్రవస్థితిక విరోధాభాసం అంటారు.

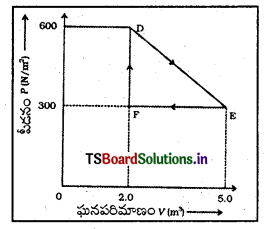
పటంలో చూపించిన మూడు పాత్రలు A, B, C లు భిన్న ఆకారాల్ని కలిగి ఉన్నాయి. వాటి అడుగు భాగాన్ని ఒక క్షితిజ సమాంతర గొట్టం సంధానం చేస్తోంది. వాటిని నీటితో నింపినప్పుడు ఆ మూడు పాత్రలలోను నీటి మట్టం, వాటిలో నిలిచి ఉన్న నీటి మొత్తాలు భిన్నమైనప్పటికీ, ఒకటిగానే ఉన్నాయి. ఇలా ఎందుకు జరుగుతుందంటే, పాత్ర యొక్క ఒక్కొక్క భాగం అడుగులో నీరు కలిగించే పీడనం సమానంగా ఉంటుంది.

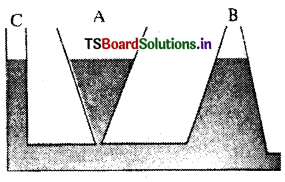
ప్రవాహి స్తంభం ఎత్తు కేవలం పీడనం మీద ఆధారపడును. ఇది ద్రవం మధ్యచ్ఛేద వైశాల్యం లేదా పీఠ వైశాల్యం లేదా పాత్ర ఆకారంపైన ఆధారపడదు.

ప్రశ్న 6.
లోతులో పీడనం ఎలా మారుతుందో వివరించండి.
జవాబు:
లోతులో పీడనంలో వచ్చే మార్పు :
ఒక పాత్రలో ఒక ప్రవాహి నిశ్చలంగా ఉందనుకొనుము. పటంలో బిందువు 2కి పైన h ఎత్తులో బిందువు 1 ఉంది. బిందువు 1, బిందువు 2 ల వద్ద పీడనాలు వరుసగా P₁, P₂ అనుకొనుము. పీఠ వైశాల్యం A, ఎత్తు ఉన్నటువంటి ఒక స్థూపాకార స్వల్పాంశ ప్రవాహి భాగాన్ని పరిగణనలోకి తీసుకొనుము. ప్రవాహి నిశ్చలంగా ఉంది కాబట్టి క్షితిజ సమాంతర బలాల వల్ల కలిగే ఫలితబలం శూన్యం కావాలి. అంతేగాక క్షితిజ లంబ బలాల ఫలిత బలం, స్వల్పాంశ ప్రవాహి భాగం భారాన్ని సంతులనం చేయాలి. స్వల్పాంశ భాగానికి నిలువు దిశలో చర్య జరిపే బలాలు (P₁ A) దానిపై భాగాన ఉండి, అధోముఖ దిశలోని పీడనం వల్ల ఏర్పడగా, అడుగు భాగంలోని ప్రవాహి వల్ల ఇలా ఏర్పడే బలాలు (P₂A) ఊర్ధ్వ దిశలో చర్య జరిపే పీడనం వల్ల ఏర్పడతాయి. మనం పరిగణనలోకి తీసుకున్న స్థూపంలోని ప్రవాహి భారం mg అయితే,
(P₂ – P₁) A = mg ……………….. (1)
ప్రవాహి ద్రవ్యరాశి సాంద్రత ρ అయితే, ఆ ప్రవాహి ద్రవ్యరాశి, m = ρv = ρhA అవుతుంది.
కావున P₂ – P₁ = ρgh ……………… (2)

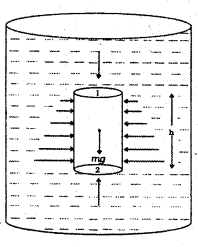
పైన సూచించిన బిందువులు 1, 2 ల మధ్య ఉండే నిలువు దూరం h పైనా, ప్రవాహి ద్రవ్యరాశి సాంద్రత p, గురుత్వ త్వరణం g పైనా పీడన వ్యత్యాసం ఆధారపడి ఉంటుంది. పరిగణనలోకి తీసుకున్న బిందువు 1ని ప్రవాహి ఉపరితలానికి మారిస్తే, అది వాతావరణ పీడనానికి (P_a) లోనయి ఉంటుంది కాబట్టి, P₁ స్థానంలో వాతావరణ పీడనం (P_a) ని, P₂ స్థానంలో P ని ప్రతిక్షేపించవచ్చు.
సమీకరణం (2) నుండి P – P_a = ρgh
లేదా P = P_a + ρgh
కాబట్టి వాతావరణ పీడనానికి లోనైనటువంటి ప్రవాహి ఉపరితలం నుంచి కొంత లోతులో ఉన్న బిందువు వద్ద పీడనం P, వాతావరణ పీడనం కంటే ρgh ఎక్కువగా ఉంటుంది.

ప్రశ్న 7.
టోరిచెల్లి నియమం అంటే ఏమిటి ? ఒక ప్రయోగంతో బహిస్రావం (efflux) వడిని ఎలా నిర్ధారిస్తారో వివరించండి.
జవాబు:
బహిస్రావం వడి :
టోరిచెల్లి నియమం : బహిస్రావం అనే పదానికి అర్థం ప్రవాహి బయటకు వెళ్ళడం. ఒక తెరచిన తొట్టి (టాంక్) నుంచి ఉండే బహిస్రావ వడి స్వేచ్ఛగా కిందకు పడుతున్న వస్తువుకు వర్తించే ఫార్ములాకు సరిసమానమైన రూపాన్నే కలిగి ఉంటుందని టోరి చెల్లి కనుక్కొన్నాడు. ρ సాంద్రతగల ద్రవంతో నిండి ఉన్న ఒక టాంక్ను పరిగణించండి. దాని అడుగు భాగం నుంచి y₁ ఎత్తులో దానికి ఒక పక్కన ఒక చిన్న రంధ్రం ఉందనుకొందాం. ద్రవం పైభాగంలో, y₂ ఎత్తు వద్ద ఉన్న దాని ఉపరితలంపైన ఉన్న గాలి (2 వద్ద) పీడనం P వద్ద ఉంది. సాంతత్య సమీకరణం నుంచి
v₁ A₁ = v₂ A₂

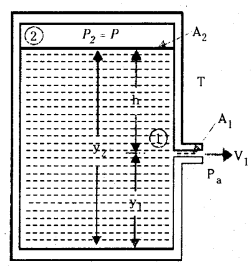
⇒ v₂ = \(\frac{A_1}{A_2}\) v₁ ……………. (1)
టాంక్ మధ్యచ్ఛేద వైశాల్యం A₂ రంధ్రం మధ్యచ్ఛేద వైశాల్యం A1 కంటే చాలా ఎక్కువగా ఉన్నట్లయితే (A₂ >> A₁) పై భాగం వద్ద ప్రవాహి (ఉజ్జాయింపుగా) విరామంలో ఉన్నట్లుగా తీసుకోవచ్చు. అంటే v₂ = 0. రంధ్రం వద్ద P₁ = P_a (P_a = వాతావరణ పీడనం) అవుతుందని గుర్తిస్తూ, బిందువులు 1, 2 ల వద్ద బెర్నౌలీ సమీకరణాన్ని అనువర్తిస్తే,
సమీకరణం నుంచి
P_a + \(\frac{1}{2}\)ρv₁² + ρgy₁ = P + ρgy₂ గా రాయవచ్చు.
y₂ – y₁ = h అని అనుకొంటే
v₁ = \(\sqrt{2 g h+\frac{2\left(\mathrm{P}-\mathrm{P}_{\mathrm{a}}\right)}{\rho}}\) ……………. (2)
P > > P_a అయినప్పుడు, 2gh ను ఉపేక్షించినప్పుడు బహిస్రావం యొక్క వడిని పాత్ర (టాంక్) పీడనం నిర్ధారిస్తుంది. ఇలాంటి పరిస్థితి రాకెట్ చోదనంలో సంభవిస్తుంది. ఒకవేళ టాంక్ను వాతవరణ పీడనానికి తెరచి ఉంచినట్లయితే, అప్పుడు P = P_a
v₁ = \(\sqrt{2 g h}\)

ప్రశ్న 8.
వెంటురి – మీటర్ అంటే ఏమిటి ? దీన్ని ఎలా ఉపయోగిస్తారో వివరించండి.
జవాబు:
వెంటురి-మీటర్ : వెంటురి మీటరును అసంపీడ్య ప్రవాహుల వడిని కొలవడానికి వాడతారు.

వెంటురి – మీటరు ఎక్కువ వైశాల్యము కలిగి మధ్యలో చిన్న నొక్కు గల గొట్టము. ‘U’ ఆకారపు మానోమీటరు యొక్క ఒక భుజము వెంటురి-మీటరు వెడల్పాటి భాగానికి రెండవ కొన వెంటురి-మీటరు నొక్కు వద్ద కలపబడి ఉంటాయి.

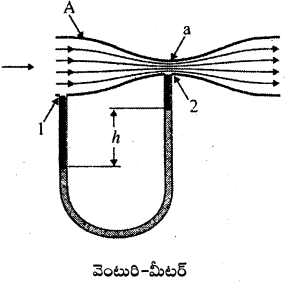
బెర్నౌలి సిద్ధాంత ప్రకారము
P₁ + \(\frac{1}{2}\)ρv₁² = P₂ + \(\frac{1}{2}\)ρv₂² (వెంటురి మీటరు గొట్టం ఒకే ఎత్తులో ఉండడం వల్ల ρgh ఇరువైపులా సమానం)
∴ P₁ – P₂ = latex]\frac{1}{2}[/latex]ρ(v₂² – v₁²)
లేదా P₁ – P₂ = \(\frac{1}{2}\)ρv₁² \(\left[\left(\frac{\mathrm{A}}{\mathrm{a}}\right)^2-1\right]\)
\(\frac{\mathrm{A}}{\mathrm{a}}\) వెంటురి మీటరు గొట్టము (A) నొక్కు (a) వద్ద గల
వైశాల్యం (a) ల నిష్పత్తి, పీడన భేదము P₁ – P₂ = ρmgh
h = మానోమీటరులో పాదరస మట్టముల బేధము
సాంతత్వ సమీకరణం నుండి \(\frac{v_2}{v_1}=\frac{A}{a}\)
∴ ప్రవాహ వడి v_i = \(\sqrt{\frac{2 \rho_{\mathrm{m}} \mathrm{gh}}{\rho}}\left[\left(\frac{\mathrm{A}}{\mathrm{a}}\right)^2-1\right]\)

ప్రశ్న 9.
రెనాల్డ్స్ సంఖ్య అంటే ఏమిటి ? దాని ప్రాముఖ్యత ఏమిటి ?
జవాబు:
రేనాల్డ్ సంఖ్య (R) : ప్రవాహులలో ఒక ప్రవాహము ధారారేఖా ప్రవాహమా లేక సంక్షుబ్ధ ప్రవాహమా అని నిర్ణయించడానికి రేనాల్డ్ సంఖ్యను వాడతారు.
రేనాల్డ్ సంఖ్య ప్రవాహుల జడత్వ బలానికి మరియు స్నిగ్ధతా బలాలకు గల నిష్పత్తిగా చెప్పవచ్చు.

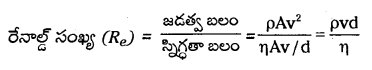
ఇక్కడ ρ అనేది v వేగంతో ప్రవహిస్తున్న ప్రవాహి సాంద్రత, d అనేది గొట్టానికి ఉండే ఒకానొక కొలతను (పొడవు లేదా వ్యాసం) సూచిస్తుంది. η ప్రవాహి స్నిగ్ధతా గుణకం. ఇక R_e ఒక మితిరహిత సంఖ్య కాబట్టి ప్రమాణాలకు ఉండే ఏ పద్ధతిలోనైనా అది మారకుండా సమానంగా ఉంటుంది.

ప్రాముఖ్యత : ఒక ప్రవాహం R_e విలువ 1000 కంటే తక్కువగా ఉన్నప్పుడు అది ధారారేఖా ప్రవాహం లేదా స్తరీయ ప్రవాహంగా ఉంటుందని కనుక్కొన్నారు. R_e > 2000 అయితే ప్రవాహం సంక్షుబ్ధ ప్రవాహం అవుతుంది. R_e విలువ 1000 నుండి 2000 ల మధ్య ఉన్నప్పుడు ఆ ప్రవాహం ‘నిలకడ రహిత’ ప్రవాహంగా మారుతుంది. ఏ R విలువ వద్ద ప్రవాహంలో సంక్షుబ్ధత మొదలవుతుందో ఆ సందిగ్ధ విలువను సందిగ్ధ రెనాల్డ్స్ సంఖ్య అంటారు.

ప్రశ్న 10.
గతిక ఉత్థాపనాన్ని ఉదాహరణలతో సహా వివరించండి.
జవాబు:
ఆత్మభ్రమణంలో గల బంతిపై గతిక ఉత్థాపన : ఆత్మభ్రమణంతో ముందుకు చలించే బంతికి రెండు రకాల చలనం
ఉంటుంది. 1) స్థానాంతరణ చలనము ; 2) భ్రమణ చలనము

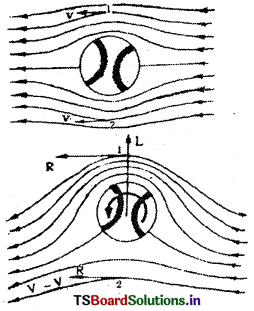
1) స్థానాంతరణ చలనం ఉన్నప్పుడు : కేవలం స్థానాంతరణ చలనం గల బంతి యానకంలో ముందుకు దూసుకొనిపోవునపుడు బంతి పై భాగాన, క్రింద భాగాన గల వేగము సమానము. కావున బంతిపై గతిక ఉత్థాపన ఉండదు.

బంతి భ్రమణ గమనం కలిగి ఉన్నపుడు : గాలిలో బంతి వేగము v మరియు బంతి ∆v అను వేగంతో సవ్యదిశలో ఆత్మభ్రమణం చేస్తున్నది అనుకొనుము. బంతి ఉపరితలం పూర్తిగా నున్నగా ఉండకపోవడం వల్ల వాయు అణువులు కూడా బంతితో పాటు ∆v వేగంతో భ్రమణం చెందుతాయి. ఈ చలనాన్ని డ్రాగ్ (Drag) అంటారు.

డ్రాగ్ ఫలితంగా బంతి పై భాగంలో గల వాయు అణువుల వేగం v + ∆v గాను, బంతి క్రింద భాగంలో గల వాయు అణువులవేగం v – ∆v గాను మారుతుంది. బంతి పై భాగంలో వాయు అణువుల వేగం ఎక్కువ. కావున బెర్నౌలి సిద్ధాంతం ప్రకారము పీడనం తక్కువ. బంతి క్రింద భాగంలో వాయు అణువుల వేగం తక్కువ కావున పీడనం ఎక్కువ. ఈ పీడన భేదం వల్ల భ్రమణంలో ఉన్న బంతిపై కొంత గతిజ ఉత్థాపకం పనిచేస్తుంది. ఫలితంగా భ్రమణంలో ఉన్న బంతి మార్గం వక్రంగా ఉంటుంది.

ప్రశ్న 11.
తలతన్యత, తలశక్తులను వివరించండి.
జవాబు:
తలతన్యత : ద్రవ ఉపరితలంపై ఏకాంక పొడవు గల ఊహాజనిత రేఖ పొడవుకు లంబంగా పనిచేసే బలాన్ని తలతన్యతగా నిర్వచించారు.
తలతన్యతా బలాలు ద్రవం ఉపరితలంపై గల అణువులపై లంబంగా ద్రవం లోపలి వైపుకు పనిచేస్తాయి.
ప్రమాణము : న్యూ/మీ
మితిఫార్ములా : MT^-2
ఉపరితల శక్తి : అణుబలాల వల్ల ప్రమాణ వైశాల్యంలో గల అధిక స్థితిజ శక్తిని ఉపరితల శక్తి అంటారు.
ఉపరితలశక్తి మరియు తలతన్యతల మధ్య సంబంధం : ఉపరితలశక్తి, ద్రవం తలతన్యతకు సమానం.

ప్రశ్న 12.
ప్రయోగాత్మకంగా తలతన్యతను కనుక్కొనే విధానాన్ని వివరించండి.
జవాబు:
ప్రయోగశాలలో ద్రవం తలతన్యతను కనుగొనటానికి విమోటన త్రాసును వాడతారు. ఇందులో ఒక ఆధారపరంగా చలించగల ఒక లోహపు కడ్డీకి ఒక వైపు గాజుపలకను మరొకవైపు బరువులు ఉంచే పళ్ళెంను కలుపుతారు.

శుభ్రమైన ఒక గాజు పలకను తీసుకొని దాని పొడవు ” మందము ‘t’ లను కనుగొంటారు. మందము t పొడవు (l) కన్న చాలా తక్కువ అయితే t ని లెక్కలోకి తీసుకోరు.

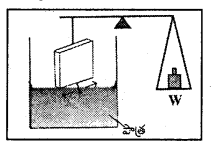
గాజు పలకను త్రాసుకు తగిలించి పళ్ళెంలో బరువులను వేసి లోహపు కడ్డీ క్షితిజ సమాంతరంగా ఉండే విధంగా పళ్ళెంలో బరువులను మారుతారు. బరువు W_o ను కనుగొంటారు.

తలతన్యత కనుగొనవలసిన ద్రవాన్ని శుభ్రమైన బీకరులో తీసుకొని ద్రవం గాజు పలకను తాకే వరకు బీకరులో ద్రవాన్ని పోస్తారు. గాజు పలక ద్రవతలాన్ని స్పర్శించినపుడు తలతన్యతా బలం వల్ల గాజు పలక లోపలికి లాగబడుతుంది. త్రాసులో అదనంగా బరువులు W ను వేసి గాజు పలక నీటి తలాన్ని తప్పించుకొని పైకి లేచే విధంగా బరువులను కొద్ది కొద్దిగా పెంచుతారు.
పలక పైకి లేవడానికి అదనంగా వేసిన బరువు W ను కొలుస్తారు.

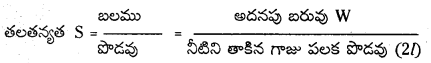
∴ తలతన్యతను S = \(\frac{\mathrm{W}}{2 l}\) ద్వారా లెక్కగడతారు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బెర్నౌలీ సూత్రాన్ని తెలపండి. ఒక గొట్టంలో ప్రవహిస్తున్న ప్రవాహికి శక్తి నిత్యత్వ నియమాన్ని అనువర్తించి బెర్నౌలీ సమీకరణాన్ని రాబట్టండి. బెర్నౌలీ సిద్ధాంతానికి ఒక అనువర్తనాన్ని ఇవ్వండి.
జవాబు:
బెర్నౌలీ సిద్ధాంతము : ధారా ప్రవాహంలో ఉన్న ప్రవాహిలోని ఏదైనా బిందువు వద్ద గల మొత్తం శక్తి స్థిరము. అనగా ఆ ప్రవాహి యొక్క ప్రమాణ ఘనపరిమాణానికి గల పీడన శక్తి, గతిజశక్తి మరియు స్థితిశక్తుల మొత్తము స్థిరము. అనగా
\(\frac{\mathrm{P}}{\rho}+\frac{\mathrm{h}}{\mathrm{g}}+\frac{\mathrm{v}^2}{2}\) = స్థిరరాశి.

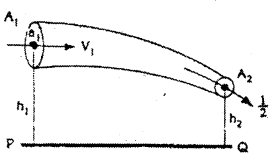
బెర్నౌలీ సిద్ధాంతము ధారా ప్రవాహంలో ఉన్న, స్నిగ్ధత లేని, అసంపీడ్య, భ్రమణ రహిత ద్రవములకు మాత్రమే వర్తించును.
నిరూపణ : A₁, A₂ అను వేరు వేరు వైశాల్యములు గల ఒక గొట్టము గుండా స్నిగ్ధత లేని, అసంపీడ్యమైన ఒక ద్రవం ప్రవహిస్తున్నది అనుకొనుము. ద్రవం A₁ వద్ద గొట్టంలోనికి v₁ వేగంతో ప్రవేశించి A₁ ద్వారా v₂ అను వేగంతో బయటకు పోయినది అనుకొనుము. A₁ వద్ద పీడము P₁, ద్రవపు సాంద్రత ρ, A₂ వద్ద పీడనము P₂ మరియు సాంద్రత ρ అనుకొనుము. ఒక స్థిరమైన ఆధారంతో పోల్చినపుడు A₁ యొక్క ఎత్తు h₁ మరియు A₂ యొక్క ఎత్తు h₂ అనుకొనుము.
dt కాలంలో A₁ వద్ద గొట్టంలోనికి ప్రవేశించిన ద్రవం
ద్రవ్యరాశి dm = ఘనపరిమాణము × సాంద్రత,
ద్రవం ఘనపరిమాణము = A₁ v₁dt ⇒ ∴ ద్రవం ద్రవ్యరాశి dm₁ = A₁V₁ρ dt . ρ ………….. (1)
A₂ గుండా dt కాలంలో బయటకుపోయిన ద్రవం ద్రవ్యరాశి dm₂ కాని dm₂= A₂ V₂ ρ dt ……………….. (2)
గొట్టంలోనికి ప్రవేశించిన ద్రవం అంతా బయటకు పోవును కావున
dm₁ = dm₂ లేదా A₁V₁ρdt = A₂V₂ ρdt = dm ……………… (3)
ద్రవం P₁ నుండి P₂ పీడనానికి ప్రయాణించునపుడు జరిగిన పని
W = పీడనము × వైశాల్యము × ద్రవం ప్రయాణించిన దూరము = P₁A₁V₁dt – P₂A₂V₂dt ……….. (4)
ద్రవం h₁ నుండి h₂ ఎత్తుకి దిగడం వల్ల జరిగిన పని W = dm₁gh₁ – dm₂gh₂ …………………. (5)
కాని పనిశక్తి సిద్ధాంతం ప్రకారం వ్యవస్థ జరిపిన మొత్తం పని దాని గతిజశక్తిలోని భేదానికి సమానము.
∴ \(\frac{1}{2}\) dm₂ v₂²– \(\frac{1}{2}\) dm₁v₁² = P₁A₁V₁dt – P₂A₂V₂dt + dm₁gh₁ – dm₂gh₂ …………….. (6)
ఇరువైపులా dm చేత భాగించగా

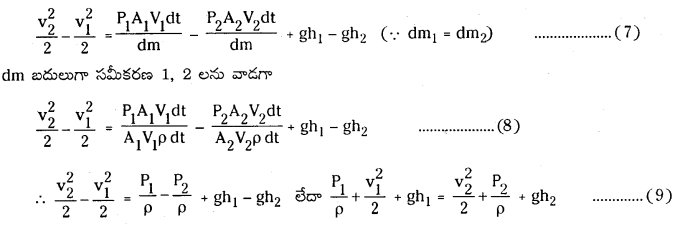
అనగా \(\frac{\mathrm{P}}{\rho}+\frac{\mathrm{v}^2}{2}\) + gh = స్థిరరాశి. ఇందులో \(\frac{P}{\rho}\) = ప్రమాణ ఘనపరిమాణానికి పీడనశక్తి
\(\frac{\mathrm{v}^2}{2}\) = ప్రమాణ ఘనపరిమాణానికి గతిజశక్తి gh = ప్రమాణ ఘనపరిమాణానికి స్థితిశక్తి
కావున ద్రవంలో ఏ బిందువు వద్ద అయినా ప్రమాణ ఘనపరిమాణం గల ద్రవానికి ఉన్న పీడనశక్తి, గతిజశక్తి మరియు స్థితిశక్తుల మొత్తం స్థిరము. అనగా బెర్నౌలి సిద్ధాంతము నిరూపించబడినది.
బెర్నౌలీ సిద్ధాంతపు అనువర్తనాలు :

1. విమానపు రెక్కపై గల గతిక ఉత్థాపన బెర్నౌలీ సిద్ధాంతం ఆధారంగా ఏర్పడినదే.
2. స్పిన్తో చలించు క్రికెట్ బంతి స్వింగ్కు గల కారణము బెర్నౌలి సిద్ధాంతం.
3. తుఫానులలో ఇళ్ళకప్పులు పైకి ఎగురుట బెర్నౌలీ సిద్ధాంత ప్రభావమే.

ప్రశ్న 2.
స్నిగ్ధతా గుణకాన్ని నిర్వచించండి. స్టోక్స్ నియమాన్ని వివరించి, ఏ పరిస్థితులలో ఒక వర్షపు బిందువు చరమవేగం v₁ ని పొందుతుందో వివరించండి. v₂ కి సమీకరణాన్ని ఇవ్వండి.
జవాబు:
స్నిగ్ధతా గుణకము : ప్రవాహి దిశకు లంబంగా పొరల మధ్య ఏకాంక వేగ ప్రవణత ఉన్నప్పుడు ఏకాంక వైశాల్యం గల పొరల మీద పనిచేసే బలపరిమణాన్ని ఆ ద్రవం స్నిగ్ధతా గుణకం అంటారు.

చరమవేగానికి సమీకరణ:
స్ట్రోక్ సిద్ధాంతం ప్రకారము ప్రవాహి గుండా క్రిందికి పడుతున్న గోళంపై పనిచేసే నిరోధక బలం F గోళం వ్యాసార్ధము (a) ; ప్రవాహి స్నిగ్ధతా గుణకం (η) మరియు గోళం వేగం (v) కి అనులోమానుపాతంలో ఉంటుందని స్ట్రోక్ కనుగొన్నాడు.
∴ F ∝ ηav లేదా F = 6 π η av. ఇక్కడ 6π అనుపాత స్థిరాంకం. ఈ బలం ప్రవాహిలో గోళం బరువుకి సమానమయితే, అది v సమవేగంతో పోతుంది. ఇదే అంత్యవేగం.
∴ F = గోళం భారం – ప్రవాహిలో అది కోల్పోయే భారం = \(\frac{4}{3}\)πa³ρg – \(\frac{4}{3}\) 4πa³σg = \(\frac{4}{3}\)πa³ (ρ – σ) g
ఇక్కడ ρ, σ గోళం మరియు ప్రవాహి సాంద్రతలు.
∴ \(\frac{4}{3}\)πa³ (ρ – σ) g = 6π ηav;
అంత్యవేగము v = \(\frac{2}{9}\) a² \(\frac{(\rho-\sigma) g}{\eta}\)

లెక్కలు

ప్రశ్న 1.
0.6 సెం.మీ. వ్యాసం గల ఒక సబ్బు బుడగను ఊదేందుకు తలతన్యతా బలానికి వ్యతిరేకంగా చేయాల్సిన పనిని లెక్కించండి. (సబ్బు ద్రావణం తలతన్యత = 2.5 × 10^-2 Nm^-1)
సాధన:
జరిగిన పని = W = తలతన్యత (S) × వైశాల్యములోని పెరుగుదల (2 × 4πr)
∴ W = S (4πr²) × 2 (నీటి బుడగకు రెండు తలములు ఉండుట వలన)
= \(\frac{2.5}{100}\) × 4π × \(\left(\frac{0.3}{100}\right)^2\) × 2 = \(\frac{20 \pi \times 9}{10^8}=\frac{1.8 \pi}{10^6}\) = 5.65 × 10^-6 J.

ప్రశ్న 2.
0.06 సెం.మీ. వ్యాసం గల గాజు గొట్టంలో మిథైల్ ఆల్కహాల్ ఎంత ఎత్తుకు ఎగబాకుతుంది ? (మిథైల్ ఆల్కహాల్ తలతన్యత = 0.023 Nm^-1, సాంద్రత = 0.8 gmcm^-3. స్పర్శకోణాన్ని శూన్యంగా పరిగణించండి.)
సాధన:
మిథైల్ ఆల్కహాల్ తలతన్యత (S) = 0.023 N/m; సాంద్రత ρ = 0.8 gr/cm³ = 800 kg/m³
గొట్టపు వ్యాసము D = 0.06 cm
⇒ వ్యాసార్ధము r = 0.03 cm = \(\frac{0.03}{100}\) m
తలతన్యత S = \(\frac{\mathrm{h} \rho \mathrm{rg}}{2 \cos \theta}\) ; ఇక్కడ θ = 0°, cos 0° = 1; ρ = 0.8 g/cm³ = 800 kg/m³
∴ h = \(\frac{2 \mathrm{~S}}{\rho \mathrm{rg}}\) = \(\frac{2 \times 0.023}{800 \times \frac{0.03}{100} \times 9.8}\)
= \(\frac{2 \times 0.023}{0.24 \times 9.8}\) = 0.0196 m. = 1.96 cm.

ప్రశ్న 3.
నీటిలో ముంచిన కేశనాళం వ్యాసార్ధం ఎంత ఉంటే దానిలో నీరు 6 సెం.మీ. ఎత్తుకు ఎగబాకుతుంది ? (నీటి తలతన్యత = 7.2 × 10^-2 Nm^-1)
సాధన:
నీటి తలతన్యత, S = 7.2 × 10^-2 N/m; నీటి స్తంభము ఎత్తు, h= 6 cm = \(\frac{6}{100}\) m
కేశనాళిక వ్యాసార్ధము r = ? ; తలతన్యత S = \(\frac{\mathrm{h} \rho \mathrm{rg}}{2}\), ఇక్కడ ρ – నీటి సాంద్రత = 10³ kg/m³
7.2 × 10^-2 = \(\frac{6}{100} \times \frac{1000 \times r \times 10}{2}\) = 300 r
∴ r = \(\frac{7.2 \times 10^{-2}}{300}\) = 2.4 × 10^-4 m = 0.24 mm.

ప్రశ్న 4.
0.4 మి.మీ. వ్యాసం గల ఒక కేశనాళికను బీకరులో ఉన్న పాదరసంలో ముంచినప్పుడు, నాళంలోని ద్రవచంద్రరేఖాకృతి (meniscus) లో కలిగే నిమ్నతను లెక్కించండి. (పాదరసం సాంద్రత = 13.6 × 10^{3/sup>.గ్రా. మీ, పాదరసం తలతన్యత = 0.49 Nm-1స్పర్శకోణం = 135°)
సాధన:
గొట్టము వ్యాసము = 0.4 mm ;
∴ వ్యాసార్ధము, (r) = 0.2 mm = \(\frac{0.2}{10^3}\) m
పాదరసం సాంద్రత = 13.6 × 103 kg/m3 ;
స్పర్శకోణం, θ = 135° ; పాదరసం తలతన్యత, S = 0.49 N/m.}

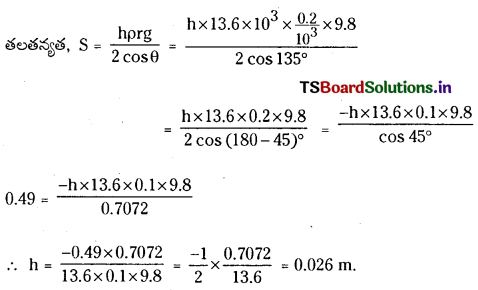
ప్రశ్న 5.
ఒక సబ్బు బుడగ వ్యాసం 10 మి.మీ. దాని తలతన్యత 0.04 Nm^-1. ఆ బుడగలోని అదనపు పీడనాన్ని కనుక్కోండి.
సాధన:
సబ్బు నీటి బుడగ వ్యాసం = 10 mm
∴ వ్యాసార్ధం, r = 5 mm = 5 × 10^-3m
తలతన్యత S = 0.04 Nm^-1
నీటి బుడగలోని అధికపీడనం P = \(\frac{4 \mathrm{~S}}{\mathrm{r}}\)
∴ P = \(\frac{4 \times 0.04}{5 \times 10^{-3}}=\frac{160}{5}\) = 32 Nm^-2 పాస్కల్

ప్రశ్న 6.
R వ్యాసార్ధం గల బుడగను రూపొందించేందుకు చేసిన పని W అయితే బుడగ వ్యాసార్ధం రెట్టింపు అయ్యేందుకు (2R అయ్యేందుకు) ఎంత శక్తి అవసరం ? (మార్చి 2014)
సాధన:
‘R’ వ్యాసార్ధము గల బుడగను ఊదుటలో జరిగిన పని W = 8πR²
2R వ్యాసార్ధము గల బుడగను ఊదుటకు జరిగిన పని W’ = 8π (2R)²(S) = 4 (8πR²S)
∴ W = 4W
∴ R నుండి 2R కు వ్యాసార్ధం పెంచుటలో జరిగిన పని
W’ – W = 4W – W = 3W

ప్రశ్న 7.
R₁, R₂ వ్యాసార్ధాలు గల రెండు సబ్బు బుడగలు శూన్యంలో సమోష్ణోగ్రతా ప్రక్రియ పరిస్థితిలో కలిసిపోయి, ఒక కొత్త బుడగను ఏర్పరచాయి. ఆ కొత్త బుడగ వ్యాసార్ధం ఎంత ? సబ్బు ద్రావణం తలతన్యతను T గా తీసుకోండి.
సాధన:
సమ ఉష్ణోగ్రత ప్రక్రియలో ఉష్ణోగ్రతలోని మార్పు సున్నా. కావున వ్యవస్థ అంతర్గత శక్తిలోని మార్పు సున్న.
మొదటి బుడగ తలశక్తి U₁ = 4πR₁²S ; రెండవ బుడగ తలశక్తి U₂ = 4πR₂²S
కొత్తగా ఏర్పడిన బుడగ తలశక్తి U = 4πR²S
కానీ 4πR²S = 4πR₁²S + 4πR₂²S
⇒ R² = R₁² + R₂²
కొత్త బుడగ వ్యాసార్ధం R = \(\sqrt{\mathrm{R}_1^2+\mathrm{R}_2^2}\)

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
ఎందుకో వివరించండి.
ఎ) మనిషి శరీరంలో పాదాల వద్ద రక్త పీడనం మెదడు వద్ద కంటే ఎక్కువ.
బి) భూమి నుంచి 100 కి.మీ. కంటే ఎక్కువగా వాతావరణం ఉన్నప్పటికీ 6కి.మీ. ఎత్తు వద్ద వాతావరణ పీడనం, సముద్రమట్టం వద్ద ఉండే వాతావరణ పీడనంలో సగం ఉంటుంది.
సి) బలాన్ని, వైశాల్యంతో భాగిస్తే వచ్చేదే పీడనం అయినప్పటికీ ఈ ద్రవస్థితిక పీడనం ఒక అదిశరాశి.
సాధన:
ఎ) మానవ శరీరంలోని రక్త స్తంభం ఎత్తు మెదడుతో పోల్చిన పాదాల వద్ద ఎక్కువ అందువల్ల రక్త పీడనము మెదడుతో పోల్చిన పాదాల వద్ద ఎక్కువ.
(∴ పీడనము = hρg)

బి) గాలి సాంద్రత భూమి ఉపరితలం మీద గరిష్టంగా వుంటుంది. మరియు ఎత్తుకు వెళుతున్నప్పుడు సాంద్రత త్వరితగతిన తగ్గుతూ ఉంటుంది. సుమారు 6 కి.మీ. ఎత్తు వద్ద సాంద్రత సముద్ర మట్టం వద్ద ఉండే సాంద్రతలో సగం ఉంటుంది. 6 కి.మీ. ఎత్తు మించిన తరువాత గాలి సాంద్రత ఎత్తుతో చాలా నెమ్మదిగా తగ్గుతుంది. ఈ కారణంగా 6 కి.మీ. ఎత్తు వద్ద వాతావరణ పీడనం, సముద్ర మట్టం వద్ద ఉంటే వాతావరణ పీడనంలో సగం
ఉంటుంది.

సి) ఏదైనా ద్రవంపై బలాన్ని ప్రయోగించినప్పుడు పీడనం ద్రవంలో అన్ని దిశలలోను సమానంగా పనిచేస్తుంది. అందువల్ల ద్రవాలలో పీడనానికి ఒక నిర్దిష్ట దిశ ఉండదు. కనుక ద్రవ స్థితిక పీడనం అదిశరాశి.

ప్రశ్న 2.
ఎందుకో వివరించండి.
ఎ) గాజుతో పాదరసం స్పర్శకోణం గురుకోణం కాని నీటితో లఘుకోణం.
బి) శుభ్రమైన గాజుపలక తలంపైన వేసిన నీరు దానిపై వ్యాపించడానికి ప్రయత్నిస్తుంది. కాని పాదరసం అయితే బిందువులుగా ఏర్పడటానికి ప్రయత్నిస్తుంది. (దీన్నే ఇంకో రకంగా చెప్పాలంటే, నీరు గాజును తడుపుతుంది. కాని పాదరసం గాజును తడపలేదు).
సి) ఒక ద్రవం తలతన్యత ఆ తలవైశాల్యంపై ఆధారపడి ఉండదు.
డి) డిటర్జంట్ కలిపిన నీరు తక్కువ స్పర్శకోణాలను కలిగి ఉంటుంది.
ఇ) బాహ్య బలాలకు లోనుకానటువంటి ద్రవబిందువు ఎప్పుడూ గోళాకారాన్నే కలిగి ఉంటుంది.
సాధన:
ఎ) ఒక ఘన వస్తువుపై అతి తక్కువ పరిమాణంలో ద్రవాన్ని పోసిన ద్రవం – ఘనం, ద్రవం-గాలి, ఘనం-గాలి అను మూడు రకాల అంతర్గత తలాలు ఏర్పడతాయి.
ఈ అంతర్గత తలాల తలతన్యతలు వరుసగా S_LA, S_SA, S_SL ద్రవం మరియు ఘనానికి మధ్య స్పర్శ కోణము ‘O’ అని అనుకొనుము. మూడు అంతర్గతా తలాలు కలుసుకున్న తలములో అణువులు సమతాస్థితిలో ఉండును. దీనివలన అణువులపై పనిచేసే మొత్తం బలం శూన్యము.
‘0’ వద్ద సమతాస్థితిలో వున్న అణువుకు
S_SL + S_LA cos θ = S_SA లేదా cos θ = \(\frac{\mathrm{S}_{\mathrm{SA}}-\mathrm{S}_{\mathrm{SL}}}{\mathrm{S}_{\mathrm{LA}}}\)
పాదరసం గాజు సందర్భములో S_SA < S_SL, అందువల్ల cos θ ఋణాత్మకము లేదా θ > 90° అనగా గురుకోణం. నీరు గాజు సందర్భంలో S_SA > S_SL అందువల్ల cos θ ధనాత్మకము లేదా θ < 90° అనగా లఘుకోణం.

బి) పాదరసం – గాజుల మధ్య స్పర్శకోణం గురుకోణం. ఇలాంటి గురుకోణం గల స్పర్శకోణం పొందాలి అంటే పాదరసం బిందువు వలె వుండాలి. నీరు – గాజు సందర్భంలో స్పర్శకోణం లఘుకోణం. ఇలాంటి లఘుకోణం పొందాలి అంటే నీరు వ్యాప్తి చెందాలి.

సి) సమతాస్థితిలో ఉన్న ఒక స్వేచ్ఛాతలంపై ఒక ఊహారేఖకు ఇరువైపులా రేఖకు లంబంగా ప్రమాణ పొడవుపై తలానికి స్పర్శీయంగా పనిచేసే బలాన్నే తలతన్యత అంటారు. ఈ బలం ద్రవ ఉపరితల వైశాల్యంపై ఆధారపడదు. అందువల్ల తలతన్యత కూడా ద్రవ ఉపరితల వైశాల్యంపై ఆధారపడదు.

డి) వస్త్రాలలో వుండే సన్నని ప్రదేశం కేశనాళికలవలె వుంటాయి. కేశనాళికలో ఎగబ్రాకే ద్రవం cos θ కి అనులోమానుపాతంలో ఉంటుంది. θ స్వల్పం అయిన cos θ హెచ్చుగా వుంటుంది. అందువల్ల కేశనాళికలో ఎగబ్రాకే ద్రవం ఎక్కువ. అందువల్ల వస్త్రాలను శుభ్రం చేయు పదార్థము (డిటర్జెంట్స్) వస్త్రం లోపలికి చొచ్చుకొని పోవును.

ఇ) బాహ్య బలాలు పనిచేయునప్పుడు ద్రవ ఉపరితలం తక్కువ ఉపరితల వైశాల్యం కలిగి ఉంటుంది. నిర్ణీత ఘనపరిమాణం గల అనేక ఆకృతులలో గోళం ఉపరితలం వైశాల్యం కనిష్టం కావున ద్రవ బిందువు గోళాకారాన్ని పొందుతుంది.

ప్రశ్న 3.
ప్రతి వాక్యానికి అనుబంధంగా ఇచ్చిన పదాలతో ఖాళీలను పూరించండి.
ఎ) ద్రవాల తలతన్యత ఉష్ణోగ్రతతో పాటు సాధారణంగా …. (పెరుగుతుంది / తగ్గుతుంది)
బి) వాయువుల స్నిగ్ధత ఉష్ణోగ్రతతో పాటు …… అదే ద్రవాల స్నిగ్ధత ఉష్ణోగ్రతతో పాటు …. (పెరుగుతుంది / తగ్గుతుంది)
సి) స్థితిస్థాపక ద్రుఢతా గుణకమున్న ఘనపదార్థాల విషయంలో విరూపణ బలం …. కు అనులోమానుపాతంలో ఉంటే ప్రవాహులకు ….. కు అనులోమానుపాతంలో ఉంటుంది. (విరూపణ వికృతి / విరూపణ వికృతి రేటు)
డి) నిలకడ ప్రవాహి ప్రవాహంలో నొక్కు (ఇరుకైన) ప్రాంతంలో ప్రవాహి వడి పెరుగుతుందనేది … అనుసరించి (ద్రవ్యరాశి నిత్యత్వం / బెర్నౌలీ సూత్రం)
ఇ) వాయు సొరంగం (wind tunnel) లో దూసుకుపోతున్న నమూనా విమానానికి సంక్షోభం ఉత్పన్నమయ్యే వేగం, వాస్తవ పరిస్థితులలో ఎగిరే నిజమైన విమానానికి సంక్షోభం ఉత్పన్నమయ్యే వేగం కంటే (ఎక్కువ/ తక్కువ).
సాధన:
ఎ) తగ్గుతుంది
బి) పెరుగుతుంది, తగ్గుతుంది
సి) విరూపణ వికృతి, విరూపణ వికృతిరేటు
డి) ద్రవ్యరాశి నిత్యత్వ నియమం, బెర్నౌలీ సూత్రం
ఇ) ఎక్కువ

ప్రశ్న 4.
ఎందుకో వివరించండి.
ఎ) ఒక కాగితాన్ని క్షితిజ సమాంతరంగా ఉంచేందుకు నీవు గాలిని దాని కింద నుంచి కాక దానిపైన ఊదాలి.
బి) ఒక కుళాయిని కట్టివేసేందుకు దాని మూతిని వేళ్లతో మూయడానికి ప్రయత్నిస్తే మన వేళ్ల మధ్య ఉన్న ఖాళీల నుంచి నీరు వేగంగా బయటకు చిమ్ముకొస్తుంది.
సి) ఒక డాక్టరు ఇంజక్షన్ ఇస్తున్నప్పుడు అతడు తన బొటనవేలితో సిరంజిపై ప్రయోగించిన పీడనం కంటే ఆ సిరంజి సూది పరిమాణమే (size) మందు ప్రవాహరేటును అదికంగా ప్రభావితం చేస్తుంది.
డి) పాత్రకు ముందువైపున్న ఒక చిన్న రంధ్రం ద్వారా ప్రవాహి వెలుపలికి ప్రవహించేటప్పుడు పాత్రపై ఒక అభిబలం వెనకకు పనిచేస్తుంది.
ఇ) ఆత్మభ్రమణం చెందే క్రికెట్ బంతి గాలిలో పరావలయ పథాన్ని అనుసరించదు.
సాధన:
ఎ) గాలిని గట్టిగా కాగితంపైన ఊదినప్పుడు, ఊదిన గాలియొక్క వేగం పెరుగుతుంది. అందువల్ల బెర్నౌలీ సిద్ధాంతము ప్రకారం దానిమీద పనిచేసే పీడనం తగ్గుతుంది. కాగితం క్రింద గాలిపీడనం వాతావరణ పీడనంకు సమానం. అందువల్ల కాగితం క్షితిజ సమాంతరంగా వుంటుంది.

బి) కుళాయి మూతిని వేళ్ళతో మూయడానికి ప్రయత్నించినపుడు కుళాయి మూతి వైశాల్యం తగ్గుతుంది. సాంతత్య సమీకరణం ప్రకారం, av = స్థిరం కావున నీటి వేగం పెరుగుతుంది.

సి) సిరంజి సూది పరిమాణం ప్రవాహి వేగాన్ని అదుపుచేస్తుంది. మరియు బ్రొటనవేలితో ప్రయోగించిన పీడనం పీడనాన్ని అదుపు చేస్తుంది. బెర్నౌలీ సిద్ధాంతము ప్రకారం
P + ρ gh + \(\frac{1}{2}\) ρ v² = a ఒక స్థిరాంకము
ఇచ్చట ‘p’ ఘాతము ‘1’ (ఒకటి) ‘v’ ఘాతం ‘2’ (రెండు) అందువలన వేగం ప్రభావం ఎక్కువ. అందువలన సిరంజి సూది పరిమాణమే మందు ప్రవాహ రేటును అధికంగా ప్రభావితం చేస్తుంది.

డి) పాత్రకు ముందువైపున్న ఒక చిన్న రంధ్రం ద్వారా ప్రవాహి వెలుపలికి ప్రవహిస్తున్న, ఆ ప్రవాహం అధికవేగమును కల్గియుంటుంది. దీనివలన ప్రవాహి ద్రవ్యవేగం అధికంగా ఉంటుంది. వ్యవస్థపై ఏ విధమైన బాహ్య బలాలు పని చేయనప్పుడు, ద్రవ్య వేగ నిత్యత్వ నియమము ప్రకారము పాత్ర తిరోగమన (వెనుకకు) వేగాన్ని పొందుతుంది. దీని ఫలితంగా పాత్రపై ఒక అభిబలం వెనుకకు పనిచేస్తుంది.

ఇ) ఆత్మ భ్రమణం చెందే క్రికెట్ బంతి మాగ్నసే ప్రభావము వలన దాని మార్గాన్ని మార్చుకొంటుంది. ఆత్మ భ్రమణం వలన బంతిపై కలిగే గతిక ఉత్థాపకాన్ని మాగ్నస్ ప్రభావం అంటారు.

ప్రశ్న 5.
ఎత్తైన మడిమలుండే చెప్పులను ధరించిన 50 kg ల ద్రవ్యరాశి గల ఒక అమ్మాయి ఒంటికాలిపై తనను తాను నిలబెట్టుకుంది. చెప్పు మడిమ 1.0 cm వ్యాసంతో వృత్తాకారంగా ఉంది. క్షితిజ సమాంతర నేలపై చెప్పుకలగచేసే పీడనం ఎంత ?
సాధన:
దత్తాంశము ప్రకారము అమ్మాయి ద్రవ్యరాశి, m = 50 kg ;
చెప్పు మడిమ వ్యాసార్ధము, r = D/2 = 1/2 cm = \(\frac{1}{200}\) m

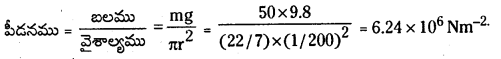
ప్రశ్న 6.
టోరిచెల్లీ బారోమీటర్లో పాదరసాన్ని ఉపయోగించాడు. పాస్కల్ 984 kg m 3. సాంద్రత గల ఫ్రెంచి సారాయి (wine) తో టోరిచెల్లీ బారోమీటర్ను పోలి ఉండేటట్లు మరొక బారోమీటర్ను తయారుచేశాడు. సాధారణ వాతావరణ పీడనాన్ని సూచించే ద్రాక్ష సారాయి స్తంభం ఎత్తు ఎంత ?
సాధన:
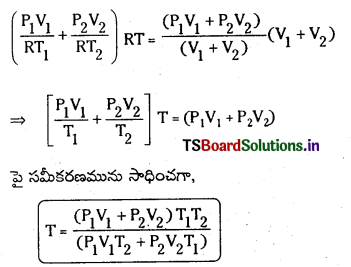
P = 0.76 × (13.6 × 10³) × 9.8 = h × 984 × 9.8
(లేదా) h = \(\frac{0.76 \times 13.6 \times 10^3 \times 9.8}{984 \times 9.8}\) = 10.5 m.

ప్రశ్న 7.
సముద్రతీర ప్రాంతంలో 10⁹ Pa పీడనాన్ని తట్టుకోగల ఒక నిలువైన నిర్మాణాన్ని రూపొందించారు. సముద్రంలోని ఒక చమురు బావి శిఖర భాగంలో ఉంచడానికి ఈ నిర్మాణం అనువైనదేనా ? సముద్రం లోతు దాదాపు 3 km అనుకోండి. సముద్ర ప్రవాహాలను ఉపేక్షించండి.
సాధన:
గరిష్ఠ ప్రతిబలం = 10⁹ Pa,
h = 3 km = 3 × 10³ m;
ρ (నీరు) = 10³ kg/m³ మరియు g = 9.8 m/s².
రూపొందించిన విలువైన నిర్మాణాన్ని చమురు బావి శిఖర భాగంలో ఉంచటానికి అనువైనది. సముద్రపు నీరు ప్రయోగించు పీడనం కన్నా, నిర్మాణం గరిష్ఠ ప్రతిబలం చాలా ఎక్కువ. అందువల్ల సముద్రపు అలల పీడనాన్ని భరిస్తుంది. సముద్రపు నీటి పీడనం
P = hρg = 3 × 10³ × 10³ × 9.8 = 2.94 × 10⁷ Pa
అందువల్ల సముద్రపు నీటి పీడనం, ఇచ్చిన నిర్మాణం ప్రతిబలం 10⁹ Pa కన్నా తక్కువ. అందువల్ల రూపొందించిన విలువైన నిర్మాణము చమురు బావి ఉపరితలంపైన వుంచుటకు సరియైనది.

ప్రశ్న 8.
గరిష్ఠంగా 3000 kg ద్రవ్యరాశి గల కార్లను ఎత్తగల హైడ్రాలిక్ లిఫ్ట్ను తయారుచేశారు. బరువులను ఎత్తే ముషలకం మధ్యచ్ఛేద వైశాల్యం 425 cm3 అయితే చిన్న ముషలకం భరించగల గరిష్ఠ పీడనం ఎంత ?
సాధన:
పెద్ద ముషలకము భరించగల గరిష్ఠ బలం,
F = 3000 kgf = 3000 × 9.8 N
ముషలకము వైశాల్యం A = 425 cm² = 425 × 10⁴ m²
∴ పెద్ద ముషలకముపై పనిచేసే గరిష్ఠ పీడనం,
P = \(\frac{F}{A}=\frac{3000 \times 9.8}{425 \times 10^{-4}}\) = 6.92 × 10⁵ Pa
ద్రవం, పీడనాన్ని అన్నివైపుల సమానంగా సరఫరా చేస్తుంది. కావున, చిన్న ముషలకము భరించు గరిష్ఠ పీడనం 6.92 × 10⁵ Pa.

ప్రశ్న 9.
U- ఆకార గొట్టంలో పాదరసంతో వేరుచేసిన నీరు, మిథిలేటెడ్ స్పిరిట్ ధ్రవస్తంభాలు ఇరువైపులా ఉన్నాయి. నీటి మట్టం 10.0 cm, స్పిరిట్ మట్టం ఎత్తు 12.5 cm ఉండే విధంగా రెండు భుజాల్లో పాదరస మట్టం ఉంది. స్పిరిట్ విశిష్ట గురుత్వం ఎంత ?
సాధన:
U గొట్టంలోని ఒక భుజంలో నీటి స్తంభం ఎత్తు
h₁ = 10.0 cm ; ρ₁ (సాంద్రత) = 1 g cm^-3
Uగొట్టంలోని వేరొక భుజంలో గల స్పిరిట్ స్తంభం
ఎత్తు h₂= 12.5cm ; ρ₂ = ?
Uగొట్టంలోని రెండు భుజాలలోని పాదరస మట్టాలు సమానం అయిన, పీడనం సమానము. అందువల్ల
h₁ρ₁g = h₂ρ₂g
(లేదా) ρ₂ = \(\frac{\mathrm{h}_1 \rho_1}{\mathrm{~h}_2}=\frac{10 \times 1}{12.5}\) = 0.8g.cm^-3
స్పిరిట్ సాపేక్ష సాంద్రత = ρ₂/ ρ₁ = 0.8 /1 = 0.8

ప్రశ్న 10.
ఇంతకుముందు లెక్కలోని గొట్టంలోని సంబంధిత భుజాల్లో 15.0 cm మట్టం పెరిగే విధంగా నీరు, స్పిరిట్లను అదనంగా కలిపితే, రెండు భుజాల్లోని పాదరస మట్టాలలోని వ్యత్యాసం ఎంత ? (పాదరసం విశిష్ఠ గురుత్వం = 13.6)
సాధన:
U గొట్టంలోని రెండు భుజాలలో 15 సెం.మీ. నీరు మరియు స్పిరిట్ను వరుసగా నింపవలెను. స్పిరిట్ గల భుజంలోని పాదరస మట్టం పెరుగును.
‘U’ గొట్టంలోని రెండు భుజములలో గల పాదరస మట్టం ఎత్తులో గల భేదం ‘h’ మరియు ‘p’ అనునది పాదరసం సాంద్రత.
∴ ‘h’ ఎత్తు గల పాదరస స్తంభం కలుగచేయు పీడనం = నీరు మరియు స్పిరిట్ కలుగచేయు పీడనం వ్యత్యాసం.
∴ h ρ g = h₁ ρ₁ g₁ – h₁ ρ₂ g₂
ఇచ్చట h = ? ; ρ = 13.6gcm^-3 ; h₁ = 15 + 10 = 25 cm;
ρ₁ = 1 g cm^-3
h₂ = 15 + 12.5 = 27.5 cm; ρ₂ = 0.8 g cm^-3
పై విలువలను సమీకరణంలో ప్రతిక్షేపించగా
h × 13.6 × g = 25 × 1 × g – 27.5 × 0.8 × g = 3g
(లేదా) h = 3/13.6 = 0.22 cm

ప్రశ్న 11.
నదిలో నీటి ప్రవాహం ఉధృతంగా ఉన్న ప్రాంతంలో ఆ నీటి ప్రవాహాన్ని వర్ణించేందుకు బెర్నౌలీ సమీకరణాన్ని ఉపయోగించవచ్చా ? వివరించండి.
సాధన:
ధారారేఖ ప్రవాహిలకు మాత్రమే బెర్నౌలీ సిద్ధాంతము ఉపయోగపడును. కావున నదిలో నీటి ప్రవాహం ఉదృతంగా ఉన్న ప్రాంతంలో ఆ నీటి ప్రవాహాన్ని వర్ణించేందుకు బెర్నౌలీ సమీకరణం ఉపయోగించలేము.

ప్రశ్న 12.
బెర్నౌలీ సమీకరణాన్ని అనువర్తించేటప్పుడు పరమ పీడనానికి బదులు గేజ్ పీడనాన్ని ఉపయోగిస్తే ఏదైనా ప్రభావం ఉంటుందా ?
సాధన:
ఉండదు. బెర్నౌలీ సూత్రం అనువర్తించే రెండు బిందువుల వద్ద ఉన్న వాతావరణ పీడనాలలో చెప్పుకోదగ్గ వ్యత్యాసం ఉన్నప్పుడే గేజ్ పీడనం ప్రభావం ఉంటుంది.

ప్రశ్న 13.
1.5 m పొడవు, 1.0 cm వ్యాసార్ధం గల ఒక క్షితిజ సమాంతర గొట్టం ద్వారా గ్లిజరిన్ నిలకడగా ప్రవహిస్తున్నది. గొట్టం ఒక చివర ఒక సెకన్ కాలంలో సేకరించిన గ్లిజరిన్ పరిమాణం 4.0 × 10^-3 kgs^-1 అయితే గొట్టం రెండు చివరల మధ్య ఉండే పీడన వ్యత్యాసం ఎంత ? (గ్లిజరిన్ సాంద్రత = 1.3 × 10³ kg m^-3, గ్లిజరిన్ స్నిగ్ధత = 0.83 Pa s). (గొట్టంలోని ప్రవాహం స్తరీయం అనే మీ ఊహ సరైందా ? లేదా ? అని పరీక్షించడంలో మీరు ఆసక్తి కనబరచవచ్చు.)
సాధన:
ఇచ్చట l = 1.5 m ; r = 1.0 cm = 10^-2m;
ρ = 1.3 × 10³kg/m³ ; η = 0.83 Ns m^-2
ఒక సెకను కాలంలో ప్రవహించు గ్లిజరిన్ ద్రవ్యరాశి
M = 4 × 10^-3 kg/s
ఒక సెకను కాలంలో ప్రవహించు గ్లిజరిన్ ఘనపరిమాణం
V = \(\frac{\mathrm{M}}{\rho}=\frac{4 \times 10^{-3}}{1.3 \times 10^3}\) m³s^-1
గొట్టం రెండు చివరల మధ్య గల పీడనం తేడా ρ అయితే పాజ్వేజ్ సూత్రము ప్రకారము
V = \(\frac{\pi \mathrm{pr}^4}{8 \eta l}\) (లేదా) P = \(\frac{\mathrm{V} \times 8 \eta l}{\pi \mathrm{r}^4}\)
∴ p = \(\left(\frac{4 \times 10^{-3}}{1.3 \times 10^3}\right) \times \frac{8 \times 0.83 \times 1.5}{3.142 \times\left(10^{-2}\right)^4}\) = 975.37 Pa

ప్రశ్న 14.
ఒక వాయు సొరంగంలో నమూనా విమానాన్ని పరీక్షించే ప్రయోగంలో విమాన రెక్కల పైతలం, క్రింది తలంపై ప్రవాహ వడులు వరుసగా 70 ms^-1, 63 ms^-1. విమాన రెక్క వైశాల్యం 2.5 m² అయితే దానిపై పనిచేసే ఉత్థాపక బలాన్ని లెక్కగట్టండి. గాలి సాంద్రతను 1.3 kg m^-3 గా తీసుకోండి.
సాధన:
విమానం రెక్కల పై తలం మరియు క్రింద తలం వద్ద వేగాలు వరుసగా v₁, v₂ అని మరియు పీడనాలను P₁, P₂ అని అనుకొనుము.
v₁ = 70 ms^-1; v₂ = 63 ms^-1, ρ = 1.3 kg m^-1.
బెర్నౌలీ సిద్ధాంతము ప్రకారము

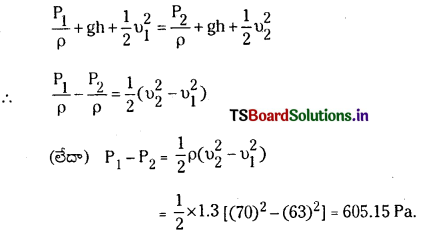
ఈ పీడనంలో వ్యత్యాసము విమానముపై ఉత్థాపక బలాన్ని కలుగచేస్తుంది.
విమానంపై పనిచేసే ఉత్థాపక బలం = పీడనంలో తేడా × రెక్కల వైశాల్యము
= 605.15 × 2.5
= 1512.875 N
= 1.51 × 10³ N

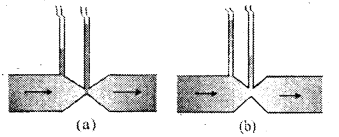
ప్రశ్న 15.
పటాలు (ఎ), (బి) లు స్నిగ్ధతారహిత ద్రవం నిలకడ ప్రవాహాన్ని సూచిస్తున్నాయి. అప్పుడు ఈ రెండు పటాల్లో ఏది సరైంది కాదు ? ఎందువల్ల?

సాధన:
పటం సరియైనది కాదు.
సాంతత్య సమీకరణం ప్రకారం av = a స్థిరం. గొట్టం అడ్డుకోత వైశాల్యం ఎక్కడ తక్కువగా ఉంటుందో అక్కడ ప్రవహించు ప్రవాహి వేగం ఎక్కువ.
గొట్టంలో మిగిలిన భాగంలో గల ప్రవాహి వేగం కన్నా సన్నని భాగంలో ప్రవాహి వేగం ఎక్కువ.
బెర్నౌలీ సిద్ధాంతము ప్రకారం, P + \(\frac{1}{2}\) ρ v² = 9 స్థిరం, ఎక్కడ వేగం ఎక్కువగా ఉంటుందో అక్కడ P పీడనం తక్కువ.
అదే విధంగా P ఎక్కువగా ఉంటుందో అక్కడ వేగం U తక్కువ.

ప్రశ్న 16.
ఒక స్ప్రే పంప్ స్తూపాకార గొట్టం మధ్యచ్ఛేద వైశాల్యం 8.0cm². దాని ఒక చివర 1.0 mm వ్యాసం గల సూక్ష్మ రంధ్రాలు 40 ఉన్నాయి. గొట్టంలో ద్రవం ప్రవాహం వడి 1.5 m min^-1 అయితే రంధ్రాల నుంచి విరజిమ్మే ద్రవం వడి ఎంత ?
సాధన:
గొట్టం అడ్డుకోత వైశాల్యం
a₁ = 8.0 cm² = 8 × 10^-4m²,
రంధ్రముల సంఖ్య = 40 ;
ఒక్కొక్క రంధ్రం వ్యాసం, D = 1.0 mm = 1.0 × 10^-3 m
∴ రంధ్రం వ్యాసార్ధం, r = \(\frac{D}{2}\) = \(\frac{1}{2}\) × 10^-3 m = 5 × 10^-4 m
ఒక్కొక్క రంధ్రం అడ్డుకోత వైశాల్యం = πr² = π(5 × 10^-4)² m²
40 రంధ్రముల మొత్తం అడ్డుకోత వైశాల్యం a₂ = 40 × π (5 × 10^-4)² m²
గొట్టం లోపల ద్రవం వేగం v₁ = 1.5 m/min = \(\frac{1.5}{60}\) ms^-1
v₂ అనునది రంధ్రం నుంచి విరజిమ్మే ద్రవం వేగం అయితే
a₁ v₁ = a₂ v₂ (లేదా) v₂ = a₁ v₁/a₂
∴ v₂ = \(\frac{\left(8 \times 10^{-4}\right) \times 1.5}{60 \times 40 \times \pi \times\left(5 \times 10^{-4}\right)^2}\) = 0.637 ms^-1

ప్రశ్న 17.
ఒక U-ఆకార తీగను సబ్బు ద్రావణంలో ముంచి తీస్తే తీగకు, తీగపై జారే మరొక తీగకు మధ్య ఒక సబ్బు పొర్ల ఏర్పడుతుంది. U-ఆకారం తీగకు దానిపై జారుతున్న తేలికైన తీగకు మధ్య ఏర్పడిన పలుచని సబ్బుపొర 1.5 × 10^-2 N(జారుడు తీగ స్వల్ప భారం కూడా ఇందులో కలిసి ఉంది). భారాన్ని మోయగలుగుతుంది. జారుడు తీగ పొడవు 30 cm. పొర తలతన్యత ఎంత ?
సాధన:
సబ్బు పొరకి రెండు ఉపరితలాలు వుంటాయి. కావున పల్చని పొర మొత్తం పొడవు = 2 l = 2 × 30 = 60 cm = 0.6 m. తలతన్యత వలన జారుడు తీగపై పనిచేసే బలము
F = S × 2l = S × 0.6 N.
సమతాస్థితి స్థానము వద్ద తలతన్యత వలన జారుడు తీగపై పనిచేస్తే బలము, భారం (mg) కు సమానంగా ఉంటుంది. (=1.5 × 10^-2 N)
F = 1.5 × 10^-2 = S × 0.6 N (లేదా)
S = \(\frac{1.5 \times 10^{-2}}{0.6}\) = 2.5 × 10^-2 Nm^-2.

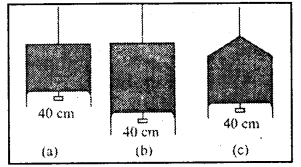
ప్రశ్న 18.
పటంలో చూపించిన ద్రవపొర 4.5 × 10^-2 N. స్వల్ప భారాన్ని మోయగలదు. పటం (b), (c) లలో చూపించిన పొరలు అదే ద్రవంతో ఏర్పడి అంతే ఉష్ణోగ్రత వద్ద ఉన్నట్లయితే ఆ పొరలు భరించగలిగే భారం ఎంతో తెలపండి. భౌతికశాస్త్ర నియమాలను అనుసరించి మీ జవాబును వివరించండి.

సాధన:
స్వల్ప భారాన్ని మోయగల ద్రవ పొర పొడవు = 40 cm = 0.4 m.
మొత్తం బరువు = 4.5 × 10^-2 N
పల్చని పొర రెండు ఉపరితలాలను కల్గియుంటుంది.
∴ తలతన్యత, S = \(\frac{4.5 \times 10^{-2}}{2 \times 0.4}\) = 5.625 × 10^-2 Nm^-1.
(a), (b) మరియు (c) అన్ని సందర్భాలలో ద్రవం ఒకటే మరియు ఉష్ణోగ్రత కూడా సమానం కావున
(b) మరియు (c) సందర్భాలలో తలతన్యత సమానం. ఇది 5.625 × 10^-2 Nm^-1 కు సమానం. పటంలో (a) లో వలె (b) మరియు (c) పటాలలో స్వల్ప భారాన్ని మోయగల ద్రవ పొర పొడవులు సమానం.
ప్రతి సందర్భంలో పొరలు భరించగలిగే భారం 4.5 × 10^-2 N.

ప్రశ్న 19.
గది ఉష్ణోగ్రత వద్ద ఉన్న 3.00mm వ్యాసార్ధం గల పాదరస బిందువు లోపల ఉండే పీడనం ఎంత ?ఆ ఉష్ణోగ్రత (20° C) వద్ద పాదరసం తలతన్యత 4.65 × 10 N m^-1. వాతావరణ పీడనం 1.01 × 10⁵ Pa. పాదరస బిందువు లోపల ఉండే అదనపు పీడనం విలువను కూడా తెలుపండి.
సాధన:
ఇచ్చట r = 3.0 mm = 3 × 10³m; S = 4.65 × 10^-1 Nm^-1; P = 1.01 × 10⁵ Pa
పాదరస బిందువు లోపల ఉండే అదనపు పీడనం, P = \(\frac{2 S}{r}\) = \(\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}}\) = 310 Pa
బిందువు లోపల మొత్తం అదనపు పీడనం = P + p = 1.01 × 10⁵ + 310 = 1,0131 × 10⁵ Pa

ప్రశ్న 20.
గది ఉష్ణోగ్రత (20° C) వద్ద సబ్బు ద్రావణం తలతన్యత 2.50 × 10^-2 Nm^-1 అని ఇచ్చినప్పుడు, 5.00 mm వ్యాసార్ధం గల సబ్బు ద్రావణపు బుడగ లోపల ఉండే అదనపు పీడనాన్ని లెక్కించండి. అంతే పరిమాణం లేదా అవే కొలతలున్న ఒక గాలి బుడగ ఒక పాత్రలో ఉన్న సబ్బు ద్రావణంలో 40.0 cm లోతున ఉంటే, ఆ బుడగ అంతర్భాగంలోని అదనపు పీడనం ఎంత ? సబ్బు ద్రావణం సాపేక్ష సాంద్రత = 1.20. ఒక వాతావరణ పీడనం – 1.01 × 10⁵ Pa.
సాధన:
ఇచ్చట S = 2.5 × 10^-2 Nm^-1,
r = 5.00 mm = 5 × 10^-3 m,
సబ్బు ద్రావణం సాంద్రత, ρ = 1.2 × 10³ kg m^-3
సబ్బు బుడగ లోపల గల అధిక పీడనం P = \(\frac{4 \mathrm{~S}}{\mathrm{r}}=\frac{4 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}\) = 20 Pa
గాలి బుడగ లోపల గల అధిక పీడనం P¹ = \(\frac{2 \mathrm{~S}}{\mathrm{r}}=\frac{4 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}\) = 10 Pa
సబ్బు ద్రావణంలో ‘h’ లోతులో ఉన్న గాలి బుడగలో మొత్తం పీడనం
= P¹ + వాతావరణ పీడనం + h ρ g
= 10 + 1.01 × 10⁵ + 0.4 × 1.2 × 10³ × 9.8 = 1.06 × 10⁵ Pa

ప్రశ్న 21.
ఒక టాంక్ అడుగు భాగం చతురస్రాకారంలో ఉంది. ఆ అడుగు భాగం లేదా ఆధారం వైశాల్యం 1.0 m²;. ఈ టాంక్ మధ్యలో ఒక నిట్టనిలువు గోడను నిర్మించి దాన్ని రెండు సమాన భాగాలుగా విభజించారు. ఈ గోడ అడుగున మడతబందు సహాయంతో తిరిగే 20 cm² వైశాల్యం గల చిన్న ద్వారం ఉంది. రెండు అర్ధభాగాల్లో ఒకదానిలో నీరు మరొక దానిలో ఆమ్లం (సాపేక్ష సాంద్రత 1.7) లతో 4.0m ఎత్తు వరకు నింపారు. ఆ ద్వారాన్ని మూసి ఉంచేందుకు అవసరమయ్యే బలాన్ని లెక్కించండి.
సాధన:

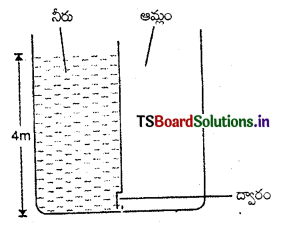
నీటిని కల్గియున్న భాగమునకు,
h₁ = 4m, ρ₁= 10³ kg m³.
టాంక్ అడుగు భాగాన గల ద్వారంపై నీటి వలన కలిగే పీడనం
P₁ = h₁ ρ₁ g = 4 × 10³ × 9.8 = 3.92 × 10⁴ Pa
ఆమ్లంను కల్గియున్న భాగమునకు,
h₂ = 4m,
P₂ = 1.7 × 10³ kg/m³
టాంక్ అడుగు భాగాన గల ద్వారంపై ఆమ్లం వలన కలిగే పీడనం,
P₂ = h₂ρ₂g = 4 × 1.7 × 10³ × 9.8 = 6.664 × 10⁴ Pa
∴ పీడనములోని తేడా = P₂ – P₁
= 6.664 × 10⁴ – 3.92 × 10⁴ = 2.774 × 10⁴ Pa
ద్వారం వైశాల్యం, A = 20 cm⁴ = 20 × 10^-4 m²
ద్వారంపై పనిచేసే బలం = పీడనములోని తేడా × వైశాల్యం
= (P₂ – P₁) × A = (2.774 × 10⁴) (20 × 10^-4) = 54.88 N ≃ 55 N
ద్వారంను మూసి ఉంచేందుకు 55 N బలాన్ని, ద్వారంపై క్షితిజ సమాంతరముగా నీటిని కల్గియున్న భాగము వైపు నుండి ఆమ్లం కలిగియున్న భాగంవైపుకు అనువర్తించవలెను.

ప్రశ్న 22.
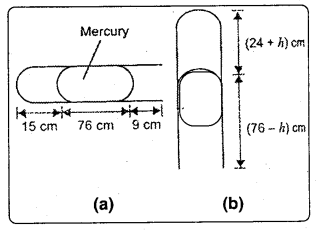
ఒక పాత్రలో బంధితమై ఉన్న వాయువు పీడనాన్ని ఒక మానోమీటర్ పటంలో చూపించిన విధంగా రీడింగ్ చూపిస్తుంది. పాత్రలోని కొంత వాయువును ఒక పంపు ద్వారా తొలగిస్తే ఉండే మానోమీటర్ రీడింగ్ను పటం (b) సూచిస్తుంది. మానోమీటర్లో ఉపయోగించిన ద్రవం పాదరసం అయి, వాతావరణ పీడనం 76 cm ల పాదరస స్తంభం ఎత్తుకు సమానమైతే,
ఎ) పటం (a) పటం (b) సూచించిన రెండు సందర్భాలలోను పాత్రలోని వాయు పరమ పీడనాన్ని, గేజ్ పీడనాన్ని పాదరస cm ప్రమాణాలలో తెలపండి.
బి) రెండో సందర్భంలో, అంటే పటం (b) లోని మానోమీటర్ కుడి భుజంలో 13.6 cm ఎత్తు పెరిగే విధంగా నీటిని (నీరు, పాదరసం కలవవు) నింపితే, మానోమీటర్ మట్టాలు ఏ విధంగా మారతాయి ? (వాయువు ఘనపరిమాణంలో వచ్చే స్వల్ప మార్పులను ఉపేక్షించండి.)

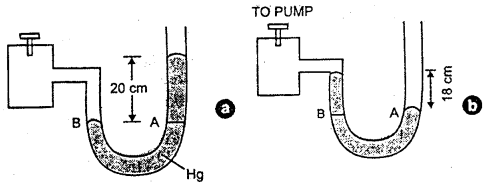
సాధన:
1) వాతావరణ పీడనం, P = 76 cm పాదరసం పటం
(a) లో పీడన శీర్షం, h = + 20 cm ల పాదరసం
∴ పరమ పీడనం, P + h = 76 + 20 = 96 cm ల పాదరసం
గేజ్ పీడనం = h = 20 cm ల పాదరసం
పటం (b) లో పీడన శీర్షం, h = -18 cm ల పాదరసం
పరమ పీడనం = P + h = 76 + (-18) = 58 cm ల పాదరసం
గేజ్ పీడనం = h = -18 cm ల పాదరసం

2) మానోమీటర్ కుడి భుజంలో 13.6 cm ఎత్తు పెరిగే విధముగా నీటిని నింపితే, అది \(\frac{13.6}{13.6}\) = 1 cm పాదరస స్తంభానికి సమానం.
ఇప్పుడు A వద్ద పీడనం, P_A = P + h’ = 76 + 1 = 77 cm ల పాదరసం
మానోమీటర్ రెండు భుజములలో పాదరస మట్టంలోని తేడా h₁ అని అనుకొనిన B వద్ద పీడనం
P_B = 58 + h₁ As, P_A = P_B
∴ 77 = 58 + h₁ (లేదా) h= 77 – 58 = 19 cm ల పాదరసం

ప్రశ్న 23.
విభిన్న ఆకారాల్లో ఉండే రెండు పాత్రల ఆధార వైశాల్యాలు సమానం. రెండు పాత్రల్లోను ఒక నిర్ణీత సమాన ఎత్తు వరకు నీటిని నింపాలంటే మొదటి పాత్ర తీసుకొనే నీటి ఘనపరిమాణం రెండో పాత్ర తీసుకొనే నీటి ఘనపరిమాణానికి రెట్టింపు. అయితే నీరు పాత్ర ఆధారంపై ప్రయోగించే బలం రెండు సందర్భాల్లోను సమానంగానే ఉంటుందా ? ఒకవేళ అలా సమానమైతే, సమాన మట్టాల వరకు నీటితో నింపిన ఆ పాత్రలు బరువు తూచే పరికరంపై రెండు వేరు వేరు రీడింగులను ఎందుకు చూపిస్తాయి ?
సాధన:
పీడనం, నీటి స్తంభము ఎత్తు మీద ఆధారపడి ఉంటుంది.

విభిన్న ఆకారాల్లో ఉన్న రెండు పాత్రలలో నీటి మట్టాలు ఒకే ఎత్తులో ఉన్నాయి కావున పాత్రల అడుగు భాగంపై పనిచేసే పీడనం సమానంగా ఉంటుంది. పాత్రల ఆధార వైశాల్యాలు సమానం కావున నీటి పీడనం వలన రెండు పాత్రల అడుగు భాగంపై పనిచేసే బలాలు సమానంగా ఉంటాయి. పాత్ర గోడల మీద కూడ నీరు బలాన్ని ప్రయోగిస్తుంది. ఒకవేళ పాత్రల గోడలు, పాత్ర అడుగు భాగానికి లంబంగా లేకపోతే పాత్ర గోడల మీద పనిచేసే నీరు శూన్యంకాని నిలువు అంశలను కల్గియుంటుంది. ఇది మొదట పాత్రలో ఎక్కువ, రెండవ పాత్రలో తక్కువ. అందువలన రెండు పాత్రలలో నింపిన నీటిని నిలువు ఎత్తు సమానంగా ఉన్నప్పటికి బరువు తూచే పరికరం వేరు వేరు పరిశీలనలను చూపుతుంది.

ప్రశ్న 24.
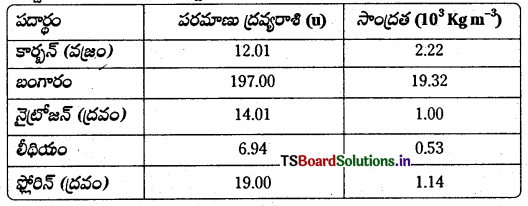
రక్త మార్పిడి చేస్తున్నప్పుడు సూదిని సిరలోకి (రక్తనాళంలోకి గుచ్చారు. అక్కడ గేజ్ పీడనం 2000 పాస్కల్, అప్పుడు ఈ సిరలోకి రక్తం ఎక్కాలంటే రక్తం ఉండే సీసాను ఎంత ఎత్తులో అమర్చాలి? (పరిపూర్ణ రక్తం సాంద్రత విలువను పట్టిక నుంచి తీసుకోండి).
సాధన:
h = \(\frac{\mathrm{P}}{\rho \mathrm{g}}\) = \(\frac{2000}{1.06 \times 10^3 \times 9.8}\) = 0.1925 m
రక్తం సిరలోకి ఎక్కాలి అంటే, రక్తం కలిగి ఉన్న సీసాను 0.1925 మీ. అనగా 0.2 మీ. కన్నా కొంచెం ఎక్కువ ఎత్తులో ఉంచాలి.

ప్రశ్న 25.
బెర్నౌలీ సమీకరణాన్ని ఉత్పాదించేటప్పుడు గొట్టంలోని ప్రవాహిపై జరిగిన పనిని ప్రవాహి స్థితిజ, గతిజ శక్తులలోని వ్యత్యాసానికి సమానం చేశాం. ఎ) 2 × 10^-3 m వ్యాసం గల ధమనిలో రక్త ప్రవాహం స్తరీయంగా కొనసాగేందుకు రక్తానికి ఉండాల్సిన గరిష్ఠ సగటు వేగం ఎంత ? బి) ప్రవాహి వేగం పెరిగే కొద్దీ దుర్వ్వయ బలాల ప్రాముఖ్యత పెరుగుతుందా ? గుణాత్మకంగా చర్చించండి.
సాధన:
ఎ) దుర్వయ బలాలు పనిచేస్తుంటే, పీడన వ్యత్యాసము వలన ప్రవాహిలో కలిగే కొన్ని బలాలు ఈ బలాలను అధిగమించటానికి ఉపయోగపడతాయి. కావున ప్రవాహి ప్రవహిస్తున్నప్పుడు పీడనంలో భారీ తగ్గుదల ఉంటుంది.

బి) ప్రవాహి వేగం పెరిగే కొద్దీ దుర్వ్యయ బలాల ప్రాముఖ్యత పెరుగుతుంది. వేగం పెరిగే కొలది స్నిగ్ధతా ఈడ్పు ఉంటుంది. అనగా దుర్వ్యయ బలాలు పెరుగుతాయి.

ప్రశ్న 26.
ఎ) 2 × 10^-3m వ్యాసం గల ధమనిలోని రక్త ప్రవాహం స్తరీయంగా కొనసాగేందుకు రక్తం కలిగి ఉండాల్సిన గరిష్ఠ సగటు వేగం ఎంత ? బి) సంబంధిత రక్త ప్రవాహరేటు ఎంత? (రక్తం స్నిగ్ధతను 2.084 × 10^-3 Pas) గా తీసుకోండి.)
సాధన:
ఇచ్చట r = 2 × 10^-3 m; D = 2 r = 2 × 2 × 10^-3 = 4 × 10^-3 m;
η = 2.084 × 10^-3 Pa-s; ρ = 1.06 × 10³ kg m^-3.
ప్రవాహం స్తరీయంగా కొనసాగేందుకు, N_R = 2000
ఎ) గరిష్ట సగటు వేగం, v_c = \(\frac{\mathrm{N}_{\mathrm{R}} \eta}{\rho D}\) = \(\frac{2000 \times\left(2.084 \times 10^{-3}\right)}{\left(1.06 \times 10^3\right) \times\left(4 \times 10^{-3}\right)}\)
బి) రక్త ప్రవాహ రేటు = πr² v_c = \(\frac{22}{7}\) × (2 × 10²)^-3 × 9.8 = 1.23 × 10^-5 m³ s^-1

ప్రశ్న 27.
ఒక్కొక్కటి 25 m² వైశాల్యం గల రెండు రెక్కలను కలిగి ఉండే విమానం ఒక నిర్ణీత ఎత్తు వద్ద స్థిరవడితో ప్రయాణిస్తున్నది. రెక్క అడుగు తలంపై గాలివేగం 180 km/h, రెక్కపై తలంపై ఉన్న గాలి వేగం 234 km/h అయితే విమానం ద్రవ్యరాశిని నిర్ధారించండి. (గాలి సాంద్రతను 1 kg m^-3 గా తీసుకోండి.)
సాధన:
ఇచ్చట v₁ = 180 km/h = 50 m/s ;
v₂ = 234 km/h = 65 m/s ;
A = 2 × 25 = 50 m² ; ρ = 1 kg/m³
P₁ – P₂ = \(\frac{1}{2}\)ρ(v₂² – v₁²) = \(\frac{1}{2}\) × 1 × [65² × 50²]
బెర్నౌలీ సిద్ధాంతము ప్రకారము, (P₁ – P₂) A = \(\frac{1}{2}\) × [65² – 50²] × 50 N
ఊర్ధ్వ దిశలో పనిచేసే బలం mg = (P₁ – P₂) A
(లేదా) m = \(\frac{\left(P_1-P_2\right) A}{g}=\frac{1 \times\left[65^2-50^2\right] \times 50}{2 \times 9.8}\) = 4.4 × 10³ kg.

ప్రశ్న 28.
మిల్లికాన్ తైల బిందు ప్రయోగంలో 2.0 × 10^-5 m వ్యాసార్ధం, 1.2 × 10³ kg m^-3 సాంద్రత గల తటస్థ బిందువు (అనావేశిత బిందువు) (uncharged particle) చరమవేగం ఎంత ? ప్రయోగ ఉష్ణోగ్రత వద్ద గాలి స్నిగ్ధతను 1.8 × 10^-5 Pasగా తీసుకోండి. ఆ చరమవేగం వద్ద బిందువుపై పనిచేసే స్నిగ్ధతాబలం ఎంత ? గాలివల్ల బిందువుపై పనిచేసే ఉత్సవన బలాన్ని ఉపేక్షించండి.
సాధన:
ఇచ్చట r = 2.0 × 10^-5 m; ρ = 1.2 × 10³ kg m^-2 ;
η = 1.8 × 10^-5 Ns m^-2, σ = 0, v = ?; F= ?
చరమవేగం, v = \(\frac{2 r^2(\rho-\sigma) g}{9 \eta}\)
= \(\frac{2 \times\left(2.0 \times 10^{-5}\right)^2\left(1.2 \times 10^3-0\right) \times 9.8}{9 \times 1.8 \times 10^{-5}}\)
= 5.8 × 10^-2 ms^-1 = 5.8 cm s^-1
బిందువుపై పనిచేసే స్నిగ్ధతా బలం, F = 6π η r v
= 6 × \(\frac{22}{7}\) × (1.8 × 10^-5) × (2.0 × 10^-5) × (5.8 × 10^-2) = 3.93 × 10^-10 N

ప్రశ్న 29.
సోడాలైమ్ గాజుతో పాదరస స్పర్శకోణం 140. ఈ రకమైన గాజుతో చేసిన 1.00 mm వ్యాసార్ధం గల సన్నని గొట్టాన్ని పాదరసం ఉండే తొట్టెలో నిలువుగా ముంచారు. పాత్రలోని పాదరస ద్రవ మట్టానికి సాపేక్షంగా నాళంలోని పాదరస మట్టం ఎంత కిందికి దిగుతుంది ? ప్రయోగ ఉష్ణోగ్రత వద్ద పాదరసం తలతన్యత 0.465 N m^-1. పాదరస సాంద్రత = 13.6 × 10³ kg m^-3.
సాధన:
ఇచ్చట θ = 140°, r = 1 × 10^-3 m; S = 0.465 Nm^-1 ; ρ = 13.6 × 10³ kg, h = ?
cos 140 ° = -cos 40° = -0.7660
ఇప్పుడు h = \(\frac{2 \mathrm{~S} \cos \theta}{\mathrm{r} \rho \mathrm{g}}\) = \(\frac{2 \times 0.465 \times \cos 140^{\circ}}{10^{-3} \times 13.6 \times 10^3 \times 9.8}\)
= \(\frac{2 \times 0.465 \times(-0.7660)}{10^{-3} \times 13.6 \times 10^3 \times 9.8}\)
= -5.34 × 10^-3 m = -5.34 mm
ఇచ్చట ఋణగుర్తు నాళంలో పాదరస మట్టం తగ్గుతుందని సూచిస్తుంది.

ప్రశ్న 30.
3.0 mm, 6.0 mm వ్యాసాలున్న రెండు సన్నని నాళాలను కలిపి రెండు చివరలలో తెరచి ఉంచిన U- ఆకార గొట్టాన్ని తయారుచేశారు. U- గొట్టంలోని నీటిని కలిగి ఉంటే, గొట్టంలోని రెండు భుజాల్లోని నీటి మట్టాల్లోని వ్యత్యాసం ఎంత? ప్రయోగ ఉష్ణోగ్రత వద్ద నీటి తలతన్యత 7.3 × 10^-2 N m^-1. స్పర్శకోణాన్ని శూన్యంగా, నీటి సాంద్రతను 1.0 × 10³ kg m^-3 గా తీసుకోండి (g = 9.8 m s^-2).
సాధన:
ఇచ్చట S = 7.3 × 10^-2 Nm^-2; ρ = 1.0 × 10³ kg m^-3; θ = 0°
సన్నని నాళముమునకు, 2 r₁ = 3.00 mm = 3 × 10^-3m
(లేదా) r₁ = 1.5 × 10^-3 m
వెడల్పు నాళమునకు, 2 r₂ = 6.00 mm = 6 × 10^-3 m (లేదా) r₂ = 3 × 10^-3 m
h₁ మరియు h₂ అనునవి సన్నని మరియు వెడల్పు నాళములలో నీరు ఎగబ్రాకిన ఎత్తులు అయిన
అప్పుడు h₁ = \(\frac{2 \mathrm{~S} \cos \theta}{\mathrm{r}_1 \rho \mathrm{g}}\)
మరియు h₂ = \(\frac{2 \mathrm{~S} \cos \theta}{\mathrm{r}_2 \rho \mathrm{g}}\)
∴ గొట్టంలోని రెండు నాళాలలోని నీటిమట్ట వ్యత్యాసం, h₁ – h₂ = \(\frac{2 S \cos \theta}{\rho g}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]\)
= \(\frac{2 \times 7.3 \times 10^{-2} \times \cos 0^{\circ}}{10^3 \times 9.8} \times\left[\frac{1}{1.5 \times 10^{-3}}-\frac{1}{3 \times 10^{-3}}\right]\) = 4.97 × 10^-3 m