TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(c)

Students must practice these TS Inter 1st Year Maths 1A Study Material Chapter 6 Trigonometric Ratios upto Transformations Ex 6(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(c)

I.
Question 1.
Simplify the following
(i) cos 100° . cos 40° + sin 100° . sin 40°
Answer:
Use cos A. cos B + sin A sin B = cos (A – B)
∴ cos 100° . cos 40° + sin 100°.sin 40°
= cos (100° – 40°)
= cos 60°
= \(\frac{1}{2}\) = R.H.S

(ii) \(\frac{\cot 55^{\circ} \cot 35^{\circ}-1}{\cot 55^{\circ}+\cot 35^{\circ}}\)
Answer:

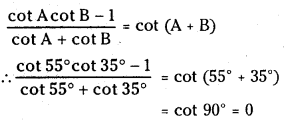
(iii) tan [\(\frac{\pi}{4}\) + θ]. tan[\(\frac{\pi}{4}\) – θ]
Answer:

(vi) Evaluate Σ\(\frac{\cos ^2 \mathrm{~B}-\cos ^2 \mathrm{~A}}{\cos ^2 \mathrm{~A} \cos ^2 \mathrm{~B}}\) if none of sin A, sin B, sin C is zero.
Answer:
Σ\(\frac{\cos ^2 \mathrm{~B}-\cos ^2 \mathrm{~A}}{\cos ^2 \mathrm{~A} \cos ^2 \mathrm{~B}}\) = Σ\(\left(\frac{\sin C \cos A-\cos C \sin A}{\sin C \sin A}\right)\)
= Σ (cot A – cot C)
= cot A – cot C + cot B – cot A + cot C – cot B = 0

Question 4.
(i) Prove that
cos 35° + cos 85° + cos 155° = 0
Answer:
cos 35° + cos 85° + cos 155°
= cos 35° + 2cos\(\left(\frac{85+155}{2}\right)\)cos\(\left(\frac{85-155}{2}\right)\)
= cos 35° + 2 cos 120° cos (-35°)
= cos 35° – cos 35° = 0

(ii) tan 72° = tan 18° + 2 tan 54°
Answer:
We have cot A – tan A = \(\frac{1}{\tan A}\) – tan A
⇒ \(\frac{1-\tan ^2 A}{\tan A}=\frac{2\left(1-\tan ^2 A\right)}{2 \tan A}\) = 2 cot 2A
∴ cot A – tan A = 2 cot 2A
⇒ cot A = tan A + 2 cot 2A°
Take A = 18°, then cot 18° = tan 18° + 2 cot 36°
⇒ cot(90 – 72) = tan 18° + 2 cot(90 – 54)
⇒ tan 72° = tan 18° + 2 tan 54°

(iii) sin 750° cos 480° + cos 120° cos 60° = –\(\frac{1}{2}\)
Answer:
L.H.S = sin [2.(360) + 30] cos[360 + 120] + cos 120 cos 60
= sin 30 cos 120 + cos 120 cos 60
= \(\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)\left(\frac{1}{2}\right)=-\frac{1}{2}\)

(iv) cos A + cos(\(\frac{4 \pi}{3}\) – A) + cos(\(\frac{4 \pi}{3}\) + A) = 0
Answer:
Use cos(A + B) + cos(A – B) = 2cos A cos B
L.H.S = cos A + 2cos\(\frac{4 \pi}{3}\)cos A
= cos A + 2 cos 240 cos A
= cos A + 2 cos ( 180 + 60) cos A
= cos A + 2 ( – cos 60) cos A
= cos A + 2\(\left(-\frac{1}{2}\right)\)cos A = cos A – cos A = 0

(v) cos²θ + cos²(\(\frac{2 \pi}{3}\) + θ) + cos²(\(\frac{2 \pi}{3}\) – θ) = \(\frac{3}{2}\)
Answer:
cos²θ + cos²( 120 + θ) + cos²( 120 – θ)
= cos²θ + cos²(120 + θ) + 1 – sin²(120 – θ)
= 1 + cos²θ + cos [ 120 + θ + 120 – θ] cos [ 120 + θ- 120 + θ]
= 1 + cos²θ + cos (240) cos 2θ
= 1 + cos²θ + cos (180 + 60) cos 2θ
[∵ Use cos²A – sin²B = cos (A + B) cos (A – B)]
= 1 + cos²θ – cos 60 ( 2 cos2θ – 1)
= 1 + cos²θ – \(\frac{1}{2}\) ( 2 cos2θ – 1)
= 1 + cos²θ – cos² θ + \(\frac{1}{2}=\frac{3}{2}\)

Question 5.
Evaluate
(i) sin²82\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
Answer:
sin²82\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
= sin[82\(\frac{1}{2}^{\circ}\) + 22\(\frac{1}{2}^{\circ}\)]
∵ Use sin²A – sin²B = sin(A + B) sin(A – B)
= sin 105° . sin 60°
= sin 60° sin (60° + 45°)
= sin 60° [sin 60° cos 45° + cos 60° sin 45°]
= \(\frac{\sqrt{3}}{2}\left[\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}}\right]=\frac{\sqrt{3}(\sqrt{3}+1)}{4 \sqrt{2}}=\frac{3+\sqrt{3}}{4 \sqrt{2}}\)

(ii) cos² 112\(\frac{1}{2}^{\circ}\) – sin²52\(\frac{1}{2}^{\circ}\)
Answer:
Use cos² A – sin² B = cos (A + B) cos (A – B)
cos²112\(\frac{1}{2}^{\circ}\) – sin² 52\(\frac{1}{2}^{\circ}\)
= cos [112\(\frac{1}{2}^{\circ}\) + 52\(\frac{1}{2}^{\circ}\)]cos[112\(\frac{1}{2}^{\circ}\) -52\(\frac{1}{2}^{\circ}\)]
= cos 165° . cos 60
= cos 60° cos (180 – 15)
= -cos 60°. cos 15°
= \(-\frac{1}{2}\left[\frac{\sqrt{3}+1}{2 \sqrt{2}}\right]=-\frac{(\sqrt{3}+1)}{4 \sqrt{2}}\)

(iii) sin²\(\left[\frac{\pi}{8}+\frac{A}{2}\right]\) – sin²\(\left[\frac{\pi}{8}-\frac{A}{2}\right]\)
Answer:

(iv) cos²52\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\) (M’ 2010, 06 Jun 08)
Answer:
[∵ cos²A – sin²B = cos (A + B) cos (A – B)]
cos²52\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
= cos[52\(\frac{1}{2}^{\circ}\) + 22\(\frac{1}{2}^{\circ}\)]cos[52\(\frac{1}{2}^{\circ}\) – 22\(\frac{1}{2}^{\circ}\)]
= cos 75° cos 30°
= cos 30° cos(90 – 15)
= cos 30° sin 15°
= \(\frac{\sqrt{3}}{2}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)=\frac{3-\sqrt{3}}{4 \sqrt{2}}\)

Question 6.
Find the minimum and maximum values of
(i) 3 cos x + 4 sin x
Answer:
Recall for a cos x + b sin x + c

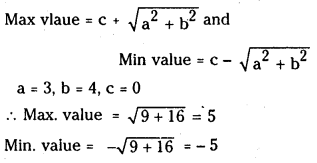
(ii) sin 2x – cos 2x
Answer:
a = 1, b = -1, c = 0

Question 7.
Find the range of
(i) 7 cos x – 24 sin x + 5
Answer:
a = -24, b = 7, c = 5

(ii) 13 cos x + 3√3 sin x – 4
Answer:
a = 3√3, b = 13, c = -4

II.
Question 1.
(i)If cos α = –\(\frac{3}{5}\) and sin β = \(\frac{7}{25}\) where \(\frac{\pi}{2}\) < α < π and 0 < β < \(\frac{\pi}{2}\), then find the values of tan(α + β) and sin(α + β).
Answer:
cos α = –\(\frac{3}{5}\), and α lies in second quadrant
sin α = \(\frac{4}{5}\) ∴ tan α = –\(\frac{4}{5}\)

(ii) If 0 < A < B < \(\frac{\pi}{4}\) and sin(A + B) = \(\frac{24}{25}\) and cos (A – B) = \(\frac{4}{5}\), then find the value of tan 2A. (March 2015-T.S)
Answer:

(iii) If A + B, A are acute angles such that sin (A + B) = \(\frac{24}{25}\) and tan A = \(\frac{3}{5}\), then find the value of cos B.
Answer:
A + B, A are acute angles ⇒ B is also acute.
Given sin (A + B) = \(\frac{24}{25}\), we have

(iv) If tan α – tan β = m, and cot α – cot β = n then prove that cot(α – β) = \(\frac{1}{\mathrm{~m}}-\frac{1}{\mathrm{n}}\).
Answer:
We have tan α – tan β = m

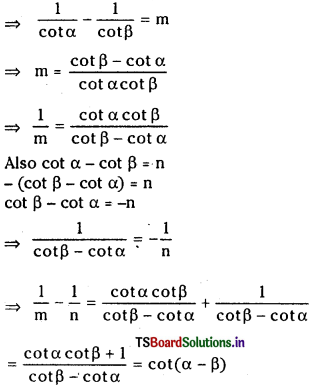
(v) If tan (α – β) = \(\frac{7}{24}\) and tan α = \(\frac{4}{3}\) where α and β are in the first quadrant prove that α + β = π/2.
Answer:

Question 2.
i) Find the expansion of sin (A + B – C).
Answer:
0 sin (A + B – C) = Sin [ (A + B) – C]
= sin (A + B) cos C – cos (A + B) sin C] – (sin A cos B + cos A sin B) cos C – (cos A cos B – sin A sin B] sin C
= sin A cos B cos C + cos A sin B cos C – cos A cos B sin C – sin A sin B sin C

ii) Find the expansion of cos (A – B – C).
Answer:
cos (A – B – C) = cos [(A – B) – C]
= cos (A – B) cos C + sin (A – B) sin C
= (cos A cos B + sin A sin B) cos C + (sin A cos B – cos A sin B] sin C
= cos A cos B cos C + sin A sin B cos C + sin A cos B sin C – cos A sin B sin C

iii) In a ΔABC, A is obtuse. If sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\), then show that sin C = \(\frac{16}{65}\)
Answer:
Given, A + B + C = 180°
⇒ A + B = 180° – C
∴ sin (A + B) = sin (180° – C)
= sin C ………………..(1)
∴ A is obtuse angle and A lies in II quadrant.

iv) If \(\frac{\sin (\alpha+\beta)}{\sin (\alpha-\beta)}=\frac{a+b}{a-b}\) then prove that a tan β = b tan α.
Answer:

III.
Question 1.
i) If A – B = \(\frac{3 \pi}{4}\), then show that (1 – tan A) (1 + tan B) = 2.
Answer:
A – B = \(\frac{3 \pi}{4}\)
⇒ tan(A – B) = tan\(\frac{3 \pi}{4}\)
⇒ \(\frac{\tan A-\tan B}{1+\tan A \tan B}\) = -1
⇒ tan A – tan B = – 1 – tan A tan B
⇒ tan A – tan B + tan A tan B = -1
⇒ – tan A + tan B – tan A tan B = 1
⇒ (1 – tan A) + tan B (1 – tan A) = 1 + 1 = 2
= (1 – tan A) (1 + tan B) = 2

ii) If A + B + C = \(\frac{\pi}{2}\) and if none of A, B, C is an odd multiple of \(\frac{\pi}{2}\), then prove that cot A + cot B + cot C = cot A cot B cot C
a) Given A + B + C = \(\frac{\pi}{2}\) ⇒ A + B = \(\frac{\pi}{2}\) – C
∴ cot(A + B) = cot(\(\frac{\pi}{2}\) – C)
= tan C = \(\frac{1}{\cot C}\)
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}=\frac{1}{\cot C}\)
⇒ cot A + cot B + cot C = cot A cot B cot C

b) tan A tan B + tan B tan C + tan C tan A = 1
Answer:
tan (A + B) = tan(\(\frac{\pi}{2}\) – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = cot C = \(\frac{1}{\tan C}\)
⇒ tan A tan C + tan B tan C= 1 – tan A tan B
⇒ tan A tan B + tan B tan C + tan C tan A = 1

c) Σ\(\frac{\cos (B+C)}{\cos B \cos C}\) = 2
Answer:
\(\Sigma \frac{\cos B \cos C-\sin B \sin C}{\cos B \cos C}\)
= Σ (1 – tan BtanC)
= 1 – tan B tan C + 1 – tan C tan A + 1 – tan A tan B
= 3 – (tan B tan C + tan C tan A + tan A tan B]
= 3 – 1 = 2 [∵ from (b) Σ tanA tan B = 1 ]

Question 2.
i) Prove that sin² α + cos² (α + β) + 2 sin α sin β cos (α + β) is independent of α.
Answer:
sin²α + cos² (α + β) + 2 sin α sin β cos (α + β)
= sin²α + cos (α + β) [cos (α + β) + 2sin α sin β ]
= sin²α + cos (α + β) [ cos (α + β) + cos (α – β) – cos (α + β)] (Formula)
= sin²α + cos (α + β) cos (α – β)
= 1 – sin²β = cos2β
Which is independent of α.

ii) Prove that cos² (α – β) + cos²β – 2 cos (α – β) cos α cos β is independent of β.
Answer:
cos² (α – β) + cos² β – 2 cos (α – β) cos α cos β
= cos² (α – β) – 2 cos (α – β)
= cos α cos β + cos² β = cos (α – β) [cos (α – β) – 2 cos α cosβ] + cos² β
= cos (α – β) [cos (α – β) – cos (α + β) – cos (α – β)] + cos2 β (Formula)
= – cos (α – β) cos (α + β) + cos2 β (Formula)
= – (cos²α – sin²β) + cos2 β = – cos² α + 1
= sin²α which is independent of β.