Class 10

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 13 Probability Ex 13.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 13 Probability Exercise 13.2

Question 1.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball selected is (i) red ? (ii) not red ? (AS₁)
Solution:
i) Total number of balls in the bag = 3 red + 5 black = 8 balls
Number of total outcomes when a ball is selected at random = 3 + 5 = 8
Now, number of favourable outcomes of red ball = 3
∴ Probability of getting a red ball
P(E) = \(\frac{\text { No. of favourable outcome }}{\text { No. of total outcomes }}\)
= \(\frac{3}{8}\)

ii) If P(\(\overline{\mathrm{E}}\)) is the probability of selecting no red balls, then
P(E) + P(\(\overline{\mathrm{E}}\)) = 1
P(\(\overline{\mathrm{E}}\)) = 1 – P(E) = 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)

Question 2.
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red ? (ii) white ? (iii) not green ? (AS₁)
Solution:
There are 5 red marbles, 8 white marbles and 4 green marbles in a bag.
∴ Total number of marbles in the bag = 5 + 8 + 4= 17
∴ Number of all possible outcomes = 17
i) Let E be the event that the marble taken out will be red.
Total number of red marbles in the bag = 5
∴ Number of outcomes favourable to E = 5
P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{5}{17}\)

ii) Let E be the event that the marble taken out will be white.
Total number of white marbles in the bag = 8
∴ Number of outcomes favourable to E = 8
P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{8}{17}\)

iii) Let E be the event that the marble taken out will be green.
Total number of green marbles in the bag = 4
∴ Number of outcomes favourable to E = 4
P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{4}{17}\)
∴ Probability that the marble taken out will not be green.
= 1 – P (Probability that the marble taken out will be green)
= 1 – P(E) = 1 – \(\frac{4}{17}\) = \(\frac{13}{17}\)

Question 3.
A Kiddy bank contains hundred 50p coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin (i) will be a 50p coin ? (ii) will not be a ₹ 5 coin ? (AS₁)
Solution:
i) Number of 50p coins = 100
Number of ₹ 1 coins = 50
Number of ₹ 2 coins = 20
Number of ₹ 5 coins = 10
∴ Total number of coins
= 100 + 50 + 20 + 10 = 180
Number of total outcomes for a coin to fall down = 180
Number of outcomes favourable to 50p coins to fall down = 100
∴ Probability of a 50p coin to fall down No. of favourable outcomes
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{100}{180}\) = \(\frac{5}{9}\)

ii) Let P(E) be the probability for a ₹ 5 coin to fall down.
= \(\frac{1}{2}\) (P(\(\overline{\mathrm{E}}\))) = \(\frac{1}{2}\) (P(\(\overline{\mathrm{E}}\)))
No. of outcomes favourable to ₹ 5 coin = 10
∴ Probability for a ₹ 5 coin to fall down
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{10}{180}\) = \(\frac{1}{18}\)
Then P(\(\overline{\mathrm{E}}\)) is the probability of a coin which fall down is not a ₹ 5 coin.
Again P(E) + P(\(\overline{\mathrm{E}}\)) = 1
∴ P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{1}{18}\)
= \(\frac{17}{18}\)

Question 4.
Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (See figure). What is the probability that the fish taken out is a male fish ? (AS₄)

Solution:
Number of male fish in the acquarium = 5
Number of female fish in the acquarium = 8
Total number of fish in the acquarium = 5 + 8 = 13
∴ Number of all possible outcomes = 13
Let E be the event that the fish taken out is a male fish.
Number of outcomes favourable to E = 5
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{5}{13}\)

Question 5.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See figure) and these are equally likely outcomes. What is the probability that it will point at

i) 8?
ii) an odd number ?
iii) a number greater than 2 ?
iv) a number less than 9 ?
Solution:
i) The figure shows the numbers from 1 to 8.
Let E be the event that the arrow comes to rest pointing at 8.
Number of outcomes favourable to E = 1
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{1}{8}\)

ii) The odd numbers shown in the figure are 1, 3, 5 and 7 = 4.
Let E be the event that the arrow will point an odd number.
Number of outcomes favourable to E = 4
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{4}{8}\) = \(\frac{1}{2}\)

iii) The numbers which are greater than 2 as per the figure given are 3, 4, 5, 6, 7 and 8 = 6
Let E be the event that the arrow will point a number greater than 2.
Number of outcomes favourable to E = 6
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{6}{8}\) = \(\frac{3}{4}\)

iv) The numbers less than 9 are 1, 2, 3. 4, 5, 6, 7,8
Let E be the event that the arrow will point a number less than 9.
Number of outcomes favourable to E = 8
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{8}{8}\) = 1

Question 6.
One card is selected from a well-shuffled deck of 52 cards. Find the probability of getting
i) a king of red colour
ii) a face card
iii) a red face card
iv) the jack of hearts
v) a spade
vi) the queen of diamonds.
Solution:
Total number of cards = 52
∴ Number of all possible outcomes in selecting a card at random = 52
i) Number of out comes favourable to the kings of red colour = 2(♥k, ♥k)
∴ Probability of getting the king of red colour
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{2}{52}\) = \(\frac{1}{26}\)

ii) Number of face cards in a deck of cards = 4 × 3 = 12(K, Q, J)
No. of outcomes favourable to select face card = 12
∴ Probability of getting a face card
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{12}{52}\) = \(\frac{3}{13}\)

iii) Number of red face cards = 2 × 3 = 6
∴ No. of outcomes favourable to select a red face card = 6
∴ Probability of getting a red face card
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{6}{52}\) = \(\frac{3}{26}\)

iv) No. of outcomes favourable to the jack of hearts = 1
∴ Probability of getting the jack of hearts.
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{1}{52}\)

v) No. of spade cards = 13
∴ No. of outcomes favourable to ‘a spade card’ = 13
∴ Probability of getting a spade card
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{13}{52}\) = \(\frac{1}{4}\)

vi) No. of outcomes favourable to the queen of diamonds = 1
∴ Probability of getting the queen of diamonds
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{1}{52}\)

Question 7.
Five cards-the ten, jack, queen, king and ace of diamonds, are well shuffled with their face downwards. One card is selected at random.
i) What is the probability that the card is the queen ?
ii) If the queen is selected and put aside (without replacement), what is the probability that the second card selected is
(a) an ace ? (b) a queen ?
Solution:
Total number of cards = 5
Well – Shuffled with their face downwards.
i) Let E be the event that the card is the queen. Therefore, the number of outcomes favourable to E = 1
So, P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{1}{5}\)

ii) If the queen is selected & put a side then the number of remaining cards is 4 (i.e.,) (5 – 1 = 4)
∴ No. of all possible outcomes = 4

a) Let E be the event that the second card picked up is an ace.
Then, the number of outcomes favourable toE = 1
So. P(E)
= \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{1}{4}\)

b) Let E be the event that the second card selected is a queen.
Then, the number of outcomes favourable to E is 0 (∵ there is no queen)
So, P(E)
= \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{0}{4}\) = 0

Question 8.
12 defective pens are accidentally mixed 10. with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Number of defective pens = 12
Number of good pens = 132
∴ Total number of pens = Number of defective pens + number of good pens
= 12 + 132 = 144
Let E be the event that the pen taken out is a good one,
Then, the number of outcomes favourable to
E = 132
So, P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{132}{144}\) = \(\frac{11}{12}\)

Question 9.
A lot of 20 bulbs contain 4 defective ones. One bulb is selected at random from the lot. What is the probability that this bulb is defective ? Suppose the bulb selected in previous case is not defective and is not replaced. Now one bulb is selected at random from the rest. What is the probability that this bulb is not defective ? (AS₁, AS₄)
Solution:
Total number of bulbs = 20
∴ No. of all possible outcomes = 20
i) Let E be the event that the bulbs drawn at random from the lot is defective.
Then, the number of outcomes favourable to E = 4
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{4}{20}\) = \(\frac{1}{5}\)

ii) As one bulb is selected at random from the rest,
Total number of bulbs = 20 – 1 = 19
Number of defective bulbs = 4
Let E be the event that the bulb selected is not defective.
Then, the number of outcomes favourable to E is 15 since, now there are 19 – 4 = 15 bulbs which are not defective.
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{15}{19}\)

Question 10.
A box contains 90 discs which are numbered from 1 to 90. If one disc is selected at random from the box, find the probability that it bears (i) a two-digit number (ii) a perfect square number (iii) a number divisible by 5. (AS₁)
Solution:
Number of discs in the box = 90
∴ Number of all possible outcomes = 90
i) Let E be the event that the disc bears a two-digit number.
One digit numbers are 1, 2, 3, 4, 5, 6, 7, 8 and 9. These are 9 in numbers.
Then, the number of outcomes favourable to E = 90 – 9 = 81
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{81}{90}\) = \(\frac{9}{10}\)

ii) Let E be the event that the disc bears a perfect square number.
The perfect square numbers from 1 to 90 are 1, 4, 9, 16, 25, 36, 49, 64, 81. These are 9.
Then, the number of outcomes favourable to E = 9
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{9}{90}\) = \(\frac{1}{10}\)

iii) Let E be the event that the disc bears a number divisible by 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90. These are 18.
Then, the number of outcomes favourable to E = 18
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{18}{90}\) = \(\frac{1}{5}\)

Question 11.
Suppose you drop a die at random on the rectangular region shown in figure. What is the probability that it will land inside the circle with diameter 1m ? (AS₄)

Solution:
Length of the rectangular region = 3 m
Breadth of the rectangular region = 2m
Area of the rectangular region =
Length × Breadth = 3 × 2 = 6m²
Diameter of the circle = 1 m
∴ Radius of the circle = \(\frac{1}{2}\) m
∴ Area of the circle = πr²
= \(\frac{22}{7}\) \(\frac{1}{2}\) \(\frac{1}{2}\) = \(\frac{11}{14}\) m²
∴ Probability that the dice will land inside the circle
= \(\frac{\frac{11}{14}}{6}\)
= \(\frac{11}{14}\) \(\frac{1}{6}\) = \(\frac{11}{84}\)

Question 12.
A lot consists of 144 ball pens of which 20 are defective and the others are good. The shopkeeper draws one pen at random and gives it to Sudha. What is the probability that
(i) She will buy it ?
(ii) She will not buy it ? (AS₄)
Solution:
Total number of ball pens = 144
i) ∴ Number of all possible outcomes = 144
Number of defective ball pens = 20
∴ Number of good ball pens
= 144 – 20 = 124
∴ Probability that Sudha will buy it
= \(\frac{124}{144}\) = \(\frac{31}{36}\)

ii) Probability that Sudha will not buy it = 1 – (Probability that Sudha will buy it)
= 1 – \(\frac{31}{36}\) = \(\frac{5}{36}\)

Question 13.
Two dice are rolled simultaneously and counts are added (i) complete the table given below :

Event: Sum on 2 dice’	2	3	4	5	6	7	8	9	10	11	12
Probability	\(\frac{1}{36}\)						\(\frac{5}{36}\)				\(\frac{12}{36}\)

i) A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of
them has a probability \(\frac{1}{11}\). Do you agree with this argument ? Justify your answer. (AS₃)
Solution:
When two dice are rolled simultaneously there are 36 possible out comes. So n(s) = 36.
i) Let E₃ denotes that event that the sum on two dice is 3 the outcomes favourable to the event E₃ = (1, 2), (2, 1)
No. of favourable out comes n(E₃) = 2
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_3\right)}{\mathrm{n}(\mathrm{S})}=\frac{2}{36}=\frac{1}{18}\)

ii) Let E₄ denotes the event that the sum on two dice is 4 the outcomes favourable to the event E₄ = (1,3), (2, 2), (3, 1).
No. of favourable outcomes n(E₄) = 3
probability = \(\frac{\mathrm{n}\left(\mathrm{E}_4\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{36}\) = \(\frac{1}{12}\)

iii) Let E₅ denotes the event that the sum on two dice is 5 the outcomes favourable to the event E₅ = (1, 4), (2, 3), (3, 2), (4, 1)
No. of favourable outcomes n(E₅) = 4
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_5\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{36}\) = \(\frac{1}{9}\)

iv) Let E₆ denotes the event that the sum on two dice is 6 the outcomes favourable to the event E6 = (1, 5), (2, 4), (3, 3), (4, 2), (5, 1)
No. of favourable outcomes n(E₆) = 5
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_6\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{5}{36}\)

v) Let E₇ denotes the event that the sum on two dice is 7 the outcomes favourable to the event E₇ = (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
No. of favourable outcomes n(E₇) = 6
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_7\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{6}{36}\) = \(\frac{1}{6}\)

vi) Let E₈ denotes the event that the sum on two dice is 8
probability = \(\frac{\mathrm{n}\left(\mathrm{E}_8\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{5}{36}\)

vii) Let E₉ denotes the event that the sum on two dice is 9 the outcomes favourable to the event E₉ = (3, 6), (4, 5), (5, 4), (6, 3), (7,2), (8,1)
No. of favourable outcomes n (E₉) = 8
probability = \(\frac{\mathrm{n}\left(\mathrm{E}_9\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{36}\) = \(\frac{1}{9}\)

viii) Let E₁₀ denotes the event that the sum on two dice is 10 the outcomes favourable to the event E₁₀ = (1, 9), (2, 8), (3, 7), (4, 6), (5, 5), (6. 4), (7, 3), (8, 2), (9, 1).
No. of favourable outcomes n(E₁₀) = 3
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_10\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{36}\) = \(\frac{1}{12}\)

ix) Let E₁₁ denotes the event that the sum on two dice is 11 the outcomes favourable to the event E₁₁ = (5, 6), (6, 5)

Question 14.
A game consists of tossing a one rupee coin 3 times and recording its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution:
Let H : Head, T : Tail
When we toss a one rupee coin 3 times,
S = {H, T} × (H, T} × {H, T} where ‘S’ denotes the cartesian product.
So, n(S) = 2 × 2 × 2 = 8
Let E be the event that Hanif will win the game
i.e., either three heads or three tails will come.
So, E = {(H, H, H), (T, T, T)}
n(E) = 2
So, probability that Hanif will win the game,
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{8}\) = \(\frac{1}{4}\)
So. probability that Hanif will lose the game,
P(\(\overline{\mathrm{E}}\)) = 1 – P(E) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

Question 15.
A dice is thrown twice. What is the probability that (i) 5 will not come up either time ? (ii) 5 will come up at least once ? [Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment.]
Solution:
When a dice is thrown twice.
S = {1, 2, 3, 4, 5, 6} × (1, 2, 3, 4, 5, 6}
So, n (S) = 6 × 6 = 36
Let E denote the event that 5 will come up at least once.
Then, E = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}.
∴ n(E) = 11
i) Probability that 5 will not come up either time = P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\)
= 1 – \(\frac{11}{36}\)
= \(\frac{25}{36}\)

ii) Probability that 5 will come up at least once,
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{11}{36}\)

Students can practice 10th Class Maths Solutions Telangana Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Exercise 4.1

Question 1.
By comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\), \(\frac{c_1}{c_2}\) find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or coincident.
a) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
b) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
c) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solution:
a) The given pair of linear equations are
5x – 4y + 8 = 0 ———- (1)
7x + 6y – 9 = 0 —— (2)
Comparing equations (1) and (2) with standard pair of linear equations (i.e.,)
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂= 0, we get
a₁ = 5; b₁ = -4; c₁ = 8
a₂ = 7; b₂ = 6; c₂ = -9
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{5}{7}\); \(\frac{b_1}{b_2}\) = \(\frac{-4}{6}\); \(\frac{c_1}{c_2}\) = \(\frac{8}{-9}\)
Since, \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\), the pair of linear equations will represent intersecting lines.

b) The given pair of linear equations are
9x + 3y + 12 = 0 —- (1)
18x + 6y + 24 = 0 —- (2)
Here, a₁ = 6; b₁ = 3; c₁ = 12
a₂ = 18; b₂ = 6; c₂ = 24
\(\frac{a_1}{a_2}\) = \(\frac{9}{18}\) = \(\frac{1}{2}\) ;
\(\frac{b_1}{b_2}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{12}{24}\) = \(\frac{1}{2}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) = \(\frac{1}{2}\), The pair of linear equations will represent coincident lines.

c) The given pair of linear equations are
6x – 3y + 10 = 0
2x – y + 9 = 0
Here,
a₁ = 6; b₁ = -3; c₁ = 10
a₂ = 2; b₂ = -1; c₂ = 9
\(\frac{a_1}{a_2}\) = \(\frac{6}{2}\) = \(\frac{3}{1}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-3}{-1}\) = \(\frac{3}{1}\);
\(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{10}{9}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\), the pair of linear equations will represent parallel lines.

Question 2.
Check whether the following equations are consistent or inconsistent. Solve them graphically.
a) 3x + 2y = 5; 2x – 3y = 7
b) 2x – 3y = 8; 4x – 6y = 9
c) \(\frac{3}{2}\)x + – y = 7; 9x – 10y = 14
d) 5x – 3y = 11; -10x + 6y = -22
e) \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
f) x + y = 5; 2x + 2y = 10
g) x – y = 8; 3x – 3y = 16
h) 2x + y – 6 = 0; 4x – 2y – 4 = 0
i) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
Solution:
a) 3x + 2y – 5 = 0
2x – 3y – 7 = 0
Here
a₁ = 3; b₁ = 2; c₁ = -5
a₂ = 2; b₂ = -3; c₂ = -7
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{3}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{2}{-3}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-5}{-7}\) = \(\frac{5}{7}\)
⇒ \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given equations are consistent.
They intersect at one point. There is an unique solution.
The given equations are 3x + 2y = 5 and 2x – 3y = 7
3x + 2y = 5 —– (1)
⇒ 2y = 5 – 3x
⇒ y = \(\frac{5-3 x}{2}\)

2x – 3y = 7 —- (2)
⇒ 3y = 2x – 7
⇒ y = \(\frac{2 x-7}{3}\)

Scale :
X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

The given lines intersect at one point. The solution is (2,-1).
x = \(\frac{29}{13}\) ; y = \(\frac{-11}{13}\)

b) 2x – 3y = 8
4x – 6y = 9
Solution:
2x – 3y – 8 = 0
4x – 6y – 9 = 0
Here,
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-3}{-6}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-8}{-9}\) = \(\frac{8}{9}\)
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations are inconsistent.
They are parallel lines. There is no solution.
The given equations are 2x – 3y = 8 and
4x — 6y = 9
2x – 3y = 8 —– (1)
⇒ 3y = 2x – 8
⇒ y = \(\frac{2 x-8}{3}\)

4x – 6y = 9
⇒ 6y = 4x – 9
⇒ y = \(\frac{4 x-9}{6}\)

The given lines parallel to each other.
There is no solution.

Scale: X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 0.5 cm

c) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
9x – 10y = 14
Solution:
\(\frac{3 x}{2}\) + \(\frac{5 y}{3}\) = 7
\(\frac{6(3 x)}{2}\) + \(\frac{6(5 y)}{3}\) = 7 × 6
(Multiplying each term by 6, we get)
⇒ 9x + 10y = 42
⇒ 9x + 10y – 42 = 0 —- (1)
⇒ 9x – 10y – 14 = 0 —- (2)
Here, a₁ = 9; b₁ = 10; c₁ = -42
a₂ = 9; b₂ = -10; c₂ = -14

∴ The given equations are consistent.
They intersect at one point. There is an unique solution.
The given equations are \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 and 9x – 10y = 14
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 —– (1)
⇒ 9x + 10y = 42 ⇒ 10y = 42 – 9x
⇒ y = \(\frac{42-9 x}{10}\)

9x – 10y = 14
⇒ 10y = 9x – 14
y = \(\frac{9 x-14}{10}\)

The given lines intersect at one point.
x = \(\frac{28}{9}\) and y = \(\frac{7}{5}\)

Scale : X-axis: 1 unit = 1 cm
Y-axis: 1 unit = 0.5 cm

d) 5x – 3y = 11
-10x + 6y = -22
Solution:
5x – 3y – 11 = 0
-10x + 6y + 22 = 0
Here, a₁ = 5; b₁ = -3; c₁ = -11
a₂ = -10: b₂ = 6; c₂ = 22
\(\frac{a_1}{a_2}\) = \(\frac{5}{-10}\) = \(\frac{-1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-3}{6}\) = \(\frac{-1}{2}\);
\(\frac{c_1}{c_2}\) = \(\frac{-11}{22}\) = \(\frac{-1}{2}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.
The given equations are 5x – 3y = 11 and -10x + 6y = -22
5x – 3y = 11 —– (1)
⇒ 3y = 5x – 11
⇒ y = \(\frac{5 x-11}{3}\)

⇒ 10x + 6y = -22 —– (2)
⇒ 6y = 10x – 22
⇒ y = \(\frac{10 x-22}{6}\)

The given lines are coincident.
There are infinitely many solutions.

Scale: X – axis: 1 cm = 1 unit
Y – axis: 1 cm = 1 unit

e) \(\frac{4}{3}\)x + 2y = 8
2x + 3y = 12
Solution:
4x + 6y = 24
Multiplying each term by (3), we get
⇒ 4x + 6y – 24 = 0 —— (1)
2x + 3y – 12 = 0 ——- (2)
a₁ = 4; b₁ = 6; c₁ = -24
a₂ = 2; b₂ = 3; c₂ = -12
Here,
\(\frac{a_1}{a_2}\) = \(\frac{4}{2}\) = 2; \(\frac{b_1}{b_2}\) = \(\frac{6}{3}\) = 2 ; \(\frac{c_1}{c_2}\) = \(\frac{-24}{-12}\) = 2
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent.
There are infinitely many solutions.
The given equations are \(\frac{4}{3}\)x + 2y = 8 and 2x + 3y = 12
\(\frac{4}{3}\)x + 2y = 8 —– (1)
⇒ 4x + 6y = 24
⇒ 6y = 24 – 4x
⇒ y = \(\frac{24-4 x}{6}\)

2x + 3y = 12 —– (2)
⇒ 3y = 12 – 2x
⇒ y = \(\frac{12-2 x}{3}\)


The given lines are coincident.
There are infinitely many solutions.

f) x + y = 5 (A.P. Jun.15)
2x + 2y = 10
Solution:
x + y – 5 = 0
2x + 2y – 10 = 0
Here, a₁ = 1; b₁ = 1; c₁ = -5
a₂ = 2; b₂ = 2; c₂ = -1O
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-5}{-10}\) = \(\frac{1}{2}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.
The given equations are x + y = 5 and 2x + 2y = 10
x + y = 5 —— (1)
⇒ y = 5 – x

2x + 2y = 10 —– (2)
⇒ 2y = 10 – 2x
⇒ y = \(\frac{10-2 \mathrm{x}}{2}\)

The given lines are coincident.
There are infinitely many solutions.

g) x – y = 8
3x – 3y = 16
Solution:
x – y – 8 = 0
3x – 3y – 16 = 0
Here, a₁ = 1; b₁ = -1; c₁ = -8
a₂ = 3; b₂ = -3; c₂ = -16
⇒ \(\frac{a_1}{a_2}\) = \(\frac{1}{3}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-1}{-3}\) = \(\frac{1}{3}\);
\(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{-8}{-16}\) = \(\frac{1}{2}\)
⇒ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
The given equations are inconsistent.
They are parallel lines. There is no
solution.
The given equations are x – y = 8 and 3x – 3y = 16
x – y = 8 —– (1)
⇒ y = x – 8

3x – 3y = 16 —- (2)
⇒ 3y = 3x – 16
⇒ y = \(\frac{3 x-16}{3}\)

The given lines are parallel to each other. There is no solution.

Scale: X – axis : 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

h) 2x + y – 6 = 0
4x – 2y – 4 = 0
Solution:
2x + y – 6 = 0
4x – 2y – 4 = 0
Here, a₁ = 2; b₁ = 1; c₁ = -6
a₂ = 4; b₂ = -2; c₂ = -4
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{1}{-2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-6}{-4}\) = \(\frac{3}{2}\)
⇒ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given equations are consistent.
They intersect at one point. There is a unique solution.
The given equations are 2x + y – 6 = 0 and 4x – 2y – 4 = 0
2x + y – 6 = 0 —– (1)
⇒ y = 6 – 2x

4x – 2y – 4 = 0 —– (2)
⇒ 2y = 4x – 4
⇒ y = \(\frac{4 x-4}{2}\)

Scale: X-axis : 1 unit = 1 cm
Y-axis : 1 unit = 1 cm

The given lines intersect at one point (2, 2).
The solution is x = 2 and y = 2.

i) 2x – 2y – 2 = 0
4x – 4y – 5 = 0
Solution:
2x – 2y – 2 = 0
4x – 4y – 5 = 0
Here, a₁ = 2; b₁ = -2; c₁ = -2
a₂ = 4; b₂ = -4; c₂ = -5
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-2}{-4}\) = \(\frac{1}{2}\)
\(\frac{\mathrm{c}_1}{\mathrm{~c}_2}\) = \(\frac{-2}{-5}\) = \(\frac{2}{5}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations are consistent.
They are parallel lines. There is no solution.
The given equations are 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0
2x – 2y – 2 = 0 —– (1)
⇒ 2y = 2x – 2
⇒ y = \(\frac{2 x-2}{2}\)

4x – 4y – 5 = 0 —– (2)
⇒ 4y = \(\frac{4 x-5}{4}\)
⇒ y = \(\frac{4 x-5}{4}\)

The given lines are parallel to each other.
There is no solution.

Scale: X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

Question 3.
Neha went to a ‘sale’ to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered “The number of skirts are two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number of pants purchased”. Help her friend to find how many pants and skirts Neha bought.
Solution:
Let the number of pants Neha bought be x.
Let the number of skirts Neha bought be y.
By problem,
y = 2x – 2
⇒ 2x – y = 2 —— (1)
y = 4x – 4
⇒ 4x – y = 4 —– (2)

Substitute x = 1 in (1) or (2), we get
⇒ 2(1) – y = 2
⇒ 2 – y = 2
⇒ -y = 2 – 2 = 0
∴ y = o
Number of pants purchased = 1
∴ Number of skirts purchased = 0

Question 4.
10 students of Class-X took part in a mathematics quiz. If the number of girls is 4 more than the number of boys then, find the number of boys and the number of girls who took part in the quiz.
Solution:
Number of boys who took part in the quiz = x
Number of girls who took part in the quiz = y
It is given that 10 students took part in the quiz.
∴ x + y = 10 ——— (1)
Since the number of girls is 4 more than the number of boys, we have
y = x + 4
⇒ -x + y = 4 —– (2)
Adding (1) and (2)

Substitute y = 7 in equation (1), we get
x + 7 = 10
x = 10 – 7 = 3
Therefore, Number of boys who took part in the quiz = 3
Number of girls who took part in the quiz = 7

Question 5.
5 pencils and 7 pens together cost ₹ 50 whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
Let the cost of one pencil = ₹ x
Cost of one pen = ₹ y
Total cost of 5 pencils and 7 pens = 5x + 7y
Total cost of 7 pencils and 5 pens = 7x + 5y
By problem, 5x + 7y = 50 —- (1)
7x + 5y = 46 —– (2)
We equate the coefficients of ‘x’ in (1) and (2).

Substitute y = 5 in equation (1), we get
5x + (7 × 5) = 50
5x + 35 = 50
5x = 50 – 35 =15
∴ x = \(\frac{15}{5}\) = 3
Therefore, cost of one pencil = ₹ 3
Cost of one pen = ₹ 5

Question 6.
Half of the perimeter of a rectangular garden, whose length is 4m more than its width is 36m. Find the dimensions of the garden.
Solution:
Let the length of the garden be x metres.
Let the breadth of the garden be y metres.
Perimeter of the garden = 2(x + y) metres.
Half of the perimeter of the garden =
\(\frac{2(x+y)}{2}\) = x + y
By problem, x + y = 36 —— (1)
It is given that the length is 4 metres more than its width.
(i.e.,) x = y + 4
⇒ x – y = 4 —– (2)
Solving (1) and (2)

Substitute, x = 20 in equation (1),
20 + y = 36
⇒ y = 36 – 20 = 16
Therefore, length of the garden = 20 metres
Breadth of the garden =16 metres

Question 7.
We have a linear equation 2x + 3y – 8 = 0. Write another linear equation in two variables such that the geometrical representation of the pair is formed intersecting lines. Now, write two more linear equations so that one forms a pair of parallel lines and the second forms coincident line with the given equation.
Solution:
The given linear equation is 2x + 3y – 8 = 0.

1. The required linear equation in two variables such that it is formed an intersecting line with the given one, is 6x – 5y – 10 = 0.
2. The linear equation in two variables (i.e.,) 4x + 6y – 10 = 0 forms a parallel line with the given one.
3. The linear equation in two variables (i.e.,) 6x + 9y – 24 = 0 forms a coincident line with the given one.

Question 8.
The area of a rectangle gets reduced by 80 sq units if its length is reduced by 5 units and breadth is increased by 2 units. If we increase the length by 10 units and decrease the breadth by 5 units, the area will increase by 50 sq units. Find the length and breadth of the rectangle.
Solution:
Let the length of the rectangle be x units and the breadth be y units.
Then the area of the rectangle = length × breadth = x × y = xy
If the length is reduced by 5 units and breadth is increased by 2 units, then its area is reduced by 80 sq. units.
∴ (x – 5) (y + 2) = xy – 80
⇒ xy + 2x – 5y – 10 = xy – 80
⇒ 2x – 5y = -70 —– (1)
When the length is increased by 10 units and breadth is decreased by 5 units, the area is increased by 50 sq. units.
∴ (x + 10) (y – 5) = xy + 50
⇒ xy – 5x + 10y – 50 = xy + 50
⇒ -5x + 10 y = 100 —– (2)
Equation (1) × 2
Solving (1) and (2), we get
4x – 10y = -140
-5x + 10y = 100 Adding
-x = -40
∴ x = 40
Substitute x = 40 in (2), we get
⇒ (-5 × 40) + 10y = 100
⇒ – 200 + 10y = 100
⇒ 10y = 100 + 200 = 300
∴ y = \(\frac{300}{10}\) = 30
Length of the rectangle = 40 units
Breadth of the rectangle = 30 units

Question 9.
In class X, if three students sit on each bench, one student will be left. If four students sit on each bench, one bench will be left. Find the number of students and the number of benches in that class.
Solution:
Let the number of students in class X be x.
Let the number of benches in that class be y.
If three students sit on each bench, one student will be left.
∴ 3y = x – 1
⇒ x – 3y = 1 —- (1)
If four students sit on each bench, one bench will be left.
∴ 4(y – 1) = x
⇒ 4y – 4 = x
⇒ x – 4y = -4 —– (2)
Solving (1) and (2), we get

Substitute y = 5 in (1), we get
x – (3 × 5) = 1
⇒ x – 15 = 1
∴ x = 1 + 15 = 16
∴ Number of students in class X = 16
Number of benches in that class = 5
Form a pair of linear equations for each of the following problems and find their solution.

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 12 Applications of Trigonometry Ex 12.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Exercise 12.1

Question 1.
A tower stands vertically on the ground. From a point which is 15 meter away from the foot of the tower, the angle of elevation of the top of the tower is 45°. What is the height of the tower ? (AS₄)
Solution:

In ∆ ABC, ∠B = 90°
AB represents the height of the tower and ∠ACB = 45°
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
1 = \(\frac{\mathrm{AB}}{15}\)
⇒ AB = 15 meters.
Therefore, the height of the tower = 15 meters.

Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground by making 30° angle with the ground. The distance between the foot of the tree and the top of the tree on the ground is 6 m. Find the height of the tree before falling. (AS₄) (A.P. Mar. ’16)
Solution:
Let AB represents the height of the tree

AC represents the broken part.
AC = CD (∵ the broken part touches the ground)
Let BC = x meters, the height of the tree after it is broken
In ∆CBD, ∠B = 90° and ∠BDC = 30°
tan 30° = \(\frac{\mathrm{BC}}{\mathrm{BD}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{x}{6}\)
⇒ \({\sqrt{3}}\) x = 6
⇒ x = \(\frac{6}{\sqrt{3}}\) (∵ \(\frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{6 \sqrt{3}}{3}=2 \sqrt{3}\))
⇒ x = \(2 \sqrt{3}\)
sin 30° = \(\frac{\mathrm{BC}}{\mathrm{BD}}\)
\(\frac{1}{2}\) = \(\frac{2 \sqrt{3}}{C D}\)
⇒ CD = 2 × 2\({\sqrt{3}}\) = 4\({\sqrt{3}}\)
∴ The height of the tree before falling down
= AB
= AC + CB
= 4\({\sqrt{3}}\) + 2\({\sqrt{3}}\) (∵ AC = CD = 4\({\sqrt{3}}\))
= 6\({\sqrt{3}}\) m

Question 3.
A contractor wants to set up a slide for the children to play in the park. He wants to set it up at the height of 2m and by making an angle of 30° with the ground. What should be the length of the slide ? (AS₄)
Solution:
In the triangle ABC, ∠B = 90°
Let AC represents the length of the side
AB = 2 m
sin 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{1}{2}\) = \(\frac{2}{\mathrm{AC}}\)
⇒ Ac = 4

Hence, length of the side = 4m

Question 4.
Length of the shadow of a 15 meter high pole is 5\({\sqrt{3}}\) m at 7 o’ clock in the morning. Then, what is the angle of elevation of the sun rays with the ground at the time ? (A.P. Mar.’15) (AS₄)
Solution:
In ∆ABC, ∠B = 90°
AB represents the height of the pole.
AB = 15m
Let BC represents its shadow at 7 o’ clock in the morning.
BC = 5\({\sqrt{3}}\) m
Let the angle of elevation of the sun rays with the ground be ‘θ’.
Now, tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
= \(\frac{15}{5 \sqrt{3}}\)
= \(\frac{3}{\sqrt{3}}\)

We know that tan 60° = \({\sqrt{3}}\)
∴ θ = 60°
Hence, the angle of elevation of the sun rays with the ground at the time = 60°.

Question 5.
You want to erect a pole of height 10 m with the support of three ropes. Each rope has to make an angle 30° with the pole. What should be the length of the rope ? (AS₄)
Solution:
In the figure,

Let AB be the height of the pole = 10 m
Let AC be the length of the rope
Angle of elevation is 30°
From right angled ∆ ABC
cos 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{10}{\mathrm{AC}}\)
⇒ AC = \(\frac{2 \times 10}{\sqrt{3}}\)
⇒ AC = \(\frac{20}{1.732}\) (∵ \({\sqrt{3}}\) = 1.732)
⇒ AC = 11.547 cm
Hence, the length of the rope is 11.547 m

Question 6.
Suppose you are shooting an arrow from the top of a building at a height of 6 m to a target on the ground at an angle of depression of 60°. What is the distance be-tween you and the object ? (AS₄) (A.P. Mar.15)
Solution:

In figure,
Let BC be the height of a building = 6 m
‘C’ be the point of the observation and A’ be the target on the ground.
Angle of depression is ∠CAB = 60°
Let AC be the distance between me and the object
From the right angled ∆ABC,
sin 60° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{6}{\mathrm{AB}}\)
⇒ AB = \(\frac{6 \times 2}{\sqrt{3}}=\frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{12 \sqrt{3}}{3}\) = 4\({\sqrt{3}}\) m
Hence, the distance between me and the object is 4\({\sqrt{3}}\) m.

Question 7.
An electrician wants to repair an electric connection on a pole of height 9 m. He needs to reach 1.8 m below the top of the pole to do repair work. What should be the length of the ladder which he should use, when he climbs it at an angle of 60° with the ground ? What will be the distance between foot of the ladder and foot of the pole ? (AS₄)
Solution:
In the figure,
Let AB be the height of a pole is 9 m
AC be the actual required height of the pole is 7.2 m
Angle of elevation is ∠CDA = 60°.
CD be the length of the ladder.
AD be the distance between foot of the ladder and foot of the pole.
From the right angled ∆ADC,
tan 60° = \(\frac{\mathrm{AC}}{\mathrm{AD}}\)
⇒ \({\sqrt{3}}\) = \(\frac{7.2}{\mathrm{AD}}\)

⇒ AD = \(\frac{7.2}{\sqrt{3}}=\frac{7.2}{1.732}\)
⇒ AD = 4.15692 m
Again, from the ∆ADC,
sin 60° = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{7.2}{\mathrm{CD}}\)
⇒ CD = \(\frac{7.2 \times 2}{\sqrt{3}}\)
⇒ CD = \(\frac{7.2 \times 2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
CD = \(\frac{7.2 \times 2 \times \sqrt{3}}{3}\)
CD = 2.4 × 2 × \({\sqrt{3}}\)
CD = 4.8 × \({\sqrt{3}}\)
CD = 8.3138 m
Hence, the distance between foot of the ladder and foot of the pole is 4.15692 m and the length of the ladder is 8.3138 m.

Question 8.
A boat has to cross a river. It crosses the river by making an angle of 60° with the bank of the river due to the stream of the river and travels a distance of 600 m to reach the another side of the river. What is the width of the river ? (AS₄)
Solution:

In the figure,
Let A’ be the required point to reach the bank of the river.
Let ‘C’ be the present position of the boat (or) observation point.
AC be the distance travelled by the boat is 600 m
Angle of elevation is ∠ACB = 60°
AB be the actual width of the river
From the right angled ∆ABC,
sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{\mathrm{AB}}{600}\)
⇒ AB = 600 × \(\frac{\sqrt{3}}{2}\)
⇒ AB = 300\({\sqrt{3}}\) m
⇒ Hence, the width of the river is 300\({\sqrt{3}}\) m

Question 9.
An observer of height 1.8m is 13.2m away from a palm tree. The angle of elevation of the top of the tree from his eyes is 45°. What is the height of palm tree ? (AS₄)
Solution:
AB represents the height of the observer.
CD denotes the height of the palm tree.
AB = 1.8 m; BC = 13.2 m AE = 13.2 m (∵ ABCE is a rectangle so, opposite sides of BC and AE are equal)
(AB and EC are also opposite sides of the rectangle ABCE)
∴ AB = EC
In ∆AED, ∠E = 90°
tan 45° = \(\frac{\mathrm{DE}}{\mathrm{AE}}\)
1 = \(\frac{\mathrm{DE}}{13.2}\)
⇒ DE = 13.2 m

Therefore, the height of the palm tree CD
= DE + EC
= 13.2 + 1.8
= 15 meters.

Question 10.
In the adjacent figure
In ∆ABC, AC = 6 cm, AB = 5 cm and ∠BAC = 30°. Find the area of the triangle. (AS₄)
Solution:
In ∆ ABC,
AB = 5 cm, AC = 6 cm
∠BAC = 30°
Draw BD ⊥ AC

In ∆ ABD, ∠ADB = 90°
sin 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
\(\frac{1}{2}\) = \(\frac{\mathrm{BD}}{5}\)
⇒ 2 × BD = 5
BD = \(\frac{5}{2}\) = 2.5 cm
Hence, area of the triangle ABC
= \(\frac{1}{2}\) × Base × Altitude
= \(\frac{1}{2}\) × AC × BD
= \(\frac{1}{2}\) × 6 × 2.5
= 3 × 2.5 = 7.5 cm²

Students can practice TS 10th Class Maths Solutions Chapter 2 Sets Ex 2.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 2 Sets Exercise 2.4

Question 1.
State which of the following sets are empty and which are not ?
a) The set of straight lines passing through a point.
b) Set of odd natural numbers divisible by 2.
c) {x : x is a natural number, x < 5 and x > 7}
d) {x : x is a common point to any two parallel lines}
e) Set of even prime numbers.
Answer:
a) The number of straight lines passing through a point is infinite. So, the given set is non-empty.
b) We know the odd natural numbers are 1, 3, 5, 7,…. are not divisible by 2. Hence the given set is empty.
c) There is no natural number satisfying the given condition. Hence the given set is empty.
d) There is no common point to any two parallel lines because they do not meet when produced on either side. Hence the given set is empty.
e) 2 is the only even prime number. Therefore the set contains one element. Hence the given set is non-empty.

Question 2.
Which of the following sets are finite or infinite ?
a) The set of months in a year.
b) {1, 2, 3,…….., 99, 100}
c) The set of prime numbers less than 99.
Answer:
a) There are 12 months in a year. The set of months in a year contains 12 elements. Hence the set is finite.
b) Obviously, the given set contains 100 elements. Hence the set is finite.
c) We can count the prime numbers less than 99. Hence the set is finite.

Question 3.
State whether each of the following sets is finite or infinite.
a) The set of letters in the english alphabet.
b) The set of lines which are parallel to the x – axis.
c) The set of numbers which are multiples of 5.
d) The set of circles passing through the origin (0, 0).
Answer:
a) The set of letters in the english alphabet contains 26 elements. Hence, the set is finite.
b) We cannot count the number of parallel lines drawn to the x – axis. Hence the set is infinite.
c) The set of numbers which are multiples of 5 is {5, 10, 15, 20, 25, …}. Hence the set contains infinite number of elements. Hence, the set is infinite.
d) The number of circles that can be drawn through the origin (0, 0) is countless. Hence the set is infinite.

Students can practice 10th Class Maths Solutions Telangana Chapter 3 Polynomials Ex 3.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 3 Polynomials Exercise 3.1

Question 1.
If p(x) = 5x⁷ – 6x⁵ + 7x – 6, find
(i) Coefficient of x⁵
(ii) degree of p(x)
(iii) constant term.
a) If P(x) = 5x⁷ – 6x⁵ + 7x – 6
Solution:
i) coefficient of x⁵ is -6
ii) degree of p(x) = highest degree of x = 7
iii) constant term is -6

Question 2.
State which of the following statements are true and which are false ? Give reasons for your choice.

i) The degree of the polynomial
\(\sqrt{2}\)x² – 3x + 1 is \(\sqrt{2}\).
Solution:
The given statement is false because \(\sqrt{2}\) is the coefficient of x² but not its degree. The degree of the polynomial is 2.

ii) The coefficient of x² in the polynomial p(x) = 3x³ – 4x² + 5x + 7 is 2.
Solution:
The given statement is false because the coeffi-cient of x² in the polynomial is -4 but not 2.

iii) The degree of a constant term is zero.
Solution:
The given statement is true. Because 3x⁰ = 3 the degree is 0

iv) \(\frac{1}{x^2-5 x+6}\) is a quadratic polynomial.
Solution:
The given statement is false because the variable ‘x’ appears in the denominator.

v) The degree of a polynomial is one more than the number of terms ¡n it.
Solution:
The given statement is false. There is a no relationship between the degree of the polynomial and the number of terms in it.

Question 3.
If p(t) = t³ – 1, find the values of p(1), p(-1), p(0), p(2). p(-2) (A.P.Mar. ’15)
Solution:
Given that p(t) = t³ – 1
∴ p(1) = (1)³ – 1 = 1 – 1 = 0
p(-1) = (-1) – 1 = -1 – 1 = -2
p(0) = (0) – 1 = 0 – 1 = -1
p(2) = (2) – 1 = 8 – 1 = 7
= (-2) – 1 = -8 – 1 = -9

Question 4.
Check whether -2 and 2 are the zeroes of the polynomial x⁴ – 16.
Solution:
p(x) = x⁴ – 16
p(-2) = (-2)⁴ – 16 = 16 – 16 = 0
p(2) = (2⁴) – 16 = 16 – 16 = 0
Yes, -2 and 2 are zeroes of the polynomial x⁴ – 16.

Question 5.
Check whether 3 and -2 are the zeroes of the polynomial p(x) when p(x) = x² – x – 6
Solution:
p(x) = x² – x – 6
= (3)² – 3 – 6 = 9 – 3 – 6 = 9 – 9 = 0
p(-2) = (-2)² – (-2) – 6 = 4 + 2 – 6 = 6 – 6 = 0
Yes, 3 and -2 are zeroes of the polynomial
p(x) = x² – x – 6

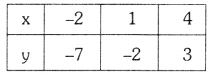
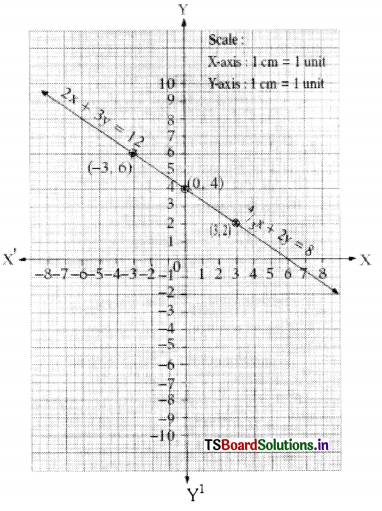
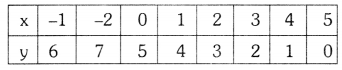
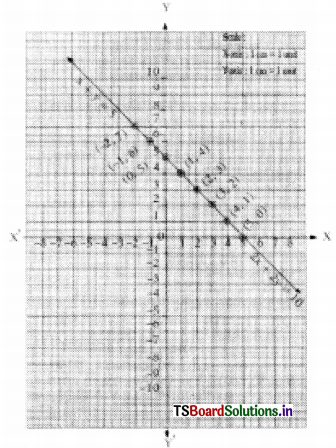
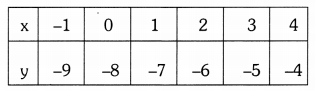
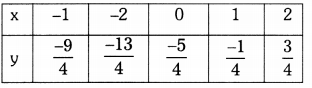
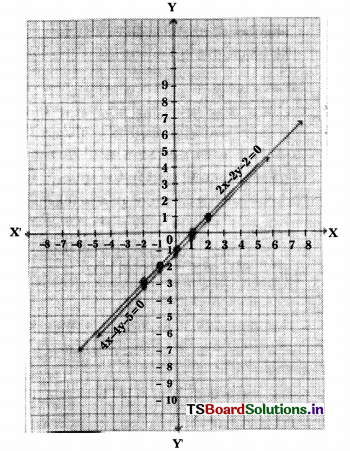
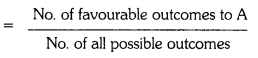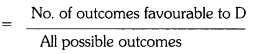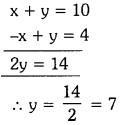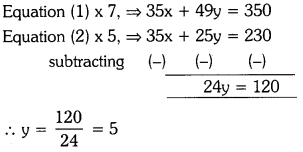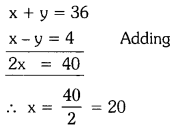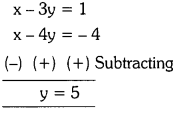Students can practice TS 10th Class Maths Solutions Chapter 2 Sets InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 2 Sets InText Questions

Do This

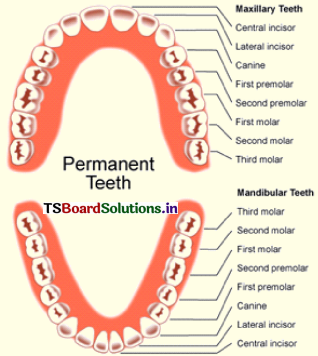
Question 1.
List the teeth under each of the following type.
i) Incisors
Solution:
Central incisors = 4
Lateral incisors = 4

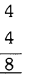
Total incisors = 8

ii) Canines
Solution:
Total Canines = 4

iii) Pre-molars
Solution:
First premolars = 4
Second premolars = 4

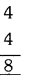
Total premolars = 8

iv) Molars
Solution:
First molars = 4
Second molars = 4
Third molars = 4

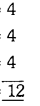
Total molars = 12

Question 2.
Identify and write the “common property” of the following collections. (Page No. 26)

1) 2, 4, 6, 8 ….
2) 3, 5, 7, 11, ….
3) 1, 4, 9, 16, ………
4) January, February, March, April,………..
5) Thumb, index finger, middle finger, ring finger, pinky.
Solution:
1) For given integers 2, 4, 6, 8 …….. 2n, n = 1, 2, 3, 4,…. is any positive integer.
2) 2, 3, 5, 7, 11, …. prime numbers.
3) For given integers 1, 4, 9, 16, …. n², where ‘n’ is any positive integer and square of the numbers.
4) January, February, March, April,…. months of the every year.
5) Thumb, index finger, middle finger, ring finger, pinky fingers of the human hand.

Question 3.
Write the following sets. (Page No. 27)
1) Set of the first five positive integers.
2) Set of multiples of 5 which are more than 100 and less than 125.
3) Set of first five cubic numbers.
4) Set of digits in the Ramanujan number.
Solution:
1) { + 1, +2, +3, +4, +5}
2) {105, 110, 115, 120}
3) {1, 8, 27, 64,125} = {1³, 2³, 3³, 4³, 5³}
4) Ramanujan Number = 1729. So the set = {1, 2, 7, 9}

Question 4.
Some numbers are given below. Decide the numbers to which number sets they belong to and does not belong to and express with correct symbols. (Page No. 27)
i) 1
ii) 0
iii) -4
iv) \(\frac{5}{6}\)
v) \(\text { 1. } \overline{3}\)
vi) \(\sqrt{2}\)
vii) log 2
viii) 0.03
ix) π
x) \(\sqrt{-4}\)
Solution:
Set of natural numbers = N
set of integers = Z
Set of rational numbers = Q
Set of real numbers = R
i) 1 ∈ (N, Z, Q, R}
ii) 0 ∉ N, 0 ∈ {Z, Q, R}
iii) -4 ∉ N, -4 ∈ (Z, Q, R}
iv) \(\frac{5}{6}\) ∉ (N, Z} But \(\frac{5}{6}\) ∈ {Q, R}
v) \(1 . \overline{3}\) ∉ {N, Z} But \(1 . \overline{3}\) ∈ {Q, R}
vi) \(\sqrt{2}\) ∉ {N, Z} But \(\sqrt{2}\) ∈ {Q, R}
vii) log2 ∉ N,Z But log 2 ∈ {Q, R}
viii) 0.03 ∉ {N, Z}But 0.03 ∈ {Q, R}
ix) π ∉ {N, Z} But π ∈ (Q, R}
x) \(\sqrt{-4}\) ∉ (N, Z, Q} But \(\sqrt{-4}\) ∈ R.

Question 5.
List the elements of the following sets.
i) G = {all the factors of 20}
ii) F = {the multiples of 4 between 17 and 61 which are divisible by 7}
iii) S = {x : x is a letter in the word MADAM’}
iv) P = {x : x is a whole number between 3.5 and 6.7} (Page No. 29)
Answer:
i) G = {1, 2, 4, 5, 10, 20}
ii) Multiples of 4 between 17 and 61.
x = {20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60}
F = {28, 56}
iii) S = {M, D, A}
iv) P = {4, 5, 6}

Question 6.
Write the following sets in the roaster form. (Page No. 29)
i) B is the set of all months in a year having 30 days.
ii) P is the set of all prime numbers less than 10.
iii) X is the set of colours of the rainbow.
Answer:
i) B = {April, June, September, November}
ii) P = {2, 3, 5, 7}
iii) X = {Violet, Indigo, Blue, Green, Yellow, Orange, Red}

Question 7.
A is the set of factors of 12. Which one of the following is not a member of A ? (Page No. 29)
A) 1
B) 4
C) 5
D) 12
Answer:
[C]

Think – Discuss

Question 1.
Observe the following collections and prepare as many as generalised statements you can describing their more properties. (Page No. 26)
i) 2, 4, 6, 8, ….
ii) 1, 4, 9, 16
Answer:
i) 3, 6, 9, 12, ….
Property : multiples of 3.

ii) 1, 8, 27, 64,….
Property : cube of the numbers, i.e., 1³, 2³, 3³, 4³, ….

Question 2.
Can you write the set of rational numbers listing elements in it ? (Page No. 28)
Solution:
No

Try This

Question 1.
Write some sets of your choice, involving algebraic and geometrical ideas. (Page No. 29)
Answer:
1) The natural number greater than three and less than twelve.
2) A two digit number such that the sum of its digits is 8.
3) The set of quadrilaterals.
4) The set of all triangles in a plane.

Question 2.
Match roaster forms with the set builder form.
i) {P, R, I, N, C, A, L}
ii) {0}
iii) {1, 2, 3, 6, 9, 18}
iv) {3, -3} (Page No. 29)
a) {x : x is a positive integer and is a divisor of 18}
b) {x : x is an integer and x² – 9 = 0}
c) {x : x is an integer and x + 1 = 1}
d) {x: x is a letter of the word PRINCIPAL}
Answer:
i) d
ii) c
iii) a
iv) b

Do This

Question 1.
A = {1, 2, 3, 4}, B = {2, 4}, C = {1, 2, 3, 4, 7}, F = { } (Page No. 33)
Fill in the blanks with ⊂ or ⊄.
i) A………B
ii) C……..A
iii) B……..A
iv) A……..C
v) B……..C
vi) F……B
Answer:
i) A⊄B
ii) C⊄A
iii) B⊂A
iv) A⊂C
v) B⊂C
vi) F⊂B

Question 2.
State which of the following statements are true. (Page No. 33)
i) { } = ϕ
ii) ϕ = 0
iii) 0 = {ϕ}
Answer:
i) True (T)
ii) False (F)
iii) False (F)

Question 3.
Let A = {1, 3, 7, 8} and B = {2, 4, 7, 9}. Find A∩B.(Page No. 37)
Solution:
Given sets
A = {1, 3, 7, 8} and B = {2, 4, 7, 9}
A ∩ B = {1, 3, 7, 8} ∩ {2, 4, 7, 9}
= {7}

Question 4.
If A = {6, 9, 11}; ϕ = { }, find A ∪ ϕ. (Page No. 37)
Solution:
Given sets A = {6, 9, 11} and B = {2, 4, 7, 9}
A ∪ ϕ = {6, 9, 11} ∪ {ϕ}
= {6, 9, 11} = A
∴ A ∪ ϕ = A

Question 5.
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
B = {2, 3, 5, 7}. Find A ∩ B. (Page No. 37) (June ’15(AP))
Solution:
Given sets A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = {2, 3, 5, 7}
A ∩ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {2, 3, 5, 7}
= {2, 3, 5, 7} = B
∴ A ∩ B = B

Question 6.
If A = {4, 5, 6}; B = {7, 8}, then show that A ∪ B = B ∪ A. (Page No. 37)
Solution:
Given sets are
A = (4, 5, 6} and B = (7, 8}
A ∪ B = {4, 5, 6} ∪ {7, 8}
= {4, 5, 6, 7, 8}
B ∪ A = {7, 8} ∪ {4, 5, 6}
= {4, 5, 6, 7, 8}
∴ A ∪ B = B ∪ A

Question 7.
If A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7} then find A-B and B-A. Are they equal ? (Page No. 38)
Solution:
Given sets are A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7}
A – B = {1, 2, 3, 4, 5} – {4, 5, 6, 7} = {1, 2, 3}
B – A = {4, 5, 6, 7} – {1, 2, 3, 4, 5} = {6, 7}
No, A – B ≠ B – A

Question 8.
If V = {a, e, i, o, u} and B = {a, i, k, u}, find V – B and B – V. (Page No. 38)
Solution:
Given sets are
V = {a, e, i, o, u} and B = {a, i, k, u}
V – B = {a, e, i, o, u} – {a, i, k, u}
= {e, o}
B – V = {a, i, k, u} – {a, e, i, o, u}
= {k}

Try This

Question 1.
A = {set of quadrilaterals}, B = {square, rectangle, trapezium, rhombus}
State whether
A ⊂ B or B ⊂ A. Justify your answer. (Page No. 33)
Answer:
A ⊄ B
B ⊂ A every element of B is also an element of A.

Question 2.
If A = {a, b, c, d}. How many subsets does the set A have? (Remember null set and equal sets). (Page No. 33)
A) 5
B) 6
C) 16
D) 65
Solution:
A = {a, b, c, d}
Subsets of A = {a}, {b}, {c}, {d};
n(A) = 4
Number of subsets for a set, which is having ‘n’ elements is 2ⁿ.
So n(A) = 4
Number of subsets for A is 2⁴ =16.
Answer:
(C)

Question 3.
P is the set of factors 5, Q is the set of factors of 25 and R is the set of factors of 125.
Which one of the following is false?
A) P ⊂ Q
B) Q ⊂ R
C) R ⊂ P
D) P ⊂ R (Page No. 33)
Solution:
P = {1, 5}
Q = {1, 5, 25}
R = {1, 5, 25, 125}
Answer:
(C)

Question 4.
A is the set of prime numbers less than 10, B is the set of odd numbers < 10 and C is the set of even numbers < 10. How many of the following statements are true ? (Page No. 33)
i) A ⊂ B
ii) B ⊂ A
iii) A ⊂ C
iv) C ⊂ A
v) B ⊂ C
vi) X ⊂ A
Solution:
A = {2, 3, 5, 7}
B = {1, 3, 5, 7, 9}
C = {2, 4, 6, 8}
The given all statements are false.

Question 5.
List out some sets A and B and choose their elements such that A and B are disjoint. (Page No. 37)
Solution:
A and B are disjoint sets.
i) A = {2, 3, 5} B = {4, 6, 8}
ii) A = {1, 2, 3} B = {4, 5, 6}
iii) A = {1, 3, 5, 7} B = {2, 4, 6, 8}

Question 6
If A = {2, 3, 5}, find A∪ϕ and ϕ∪A and compare. (Page No. 37)
Solution:
A = {2, 3, 5}; ϕ = { }
A∪ϕ = {2, 3, 5} ∪ { } = {2, 3, 5}
ϕ∪A = { } ∪ {2, 3, 5} = {2, 3, 5}
∴ A∪ϕ = ϕ∪A

Question 7.
If A = {1, 2, 3, 4}; B = {1, 2, 3, 4, 5, 6, 7, 8} then find A ∪ B, A ∩ B. What do you notice about the result ? (Pg. No. 37)
Solution:
A = {1, 2, 3, 4};
B = {1, 2, 3, 4, 5, 6, 7, 8}
A∪B = {1, 2, 3, 4} ∪ {1, 2, 3, 4, 5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}
The common elements in both A and B sets are 1, 2, 3, 4.
A∩B = {1, 2, 3, 4}
Result :
i) A∪B = B
ii) A∩B = A
iii) A ∩ B ⊂ A ∪ B

Question 8.
A = {1, 2, 3, 4, 5, 6}; B = {2, 4, 6, 8, 10}. Find the intersection of A and B. (Page No. 37)
Solution:
A = {1, 2, 3, 4, 5, 6}
B = {2, 4, 6, 8, 10}
The common elements in both A and B are 2, 4, 6.
∴ A ∩ B = {2, 4, 6}

Think : Discuss

Question 1.
Is empty set subset to every set? (Page No. 34)
Solution:
Yes.

Question 2.
Is any set subset to itself? (Page No. 34)
Solution:
Yes.

Question 3.
You are given two sets such that a set is not a subset of the other. If you have to prove this, how do you prove ? Justify your answers. (Page No. 34)
Solution:
The above statement is true only in the two sets does not have common elements.
Ex : A = {1, 2, 3}; B = {4, 5, 6}
So, A⊊B.

Question 4.
The intersection of any two disjoint sets is a null set. Justify your answer. (Page No. 37)
Answer:
Yes, this statement is true because A ∩ B = ϕ when A and B are disjoint sets.

Question 5.
The sets A – B, B – A and A ∩ B are mutually disjoint sets. Use examples to observe if this is true. (Page No. 38)
Solution:
Let the sets are
A = {1, 2, 3, 4} and B = {5, 6, 7, 8}
A – B = {1, 2, 3, 4} – {5, 6, 7, 8} = {1, 2, 3, 4}
B – A = {5, 6, 7, 8} – {1, 2, 3, 4} = {5, 6, 7, 8}
A ∩ B = {1, 2, 3, 4} ∩ {5, 6, 7, 8} = { } = ϕ
∴ A – B, B – A and A ∩ B are disjoint sets.

Do This

Question 1.
Which of the following are empty sets? Justify your answer. (Page No. 44)
i) Set of integers which lie between 2 and 3.
ii) Set of natural numbers that are less than 1.
iii)Set of odd numbers that have remainder zero, when divided by 2.
Answer:
i) This is null set. We know that there is no integer that lie between 2 and 3.
ii) This is also a null set. We know that there is natural number less than ‘1’.
iii) This is a null set. We know that odd numbers do not leave remainder zero when divided by 2.

Question 2.
State which of the following sets are finite and which are infinite. Give reasons for your answers.
i) A = {x: x ∈ N and x < 100}
ii) B = {x : x ∈ N and x ≤ 5}
iii)C = {1², 2², 3², ………… )
iv)D = {1, 2, 3, 4)
v) {x : x is a day of the week) (Page No. 44)
Answer:
i) A = {1, 2, 3, ………., 98, 99}
This set is finite, because there are 99 numbers possible to count.

ii) B = {1, 2, 3. 4, 5}
This set is finite, because there are 5 numbers possible to count.

iii) C = {1², 2², 3²,………)
This set is infinite, because there are infinite numbers.

iv) D = {1, 2, 3, 4}
This set is finite because there are 4 numbers that are possible to count.

v) E = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday)
This set is finite, because there are 7 days in a week possible to count.

Question 3.
Tick the set which is infinite
A) The set of whole numbers < 10
B) The set of prime numbers < 10
C) The set of integers < 10
D) The set of factors of 10 (Page No. 44)
Answer:
[C]
The set of integers < 10
{……., -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Try This

Question 1.
Which of the following sets are empty sets? Justify your answer.
i) A = {x : x² = 4 and 3x = 9}
ii) The set of all triangles in a plane having the sum of their three angles less than 180. (Page No. 44)
Answer:
i) Empty set.
To satisfy these equations same x value is not possible.
ii) Empty set.
The sum of the three angles of a triangle is equal to 180°.

Question 2.
B = {x : x + 5 = 5} is not an emptyset. Why? (Page No. 44)
Solution:
x + 5 = 5
x = 5 – 5
x = 0
For x = 0 it is true
Only one element is there.
So it is not an empty set.

Think — Discuss

Question 1.
An empty set is a finite set. Is this statement true or false? Why? (Page No. 44)
Answer:
Yes, it is a finite set because there is finite number i.e., ‘0’ elements it consists.

Question 2.
What is the relation between n(A), n(B), n(A ∩ B) and n (A ∪ B)? (Page No. 45)
Solution:
n(A) = elements in set A, n(B) = elements in set B
n(A ∩ B) = set of all elements which are common to both A and B.
n(A ∪ B) = elements in set A and set B (or) union of sets A and B.
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Question 3.
If A and B are disjoint sets, then how can you find n(A ∪ B)? (Page No. 45)
Solution:
n(A) = elements in set A.
n(B) = elements in set B.
n(A ∩ B) = elements in set A and set B
Here it is ‘0’ (∴ A and B are disjoint sets)
n(A ∪ B) = elements in set A or set B.
∴ n(A ∪ B) = n(A) ÷ n(B) – n(A ∩ B)
= n(A) + n(B) – 0
= n(A) + n(B).

Students can practice TS 10th Class Maths Solutions Chapter 2 Sets Ex 2.3 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 2 Sets Exercise 2.3

Question 1.
Which of the following sets are equal ?
a) A = {x : x is a letter in the word FOLLOW’}
b) B = {x : x is a letter in the word ‘FLOW’}
c) C = {x : x is a letter in the word ‘WOLF’}
Answer:
a) Writing the given set in the roaster form, we have A = {F, O, L, W}
b) Writing the given set in the roaster form, we have B = {F, L, O, W}
c) Writing the given set in the roaster form, we have C = {W, O, L, F}
Therefore, A, B, C are equal sets.
[∴ The sets A, B, C have exactly the same elements]

Question 2.
Consider the following sets and fill up the blank in the statement given below with = or ≠ so as to make the statement true.
A = {1, 2, 3};
B = {The first three natural numbers}
C = {a, b, c, d};
D = {d, c, a, b}
E = {a, e, i, o, u};
F = {set of vowels in English Alphabet}
i) A ……… B
ii) A …….. E
iii) C ……. D
iv) D …… F
v) F ……. A
vi) D …… E
vii) F ……. B
Answer:
i) A = B
ii) A ≠ E
iii) C=D
iv) D ≠ F
v) F ≠ A
vii) D ≠ E
viii) F ≠ B

Question 3.
In each of the following, state whether
A = B or not.
i) A = {a, b, c, d}; B = {d, c, a, b}
ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
iii) A = (2, 4, 6, 8, 10)
B = {x: x is a positive even integer and x ≤ 10}
iv) A = {x: x ¡s a multiple of 10};
B = {10, 15, 20, 25, 30,……. }
Answer:
i) A = B because A and B have exactly the same elements i.e., a, b, c, d.
ii) A ≠ B because A and B have not exactly the same elements.
iii) A = B because A and B have exactly the same elements.
Writing B in roaster form, we have
B = {2, 4, 6, 8, 10}
iv) A = {10, 20, 30, 40,……..}
B = {10, 15, 20, 25,……..}
A ≠ B because A and B have not exactly the same elements.

Question 4.
State the reasons for the following:
i) {1,2, 3,…, 10} ≠ {x : x ∈ N and 1 < x < 10}
ii) {2, 4, 6, 8, 10} ≠ {x : x = 2n + 1 and x ∈ N}
iii) {5, 15, 30, 45} ≠ {x : x is a multiple of 15
iv) {2, 3, 5, 7, 9} ≠ {x : x is a prime number}
Solution:
The first set is {1, 2, 3, ……, 10}
Writing the second set in roaster form, we have {2, 3, 4, ……, 9}
The first set and the second set have not exactly the same elements.
∴ {1, 2, 3,……10} ≠ {x : x ∈ N and 1 < x < 10}

ii) The first set is {2, 4, 6, 8, 10}
Writing the second set in roaster form, we have {3, 5, 7, 9, ….}
∴ {2, 4, 6, 8, 10} ≠ {3, 5, 7, 9, ….}
x = 2n + 1 means x is odd.

iii) The first set is {5, 15, 30, 45}
Writing the second set in roaster form, we have {15, 30, 45, 60, …}
∴ {5, 15, 30, 45} ≠ {15, 30, 45, 60,…}
5 does not exist, since x is multiple of 15.

iv) The first set is {2, 3, 5, 7, 9}
Writing the second set in roaster form, we have {2, 3, 5, 7, 11, 13,…}
∴ {2, 3, 5, 7, 9} ≠ {2, 3, 5, 7, 11, 13 }
9 is not a prime number.

Question 5.
List all the subsets of the following sets.
i) B = {p, q}
ii) C = {x, y, z}
iii) D = {a, b, c, d}
iv) E = {1, 4, 9, 16}
v) F = {10, 100, 1000}
Solution:
i) {p}, {q}, {p, q}, { ϕ }
ii) {x}, {y}, {z}, {x, y}, {y, z}, {x, z}, {x, y, z}, {ϕ}
iii) {a}, {b}, {c}, {d}, {a, b}, {b, c}, {c, d}, {a, c}, [a, d}, {b, d}, {a, b, c}, {b, c, d}, {a, b, d}, {a, c, d}, {a, b, c, d}, {ϕ}
iv) {1}, {4}, {9}, {16}, {1, 4}, {4, 9}, {9, 16}, {1, 9}, {1, 16}, {4, 16}, {1, 4, 9}, {4, 9, 16}, {1, 4, 16}, {1, 9, 16}, {1, 4, 9, 16}, {ϕ}
v) {10}, {100}, {1000}, {10, 100}, {100, 1000}, {10, 1000}, {10, 100, 1000}, {ϕ}

Students can practice TS 10th Class Maths Solutions Chapter 2 Sets Ex 2.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 2 Sets Exercise 2.2

Question 1.
If A = {1, 2, 3, 4} and B = {3, 4, 5, 6}, then find A ∩ B and B ∩ C. Are they same ?
Solution:
A = {1, 2, 3, 4}; B = {1, 2, 3, 5, 6}
∴ A ∩ B = {1, 2, 3, 4} ∩ {1, 2, 3, 5, 6}
= {1, 2, 3}
B ∩ A = {1, 2, 3, 5, 6} ∩ {1, 2, 3, 4)
= {1, 2, 3}
Yes, A ∩ B and B ∩ A are same.

Question 2.
A = {0, 2, 4}, find A ∩ ϕ and A ∩ A. Comments. (June 15(A.P.))
Solution:
A = {0, 2, 4}
A ∩ ϕ = {0, 2, 4} ∩ ϕ
= ϕ
A ∩ A = {0, 2, 4} ∩ {0, 2, 4}
= {0, 2, 4} = A

Question 3.
If A = {2, 4, 6, 8, 10} and B = {3, 6, 9, 12, 15}, find A – B and B – A.
Solution:
A = {2, 4, 6, 8, 10);
B = {3, 6, 9, 12, 15)
A – B = {2, 4, 8, 10}
B – A = {3, 9, 12, 15}

Question 4.
If A and B are two sets such that A ⊂ B then what is A ∪ B?
Solution:
Let us consider A ⊂ B.
Set A = {1, 2, 3}
Set B = {1, 2, 3, 4, 5}
A ∪ B = {1, 2, 3} ∪ {1, 2, 3, 4, 5)
= {1, 2, 3, 4, 5}
= B
A ∪ B = B

Question 5.
If A = {x : x is a natural number}
B = {x : x is an even natural number}
C = {x : x is an odd natural number}
D = {x : x is a prime number
Find A∩B, A∩C, A∩D, B∩C, B∩D, C∩D.
Solution:
A = {1, 2, 3, 4, …….. }
B = {2, 4, 6, 8, ……….}
C = {1, 3, 5,7, ……….}
D = {2, 3, 5, 7, ……….}
A ∩ B = {1, 2, 3, 4,………. } ∩ {2, 4, 6, 8,………. }
= {2, 4, 6,…… }
= {even natural numbers)
A ∩ C = {1, 2, 3, 4,……} ∩ {1, 3, 5,……}
= {1, 3, 5,………}
= {odd natural numbers}
A ∩ D = {1, 2, 3, 4,……} ∩ {2, 3, 5, 7, ……..}
= {2, 3, ………}
= {prime natural numbers}
B ∩ C = {2, 4, 6, 8,…..} ∩ {1, 3, 5, 7, …….}
= ϕ
= Null set (Or) empty set
B ∩ D = {2, 4, 6, 8,…….. } ∩ {2, 3, 5, 7,…….. }
= {2} = {even natural number}
C ∩ D = {1, 3, 5, 7,……. } ∩ {2, 3, 5, 7,…….}
= {3, 5, 7,…….. }
= {All odd prime numbers)

Question 6.
If A = {3, 6, 9, 12, 15, 18, 21);
B = {4, 8, 12, 16, 20};
C = {2, 4, 6, 8, 10, 12, 14, 16};
D = {5, 10, 15, 20}, find
i) A – B
ii) A – C
iii) A – D
iv) B – A
v) C – A
vi) D – A
vii) B – C
viii) B – D
ix) C – B
x) D – B
Solution:
i) A – B = {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}

ii) A – C = {3, 6, 9, 12, 15, 18, 21} – {2, 4, 6, 8, 10, 12, 14, 16)
= {3, 9, 15, 18, 21}

iii) A – D = {3, 6, 9, 12, 15, 18, 21} – {5, 10, 15, 20}
= {3, 6, 9, 12, 18, 21}

iv) B – A = {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21}
= {4, 8, 16, 20}

v) C – A = {2, 4, 6, 8, 10, 12, 14, 16} – {3, 6, 9, 12, 15, 18, 21}
= {2, 4, 8, 10, 14, 16}

vi) D – A = {5, 10, 15, 20} — {3, 6, 9, 12, 15, 18, 21)
= (5, 10, 20)

vii) B – C = {4, 8, 12, 16, 20) – {2, 4, 6, 8, 10, 12, 14, 16}
= {20}

viii) B — D = {4, 8, 12, 16, 20} – {5, 10, 15, 20}
= {4, 8, 12, 16)

ix) C – B = {2, 4, 6, 8, 10, 12, 14, 16} – {4, 8, 12, 16, 20}
= {2, 6, 10, 14)

x) D – B = {5, 10, 15, 20} – {4, 8, 12, 16, 20}
= {5, 10, 15}

Question 7.
State whether each of the following statement is true or false. Justify your answers.
i) {2, 3, 4, 5} and {3, 6) are disjoint sets.
ii) {a, e, i, o, u) and {a, b, c, d) are disjoint sets.
iii){2, 6, 10, 14) and {3, 7, 11, 15) are disjoint sets.
iv) (2, 6, 10) and {3, 7, 11) are disjoint sets.
Answer:
Two sets are said to be disjoint sets when they have no elements in common.
i) In the given two sets. ‘3’ is common. So, they are not disjoint sets. Hence, the given statement is false.
ii) In the given two sets, ‘a’ is common. So, they are not disjoint sets. Hence, the given statement is false.
iii) There are no elements common in the given two sets. So they are disjoint sets. Hence, the given statement is true.
iv) There are no elements common in the given two sets, So they are disjoint sets. Hence. the given statement is true.

Students can practice TS 10th Class Maths Solutions Chapter 2 Sets Ex 2.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 2 Sets Exercise 2.1

Question 1.
Which of the following are sets? Justify your answer.
(i) The collection of all the months of a year begining with the letter “J”.
Answer:
The months of a year which begin with the letter “J” are January, June and July.
The required set is {January, June, July}.
∴ The given statement is a well defined collection of objects. So, it is a set.

(ii) The collection of ten most talented writers of India.
Answer:
The given statement is not a set because the criterion for determining as most talented writers of India may vary from person to person. Thus, it is not a well defined collection.

(iii) A team of eleven best cricket batsmen of the world.
Answer:
The given statement is not a set because the criterion for determining eleven best cricket batsmen of the world may vary from person to person.

(iv) The collection of all boys in your class.
Answer:
The given statement is a set because given a student we can divide whether he/she belongs to the set or not.

(v) The collection of all even integers.
Answer:
The given statement is a set because given a number we can divide whether the number belongs to the given set or not.

Question 2.
If A = {0, 2, 4, 6}, B = {3, 5, 7} and C = {p, q, r}, then fill the appropriate symbol, ∈ or ∉ in the blanks.
(i) 0 ….. A
Answer:
0 ∈ A

(ii) 3 …… C
Answer:
3 ∉ C

(iii) 4 ….. B
Answer:
4 ∉ B

(iv) 8 ….. A
Answer:
8 ∉ A

(v) p …… C
Answer:
p ∈ C

(vi) 7 …… B
Answer:
7 ∈ B

Question 3.
Express the following statements using symbols.
(i) The element ‘x’ does not belong to ‘A’.
Answer:
x ∉ A

(ii) ‘d’ is an element of the set ‘B’.
Answer:
d ∈ B

(iii) ‘1’ belongs to the set of Natural numbers.
Answer:
1 ∈ N

(iv) ‘8’ does not belong to the set of prime numbers P.
Answer:
8 ∉ P

Question 4.
State whether the following statements are true or false. Justify your answer
(i) 5 ∉ set of prime numbers
Answer:
Not true (5 is a prime number)

(ii) S ∈ {5, 6, 7} implies 8 ∈ S.
Answer:
Not true (8 is not a member of S)

(iii) -5 ∉ W where ‘W’ is the set of whole numbers
Answer:
True (-5 is not a member of W)

(iv) \(\frac{8}{11}\) ∈ Z Where ‘Z’ is the set of integers.
Answer:
Not true (\(\frac{8}{11}\) is a rational number)

Question 5.
Write the following sets in roster form.

(i) B = {x : x is a natural number smaller than 6}
Answer:
B = {1, 2, 3, 4, 5}

(ii) C = {x : x is a two-digit natural number such that the sum of its digits is 8}.
Answer:
C = {17, 26, 35, 44, 53, 62, 71}

(iii) D = {x : x is a prime number which is a divisor of 60}.
Answer:
D = {3, 5}

(iv) E = {x : x is an alphabet in BETTER}.
Answer:
E = {B, E, T, R}

Question 6.
Write the following sets in the set-builder form.
(i) {3, 6, 9, 12}
Answer:
A = {x: x is multiple of 3 and less than 13}

(ii) {2, 4, 8, 16, 32}
Answer:
B = {x : x is in power of 2 and x is less than 6}

(iii) {5, 25, 125, 625}
Answer:
C = {x : x is in power of 5 and x is less than 5}

(iv) {1, 4, 9, 16, 25, 100}
Answer:
D = {x : x is in square of natural number and not greater than 10)

Question 7.
Write the following sets in roster form.
(i) A = {x : x is a natural number greater than 50 but smaller than 100}
Answer:
A = {51, 52, 53, 54….., 98, 99}

(ii) B = {x : x is an integer, x = 4}
Answer:
B = {+2, -2}

(iii) D = {x : x is a letter in the word “LOYAL”}
Answer:
D = {L, O, Y, A}

Question 8.
Match the roster form with set builder form.

Answer:
i) c
ii) a
iii) d
iv) b

Students can practice TS 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.5 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 1 Real Numbers Exercise 1.5

Question 1.
Determine the value of the following.

(i) log₂₅5
Solution:
Let log₂₅5 = x ∵ log_aN = x ⇒ a^x = N
25^x = 5; 5^2x = 5¹ ⇒ a^x = N
⇒ 2x = 1 ⇒ x = \(\frac{1}{2}\)
log₂₅5 = \(\frac{1}{2}\)

(ii) log₈₁3
Solution:
log₈₁3 = x ∵ log<sub.aN = x
81^x = 3 ⇒ (3⁴)^x = 3¹ ⇒ a^x = N
⇒ 4x = 1 ⇒ x = \(\frac{1}{4}\)
log₈₁3 = \(\frac{1}{4}\)

(iii) log₂ \(\left(\frac{1}{16}\right)\)
Solution:
log₂\(\frac{1}{16}\) = x ∵ log_aN = x ⇒ a^x = N
⇒ Then 2^x = \(\frac{1}{16}\) ⇒ 2^x = \(\frac{1}{2^4}\) = 2^-4
⇒ x = – 4
los₂(\(\frac{1}{16}\)) = -4

(iv) log₇1
Solution:
log₇1 = x ∵ log_aN = x ⇒ a^x = N
⇒ Then 7^x = 1 ⇒ 7^x – 7⁰ ⇒ x = 0
⇒ log₁a = 0

(v) log_x \(\sqrt{x}\)
Solution:
log_x \(\sqrt{x}\) ∵ log_aN = x ⇒ a^x = N
⇒ Then x^y = \(\sqrt{x}\) ⇒ x^y = x^1/2
⇒ y = \(\frac{1}{2}\)
log_x \(\sqrt{x}\) = \(\frac{1}{2}\)

(vi) log₂512
Solution:
log₂ 512 ∵ log_aN = x ⇒ a^x = N
⇒ Then 2^x = 512 ⇒ 2^x = 2⁹
⇒ x = 9
log₂512 = 9

(vii) log₁₀0.01
Solution:
log₁₀0.01 = x ∵ log_aN = x ⇒ a^x = N
Then 10^x = 0.01
⇒ 10^x = 10^-2
⇒ x = -2
log₁₀0.01 = -2

(viii) \(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\)
Solution:
\(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\) ∵ log_aN = x ⇒ a^x = N
\(\left(\frac{2}{3}\right)^x\) = \(\frac{8}{27}\)
\(\left(\frac{2}{3}\right)^2\) = \(\left(\frac{2}{3}\right)^3\) ⇒ x = 3
\(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\) = 3

(ix) \(2^{2+\log _2^3}\)
Solution:
\(2^{2+\log _2^3}\) ∵ \(a^{\log _a^m}\) = m
= 2² × \(2^{\log _2^3}\)
= 4 × 3 = 12

Question 2.
Write the following expressions as log N and find their values.

(i) log 2 + log 5
Solution:
log 2 + log 5
∵ log x + log y = log xy
log 2 + log 5 = log (2 × 5)
= log (2 × 5)
= log 10

(ii) log 16 – log 2
Solution:
log 16 – log 2
∵ log x – log y = log \(\left(\frac{x}{y}\right)\)
log 16 – log 2 = log \(\left(\frac{16}{2}\right)\) = log 8

(iii) 3 log 4
Solution:
3 log 4
∵ m log_ax = log_ax^m
3 log 4 = log 4³ = log 64

(iv) 2 log 3 – 3 log 2
Solution:
2 log 3 – 3 log 2 ∵ m log a = log a^m
log x – log y = log\(\frac{x}{y}\)

log 3² – log 2³
log \(\frac{3^2}{2^3}\) = log \(\frac{9}{8}\)

(v) log 243 + log 1
Solution:
log 243 + log 1 ∵ log x + log y = log xy
= log 243 × 1
= log 243

(vi) log 10 + 2 log 3 – log 2
Solution:
log 10 + 2 log 3 – log 2
= log 10 + log 3² – log 2
= log 10 + log 9 – log 2
= log 90 – log 2
= log \(\frac{90}{2}\) = log 45

Question 3.
Evaluate each of the following in terms of x and y, if it is given that x = log₂3 and y = log₂5
(i) log₂ 15
(ii) log₂ 7.5
(iii) log₂60
(iv) log₂6750
Solution:

Question 4.
Expand the following.

(i) log 1000
Solution:

= 3 log 2 + 3 log 5
= 3 [log 2 + log 5]

(ii) log₂\(\left(\frac{128}{625}\right)\)
Solution:
log \(\left(\frac{128}{625}\right)\)

(iii) log x²y³z⁴
Solution:
log x²y³z⁴
= log x² + log y³ + log z⁴
= 2 log x + 3 log y + 4 log z

(iv) log \(\frac{p^2 q^3}{r}\)
Solution:
log \(\frac{p^2 q^3}{r}\)
log (p²q³) – log r
= log p² + log q³ – log r
= 2 log p + 3 log q – log r

(v) \(\log \sqrt{\frac{x^3}{y^2}}\)
Solution:
log \(\sqrt{\frac{x^3}{y^2}}\) ∵ log x^m = m log x
= log \(\left(\frac{x^3}{y^2}\right)^{1 / 2}\) = \(\frac{1}{2} \log \left(\frac{x^3}{y^2}\right)\)
= \(\frac{1}{2}\)[log x³ – log y²]
= \(\frac{1}{2}\)[3 log x – 2 log y]

Question 5.
If x² + y² = 25xy, then prove that 2 log(x + y) = 3log3 + logx + logy.
Solution:
Given x² + y² = 25xy
Adding ‘2xy’ on both sides.
x² + y² + 2xy = 25xy + 2xy
(x + y)² = 27xy
Applying ‘log’ on both sides
log(x + y)² = log 27xy
2log(x + y) = log(3³ × x × y)
= log3³ + log x + log y
∴ 2log(x + y) = 31og3 + logx + logy

Question 6.
If log\(\left(\frac{x+y}{3}\right)\) = \(\frac{1}{2}\)log(x + y) = 3log3 + logx + logy.
Solution:

Squaring on both sides

Question 7.
If (2.3)^x = (0.23)^y = 1000, then find the value of \(\frac{1}{x}\) – \(\frac{1}{y}\).
Solution:
Given : (2.3)^x = (0.23)^y = 1000
(2.3)^x = 1000 = 10³
∴ 2.3 = \(10^{\frac{3}{x}}\)
Also (0.23)^y = 10³
∴ 0.23 = \(10^{\frac{3}{y}}\)
Now 0.23 = \(\frac{2.3}{10}\)

Question 8.
If 2^x+1 = 3^1-x then find the value of x.
Solution:
Given : 2^{x + 1} = 3^{1 – x}
Taking log on b.t.s
log 2^{x + 1} = log 3^{1 – x}
(x + 1) log 2 = (1 – x) log 3
x log 2 + log 2 = log 3 – x log 3
x log 2 + x log 3 = log 3 – log 2
x (log 3 + log 2) = log 3 – log 2
∴ x = \(\frac{\log 3-\log 2}{\log 3+\log 2}\) = \(\frac{\log \frac{3}{2}}{\log 6}\)

Question 9.
Is (i) log 2 rational or irrational? Justify your answer.
(ii) log 100 rational or irrational? Justify your answer.
Solution:
i) log2 is rational. Since the value of log₁₀2
= 0.3010

(ii) log 100 rational or irrational? Justify your answer.
Solution:
log 100 is rational
∴ log₁₀100 = log₁₀10²
= 2 log₁₀10 = 2

Students can practice TS 10th Class Maths Solutions Chapter 1 Real Numbers InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 1 Real Numbers InText Questions

Do This

Question 1.
Find ‘q’ and ‘r’ for the following pairs of positive integers ‘a’ and ‘b’, satisfied a = bq + r
i) a = 13, b = 3
Solution:
a = 13, b = 3
a = bq + r
13 = 3(4) + 1 Here q = 4; r = 1
13 = 13

ii) a = 8, b = 80
Solution:
a = 8, b = 80
a = bq + r Here q = \(\frac{1}{10}\) and r = 0
8 = 80\(\left(\frac{1}{10}\right)\) + 0, 8 = 8

iii) a = 125; b = 5
Solution:
a = 125; b = 5
a = bq + r
q = 25, r = 0
125 = 5(25) + 0
125 = 125

iv) a = 132; b = 11
Solution:
a = 132; b = 11
a = bq + r
q = 12, r = 0
132 = 11(12) + 0
132 = 132

Question 2.
Find the HCF of the following by using Euclid division lemma (Page No. 4)
i) 50 and 70
ii) 96 and 72
iii) 300 and 550
iv) 1860 and 2615
Euclid Division Lemma
a = bq + r, q > 0 and 0 ≤ r < b
Solution:
i) 50 and 70 When 70 is divided by 50, the remainder is 20 to get 70 = 50 × 1 + 20
Now consider the division of 50, with the remainder 20 in the above and apply the division lemma to get 50 = 20 × 2 + 10
Now consider the division of 20, with the remainder 10 in apply the division lemma to get 20 = 10 × 2 + 0
The remainder = 0, when we cannot proceed further.
We conclude that the HCF of 50 and 70 is the divisor at this stage, i.e., 10
∴ So, HCF of 50 and 70 is 10.

ii) 96 and 72 When 96 is divided by 72, the remainder is 24 to get 96 = 72 × 1 + 24
Now consider the division of 72, with the remainder 24 in the above and apply the division lemma to get, 72 = 24 x 3 + 0
The remainder = 0, when we cannot proceed further.
We conclude that the HCF of 96 and 72 is the divisor at this stage, i.e., 24 so, the HCF of 96 and 72 is 24

iii) 300 and 550 When 550 is divided by 300, the remainder is 250, to get 550 = 300 × 1 + 250
Now consider the division of 300 with the remainder 250, and apply the division lemma to get 300 = 250 × 1 + 50
Now consider the division of 250 with the remainder 50, and apply the division lemma to get 250 = 50 × 5 + 0. The remainder is zero, when we cannot proceed further. We conclude that the H.C.F of 300 and 550 is the divisor at this stage i.e., 50. So, the H.C.F of 300 and 550 is 50.

iv) 1860 and 2015 When 2015 is divided by 1860, the remainder is 155, to get 2015 = 1860 × 1 + 155
Now consider the division of 1860 with the remainder 155, and apply the division lemma to get 1860 = 155 × 12 + 0
The remainder is zero, then we cannot proceed further.
We conclude that the HCF of 1860 and 2015 is the divisor at this stage i.e., 155 So, the HCF of 1860 and 2015 is 155

Think – Discuss

Question 1.
From the above questions in do this what is the nature of q and r ? (Page No. 3)
Solution:
Given a = bq + r q > 0 and r ≤ 0 r < b r lies between 0 and b

Question 2.
Can you find the HCF of 1.2 and 0.12 ? Justify your answer. (Page No. 4)
Solution:
1.2 = \(\frac{12}{10}\) and 0.12 = \(\frac{12}{100}\)
When \(\frac{12}{10}\) is divided by \(\frac{12}{100}\), then the remainder is 0.
\(\frac{12}{10}\) = \(\frac{12}{100}\) × 10 + 0
∴ yes, we can find the HCF of 1.2 and 0.12 HCF (1.2, 0.12) = 10

Textual Examples

Question 1.
Show that every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer. (Page No. 5)
Solution:
Let a be any positive integer and b = 2. Then, by Euclid’s algorithm, a = 2q + r, for some integer q ≥ 0, and r = 0 or r = 1, because 0 ≤ r < 2. So, a = 2q or 2q + 1.
If a is of the form 2q, then a is an even integer. Also, a positive integer can be either even or odd. Therefore, any positive odd integer is of the form 2q + 1.

Question 2.
Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer. (Page No. 5)
Solution:
Let us start with taking a, where a is a positive odd integer. We apply the division algorithm with a and b = 4. Since 0 ≤ r < 4, the possible remainders are 0, 1, 2 and 3.
That is, a can be 4q, or 4q + 1, or 4q + 2, or 4q + 3, where q is the quotient. However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Therefore, any odd integer is of the form 4q + 1 or 4q + 3.

Think – Discuss

Question 1.
If r = 0, then what is the relationship between a, b and q in a = bq + r of Euclid division lemma? (Page No. 6)
Solution:
a = bq + 0 (∵ r = 0) ⇒ a = bq

Do This

Question 1.
Express 2310 as a product of prime factors. Also see how your friends have factorized the number. Have they done it like you ? Verify your final product with your friend’s result. Try this for 3 or 4 more numbers. What do you conclude ?
(Page No. 7)
Solution:
2310 = 2 × 1155
= 2 × 5 × (231)
= 2 × 5 × 3 × 77
= 2 × 5 × 3 × 7 × 11
= 2 × 3 × 5 × 7 × 11
Ramu, Kiran and Mohan are my friends. They factorized the number in the following way :
Ramu : 2310 = 231 × 10
= 3 × 77 × 2 × 5
= 3 × 7 × 11 × 2 × 5
Kiran : 2310 = 3 × 770
= 3 × 10 × 77
= 3 × 10 × 11 × 7
= 3 × 2 × 5 × 11 × 7
Mohan : 2310 = 7 × 330
= 7 × 3 × 110
= 7 × 3 × 11 × 10
= 7 × 3 × 11 × 2 × 5
No, but the prime factors are same.
The final product with your friends result is same.
Conclusion : The order in which the prime factors occur, the composite number is unique.

Question 2.
Find the HCF and LCM of the following given pairs of numbers by prime factorisation.
i) 120, 90
ii) 50, 60
iii) 37, 49 (Page No. 8)
H.C.F. : (Product of smallest power of each common prime factor of the numbers)
L.C.M. : (Product of greatest power of each prime factors of the numbers)
Solution:
i) 120, 90
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3¹ × 5¹
90 = 2 × 3 × 3 × 5 = 2¹ × 3² × 5¹
HCF (120, 90) = 2¹ × 3¹ × 5¹ = 30
LCM (120, 90) = 2³ × 3² × 5¹ = 360

ii) 50, 60
50 = 2 × 5 × 5 = 2¹ × 5²
60 = 2 × 2 × 3 × 5 = 2² × 3¹ × 5¹
HCF (50, 60) = 2¹ × 5¹ = 10 (Product of smallest power of each common prime factors of the numbers)
LCM (50, 60) = 2² × 5² × 3¹ = 300 (Product of greatest power of each prime factors of the numbers)

iii) 37, 49
37 is a prime number and 49 is a composite number, so the HCF(37, 49) is 1 and LCM(37, 49) is 1813.

Textual Examples

Question 1.
Consider the numbers 4ⁿ, where n is a natural number. Check whether there is any value of n for which 4ⁿ ends with the digit zero. (Page No. 5)
Solution:
For the number 4ⁿ to end with digit zero for any natural number n, it should be divisible by 5. This means that the prime factorisation of 4ⁿ should contain the prime number 5. But it is not possible because 4ⁿ = (2)²ⁿ so 2 is the only prime in the factorization of 4ⁿ. Since 5 is not present in the prime factorization, so there is no natural number n for which 4ⁿ ends with the digit zero.

Question 2.
Find the HCF and LCM of 12 and 18 by the prime factorization method. (Page No. 7)
Solution:
We have 12 = 2 × 2 × 3 = 2² × 3¹
18 = 2 × 3 × 3 = 2¹ × 3²
Note that HCF (12, 18) = 21 x 31 = 6
HCF : Product of the smallest power of each common prime factors in the numbers.
LCM (12, 18) = 2² × 3² = 36 = Product of the greatest power of each prime factors in the numbers.

Try This

Question 1.
Show that 3ⁿ × 4^m cannot end with the digit 0 or 5 for any natural numbers ‘n’ and ‘m’. (Page No. 8)
Solution:
Let the number 3ⁿ × 4^m
= 3ⁿ × (2²)^m
= 3ⁿ × 2^2m
Number 3ⁿ × 22^m to end with ‘0’ or ‘5’. It should be divisible by 2 and 5. This means that the prime factorization of 3ⁿ × 4^m should contain prime numbers. But it is not possible because 3ⁿ × 4^m = 3ⁿ × 22^m
So 2 or 3 are the only prime factors in its factorization. Since 5 is not present in the prime factorization 3ⁿ × 4^m can not end with the digits 0 or 5.

Try This

Question 1.
Show that 3ⁿ × 4^m cannot end with the digit 0 or 5 for any natural numbers ‘n’ and’m’. (Page No. 8)
Solution:
Let the number 3ⁿ × 4^m = 3ⁿ × (2²)^m
= 3ⁿ × 2^2m
Number 3ⁿ × 2^2m to end with ‘0’ or ‘5’. It should be divisible by 2 and 5. This means that the prime factorization of 3ⁿ × 4^m should contain prime numbers. But it is not possible because 3ⁿ × 4^m = 3ⁿ × 2^2m
So 2 or 3 are the only prime factors in its factorization. Since 5 is not present in the prime factorization 3ⁿ × 4^m can not end with the digits 0 or 5.

Do This

Question 1.
Write the following terminating decimals in the form of \(\frac{\mathbf{p}}{\mathbf{q}}\). q ≠ 0 and p, q are co-primes.
i)15.265
ii) 0.1255
iii) 0.4
iv) 23.34
v) 1215.8
What can you conclude about the denominators through this process? (Page No. 6)
Solution:
i) 15.265 = \(\frac{15265}{10^3}\) = \(\frac{152625}{2^3 \times 5^3}\) = \(\frac{3053}{2^3 \times 5^2}\) = \(\frac{3053}{200}\)

ii) 0.1255 = \(\frac{1255}{10^4}\) = \(\frac{1255}{2^4 \times 5^4}\) = \(\frac{3053}{200}\)

iii) 0.4 = \(\frac{4}{10}\) = \(\frac{2}{5}\)

iv) 23.34 = \(\frac{2334}{10^2}\) = \(\frac{2334}{2^2 \times 5^2}\) = \(\frac{1167}{50}\)

v) 1215.8 = \(\frac{12158}{10}\) = \(\frac{12158}{2 \times 5}\) = \(\frac{6079}{5}\)

We can conclude that the denominator in the problems have only power of 2 or power of 5 or both.

Question 2.
Write the following rational numbers in the form of \(\frac{\mathbf{p}}{\mathbf{q}}\), where q is of the form 2ⁿ5^m where n, m are non-negative integers and these write the negative Integers and then write the numbers in their decimal form.

i) \(\frac{3}{4}\)
ii) \(\frac{7}{5}\)
iii) \(\frac{51}{64}\)
iv) \(\frac{14}{25}\)
v) \(\frac{80}{100}\)
Solution:

Question 3.
Write the following rational numbers as decimals and find out the block of digits, repeating ¡n the quotient.
i) \(\frac{1}{3}\)
ii) \(\frac{2}{7}\)
iii) \(\frac{5}{11}\)
iv) \(\frac{10}{13}\) (Page No. 11)
Solution:
i) \(\frac{1}{3}\) = 0.33333 …….

The block of digits repeating in the quotient is only 3.

ii) \(\frac{2}{7}\) = 0.285714285714 ……


The block of digits repeating in the quotient is only 285714.

iii) \(\frac{5}{11}\) = 0.454545…..

The block of digits repeating in the quotient is only 45.

iv) \(\frac{10}{13}\) = 0.769230769230 …..


The block of digits repeating in the quotient is only 769230.

Textual Examples

Question 1.
Using the above theorems, without actual division, state whether the following rational numbers are terminating or non-terminating, repeating decimals.
i) \(\frac{16}{125}\)
ii) \(\frac{25}{32}\)
iii) \(\frac{100}{81}\)
iv) \(\frac{41}{75}\)
Solution:
\(\frac{16}{125}\) = \(\frac{16}{555}\) = \(\frac{16}{5^3}\)
is terminating decimal.

ii) \(\frac{25}{32}\) = \(\frac{25}{2 \times 2 \times 2 \times 2 \times 2}\) = \(\frac{25}{2^5}\)
is terminating decimal.

iii) \(\frac{100}{81}\) = \(\frac{100}{3 \times 3 \times 3 \times 3}\) = \(\frac{10}{3^4}\)
is non-terminating, repeating decimal.

iv) \(\frac{41}{75}\) = \(\frac{41}{3 \times 5 \times 5}\) = \(\frac{41}{3 \times 5^2}\)
is non-terminating, repeating decimal.

Question 2.
Write the decimal expansion of the following rational numbers without actual division.
i) \(\frac{35}{40}\)
ii) \(\frac{21}{25}\)
iii) \(\frac{7}{8}\)
Solution:

Do This

Question 1.
Verify the statement proved above for p = 2, p = 5 and for a² = 1, 4, 9, 25, 36, 49, 64 and 81. (Page No. 14)
Solution:
The statement proved already is as follow.
Let p be a prime number.
If p divides a² where ‘a’ is a positive integer then ‘p’ divides ‘a’ when p = 2 if 2 divides a (= 4, 36, 64) then p divide ‘a’ (= 2, 6, 8)
In other cases when a² = 1, 9, 25, 49 and 81 the statement is not correct.
When p = 5 if 5 divide a² then p divide ‘a’
In other cases i.e., when a²(= 1, 4, 9, 16, 36, 49, 64, 81). the statement is not correct.

Textual Examples

Question 1.
Prove that \(\sqrt{2}\) is irrational. (Page No. 14)
Solution:
Since we are using proof by contradiction, let us assume the contrary, i.e., \(\sqrt{2}\) is rational.
If it is rational, then there must exist two integers r and s (s ≠ 0) such that
\(\sqrt{2}\) = \(\frac{\mathrm{r}}{\mathrm{s}}\)
Suppose r and s have a common factor other than 1. Then, we divide by the common factor to get \(\sqrt{2}\) = \(\frac{a}{b}\)’ w^ere a and b are co-primes.
So, b\(\sqrt{2}\) = a
On squaring both sides and rearranging, we get 2b² = a². Therefore, 2 divides a².
Now, by statement 1, it follows that if 2 divides a² it also divides a.
So, we can write a = 2c for some integer c. Substituting for a, we get 2b² = 4c², that is, b² = 2c².
This means that 2 divides b², and so 2 divides b (again using statement 1 with p = 2).
Therefore, both a and b have 2 as a common factor.
But this contradicts the fact that a and b are co-prime and have no common factors other than 1.
This contradiction has arisen because of our assumption that \(\sqrt{2}\) is rational. So, we conclude that \(\sqrt{2}\) is irrational.

Question 2.
Show that 5 – \(\sqrt{3}\) is irrational. (Page No. 14)
Solution:
Let us assume, to the contrary, that 5 – \(\sqrt{3}\) is rational.
That is, we can find co-primes a and b (b ≠ 0)
such that 5 – \(\sqrt{3}\) = \(\frac{\mathrm{a}}{\mathrm{b}}\)
Therefore, 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) = \(\sqrt{3}\)
Rearranging this equation,
we get \(\sqrt{3}\) = 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) = \(\frac{5 b-a}{b}\)
Since a and b are integers, we get 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) is rational so \(\sqrt{3}\) is rational.
But this contradicts the fact that \(\sqrt{3}\) is irrational.
This contradiction has arisen because of our incorrect assumption that
5 – \(\sqrt{3}\) is rational.
So, we conclude that 5 – \(\sqrt{3}\) is irrational.

Question 3.
Show that 3\(\sqrt{2}\) is irrational.(Page No. 15)
Solution:
Let us assume, the contrary, that 3\(\sqrt{2}\) is rational.
i.e., we can find co-primes a and b (b ≠ 0) such that 3\(\sqrt{2}\) = \(\frac{\mathrm{a}}{\mathrm{b}}\)
Rearranging, we get \(\sqrt{2}\) = \(\frac{a}{3 b}\)
Since 3, a and b are integers, \(\frac{a}{3 b}\) is rational, and so \(\sqrt{2}\) is rational.
But this contradicts the fact that \(\sqrt{2}\) is irrational.
So, we conclude that 3\(\sqrt{2}\) is irrational.

Question 4.
Prove that \(\sqrt{2}\) + \(\sqrt{3}\) is irrational. (Page No. 15)
Solution:
Let us suppose that \(\sqrt{2}\) + \(\sqrt{3}\) is rational.
Let \(\sqrt{2}\) + \(\sqrt{3}\) = \(\frac{a}{b}\), where a, b are integers and
b ≠ 0.
Therefore, \(\sqrt{2}\) = \(\frac{a}{b}\) – \(\sqrt{3}\)
Squaring on both sides, we get

∴ Since a, b are intetgers, \(\frac{a^2+b^2}{2 a b}\) is rational, and so, \(\sqrt{3}\) is rational.
This contradicts the fact that \(\sqrt{3}\) is irrational.
∴ Hence, \(\sqrt{2}\) + \(\sqrt{3}\) is irrational

Think – Discuss

Question 1.
Draw the graphs of y = 2^x; y = 4^x; y = 8^x and y = 10^x in a single graph and mention your observation. (Page No. 17)

Observations:

1. The curve never cuts the X – axis.
2. The value of y is same x = 0.
i.e., y = 2^x = 4^x = 8 = 1o^x = 1 where x = 0.
3. The value of y gets very close to zero for the values of x.
4. All curves meet Y-axis at the same point when x = 0.
Solution:

Question 2.
Write the nature of y, a and x in y = a,sup>x. Can you determine the value of x ford given y justify your answer. (Page No. 17)
Solution:
y = a^x means, the relative change is not same for all real values of x.
We are unable to determine the value of x for a given value of y in y = a^x.
For example y = 3 in y = 7^x
What should be the power to which 7 must be raised to get 3.

Question 3.
From the graph y = 2^x, y = 4^x, y = 8^x and y = 10^x you have drawn earlier have you noticed the value log 1 (any base) (Page No. 18)
Solution:
Yes, log 1 to any base is zero.

Question 4.
You know that 2¹ = 2, 4¹ = 4, 8¹ = 8 and 10¹ = 10. What do you notice about the values of \(\log _2^2\), \(\log _4^4\), \(\log _8^8\) and \(\log _10^10\)?
What can you generalise from this? (Page No. 18)
Solution:
We know that 2¹ = 2, 4¹ = 4, 8¹ = 8 and 10¹ = 10.
\(\log _2^2\) = 1, \(\log _4^4\) = 1, \(\log _8^8\) = 1 and \(\log _10^10\) = 1
∴ We generalise from this, a = N then the \(\log _a^a\) = 1

Question 5.
Does \(\log _0^10\) exist?
Solution:
No, \(\log _0^10\) does not exist.
a^x ≠ 0, a, x ∈ N

Question 6.
We know that, if 7 = 2^x then x = \(\log _2 7\). Then what is the value of \(2^{\log _2^7}\) = ? Justify your answer. Generalise the above by taking same more examples for \(a^{\log _a^N}\). (Page No. 23)
Solution:

Do THIS

Question 1.
Write the powers to which the bases to be raised in the following:

i) 7 = 2^x
ii) 10 = 5^b
iii) \(\frac{1}{81}\) = 3^c
iv) 100 = 10^z
v) \(\frac{1}{257}\) = 4^a.
Solution:
i) 7 = 2^x
We cannot determined the power of x.

ii) 10 = 5^b
2 × 5 = 5^b
We can not determined the power of b.

iii) \(\frac{1}{81}\) = 3^c
(81)^-1 = 3^c
(3⁴)^-1 = 3^c
(3)^-4 = 3^c
∴ C = -4

iv) 100 = 10^z
10² = 10^z
∴ z = 2

v) \(\frac{1}{257}\) = 4^a
We cannot determine the power of a.

Question 2.
Express the logarithms of the following Into sum of the logarithms:
i) 35 × 46
ii) 235 × 437
iii) 2437 × 3568 (Page No. 19)
Solution:
i) 35 × 46
log xy = log x + log y
∴ log₁₀ 35 × 46 = log₁₀ 35 + log₁₀ 46

ii) 235 × 437
log₁₀ 35 × 437 = log₁₀ 235 + log₁₀ 437
[∵ log xy = log x + log y]

iii) 2437 × 3568
log₁₀ 2437 × 3568 = log₁₀ 2437 + log₁₀ 3568
[∵ log xy = log x + log y]

Question 3.
Express the logarithms of the following into difference of the logarithms

i) \(\frac{23}{34}\)
ii) \(\frac{373}{275}\)
iii) 4525 ÷ 3734
iv) 5055/3303
Solution:

Question 4.
By using the formula \(\log _a^{x^n}\) = \(n \log _a^{\mathbf{x}}\) convert the following

i) \(\log _2^{7^{25}}\)
ii) \(\log _5^{8^{50}}\)
iii) \(\log 5^{23}\)
iv) log¹⁰²⁴ (Page No. 21)
Solution:

TRY THIS

Question 1.
Write the following relation in exponential form and find the values of respective variables. (Page No. 18)
i) \(\log _2^{32}\) = x
ii) \(\log _5^{625}\) = y
iii) \(\log _{10}^{10000}\) = z
iv) \(\log _7\left(\frac{1}{343}\right)\) = -a
Solution:

Question 2.
i) Find the value of \(\log _2^{32}\) (Page No. 21)
log x^m = m log x and \(\log _a^a\) = 1
Solution:
= \(\log _2^{2^5}\) = \(5 \log _2^2\) = 5 × 1 = 5

ii) Find the value of \(\log _c^{\sqrt{c}}\) (Page No. 21)
Solution:

iii) Find the value of \(\log _{10}^{0.001}\) (Page No. 21)
Solution:

iv) Find the value of (Page No. 21)
Solution:

Textual Examples

Question 1.
Expand log \(\frac{343}{125}\).
Solution:
As you know, log_a \(\frac{x}{y}\) = log_ax – log_ay
So, log \(\frac{343}{125}\) = log343 – log125
= log7³ – log5³
∴ Since, log_ax^m = m log_ax
= 3log7 – 3log5

Question 2.
Write 2log3 + 3log5 – 5log2 as a single logarithm.
Solution:
2log3 + 3log5 – 5log2
= log3² + log5³ – log2⁵
(Since in m log_ax=log_ax^m)
= log9 + log125 – log32
= log (9 × 125) – log32
(Since log_ax + log_ay = log_axy)
= log1125 – log32
= logl \(\frac{1125}{32}\) (Since log_ax – log_ay = \(\log _a \frac{x}{y}\))

Question 3.
Solve 3^x = 5^x-2 (Page No. 22)
Solution:
Taking log on both the sides
x log₁₀ 3 = (x – 2) log₁₀ 5
x log₁₀ 3 = x log₁₀ 5 – 2 log₁₀ 5
x log₁₀ 5 – 2 log₁₀ 5 = x log₁₀ 3
x(log₁₀ 5 – log₁₀ 3) = 2 log₁₀ 5

Question 4.
Find x if 2 log 5 + \(\frac{1}{2}\) log 9 – log 3 = log x. (Page No. 22)
Solution:
log x = 21og 5 + \(\frac{1}{2}\) log 9 – log 3
= log 5² + log \(9^{\frac{1}{2}}\) – log 3
= log 25 + log \(\sqrt{9}\) – log 3
= log 25 + log 3 – log 3
log x = log 25
∴ x = 25