TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1

Students can practice 10th Class Maths Solutions Telangana Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Exercise 4.1

Question 1.
By comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\), \(\frac{c_1}{c_2}\) find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or coincident.
a) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
b) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
c) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solution:
a) The given pair of linear equations are
5x – 4y + 8 = 0 ———- (1)
7x + 6y – 9 = 0 —— (2)
Comparing equations (1) and (2) with standard pair of linear equations (i.e.,)
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂= 0, we get
a₁ = 5; b₁ = -4; c₁ = 8
a₂ = 7; b₂ = 6; c₂ = -9
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{5}{7}\); \(\frac{b_1}{b_2}\) = \(\frac{-4}{6}\); \(\frac{c_1}{c_2}\) = \(\frac{8}{-9}\)
Since, \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\), the pair of linear equations will represent intersecting lines.

b) The given pair of linear equations are
9x + 3y + 12 = 0 —- (1)
18x + 6y + 24 = 0 —- (2)
Here, a₁ = 6; b₁ = 3; c₁ = 12
a₂ = 18; b₂ = 6; c₂ = 24
\(\frac{a_1}{a_2}\) = \(\frac{9}{18}\) = \(\frac{1}{2}\) ;
\(\frac{b_1}{b_2}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{12}{24}\) = \(\frac{1}{2}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) = \(\frac{1}{2}\), The pair of linear equations will represent coincident lines.

c) The given pair of linear equations are
6x – 3y + 10 = 0
2x – y + 9 = 0
Here,
a₁ = 6; b₁ = -3; c₁ = 10
a₂ = 2; b₂ = -1; c₂ = 9
\(\frac{a_1}{a_2}\) = \(\frac{6}{2}\) = \(\frac{3}{1}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-3}{-1}\) = \(\frac{3}{1}\);
\(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{10}{9}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\), the pair of linear equations will represent parallel lines.

Question 2.
Check whether the following equations are consistent or inconsistent. Solve them graphically.
a) 3x + 2y = 5; 2x – 3y = 7
b) 2x – 3y = 8; 4x – 6y = 9
c) \(\frac{3}{2}\)x + – y = 7; 9x – 10y = 14
d) 5x – 3y = 11; -10x + 6y = -22
e) \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
f) x + y = 5; 2x + 2y = 10
g) x – y = 8; 3x – 3y = 16
h) 2x + y – 6 = 0; 4x – 2y – 4 = 0
i) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
Solution:
a) 3x + 2y – 5 = 0
2x – 3y – 7 = 0
Here
a₁ = 3; b₁ = 2; c₁ = -5
a₂ = 2; b₂ = -3; c₂ = -7
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{3}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{2}{-3}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-5}{-7}\) = \(\frac{5}{7}\)
⇒ \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given equations are consistent.
They intersect at one point. There is an unique solution.
The given equations are 3x + 2y = 5 and 2x – 3y = 7
3x + 2y = 5 —– (1)
⇒ 2y = 5 – 3x
⇒ y = \(\frac{5-3 x}{2}\)

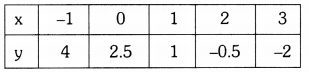
2x – 3y = 7 —- (2)
⇒ 3y = 2x – 7
⇒ y = \(\frac{2 x-7}{3}\)

Scale :
X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

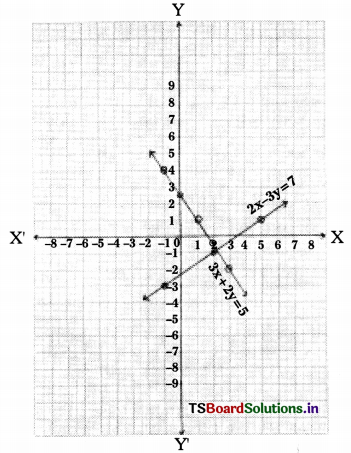
The given lines intersect at one point. The solution is (2,-1).
x = \(\frac{29}{13}\) ; y = \(\frac{-11}{13}\)

b) 2x – 3y = 8
4x – 6y = 9
Solution:
2x – 3y – 8 = 0
4x – 6y – 9 = 0
Here,
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-3}{-6}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-8}{-9}\) = \(\frac{8}{9}\)
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations are inconsistent.
They are parallel lines. There is no solution.
The given equations are 2x – 3y = 8 and
4x — 6y = 9
2x – 3y = 8 —– (1)
⇒ 3y = 2x – 8
⇒ y = \(\frac{2 x-8}{3}\)

4x – 6y = 9
⇒ 6y = 4x – 9
⇒ y = \(\frac{4 x-9}{6}\)

The given lines parallel to each other.
There is no solution.

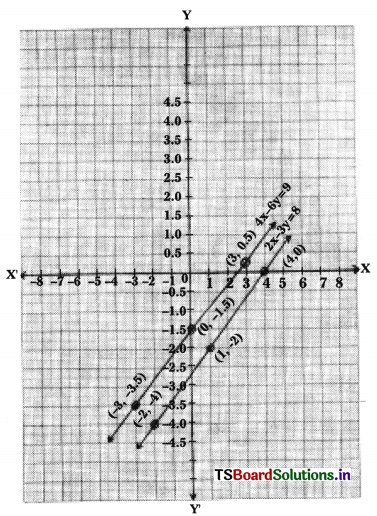
Scale: X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 0.5 cm

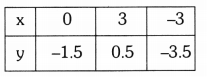
c) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
9x – 10y = 14
Solution:
\(\frac{3 x}{2}\) + \(\frac{5 y}{3}\) = 7
\(\frac{6(3 x)}{2}\) + \(\frac{6(5 y)}{3}\) = 7 × 6
(Multiplying each term by 6, we get)
⇒ 9x + 10y = 42
⇒ 9x + 10y – 42 = 0 —- (1)
⇒ 9x – 10y – 14 = 0 —- (2)
Here, a₁ = 9; b₁ = 10; c₁ = -42
a₂ = 9; b₂ = -10; c₂ = -14

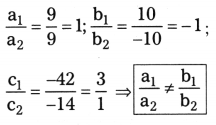
∴ The given equations are consistent.
They intersect at one point. There is an unique solution.
The given equations are \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 and 9x – 10y = 14
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 —– (1)
⇒ 9x + 10y = 42 ⇒ 10y = 42 – 9x
⇒ y = \(\frac{42-9 x}{10}\)

9x – 10y = 14
⇒ 10y = 9x – 14
y = \(\frac{9 x-14}{10}\)

The given lines intersect at one point.
x = \(\frac{28}{9}\) and y = \(\frac{7}{5}\)

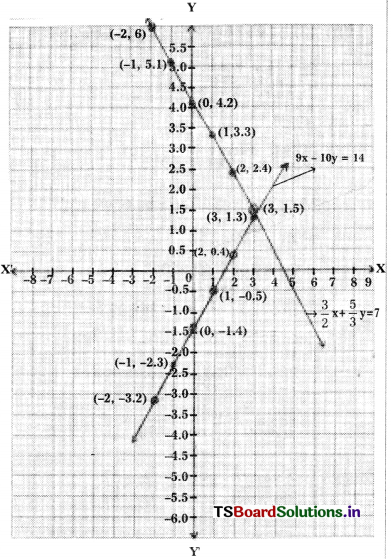
Scale : X-axis: 1 unit = 1 cm
Y-axis: 1 unit = 0.5 cm

d) 5x – 3y = 11
-10x + 6y = -22
Solution:
5x – 3y – 11 = 0
-10x + 6y + 22 = 0
Here, a₁ = 5; b₁ = -3; c₁ = -11
a₂ = -10: b₂ = 6; c₂ = 22
\(\frac{a_1}{a_2}\) = \(\frac{5}{-10}\) = \(\frac{-1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-3}{6}\) = \(\frac{-1}{2}\);
\(\frac{c_1}{c_2}\) = \(\frac{-11}{22}\) = \(\frac{-1}{2}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.
The given equations are 5x – 3y = 11 and -10x + 6y = -22
5x – 3y = 11 —– (1)
⇒ 3y = 5x – 11
⇒ y = \(\frac{5 x-11}{3}\)

⇒ 10x + 6y = -22 —– (2)
⇒ 6y = 10x – 22
⇒ y = \(\frac{10 x-22}{6}\)

The given lines are coincident.
There are infinitely many solutions.

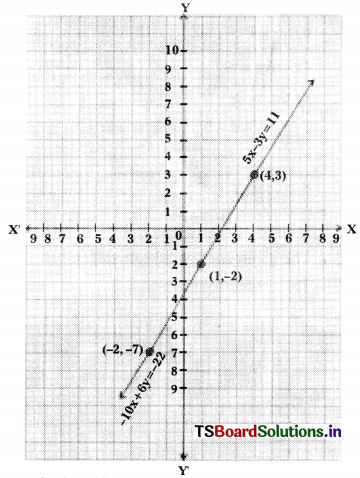
Scale: X – axis: 1 cm = 1 unit
Y – axis: 1 cm = 1 unit

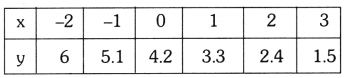
e) \(\frac{4}{3}\)x + 2y = 8
2x + 3y = 12
Solution:
4x + 6y = 24
Multiplying each term by (3), we get
⇒ 4x + 6y – 24 = 0 —— (1)
2x + 3y – 12 = 0 ——- (2)
a₁ = 4; b₁ = 6; c₁ = -24
a₂ = 2; b₂ = 3; c₂ = -12
Here,
\(\frac{a_1}{a_2}\) = \(\frac{4}{2}\) = 2; \(\frac{b_1}{b_2}\) = \(\frac{6}{3}\) = 2 ; \(\frac{c_1}{c_2}\) = \(\frac{-24}{-12}\) = 2
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent.
There are infinitely many solutions.
The given equations are \(\frac{4}{3}\)x + 2y = 8 and 2x + 3y = 12
\(\frac{4}{3}\)x + 2y = 8 —– (1)
⇒ 4x + 6y = 24
⇒ 6y = 24 – 4x
⇒ y = \(\frac{24-4 x}{6}\)

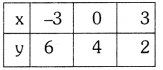
2x + 3y = 12 —– (2)
⇒ 3y = 12 – 2x
⇒ y = \(\frac{12-2 x}{3}\)


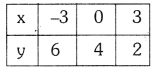
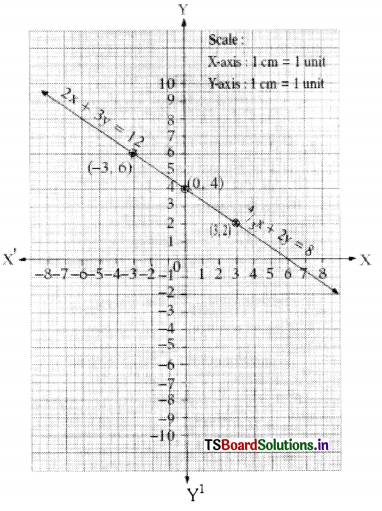
The given lines are coincident.
There are infinitely many solutions.

f) x + y = 5 (A.P. Jun.15)
2x + 2y = 10
Solution:
x + y – 5 = 0
2x + 2y – 10 = 0
Here, a₁ = 1; b₁ = 1; c₁ = -5
a₂ = 2; b₂ = 2; c₂ = -1O
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-5}{-10}\) = \(\frac{1}{2}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.
The given equations are x + y = 5 and 2x + 2y = 10
x + y = 5 —— (1)
⇒ y = 5 – x

2x + 2y = 10 —– (2)
⇒ 2y = 10 – 2x
⇒ y = \(\frac{10-2 \mathrm{x}}{2}\)

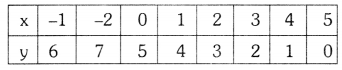
The given lines are coincident.
There are infinitely many solutions.

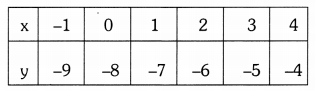
g) x – y = 8
3x – 3y = 16
Solution:
x – y – 8 = 0
3x – 3y – 16 = 0
Here, a₁ = 1; b₁ = -1; c₁ = -8
a₂ = 3; b₂ = -3; c₂ = -16
⇒ \(\frac{a_1}{a_2}\) = \(\frac{1}{3}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-1}{-3}\) = \(\frac{1}{3}\);
\(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{-8}{-16}\) = \(\frac{1}{2}\)
⇒ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
The given equations are inconsistent.
They are parallel lines. There is no
solution.
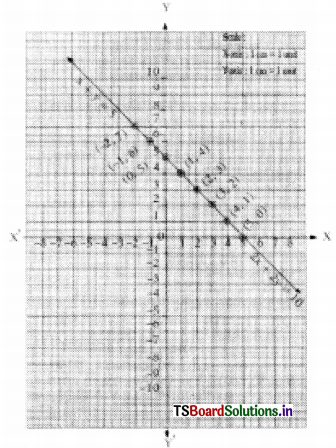
The given equations are x – y = 8 and 3x – 3y = 16
x – y = 8 —– (1)
⇒ y = x – 8

3x – 3y = 16 —- (2)
⇒ 3y = 3x – 16
⇒ y = \(\frac{3 x-16}{3}\)

The given lines are parallel to each other. There is no solution.

Scale: X – axis : 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

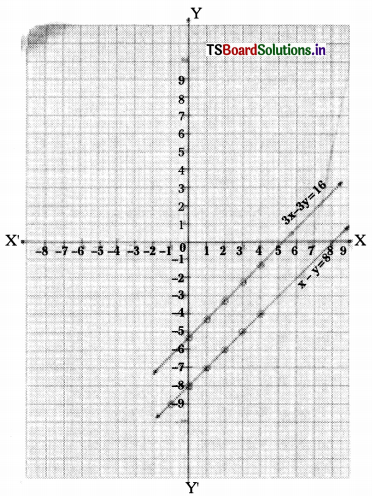
h) 2x + y – 6 = 0
4x – 2y – 4 = 0
Solution:
2x + y – 6 = 0
4x – 2y – 4 = 0
Here, a₁ = 2; b₁ = 1; c₁ = -6
a₂ = 4; b₂ = -2; c₂ = -4
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{1}{-2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-6}{-4}\) = \(\frac{3}{2}\)
⇒ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given equations are consistent.
They intersect at one point. There is a unique solution.
The given equations are 2x + y – 6 = 0 and 4x – 2y – 4 = 0
2x + y – 6 = 0 —– (1)
⇒ y = 6 – 2x

4x – 2y – 4 = 0 —– (2)
⇒ 2y = 4x – 4
⇒ y = \(\frac{4 x-4}{2}\)

Scale: X-axis : 1 unit = 1 cm
Y-axis : 1 unit = 1 cm

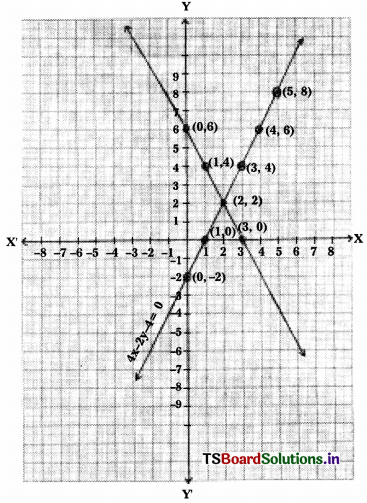
The given lines intersect at one point (2, 2).
The solution is x = 2 and y = 2.

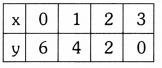
i) 2x – 2y – 2 = 0
4x – 4y – 5 = 0
Solution:
2x – 2y – 2 = 0
4x – 4y – 5 = 0
Here, a₁ = 2; b₁ = -2; c₁ = -2
a₂ = 4; b₂ = -4; c₂ = -5
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-2}{-4}\) = \(\frac{1}{2}\)
\(\frac{\mathrm{c}_1}{\mathrm{~c}_2}\) = \(\frac{-2}{-5}\) = \(\frac{2}{5}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations are consistent.
They are parallel lines. There is no solution.
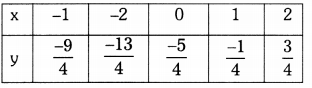
The given equations are 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0
2x – 2y – 2 = 0 —– (1)
⇒ 2y = 2x – 2
⇒ y = \(\frac{2 x-2}{2}\)

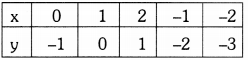
4x – 4y – 5 = 0 —– (2)
⇒ 4y = \(\frac{4 x-5}{4}\)
⇒ y = \(\frac{4 x-5}{4}\)

The given lines are parallel to each other.
There is no solution.

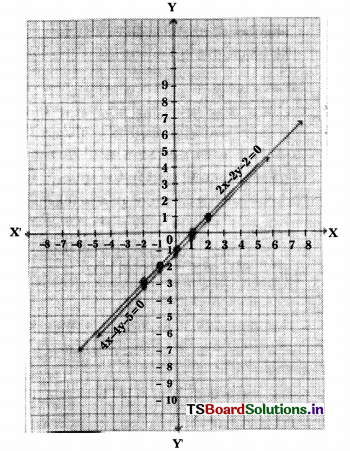
Scale: X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

Question 3.
Neha went to a ‘sale’ to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered “The number of skirts are two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number of pants purchased”. Help her friend to find how many pants and skirts Neha bought.
Solution:
Let the number of pants Neha bought be x.
Let the number of skirts Neha bought be y.
By problem,
y = 2x – 2
⇒ 2x – y = 2 —— (1)
y = 4x – 4
⇒ 4x – y = 4 —– (2)

Substitute x = 1 in (1) or (2), we get
⇒ 2(1) – y = 2
⇒ 2 – y = 2
⇒ -y = 2 – 2 = 0
∴ y = o
Number of pants purchased = 1
∴ Number of skirts purchased = 0

Question 4.
10 students of Class-X took part in a mathematics quiz. If the number of girls is 4 more than the number of boys then, find the number of boys and the number of girls who took part in the quiz.
Solution:
Number of boys who took part in the quiz = x
Number of girls who took part in the quiz = y
It is given that 10 students took part in the quiz.
∴ x + y = 10 ——— (1)
Since the number of girls is 4 more than the number of boys, we have
y = x + 4
⇒ -x + y = 4 —– (2)
Adding (1) and (2)

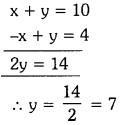
Substitute y = 7 in equation (1), we get
x + 7 = 10
x = 10 – 7 = 3
Therefore, Number of boys who took part in the quiz = 3
Number of girls who took part in the quiz = 7

Question 5.
5 pencils and 7 pens together cost ₹ 50 whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
Let the cost of one pencil = ₹ x
Cost of one pen = ₹ y
Total cost of 5 pencils and 7 pens = 5x + 7y
Total cost of 7 pencils and 5 pens = 7x + 5y
By problem, 5x + 7y = 50 —- (1)
7x + 5y = 46 —– (2)
We equate the coefficients of ‘x’ in (1) and (2).

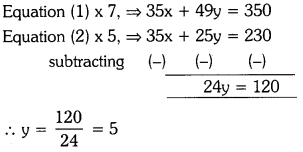
Substitute y = 5 in equation (1), we get
5x + (7 × 5) = 50
5x + 35 = 50
5x = 50 – 35 =15
∴ x = \(\frac{15}{5}\) = 3
Therefore, cost of one pencil = ₹ 3
Cost of one pen = ₹ 5

Question 6.
Half of the perimeter of a rectangular garden, whose length is 4m more than its width is 36m. Find the dimensions of the garden.
Solution:
Let the length of the garden be x metres.
Let the breadth of the garden be y metres.
Perimeter of the garden = 2(x + y) metres.
Half of the perimeter of the garden =
\(\frac{2(x+y)}{2}\) = x + y
By problem, x + y = 36 —— (1)
It is given that the length is 4 metres more than its width.
(i.e.,) x = y + 4
⇒ x – y = 4 —– (2)
Solving (1) and (2)

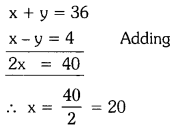
Substitute, x = 20 in equation (1),
20 + y = 36
⇒ y = 36 – 20 = 16
Therefore, length of the garden = 20 metres
Breadth of the garden =16 metres

Question 7.
We have a linear equation 2x + 3y – 8 = 0. Write another linear equation in two variables such that the geometrical representation of the pair is formed intersecting lines. Now, write two more linear equations so that one forms a pair of parallel lines and the second forms coincident line with the given equation.
Solution:
The given linear equation is 2x + 3y – 8 = 0.

1. The required linear equation in two variables such that it is formed an intersecting line with the given one, is 6x – 5y – 10 = 0.
2. The linear equation in two variables (i.e.,) 4x + 6y – 10 = 0 forms a parallel line with the given one.
3. The linear equation in two variables (i.e.,) 6x + 9y – 24 = 0 forms a coincident line with the given one.

Question 8.
The area of a rectangle gets reduced by 80 sq units if its length is reduced by 5 units and breadth is increased by 2 units. If we increase the length by 10 units and decrease the breadth by 5 units, the area will increase by 50 sq units. Find the length and breadth of the rectangle.
Solution:
Let the length of the rectangle be x units and the breadth be y units.
Then the area of the rectangle = length × breadth = x × y = xy
If the length is reduced by 5 units and breadth is increased by 2 units, then its area is reduced by 80 sq. units.
∴ (x – 5) (y + 2) = xy – 80
⇒ xy + 2x – 5y – 10 = xy – 80
⇒ 2x – 5y = -70 —– (1)
When the length is increased by 10 units and breadth is decreased by 5 units, the area is increased by 50 sq. units.
∴ (x + 10) (y – 5) = xy + 50
⇒ xy – 5x + 10y – 50 = xy + 50
⇒ -5x + 10 y = 100 —– (2)
Equation (1) × 2
Solving (1) and (2), we get
4x – 10y = -140
-5x + 10y = 100 Adding
-x = -40
∴ x = 40
Substitute x = 40 in (2), we get
⇒ (-5 × 40) + 10y = 100
⇒ – 200 + 10y = 100
⇒ 10y = 100 + 200 = 300
∴ y = \(\frac{300}{10}\) = 30
Length of the rectangle = 40 units
Breadth of the rectangle = 30 units

Question 9.
In class X, if three students sit on each bench, one student will be left. If four students sit on each bench, one bench will be left. Find the number of students and the number of benches in that class.
Solution:
Let the number of students in class X be x.
Let the number of benches in that class be y.
If three students sit on each bench, one student will be left.
∴ 3y = x – 1
⇒ x – 3y = 1 —- (1)
If four students sit on each bench, one bench will be left.
∴ 4(y – 1) = x
⇒ 4y – 4 = x
⇒ x – 4y = -4 —– (2)
Solving (1) and (2), we get

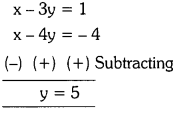
Substitute y = 5 in (1), we get
x – (3 × 5) = 1
⇒ x – 15 = 1
∴ x = 1 + 15 = 16
∴ Number of students in class X = 16
Number of benches in that class = 5
Form a pair of linear equations for each of the following problems and find their solution.