TS 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Ex 12.2

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 12 Applications of Trigonometry Ex 12.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Exercise 12.2

Question 1.
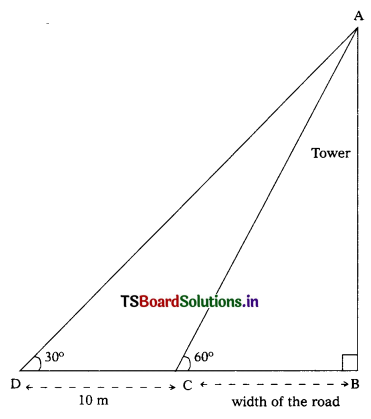
A TV tower stands vertically on the side of a road. From a point on the other side directly opposite to the tower, the angle of elevation of the top of tower is 60°. From another point 10 m away from this point, on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the road. (AS₄)
Solution:
In the adjacent figure,
AB denotes the height of the tower.
BC denotes the width of the road.
CD = 10 cm
∠ACB = 60° and ∠ADC = 30°
In ∆ACB, ∠B = 90°
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)

\(\frac{\sqrt{3}}{1}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) ………….. (1)
In ∆ ABD, ∠ABD = 90°
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}+\mathrm{CD}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}+10}\) ………….. (2)
dividing eq. (1) by eq. (2) we have
\(\frac{\mathrm{eq} \mathrm{(1)}}{\mathrm{eq} \mathrm{(2)}}=\frac{\sqrt{3} \times \sqrt{3}}{1}=\frac{\mathrm{AB}}{\mathrm{BC}} \times \frac{\mathrm{BC}+10}{\mathrm{AB}}\)
\(\frac{3}{1}\) = \(\frac{\mathrm{BC}+10}{\mathrm{BC}}\)
3BC = BC + 10
3BC – BC = 10
2BC = 10
BC = \(\frac{10}{2}\) = 5 …………… (3)
from (1),
\(\sqrt{3}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
\(\frac{\sqrt{3}}{1}\) = \(\frac{\mathrm{AB}}{5}\)
⇒ AB = 5\(\sqrt{3}\)
Hence, the height of the tower = 5 \(\sqrt{3}\) m and the width of the road = 5 m.

Question 2.
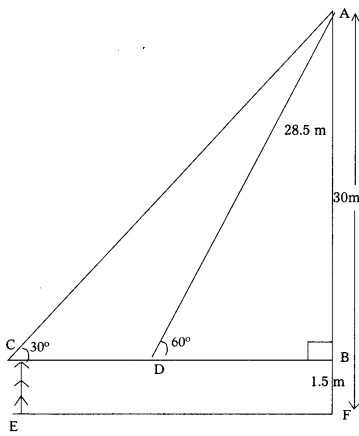
A 1.5 m tall boy is looking at the top of a temple which is 30 meter in height from a point of certain distance. The angle of elevation from his eye to the top of the crown of the temple increases from 30° to 60° as he walks towards the temple. Find the distance he walked towards the temple. (AS₄)
Solution:
CE denotes the height of the boy CE = 1.5 m
AF denotes the height of the temple AF = 30 m
CB || EF
CEFB is a rectangle
∴ CE = 8F = 1.5 m
∴ AB = AF – BF
= 30 – 1.5
= 28.5 m

In ∆ ABC, ∠B = 90°
∴ tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{28.5}{\mathrm{BC}}\)
⇒ BC = 28.5 × \(\sqrt{3}\) …………… (1)
In ∆ ABD, ∠B = 90°
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ \(\frac{\sqrt{3}}{1}\) = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ \(\frac{\sqrt{3}}{1}\) = \(\frac{28.5}{\mathrm{BD}}\)
⇒ BD × \(\sqrt{3}\) = 28.5
⇒ BD = \(\frac{28.5}{\sqrt{3}}\)
Therefore, the distance, the boy walked towards the temple is CD
CD = BC – BD

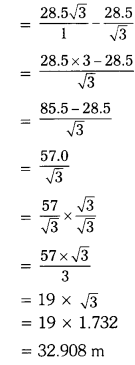
Question 3.
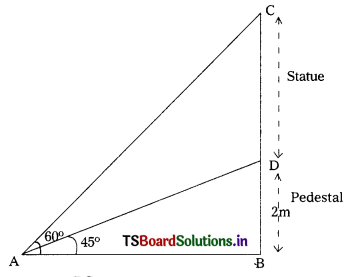
A statue stands on the top of a 2m tall pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the statue. (AS₄)
Solution:
In ∆ABD, ∠B = 90° and ∠DAB = 45°
∴ tan 60° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
\(\frac{\sqrt{3}}{1}\) = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
AB × \(\sqrt{3}\) = BC

AB = \(\frac{\mathrm{BC}}{\sqrt{3}}\) …………….. (1)
In ∆ABD, ∠B = 90° and ∠DAB = 45°
∴ tan 45° = \(\frac{\mathrm{DB}}{\mathrm{AB}}\)
\(\frac{1}{1}\) = \(\frac{2}{\mathrm{AB}}\)
⇒ AB = 2 m ………………. (2)
from (i), \(\frac{\mathrm{BC}}{\sqrt{3}}\) = \(\frac{2}{1}\)
⇒ BC = 2\(\sqrt{3}\)
= 2 × 1.732 = 3.464 m
Therefore, the height of the statue
CD = BC – BD
= 3.464 – 2 = 1.464 m

Question 4.
From the top of a building, the angle of elevation of the top of a cell tower is 60° and the angle of depression to its foot is 45°. If distance of the building from the tower is 7m, then find the height of the tower. (AS₄)
Solution:
From the figure,
Let AB be the height of the tower.
CD be the height of the building.
Distance between the building from the tower is 7m

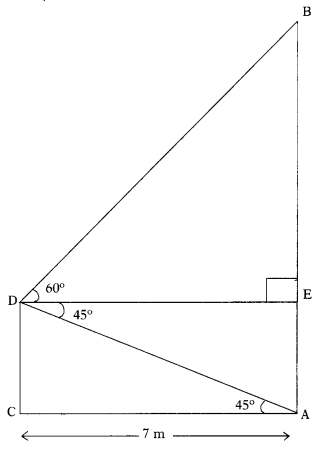
Angles of elevation and depression are
∠BDE = 60° and ∠EDA = 45° and DE = AC = 7m and DC = AE
From the right angled ∆BDE,
We have
tan 60° = \(\frac{\mathrm{BE}}{\mathrm{DE}}\)
⇒ \(\sqrt{3}\) = \(\frac{\mathrm{BE}}{7}\)
⇒ BE = 7 \(\sqrt{3}\) ……………….. (1)
From the right angled ∆ADC, we have
tan 45° = \(\frac{\mathrm{CD}}{\mathrm{AC}}\)
1 = latex]\frac{\mathrm{CD}}{7}[/latex]
⇒ CD = 7 ………………. (2)
From the equations (1) and (2)
Height of the tower = AB = AE + BE
= 7 + 7 \(\sqrt{3}\) = 7(1 + \(\sqrt{3}\))
= 7(1 + 1.732)
= 7(2.732) = 19.124 m
Hence, the height of the tower is 19.124 m.

Question 5.
A wire of length 18 m had been tied with electric pole at an angle of elevation 30° with the ground. Because it was covering a long distance, it was cut and tied at an angle of elevation 60° with the ground. How much length of the wire was cut ? (AS₄)
Solution:
In the figure,
Let AB be the height of the electric pole = h m.
BC be the actual length of the wire = 18 m.
X and Y are the first and second points of observations.

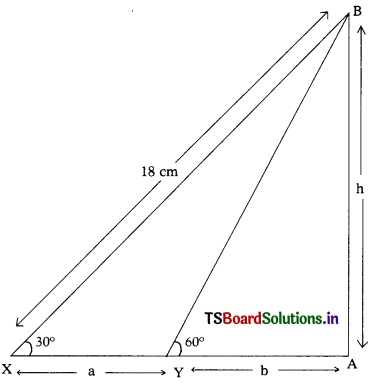
Let AX = a + b and AY = b
Angles of elevations are ∠BXA = 30° and ∠BYA = 60°

Again from the ∆ ABY
Cos 60° = \(\frac{\mathrm{AY}}{\mathrm{BY}}\)
\(\frac{1}{2}\) = \(\frac{\mathrm{b}}{\mathrm{BY}}\)
BY = 2b
BY = 2(3\(\sqrt{3}\))
= 6\(\sqrt{3}\)
= 6 (1.732)
∴ BY = 10. 3920
∴ BY = 10.39230
The length of the cut wire = BX – BY
= 18 – 10.39230
= 7.6076 m
= 7.608 m

Question 6.
The angle of elevation of the top of a build¬ing from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of building is 60°. If the tower is 30 m high, find the height of the building. (AS₄)
Solution:
From the figure,
Let ‘BC’ be the height of the tower is 30 m.
Let ‘AD’ be the height of the building is h m_C

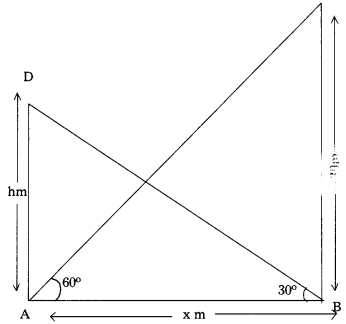
Angle of elevation, from the bottom of building and tower as well as
∠BAC = 60° and ∠ABD = 30°
Also, let AB = x be the distance between foot of the tower and building.
In right angled ∆ABD, we have
tan 30° = \(\frac{\mathrm{AD}}{\mathrm{AB}}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{h}}{\mathrm{x}}\)
⇒ h = \(\frac{\mathrm{x}}{\sqrt{3}}\) ………….. (1)
Again, in right angled ∆BAC, we have
tan 60° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ \(\sqrt{3}\) = \(\frac{30}{\mathrm{x}}\)
x = \(\frac{30}{\sqrt{3}}\) m
Substituting x = \(\frac{30}{\sqrt{3}}\) in equation (1) we get
h = \(\frac{30}{\sqrt{3}} \times \frac{1}{\sqrt{3}}\) = \(\frac{30}{3}\) = 10 m
Hence, the height of the building is 10 m.

Question 7.
Two poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles. (AS₄)
Solution:
AB and CD are two poles of equal height.
Let BE = x, then ED = (120 – x)
In ∆ABE, ∠B = 90°, ∠AEB = 60°
∴ tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BE}}\)

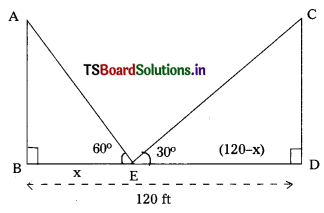
⇒ \(\frac{\sqrt{3}}{1}\) = \(\frac{\mathrm{AB}}{\mathrm{x}}\)
⇒ AB = \(\sqrt{3}\) x ……………… (1)
In ∆CDE, ∠D = 90° and ∠CED = 30°
∴ tan 30° = \(\frac{\mathrm{CD}}{\mathrm{ED}}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{CD}}{120-\mathrm{x}}\)
⇒ CD × \(\sqrt{3}\) = 120 – x
⇒ CD = \(\frac{120-x}{\sqrt{3}}\) ………………… (2)
from (1) & (2), we have
\(\frac{120-x}{\sqrt{3}}\) = \(\frac{\sqrt{3} x}{1}\) (∵ AB = CD)
\(\sqrt{3}\) × \(\sqrt{3}\)x = 120 – x
3x = 120 – x
3x + x = 120
4x = 120
x = \(\frac{120}{4}\) = 30
AB = \(\sqrt{3}\) x
= \(\sqrt{3}\) × 30
= 30\(\sqrt{3}\) = 30 × 1.732
= 51.96 ft
The height of the pole = 51.96 ft.
The distance of one pole AB from the point E = 30 ft.
The distance of another pole CD from the point E = 120 – 30 = 90 ft.

Question 8.
The angles of elevation of the top of a tower from two points are at a distance of 4m and 9 m, find the height of the tower from the base of the tower and in the same straight line with it are complementary. (AS₄)
Solution:
From the figure,
AB be the height of a tower = h m
Let the two points on the ground are ‘C’ and
‘D’, such that they make a distance 4 m and
AC = 4 m and AD = 9 m

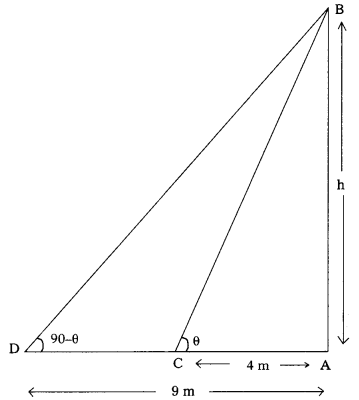
Angles of elevation are ∠ACB = θ and ∠ADB = 90 – θ
In the right angled ∆ABC, we have
tan θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ tan θ = \(\frac{\mathrm{h}}{4}\)
Again from the right angled ∆ABD, we have
tan (90 – θ) = \(\frac{\mathrm{AB}}{\mathrm{AD}}\)
⇒ cot θ = \(\frac{\mathrm{h}}{9}\)
⇒ \(\frac{1}{\tan \theta}\) = \(\frac{\mathrm{h}}{9}\)
⇒ tan θ = \(\frac{9}{\mathrm{h}}\) …………….. (2)
From the equations (1) and (2) :
\(\frac{\mathrm{h}}{4}\) = \(\frac{9}{\mathrm{h}}\)
⇒ h² = 36
h = \(\sqrt{36}\) = 6 m
The height of the tower is 6 m.

Question 9.
The angle of elevation of jet plane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of 1500 \(\sqrt{3}\) meters, find the speed of the jet plane. (\(\sqrt{3}\) = 1.732) (AS₄)
Solution:
From the figure,
Let P and Q be the two positions of the plane.

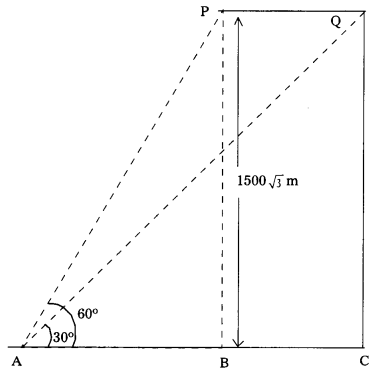
Let A’ be the point of observation.
Let ABC be the horizontal line through A.
It is given that angle of elevation of the plane Q
from a point A’ are 60° and 30° respectively.
∴ ∠PAB = 60°, ∠QAB = 30°
Constant height of jet plane = 1500 \(\sqrt{3}\) m
In the right angled ∆ABP we have
tan 60° = \(\frac{\mathrm{BP}}{\mathrm{AB}}\)
⇒ \(\sqrt{3}\) = \(\frac{1500 \sqrt{3}}{\mathrm{AB}}\)
⇒ AC = \(\frac{1500 \sqrt{3}}{\sqrt{3}}\) = 1500 m
In the right angled ∆ACQ, we have
tan 30° = \(\frac{\mathrm{CQ}}{\mathrm{AC}}\) ⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{1500 \sqrt{3}}{\mathrm{AC}}\)
⇒ AC = 1500 × \(\sqrt{3}\) × \(\sqrt{3}\)
= 1,500 × 3 = 4,500 m
From the figure
PQ = BC = AC – AB
= 4500 – 1500 = 3000 m
Thus, the plane travels 3000 m in 15 seconds.
Hence, speed of a plane = \(\frac{3000}{15}\)
= 200m/sec.

Question 10.
The angle of elevation of the top of a tower from the foot of the building is 30° and the angle of elevation of the top of the building from the foot of the tower is 60°. What is the ratio of heights of tower and building ? (AS₄)
Solution:
Let the height of the tower = x m
Let the height of the building = y m

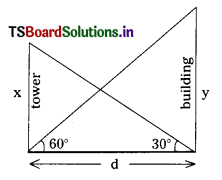
Distance between the tower and building = d m.
Angle of elevation of the top of the tower = 30°
From the figure,
tan 30° = \(\frac{\mathrm{x}}{\mathrm{d}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{x}}{\mathrm{d}}\)
d = \(\sqrt{3}\)x …………….. (1)
Also tan 60° = \(\frac{\mathrm{y}}{\mathrm{d}}\)
\(\sqrt{3}\) = \(\frac{\mathrm{y}}{\mathrm{d}}\)
d = \(\frac{y}{\sqrt{3}}\) …………….. (2)
From (1) and (2)
\(\sqrt{3}\)x = \(\frac{y}{\sqrt{3}}\)
\(\frac{x}{y}=\frac{1}{\sqrt{3} \cdot \sqrt{3}}=\frac{1}{3}\)
∴ x : y = 1 : 3
∴ The ratio of heights of tower and building = 1 : 3.