Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 13 Probability InText Questions to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 13 Probability InText Questions
Do This
(a) Outcomes of which of the following experiments cure equally likely. (AS3)(Page No. 307)
Question 1.
Getting a digit 1, 2, 3, 4, 5 or 6 when a die is rolled.
Solution:
Equally likely
Question 2.
Selecting a different colour ball from a bag of 5 red balls, 4 blue balls and 1 black ball.
Note : Picking two different colour balls, i.e., Picking a red, a blue (or) black ball from a ………
Solution:
Not equally likely
Question 3.
Winning in a game of carrom.
Solution:
Not equally likely
Question 4.
Units place of a two digit number selected may be 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9.
Solution:
equally likely
Question 5.
Selecting a different colour ball from a bag of 10 red balls, 10 blue balls and 10 black balls.
Solution:
equally likely
![]()
Question 6.
Raining on a particular day of July.
Solution:
equally likely
(b) Are the outcomes of every experiment equally likely ?
Solution:
Outcomes of all experiments need not necessarily be equally likely.
(c) Give examples of 5 experiments that have equally likely outcomes and five more examples that do not have equally likely outcomes.
Solution:
Equally likely events :
a) Getting an even or odd number when a die is rolled.
b) Getting tail or head when a coin is tossed.
c) Getting an even (or) odd number when a card is drawn at random from a pack of cards numbered from 1 to 10.
d) Picking a green or black ball from a bag containing 8 green balls and 8 black balls.
e) Selecting a boy or girl from a class of 20 boys and 20 girls.
f) Selecting a red or black card from a deck of cards.
Events which are not equally likely :
a) Getting a prime (or) composite number when a die is thrown.
b) Getting an even or odd number when a card is drawn at random from a pack of cards numbered from 1 to 5.
c) Getting a number which is a multiple of 3 (or) not a multiple of 3 from numbers 1, 2, …….., 10.
d) Getting a number less than 5 or greater than 5.
e) Drawing a white ball or green ball from a bag containing 5 green balls and 8 white balls.
Think of 5 situations with equally likely events and find the sample space.
a) Tossing a coin : Getting a tail or head when a coin is tossed.
Sample space = {T, H}
b) Getting an even (or) odd number when a die is rolled.
Sample space = {1, 2, 3, 4, 5, 6}
c) Winning a game of shuttle Sample space = {win, loss}
d) Picking a black (or) blue ball from a bag containing 3 blue balls and 3 black balls = {blue, black}
e) Drawing a red coloured card or black coloured card from a deck of cards = {black, red}
![]()
d) Is getting a head complementary to getting a tail ? Give reasons.
Solution:
Number outcomes favourable to head = 1
Probability of getting a head = \(\frac{1}{2}\) [P(E)]
Number of outcomes not favourable to head = 1
Probability of not getting a head = \(\frac{1}{2}\) (P (\(\overline{\mathrm{E}}\)))
Now P(E) + P(\(\overline{\mathrm{E}}\)) = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
∴ Getting a head is complementary to getting a tail.
e) In case of a die is getting a 1 complementary to events getting 2, 3, 4, 5, 6 ? Give reasons for your answer.
Solution:
Yes, complementary events
∴ Probability of getting a 1 = \(\frac{1}{6}\) [P(E)]
Probability of getting 2, 3, 4, 5, 6
= P (\(\overline{\mathrm{E}}\)) = \(\frac{5}{6}\)
p(E) + P(\(\overline{\mathrm{E}}\)) = \(\frac{1}{6}\) + \(\frac{5}{6}\) = \(\frac{6}{6}\) = 1
f) Write of five new pair of events that are complementary.
Solution:
a) When a die is thrown, getting an even number is complementary to getting an odd number.
b) Drawing a red card from a deck of cards is complementary to getting a black card.
c) Getting an even number is complementary to getting an odd number from numbers 1, 2, ……….., 8.
d) Getting a Sunday is complementary to getting any day other than Sunday in a week.
e) Winning a running race is complementary to loosing it.
Try This
Question 1.
A child has a die whose six faces show the letters A, B, C, D, E and F. The die is thrown once. What is the probability of getting (i) A ? (ii) D ? (AS4)(Page No. 312)
Solution:
Total number of outcomes [A, B, C, D, E and F] = 6
i) Number of favourable outcomes to A = 1
Probability of getting A = P(A)
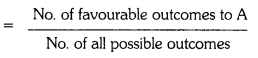
= \(\frac{1}{6}\)
![]()
ii) Number of outcomes favourable to D = 1
Probability of getting D
= P(D)
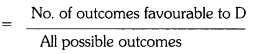
= \(\frac{1}{6}\)
Question 2.
Which of the following cannot be the probability of an event ? (AS3)(Page No. 312)
a) 2.3
b) – 1.5
c) 15%
d) 0.7
Solution:
a) 2.3 – Not possible
b) -1.5 – Not possible
c) 15% – May be the probability
d) 0.7 – May be the probability
Question 3.
You have a single deck of well shuffled cards. Then,
i) What is the probability that the card drawn will be a queen ? (AS4)(Page No. 313)
Solution:
Number of all possible outcomes
= 4 × 13 = 1 × 52 = 52
Number of outcomes favourable to Queen
= 4[♥Q ♥Q ♥Q ♥Q]
Probability P(E)
= \(\frac{\text { No. of favourable outcomes }}{\text { Total no.of outcomes }}\)
= \(\frac{4}{52}\)
= \(\frac{1}{13}\)
ii) What is the probability that it is a face card ? (Page No. 314)
Solution:
Face cards are J, Q, K.
∴ Number of outcomes favourable to face cards = 4 × 3 = 12
No. of all possible outcomes = 52
P(E) = \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\)
= \(\frac{12}{52}\) = \(\frac{3}{13}\)
![]()
iii) What is the probability that it is a spade ? (Page No. 314)
Solution:
Number of spade cards = 13
Total number of cards = 52
Probability = \(\frac{\text { Number of outcomes favourable to spade }}{\text { Number of all outcomes }}\)
= \(\frac{13}{52}\) = \(\frac{1}{4}\)
iv) What is the probability that is the face cards of spades ? (Page No. 314)
Solution:
Number of outcomes favourable to face cards of spades = (K, Q, J) = 3
Number of all outcomes = 52 3
∴ P(E) = \(\frac{3}{52}\)
v) What is the probability it is not a face card ? (Page No. 314)
Solution:
Probability of a face card = \(\frac{12}{52}\)
∴ Probability that the card is not a face card
= 1 – \(\frac{12}{52}\) [P (\(\overline{\mathrm{E}}\)) = 1 – P(E)]
= \(\frac{52-12}{52}\)
= \(\frac{40}{52}\) = \(\frac{10}{13}\)
(Or)
Number of favourable outcomes = 4 × 10 = 40
Number of all outcomes = 52
∴ Probability = \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\)
= \(\frac{40}{52}\) = \(\frac{10}{13}\)
Think – Discuss
Question 1.
Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of any game ? (Page No. 312)
Solution:
Probability of getting a head is \(\frac{1}{2}\) and a tail is
\(\frac{1}{2}\) = 1
Hence, tossing a coin is a fair way.
![]()
Question 2.
Can \(\frac{7}{2}\) be the probability of an event ? Explain. (AS3) (Page No. 312)
Solution:
\(\frac{7}{2}\) can’t be the probability of any event. Since probability of any event should lie between 0 and 1.
Question 3.
Which of the following arguments are correct and which are not correct ? Given reasons. (Page No. 312)
i) If two coins are tossed simultaneously, there are three possible outcomes – two heads, two tails (or) one of each. Therefore, for each. If these outcomes, the probability is \(\frac{1}{3}\)
Solution:
False
Reason :
All possible outcomes are 4. They are HH, HT, TH, TT
Thus, probability of two heads = \(\frac{1}{4}\)
Probability of two tails = \(\frac{1}{4}\)
Probability of one each = \(\frac{2}{4}\) = \(\frac{1}{2}\)
![]()
ii) If a die is thrown, there are two possible outcomes – an odd number (or) an even number. Therefore, the probability of getting an odd number is \(\frac{1}{2}\).
Solution:
True
Reason :
All possible outcomes = (1, 2, 3, 4, 5, 6) = 6
Outcomes favourable to an odd number = (1, 3, 5) = 3
Outcomes favourable to an even number = (2, 4, 6) = 3
∴ Probability (odd number)
= \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)