TS 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Ex 12.1

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 12 Applications of Trigonometry Ex 12.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Exercise 12.1

Question 1.
A tower stands vertically on the ground. From a point which is 15 meter away from the foot of the tower, the angle of elevation of the top of the tower is 45°. What is the height of the tower ? (AS₄)
Solution:

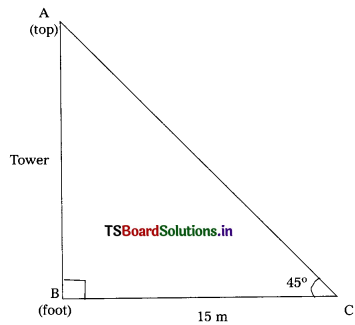
In ∆ ABC, ∠B = 90°
AB represents the height of the tower and ∠ACB = 45°
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
1 = \(\frac{\mathrm{AB}}{15}\)
⇒ AB = 15 meters.
Therefore, the height of the tower = 15 meters.

Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground by making 30° angle with the ground. The distance between the foot of the tree and the top of the tree on the ground is 6 m. Find the height of the tree before falling. (AS₄) (A.P. Mar. ’16)
Solution:
Let AB represents the height of the tree

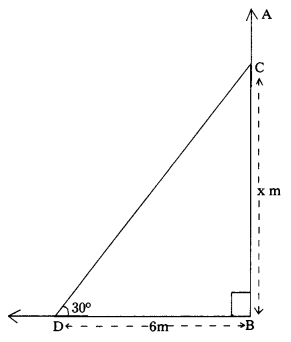
AC represents the broken part.
AC = CD (∵ the broken part touches the ground)
Let BC = x meters, the height of the tree after it is broken
In ∆CBD, ∠B = 90° and ∠BDC = 30°
tan 30° = \(\frac{\mathrm{BC}}{\mathrm{BD}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{x}{6}\)
⇒ \({\sqrt{3}}\) x = 6
⇒ x = \(\frac{6}{\sqrt{3}}\) (∵ \(\frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{6 \sqrt{3}}{3}=2 \sqrt{3}\))
⇒ x = \(2 \sqrt{3}\)
sin 30° = \(\frac{\mathrm{BC}}{\mathrm{BD}}\)
\(\frac{1}{2}\) = \(\frac{2 \sqrt{3}}{C D}\)
⇒ CD = 2 × 2\({\sqrt{3}}\) = 4\({\sqrt{3}}\)
∴ The height of the tree before falling down
= AB
= AC + CB
= 4\({\sqrt{3}}\) + 2\({\sqrt{3}}\) (∵ AC = CD = 4\({\sqrt{3}}\))
= 6\({\sqrt{3}}\) m

Question 3.
A contractor wants to set up a slide for the children to play in the park. He wants to set it up at the height of 2m and by making an angle of 30° with the ground. What should be the length of the slide ? (AS₄)
Solution:
In the triangle ABC, ∠B = 90°
Let AC represents the length of the side
AB = 2 m
sin 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{1}{2}\) = \(\frac{2}{\mathrm{AC}}\)
⇒ Ac = 4

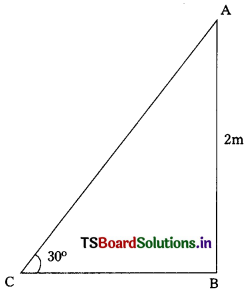
Hence, length of the side = 4m

Question 4.
Length of the shadow of a 15 meter high pole is 5\({\sqrt{3}}\) m at 7 o’ clock in the morning. Then, what is the angle of elevation of the sun rays with the ground at the time ? (A.P. Mar.’15) (AS₄)
Solution:
In ∆ABC, ∠B = 90°
AB represents the height of the pole.
AB = 15m
Let BC represents its shadow at 7 o’ clock in the morning.
BC = 5\({\sqrt{3}}\) m
Let the angle of elevation of the sun rays with the ground be ‘θ’.
Now, tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
= \(\frac{15}{5 \sqrt{3}}\)
= \(\frac{3}{\sqrt{3}}\)

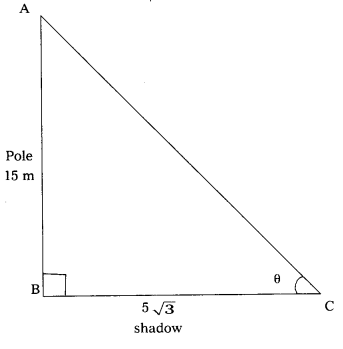
We know that tan 60° = \({\sqrt{3}}\)
∴ θ = 60°
Hence, the angle of elevation of the sun rays with the ground at the time = 60°.

Question 5.
You want to erect a pole of height 10 m with the support of three ropes. Each rope has to make an angle 30° with the pole. What should be the length of the rope ? (AS₄)
Solution:
In the figure,

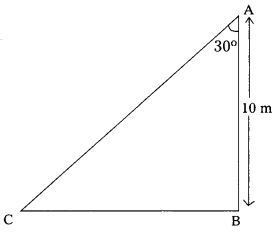
Let AB be the height of the pole = 10 m
Let AC be the length of the rope
Angle of elevation is 30°
From right angled ∆ ABC
cos 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{10}{\mathrm{AC}}\)
⇒ AC = \(\frac{2 \times 10}{\sqrt{3}}\)
⇒ AC = \(\frac{20}{1.732}\) (∵ \({\sqrt{3}}\) = 1.732)
⇒ AC = 11.547 cm
Hence, the length of the rope is 11.547 m

Question 6.
Suppose you are shooting an arrow from the top of a building at a height of 6 m to a target on the ground at an angle of depression of 60°. What is the distance be-tween you and the object ? (AS₄) (A.P. Mar.15)
Solution:

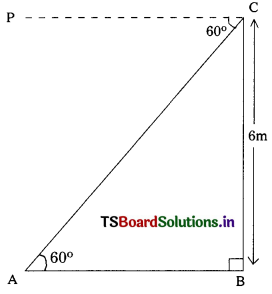
In figure,
Let BC be the height of a building = 6 m
‘C’ be the point of the observation and A’ be the target on the ground.
Angle of depression is ∠CAB = 60°
Let AC be the distance between me and the object
From the right angled ∆ABC,
sin 60° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{6}{\mathrm{AB}}\)
⇒ AB = \(\frac{6 \times 2}{\sqrt{3}}=\frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{12 \sqrt{3}}{3}\) = 4\({\sqrt{3}}\) m
Hence, the distance between me and the object is 4\({\sqrt{3}}\) m.

Question 7.
An electrician wants to repair an electric connection on a pole of height 9 m. He needs to reach 1.8 m below the top of the pole to do repair work. What should be the length of the ladder which he should use, when he climbs it at an angle of 60° with the ground ? What will be the distance between foot of the ladder and foot of the pole ? (AS₄)
Solution:
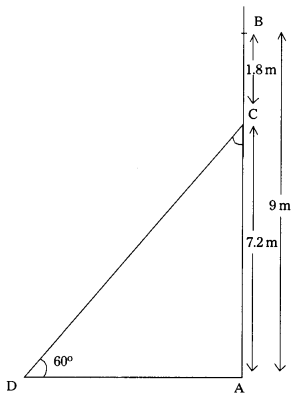
In the figure,
Let AB be the height of a pole is 9 m
AC be the actual required height of the pole is 7.2 m
Angle of elevation is ∠CDA = 60°.
CD be the length of the ladder.
AD be the distance between foot of the ladder and foot of the pole.
From the right angled ∆ADC,
tan 60° = \(\frac{\mathrm{AC}}{\mathrm{AD}}\)
⇒ \({\sqrt{3}}\) = \(\frac{7.2}{\mathrm{AD}}\)

⇒ AD = \(\frac{7.2}{\sqrt{3}}=\frac{7.2}{1.732}\)
⇒ AD = 4.15692 m
Again, from the ∆ADC,
sin 60° = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{7.2}{\mathrm{CD}}\)
⇒ CD = \(\frac{7.2 \times 2}{\sqrt{3}}\)
⇒ CD = \(\frac{7.2 \times 2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
CD = \(\frac{7.2 \times 2 \times \sqrt{3}}{3}\)
CD = 2.4 × 2 × \({\sqrt{3}}\)
CD = 4.8 × \({\sqrt{3}}\)
CD = 8.3138 m
Hence, the distance between foot of the ladder and foot of the pole is 4.15692 m and the length of the ladder is 8.3138 m.

Question 8.
A boat has to cross a river. It crosses the river by making an angle of 60° with the bank of the river due to the stream of the river and travels a distance of 600 m to reach the another side of the river. What is the width of the river ? (AS₄)
Solution:

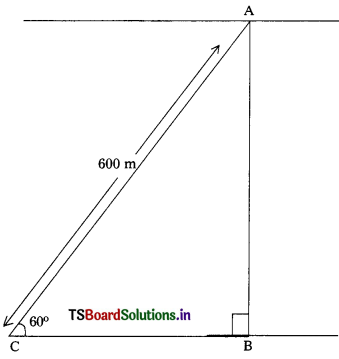
In the figure,
Let A’ be the required point to reach the bank of the river.
Let ‘C’ be the present position of the boat (or) observation point.
AC be the distance travelled by the boat is 600 m
Angle of elevation is ∠ACB = 60°
AB be the actual width of the river
From the right angled ∆ABC,
sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{\mathrm{AB}}{600}\)
⇒ AB = 600 × \(\frac{\sqrt{3}}{2}\)
⇒ AB = 300\({\sqrt{3}}\) m
⇒ Hence, the width of the river is 300\({\sqrt{3}}\) m

Question 9.
An observer of height 1.8m is 13.2m away from a palm tree. The angle of elevation of the top of the tree from his eyes is 45°. What is the height of palm tree ? (AS₄)
Solution:
AB represents the height of the observer.
CD denotes the height of the palm tree.
AB = 1.8 m; BC = 13.2 m AE = 13.2 m (∵ ABCE is a rectangle so, opposite sides of BC and AE are equal)
(AB and EC are also opposite sides of the rectangle ABCE)
∴ AB = EC
In ∆AED, ∠E = 90°
tan 45° = \(\frac{\mathrm{DE}}{\mathrm{AE}}\)
1 = \(\frac{\mathrm{DE}}{13.2}\)
⇒ DE = 13.2 m

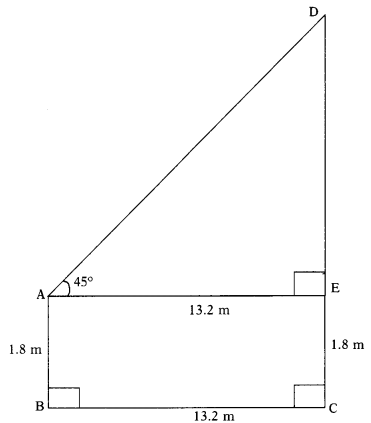
Therefore, the height of the palm tree CD
= DE + EC
= 13.2 + 1.8
= 15 meters.

Question 10.
In the adjacent figure
In ∆ABC, AC = 6 cm, AB = 5 cm and ∠BAC = 30°. Find the area of the triangle. (AS₄)
Solution:
In ∆ ABC,
AB = 5 cm, AC = 6 cm
∠BAC = 30°
Draw BD ⊥ AC

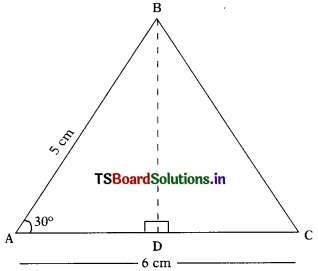
In ∆ ABD, ∠ADB = 90°
sin 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
\(\frac{1}{2}\) = \(\frac{\mathrm{BD}}{5}\)
⇒ 2 × BD = 5
BD = \(\frac{5}{2}\) = 2.5 cm
Hence, area of the triangle ABC
= \(\frac{1}{2}\) × Base × Altitude
= \(\frac{1}{2}\) × AC × BD
= \(\frac{1}{2}\) × 6 × 2.5
= 3 × 2.5 = 7.5 cm²