Class 10

We are offering TS 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle to learn maths more effectively.

TS 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle

→ Secant: A line which intersects a circle in two distinct points is called a secant.

PAB is secant of the circle with centre ‘o’

→ Tangent: A tangent to a circle is a line that intersects the circle is exactly one point.

Tt is the tangent to the circle with centre ‘o’

• No tangent can be drawn to a circle from a point lying inside it.
• One and only one tangent can be drawn to a circle at a point on a circle.
• Two tangents can be drawn to a circle from a point lying outside it.
• The lengths of two tangents drawn from an external point to a circle are equal.
• A tangent to a circle is perpendicular to the radius drawn through the point of contact.
• A line drawn through the end point of a radius and perpendicular to it is a tangent to the circle.
• The common point of a tangent to a circle is called point of contact.
• The line containing the radius through the point of contact the normal to the circle at the point.

→ Sector: The portion of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.
OAPB is a sector of the circle with centre ‘O’
∠AOB is called the angle of the sector. OAPB is called the minor sector and OAQB is called the major sector.

Area of the sector = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × πr² where x° is the angle of the sector & ‘r’ is the radius.
Length of arc = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × 2πr

→ Segment: The chord AB divides the circle with centre ‘O’ into two parts. APB is called the minor segment where as AQB is called the major segment.

Area of the segment: Area of the segment APB = Area of the sector OAPB – Area of OAB.
Area of the major sector OAQB = Area of the circle – Area of the minor sector OAPB
Area of major segment of a circle = Area of the corresponding sector – Area of the corresponding triangle.

→ The locus of points which are joined by a curve and are equidistant from a fixed point is called a circle. The fixed point here is called the centre of the circle.

(Or)
A simple closed curve consisting of all points in a plane which are equidistant from a fixed point is called a circle. The fixed point is its centre and the fixed distance is its radius.

→ The path followed by circular object is a straight line.

→ The line segment joining any two points on a circle is called a ‘chord’. The longest of all chords of a circle passes through the centre and is called a diameter.

\(\overline{\mathrm{AB}}\) is a chord and \(\overline{\mathrm{PQ}}\) is a diameter. (PO and OQ is the radius of the circle.
Diameter = 2 × radius
d = 2r
r = \(\frac{r}{2}\)

→ There are three different possibilities for a given line and a circle.

Case (i): The line PQ and the circle have no point in common (or) they do not touch each other.
Case (ii): The line PQ and the circle have two common points (or) a line which intersects a circle at two distinct points is called a “secant” of the circle.
The line PQ intersects the circle at two distinct points A and B. Here the line PQ is a “secant” of the circle.
Case (iii): The line PQ touches the circle at an unique point A(or) there is one and only one point common to both the line and circle.
Here \(\overleftrightarrow{\mathrm{PQ}}\) is called a tangent to the circle at ‘A’.

→ The word tangent is derived from the Latin word “TANGERE” which means “to touch” and was introduced by Danish mathematician “Thomas Fineke” in 1583.

→ There is only one tangent to the circle at one point.

→ The tangent at any point of a circle is perpendicular to the radius through the point of contact.

The radius OP is perpendicular to \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) at P. i.e., OP ⊥ AB.

→ Construction of a tangent to a circle :

• Draw a circle with centre ‘O’.
• Draw a perpendicular line to OP through ‘P’.
• Let it be \(\stackrel{\leftrightarrow}{\mathrm{XY}}\).
• XY is the required tangent to the given circle passing through P.

→ Let ‘O’ be the centre of the given circle and \(\overline{\mathrm{AP}}\) is a tangent through a Where OA is the radius, then the length of the tangent AP = \(\sqrt{O P^2-\mathrm{OA}^2}\)

→ Two tangents can be drawn to a circle from an external point.

Important Formula:

• Area of Sector = \(\frac{\mathrm{X}^{\circ}}{360^{\circ}}\) × πr²
• Length of arc = \(\frac{\mathrm{X}^{\circ}}{360^{\circ}}\) × 2πr
• A line which intersects a circle In two distinct points Is called a secant.
• A tangent to a circle is a line that Intersects the circle Is exactly one point.

Flow Chat:

Archimedes (287 – 212 B.C):

• “Archimedes of Syracuse” was a Greek mathematician, physicist and engineer.
• He is regarded as one of the leading scientists in classical antiquity.
• He made several discoveries in the fields of mathematics particularly in geometry.

Solving these TS 10th Class Maths Bits with Answers Chapter 8 Similar Triangles Bits for 10th Class will help students to build their problem-solving skills.

Similar Triangles Bits for 10th Class

Question 1.
From the figure ∠DAC = ……………….

A) 35°
B) 55°
C) 45°
D) 60°
Answer:
A) 35°

Question 2.
The ratio of the corresponding sides of two similar triangles is 5 : 3 then the ratio of their areas
A) 5 : 3
B) 3 : 5
C) 6 : 10
D) 25 : 9
Answer:
D) 25 : 9

Question 3.
If ∆ABC ~ ∆DEF; BC = 4 cm, EF = 5 cm and ∆ABC = 80 cm² then ∆DEF = ………………….
A) 100 cm²
B) 150 cm²
C) 125 cm²
D) 225 cm²
Answer:
C) 125 cm²

Question 4.
In the figure DE // BC and AD : DB = 1 : 2 then ∆ADE : ∆ABC =
A) 1 : 4
B) 4 : 1
C) 1 : 9
D) 2 : 9
Answer:
C) 1 : 9

Question 5.
∆ABC ~ ∆PQR. M is the mid point of BC. N is the mid point of QR. If the area of ∆ABC = 100 cm² and area of ∆PQR = 144 cm2 and AM = 4 cm then PN = ………………… cm
A) 5 cm
B) 4.8 cm
C) 4 cm
D) 3.8 cm
Answer:
B) 4.8 cm

Question 6.
In ∆PQR, PQ = 6\(\sqrt{3}\) cm; PR = 12 cm, QR = 6 cm then ∠B = ………………..
A) 30°
B) 45°
C) 90°
D) 60°
Answer:
B) 45°

Question 7.
The lengths of diagonals of a rhombus are 24 cm and 32 cm then the perimeter of rhombus
A) 180°
B) 120°
C) 220°
D) 112°
Answer:
A) 180°

Question 8.
Which of the following does not belongs to side of right triangle ?
A) 9cm, 15cm, 12cm
B) 9cm, 5cm, 7cm
C) 400mm, 300mm, 500mm
D) 2cm, \(\sqrt{5}\) cm, 1cm
Answer:
B) 9cm, 5cm, 7cm

Question 9.
In an isosceles ∆PQR, PR = QR and PQ² = 2PR² then ∠R = ……………….
A) 60°
B) 30°
C) 90°
D) 45°
Answer:
C) 90°

Question 10.
In ∆ABC the mid points are D, E and F of the sides AB, BC, CA then ∆DEF : ∆ABC
A) 1 : 1
B) 1 : 3
C) 1 : 2
D) 1 : 4
Answer:
D) 1 : 4

Question 11.
The diagonal of a square is 7\(\sqrt{2}\) cm then its area
A) 28 cm²
B) 14\(\sqrt{2}\) cm²
C) 21 cm²
D) 49 cm²
Answer:
D) 49 cm²

Question 12.
In the figure AB = 2.5 cm, AC = 3.5 cm. If AD is the bisector of ∠BAC then BD : DC = …………..

A) 5 : 3
B) 3 : 5
C) 5 : 7
D) 2 : 7
Answer:
C) 5 : 7

Question 13.
In the figure DE divides AB and AC in the ratio 1 : 3 If DE = 2.4 cm then BC = ………………

A) 4.8 cm
B) 7.2 cm
C) 9.6 cm
D) 12 cm
Answer:
B) 7.2 cm

Question 14.
The height of an equilateral triangle whose side is a unit
A) \(\frac{\mathrm{a}}{2}\)
B) \(\frac{\sqrt{3}}{2}\)a
C) \(\sqrt{3}\)a
D) \(\frac{\sqrt{3}}{4}\)a
Answer:
B) \(\frac{\sqrt{3}}{2}\)a

Question 15.
If ∆ABC ~ ∆XYZ, ∠C = 60° ∠B = 75° then ∠Z = ……………….
A) 90°
B) 75°
C) 45°
D) 60°
Answer:
D) 60°

Question 16.
Maximum possible tangents that can drawn to a circle is ………. (A.P. Mar. ’15)
A) Infinity
B) 4
C) 100
D) 2
Answer:
A) Infinity

Question 17.
∆ABC ~ ∆DEF and areas of ∆ABC, ∆DEF are 64 cm² and 121 cm² then the ratio of corresponding sides. (A.P. Mar. ’15)
A) 11 : 8
B) 8 : 11
C) 3 : 11
D) 19 : 8
Answer:
B) 8 : 11

Question 18.
Area of a regular hexagon whose side is ‘a’ cm is ………………. (A.P. Mar. ’15)
A) 6 \(\left(\frac{\sqrt{3}}{4} a^2\right)\)
B) 6 \(\left(\frac{3}{4} a^2\right)\)
C) \(\sqrt{6}\left(\frac{3}{4} a^2\right)\)
D) 6\(\left(\frac{\sqrt{3}}{4} a^2\right)\)
Answer:
D) 6\(\left(\frac{\sqrt{3}}{4} a^2\right)\)

Question 19.
If a man walks 6 m to East and 8m to North. Now he is at a distance of ……………… from origin point. (A.P. Mar.’15 )
A) 10 m
B) 48 m
C) 14 m
D) 2 m
Answer:
A) 10 m

Question 20.
∠CAD in the given figure is …………………

A) 50°
B) 60°
C) 40°
D) 90°
Answer:
A) 50°

Question 21.
Example for the sides of a Right angled triangle is …………….. (A.P. June ’15)
A) 5, 6, 9
B) 5, 12, 13
C) 5, 11, 12
D) 7, 8, 9
Answer:
B) 5, 12, 13

Question 22.
Height of an equilateral triangle whose side is ‘a’ cm is ……………. (A.P. Mar. ’16)
A) \(\frac{\sqrt{3}}{2}\)a
B) \(\frac{2}{\sqrt{3}}\)a²
C) \(\sqrt{\frac{3}{2}}\)a
D) \(\frac{\sqrt{3}}{2}\)a²
Answer:
A) \(\frac{\sqrt{3}}{2}\)a

Question 23.
∆ABC ~ ∆XYZ, ∠C = 60° ∠B = 70° then ∠ X = ……………… (A.P. Mar.’16)
A) ∠ X = 70°
B) ∠ X = 50°
C) ∠X = 60°
D) ∠X = 10°
Answer:
B) ∠ X = 50°

Question 24.
When we construct a triangle similar to a given triangle as per given scale factor, we construct on the basis of ………….. (T.S. Mar. ’15)
A) SSS similarity
B) AAA similarity
C) Basic proportionality theorem
D) A and C are correct
Answer:
C) Basic proportionality theorem

Question 25.
∆ABC ~ ∆DEF is given then which of the following is correct. (T.S. Mar. ’15)


Answer:
(A)

Question 26.
In ∆ABC ∠C = 90°, BC = a, AB = c, AC = b and ‘p‘ is length of height drawn from ‘C’ to AB then ……… is correct. (T.S. Mar. ’15)
A) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) – \(\frac{1}{\mathrm{b}^2}\)
B) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{b}^2}\) – \(\frac{1}{\mathrm{a}^2}\)
C) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) + \(\frac{1}{\mathrm{b}^2}\)
D) \(\frac{2}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) + \(\frac{1}{\mathrm{b}^2}\)
Answer:
C) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) + \(\frac{1}{\mathrm{b}^2}\)

Question 27.
From the figure, x = …………………

A) 10
B) 15
C) 12
D) 25
Answer:
B) 15

Question 28.
In the given figure, DE // BC and AD : DB = 5 : 4, then \(\frac{\text { D DEF }}{\text { D CFB }}\) =

A) \(\frac{81}{25}\)
B) \(\frac{5}{9}\)
C) \(\frac{5}{4}\)
D) \(\frac{25}{81}\)
Answer:
D) \(\frac{25}{81}\)

Question 29.
In the figure, ∆ ABC is an isosceles triangle right angled at B. Two equilateral triangles are constructed with sides AC and BC. Then ∆ BCD = …………

A) ∆ ACE
B) ∆ ABC
C) \(\frac{1}{2}\) (∆ ABC)
D) \(\frac{1}{2}\) (∆ ACE)
Answer:
D) \(\frac{1}{2}\) (∆ ACE)

Question 30.
In the figure ∆PQR and ∆SQR are two triangles on the same base QR. If PS intersects QR at ‘O’, then ∆PQR : ∆SQR = …………

A) PO : SO
B) PQ : QS
C) PR : SR
D) PQ : SR
Answer:
A) PO : SO

Question 31.
In the figure, ∠BAD = ∠CAD; AB = 3.4 cm, BD = 4 cm, BC = 10 cm, then AC = ……………

A) 5.1 cm
B) 3.4 cm
C) 6 cm
D) 5.3 cm
Answer:
A) 5.1 cm

Question 32.
All ……………… triangles similar.
A) equilateral
B) scalene
C) isosceles
D) none
Answer:
A) equilateral

Question 33.
Two polygons are similar if …………………
A) corresponding angles are equal
B) corresponding sides are equal
C) both A & B
D) none
Answer:
C) both A & B

Question 34.
The ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding ……………
A) sides
B) areas
C) angles
D) none
Answer:
A) sides

Question 35.
A perpendicular is drawn from the vertex of a right angle to the hypotenuse then the tri-angles on each side of the perpendicular are ……………..
A) similar
B) not similar
C) square
D) none
Answer:
A) similar

Question 36.
If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar. This property is …………………
A) SSS
B) ASA
C) AAA
D) SAS
Answer:
D) SAS

Question 37.
If the sides of two similar triangles are in the ratio 7 : 2 then the ratio of their areas is …………….
A) 9 : 2
B) 8 : 9
C) 4 : 49
D) 49 : 4
Answer:
D) 49 : 4

Question 38.
∆ABC ~ ∆PQR, ∠A = 32°, ∠R = 65° then ∠B = ………………
A) 64°
B) 73°
C) 83°
D) none
Answer:
C) 83°

Question 39.

If ∆ABC ~ ∆PQR then y + z = ……………..
A) 1 + 3\(\sqrt{3}\)
B) 4 + 3\(\sqrt{3}\)
C) 3\(\sqrt{3}\) + 7
D) 9 + \(\sqrt{3}\)
Answer:
B) 4 + 3\(\sqrt{3}\)

Question 40.
In ∆LMN, ∠L = 60°, ZM = 50° and ∆LMN ~ ∆PQR then ∠R = ……………..
A) 70°
B) 80°
C) 90°
D) none
Answer:
A) 70°

Question 41.
The perimeter of ∆ABC ~ ∆LMN are 60 cm and 48 cm of LM = 8 cm then AB = ………………. cm.
A) 19
B) 11
C) 7
D) 10
Answer:
D) 10

Question 42.
In ∆ABC, BC² + AB² = AC² then ……………… is the right angle.
A) ∠B
B) ∠A
C) ∠C
D) none
Answer:
A) ∠B

Question 43.
The bisector of ∠A of ∆ABC intersects BC at D. If BD : DC = 4 : 7 and AC = 3.5. Then AB = ……………..
A) 2
B) 8
C) 10
D) 11
Answer:
A) 2

Question 44.
∆ABC ~ ∆PQR, ∠A = 50° then ∠Q + ∠R = ……………….
A) 120°
B) 110°
C) 130°
D) 180°
Answer:
C) 130°

Question 45.
In the figure, CD = …………….. cm.

A) \(\sqrt{3}\)
B) 2\(\sqrt{3}\)
C) 3\(\sqrt{3}\)
D) 6\(\sqrt{3}\)
Answer:
D) 6\(\sqrt{3}\)

Question 46.
In the figure, AC = ……………. cm.

A) 19
B) 9
C) 12
D) 10
Answer:
C) 12

Question 47.
The ratio of corresponding sides of two similar triangles is 3 : 2 then the ratio of their corresponding heights is …………….
A) 3 : 2
B) 2 : 3
C) 1 : 4
D) 1 : 7
Answer:
A) 3 : 2

Question 48.
In the figure, ∠ABC = ………………..

A) 30°
B) 70°
C) 50°
D) 60°
Answer:
D) 60°

Question 49.
In ∆ABC, XY || BC, AX : XB = 2 : 1 then ∆ AXY : ∆ABC = ………………
A) 9 : 4
B) 4 : 9
C) 1 : 9
D) 2 : 3
Answer:
B) 4 : 9

Question 50.
In a square, the diagonal is ………………. times of its side.
A) \(\sqrt{7}\)
B) \(\sqrt{3}\)
C) \(\sqrt{2}\)
D) 2
Answer:
C) \(\sqrt{2}\)

Question 51.
The side of an equilateral triangle is ‘a’ units. Its height is …………….. units.
A) \(\frac{\sqrt{3 a}}{2}\)
B) \(\frac{\sqrt{3}}{4}\)a
C) \(\frac{3}{a}\)
D) \(\frac{3}{2}\)
Answer:
A) \(\frac{\sqrt{3 a}}{2}\)

Question 52.
The ratio of the areas of two similar triangles is 1 : 4 then the ratio of their corresponding sides …………….
A) 9 : 1
B) 1 : 1
C) 2 : 1
D) 1 : 2
Answer:
D) 1 : 2

Question 53.
∆ABC ~ ∆PQR then AB : PQ = ……………….
A) AC : PR
B) AC : PQ
C) AB : PR
D) none
Answer:
A) AC : PR

Question 54.
∆ABC is an isosceles right triangle ∠C = 90° then AB² = ……………….
A) AB² + BC²
B) AC² + BC²
C) AC² + 2
D) none
Answer:
B) AC² + BC²

Question 55.
Each angle in an equilateral triangle is ……………….
A) 60°
B) 80°
C) 100°
D) 70°
Answer:
A) 60°

Question 56.
Each exterior angle of an equilateral triangle is …………….
A) 180°
B) 130°
C) 110°
D) 120°
Answer:
D) 120°

Question 57.
The longest side in a right triangle is ……………..
A) smaller
B) hypotenuse
C) adjacent
D) none
Answer:
B) hypotenuse

Question 58.
In the figure, ∆ABC, DE // BC and \(\frac{A D}{D B}\) = \(\frac{3}{5}\), AC = 5.6 then AE = …………….. cm.

A) 1.8
B) 3.5
C) 1.2
D) 2.1
Answer:
D) 2.1

Question 59.
From the figure, AD = ……………. cm.

A) 2.4
B) 4.2
C) 8.2
D) 9.2
Answer:
A) 2.4

Question 60.
In the figure, LM // CB and LN // CD then \(\frac{A M}{A B}\) = ……………….

Answer:
(A)

Question 61.
In a trapezium, diagonals divide each other ………………
A) proportionally
B) not proportional
C) congruent
D) none
Answer:
A) proportionally

Question 62.
In ∆ABC, AB = BC = AC then ∠A = ∠B = ∠C = …………..
A) 70°
B) 60°
C) 80°
D) 90°
Answer:
B) 60°

Question 63.
In the figure, two triangles are similar then x = ……………… cm.

A) 9.3
B) 1.5
C) 7.5
D) 8.5
Answer:
C) 7.5

Question 64.
In the figure, x = …………… cm

A) 10
B) 12
C) 9
D) 8
Answer:
D) 8

Question 65.
In the figure, x = ……………. cm.

A) 12 cm
B) 8 cm
C) 3 cm
D) data is not sufficient
Answer:
D) data is not sufficient

Question 66.
∆ABC ~ ∆PQR, ∠A + ∠B = 100°, ∠R = ……………
A) 60°
B) 80°
C) 90°
D) 100°
Answer:
B) 80°

Question 67.
∆ABC ~ ∆DEF and their areas are respectively 64 cm² and 121 cm² if EF = 15.4 cm then BC = …………….. cm.
A) 10.2
B) 8.7
C) 11.2
D) 10.3
Answer:
C) 11.2

Question 68.
Which of the following are the sides of a right triangle ?
A) 10 cm, 8 cm, 6 cm
B) 12 cm, 1 cm, 9 cm
C) 3 cm, 5 cm, 12 cm
D) all
Answer:
A) 10 cm, 8 cm, 6 cm

Question 69.
From the figure y = …………….. cm.

A) 9
B) 10
C) 12
D) 15
Answer:
D) 15

Question 70.
The diagonal of a trapezium ABCD in which AB // CD intersect at ‘O’. If AB = 2CD then the ratio of areas of triangles AOB and COD is …………….
A) 14 : 1
B) 1 : 2
C) 1 : 9
D) none
Answer:
D) none

Question 71.
∆ABC ~ ∆DEF and 2AB = DE and BC = 8 cm then EF = ………………. cm.
A) 16
B) 19
C) 12
D) none
Answer:
A) 16

Question 72.
∆ABC ~ ∆DEF, BC = 4 cm, EF = 5 cm and area of ∆ABC = 80 cm² then area of ∆DEF = …………… cm².
A) 105
B) 165
C) 125
D) none
Answer:
C) 125

Question 73.
In the figure PQR, ∠QPR = 90°, PQ = 24 cm and QR = 26 cm and in ∆PKR, ∠PKR = 90° and KR = 8 cm then PK = ……………… cm.

A) 10
B) 6
C) 19
D) 8
Answer:
B) 6

Question 74.
In the figure, QA ⊥ AB and PB ⊥ AB if AO = 20 cm, BO = 12 cm, PB = 18 cm then AQ = ……………. cm.

A) 70
B) 60
C) 40
D) 30
Answer:
D) 30

Question 75.
In the figure, ∠A = ∠B and AD = BE then …………

A) DE // AB
B) DE = AB
C) CD = EB
D) none
Answer:
A) DE // AB

Question 76.
In the figure, in ∆PQR, QR // ST, \(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{3}{5}\) and PR = 28 cm then PT = ……………. cm.

A) 6.5
B) 10.5
C) 8.1
D) 3.3
Answer:
B) 10.5

Question 77.
In an equilateral triangle ABC, AD ⊥ BC meeting BC in D then AD² = …………….
A) 3 BD²
B) BD²
C) AB²
D) none
Answer:
A) 3 BD²

Question 78.
In the figure, if AB // CD then x = …………….. cm.

A) 10
B) 12
C) 7
D) 9
Answer:
C) 7

Question 79.
If the diagonals in a quadrilateral divide each other proportionally then it is ………….
A) square
B) trapezium
C) triangle
D) none
Answer:
B) trapezium

Question 80.
In the figure, DE // AB and FE // DB then DC² …………….

A) CF × AC
B) FE × AB
C) CF × FD
D) none
Answer:
A) CF × AC

Question 81.
D, E and F are the mid points of the sides BC, CA and AB respectively of ∆ABC then the ratio of the areas of ∆DEF and ABC = …………..
A) 1 : 9
B) 2 : 1
C) 1 : 2
D) 1 : 4
Answer:
D) 1 : 4

Question 82.
In the figure \(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{\mathrm{PT}}{\mathrm{TR}}\) and ∠PST = ∠PRQ then ∆PQR is ………………. triangle.
A) isosceles
B) equilateral
C) scalene
D) none
Answer:
A) isosceles

Question 83.
Side of a rhombus is 4 cm then its perimeter is ……………. cm
A) 22
B) 21
C) 16
D) 20
Answer:
C) 16

Question 84.
In the figure, x = ………………

A) 130°
B) 135°
C) 45°
D) 15°
Answer:
B) 135°

Question 85.
Two sides of a right triangle are 3 cm and 4 cm then the third side is …………… cm.
A) 9
B) 6
C) 6.1
D) 5
Answer:
D) 5

Question 86.
∆ABC ~ ∆PQR, AB : PQ = 3 : 4 then ar ∆ ABC : ar ∆ PQR = ……………
A) 9 : 16
B) 9 : 1
C) 16 : 9
D) none
Answer:
A) 9 : 16

Question 87.
If 8² + 15² = k² then k = ………………
A) 16
B) 17
C) 19
D) 20
Answer:
B) 17

Question 88.
The angles of a triangle arc in the ratio 1 : 2 : 3 then the largest angle is ………………
A) 70°
B) 60°
C) 90°
D) 20°
Answer:
C) 90°

Question 89.
Straight angle means ………………..
A) 180°
B) 190°
C) 200°
D) 100°
Answer:
A) 180°

Question 90.
In the figure, PQ // MN, \(\frac{\mathrm{K P}}{\mathrm{P M}}\) = \(\frac{4}{13}\) and KN = 20.4 cm then KQ ……………… = cm.

A) 6.3
B) 4.8
C) 1.8
D) 2.8
Answer:
B) 4.8

Question 91.
In the figure DE // BC if AD = x, AE = x + 2, DB = x – 2 and CE = x – 1 then x = ………………

A) 4
B) 5
C) 6
D) 7
Answer:
A) 4

Question 92.
∆ABC ~ ∆DEF if DE : AB = 2 : 3 and ar ∆DEF = 44 sq. units then ar ∆ABC = ……………. sq.units.
A) 90
B) 101
C) 99
D) 110
Answer:
C) 99

We are offering TS 10th Class Maths Notes Chapter 8 Similar Triangles to learn maths more effectively.

TS 10th Class Maths Notes Chapter 8 Similar Triangles

→ The geometrical figures which have the same shape but are not necessarily of the same size are called similar figures.

→ The heights and distances of distant objects can be found using the principles of similar figures.

→ Two polygons with same number of sides are said to be similar if their corresponding angles are equal and their corresponding sides are in proportion.

→ A polygon in which all sides and all its angles are equal is called a regular polygon.

→ The ratio of the corresponding sides is referred to as scale factor or representative factor.

→ All squares are similar.

→ All circles are similar.

→ All equilateral triangles are similar.

→ Two congruent figures are similar but two similar figures need not be congruent.

→ A square ABCD and a rectangle PQRS are of equal corresponding angles, but their corresponding sides are in proportion.
∴ The square ABCD and the rectangle PQRS are not similar.

→ The corresponding sides of a square ABCD and a rhombus PQRS are equal but their corresponding angles are not equal. So they are not similar.

→ If a line is draw parallel to one side of a triangle inter-secting the other two sides at two distinct points then the other two sides are divided in the same ratio.

In ΔABC; DE ∥ BC then \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
This is called Basic Proportionality theorem (or) Thale’s theorem.

→ If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
In ΔABC, a line intersecting AB in D and AC in E such that \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
Then l ∥ BC.
This is converse of Thale’s theorem.

→ Two triangles are similar, if
i) their corresponding angles are equal.
ii) their corresponding sides are in the same ratio.
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio or proportional and hence the two triangles are similar.

In ΔABC, ΔDEF
∠A = ∠D
∠B = ∠E
∠C = ∠F ⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
∴ ΔABC ~ ΔDEF (A . A. A)

→ If in two triangles, sides of one triangle are proportional to the sides of other triangle, then their corre-sponding angles are equal and hence the two triangles are similar.

In ΔABC, ΔDEF
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) ⇒ ∠A = ∠D
∠B = ∠E
∠C = ∠F
Hence, ΔABC ~ ΔDEF (S.S.S)

→ If two angles of a triangle are equal to two corresponding angles of another triangle then the two triangles are similar.

In ΔABC, ΔDEF
∠A = ∠D
∠B = ∠E
⇒ ∠C = ∠F (By Angle sum property)
∴ ΔABC ~ ΔDEF (A.A)

→ If one angle of a triangle is equal to one angle of other triangle and the sides including these angles are proportional, then the two triangles are similar.

In ΔABC, ΔDEF
∠A = ∠D
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
∴ ΔABC ~ ΔDEF (S.A.S)
The ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
\(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{DEF}}=\frac{\mathrm{AB}^2}{\mathrm{DE}^2}=\frac{\mathrm{BC}^2}{\mathrm{EF}^2}=\frac{\mathrm{AC}^2}{\mathrm{DF}^2}\)

→ If a perpendicular is drawn from the vertex, containing the right angle of a right triangle to the hypotenuse, then the triangles on each side of perpendicular are similar to one another and to the original triangle. Also the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.

In ΔABC, ∠B = 90°
BD ⊥ AC
Then ΔADB – ΔBDC ~ ΔABC
and BD² = AD. DC

→ Pythagoras theorem: In a right angled triangle the square of hypotenuse is equal to the sum of the squares of other two sides.

In ΔABC; ∠A = 90°; AB² + AC² = BC²

→ In a triangle, if square of one side is equal to sum of squares of the other two sides, then the angle opposite to the first side is right angle.

In ΔABC, AC² = AB² + BC² then ∠B = 90°
This is converse of Pythagoras theorem.

→ Baudhayan Theorem (about 800 BC) : The diagonal of a rect¬angle produces itself the same area as produced by its both sides.
(i.e., length and breadth)

In rectangle ABCD, area produced by the diagonal AC = AC . AC = AC², area produced by the length = AB . BA = AB², area produced by the breadth = BC. CB = BC²
Hence, AC² = AB² + BC²

→ A sentence which is either true or false but not both is called a simple statement.

→ A statement formed by combining two or more simple statements is called a compound statement.

→ A compound statement of the form “If… then…” is called a Conditional or Implication.

→ A statement obtained by modifying the given statement by ‘NOT’ is called its negation.

Important Formulas:

• Pythagoras Theorem AC² = AB² + BC²
• If ΔABC ~ ΔPQR then \(\frac{\operatorname{ar}(\mathrm{ABC})}{\operatorname{ar}(\mathrm{PQR})}=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^2=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^2=\left(\frac{\mathrm{CA}}{\mathrm{RP}}\right)^2\)

Flow Chat:

Pythagoras (570 – 495 B.C):

• Pythagoras was an Ionian Greek philosopher, mathematician and founder of the religious movement called Pythagoreanism.
• Pythagoras made influential contributions to philosophy and religious teaching in the late 6th century BC.
• He is often revered as a great mathematician, mystic and scientist, but he is best) known for the Pythagorean theorem which bears his name.

We are offering TS 10th Class Maths Notes Chapter 7 Coordinate Geometry to learn maths more effectively.

TS 10th Class Maths Notes Chapter 7 Coordinate Geometry

→ A French mathematician Rene Descartes (1596 – 1650) has developed the study of Co-ordinate Geometry.

→ The cartesian plane is also called co-ordinate plane or xy plane.

→ The X-co-ordinate is called the Abscissa and the y-co-ordinate is called the ordinate.

→ The intersection of x-axis and y-axis is called the origin. The co-ordinates of origin = 0 (0, 0).

→ Area of Rhombus = \(\frac{1}{2}\) × product of its diagonals.

→ Area of a triangle = \(\frac{1}{2}\) × base × height.

→ The distance between two points P(x₁, y₁) and Q(x₂, y₂) is \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

→ The distance of a point (x, y) from the origin is \(\)

→ The distance between two points (x₁, y₁) and (x₂, y₂) on a line parallel to Y – axis is |y₂ – y₁|.

→ The distance between two points (x₁, y₁) and (x₂, y₂) on a line parallel to X-axis is |x₂ – x₁|.

→ The co-ordinates of the point P(x, y) which divides the line segment joining the points A(x₁, y₁) and B(x₂, y₂) internally in the ratio m₁ : m₂ are
\(\left[\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right]\)

→ The midpoint of the line segment joining the points P(x₁, y₁) and Q(x₂, y₂) is
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

→ The point of intersection of the medians of a triangle is called the centroid. It is usually denoted by G. it divides each median in the ratio 2 :1.

→ The vertices of ΔABC are A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃), then the co-ordinates of the centroid of the ΔABC is \(\left[\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right]\)

→ The area of the triangle formed by the points (x₁, y₁) (x₂, y₂) and (x₃, y₃) is the numerical value of the expression
\(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|.

→ Area of a triangle formula or Heron’s Formula A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
S = \(\frac{a+b+c}{2}\)

→ Slope of the line (m) = \(\frac{y_2-y_1}{x_2-x_1}\)

Important Formula:

• AB = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
• Point (x, y) form the origin is \(\sqrt{x^2+y^2}\)
• Mid Point = \(\left[\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right]\)
• Centroid = \(\left[\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right]\)
• Area = \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|.
• Heron’s Formula A = \(\sqrt{S(S-a)(S-b)(S-c)}\)
• S = \(\frac{a+b+c}{2}\)
• Slope m = \(\frac{y_2-y_1}{x_2-x_1}\)

Flow Chat:

Rene Descartes (1596 – 1650):

• Rene Descartes was a French Mathematician.
• Rene Descartes is a Father of Modern Mathematics.
• The Cartesian co-ordinate system – allowing reference to a point in space as a set of numbers, and allowing algebraic equations to be expressed as geometric shapes in a two – dimensional co-ordinate system was named after him.
• Descartes theory provided the basis for the calculus of Newton and Leibnitz.

We are offering TS 10th Class Maths Notes Chapter 6 Progressions to learn maths more effectively.

TS 10th Class Maths Notes Chapter 6 Progressions

→ The array of numbers following some rule is called a number pattern.
E.g.: 4, 6, 4, 6, 4, 6,…

→ There is a relationship between the numbers of a pattern.

→ Each number in a pattern is called a term.

→ The series or list of numbers formed by adding or subtracting a fixed number to / from the preceding terms is called an Arithmetic Progression, simply A.P.
E.g.: 3, 5, 7, 9, 11,

→ In the above list, each term is obtained by adding ‘2’ to the preceding term except the first term.

→ Also, we find that the difference between any two successive terms is the same throughout the series. This is called “common difference”.

→ The general form of an A.P. is a – the first term; d – the common difference.
a, a + d, a + 2d, a + 3d,…. a + (n – l)d. Here d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = ………………… = a_n – a_n-1.

→ If the number of terms of an A.P. is finite, then it is a finite A.P.
E.g.: 10, 8, 6, 4, 2.

→ If the number of terms of an A.P. is infinite, then it is an infinite A.P.
E.g.: 4, 8,12,16, …

→ If d > 0, then a_n > a_n-1 and if d < 0, then a_n < a_n-1

→ The general term or nth term of an A.P. is an = a + (n – 1)d.
E.g.: The 10th term of 10, 6, 2, – 2, is Here a = 10; d = a₂ – a₁ = 6 -10 = – 4
∴ a₁₀ = a + (n – 1)d = 10 + (10 – 1) × – 4 = 10 – 40 + 4 = – 26.

→ Sum of first n – terms of an A.P. is S_n = \(\frac{n}{2}\)(a + l), where a is the first term and l is the last term.
E.g : 1 + 2 + 3 + ………… + 80 = \(\frac{80}{2}\)(1 + 80) = 40 × 81 = 3240

→ Sum of the first n – terms of an A.P. is given by,
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]. Also, a_n = S_n – S_n-1

→ In a series of numbers, if every number is obtained by multiplying the preceding number by a fixed number except for the first term, such arrangement is called geometric progression or G.P.
E.g.: 4, 8, 16, 32, 64,…
Here, starting from the second term, each term is obtained by multiplying the preceding term by 2. The first term may be denoted by ‘a’, then we also see that
\(\frac{a_2}{a_1}=\frac{a_3}{a_2}=\frac{a_4}{a_3}=\ldots=\frac{a_n}{a_{n-1}}\) = r
We call it “common ratio”, denoted by ‘r’.

→ The general form of a G.P. is a, ar, ar², ar³,…., ar^n-1
i.e a₁ = a, a₂ = ar, a₃ = ar², ……… a_n = ar^n-1

Important Formula:

• a = First term
• d = T_n – T_n-1
• T_n = a + (n – 1)d
• S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
• S_n = \(\frac{n}{2}\)[a + l]
• r = \(\frac{T_n}{T_{n-1}}\)
• T_n = ar^n-1
• S_n = \(\frac{a\left(r^n-1\right)}{r-1}\); r ≥ 1
• S_n = \(\frac{a\left(1-r^n\right)}{1-r}\); r ≤ 1
• S_∞ = \(\frac{a}{1-r}\); |r| < 1

Flow Chat:

Carl Fredrich Gauss(1777 – 1855):

• Carl Fredrich Gauss was a German mathematician and physical scientist who contributed significantly to many fields of mathematics.
• Gauss was asked to find the sum of the positive integers from 1 to 100. He immediately replied that the sum is 5050.
• Gauss had a remarkable influence in many fields of mathematics and science and is ranked as one of history’s most influential mathematicians.

We are offering TS 10th Class Maths Notes Chapter 5 Quadratic Equations to learn maths more effectively.

TS 10th Class Maths Notes Chapter 5 Quadratic Equations

→ The general form of a linear equation in one variable is ax + b = c.

→ Any equation of the form p(x) = 0 where p(x) is a polynomial of degree 2, is a quadratic equation.

→ If p(x) = 0 whose degree is 2 is written in descending order of their degrees, then we say that the quadratic equation is written in the standard form.

→ The standard form of a quadratic equation is ax² + bx + c = 0 where a ≠ 0. We can write it as y = ax² + bx + c.

→ There are various occasions in which we make use of Q.E. in our day-to-day life.
Eg : The height of a rocket is defined by a Q.E.

→ Let ax² + bx + c = be a quadratic equation. A real number a is called a root of the Q.E. if aα² + bα + c = 0. And x = a is called a solution of the Q.E. (i.e.) the real value of x for which the Q.E ax² + bx + c = 0 is satisfied is called its solution.

→ Zeroes of the Q.E. ax² + bx + c = 0 and the roots of the Q.E. ax² + bx + c = 0 are the same.

→ To factorise a Q.E. ax² + bx + c = 0, we find p, q ∈ R such that p + q = b and pq = ac.
This process is called Factorising a Q.E. by splitting its middle term.
Eg : 12x² + 13x + 3 = 0
here a = 12; b = 13; c = 3
a.c = 12 × 3 = 36
b = 4 + 9 where 4 × 9 = 36
Now 12x² + 9x + 4x +3 = 0
⇒ 12x² + 9x + 4x + 3 = 0
⇒ 3x(4x + 3) + 1 (4x + 3) = 0
⇒ (4x + 3) (3x + 1) = 0
Here 4x + 3 = 0 or 3x + 1 = 0
⇒ 4x = -3 or 3x = -1
⇒ x = \(\frac{-3}{4}\) or x = \(\frac{-1}{3}\)

\(\frac{-3}{4}\) and \(\frac{-1}{3}\) are called the roots of the Q.E. 12x² + 13x + 3 = 0 and x = \(\frac{-3}{4}\) or \(\frac{-1}{3}\) is the solution of the Q.E 12x² + 13x + 3 = 0.

→ In the above example, (4x + 3) and (3x + 1) are called the linear factors of the Q.E. 12x² + 13x + 3 = 0

→ We can factorise a Q.E. by adjusting its left side so that it becomes a perfect square.
Eg : x² + 6x + 8 = 0 ⇒ x² + 2. x. 3 + 8 = 0 ⇒ x² + 2.x.3 = -8
The L.H.S. is of the form a2 + 2ab
∴ By adding b² it becomes a perfect square
∴ x² + 2.x.3 + 3² = -8 + 3²
⇒ (x + 3)² = -8 + 9
⇒ (x + 3)² = 1
⇒ x + 3 = ±1
Now we take x + 3 = 1 or x + 3=-1
⇒ x = -2 or x = -4

→ Adjusting a Q.E. of the form ax² + bx + c = 0 so that it becomes a perfect square.
Step -1: ax² + bx + c = 0 ⇒ ax² + bx = -c
⇒ x² + \(\frac{b}{a}\)x = \(\frac{-c}{a}\)

Step – 2: x² + \(\frac{\mathrm{bx}}{\mathrm{a}}+\left[\frac{1}{2}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\right]^2=\frac{-\mathrm{c}}{\mathrm{a}}+\left[\frac{1}{2}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\right]^2\)

Step – 3: \(\left(x+\frac{b}{2 a}\right)^2=\frac{b^2-4 a c}{4 a^2}\)

Step – 4: Solve the above
Eg: 5x² – 6x + 2 = 0 ⇒ x² – \(\frac{6 x}{5}=\frac{-2}{5}\)

→ Let ax² + bx + c = 0 (a ≠ 0) be a Q.E., then b² – 4ac is called the Discriminant of the Q.E.

→ If b² – 4ac > 0, then the roots of the Q.E. ax² + bx + c = 0 are given by
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\). This is called quadratic formula to find the roots

→ The nature of the roots of a Q.E. can be determined either by its discriminant or its graph.
Q.E.: y = ax² + bx + c.

Important Formulas:

• Quadratic Formula for find the roots x = \(\frac{-b – \sqrt{b^2-4 a c}}{2 a}\)
• Sum of the roots α + β = \(\frac{-b}{a}\)
• Product of the roots αβ = \(\frac{c}{a}\)
• Discriminant = b² – 4ac
• If b² – 4ac > 0 then the roots are real and distinct.
• If b² – 4ac = 0 the roots are real and equal.
• If b² – 4ac < 0 then the roots are not real.

Flow Chat:

Al – Khwarizmi (780 – 850):

• Muhammad ibn Musa al-Khwarizmi was a Persian mathematician, astronomer, astrologer and geographer, it He was born around 780 A.D. in Khwarizmi (now Khiva, Uzbekishtan) and died around 850.
• He worked most of his life as a scholar in the House of Wisdom in Baghdad, it His ‘Algebra’ was the first book on the systematic solutions of linear and quadratic equations.

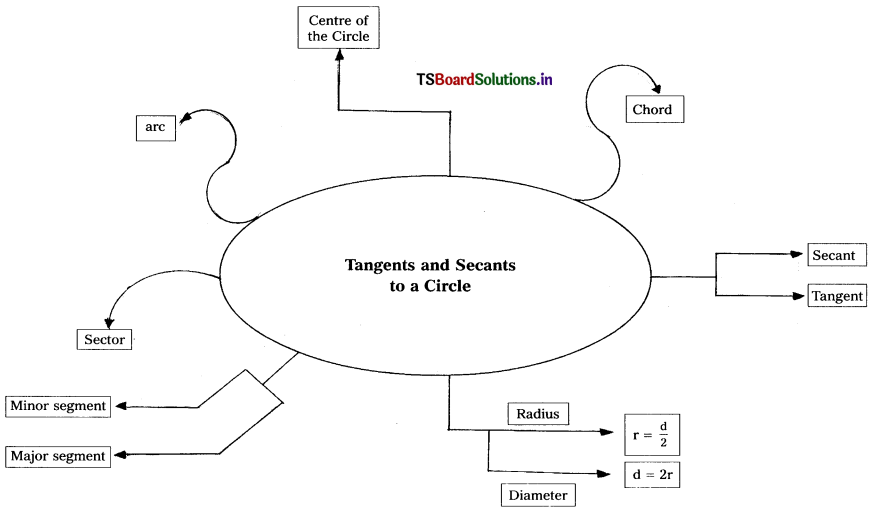
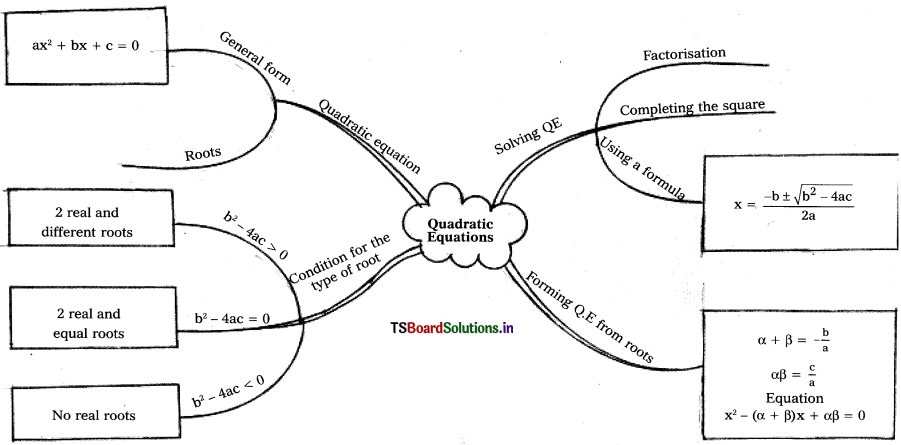
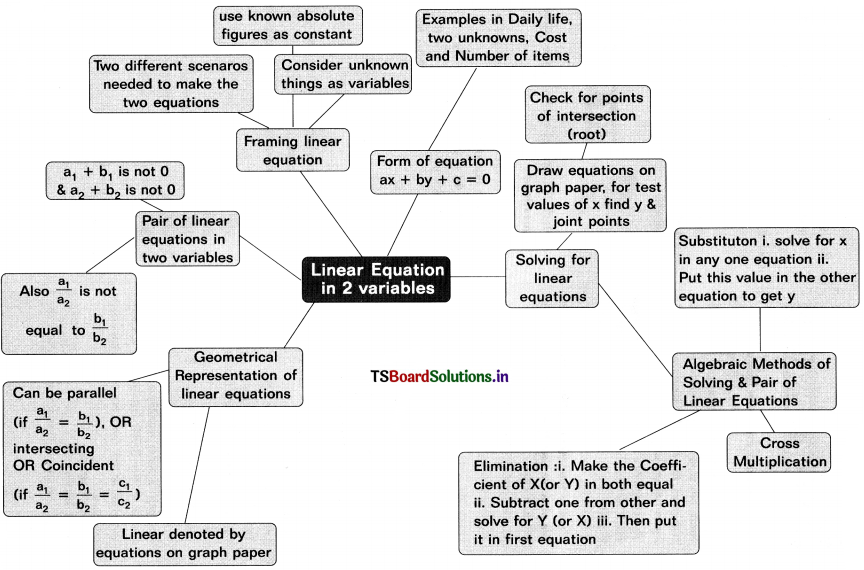
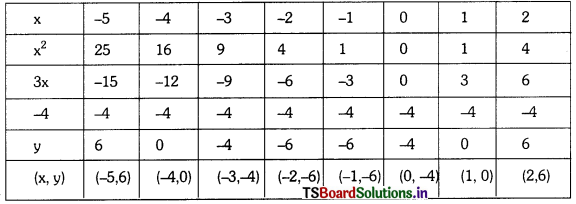
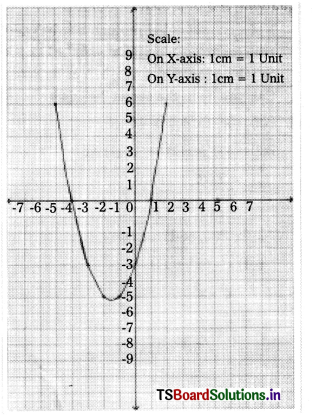
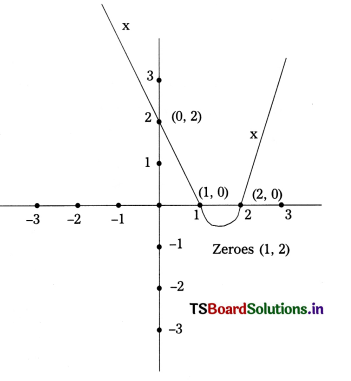
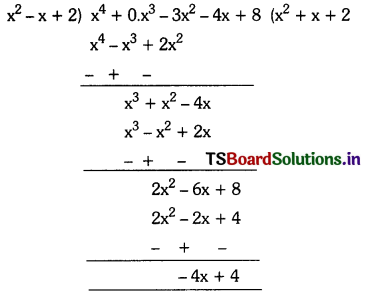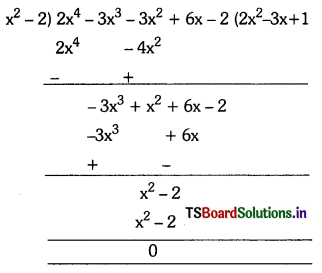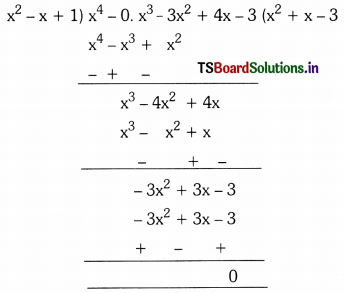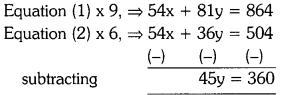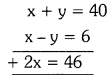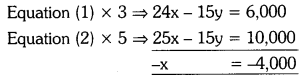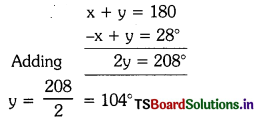Solving these TS 10th Class Maths Bits with Answers Chapter 9 Tangents and Secants to a Circle Bits for 10th Class will help students to build their problem-solving skills.

Tangents and Secants to a Circle Bits for 10th Class

Question 1.
The angle between the tangent to a circle and the radius drawn through the point of contact is
A) 90°
B) 60°
C) 45°
D) 30°
Answer:
A) 90°

Question 2.
From a point P, length of the tangent to a circle is 12 cm and the distance of P from the centre is 13 cm. then the radius of circle is
A) 7 cm
B) 6 cm
C) 5 cm
D) 12.5 cm
Answer:
C) 5 cm

Question 3.
If the tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at an angle of 80° then ∠POA = …………..
A) 50°
B) 60°
C) 70°
D) 80°
Answer:
A) 50°

Question 4.
If TP and TQ are two tangents to a circle with centre ‘O’ so that ∠POQ = 110°, then ∠PTQ =
A) 60°
B) 70°
C) 80°
D) 90°
Answer:
B) 70°

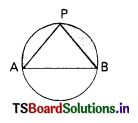
Question 5.
In the adjacent figure, if quadrilateral PQRS circumscribes a circle then PB + SD = ………………

A) SR
B) PR
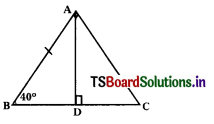
C) QS
D) PS
Answer:
D) PS

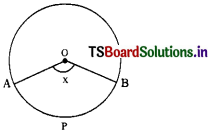
Question 6.
In the adjacent figure, APB is a tangent to the circle with centre ‘O’ at a point P. If ∠QPB = 50° then the measure of ∠POQ =
A) 25°
B) 75°
C) 100°
D) 120°

C) 100°

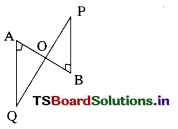
Question 7.
In the adjacent figure AB, BC and AC of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 6 cm and AC = 11cm then length of BC =
A) 15 cm
B) 14 cm
C) 7 cm
D) 10 cm

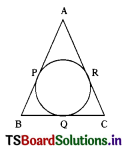
Answer:
D) 10 cm

Question 8.
In the adjacent figure, if BP = 5 cm, QC = 7 cm and AR = 6 cm then AB + BC + AC =
A) 18 cm
B) 36 cm
C) 25 cm
D) 30 cm

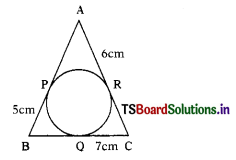
Answer:
B) 36 cm

Question 9.
The length of the tangent drawn from a point 17 cm away from the centre of a circle of radius 8 cm is
A) 25 cm
B) 9 cm
C) 15 cm
D) 8.5 cm
Answer:
C) 15 cm

Question 10.
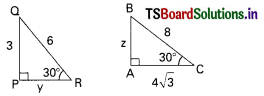
In the adjacent figure, the length of the chord AB if PA = 6 cm and ∠PAB = 60° is
A) 5 cm
B) 6 cm
C) 7 cm
D) 4 cm

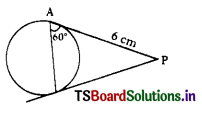
Answer:
B) 6 cm

Question 11.
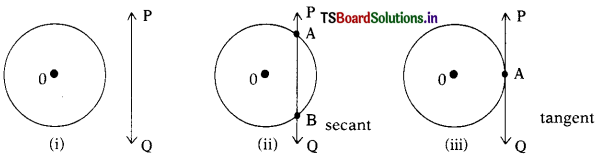
A line which intersects a circle in two points is called
A) a secant
B) a tangent
C) a chord
D) an arc
Answer:
A) a secant

Question 12.
The number of tangents that can be drawn to a circle at any point on it is
A) 2
B) 1
C) 3
D) infinetly many
Answer:
B) 1

Question 13.
The number of parallel tangents that can be drawn to a circle can have at the most is
A) 1
B) 2
C) 3
D) 4
Answer:
B) 2

Question 14.
The number of tangents that can be drawn to a circle from outside the circles is
A) 2
B) 1
C) infinetly many
D) 4
Answer:
A) 2

Question 15.
Two concentric circles of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle
A) 10 cm
B) 6 cm
C) 8 cm
D) 2 cm
Answer:
C) 8 cm

Question 16.
Length of the arc of a quadrant of a circle of radius ‘r’ is
A) πr
B) 3πr
C) \(\frac{\pi \mathrm{r}}{2}\) + 2r
D) \(\frac{\pi \mathrm{r}}{2}\)
Answer:
D) \(\frac{\pi \mathrm{r}}{2}\)

Question 17.
The length of the arc A × B in the adjacent figure is
A) 11 cm
B) 22 cm
C) 33 cm
D) 44 cm

Answer:
B) 22 cm

Question 18.
The area of a sector of a circle of radius 7 cm and central angle 45° is
A) 5.5 cm²
B) 19.25 cm²
C) 154 cm²
D) 77 cm²
Answer:
B) 19.25 cm²

Question 19.
The measure of central angle of a circle
A) 90°
B) 180°
C) 170°
D) 360°
Answer:
D) 360°

Question 20.
In the adjacent figure, ‘O’ is the centre of the circle. The area of the sector OAPB is \(\frac{5}{18}\) part of the area of the circle. Then the value
A) 30°
B) 60°
C) 45°
D) 100°

Answer:
D) 100°

Question 21.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm, then PQ =
A) \(\sqrt{79}\)
B) \(\sqrt{119}\)
C) 119
D) 169
Answer:
B) \(\sqrt{119}\)

Question 22.
The number of parallel tangents of a circle with a given tangent is
A) 1
B) 2
C) 3
D) 4
Answer:
A) 1

Question 23.
The length of the tangent drawn from an exterior point is 8 cm away from the centre of a circle of radius 6 cm is
A) 8 cm
B) 10 cm
C) 6 cm
D) 12 cm
Answer:
B) 10 cm

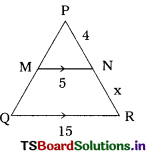
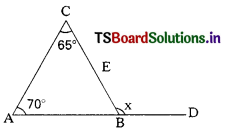
Question 24.
In the figure x = ………………

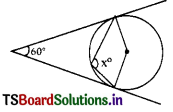
A) 60°
B) 100°
C) 110°
D) 120°
Answer:
D) 120°

Question 25.
The semi perimeter of ∆ABC = 28 cm then AF + BD + EC is …………………..

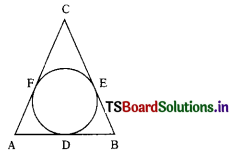
A) 23 cm
B) 28 cm
C) 56 cm
D) 14 cm
Answer:
B) 28 cm

Question 26.
The length of the drawn from a point 8 cm away from the centre of circle with radius 6 cm is
A) 2\(\sqrt{7}\) cm
B) 3\(\sqrt{7}\) cm
C) \(\sqrt{7}\) cm
D) 10 cm
Answer:
A) 2\(\sqrt{7}\) cm

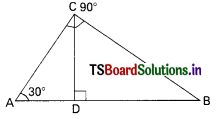
Question 27.
In the figure ‘O’ is the centre of the circle and PA, PB are tangents, then their lengths are,

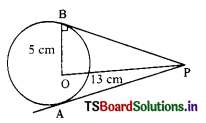
A) 5 cm, 13 cm
B) 13 cm, 13 cm
C) 13 cm, 12 cm
D) 12 cm, 12 cm
Answer:
D) 12 cm, 12 cm

Question 28.
Angle in a major segment is
A) an obtuse angle
B) an acute angle
C) right angle
D) none
Answer:
B) an acute angle

Question 29.
The length of the tangent drawn to a circle with radius ‘r’ from a point P which is ‘d’ units from the centre is
A) \(\sqrt{d^2-r^2}\)
B) \(\sqrt{r^2+d^2}\)
C) \(\sqrt{d r}\)
D) \(\sqrt{d + r}\)
Answer:
A) \(\sqrt{d^2-r^2}\)

Question 30.
If the arc is a minor arc then the segment is a …………………. segment
A) Minor
B) Major
C) Semi-circle
D) None
Answer:
A) Minor

Question 31.
The radius of a circle is equal to the sum of the circumferences of two circles of diameters 36 cm and 20 cm is ……………
A) 16 cm
B) 28 cm
C) 42 cm
D) 56 cm
Answer:
B) 28 cm

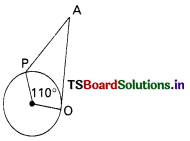
Question 32.
If tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at an angle of 110° then ∠PAO =
A) 45°
B) 50°
C) 70°
D) 35°
Answer:
D) 35°

Question 33.
How many tangent lines can be drawn to a circle from a point outside the circle ?
A) 1
B) 4
C) 2
D) none
Answer:
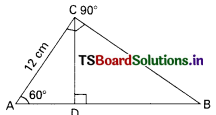
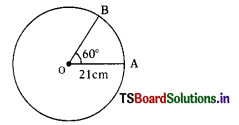
B) 4

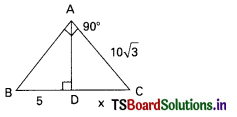
Question 34.
In the given figure ∠APB = 60° and OP = 10 cm. then PA = …………….. cm. (A.P. Mar. ’16, ’15)

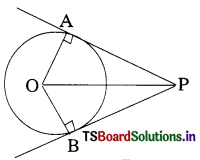
A) 5
B) 5\(\sqrt{2}\)
C) 5\(\sqrt{3}\)
D) 20
Answer:
C) 5\(\sqrt{3}\)

Question 35.
The maximum number of possible tangents that can be drawn to a circle is ……………. (A.P. Mar. ’15)
A) infinity
B) 2
C) 4
D) 1
Answer:
A) infinity

Question 36.
The angle between the tangent and the radius drawn at the point of contact is ………………. (A.P. June ’15)
A) 60°
B) 30°
C) 45°
D) 90°
Answer:
D) 90°

Question 37.
If a circle is inscribed in a Quadrilateral then AB + CD = …………….. (A.P. June ’15)
A) BC + DA
B) AC + BD
C) 2AC + 2BD
D) 2BC + 2DA
Answer:
A) BC + DA

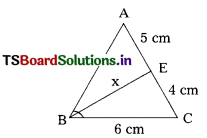
Question 38.
In the adjoint figure AC = 5, So BC = ………………… cm. (A.P. June ’15)

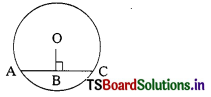
A) 5 cm
B) 7.5 cm
C) 2.5 cm
D) 10 cm
Answer:
C) 2.5 cm

Question 39.
The angle made at the centre of a circle is ………………. (A.P. Mar. ’16)
A) 360°
B) 90°
C) 280°
D) 60°
Answer:
A) 360°

Question 40.
The number of secants that can be drawn to a circle is ………………… (T.S. Mar. ’16)
A) 2
B) 1
C) infinity
D) 0
Answer:
C) infinity

Question 41.
The diameter of a circle is 10.2 cm then its radius is ……………… cm. (A.P. Mar. ’16)
A) 5.1 cm
B) 20.4
C) 10.5
D) 15.3
Answer:
A) 5.1 cm

Question 42.
If ‘r’ is the radius of a semi-circle then its perimeter is ………………….
A) πr + 2r (or) r[π + 2] (or) \(\frac{36}{7}\) r
B) πr + r
C) πr + 3r
D) πr
Answer:
A) πr + 2r (or) r[π + 2] (or) \(\frac{36}{7}\) r

Question 43.
Which of the following is not correct? (A.P. Mar. ’16 )
i) Maximum possible tangents that can be drawn to a circle from a point ‘p’ is 2.
ii) The number of secants drawn to a circle from a point at exterior is 2.

A) i only
B) ii only
C) i and ii
D) neither (i) nor (ii)
Answer:
A) i only

Question 44.
In the figure PT is a tangent to the circle with centre O’ then x = ………………….

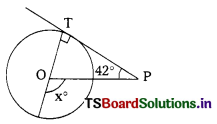
A) 148°
B) 58°
C) 52°
D) 42°
Answer:
D) 42°

Question 45.
Angle in a major segment is …………………
A) an obtuse angle
B) an acute angle
C) right angle
D) none
Answer:
B) an acute angle

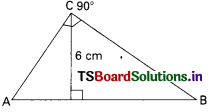
Question 46.
In the figure PT is a tangent drawn from P. If the radius is 7 cm and OP is 25 cm, then the length of the tangent is ………………. cm.

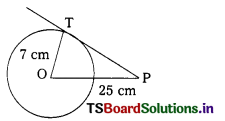
A) 18
B) 20
C) 24
D) 26
Answer:
C) 24

Question 47.
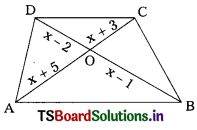
PQ is the chord of a circle. The tangent XR drawn at X meets PQ at R when produced. If XR = 12 cm, PQ = x cm, QR = (x – 2) cm. then x = ………………..
A) 6 cm
B) 7 cm
C) 14 cm
D) 10 cm
Answer:
D) 10 cm

Question 48.
The angle between the tangent to a circle and the radius drawn through the point of contact is ………………
A) 90°
B) 60°
C) 45°
D) 30°
Answer:
A) 90°

Question 49.
Two circles intersect at A, B, PS, PT are two tangents drawn from P which lies on AB to the two circles, then ……………..

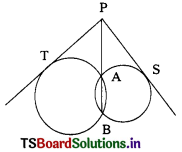
A) PS = 2PT
B) PT = 2PS
C) PS = PT
D) PS ≠ PT
Answer:
C) PS = PT

Question 50.
In the figure AB is a diameter and AC is chord of the circle such that ∠BAC = 30°. If DC is a tangent, then ABCD is ……………..
A) isosceles
B) equilateral
C) right angled
D) acute angled
Answer:
A) isosceles

Question 51.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60° it is required to draw the tangents at the end points of two radii inclined at an angle of ……………….
A) 30°
B) 60°
C) 90°
D) 120°
Answer:
D) 120°

Question 52.
If the radii of two concentric circles are 5 cm and 13 cm then the length of the chord of one circle which is tangent to the other circle is ……………
A) 24 cm
B) 18 cm
C) 12 cm
D) 6 cm
Answer:
A) 24 cm

Question 53.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 110° then ∠PAO = …………….
A) 45°
B) 50°
C) 70°
D) 35°
Answer:
D) 35°

Question 54.
In a right triangle ABC, right angled at B, BC = 15 cm and AB = 8 cm. A circle is inscribed in the triangle ABC. The radius of the circle is ……………..
A) 1cm
B) 3 cm
C) 5 cm
D) 2 cm
Answer:
B) 3 cm

Question 55.
Three circles are drawn with the vertices of a triangle as centres such that each circle touches the other two. If the sides of the triangle are 2 cm, 3 cm, 4 cm find the diameter of the smallest circle.
A) 4 cm
B) 2 cm
C) 1 cm
D) 5 cm
Answer:
C) 1 cm

Question 56.
A circle may have ……………… parallel tangents atmost.
A) 10
B) 12
C) 9
D) 2
Answer:
D) 2

Question 57.
A tangent to a circle intersects it in ………………. point(s).
A) 1
B) 2
C) 3
D) 4
Answer:
A) 1

Question 58.
A line segment joining any point on a circle is called its ………………..
A) diameter
B) tangent
C) chord
D) none
Answer:
C) chord

Question 59.
A line which intersects the given circle at two distinct points is called a ……………….
A) tangent
B) secant
C) circle
D) centre
Answer:
B) secant

Question 60.
The common point to a tangent and a circle is called …………………
A) point of contact
B) circle
C) tangent
D) none
Answer:
A) point of contact

Question 61.
Angle between the tangent and radius drawn through the point of contact is ……………..
A) 100°
B) 70°
C) 80°
D) 90°
Answer:
D) 90°

Question 62.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ……………… cm.
A) \(\frac{1}{\pi}\)
B) \(\frac{5 \sqrt{2}}{\pi}\)
C) \(\frac{50 \sqrt{2}}{\pi}\)
D) 50\(\sqrt{2}\)
Answer:
C) \(\frac{50 \sqrt{2}}{\pi}\)

Question 63.
The area of a square inscribed in a circle of radius 8 cm is …………………… cm².
A) 118
B) 129
C) 160
D) 128
Answer:
D) 128

Question 64.
The area of a circle that can be inscribed in a square of side 6 cm is …………………… cm².
A) 9π
B) 12π
C) 120π
D) none
Answer:
A) 9π

Question 65.
The perimeter of a quadrant of a circle of radius \(\frac{7}{2}\) cm is …………………. cm.
A) 9.5
B) 12.5
C) 10.5
D) 2
Answer:
B) 12.5

Question 66.
The number of tangents at one point of a circle is ………………..
A) 1
B) 2
C) 3
D) 10
Answer:
A) 1

Question 67.
Number of tangents to a circle which are parallel to a secant are …………………
A) 1
B) 10
C) 9
D) 2
Answer:
D) 2

Question 68.
………………. tangent can be drawn from a point inside a circle.
A) No
B) 1
C) 4
D) None
Answer:
A) No

Question 69.
A line which is perpendicular to the radius of the circle through the point of contact is called a …………………..
A) secant
B) tangent
C) chord
D) none
Answer:
B) tangent

Question 70.
The tangents drawn at the ends of a diameter are ………………
A) parallel
B) 0
C) perpendicular
D) none
Answer:
B) 0

Question 71.
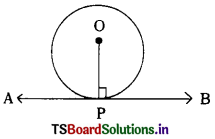
The tangent drawn at the end point of radius is ………………….
A) 0
B) parallel
C) perpendicular
D) none
Answer:
C) perpendicular

Question 72.
Tangents drawn from an exterior point are ……………..
A) not equal
B) parallel
C) equal
D) none
Answer:
C) equal

Question 73.
A secant meets a circle in ……………… points.
A) 2
B) 4
C) 3
D) 1
Answer:
A) 2

Question 74.
A tangent meets a circle in ……………… points.
A) 10
B) 9
C) 7
D) 1
Answer:
D) 1

Question 75.
Sum of the central angles in a circle is ………………..
A) 360°
B) 300°
C) 180°
D) 110°
Answer:
A) 360°

Question 76.
Angle is a semi-circle at the centre is …………………….
A) 100°
B) 180°
C) 200°
D) 80°
Answer:
B) 180°

Question 77.
From the figure, x = ……………… cm.

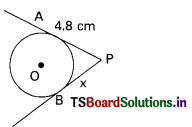
A) 8.4
B) 8.8
C) 4.8
D) 4
Answer:
C) 4.8

Question 78.
Angle in a semi-circle is ……………..
A) 80°
B) 90°
C) 100°
D) 110°
Answer:
B) 90°

Question 79.
Number of tangents drawn to a circle is ……………….
A) 1
B) 4
C) 3
D) infinite
Answer:
D) infinite

Question 80.
In the figure, x = ……………….. cm.

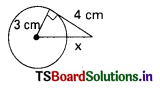
A) 5
B) 6
C) 8.2
D) 10
Answer:
A) 5

Question 81.
Angle in a minor segment is ………………
A) acute
B) 60°
C) obtuse
D) none
Answer:
C) obtuse

Question 82.
In a circle d = 10.2 cm then r = …………… cm.
A) 4.1
B) 5.1
C) 4.6
D) 5.6
Answer:
B) 5.1

Question 83.
The longest chord in a circle is ……………..
A) diameter
B) radius
C) chords
D) none
Answer:
A) diameter

Question 84.
Circles having same centre are called ……………. circles.
A) triangle
B) concentric
C) trapezium
D) none
Answer:
B) concentric

Question 85.
Circles having same radii are ………………
A) congruent
B) not congruent
C) only similar
D) none
Answer:
A) congruent

Question 86.
Area of circle is ………….. sq. units.
A) \(\frac{\pi}{\mathrm{r}^2}\)
B) πr³
C) πr²
D) π²r²
Answer:
C) πr²

Question 87.
The shaded portion represents ……………….

A) minor segment
B) major segment
C) chord
D) none
Answer:
A) minor segment

Question 88.
Area of semi-circle is ……………….
A) πr²
B) π² r
C) \(\frac{\pi \mathrm{r}^2}{2}\)
D) πr
Answer:
C) \(\frac{\pi \mathrm{r}^2}{2}\)

Question 89.
Number of circle passing through 3 collinear points in a plane is ……………….
A) 1
B) 0
C) 9
D) 12
Answer:
B) 0

Question 90.
Sum of opposite angles in a cyclic quadrilateral is …………….
A) 100°
B) 180°
C) 190°
D) 200°
Answer:
B) 180°

Question 91.
Cyclic rhombus is a ………………
A) rhombus
B) parallelogram
C) triangle
D) none
Answer:
A) rhombus

Question 92.
In the figure, ∠BAC = ………………

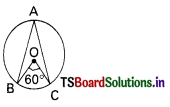
A) 90°
B) 70°
C) 30°
D) none
Answer:
C) 30°

Question 93.
Area of sector = ……………….
A) \(\frac{x^{\circ}}{360}\) × πr²
B) \(\frac{x^{\circ}}{360}\) × 2πr
C) lb
D) none
Answer:
A) \(\frac{x^{\circ}}{360}\) × πr²

Question 94.
Area of ring = ……………….
A) π(R² – r²)
B) π(R – r)
C) R² – r²
D) π(R² – r² + 2r)
Answer:
A) π(R² – r²)

Question 95.
Side of a square is 4 cm then A = ……………….. cm².
A) 64
B) 12
C) 16
D) 20
Answer:
C) 16

Question 96.
Diameter of a circle passes through ……………
A) equal
B) point
C) centre
D) none
Answer:
C) centre

Question 97.
The shaded portion represents …………… segment.

A) major
B) minor
C) acute
D) none
Answer:
A) major

Question 98.
Which of the following is a semicircle ?

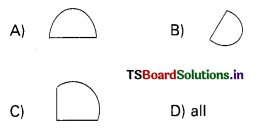
Answer:
(A)

Question 99.
Angles in the same segment of the circle ………………
A) 30°
B) equal
C) not equal
D) none
Answer:
B) equal

Question 100.
In the figure, x° = …………

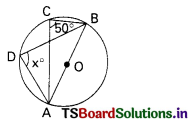
A) 30°
B) 110°
C) 60°
D) none
Answer:
D) none

Question 101.
In the figure, x = …………………

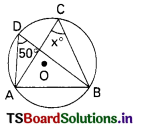
A) 20°
B) 90°
C) 60°
D) 80°
Answer:
C) 60°

Question 102.
Area of triangle = ………………. sq.units.
A) bh
B) \(\frac{1}{2}\)bh
C) \(\frac{\mathrm{b}+\mathrm{h}}{2}\)
D) none
Answer:
B) \(\frac{1}{2}\)bh

Question 103.
Area of square whose is 3 cm in …………………… cm².
A) 6
B) 12
C) 10
D) 9
Answer:
D) 9

Question 104.
Area of circle with radius r = …………………
A) πr⁴
B) πr
C) πr²
D) \(\frac{\pi}{2}\)
Answer:
C) πr²

Question 105.
The area of square is 49 cm² then side is …………….. cm.
A) 12
B) 6
C) 8
D) 7
Answer:
D) 7

Question 106.
In the above problem perimeter = ……………. cm.
A) 19
B) 16
C) 28
D) none
Answer:
C) 28

Question 107.
Angle made by minute hand in 1 m = ………………..
A) 6°
B) 12°
C) 10°
D) none
Answer:
A) 6°

Question 108.
x° = 60°, r = 14 cm then area of sector = ………………. cm².
A) 100.6
B) 102.66
C) 811.6
D) none
Answer:
B) 102.66

Question 109.
Area of regular hexagon of side ‘a’ units is ……………… sq. units.
A) \(\frac{6 \sqrt{3}}{4}\)a²
B) \(\frac{6 \sqrt{3}}{7}\)a²
C) \(\frac{6}{7} \sqrt{3}\)a²
D) none
Answer:
A) \(\frac{6 \sqrt{3}}{4}\)a²

Question 110.
Parallelogram circumscribing a circle is a ……………
A) parallelogram
B) rhombus
C) circle
D) none
Answer:
B) rhombus

Question 111.
In the figure, XY and X¹Y¹ are two parallel tangents to a circle with centre ‘O’ and another tangent AB with point of contact C intersecting XY at A and X¹Y¹ at B then ∠AOB = ………………..

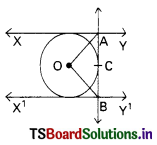
A) 75°
B) 95°
C) 70°
D) 90°
Answer:
D) 90°

Question 112.
The angle between a tangent to a circle and the radius drawn at the point of contact is ……………….
A) 60°
B) 70°
C) 90°
D) 20°
Answer:
C) 90°

Question 113.
If AP and AQ are the two tangents to a circle with centre ‘O’. So that POQ = 110° then ∠PAQ = ……………..

A) 70°
B) 60°
C) 65°
D) 75°
Answer:
A) 70°

Question 114.
Area of circle interms of diameter is ……………..
A) \(\frac{\pi \mathrm{d}^2}{4}\)
B) πr²
C) \(\frac{\pi \mathrm{d}^2}{14}\)
D) all
Answer:
A) \(\frac{\pi \mathrm{d}^2}{4}\)

Question 115.
In the figure, AP = 12 cm, PB = 16 cm and π = 3.14 then perimeter of shaded region is …………………… cm.

A) 51
B) 70
C) 58
D) 68
Answer:
C) 58

Question 116.
A bicycle wheel makes 75 revolutions per minute to maintain a speed of 8.91 km per hour then diameter of the wheel is ………………. m.
A) 6.3
B) 0.63
C) 8.1
D) none
Answer:
B) 0.63

Question 117.
Angle described by hour hand in 12 hours is ………………….
A) 90°
B) 200°
C) 360°
D) 180°
Answer:
C) 360°

Question 118.
Each angle in a square is …………….
A) 85°
B) right angle
C) 60°
D) 70°
Answer:
B) right angle

Question 119.
In the figure, the area of shaded region is ……………… cm².

A) 74
B) 60
C) 82
D) 42
Answer:
D) 42

Question 120.
Perimeter of semicircle is ………… units.
A) \(\frac{36 \mathrm{r}}{7}\)
B) \(\frac{18}{7}\)r
C) \(\frac{9}{17}\)r
D) none
Answer:
A) \(\frac{36 \mathrm{r}}{7}\)

Question 121.
In the figure the relation among a, b and c is ………………

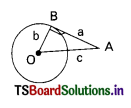
A) c² = a² + b²
B) c² – a² = 2b²
C) c² + b² = a²
D) all
Answer:
A) c² = a² + b²

Question 122.
In the figure, a = ……………….

A) 100°
B) 170°
C) 80°
D) 90°
Answer:
C) 80°

Question 123.
Perimeter of sectors = …………….
A) l + 2r
B) l – r
C) l – 2r
D) none
Answer:
A) l + 2r

Question 124.
What do you observe from the below

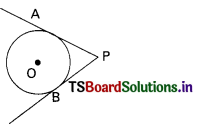
A) PA < PB B) PA > PB
C) PA = PB
D) none
Answer:
C) PA = PB

Question 125.
The radius of a circle is doubled then its area becomes ……………… times.
A) 5
B) 4
C) 9
D) none
Answer:
B) 4

We are offering TS 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables to learn maths more effectively.

TS 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables

→ An Equation of the form ax + by + c = 0, where a, b, c e R and a and b are not both zero, is called a linear equation in two variables x and y.

→ A pair of linear equations in two variables x and y can be represented as follows :
a₁x + b₁y + C₁ = 0
a₂x + b₂y + c₂ = 0
Where a₁, a₂, b₁, b₂, c₁, c₂ are real numbers such that a₁² + b₁² ≠ 0; a₂² + b₂² ≠ 0.

→ A pair of linear Equations in two variables forms a system of simultaneous linear equations.
Example : 3x – 4y = 2
2x + 5y = 9

→ A pair of values of the variables x and y satisfying each one of the equations that are given is called a solution of the system.
x = 2, y = 1 is a solution of the system of simultaneous linear equations.
3x-4y = 2 …………… (1)
2x + 5y = 9 …………… (2)
Putting x = 2 and y = 1 in equation (1), we get
L.H.S. = 3 × 2 – 4 × 1 = 6 – 4 = 2
R.H.S = 2
L.H.S = R.H.S
Similarly, put x = 2 and y = 1 in equation (2), we get
L.H.S = 2 × 2 + 5 × 1 = 4 + 5 = 9
R.H.S = 9
∴ L.H.S = R.H.S

→ A pair of linear equations in two variables can be solved using

• Graphical method
• Model method
• Algebraic method :
  (a) Substitution method
  (b) Elimination method
  (c) Cross-Multiplication method

→ Graphical method: The graph of a pair of linear equations in two variables is represented by two straight lines.

• If the lines intersect at a point, then that point gives the unique solution of the two equations. In this case, the pair of equations is consistent.
• If the lines coincide, then there are infinitely many solutions – each point on the line being a solution. In this case, the pair of equations is dependent (consistent).
• If the lines are parallel, then the pair of equations has no solution.
  In this case, the pair of equations is inconsistent.

→ The relation that exists between the coefficients and nature of system of equations.

→ If a pair of linear equations is given by a₁x + b₂y + c₂ = 0 and a₂x + b₂y + c₂ = 0, then

• The pair of linear equations is consistent if \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
• The pair of linear equation is inconsistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
• The pair of linear equation is dependent and consistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Important Formulas:

• The pair of linear equations is consistent if \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
• The pair of linear equation is inconsistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
• The pair of linear equation is dependent and consistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Flow Chat:

William George Horner(1786 – 1832):

• A William George Horner was a British mathematician; he was a schoolmaster; headmaster and schoolkeeper, proficient in classics as well as mathematics.
• A He wrote extensively on functional equations, number theory and approximation theory.
• A His contribution to approximation theory is honoured in the designation Horner’s method. The modern invention of the zoetrope, under the name Daedaleum in 1834 has been attributed to him.

Telangana SCERT TS 10th Class Physical Science Study Material Pdf 8th Lesson Chemical Bonding Textbook Questions and Answers.

TS 10th Class Physical Science 8th Lesson Questions and Answers Chemical Bonding

Improve Your Learning
I. Reflections on concepts

Question 1.
Explain the difference between the valence electrons and the covalency of an element. \
Answer:

Question 2.
A chemical compound has the following Lewis notation:

(a) How many valence electrons does element Y have?
(b) What ¡s the valency of element Y’ x . X
(c) What is the valency of element X?
(d) How many covalent bonds are there in the molecule? H
(e) To which groups the elements X and Y belong?
Answer:
(a) Six electrons.
(b) Two. because it has combined with two elements namely X and H.
(c) One
(d) Two covalent bonds one in Y – X and another one is Y – H.
(e) X is Hydrogen and Y is oxygen. I suggest the molecule is H₂O (water).

Question 3.
How bond energies and bond lengths of molecule help us in predicting their chemical properties? Explain with examples.
Answer:
1. Bond length: Bond length or bond distance ¡s the equilibrium distance between the nuclei of two atoms which form a covalent bond.

2. Bond energy: Bond energy or bond dissociation energy ¡s the energy needed to break a covalent bond between two atoms of a diatomic covalent compound in its gaseous state.

3. If the nature of the bond between the same two atoms changes, the bond length also changes. For example, the bond lengths between two carbon atoms are C-C>C=C>C ≡ C.

4. Thus the various bond lengths between the two carbon atoms are ¡n ethane 1.54 Å, ethylene 1.34 Å. acetylene 1.20 Å.

5. The bond lengths between two oxygen atoms are in H₂O₂ (O-O) Is 1.48 A° and in O₂ (O = O) is 1.21 Å.

6. Observe the table.

7. When bond length decreases, then bond dissociation energy Increases.
8. When bond length increases, then bond dissociation energy decreases.
9. Bond length of H -H in H₂ molecule is 0.74 Å and its bond dissociation energy is 436 KJ/mol, whereas bond length of F – F In F₂ molecule is 1.44 Å and its bond dissociation energy Is 159 K/mol.
10. Melting and boiling points of substances also can be determined by these bond energies and bond lengths.

Question 4.
Draw simple diagrams to show how electrons are arranged in the following covalent molecules:
(a) Calcium oxide (CaO)
(b) Water (H₂O)
(c) Chlorine (Cl₂)
Answer:
(a) Calcium oxide (CaO)

(b) Water (H₂O):

One oxygen and two hydrogen atoms form a water molecule, H₂O

(c) Chlorine (Cl₂):

Question 5.
Represent each of the following atoms using Lewis notation.
(a) Beryllium
(b) Calcium
(c) Lithium
(d) Bromine gas(Br₂)
(e) Calcium Chloride (CaCl₂)
(f) Carbon dioxide (CO₂)
Answer:
(a) Beryllium:
Beryllium atomic number = 4
Be – Valency electrons = 2

(b) Calcium:
Calcium atomïc number = 20
Ca – Valency electrons = 2

(C) Lithium:
Lithium atomic number = 3
Li – Valency electron = 1

(d) Bromine gas (Br₂):

(e) Calcium Chloride (CaCl₂):

(f) Carbon dioxide (CO₂):

Question 6.
Why do only valence electrons involve in bond formation? Why not electron of Inner shells? Explain.
Answer:

1. When two atoms come sufficiently close together the valence electrons of each atom experience the attractive force of the nucleus in the other atom.
2. The nucleus and the electrons ¡n the inner shell remain unaffected when atoms come close together.
3. only the electrons in outermost shell of an atom get affected.
4. Thus electrons in valence shell are responsible for the formation of bond between atoms.

Question 7.
List the factors that determine the type of bond that will be formed between two atoms.
Answer:
There are several factors that determine the type of bond which will be formed between two atoms. They are

• The force of attraction or repulsion between the electrons and protons.
• Number of valence electrons present in the valence shell of the atom.
• Electronegative difference between the atoms.
  If the E.N difference between the two atoms is > 1.9, ionic bond is formed.
  If the E.N difference between the two atoms is <1.9, covalent bond is formed.
• Atomic size
• Ionisation potential
• Electron affinity.

Question 8.
Represent the molecule H₂O using Lewis notation.
Answer:

Question 9.
What is octet rule? How do you appreciate the role of the ‘Octet rule’ in explaining the chemical properties of elements?
Answer:
Octet rule: “The atoms of element tend to undergo chemical changes that help to leave their atoms with eight outer-shell electrons”.

→ Role of ‘Octet Rule :

• ‘Octet rule’ helps to explain the chemical activities of atoms of many elements.
• It explains why some elements are more reactive towards chemical reaction and some are not.
• It can explain the high reactivity of Alkali, Alkaline earth metals.
• It can also explain the high reactivity of halogens.

Question 10.
What is hybridization? Explain the formation of the following molecules using hybridization.
(a) BeCl₂
(b) BF₃
Answer:
(i) Hybridisation is a phenomenon of intermixing of atomic orbitals of almost equal energy which are present in the outer shells of the atom and their reshuffling or redistribution into the same number of orbitals but with equal properties like energy and shape.

(a) Formation of BeCl₂ (Beryllium chloride) molecule:
(ii) The atomic number of Beryllium is 4
(iii) The electronic configuration of Beryllium atom in its ground state is 1s²2s².
(iv) The electronic configuration of Beryllium atom in its excited state is 1s² 2s¹2p¹.

(i) In the excited Beryllium atom its ‘2s’ and ‘2p_x‘ orbitals intermix to give two equivalent ‘ sp ‘ hybrid orbitals.
(ii) The electronic configuration of Be is 1S²2s¹2p_x¹. It has one half-filled ‘p’ orbital.
(iii) The electronic configuration of 17 Cl is 1s² 2 s²2p⁶3s²3p_x²3p_y²3p_z¹

(iv) The half-filled 3p_z orbitals of two chlorine atoms overlap with ‘sp’ hybrid orbitals of beryllium atom in their axes to form two σ _sp-p bonds.
(v) BeCl₂ molecule so formed has linear shape. The bond angle in BeCl₂ is 180°.

(b) Formation of Boron Trifluoride BF₃:
(i) The central atom in BF₃ is boron.
(ii) The electronic configuration of boron atom in its excited state is 1s² 2s¹ 2p²
B(Z=5)is

(iii) In the excited boron atom 2s’ orbital and two ‘2p’ orbitals intermix to give three equivalent sp² hybrid orbitals.
(iv) In the formation of BF₃ molecule, three sp² hybrid orbitals of boron overlap with half-filled 2p_z orbitals of three fluorine atoms. in their axes to give three bonds.
(v) BF₃ molecule so formed has trigonal planar structure.

(iv) The bond angle ¡n BF₃ is 120°.

Application of Concepts

Question 1.
Explain the formation of sodium chloride and calcium oxide on the basis of the concept of electron transfer from one atom to another atom.
Answer:
1. Formation of sodium chloride (NaCl): Sodium chloride is formed from the elements sodium and chlorine. It can be explained as follows.
(a) Formation of Cation: When sodium atom loses one electron to get octet electron configuration it forms a cation (Na⁺) and gets electron configuration that of Neon (Ne)
Na → Na⁺+e^–
E.C: 2, 8, 1 2,8 +₁e^–

(b) Formation of anion: Chlorine has shortage of one electron to get octet in its valence shell. So It gains the election that was lost by Na to form anion (Cl^–) and gets electron configuration of Argon (Ar)
Cl + e^– → Cl^–
E.C: 2,8,7 2,8,8

(c) Formation of the compound NaCl from ions: Transfer of electrons take place between ‘Na’ and ‘Cl’ atoms while they form Na⁺ and Cl^– ions. These oppositely charged ions get attracted towards each other due to
electrostatic forces and form the compound sodium chloride (NaCl).
Na⁺_(g) + Cl^–_(g) → NaCl_(s)

2. FormatIon of calcium oxide (CaO) Calcium Oxide Is formed from the elements Calcium and Oxygen. It can be explained as follows :
(a) Formation of Cation: When Calcium atom loses two electrons to get octet electronic configuration it forms a cation (Ca⁺²) and gets electron configuration of Argon (Ar)

(b) Formation of anion: Oxygen has shortage of two electrons to get octet in its valence shell. So it gains the electrons that were lost by Ca to form anion (O^-2) and gets electron configuration of Neon (Ne)
O + 2e^– → O^-2
E.C: 2, 6 → 2,8

(c) Formation of the compound CaO from ions : Transfer of electrons between ‘Ca’ and ‘O’ atoms takes place while they form Ca⁺² and O^-2 ions. These oppositely charged ions get attracted towards each other due to
electrostatic forces and form the compound calcium oxide (CaO).
Ca⁺²_(g) + O^-2_(g) →CaO_(s)

Question 2.
A, B and C are three elements with atomic numbers 6, 11. and 17 respectively.
(i) Which of these cannot form Ionic bond? Why?
(ii) Which of these cannot form covalent bond? Why?
(iii) Which of these can form Ionic as well as covalent bonds?
Answer:
(i) ‘A’ cannot form ionic bond. Its valence electrons are 4. It is difficult to lose or gain 4e^– to get octet configuration. So it forms covalent bond [Z of A is 6 so it is carbon (c)].

(ii) ‘B’ cannot form covalent bond. Its valence electrons are 1 only. So it is easy to donate the electron for other atom and become an ion. So it can form ionic bond [Z of B is 11, so it is sodium (Na)].

(iii) Element C can form ionic as well as covalent bonds. The element with atomic number 17 is Cl. It is able to participate with Na in ionic bond forming NaCl and with hydrogen in HCl molecule as covalent bond.

Question 4.
How Lewis dot structure helps in understanding bond formation between atoms?
Answer:

1. The valence electrons in an atom are represented by putting dots (.)on the symbol of the element, one dot for each valence electron.
2. By knowing the valence electrons of two different atoms by Lewis dot structure, we can understand which type of bond is going to establish between them and forms corresponding molecule.

Question 5.
Explain the formation of the following molecules using valence bond theory.
(a) N₂ molecule,
(b) O₂ molecule
Answer:
(a) Formation of N₂ molecule:
₇N has electronic configuration 1s² 2s² 2p_x¹ 2p_y¹2p_z¹ Suppose that ‘p_x’orbital of one ‘N’ atom overlaps the ‘p_x’ orbital of the other ‘N’ atom giving σ_px-px bond along the inter-nuclear axis. The p_y and p_z orbitals of one ‘N’ atom overlap the p_y and p_z orbital of other ‘N’ atom laterally, respectively perpendicular to internuclear axis giving 2π p_y-p_y and p_z – p_z bonds. Therefore N₂ molecule has a triple bond between two nitrogen atoms. (N ≡ N)

b) Formation of O₂ molecule:

• ₈O has electronic configuration 1s²2s²2p_x²2p_y¹2p_z¹
• If the ‘p_y’ orbital of one ‘O’ atom overlaps the ‘p_y’ orbital of other ‘O’ atom along the internuclear axis, a sigma p_y– p_y bond ((σ_{py- py}) is formed.
• p_z orbital of one ‘O’ atom overlaps the p_z orbital of other ‘O’ atom laterally, perpendicular to the inter-nuclear axis giving a Π_pz-pz bond.
• O₂ molecule has a double bond between two oxygen atoms. (O=O)

Question 6.
Predict the reasons for low melting points for covalent compounds when compared with ionic compounds.
Answer:

1. The melting point is low due to the weak Vander Waal’s forces of attraction between the covalent molecules.
2. The force of attraction between the molecules of a covalent compound is very weak.
3. Only a small amount of heat energy is required to break these weak molecular forces, due to which covalent compounds have low melting points and low boiling points. :
4. But some of the covalent solids like diamond and graphite have, however very high melting points and boiling points.

Higher Order Thinking questions

Question 1.
Two chemical reactions are described below.
(i) Nitrogen and hydrogen react to form ammonia.
(ii) Carbon and hydrogen bond together to form a molecule of methane (CH₄)
For each reaction, give
a) The valence of each of the atoms involved in the reaction.
b) The Lewis structure of the product that ¡s formed.
Answer:
i) Nitrogen reacts with hydrogen to form Ammonia. The reaction is
N₂ + 3H₂ → 2NH₃
a) The valency of each atom involved in the reaction.
Valence of Nitrogen = 3
Valence of Hydrogen = 1

(b) The Lewis structure of the product that is formed

(i) Carbon reacts with hydrogen to form a molecule of methane. The reaction is
C + 2H₂ → CH₄
(a) The valency of each atom involved in the reaction
Valence of Carbon = 4
Valence of Hydrogen = 1

(b) The Lewis structure of the product

Multiple choice questions

Question 1.
Which one of the following four elements is more electronegative? [ ]
(a) Sodium
(b) Oxygen
(c) Magnesium
(d) Calcium
Answer:
(b) Oxygen

Question 2.
An element, ₁₁X²³ forms an ionic compound with another element ‘Y’. Then the charge on the ior formed by X is [ ]
(a) +1
(b)+2
(c) -1
(d)-2
Answer:
(a) +1

Question 3.
An element ‘A’ forms a chloride ACl₄. The number electrons in the valence shell of ‘A’ is [ ]
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 4.
The inert gas element which does not have octet electronic configuration in its outermost orbit is [ ]
(a) Helium
(b) Argon
(c) Krypton
(d) Radon
Answer:
(a) Helium

Question 5.
Number of covalent bonds in methane molecule [ ]
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 6.
The concept hybridisation of orbitals of an atoms was introduced by  [ ]
(a) Lives pooling
(b) Mosley
(c) Lewis
(d) Kossel
Answer:
(a) Lives pooling

Question 7.
The value of bond angle in Berileum chloride molecule is [ ]
(a) 180°
(b) 120°
(c) 110°
(d) 104°.31′
Answer:
(a) 180°

Suggested Projects

Question 1.
Collect the information about properties and uses of covalent compounds and prepare a report?
Answer:
A. Properties of covalent compounds:

1. Covalent compounds are usually liquids or gases, only some of them are solids.
2. They are usually liquids or gases due to the weak force of attraction between their molecules.
3. They have usually low melting and low boiling points.
4. They are usually insoluble in water but they are soluble in organic solvents.
5. They do not conduct electricity.
6. They show molecular reactions.

Uses of covalent compounds:

1. Covalent compounds form 99% of our body.
2. Water is a covalent compound. We know many uses of water.
3. Sugars, food substances, tea, and coffee are all covalent compounds.
4. Air we breathe in contains covalent molecules of oxygen and nitrogen.
5. Almost everything on earth other than most simple inorganic salts are covalent compounds.

TS 10th Class Physical Science Chemical Bonding Intext Questions

Page 150

Question 1.
How do they(elements)usually exist?
Answer:
Elements usually exist as group of atoms.

Question 2.
Do they exist as a single atom or as a group of atoms?
Answer:
Except inert elements, all others exist as group of atoms. Inert elements exist as single atoms.

Question 3.
Are there elements which exist as atoms?
Answer:
Inert elements exist freely as atoms.

Question 4.
Why do some elements exist as molecules and some as atoms?
Answer:
Inert elements exist as atoms as they won’t form any bond other atoms form bonds and exist as molecules.

Question 5.
Why do some elements and compounds react vigorously while others are inert?
Answer:
Elements which do not have octet conflgurtion in their valence shelf react vigorously with other elements to form stable entities and which have octet configuration in their valence shell are chemically inert in nature.

Question 6.
Why is the chemical formula for water H₂0 and for sodium chloride NaCl, why not HO₂ and NaCl₂’?
Answer:
In water, oxygen atom bonds with two hydrogen atoms where as sodi + ion forms single bond with chloride in NaCl – ion.

Question 7.
Why do some atoms combine while others do not?
Answer:
Elements which do not have octet configuration in their valence shell combine with other elements and which have octet in their valence shell are chemically inert in nature.

Question 8.
Are elements and Compounds simply made up of separate atoms Individually arranged?
Answer:
No. They are arranged

Question 9.
Is there any attraction between atoms?
Answer:
Yes, there is attraction chemical bond.

Question 10.
What is that holdlng them together?
Answer:
Force of attraction called chemical bond.

Page 152

Question 11.
Why there is absorption of energy in certain chemical reactions and release of energy In other reactions?
Answer:
The absorption of energy in chemical reactions occurs when the reactants ‘‘ less chemical energy than the product where as release of energy in chemical reactions occurs when the reactants have higher chemical energy than the products.

Question 12.
Where the absorbed energy goes?
Answer:
The energy absorbed by the molecules makes electrons to reach excited s e and Increases kinetic energy of the molecule.

Question 13.
Is there any relation to energy and bond formation between atoms?
Answer:
The interacting energy is the potential energy between the atoms. It is negative if the atoms are bound and positive if they can move away from each other. The interaction energy is the integral of the force over the separation distance so these two quantities are directly related. The interaction energy is turning at the equilibrium position. This value of the energy Is called the bond energy and is the energy needed to separate completely to infinity (the work that needs to be done to overcome the attractive force.)

Question 14.
What could be the reason for the change in reactivity of elements?
Answer:
Number of valence electrons In the atoms of the element.

Question 15.
What could be the reason for the less reactivity of noble gases?
Answer:
All the noble gases have eight electrons in the outermost shell, except Helium (He). Thus they have no valency electrons and are less reactive or not at all reactive.

Page 155

Question 16.
What have you observed from tSe above conclusions about the main groups?
Answer:
Main group elements lose or gain electrons to get noble gas electronic configuration.

Question 17.
Why do atoms of elements try to combine and form molecules?
Answer:
To get stable electronic configuration In their valence shell.

Page 156

Question 18.
Is it accidental that IA to VIlA main group elements durIng chemical reactions get eight electrons In the outermost shells of their ions, similar to noble gas atoms?
Answer:
No. It cannot be simply accidental, Eight electrons in the outermost shell definitely gives stability to the ion or atom. Based on the above observations a statement known as The Octet Rule” Is framed.

Page 157

Question 19.
Explain the formation of ionic compounds NaCl, MgCl₂, Na₂O and AlCl₃ through Lewis electron-dot symbols (formulae).
Answer:
(1) Lewis electron-dot symbol for NacI :

Formation of sodium chloride (NaCl) :
Sodium chloride Is formed from the elements sodium and chlorine. It can be explained as follows.
Na_(s) + 1/2 Cl_2(g) → Nacl_(s)

Cation formation: When Sodium (Na) atom loses one electron to get octet electron configuration it forms a cation (Na+) and gets electron configuration that of Neon (Ne) atom.

Anion formation: Chlorine has shortage of one electron to get octet in its valence shell. So It gains the electron from Na atom to form anion and gets electron configuration as that of argon (Ar).

Formation of compound NaCl from its ions: Transfer of electrons between Na and cl atoms, results in the formation of Na+, and Cl- ions. These oppositely charged ions get attracted towards each other due to electrostatic forces and form the compound sodium chloride (NaCl).
Na⁺_(g)+ Cl^–_(g) → Na⁺_(g)Cl^–_(a) or NaCl

2. Lewis electron-dot symbol for MgCl₂ :

Formation of magnesium chloride (MgCl₂) :
Magnesium chloride is formed from the elements magnesium and chlorine. The bond formation MgCl₂ in brief using chemical equation is as follows :
Mg_(a)+Cl_2(g) → MgCl_2(a)
Cation Formation :

Anion formation :

The compound MgCl₂ formation from its ions :
Mg²⁺ gets Ne configuration and Each Cl- gets Ar configuration.
Mg²⁺_(g) + 2Cl^–_(g) → MgCl_2(a)
One ‘Mg’ atom transfers two electrons one each to two ‘Cl’ atoms and so formed Mg²⁺ and 2Cl- attract to form MgCl₂.

3. Lewis electron-dot symbol for (Na₂O) :

Formation of di-sodium monoxide (Na₂O) :
Di-sodium monoxide formation can be explained as follows :
Cation formation (Na+ formation) :

Anion formation (O2-, the oxide formation) Electronic configuration

The compound Na20 formation from Its ions is as shown.
2Na⁺_(g) + O^2-_(g) → Na₂O_(g)
Two ‘Na; atoms transfer one electrons each to one oxygen atom to form 1Na+ and 02-.
Each Na+ gets ‘Ne’ configuration and 02- gets ‘Ne’ configuration.
These ions (2Na+ and 02-) attract to form Na2O.

4. Lewis electron-dot symbol for (AlCl₃) :

Formation of aluminium chloride (AlCl₃) :
Aluminium chloride formation can be explained as follows :
Formation of aluminium ion (Al3+)0 the cation :

Formation of chloride ion (Cl-) the anIon :

Each aluminium atom loses three electrons and three chlorine atoms gain them, one electron each. The compound AlCl₃ is formed from its component Ions by the electrostatic forces of attraction.
Al^{+ 3}_(g)+3Cl^–_(g)

Page 160

Question 20.
How do cations and anions of an ionic compound exIst in its solid state?
Answer:
Cations and anions are surrounded themselves In three-dimensional lattices to give properly shaped crystals.

Question 21.
Do you think that pairs of Na⁺ Cl^– as units would be present in the solid crystal?
Answer:
No, electrostatic forces are non-directional. Therefore, it is not possible for one Na⁺ to be attracted by one Cl^– and vice-versa. Depending upon the size and charge of a particular ion, number of oppositely charged Ions get attracted by it, but, in a definite number. In sodium chloride crystal each Na is surrounded by 6 Cl^– and each Cl^– by six Na ions. Ionic compounds in the crystalline state consist of orderly arranged cations and anions held together by electrostatic forces of attractions in three dimensions

Page 161

Question 22.
Can you explain the reasons for all these?
Answer:
An ionic bond is formed between atoms of elements with electronegativity difference equal to or greater than 1.9.

Page 162

Question 23.
Can you say what type of bond exists between atoms of nitrogen molecules?
Answer:
Triple Bond

Page 164

Question 24.
What do you understand from bond lengths and bond energies?
Answer:
Bonds formed between two atoms in different molecules have different bond lengths and bond energies

Page 165

Question 25.
Are the values not different for the bonds between different types of atoms?
Answer:
Different for different molecules.

Page 167

Question 26.
What is the bond angle in a molecule?
Answer:
It is the angle subtended by two imaginary lines that pass from the nuclei of two atoms which form the covalent bonds with the central atom through the nucleus of the central atom at the central atom.

Page 169

Question 27.
How is HCl molecule formed?
Answer:
The ‘is’ orbital of ‘H’ atom containing unpaired electron overlaps with ‘3p’ orbital of chlorine atom containing unpaired electron of opposite spin.

TS 10th Class Physical Science Chemical Bonding Activities

Activity 1

Question 1.
Write the Lewis structure of the given elements ¡n the table. Also, consult the periodic table and fill in the group number of the element.
Answer:

Question 2.
Look at the periodic table. Do you see any relation between the number of valence electrons and group numbers’?
Answer:
For groups 2-6 the number of valence electrons is its group number. Group 1 has one outer electron, group 2 has two, where groups 13-17 number of valence electrons is (Group number-10). 3, 2, 1 respectively. (ie, 8-5=3;8-6=2;8-7= 1)

Question 3.
What did you notice in Lewis dot structure of noble gases and electronic configurations of the atoms of these elements shown in table – 1.
Answer:
It was found that the elements get octet or ns2 np6 configuration except helium, duplet.

These TS 10th Class Maths Chapter Wise Important Questions Chapter 3 Polynomials given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 3 Polynomials

Previous Exams Questions

Question 1.
Find p(3) if p(x) = x² – 5x + 6 is given.
Solution:
p(x) = x² – 5x + 6 (given)
then p(3) = 3² – 5(3) + 6
= 9 – 15 + 6 = 15 – 15 = 0
∴ p(3) = 0.

Question 2.
Find p(3) if p (x) = x² – 5x – 6 is given. (A.P.Mar.’16)
Solution:
p(x) = x² – 5x + 6 (given)
p (3) = 3² – 5(3) + 6
= 9 – 15 + 6 = 15 – 15 = 0
∴ p(3) = 0.

Question 3.
Find the quotient \(\frac{x^5+x^4+x^3+x^2}{x^3+x^2+x+1}\) when x ≠ 1.
Solution:
\(\frac{x^5+x^4+x^3+x^2}{x^3+x^2+x+1}\)
= \(\frac{x^2\left(x^3+x^2+x+1\right)}{\left(x^3+x^2+x+1\right)}\)
= x²
So the quotient is [x²]

Question 4.
We can write a trinomial having degree 7^th. Justify the given statement by giving one example. (T.S. Mar.15)
Solution:
Since the required is a trinomial, it should have 3 terms. As its degree is 7 the highest exponent (power) of the variable is 7. So the required will be
1) x⁷ – x⁶ + x⁵ (or) x⁷ – x + 10 (or) x⁷ – x⁵ – x (or) x⁷ + 5x⁶ + 6x⁵ or …

Question 5.
If we multiply or divide both sides of a linear equation by a non zero number, then the roots of linear equation will remain the same. Is it true ? If so justify with an example. (T.S. Mar. ’15)
Solution:
Let linear equation be 2x + 8 = 11
Its solution is 2x = 11 – 8 ⇒ 2x = 3
So x = \(\frac{3}{2}\)
Then 2x + 8 = 11 linear equation is divided by 10 on both sides.
\(\frac{2 x+8}{10}\) = \(\frac{11}{10}\) = 20x + 80 = 110
⇒ 20x = 110 – 80 = 30
then x = \(\frac{30}{2}\) = \(\frac{3}{2}\)
So its solution doesn’t change.
So the given statement is true.

Question 6.
Laxmi does not want to disclose the l, b, h of a cuboid of her project. She has constructed a polynomial x³ – 6x² + 11x – 6 by taking the values of l, b, h as its zeros. Can you open the secret ? (T.S. Mar. 15)
Solution:
P(x) = x³ – 6x² + 11x – 6
P(1) = (1)³ – 6(1)² + 11 (1) – 6
= 1 – 6 + 11 – 6
= 12 – 12 = 0
∴ for P(x), (x – 1) is a factor

x² – 5x + 6 = x² – 3x – 2x + 6
= x (x – 3) – 2(x – 3)
= (x – 3) (x – 2)
P(x) = (x – 1) (x – 2) (x – 3)
P(x) zeroes of the polynomial are 1, 2,3
∴ Measurements of the cuboid are 1,2 and 3 units.
Its solution doesn’t change
So it is true.

Question 7.
Draw a graph for the polynomial p(x) = x² + 3x – 4 and find its zeros from the graph.
Solution:
p(x) = x² + 3x – 4


∴ Zeroes of polynomial are -4 and 1

Question 8.
Given an example for a quadratic polynomial which has no zeroes.
Solution:
A quadratic polynomial is in the form of ax² + bx + c. As this has no zeroes. Its discriminant will not be a real number.
So b² – 4ac < 0
So we can choose certain a, b, c values where
b² – 4ac < 0
For examples a = 1, b = 4 and c = 9
So ax² + bx + c = 0
⇒ x² + 4x + 9 = 0 will not have zeroes.

Question 9.
The length of a rectangle is 5 more than its breadth. So express its perimeter in the form of polynomial.
Solution:
Let the breadth of rectangle = xm and its
length = x + 5m.
So the perimeter = 2(l + b)
= 2(x + 5 + x)
= 2(2x + 5)
= 4x + 10m

4x + 10 is the polynomial which represents the perimeter of above rectangle.

Question 10.
Draw the graph of polynomial
p(x) = x² – 3x + 2 and find its zeros.
Sol, let y = p(x) = x² – 3x + 2
If x = 0 then p(0) = 0 – 0 + 2
= 2 So (0, 2)
x = 1 then p(1) = 1² – 3(1) + 2
= 1 – 3 + 2
= 0 So (1, 0)
x = 2 then p(2) = 2² – 3(2) + 2
= 4 – 6 + 2
= 0 So (2, 0)
x = 3 then p(3) = 3² – 3(3) + 2
= 9 – 9 + 2
= 2 So (3, 2)
and if x = -1 then p(-1)
= (-1)² – 3(-1) + 2
= 1 + 3 + 2
= 6 So (-1, 6)
x = -2 then p(-2) = (-2)² – 3(2) + 2
= 4 + 6 + 2 = 12 So (-2, 12)
that means the graph of the polynomial
p(x) = x² – 3x + 2 passes through the points. (0, 2), (1, 0) (2, 0) (3, 2) (-1, 6) and (-2, 12)

So 1 and 2 are zeroes of the given polynomial.

Question 11.
Draw the graphs of the following two linear equations and find their solution.
Solution:
First we have to recognise the points through which the line 3x – 2y = 2 passes then after 2x + y = 6 pass. Let us find the points
3x – 2y = 2
So y = \(\frac{3 x-2}{2}\) —- (1)
Put x = 0 in above equation
∴ y = \(\frac{3(0)-2}{2}\) = \(\frac{0-2}{2}\) = 1
So (0, 1)
Now x = 1 then
y = \(\frac{3(1)-2}{2}\) = \(\frac{3-2}{2}\) = \(\frac{1}{2}\) So(1, \(\frac{1}{2}\))
Now x = 2 then
y = \(\frac{3(2)-2}{2}\) = \(\frac{6-2}{2}\) = \(\frac{4}{2}\) So(2, 2)
that means the line 3x – 2y = 2 passes through the points (0, -1), (1, \(\frac{1}{2}\)) and (2, 2)
Similarly
2x + y = 6
⇒ y = 6 – 2x —– (2)
Put x = 0 in the above equation (2) we get
y = 6 – 2(0) = 6 – 0 = 6 So(0, 6)
and x = 1 ⇒ y = 6 – 2(1) = 6 – 2 = 4
So(1, 4)
and x = 2 ⇒ y = 6 – 2(2) = 6 – 4 = 2
So (2, 2)
So the line 2x + y = 6 passes through the points (0, 6) (1, 4) and (2, 2)
Here we observe (2, 2) is the common point.
That means they intersert at (2, 2)
So x = 2 and y = 2 will be the solution of above the equations.

Additional Questions

Question 1.
If p(x) = 6x⁷ – 2x⁵ + 4x – 8, find
(i) coefficient of x⁵
(ii) degree of p(x)
(iii) constant term. (Each 1 Mark)
Solution:
If p(x) = 6x⁷ – 2x⁵ + 4x – 8,

i) coefficient of x⁵ = – 2
ii) degree of p(x) = highest degree of x – 7
iii) constant term = – 8

Question 2.
If p(t) = 3t³ + 4t – 5, find the values of p(1), p(-1), P(0), p(2), p(-2).
Solution:
given p(t) = 3t³ + 4t – 5
∴ p(1) = 3(1)³ + 4(1) – 5 = 3 + 4 – 5 = 2
p(-1) = 3(-1)³ + 4(-1) – 5 = -3 – 4 – 5 = -12
p(0) = 3(0)³ + 4(0) – 5 = 0 + 0 – 5 = -5
p(2) = 3(2)³ + 4(2) – 5 = 3(8) + 8 – 5
= 24 + 8 – 5 = 27
p(-2) = 3(-2)³ + 4 (-2) – 5
= – 24 – 8 – 5 = – 37

Question 3.
Check whether – 4 and 4 are the zeroes of the polynomial x⁴ – 256.
Solution:
given p(x) = x⁴ – 256
p(-4) = (-4)⁴ – 256 = 256 – 256 = 0
p(4) = (4)⁴ – 256 = 256 – 256 = 0
yes, -4 and 4 are zeroes of the given polynomial

Question 4.
Check whether 5 and -4 are the zeroes of the polynomial p(x) when p(x) = x² – x – 20
Solution:
given p(x) = x² – x – 20
p(5) = (5)² – 5 – 20 = 25 – 5 – 20 = 25 – 25 = 0
P(-4) = (-4)² – (-4) – 20
= 16 + 4 – 20 = 20 – 20 = 0
yes, 5 and – 4 are the zeroes of the polynormial
p(x) = x² – x – 20.

Question 5.
Check whether 3 and – 7 are the zeroes of the polynomial p(x) = x² + 4x – 21.
Solution:
given p(x) = x² + 4x – 21
p(3) = 3² + 4(3) – 21
= 9 + 12 – 21 = 21 – 21 = 0
p(-7) = (-7)² + 4(-7) – 21
= 49 – 28 – 21 = 49 – 49 = 0
yes, 3 and – 7 are the zeroes of the polynomial p(x) = x² + 4x – 21.

Question 6.
Find the zeroes of the given polynomials.
i) p(x) = 4x
ii) p(x) = x² – 9x + 20
iii) p(x) = (x + 5) (x + 6)
iv) p(x) = x⁴ – 81
Solution:
i) p(x) = 4x
p(0) = 4 × 0 = 0
∴ The zero of p(x) = 4x is 0.

ii) p(x) = x² – 9x + 20
= x² – 4x – 5x + 20
= x (x – 4) -5 (x – 4)
= (x – 4) (x – 5)
To find zeroes, let p(x) = 0
⇒ (x – 4) (x – 5) = 0
⇒ x – 4 = 0 or x – 5 = 0
⇒ x = 4 or x = 5
∴ The zeroes of x² – 9x + 20 are 4 nd 5.

iii) p(x) = (x + 5) (x + 6)
To find zeroes, let p(x) = 0
⇒ (x + 5) (x + 6) = 0
⇒ x + 5 = 0 or x + 6 = 0
⇒ x = -5 or x = -6
∴ The zeroes of (x + 5) (x + 6) are – 5 and – 6

iv) p(x) = x⁴ – 81.
To find zeroes, let p(x) = 0
⇒ x⁴ – 81 = 0
⇒ (x²)² – (9)² = 0
⇒ (x² + 9) (x² – 9) = 0
⇒ x² + 9 = 0 or x² – 9 = 0
x² = -9 or (x + 3) (x – 3) = 0
x = ±\(\sqrt{-9}\) = 9 or x + 3 = 0 or x – 3 = 0
x = -3 or x = 3
∴ The zeroes of the polynomial x⁴ – 81 are -3, 3 and ± \(\sqrt{-9}\).

Question 7.
Find the zeroes of the given polynomials.
i) p(x) = x² – x – 12
ii) p(x) = x² – 6x + 9
iii) x² p(x) = x² – 4x + 5
iv) p(x) = x² + 3x – 4
Solution:
i) p(x) = x² – x – 12
To find zeroes, let p(x) = 0
⇒ x² – x – 12 = 0
x² – 4x + 3x – 12 = 0
x(x – 4) + 3 (x – 4) = 0
(x – 4) (x + 3) = 0
⇒ x – 4 = 0 or x + 3 = 0
∴ The zeroes of x² – x – 12 are 4 and – 3

ii) p(x) = x² – 6x + 9
To find zeroes, let p(x) = 0
x² – 6x + 9 = 0
x² – 3x – 3x + 9 = 0
x(x – 3) – 3 (x – 3) = 0
⇒ (x – 3) (x – 3) = 0
⇒ x – 3 = 0 or x – 3 = 0
⇒ x = 3 or x = 3
∴ The zeroes of x² – 6x + 9 is 3.

iii) p(x) = x² – 4x – 5
To find zeroes, let p(x) = 0
x² – 4x – 5 = 0
x² – 5x + x – 5 = 0
⇒ x (x – 5) + 1(x – 5) = 0
⇒ (x – 5) (x + 1) = 0
⇒ x – 5 = 0 or x + 1 = 0
⇒ x = 5 or x = -1
∴ The zeroes of x² – 4x – 5 are 5 and – 1

iv) p(x) = x² + 3x – 4
To find zeroes, let p(x) = 0
x² + 3x – 4 = 0
⇒ x² + 4x – x – 4 = 0
⇒ x(x + 4) – 1(x + 4) = 0
⇒ (x + 4) (x – 1) = 0
⇒ x + 4 = 0 or x – 1 = 0
⇒ x = -4 or x = 1
∴ The zeroes of x² + 3x – 4 are -4 and 1.

Question 8.
Why are \(\frac{1}{3}\) and -2 zeroes of polynomial
p(x) = 3x² + 5x – 2 ?
Solution:
p(x) = 3x² + 5x – 2
Now p(\(\frac{1}{3}\)) = 3(\(\frac{1}{3}\))² + 5(\(\frac{1}{3}\)) – 2
= \(\frac{1}{3}\) + \(\frac{5}{3}\) – 2
= \(\frac{1+5-6}{3}\) = \(\frac{6-6}{3}\) = \(\frac{0}{3}\) = 0
p(-2) = 3 (-2)² + 5(-2) – 2
= 3(4) – 10 – 2
= 12 – 12 = 0
since p(\(\frac{1}{3}\)) and p(-2) are equal to zero
–\(\frac{1}{3}\) and – 2 are zeroes of the polynomial.

Question 9.
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and coefficients.
i) x² – 5x + 6
ii) 3x² – 7x + 4
iii) 5x² + 10x
iv) t² – 12
Solution:
i) Let p(x) = x² – 5x + 6
= x² – 3x – 2x + 6
= x(x – 3) -2 (x – 3)
= (x – 3) (x – 2)
To find zeroes, let p(x) = 0
Hence the zeroes of p(x) are 3 and 2
sum of the zeroes = 3 + 2 = 5 = –\(\frac{(-5)}{1}\)

Product of zeroes = 3 × 2 = 6 = \(\frac{6}{1}\) constant term

ii) 3x² – 7x + 4
Let p(x) = 3x² – 7x + 4
= 3x² – 3x – 4x + 4
= 3x (x – 1) -4 (x – 1)
= (x – 1) (3x – 4)
To find zeroes, let p(x) = 0
⇒ (x – 1) (3x – 4) = 0
x = 1 or x = 4/3
Hence, the zeroes of p(x) are 1 and \(\frac{4}{3}\).
sum of the zeroes = 1 + \(\frac{4}{3}\) = \(\frac{3+4}{3}\) = \(\frac{7}{3}\)

product of zeroes = 1 × \(\frac{4}{3}\) = \(\frac{4}{3}\)

iii) Let p(x) = 5x² + 10x
= 5x (x + 2)
To find zeroes, Let p(x) = 0
⇒ 5x (x + 2) = 0
⇒ x = 0 or x + 2 = 0
⇒ x = 0 or x = -2
Hence the zeroes of p(x) are 0 and -2.
sum of the zeroes = 0 + (-2) = -2

coefficient of x Product of zeroes = 0 x – 2 = 0

iv) t² – 12
let p(t) = t² – 12
to find zeroes, let p(t) = 0
⇒ t² – 12 = 0
⇒ t² = 12 ⇒ t = ±\(\sqrt{12}\) = \(\sqrt{12}\) and –\(\sqrt{12}\)
Hence the zeroes of p(t) are \(\sqrt{12}\) and –\(\sqrt{12}\)
sum of zeroes = \(\sqrt{12}\) + (-\(\sqrt{12}\))
= \(\sqrt{12}\) – \(\sqrt{12}\) = 0 = \(\frac{0}{1}\)

product of zeroes = \(\sqrt{12}\) × (-\(\sqrt{12}\))
= -12 = \(-\frac{12}{1}\)

Question 10.
Find the quadratic polynomial in each case, with the given numbers as the sum and product of its zeroes.
i) \(\frac{1}{3}\), -2
ii) 0, \(\sqrt{3}\)
iii) 3, 5
iv) –\(\frac{1}{2}\), \(\frac{1}{2}\)
Solution:
i) \(\frac{1}{3}\), -2
Let α, β be the zeroes of the quadratic polynomial sum of zeroes = α + β = \(\frac{1}{3}\)
product of zeroes = αβ = -2
The required quadratic polynomial will be
k [x² – x(α + β) + αβ] when k is a constant
⇒ k[x² – \(\frac{x}{3}\) – 2]
If k = 3, then the polynomial will be
3[x² – \(\frac{x}{3}\) – 2] = 3x² – x – 6

ii) 0, \(\sqrt{3}\)
Let α, β be the zeroes of quadratic polynomial.
sum of the zeroes = α + β = 0
product of the zeroes = αβ = \(\sqrt{3}\)
The required quadratic polynomial will be k[x² – x(α + β) + αβ] where k is a constant.
⇒ k [x² – x(0) + \(\sqrt{3}\))
⇒ k [x² – 0 + \(\sqrt{3}\)] ⇒ k[x² + \(\sqrt{3}\)
If k = 1, then the polynomial will be 1[x² + \(\sqrt{3}\)] = x² + \(\sqrt{3}\).

iii) 3, 5
Let α, β be the zeroes of quadratic polynomial.
sum of the zeroes = α + β = 3
product of the zeroes = αβ = 5
The required quadratic polynomial will be k[x² – x(α + β) + αβ] where k is a constant
⇒ k [x² – x(3) + 5]
⇒ k [x² – 3x + 5]
If k = 1, then the polynomial will be
1[x² – 3x + 5] = x² – 3x + 5

iv) –\(\frac{1}{2}\), \(\frac{1}{2}\)
Let α, β be the zeroes of quadratic polynomial sum of the zeroes = α + β
= –\(\frac{1}{2}\)
product of the zeroes αβ = \(\frac{1}{2}\)
The required quadratic polynomial will be k[x² – x(α + β) + αβ] when k is a constant
k[x² – x(-\(\frac{1}{2}\)) + \(\frac{1}{2}\)]
⇒ k[x² + \(\frac{x}{2}\) + \(\frac{1}{2}\)]
If k = 2, then the polynomial will be 2[x² + \(\frac{x}{2}\) + \(\frac{1}{2}\)] = 2x² + x + 1

Question 11.
Find the quadratic polynomial the zeroes α, β given in each case

i) 4, -3
ii) \(\sqrt{5}\) – \(\sqrt{5}\)
iii) \(\frac{1}{3}\), \(\frac{5}{3}\)
Solution:
i) 4, -3
Let the quadratic polynomial be ax² + bx + c, a ≠ 0,
and its zeroes be a and b.
then α = 4, β = – 3
sum of the zeroes = a + b = 4 – 3 = 1
product of the zeroes = a . b = 4 × -3
= -12
The requiral quadratic polynomial is k [x² – x (α + β) + αβ] where k is a constant
⇒ k[x² – x(1) + (-12)]
⇒ k[x² – x – 12]
When k = 1, the quadratic polynomial will be x² – x – 12.

ii) \(\sqrt{5}\) – \(\sqrt{5}\)
Let the quadratic polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be a and b, Here α = \(\sqrt{5}\), β = –\(\sqrt{5}\)
sum of the zeroes = α + β = \(\sqrt{5}\) – \(\sqrt{5}\) = 0
product of the zeroes = α . β
= \(\sqrt{5}\) × –\(\sqrt{5}\) = -5
The required quadratic polynomial is
k² [x – x (α + β) + αβ] where k is a constant
⇒ k² [x² – x(0) + (-5)]
⇒ k[x² – 5]
wherek k = 1, the quadratic polynomial will be x² – 5

iii) \(\frac{1}{3}\), \(\frac{5}{3}\)
Let the quadrate polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be α and β.
Then α = \(\frac{1}{3}\) and β = \(\frac{5}{3}\)
sum of the zeroes = α + β = \(\frac{1}{3}\) + \(\frac{5}{3}\)
= \(\frac{6}{3}\) = 2
Product of the zeroes = αβ = \(\frac{1}{3}\) . \(\frac{5}{3}\)
= \(\frac{5}{9}\)
The required quadratic polynomial is
k[x² – x(α + β) + αβ] where k is a constant
⇒ k[x² – x(2) + \(\frac{5}{9}\)]
⇒ k[x² – 2x + \(\frac{5}{9}\)]
Where k = 9, the quadratic polynomial will be a [x² – 2x + \(\frac{5}{9}\)] = 9x² – 18x + 5

Question 12.
Verify that 1, -2 and -3 are the zeroes of the cubic polynomial x³ + 4x² + x – 6 and check the relationship between zeroes and the coefficients.
Solution:
The given polynomial is x³ + 4x² + x – 6.
Comparing the given polynomial with
ax³ + bx² + cx + d, we get
a = 1, b = 4, c = 1, d = – 6
Let p(x) = x³ + 4x² + x – 6
p(1) = (1)³ + 4(1)² + 1 – 6
= 1 + 4 + 1 – 6 = 6 – 6 = 0
p(-2) = (-2)³ + 4(-2)² + (-2) – 6
= – 8 + 4(4) – 2 – 6
= – 8 + 16 – 2 – 6 = 16 – 16 = 0
p(-3) =(-3)³ + 4(-3)² + (-3) – 6
= – 27 + 4(9) – 3 – 6
= 36 – 36 = 0
∴ 1, -2 and – 3 are the zeroes of given polynomial. So, α = 1, β = -2, ∝= – 3

Question 13.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following.

i) p(x) = x³ + 4x² + 5x + 6, g(x) = x² + 3
ii) p(x) = x⁴ + 3x² – 4x + 8
g(x) = x² + 2 – x
Solution:
i) p(x) = x³ + 4x² + 5x + 6,
g(x) = x² + 3

The degree of x² + 3 is 2. The degree of 2x – 6 is 1
Since degree of (2x – 6)² < degree of (x² + 3)
∴ we stop here.
So, the quotient is x + 4 and the remainder is 2x – 6.

ii) p(x) = x⁴ + 3x² – 4x + 8
g(x) = x² + 2 – x = x² – x + 2
(∴ writing it in standard form)

since degree of (-4x + 4) < degree of x² – x + 2
∴ we stop here
So, the quotient is x² + x + 2 and the remainder is (-4x + 4).

Question 14.
Check in each case the first polynomial is a factor of the second polynomial.
i) x² – 2, 2x⁴ – 3x³ – 3x² + 6x – 2
ii) x² – x + 1, x⁴ – 3x² + 4x – 3
Solution:
Hint : If the remainder is zero, then the first polynomial is a factor of the second one

i) x² – 2, 2x⁴ – 3x³ – 3x² + 6x – 2
The given polynomials are in standard form.

Since the remainder is zero, x² – 2 is the factor of 2x⁴ – 3x³ – 3x² + 6x – 2.

ii) x² – x + 1, x⁴ – 3x² + 4x – 3
The given polynomials is standard form.

Since the remainder is zero, x² – x + 2 is the factor of x⁴ – 3x² + 4x – 3.

Question 15.
Draw the graph of the polynomial x² + x – 6 and mark the zeroes by the …….
Solution:
given that y = x² + x – 6
= x² + x – 6


zeroes of the polynomial x² + x – 6 are the x – co-ordinates of the points on the – 3 and 2 are the zeroes of the given polynomial on graph.

Question 16.
Check whether \(\frac{1}{2}\) is the zero of the polynomial 2x² + x – 1 or not. (AP-SA-II : 2016)
Solution:
Let p(x) = 2x² + x – 1
we have p(\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\))² + \(\frac{1}{2}\) – 1
= 2 × \(\frac{1}{4}\) + \(\frac{1}{2}\) – 1
= \(\frac{1}{2}\) + \(\frac{1}{2}\) – 1 = 1 – 1
= 0
∴\(\frac{1}{2}\) is the zero of the polynomial.

Question 17.
Verify the relationship between the zeroes and the coefficient of x² – 25 by finding its zeroes. (AP-SA-II : 2016)
Solution:
Given polynomial is x² – 25
we have x² – 25 = 0
⇒ (x + 5) (x – 5) = 0
⇒ x = -5 or x = 5
∴ The zeroes of x² – 25 are – 5 and 5
∴ The sum of zeroes = -5 + 5 = 0 coefficient of x

= –\(\frac{0}{1}\) = 0
And product of the zeroes = (-5) × (5) = – 25

= –\(\frac{25}{1}\) = -25
Hence verified.

Question 18.
Give two examples of the polynomials p(x) and g(x) satisfying division algori-tham. (AP-SA-II : 2016)
Solution:
Using division alogaritham,
We have p(x) = q(x) × g(x) + r(x)
Example (1) : on dividing 12x² + 8x + 24 by 3x² + 2x + 6, we get

Here p(x) = 12x² + 8x + 24
g(x) = 3x² + 2x + 6
g(x) = 4
r(x) = 0

Example – 2 : an dividing 3x³ + 6x² + 18x by x² + 2x + 6

Here p(x) = 3x² + 6x² + 18x
g(x) = x² + 2x + 6
g(x) = 3x
r(x) = 0

Question 19.
Verify that 4, -1, –\(\frac{1}{4}\) are the zeroes of the cubic polynomial 4x³ – 11x² – 19x – 4 and check. (AP-SA-II: 2016)
Solution:
Given polynomial is 4x³ – 11x² – 19x – 4
p(x) comparing the given polynomial with
ax³ + bx² + cx + d, we get
a = 4, b = – 11, c = -19, d = – 4
Further p(4) = 4(4)³ – 11(4)² – 19(4) – 4
= 4 × 64 – 11(16) – 19(4) – 4
= 256 – 176 – 76 – 4
= 256 – 256 = 0
p(-1) = 4(-1)³ – 11(-1)² – 19(-1) – 4
= 4(-1) – 11(1) + 19-4
= -4 – 11 + 19 – 4
= -19 + 19 = 0


Therefore 4, -1, –\(\frac{1}{4}\) are the zeroes of
4x³ – 11x² – 19x – 4.
We take α = 4, β = – 1 and γ = –\(\frac{1}{4}\)
now α + β + γ = 4 – 1 – \(\frac{1}{4}\) = 3 – \(\frac{1}{4}\) = \(\frac{11}{4}\)
= \(\frac{-(-11)}{4}\) = –\(\frac{b}{a}\)

Question 20.
Draw the graph of the polynomial x² + x – 6 and mark the zeroes of the polynomial
Solution:
Given that y = x² + x – 6


Scale : On X-axis :1 cm = 1 unit
On Y-axis :1 cm = 1 unit
Zeroes of the polynomial x² + x – 6 are the x – coordinates of the points on the x – axis.
-3 and 2 are the zeroes of the given polynomial on graph.

Question 21.
If α, β are zeroes of the polynomial 2x² + 7x + 5, find the value of α + β + αβ? (AP New SCERT Model Paper) Solution:
2x² + 7x + 5
α + β = \(\frac{-b}{a}\) = \(\frac{-7}{2}\)
α.β = \(\frac{\mathrm{c}}{\mathrm{a}}\) = \(\frac{5}{2}\)
∴ α + β + α.β = \(\frac{-7}{2}\) + \(\frac{5}{2}\) = \(\frac{-2}{2}\) = -1

Question 22.
If a, b and c are the zeroes of a polynomial of degree 3, then give the relations between the zeroes and the coefficients of the polynomial. (AP New SCERT Model Paper)
Solution:
α + β + γ = \(\frac{-b}{a}\)
αβ + βγ + γα = \(\frac{c}{a}\)
αβγ = \(\frac{-d}{a}\)

Question 23.
Solve the quadratic polynomial x² – 3x – 4 graphically. (AP New SCERT Model Paper)
Solution:
Let y = x² – 3x – 4

o.p. = (-2, 6), (-1, 0), (0, -4), (1, -6), (2, -6) (3, -4), (4, 0), (5, 6)
Scale : On X-axis 1 cm = 1 unit
On Y-axis 1 cm = 1 unit
The graph of y = x² – 3x – 4 intersects X-axis at (-1, 0) and (4, 0).
Hence the zeroes of p(x) are -1 and 4.

These TS 10th Class Maths Chapter Wise Important Questions Chapter 4 Pair of Linear Equations in Two Variables given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 4 Pair of Linear Equations in Two Variables

Previous Exams Questions

Question 1.
Solve the following equations by substitution method (A.P.Jun.’15)

i) 2x – 7y = 3
ii) 4x + y = 21
Solution:
The given two linear equations are
2x – 7y = 3 —- (1)
4x + y = 21 — (2)
From the equation (2) we get y = 21 – 4x now we substitute this ‘Y’ value in equation (1)
We get
2x – 7(21 – 4x) = 3
⇒ 2x – 147 + 28x = 3
⇒ 30x = 147 + 3 = 150
then x = \(\frac{150}{30}\) = 5
∴ x = 5
Now put x = 5 in equation (2) we get
4(5) + y = 21
20 + y = 21
y = 21 – 20 = 1
So x = 5 and y = 1 are the solution of the system.

Question 2.
10 students of 10th class participated in a Quiz programme. The number of girls participated in it is 4 more than boys. So find the number of boys and girls participated in Quiz. (A.P. Mar. 16)
Solution:
Let the number of girls = x (say)
and the number of boys = y (say)
then total students = x + y = 10 ——- (1)
and also
The number of girls = number of boys + 4
x = y + 4 —— (2)
Put this ‘x’ value in equation (1), we get
y + 4 + y = 10
⇒ 2y + 4 = 10
⇒ 2y = 10 – 4 = 6
∴ y = \(\frac{6}{2}\) = 3
So y = 3 then
x + y = 10 becomes
x + 3 = 10 ⇒ x = 10 – 3
⇒ x = 7
So the number of girls = 7 and the number of boys = 3.

Question 3.
Solve the given pair of linear equations by elimination method.
i) 2x + y – 5 = 0 and
ii) 3x – 2y – 4 = 0. (A.P. Mar.’16)
Solution:
In this elimination method, we solve this pair of linear equation by making either of coefficients equal.
The given equations are
2x + y = 5 ——— (1)
3x – 2y = 4 —– (2)
To make the coefficients of ‘x’ equal let us multiply the equation (1) by 3 and the equation (2) by 2 on both sides.
We get
(2x + y = 5) × 3
(3x – 2y = 4) × 2

then 2x + y = 5 becomes
2x + 1 = 5 ⇒ 2x = 5 – 1 = 4
∴ x = \(\frac{4}{2}\) so x = 2
x = 2 and y = 1 are the solutions of the given equations.

Verification : Put x = 2 and y = 1 in equation (1) and (2)

2x + y = 5
2(2) + 1 = 5
4 + 1 = 5
5 = 5
LHS = RHS

3x – 2y – 4 = 0
3(2) – 2(1) = 4
6 – 2 = 4
4 = 4
LHS = RHS

Question 4.
For what value of k, the following system of equations has a unique solution, x – ky = 2; 3x + 2y = – 5 (T.S. Mar.15)
Solution:
a₁x + b₁y + c₁x = 0 and
a₂x + b₂y + c₂ = 0 will have a unique solution.
will have a unique solution.
If \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\) in the given system of equations
a₁ = 1,
b₁ = – k,
a₂ = 3,
b₂ = 2
So \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\) means
\(\frac{1}{3}\) ≠ \(\frac{-k}{2}\) ⇒ -k ≠ \(\frac{2}{3}\)
So the system of equations will have a unique solutions for k = R – (\(\frac{-2}{3}\))

Question 5.
For what value of m the following system of equations will have a unique solution. 3x + my = 10 and 9x + 12y = 30
(T.S.Mar. 16)
Solution:
We know that the system of equations
a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
will have unique solutions.
If \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\)
Here in the given system
a₁ = 3, b₁ = m and a₂ = 9, b₂ = 12
So \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\) becomes
\(\frac{3}{9}\) ≠ \(\frac{m}{12}\)
⇒ m ≠ \(\frac{12 \times 3}{9}\) = 4
So for m ≠ 4 the above system will have unique solution i.e., R – (4).

Question 6.
Solve the following pair of linear equations by substitution method,
i) 2x – 3y = 19 and 3x – 2y = 21 (T.S. Mar.’16)
Solution:
The given equations are
2x – 3y = 19 —– (1)
and 3x – 2y = 21 —– (2)
From the equation (1) 2x = 19 + 3y and x = \(\frac{19+3 y}{2}\)
Now substituting this value of
x = \(\frac{19+3 y}{2}\) in equation (2) we get
3x – 2y = 21 becomes
\(\frac{3(19+3 y)}{2}\) – 2(y) = 21
∴ 57 + 9y – 4y = 21 × 2
9y – 4y = 42 – 57
5y = – 15
∴ y = \(\frac{-15}{5}\) = -3
So y = – 3 Now put this y = – 3 value in
x = \(\frac{19+3 y}{2}\) we get
y = \(\frac{19+3(-3)}{2}\)
x = \(\frac{19-9}{2}\) = \(\frac{10}{2}\)
So x = 5 and y = – 3 are the solutions of given equations.

Verification :

2x – 3y = 19
2(5) – 3(- 3) = 19
10 + 9 = 19
19 = 19
LHS= RHS

3x – 2y = 21
3(5) – 2(-3) = 21
15 + 6 = 21
21 = 21
LHS = RHS

Additional Questions

Question 1.
By comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\), \(\frac{c_1}{c_2}\), find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or coincident.

a) 3x + 4y + 5 = 0; 2x – 3y + 6 = 0
b) 3x + 5y + 6 = 0; 9x + 15y + 18 = 0
c) 4x – 2y + 5 = 0; 2x – y + 6 = 0
Solution:
a) The given pair of linear equations are
3x + 4y + 5 = 0 ——- (1)
2x – 3y + 6 = 0 —— (2)
Comparing equations (1) and (2) with stan-dard equations i.e.,
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0, we get
a₁ = 2; b₁ = 3; c₁ = -5
a₂ = 3; b₂ = 4; c₂ = -6
Since \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)

b) 4x + 6y = 9 —– (1)
⇒ 4x + 6y – 9 = 0
⇒ 2x + 3y = 5 —— (2)
⇒ 2x + 3y – 5 = 0
Here, a₁ = 4; b₁ = 6; c₁ = -9
a₂ = 2; b₂ = 3; c₂ = -5
Since
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations will represent inconsistent.

c) 3x – 5y = 11 —– (1)
6x – 10y = 22 —- (2)
3x – 5y – 11 = 0
6x – 10y – 22 = 0
Here, a₁ = 3; b₁ = -5; c₁ = -11
a₂ = 6; b₂ = -10; c₂ = -22
\(\frac{a_1}{a_2}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-5}{-10}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-11}{-22}\) = \(\frac{1}{2}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given pair of linear equations are consistent.

Question 3.
15 students of Class – X took part in a science quiz. If the number of boys is 5 more than the number of girls then, find the number of boys and the number of girls who took part in the quiz.
Solution:
Let the number of boys who took part in the quiz = x
Let the number of girls who took part in the quiz = y
15 students took part in quiz
⇒ x + y = 15 —– (1)
Since the number of boys is 5 more than the number of girls, we have
x = y + 5
⇒ x – y = 5 —- (2)
⇒ x – y = 5
Adding (1) and (2)

x = \(\frac{20}{2}\) = 10
Substitutes x = 10 in equation (1)
10 + y = 15 ⇒ y = 15 – 10 = 5
∴ The number of boys who took part in quiz = x = 10 and the number of girls who took part in quiz = y = 5

Question 4.
6 pencils and 9 pens together cost ₹ 96 whereas 9 pencils and 6 pens together cost ₹ 84. Find the cost of one pencil and that of one pen.
Solution:
Let the cost of one pencil = ₹ x
Cost of one pen = ₹ y
Total cost of 6 pencils and 9 pens = 6x + 9y
Total cost of 9 pencils and 6 pens = 9x + 6y
By the given problem, 6x + 9y = 96 —- (1)
9x + 6y = 84 —- (2)

∴ y = \(\frac{360}{45}\) = 8
Substitute y = 8 in equation (1),
6x + 9(8) = 96
6x + 72 = 96 ⇒ 6x = 96 – 72 = 24
x = \(\frac{24}{6}\) = 4
∴ Cost of one pencil = ₹ 4
Cost of one pen = ₹ 8

Question 5.
Half of the perimeter of a rectangular! garden, whose length is 6 m more than its width is 40 m. Find the dimensions of the garden.
Solution:
Let the length of the garden be x metres.
Let the breadth of the garden be y metres.
Perimeter of the rectangular garden = 2(x + y) metres.
\(\frac{2(x+y)}{2}\) = x + y
By the problem, x + y = 40 —- (1)
Since given length is 6 m more than its width.
∴ x = y + 6
⇒ x – y = 6 — (2)
Solving (1) and (2)

∴ x = \(\frac{46}{2}\) = 23
Substituting x = 23 in equation (1),
23 + y = 40
⇒ y = 40 – 23 = 17
∴ Lengthofthegarden = x = 23 m
Breadth of the garden = y = 17 m

Question 6.
The ratio of income of two persons is 8 : 5 and the ratio of their expenditure is 5 : 3. If each of them manages to save ₹ 2,000 per month find their monthly income.
Solution:
Let the income of the first person be ₹ 8x and that of the second person be ₹ 5x. And let the expenditure of the first person and second person be ₹ 5y and 3y respectively. Then saving of the first person = 8x – 5y
By the problem. 8x – 5y = 2,000 —- (1)
The saving of the second person = 5x – 3y
By the problem, 5x – 3y = 2,000 —- (2)
Solving equations (1) and (2)

x = 4,000
Substituting x = 4,000 in equation (1)
8 × 4,000 – 5y = 2,000
32,000 – 5y = 2,000
-5y = 2,000 – 32,000
-5y = -30,000
y = 6,000
∴ Monthly income of the first person = ₹ 8x
= ₹ 8x
= ₹ 8 × 4,000
= ₹ 32,000
and monthly income of the second person
= ₹ 5x
= ₹5 × 4,000
= ₹ 20,000

Question 7.
The sum of a two digit number and the number obtained by reversing the digit is 55. If the digits of the number differ by 3, find the number. How many such numbers are there ?
Solution:
Let the digit at units place be x.
and the digit at tens place be y.
The number will be yx

The value of the number = y × 10 + x + 1
= 10y + x
Number obtained by reversing the digits = xy
The value of the reversed number
= 10 × x + y + 1
= 10x + y
By the problem, we have
(10y + x) + (10x + y) = 55
⇒ 11x + 11y = 55 (Dividing by 11)
⇒ x + y = 5 — (1)
given that digits of the number differ by 3
so, x – y = 3 (or) y – x = 3 —- (2)
Solving (1) and (2)

Substitute x = 4 in equation (1), we get
4 + y = 5 ⇒y = 5 – 4 = 1
Substitute y = 4 in equation (1), we get
x + 4 = 5
x = 5 – 4 = 1
∴ The required numbers are 41 and 14.

Question 8.
The larger of two supplementary angles exceed the smaller by 28°. Find the angles.
Solution:
Two angles are said to be supplementary
⇒ sum of angles is 180°
Let the smaller supplementary angle be x°.
and the larger supplementary angle be y°.
We know that x + y = 180° —- (1)
The larger angle exceed the smaller by 28°
⇒ y = x + 28°
⇒ -x + y = 28° —- (2)
Solving equations (1) and (2)

Substitute y = 104° in (1)
x + 104° = 180°
x = 180 – 104° = 76°
∴ The required angles are 76° and 104°.

Question 9.
The taxi charges in Calcutta are fixed along with the charge for the distance covered. For a distance of 12 km, the charge paid ₹ 250. For a journey of 18 km, the charge paid ₹ 370.
i) What are the fixed charges and charge per km.
ii) How much does a person have to pay for travelling a distance of 35 km.
Solution:
Let the fixed charge be ₹ x.
i) and charge per km be ₹ y.
For a distance of 12 km, the charge paid is ₹ 250.
Then x + 12y = 250 —- (1)
For a distance of 18 km, the charge paid is ₹ 370.
Then x + 18y = 370 —– (2)
Solving equations (1) and (2)

Substitute y = 20 in equation (1)
x + 12 × 20 = 250
x + 240 = 250
x = 250 – 240 = 10
∴Fixed charge = ₹ 10
Change per km = ₹ 20

ii) Person has to pay for travelling a distance of 35 km = 20 × 35 = ₹ 700

Question 10.
A fraction becomes \(\frac{3}{4}\) if 1 is added to both numerator and denominator. If, however 5 is subtracted from both numerator and denominator, the fraction becomes \(\frac{1}{2}\) . What is the fraction ?
Solution:
Let the fraction be \(\frac{x}{y}\).
If 1 is added to both numerator and denominator then the fraction \(\frac{x+1}{y+1}\)
By problem \(\frac{x+1}{y+1}\) = \(\frac{3}{4}\)
⇒ 4(x + 1) = 3(y + 1)
⇒ 4x + 4 = 3y + 3
⇒ 4x – 3y = -1 ——- (1)
If 5 is subtracted from both numerator and denominator, then the fraction = \(\frac{x-5}{y-5}\)
By problem, \(\frac{x-5}{y-5}\) = \(\frac{1}{2}\)
⇒ 2(x – 5) = 1(y – 5)
⇒ 2x – 10 = y – 5
⇒ 2x – y = -5 + 10
2x – y = 5 ——– (2)
Solving equations (1) and (2)
4x – 3y = -1 —– (1)
2x – y = 5 —– (2)

x = \(\frac{16}{2}\) = 8
Substitute x = 8 in equation (1)
4 × 8 – 3y = -1
32 – 3y – = -1
-3y = -1 – 32 = -33
y = \(\frac{33}{3}\) = 11
∴ The required fraction is \(\frac{x}{y}\) = \(\frac{8}{11}\)

Question 11.
Solve each of the following pairs of equations by reducing them to a pair of linear equations.

i) \(\frac{4}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{8}{x-1}\) – \(\frac{1}{y-2}\) = -1
Solution:
Given \(\frac{4}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{8}{x-1}\) – \(\frac{1}{y-2}\) = -1
Put \(\frac{1}{x-1}\) = a and \(\frac{1}{y-2}\) = b
Then the given equations reduce to
4a + b = 2 —- (1)
and 8a – 3b = -1 —- (2)
Solving the above equations

Substitute value of a = \(\frac{1}{4}\) in equation (1)
4(\(\frac{1}{4}\)) + b = 2
1 + b = 2
b = 2 – 1 = 1 ⇒ b = 1
But a = \(\frac{1}{x-1}\) ⇒ \(\frac{1}{4}\) = \(\frac{1}{x-1}\)
⇒ x – 1 = 4 ⇒ x = 4 + 1 = 5
and b = \(\frac{1}{y-2}\) ⇒ 1 = \(\frac{1}{y-2}\)
⇒ y – 2 = 1 ⇒ y = 2 + 1 = 3
∴ Solution (x, y) = (5, 3)

ii) \(\frac{x+y}{x y}\) = 6 ; \(\frac{x-y}{x-y}\) = 2
Solution:
Given \(\frac{x+y}{x y}\) = 6 ⇒ \(\frac{x}{x y}\) + \(\frac{y}{x y}\) = 6
⇒ \(\frac{1}{y}\) + \(\frac{1}{x}\) = 6
and \(\frac{x-y}{x y}\) = 2 ⇒ \(\frac{x}{x y}\) – \(\frac{y}{x y}\) = 2
⇒ \(\frac{1}{y}\) – \(\frac{1}{x}\) = 2
take \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = b
Then the above equations reduces to
b + a = 6 ⇒ a + b = 6 —— (1)
b – a = 6 ⇒ -a + b = 2 —- (2)
Adding equations (1) and (2)

b = 4
Substitute b = 4 in equation (1)
a + 4 = 6
a = 6 – 4 = 2
But a = \(\frac{1}{x}\) ⇒ 2 = \(\frac{1}{x}\) ⇒ x = \(\frac{1}{2}\)
and b = \(\frac{1}{y}\) ⇒ 4 = \(\frac{1}{y}\) ⇒ y = \(\frac{1}{4}\)
∴ The solution (x, y) = (\(\frac{1}{2}\), \(\frac{1}{4}\) )

iii) \(\frac{3}{\sqrt{x}}\) + \(\frac{4}{\sqrt{y}}\) = 2; \(\frac{3}{\sqrt{x}}\) – \(\frac{12}{\sqrt{y}}\) = -2
Solution:
Take \(\frac{1}{\sqrt{x}}\) = a and \(\frac{1}{\sqrt{y}}\) = b
Then the above equations reduce to
3a + 4b = 2 —– (1)
3a – 12b = -2 —– (2)
Solving the above equations.

Substitute b = \(\frac{1}{4}\) in equation (1)
3a + 4(\(\frac{1}{4}\)) = 2
3a + 1 = 2
3a = 2 – 1
a = \(\frac{1}{3}\)

∴ Solution (x, y) = (9, 16)

iv) \(\frac{4}{x}\) + \(\frac{5}{y}\) = 32; \(\frac{6}{x}\) – \(\frac{5}{y}\) = -2
Solution:
Take \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = 6
Then the above equations reduces to
4a + 5b = 32 —- (1)
6a – 5b = -2 —- (2)
and Adding equations

Substitute a = 3 in equation (1)
4 × 3 + 5b = 32
12 + 5b = 32
5b = 32 – 12 = 20
b = \(\frac{20}{5}\) = 4
But a = \(\frac{1}{x}\) ⇒ 3 = \(\frac{1}{x}\) ⇒ x = \(\frac{1}{3}\)
b = \(\frac{1}{y}\) ⇒ 4 = \(\frac{1}{y}\) ⇒ y = \(\frac{1}{4}\)
∴ Solution (x, y) = (\(\frac{1}{3}\), \(\frac{1}{4}\))

vi) \(\frac{14}{x+y}\) + \(\frac{1}{x-y}\) = 3, \(\frac{21}{x+y}\) – \(\frac{2}{x-y}\) = 1
Solution:
Take \(\frac{1}{x+y}\) = a and \(\frac{1}{x-y}\) = b, then the above equation reduces to
14a + b = 3 —– (1)
21a – 2b = 1 —- (2)
Solving the above equations

Substitute b = \(\frac{1}{13}\) in equation (1)
28a + 39 × \(\frac{1}{13}\) = 7
28a + 3 = 7 ⇒ 28a = 7 – 3 = 4
a = \(\frac{4}{28}\) = \(\frac{1}{7}\)
But a = \(\frac{1}{x-y}\) ⇒ \(\frac{1}{7}\) = \(\frac{1}{x-y}\)
⇒ x – y = 7 —- (3)
and b = \(\frac{1}{x+y}\) ⇒ \(\frac{1}{13}\) = \(\frac{1}{x+y}\)
⇒ x + y = 13 —– (4)
Solving equations (3) and (4)

Substitute x = 10 in equation (3), 10 – y = 7
⇒ y = 3
∴ Speed of the boat in still water = x = 10 kmph
and speed of the stream = y = 3 kmph.

Question 12.
The height of a rectangular stockroom is 5m and perimeter of its floor is 50 m. Find the outer area of the four walls to be painted. (AP New SCERT Model Paper)
Solution:
Given,
Height of a rectangular stockroom (h) = S m
perimeter of its floor 2 (l + b) = 50 m
∴ Area of the four walls = 2h (l + b)
= 5 × 50
= 250 m²

Question 13.
Find whether the equations x² – 4x + 1.5 = 0 and 2x² + 3 = 8x are consistent or not. (AP New SCERT Model Paper)
Solution:
x² – 4x + 1.5 = 0 and 2x² – 8x + 3 = 0 consistent.
x² – 4x + 1.5 = 0
a₁ = 1; b₁ = -4; c₁ = 1.5
2x² – 8x + 3 = 0
a₂ = 2, b₂ = -8, c₂ = 3
Here \(\frac{a_1}{a_2}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-4}{-8}\) = \(\frac{1}{2}\); \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{1.5}{3}\) = \(\frac{1}{2}\)
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.

Question 14.
Solve the equations \(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4 and \(\frac{15}{x+y}\) + \(\frac{5}{x-y}\) = -2. (AP New SCERT Model Paper)
Solution:
Given, \(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4 and
\(\frac{15}{x+y}\) + \(\frac{5}{x-y}\) = -2.
Taking \(\frac{1}{x+y}\) = a, and \(\frac{1}{x-y}\) = b then the given equations reduce to
10a + 2b = 4 —– (1)
15a – 5b = -2 —– (2)

Substituting b = 1 in equation (1), we get 10a + 2(1) = 4
10a + 2(1) = 4
⇒ 10a = 4 – 2 = 2 ⇒ a = \(\frac{2}{10}\) = \(\frac{1}{5}\)
But a = \(\frac{1}{x+y}\) = \(\frac{1}{5}\) ⇒ x + y = 5 ——– (3)
b = \(\frac{1}{x-y}\) = 1 ⇒ x – y = 1 ——- (4)
Adding (3) and (4)

∴ x = \(\frac{6}{2}\) = 3
Substituting x = 3 in x + y = 5, we get 3 + y = 5 ⇒ y = 5 – 3 = 2
∴ The solution (x, y) = (3, 2)

Question 15.
The Coach of a cricket team buys 3 bats and 6 balls for ₹ 3,900. Later he buys another bat and two more balls of the same kind for ₹ 1,300. What is the cost price of each ? Solve the situation graphically. (AP New SCERT Model Paper)
Solution:
Let the cost of a bat = ₹ x
The cost of a bat = ₹ y
It is given that, the cost of 3 hats and 6 balls together is ₹ 3,900
⇒ 3x + 6y = 3,900
∴ x + 2y = 1,300 —– (1)
It is also given that the cost of a bat and 2 balls together is ₹ 1,300.
∴ x + 2y = 1,300 —- (2)
By the observations equation (1). equation (2) are dependent equation,
x + 2y = 1,300
2y = 1,300 – x
y = 1,300 – x
y = \(\frac{1,300-x}{2}\)