We are offering TS 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle to learn maths more effectively.
TS 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle
→ Secant: A line which intersects a circle in two distinct points is called a secant.
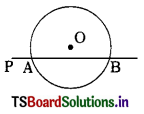
PAB is secant of the circle with centre ‘o’
→ Tangent: A tangent to a circle is a line that intersects the circle is exactly one point.

Tt is the tangent to the circle with centre ‘o’
- No tangent can be drawn to a circle from a point lying inside it.
- One and only one tangent can be drawn to a circle at a point on a circle.
- Two tangents can be drawn to a circle from a point lying outside it.
- The lengths of two tangents drawn from an external point to a circle are equal.
- A tangent to a circle is perpendicular to the radius drawn through the point of contact.
- A line drawn through the end point of a radius and perpendicular to it is a tangent to the circle.
- The common point of a tangent to a circle is called point of contact.
- The line containing the radius through the point of contact the normal to the circle at the point.
![]()
→ Sector: The portion of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.
OAPB is a sector of the circle with centre ‘O’
∠AOB is called the angle of the sector. OAPB is called the minor sector and OAQB is called the major sector.
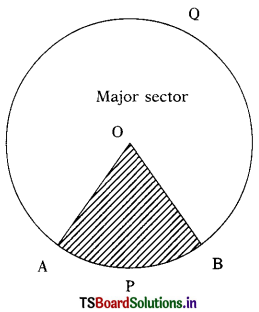
Area of the sector = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × πr2 where x° is the angle of the sector & ‘r’ is the radius.
Length of arc = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × 2πr
→ Segment: The chord AB divides the circle with centre ‘O’ into two parts. APB is called the minor segment where as AQB is called the major segment.
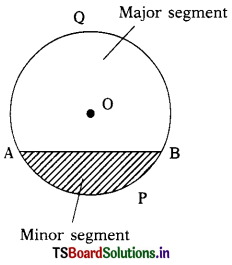
Area of the segment: Area of the segment APB = Area of the sector OAPB – Area of OAB.
Area of the major sector OAQB = Area of the circle – Area of the minor sector OAPB
Area of major segment of a circle = Area of the corresponding sector – Area of the corresponding triangle.
→ The locus of points which are joined by a curve and are equidistant from a fixed point is called a circle. The fixed point here is called the centre of the circle.
(Or)
A simple closed curve consisting of all points in a plane which are equidistant from a fixed point is called a circle. The fixed point is its centre and the fixed distance is its radius.
→ The path followed by circular object is a straight line.

→ The line segment joining any two points on a circle is called a ‘chord’. The longest of all chords of a circle passes through the centre and is called a diameter.
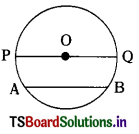
\(\overline{\mathrm{AB}}\) is a chord and \(\overline{\mathrm{PQ}}\) is a diameter. (PO and OQ is the radius of the circle.
Diameter = 2 × radius
d = 2r
r = \(\frac{r}{2}\)
→ There are three different possibilities for a given line and a circle.
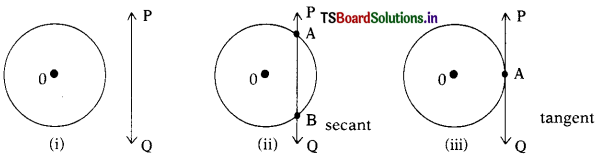
Case (i): The line PQ and the circle have no point in common (or) they do not touch each other.
Case (ii): The line PQ and the circle have two common points (or) a line which intersects a circle at two distinct points is called a “secant” of the circle.
The line PQ intersects the circle at two distinct points A and B. Here the line PQ is a “secant” of the circle.
Case (iii): The line PQ touches the circle at an unique point A(or) there is one and only one point common to both the line and circle.
Here \(\overleftrightarrow{\mathrm{PQ}}\) is called a tangent to the circle at ‘A’.
→ The word tangent is derived from the Latin word “TANGERE” which means “to touch” and was introduced by Danish mathematician “Thomas Fineke” in 1583.
→ There is only one tangent to the circle at one point.
→ The tangent at any point of a circle is perpendicular to the radius through the point of contact.
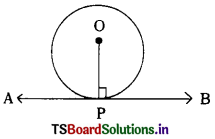
The radius OP is perpendicular to \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) at P. i.e., OP ⊥ AB.
→ Construction of a tangent to a circle :
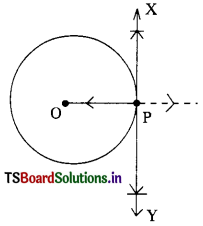
- Draw a circle with centre ‘O’.
- Draw a perpendicular line to OP through ‘P’.
- Let it be \(\stackrel{\leftrightarrow}{\mathrm{XY}}\).
- XY is the required tangent to the given circle passing through P.
![]()
→ Let ‘O’ be the centre of the given circle and \(\overline{\mathrm{AP}}\) is a tangent through a Where OA is the radius, then the length of the tangent AP = \(\sqrt{O P^2-\mathrm{OA}^2}\)

→ Two tangents can be drawn to a circle from an external point.
Important Formula:
- Area of Sector = \(\frac{\mathrm{X}^{\circ}}{360^{\circ}}\) × πr2
- Length of arc = \(\frac{\mathrm{X}^{\circ}}{360^{\circ}}\) × 2πr
- A line which intersects a circle In two distinct points Is called a secant.
- A tangent to a circle is a line that Intersects the circle Is exactly one point.
Flow Chat:
Archimedes (287 – 212 B.C):
- “Archimedes of Syracuse” was a Greek mathematician, physicist and engineer.
- He is regarded as one of the leading scientists in classical antiquity.
- He made several discoveries in the fields of mathematics particularly in geometry.