TS 10th Class Maths Important Questions Chapter 4 Pair of Linear Equations in Two Variables

These TS 10th Class Maths Chapter Wise Important Questions Chapter 4 Pair of Linear Equations in Two Variables given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 4 Pair of Linear Equations in Two Variables

Previous Exams Questions

Question 1.
Solve the following equations by substitution method (A.P.Jun.’15)

i) 2x – 7y = 3
ii) 4x + y = 21
Solution:
The given two linear equations are
2x – 7y = 3 —- (1)
4x + y = 21 — (2)
From the equation (2) we get y = 21 – 4x now we substitute this ‘Y’ value in equation (1)
We get
2x – 7(21 – 4x) = 3
⇒ 2x – 147 + 28x = 3
⇒ 30x = 147 + 3 = 150
then x = \(\frac{150}{30}\) = 5
∴ x = 5
Now put x = 5 in equation (2) we get
4(5) + y = 21
20 + y = 21
y = 21 – 20 = 1
So x = 5 and y = 1 are the solution of the system.

Question 2.
10 students of 10th class participated in a Quiz programme. The number of girls participated in it is 4 more than boys. So find the number of boys and girls participated in Quiz. (A.P. Mar. 16)
Solution:
Let the number of girls = x (say)
and the number of boys = y (say)
then total students = x + y = 10 ——- (1)
and also
The number of girls = number of boys + 4
x = y + 4 —— (2)
Put this ‘x’ value in equation (1), we get
y + 4 + y = 10
⇒ 2y + 4 = 10
⇒ 2y = 10 – 4 = 6
∴ y = \(\frac{6}{2}\) = 3
So y = 3 then
x + y = 10 becomes
x + 3 = 10 ⇒ x = 10 – 3
⇒ x = 7
So the number of girls = 7 and the number of boys = 3.

Question 3.
Solve the given pair of linear equations by elimination method.
i) 2x + y – 5 = 0 and
ii) 3x – 2y – 4 = 0. (A.P. Mar.’16)
Solution:
In this elimination method, we solve this pair of linear equation by making either of coefficients equal.
The given equations are
2x + y = 5 ——— (1)
3x – 2y = 4 —– (2)
To make the coefficients of ‘x’ equal let us multiply the equation (1) by 3 and the equation (2) by 2 on both sides.
We get
(2x + y = 5) × 3
(3x – 2y = 4) × 2

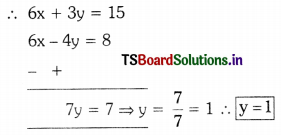
then 2x + y = 5 becomes
2x + 1 = 5 ⇒ 2x = 5 – 1 = 4
∴ x = \(\frac{4}{2}\) so x = 2
x = 2 and y = 1 are the solutions of the given equations.

Verification : Put x = 2 and y = 1 in equation (1) and (2)

2x + y = 5
2(2) + 1 = 5
4 + 1 = 5
5 = 5
LHS = RHS

3x – 2y – 4 = 0
3(2) – 2(1) = 4
6 – 2 = 4
4 = 4
LHS = RHS

Question 4.
For what value of k, the following system of equations has a unique solution, x – ky = 2; 3x + 2y = – 5 (T.S. Mar.15)
Solution:
a₁x + b₁y + c₁x = 0 and
a₂x + b₂y + c₂ = 0 will have a unique solution.
will have a unique solution.
If \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\) in the given system of equations
a₁ = 1,
b₁ = – k,
a₂ = 3,
b₂ = 2
So \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\) means
\(\frac{1}{3}\) ≠ \(\frac{-k}{2}\) ⇒ -k ≠ \(\frac{2}{3}\)
So the system of equations will have a unique solutions for k = R – (\(\frac{-2}{3}\))

Question 5.
For what value of m the following system of equations will have a unique solution. 3x + my = 10 and 9x + 12y = 30
(T.S.Mar. 16)
Solution:
We know that the system of equations
a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
will have unique solutions.
If \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\)
Here in the given system
a₁ = 3, b₁ = m and a₂ = 9, b₂ = 12
So \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\) becomes
\(\frac{3}{9}\) ≠ \(\frac{m}{12}\)
⇒ m ≠ \(\frac{12 \times 3}{9}\) = 4
So for m ≠ 4 the above system will have unique solution i.e., R – (4).

Question 6.
Solve the following pair of linear equations by substitution method,
i) 2x – 3y = 19 and 3x – 2y = 21 (T.S. Mar.’16)
Solution:
The given equations are
2x – 3y = 19 —– (1)
and 3x – 2y = 21 —– (2)
From the equation (1) 2x = 19 + 3y and x = \(\frac{19+3 y}{2}\)
Now substituting this value of
x = \(\frac{19+3 y}{2}\) in equation (2) we get
3x – 2y = 21 becomes
\(\frac{3(19+3 y)}{2}\) – 2(y) = 21
∴ 57 + 9y – 4y = 21 × 2
9y – 4y = 42 – 57
5y = – 15
∴ y = \(\frac{-15}{5}\) = -3
So y = – 3 Now put this y = – 3 value in
x = \(\frac{19+3 y}{2}\) we get
y = \(\frac{19+3(-3)}{2}\)
x = \(\frac{19-9}{2}\) = \(\frac{10}{2}\)
So x = 5 and y = – 3 are the solutions of given equations.

Verification :

2x – 3y = 19
2(5) – 3(- 3) = 19
10 + 9 = 19
19 = 19
LHS= RHS

3x – 2y = 21
3(5) – 2(-3) = 21
15 + 6 = 21
21 = 21
LHS = RHS

Additional Questions

Question 1.
By comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\), \(\frac{c_1}{c_2}\), find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or coincident.

a) 3x + 4y + 5 = 0; 2x – 3y + 6 = 0
b) 3x + 5y + 6 = 0; 9x + 15y + 18 = 0
c) 4x – 2y + 5 = 0; 2x – y + 6 = 0
Solution:
a) The given pair of linear equations are
3x + 4y + 5 = 0 ——- (1)
2x – 3y + 6 = 0 —— (2)
Comparing equations (1) and (2) with stan-dard equations i.e.,
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0, we get
a₁ = 2; b₁ = 3; c₁ = -5
a₂ = 3; b₂ = 4; c₂ = -6
Since \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)

b) 4x + 6y = 9 —– (1)
⇒ 4x + 6y – 9 = 0
⇒ 2x + 3y = 5 —— (2)
⇒ 2x + 3y – 5 = 0
Here, a₁ = 4; b₁ = 6; c₁ = -9
a₂ = 2; b₂ = 3; c₂ = -5
Since
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations will represent inconsistent.

c) 3x – 5y = 11 —– (1)
6x – 10y = 22 —- (2)
3x – 5y – 11 = 0
6x – 10y – 22 = 0
Here, a₁ = 3; b₁ = -5; c₁ = -11
a₂ = 6; b₂ = -10; c₂ = -22
\(\frac{a_1}{a_2}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-5}{-10}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-11}{-22}\) = \(\frac{1}{2}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given pair of linear equations are consistent.

Question 3.
15 students of Class – X took part in a science quiz. If the number of boys is 5 more than the number of girls then, find the number of boys and the number of girls who took part in the quiz.
Solution:
Let the number of boys who took part in the quiz = x
Let the number of girls who took part in the quiz = y
15 students took part in quiz
⇒ x + y = 15 —– (1)
Since the number of boys is 5 more than the number of girls, we have
x = y + 5
⇒ x – y = 5 —- (2)
⇒ x – y = 5
Adding (1) and (2)

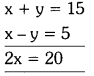
x = \(\frac{20}{2}\) = 10
Substitutes x = 10 in equation (1)
10 + y = 15 ⇒ y = 15 – 10 = 5
∴ The number of boys who took part in quiz = x = 10 and the number of girls who took part in quiz = y = 5

Question 4.
6 pencils and 9 pens together cost ₹ 96 whereas 9 pencils and 6 pens together cost ₹ 84. Find the cost of one pencil and that of one pen.
Solution:
Let the cost of one pencil = ₹ x
Cost of one pen = ₹ y
Total cost of 6 pencils and 9 pens = 6x + 9y
Total cost of 9 pencils and 6 pens = 9x + 6y
By the given problem, 6x + 9y = 96 —- (1)
9x + 6y = 84 —- (2)

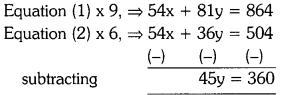
∴ y = \(\frac{360}{45}\) = 8
Substitute y = 8 in equation (1),
6x + 9(8) = 96
6x + 72 = 96 ⇒ 6x = 96 – 72 = 24
x = \(\frac{24}{6}\) = 4
∴ Cost of one pencil = ₹ 4
Cost of one pen = ₹ 8

Question 5.
Half of the perimeter of a rectangular! garden, whose length is 6 m more than its width is 40 m. Find the dimensions of the garden.
Solution:
Let the length of the garden be x metres.
Let the breadth of the garden be y metres.
Perimeter of the rectangular garden = 2(x + y) metres.
\(\frac{2(x+y)}{2}\) = x + y
By the problem, x + y = 40 —- (1)
Since given length is 6 m more than its width.
∴ x = y + 6
⇒ x – y = 6 — (2)
Solving (1) and (2)

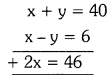
∴ x = \(\frac{46}{2}\) = 23
Substituting x = 23 in equation (1),
23 + y = 40
⇒ y = 40 – 23 = 17
∴ Lengthofthegarden = x = 23 m
Breadth of the garden = y = 17 m

Question 6.
The ratio of income of two persons is 8 : 5 and the ratio of their expenditure is 5 : 3. If each of them manages to save ₹ 2,000 per month find their monthly income.
Solution:
Let the income of the first person be ₹ 8x and that of the second person be ₹ 5x. And let the expenditure of the first person and second person be ₹ 5y and 3y respectively. Then saving of the first person = 8x – 5y
By the problem. 8x – 5y = 2,000 —- (1)
The saving of the second person = 5x – 3y
By the problem, 5x – 3y = 2,000 —- (2)
Solving equations (1) and (2)

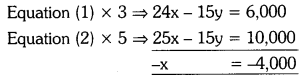
x = 4,000
Substituting x = 4,000 in equation (1)
8 × 4,000 – 5y = 2,000
32,000 – 5y = 2,000
-5y = 2,000 – 32,000
-5y = -30,000
y = 6,000
∴ Monthly income of the first person = ₹ 8x
= ₹ 8x
= ₹ 8 × 4,000
= ₹ 32,000
and monthly income of the second person
= ₹ 5x
= ₹5 × 4,000
= ₹ 20,000

Question 7.
The sum of a two digit number and the number obtained by reversing the digit is 55. If the digits of the number differ by 3, find the number. How many such numbers are there ?
Solution:
Let the digit at units place be x.
and the digit at tens place be y.
The number will be yx

The value of the number = y × 10 + x + 1
= 10y + x
Number obtained by reversing the digits = xy
The value of the reversed number
= 10 × x + y + 1
= 10x + y
By the problem, we have
(10y + x) + (10x + y) = 55
⇒ 11x + 11y = 55 (Dividing by 11)
⇒ x + y = 5 — (1)
given that digits of the number differ by 3
so, x – y = 3 (or) y – x = 3 —- (2)
Solving (1) and (2)

Substitute x = 4 in equation (1), we get
4 + y = 5 ⇒y = 5 – 4 = 1
Substitute y = 4 in equation (1), we get
x + 4 = 5
x = 5 – 4 = 1
∴ The required numbers are 41 and 14.

Question 8.
The larger of two supplementary angles exceed the smaller by 28°. Find the angles.
Solution:
Two angles are said to be supplementary
⇒ sum of angles is 180°
Let the smaller supplementary angle be x°.
and the larger supplementary angle be y°.
We know that x + y = 180° —- (1)
The larger angle exceed the smaller by 28°
⇒ y = x + 28°
⇒ -x + y = 28° —- (2)
Solving equations (1) and (2)

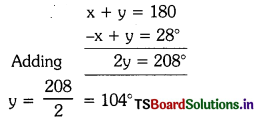
Substitute y = 104° in (1)
x + 104° = 180°
x = 180 – 104° = 76°
∴ The required angles are 76° and 104°.

Question 9.
The taxi charges in Calcutta are fixed along with the charge for the distance covered. For a distance of 12 km, the charge paid ₹ 250. For a journey of 18 km, the charge paid ₹ 370.
i) What are the fixed charges and charge per km.
ii) How much does a person have to pay for travelling a distance of 35 km.
Solution:
Let the fixed charge be ₹ x.
i) and charge per km be ₹ y.
For a distance of 12 km, the charge paid is ₹ 250.
Then x + 12y = 250 —- (1)
For a distance of 18 km, the charge paid is ₹ 370.
Then x + 18y = 370 —– (2)
Solving equations (1) and (2)

Substitute y = 20 in equation (1)
x + 12 × 20 = 250
x + 240 = 250
x = 250 – 240 = 10
∴Fixed charge = ₹ 10
Change per km = ₹ 20

ii) Person has to pay for travelling a distance of 35 km = 20 × 35 = ₹ 700

Question 10.
A fraction becomes \(\frac{3}{4}\) if 1 is added to both numerator and denominator. If, however 5 is subtracted from both numerator and denominator, the fraction becomes \(\frac{1}{2}\) . What is the fraction ?
Solution:
Let the fraction be \(\frac{x}{y}\).
If 1 is added to both numerator and denominator then the fraction \(\frac{x+1}{y+1}\)
By problem \(\frac{x+1}{y+1}\) = \(\frac{3}{4}\)
⇒ 4(x + 1) = 3(y + 1)
⇒ 4x + 4 = 3y + 3
⇒ 4x – 3y = -1 ——- (1)
If 5 is subtracted from both numerator and denominator, then the fraction = \(\frac{x-5}{y-5}\)
By problem, \(\frac{x-5}{y-5}\) = \(\frac{1}{2}\)
⇒ 2(x – 5) = 1(y – 5)
⇒ 2x – 10 = y – 5
⇒ 2x – y = -5 + 10
2x – y = 5 ——– (2)
Solving equations (1) and (2)
4x – 3y = -1 —– (1)
2x – y = 5 —– (2)

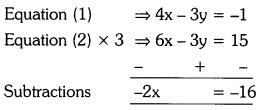
x = \(\frac{16}{2}\) = 8
Substitute x = 8 in equation (1)
4 × 8 – 3y = -1
32 – 3y – = -1
-3y = -1 – 32 = -33
y = \(\frac{33}{3}\) = 11
∴ The required fraction is \(\frac{x}{y}\) = \(\frac{8}{11}\)

Question 11.
Solve each of the following pairs of equations by reducing them to a pair of linear equations.

i) \(\frac{4}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{8}{x-1}\) – \(\frac{1}{y-2}\) = -1
Solution:
Given \(\frac{4}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{8}{x-1}\) – \(\frac{1}{y-2}\) = -1
Put \(\frac{1}{x-1}\) = a and \(\frac{1}{y-2}\) = b
Then the given equations reduce to
4a + b = 2 —- (1)
and 8a – 3b = -1 —- (2)
Solving the above equations

Substitute value of a = \(\frac{1}{4}\) in equation (1)
4(\(\frac{1}{4}\)) + b = 2
1 + b = 2
b = 2 – 1 = 1 ⇒ b = 1
But a = \(\frac{1}{x-1}\) ⇒ \(\frac{1}{4}\) = \(\frac{1}{x-1}\)
⇒ x – 1 = 4 ⇒ x = 4 + 1 = 5
and b = \(\frac{1}{y-2}\) ⇒ 1 = \(\frac{1}{y-2}\)
⇒ y – 2 = 1 ⇒ y = 2 + 1 = 3
∴ Solution (x, y) = (5, 3)

ii) \(\frac{x+y}{x y}\) = 6 ; \(\frac{x-y}{x-y}\) = 2
Solution:
Given \(\frac{x+y}{x y}\) = 6 ⇒ \(\frac{x}{x y}\) + \(\frac{y}{x y}\) = 6
⇒ \(\frac{1}{y}\) + \(\frac{1}{x}\) = 6
and \(\frac{x-y}{x y}\) = 2 ⇒ \(\frac{x}{x y}\) – \(\frac{y}{x y}\) = 2
⇒ \(\frac{1}{y}\) – \(\frac{1}{x}\) = 2
take \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = b
Then the above equations reduces to
b + a = 6 ⇒ a + b = 6 —— (1)
b – a = 6 ⇒ -a + b = 2 —- (2)
Adding equations (1) and (2)

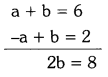
b = 4
Substitute b = 4 in equation (1)
a + 4 = 6
a = 6 – 4 = 2
But a = \(\frac{1}{x}\) ⇒ 2 = \(\frac{1}{x}\) ⇒ x = \(\frac{1}{2}\)
and b = \(\frac{1}{y}\) ⇒ 4 = \(\frac{1}{y}\) ⇒ y = \(\frac{1}{4}\)
∴ The solution (x, y) = (\(\frac{1}{2}\), \(\frac{1}{4}\) )

iii) \(\frac{3}{\sqrt{x}}\) + \(\frac{4}{\sqrt{y}}\) = 2; \(\frac{3}{\sqrt{x}}\) – \(\frac{12}{\sqrt{y}}\) = -2
Solution:
Take \(\frac{1}{\sqrt{x}}\) = a and \(\frac{1}{\sqrt{y}}\) = b
Then the above equations reduce to
3a + 4b = 2 —– (1)
3a – 12b = -2 —– (2)
Solving the above equations.

Substitute b = \(\frac{1}{4}\) in equation (1)
3a + 4(\(\frac{1}{4}\)) = 2
3a + 1 = 2
3a = 2 – 1
a = \(\frac{1}{3}\)

∴ Solution (x, y) = (9, 16)

iv) \(\frac{4}{x}\) + \(\frac{5}{y}\) = 32; \(\frac{6}{x}\) – \(\frac{5}{y}\) = -2
Solution:
Take \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = 6
Then the above equations reduces to
4a + 5b = 32 —- (1)
6a – 5b = -2 —- (2)
and Adding equations

Substitute a = 3 in equation (1)
4 × 3 + 5b = 32
12 + 5b = 32
5b = 32 – 12 = 20
b = \(\frac{20}{5}\) = 4
But a = \(\frac{1}{x}\) ⇒ 3 = \(\frac{1}{x}\) ⇒ x = \(\frac{1}{3}\)
b = \(\frac{1}{y}\) ⇒ 4 = \(\frac{1}{y}\) ⇒ y = \(\frac{1}{4}\)
∴ Solution (x, y) = (\(\frac{1}{3}\), \(\frac{1}{4}\))

vi) \(\frac{14}{x+y}\) + \(\frac{1}{x-y}\) = 3, \(\frac{21}{x+y}\) – \(\frac{2}{x-y}\) = 1
Solution:
Take \(\frac{1}{x+y}\) = a and \(\frac{1}{x-y}\) = b, then the above equation reduces to
14a + b = 3 —– (1)
21a – 2b = 1 —- (2)
Solving the above equations

Substitute b = \(\frac{1}{13}\) in equation (1)
28a + 39 × \(\frac{1}{13}\) = 7
28a + 3 = 7 ⇒ 28a = 7 – 3 = 4
a = \(\frac{4}{28}\) = \(\frac{1}{7}\)
But a = \(\frac{1}{x-y}\) ⇒ \(\frac{1}{7}\) = \(\frac{1}{x-y}\)
⇒ x – y = 7 —- (3)
and b = \(\frac{1}{x+y}\) ⇒ \(\frac{1}{13}\) = \(\frac{1}{x+y}\)
⇒ x + y = 13 —– (4)
Solving equations (3) and (4)

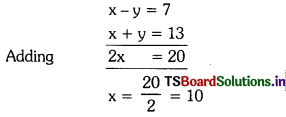
Substitute x = 10 in equation (3), 10 – y = 7
⇒ y = 3
∴ Speed of the boat in still water = x = 10 kmph
and speed of the stream = y = 3 kmph.

Question 12.
The height of a rectangular stockroom is 5m and perimeter of its floor is 50 m. Find the outer area of the four walls to be painted. (AP New SCERT Model Paper)
Solution:
Given,
Height of a rectangular stockroom (h) = S m
perimeter of its floor 2 (l + b) = 50 m
∴ Area of the four walls = 2h (l + b)
= 5 × 50
= 250 m²

Question 13.
Find whether the equations x² – 4x + 1.5 = 0 and 2x² + 3 = 8x are consistent or not. (AP New SCERT Model Paper)
Solution:
x² – 4x + 1.5 = 0 and 2x² – 8x + 3 = 0 consistent.
x² – 4x + 1.5 = 0
a₁ = 1; b₁ = -4; c₁ = 1.5
2x² – 8x + 3 = 0
a₂ = 2, b₂ = -8, c₂ = 3
Here \(\frac{a_1}{a_2}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-4}{-8}\) = \(\frac{1}{2}\); \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{1.5}{3}\) = \(\frac{1}{2}\)
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.

Question 14.
Solve the equations \(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4 and \(\frac{15}{x+y}\) + \(\frac{5}{x-y}\) = -2. (AP New SCERT Model Paper)
Solution:
Given, \(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4 and
\(\frac{15}{x+y}\) + \(\frac{5}{x-y}\) = -2.
Taking \(\frac{1}{x+y}\) = a, and \(\frac{1}{x-y}\) = b then the given equations reduce to
10a + 2b = 4 —– (1)
15a – 5b = -2 —– (2)

Substituting b = 1 in equation (1), we get 10a + 2(1) = 4
10a + 2(1) = 4
⇒ 10a = 4 – 2 = 2 ⇒ a = \(\frac{2}{10}\) = \(\frac{1}{5}\)
But a = \(\frac{1}{x+y}\) = \(\frac{1}{5}\) ⇒ x + y = 5 ——– (3)
b = \(\frac{1}{x-y}\) = 1 ⇒ x – y = 1 ——- (4)
Adding (3) and (4)

∴ x = \(\frac{6}{2}\) = 3
Substituting x = 3 in x + y = 5, we get 3 + y = 5 ⇒ y = 5 – 3 = 2
∴ The solution (x, y) = (3, 2)

Question 15.
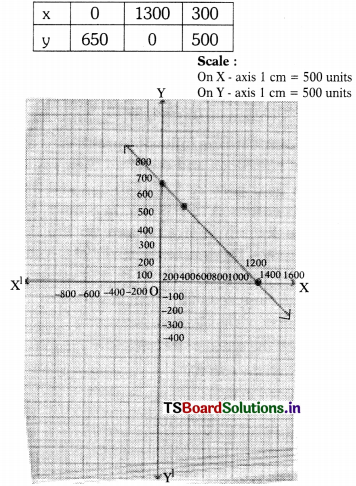
The Coach of a cricket team buys 3 bats and 6 balls for ₹ 3,900. Later he buys another bat and two more balls of the same kind for ₹ 1,300. What is the cost price of each ? Solve the situation graphically. (AP New SCERT Model Paper)
Solution:
Let the cost of a bat = ₹ x
The cost of a bat = ₹ y
It is given that, the cost of 3 hats and 6 balls together is ₹ 3,900
⇒ 3x + 6y = 3,900
∴ x + 2y = 1,300 —– (1)
It is also given that the cost of a bat and 2 balls together is ₹ 1,300.
∴ x + 2y = 1,300 —- (2)
By the observations equation (1). equation (2) are dependent equation,
x + 2y = 1,300
2y = 1,300 – x
y = 1,300 – x
y = \(\frac{1,300-x}{2}\)