TS 10th Class Maths Notes Chapter 7 Coordinate Geometry

by

We are offering TS 10th Class Maths Notes Chapter 7 Coordinate Geometry to learn maths more effectively.

TS 10th Class Maths Notes Chapter 7 Coordinate Geometry

→ A French mathematician Rene Descartes (1596 – 1650) has developed the study of Co-ordinate Geometry.

→ The cartesian plane is also called co-ordinate plane or xy plane.

→ The X-co-ordinate is called the Abscissa and the y-co-ordinate is called the ordinate.

→ The intersection of x-axis and y-axis is called the origin. The co-ordinates of origin = 0 (0, 0).

→ Area of Rhombus = \(\frac{1}{2}\) × product of its diagonals.

→ Area of a triangle = \(\frac{1}{2}\) × base × height.

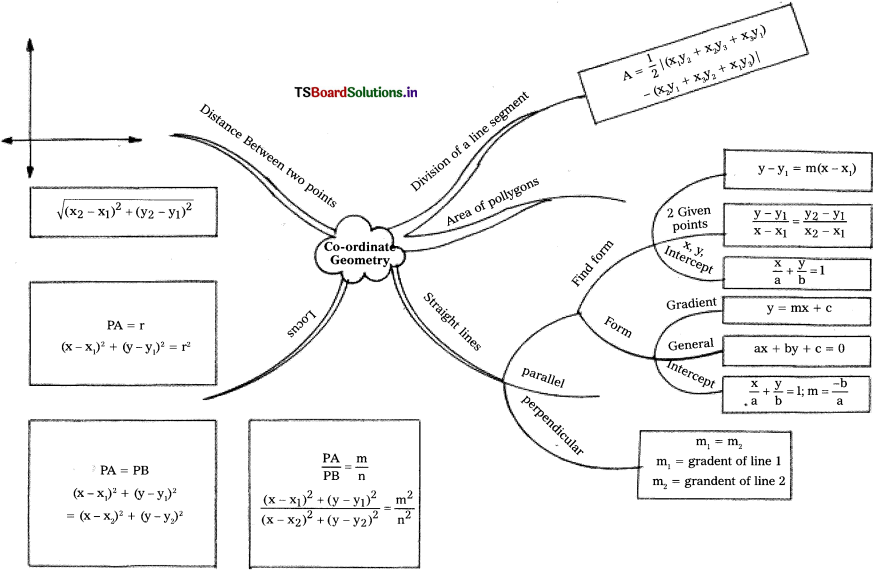
→ The distance between two points P(x1, y1) and Q(x2, y2) is \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

→ The distance of a point (x, y) from the origin is \(\)

→ The distance between two points (x1, y1) and (x2, y2) on a line parallel to Y – axis is |y2 – y1|.

→ The distance between two points (x1, y1) and (x2, y2) on a line parallel to X-axis is |x2 – x1|.

→ The co-ordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) internally in the ratio m1 : m2 are
\(\left[\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right]\)

TS 10th Class Maths Notes Chapter 7 Coordinate Geometry

→ The midpoint of the line segment joining the points P(x1, y1) and Q(x2, y2) is
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

→ The point of intersection of the medians of a triangle is called the centroid. It is usually denoted by G. it divides each median in the ratio 2 :1.

→ The vertices of ΔABC are A(x1, y1), B(x2, y2) and C(x3, y3), then the co-ordinates of the centroid of the ΔABC is \(\left[\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right]\)

→ The area of the triangle formed by the points (x1, y1) (x2, y2) and (x3, y3) is the numerical value of the expression
\(\frac{1}{2}\)|x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|.

→ Area of a triangle formula or Heron’s Formula A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
S = \(\frac{a+b+c}{2}\)

→ Slope of the line (m) = \(\frac{y_2-y_1}{x_2-x_1}\)

Important Formula:

  • AB = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
  • Point (x, y) form the origin is \(\sqrt{x^2+y^2}\)
  • Mid Point = \(\left[\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right]\)
  • Centroid = \(\left[\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right]\)
  • Area = \(\frac{1}{2}\)|x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|.
  • Heron’s Formula A = \(\sqrt{S(S-a)(S-b)(S-c)}\)
  • S = \(\frac{a+b+c}{2}\)
  • Slope m = \(\frac{y_2-y_1}{x_2-x_1}\)

Flow Chat:
TS 10th Class Maths Notes Chapter 7 Coordinate Geometry 1

TS 10th Class Maths Notes Chapter 7 Coordinate Geometry

Rene Descartes (1596 – 1650):

  • Rene Descartes was a French Mathematician.
  • Rene Descartes is a Father of Modern Mathematics.
  • The Cartesian co-ordinate system – allowing reference to a point in space as a set of numbers, and allowing algebraic equations to be expressed as geometric shapes in a two – dimensional co-ordinate system was named after him.
  • Descartes theory provided the basis for the calculus of Newton and Leibnitz.

Leave a Comment