TS 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables

We are offering TS 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables to learn maths more effectively.

TS 10th Class Maths Notes Chapter 4 Pair of Linear Equations in Two Variables

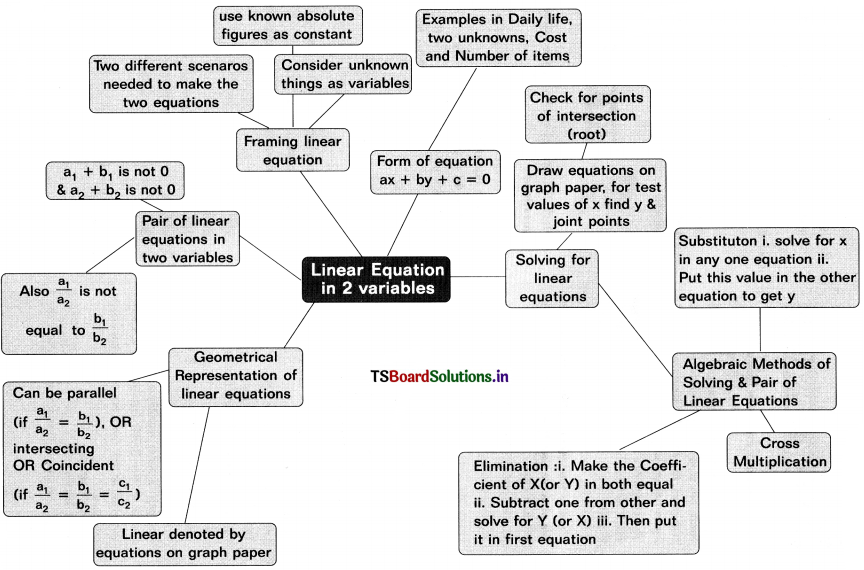
→ An Equation of the form ax + by + c = 0, where a, b, c e R and a and b are not both zero, is called a linear equation in two variables x and y.

→ A pair of linear equations in two variables x and y can be represented as follows :
a₁x + b₁y + C₁ = 0
a₂x + b₂y + c₂ = 0
Where a₁, a₂, b₁, b₂, c₁, c₂ are real numbers such that a₁² + b₁² ≠ 0; a₂² + b₂² ≠ 0.

→ A pair of linear Equations in two variables forms a system of simultaneous linear equations.
Example : 3x – 4y = 2
2x + 5y = 9

→ A pair of values of the variables x and y satisfying each one of the equations that are given is called a solution of the system.
x = 2, y = 1 is a solution of the system of simultaneous linear equations.
3x-4y = 2 …………… (1)
2x + 5y = 9 …………… (2)
Putting x = 2 and y = 1 in equation (1), we get
L.H.S. = 3 × 2 – 4 × 1 = 6 – 4 = 2
R.H.S = 2
L.H.S = R.H.S
Similarly, put x = 2 and y = 1 in equation (2), we get
L.H.S = 2 × 2 + 5 × 1 = 4 + 5 = 9
R.H.S = 9
∴ L.H.S = R.H.S

→ A pair of linear equations in two variables can be solved using

• Graphical method
• Model method
• Algebraic method :
  (a) Substitution method
  (b) Elimination method
  (c) Cross-Multiplication method

→ Graphical method: The graph of a pair of linear equations in two variables is represented by two straight lines.

• If the lines intersect at a point, then that point gives the unique solution of the two equations. In this case, the pair of equations is consistent.
• If the lines coincide, then there are infinitely many solutions – each point on the line being a solution. In this case, the pair of equations is dependent (consistent).
• If the lines are parallel, then the pair of equations has no solution.
  In this case, the pair of equations is inconsistent.

→ The relation that exists between the coefficients and nature of system of equations.

→ If a pair of linear equations is given by a₁x + b₂y + c₂ = 0 and a₂x + b₂y + c₂ = 0, then

• The pair of linear equations is consistent if \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
• The pair of linear equation is inconsistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
• The pair of linear equation is dependent and consistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Important Formulas:

• The pair of linear equations is consistent if \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
• The pair of linear equation is inconsistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
• The pair of linear equation is dependent and consistent if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Flow Chat:

William George Horner(1786 – 1832):

• A William George Horner was a British mathematician; he was a schoolmaster; headmaster and schoolkeeper, proficient in classics as well as mathematics.
• A He wrote extensively on functional equations, number theory and approximation theory.
• A His contribution to approximation theory is honoured in the designation Horner’s method. The modern invention of the zoetrope, under the name Daedaleum in 1834 has been attributed to him.