TS 10th Class Maths Notes Chapter 5 Quadratic Equations

We are offering TS 10th Class Maths Notes Chapter 5 Quadratic Equations to learn maths more effectively.

TS 10th Class Maths Notes Chapter 5 Quadratic Equations

→ The general form of a linear equation in one variable is ax + b = c.

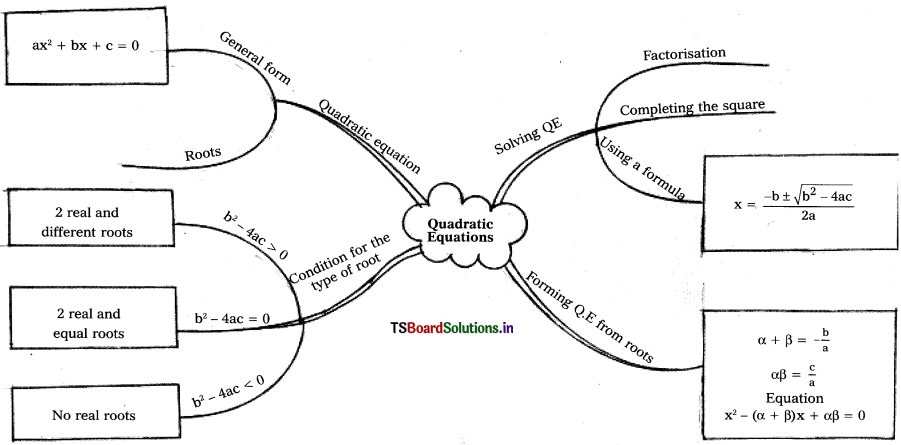
→ Any equation of the form p(x) = 0 where p(x) is a polynomial of degree 2, is a quadratic equation.

→ If p(x) = 0 whose degree is 2 is written in descending order of their degrees, then we say that the quadratic equation is written in the standard form.

→ The standard form of a quadratic equation is ax² + bx + c = 0 where a ≠ 0. We can write it as y = ax² + bx + c.

→ There are various occasions in which we make use of Q.E. in our day-to-day life.
Eg : The height of a rocket is defined by a Q.E.

→ Let ax² + bx + c = be a quadratic equation. A real number a is called a root of the Q.E. if aα² + bα + c = 0. And x = a is called a solution of the Q.E. (i.e.) the real value of x for which the Q.E ax² + bx + c = 0 is satisfied is called its solution.

→ Zeroes of the Q.E. ax² + bx + c = 0 and the roots of the Q.E. ax² + bx + c = 0 are the same.

→ To factorise a Q.E. ax² + bx + c = 0, we find p, q ∈ R such that p + q = b and pq = ac.
This process is called Factorising a Q.E. by splitting its middle term.
Eg : 12x² + 13x + 3 = 0
here a = 12; b = 13; c = 3
a.c = 12 × 3 = 36
b = 4 + 9 where 4 × 9 = 36
Now 12x² + 9x + 4x +3 = 0
⇒ 12x² + 9x + 4x + 3 = 0
⇒ 3x(4x + 3) + 1 (4x + 3) = 0
⇒ (4x + 3) (3x + 1) = 0
Here 4x + 3 = 0 or 3x + 1 = 0
⇒ 4x = -3 or 3x = -1
⇒ x = \(\frac{-3}{4}\) or x = \(\frac{-1}{3}\)

\(\frac{-3}{4}\) and \(\frac{-1}{3}\) are called the roots of the Q.E. 12x² + 13x + 3 = 0 and x = \(\frac{-3}{4}\) or \(\frac{-1}{3}\) is the solution of the Q.E 12x² + 13x + 3 = 0.

→ In the above example, (4x + 3) and (3x + 1) are called the linear factors of the Q.E. 12x² + 13x + 3 = 0

→ We can factorise a Q.E. by adjusting its left side so that it becomes a perfect square.
Eg : x² + 6x + 8 = 0 ⇒ x² + 2. x. 3 + 8 = 0 ⇒ x² + 2.x.3 = -8
The L.H.S. is of the form a2 + 2ab
∴ By adding b² it becomes a perfect square
∴ x² + 2.x.3 + 3² = -8 + 3²
⇒ (x + 3)² = -8 + 9
⇒ (x + 3)² = 1
⇒ x + 3 = ±1
Now we take x + 3 = 1 or x + 3=-1
⇒ x = -2 or x = -4

→ Adjusting a Q.E. of the form ax² + bx + c = 0 so that it becomes a perfect square.
Step -1: ax² + bx + c = 0 ⇒ ax² + bx = -c
⇒ x² + \(\frac{b}{a}\)x = \(\frac{-c}{a}\)

Step – 2: x² + \(\frac{\mathrm{bx}}{\mathrm{a}}+\left[\frac{1}{2}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\right]^2=\frac{-\mathrm{c}}{\mathrm{a}}+\left[\frac{1}{2}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\right]^2\)

Step – 3: \(\left(x+\frac{b}{2 a}\right)^2=\frac{b^2-4 a c}{4 a^2}\)

Step – 4: Solve the above
Eg: 5x² – 6x + 2 = 0 ⇒ x² – \(\frac{6 x}{5}=\frac{-2}{5}\)

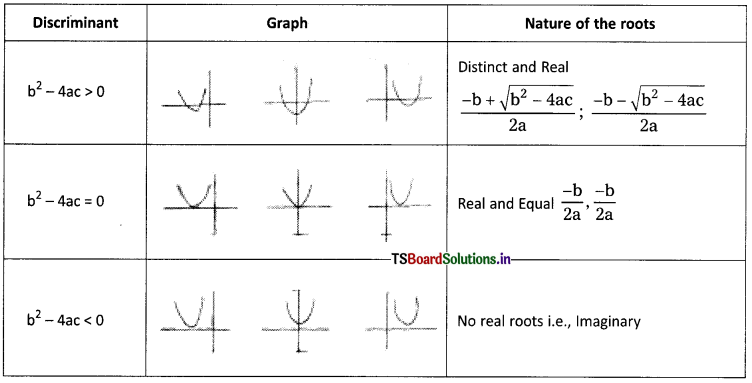
→ Let ax² + bx + c = 0 (a ≠ 0) be a Q.E., then b² – 4ac is called the Discriminant of the Q.E.

→ If b² – 4ac > 0, then the roots of the Q.E. ax² + bx + c = 0 are given by
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\). This is called quadratic formula to find the roots

→ The nature of the roots of a Q.E. can be determined either by its discriminant or its graph.
Q.E.: y = ax² + bx + c.

Important Formulas:

• Quadratic Formula for find the roots x = \(\frac{-b – \sqrt{b^2-4 a c}}{2 a}\)
• Sum of the roots α + β = \(\frac{-b}{a}\)
• Product of the roots αβ = \(\frac{c}{a}\)
• Discriminant = b² – 4ac
• If b² – 4ac > 0 then the roots are real and distinct.
• If b² – 4ac = 0 the roots are real and equal.
• If b² – 4ac < 0 then the roots are not real.

Flow Chat:

Al – Khwarizmi (780 – 850):

• Muhammad ibn Musa al-Khwarizmi was a Persian mathematician, astronomer, astrologer and geographer, it He was born around 780 A.D. in Khwarizmi (now Khiva, Uzbekishtan) and died around 850.
• He worked most of his life as a scholar in the House of Wisdom in Baghdad, it His ‘Algebra’ was the first book on the systematic solutions of linear and quadratic equations.