Srinivas

Students must practice these TS Inter 1st Year Maths 1A Study Material Chapter 6 Trigonometric Ratios upto Transformations Ex 6(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(a)

I.
Question 1.
Convert the following into simplest form
(i) tan (θ – 14π)
Answer:
tan (θ – 14π) = tan [- (14π – θ)]
= – tan (14π – θ)
= – tan [ 2(7π) – θ)
= – tan (-θ) = tan θ

(ii) cot (\(\frac{21 \pi}{2}\) – θ)
Answer:
cot (\(\frac{21 \pi}{2}\) – θ) = cot[10π + (\(\frac{\pi}{2}\) – θ)]
= cot (\(\frac{\pi}{2}\) – θ) = tan θ

(iii) cosec (5π + θ)
Answer:
cosec (5π + θ) = cosec [4π + (π + θ)]
= cosec(π + θ) = – cosec θ

(iv) sec (4π – θ)
Answer:
sec (4π – θ) = sec [2(2π) – θ]
= sec (- θ) = sec θ

Question 2.
Find the values of each of the following
(i) sin (-405°)
Answer:
sin (-405°) = -sin 405° = -sin (360°+45°)
= – sin 45° = \(-\frac{1}{\sqrt{2}}\)

(ii) cos \(\left(-\frac{7 \pi}{2}\right)\)
Answer:
cos \(\left(-\frac{7 \pi}{2}\right)\) = cos \(\frac{7 \pi}{2}\) = cos (630°)
= cos (360 + 270°) = cos 270°
= cos (180 + 90) = -cos 90 = 0
(or) cos \(\left(-\frac{7 \pi}{2}\right)\) = 0 (∵ cos(2n + 1)\(\frac{\pi}{2}\) = 0)

(iii) sec (2100°)
Sol. sec (2100°) = sec [5 × 360° + 300°]
= sec 300° = sec (360° – 60°)
= sec 60° = 2

(iv) cot (-315°)
Answer:
cot (-315°) = – cot 315° = – cot (270 + 45°)
= cot 45° = 1

Question 3.
Evaluate
(i) cos² 45° + cos² 135° + cos² 225° + cos² 315°
Answer:
cos 45° = \(\frac{1}{\sqrt{2}}\), cos 135° = cos (180 – 45°)
= – cos 45° = \(-\frac{1}{\sqrt{2}}\)

cos 225° = cos (180 + 45°)
= – cos 45° = –\(\frac{1}{\sqrt{2}}\)

cos 315° = cos(360 – 45°)
= cos 45° = \(\frac{1}{\sqrt{2}}\)

∴ cos² 45° + cos² 135° + cos² 225° + cos² 315°
= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}\) = 2

(ii) sin²\(\frac{2 \pi}{3}\) + cos²\(\frac{5 \pi}{6}\) – tan²\(\frac{3 \pi}{4}\)
Answer:

(iii) cos 225° – sin 225° + tan 495° – cot 495°
Answer:
cot (180 + 45) – sIn (180 + 45) + tan (360 + 135) – cot (360 + 135)
= – cot 45° + sin 45° + tan 135 – cot 135°
= – cos 45° + sin 45° +tan(180 – 45) – cot(180 – 45)
= – cos 45° + sin 45° – tan 45° + cot 45°
= \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) – 1 + 1 = 0

(iv) (cos θ – sin θ) if
(a) θ = \(\frac{7 \pi}{4}\)
(b) θ = \(\frac{11 \pi}{4}\)
Answer:

Question 4.
(i) If sin θ = –\(\frac{1}{3}\) and 0 does not lie in the third 3 quadrant, find the values of (a) cos θ and (b) cot θ. (March 2013)
Answer:
sin θ = –\(\frac{1}{3}\) and sin θ is negative and does not lie in third quadrant,
⇒ θ lies in fourth quadrant. In IVth quadrant cos θ is positive and cot θ is negative.
a) cos θ = \(\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{1}{9}}=\frac{2 \sqrt{2}}{3}\)
b) cot θ = \(\frac{\cos \theta}{\sin \theta}\) = -2√2

(ii) If cos θ = t (0 < t < 1) and θ does not lie in the first quadrant, find the values of a) sin θ b) tan θ
Answer:
cos θ = t, (0 < t < 1)
⇒ cos θ is positive and 0 does not lie in first quadrant
⇒ θ lies in IVth quadrant
a) sin θ = \(-\sqrt{1-\cos ^2 \theta}=-\sqrt{1-t^2}\)
b) tan θ = \(\frac{\sin \theta}{\cos \theta}=-\frac{\sqrt{1-t^2}}{t}\)

(iii) Find the value of sin 330°. cos 120° + cos 210°. sin 300°
Answer:
sin 330° cos 120° + cos 210° sin 300°
= sin (360 – 30) cos (180 – 60) + cos ( 180 + 30) sin (360 – 60)
= (-sin 30°) (-cos 60°) + (-cos 30°) (- sin 60°)
= sin 30 cos 60 + cos 30 sin 60 = sin (30 + 60)
= sin 90° = 1

(iv) If cosec θ + cot θ = \(\frac{1}{3}\), find cos θ and determine the quadrant in which θ lies.
Answer:
we have coses²θ – cot² θ = 1
⇒ (cosec θ + cot θ) (cosec θ – cot θ) = 1

∴ sin θ is positive and cos θ is negative,
⇒ θ lies in IInd quadrant.

Question 5.
(i) If sin α + cosec α= 2, find the value of sinⁿ α + cosecⁿ α; n ∈ Z.
Answer:
Given sin α + cosec α = 2
Squaring both sides
sin² α = cosec² α + 2 = 4
⇒ sin α + cosec α = 2
cubing on both sides
sin³ α + cosec³ α + 3 sin α cosec α (sin α + cosec α) = 8
sin³ α + cosec³ α + 3 (2) = 8
⇒ sin³ α + cosec³ α = 2
In the same way sinⁿ α + cosecⁿ α = 2 (n ∈ z)

(ii) If sec θ + tan θ = 5, find the quadrant in which θ lies and find the value of sin θ
Answer:
We have sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
Also given sec θ + tan θ = 5 ………….(2)

Adding (1) and (2)

tan θ is +ve, sec θ is + ve
⇒ θ lies is first quadrant.

II.
Question 1.
Prove that
(i) \(\frac{\cos (\pi-A) \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left(\frac{3 \pi}{2}+A\right) \sin (2 \pi-A)}\) = cos A
Answer:

(ii) \(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\)
Answer:

(iii) sin 780°. sin 480° + cos 240°. cos 300° = \(\frac{1}{2}\)
Answer:
sin [2 × 360 + 60] sin [360 + 120] + cos [180 + 60] cos [360-60]
= sin 60 sin 120 – cos 60 cos 60
= sin 60 sin 60 – cos 60. cos 60
= \(\frac{\sqrt{3}}{2} \frac{\sqrt{3}}{2}-\frac{1}{2} \cdot \frac{1}{2}=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}\)

(iv) \(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\) = -2
Answer:

(v) cot\(\left(\frac{\pi}{20}\right)\). cot\(\left(\frac{3 \pi}{20}\right)\). cot\(\left(\frac{5 \pi}{20}\right)\). cot\(\left(\frac{7 \pi}{20}\right)\). cot\(\left(\frac{9 \pi}{20}\right)\) = 1
Answer:
cot\(\left(\frac{\pi}{20}\right)\). cot\(\left(\frac{3 \pi}{20}\right)\). cot\(\left(\frac{5 \pi}{20}\right)\). cot\(\left(\frac{7 \pi}{20}\right)\). cot\(\left(\frac{9 \pi}{20}\right)\)
= cot 9°. cot 27°. cot 45°. cot 63°. cot 81°
= cot 9°. cot 27°. 1.cot (90 – 27) . cot (90 -9)
= cot 9°. cot 27°. 1. tan 27°. tan 9°
= 1

Question 2.
(i) Simplify \(\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}\)
Answer:

(ii) If tan 20 ° = p, prove that
\(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}\)
Answer:
Given that tan 20° = p then

(iii) If α, β are complementary angles such that b sin α = a, then find the value of (sin α cos β – cos α sin β)
Answer:
Given α, β are complementary angles α + β = 90°
⇒ β = 90° – α
∴ sin α cos β – cos α sin β
= sin (α – β)
= sin[α – (90 – α)]
= sin [2α – 90°]
= -sin[90 – 2α]
= -cos 2α
= -(1 – 2sin²α) = -1 + 2sin²α
= -1 + 2\(\left(\frac{a^2}{b^2}\right)\)
= \(\frac{2 a^2-b^2}{b^2}\)

Question 3.
(i) If cos A = cos B = – \(\frac{1}{2}\), A does not lie in the second quadrant and B does not lie in third quadrant, then find the value of \(\frac{4 \sin B-3 \tan A}{\tan B+\sin A}\)
Answer:
cos A = –\(\frac{1}{2}\) and A does not lie in second quadrant
⇒ A lies in third quadrant
cos B = –\(\frac{1}{2}\) and B does not lie in third quadrant
⇒ B lies in second quadrant
cos A = –\(\frac{1}{2}\) and A lie in third quadrant
⇒ A = 240°
cos B = –\(\frac{1}{2}\) and B lies in second quadrant.
⇒ B = 120°

(ii) If 8 tan A = -15 and 25 sin B = -7 and neither A nor B is in the fourth quadrant, then show that sin A cos B + cos A sin B = \(\frac{-304}{425}\)
Answer:
8 tan A = -15 25 sin B = -7
⇒ tan A = \(\frac{-15}{8}\) ⇒ sin B = \(\frac{-7}{25}\)
Given neither A nor B is in the fourth quadrant, clearly A is in second quadrant and B is in third quadrant,
sin A cos B + cos A sin B

(iii) If A, B, C, D are angle of a cyclic quadrilateral then prove that
a) sin A – sin C = sin D – sin B
b) cos A + cos B + cos C + cos D = 0
Answer:
A, B, C, D are angles of a cyclic quadrilateral
⇒ A + C = 180°, and B + D = 180° ……………(1)
C = 180 – A and D = 180° – B
a) LHS = sin A – sin C
= Sin A – sin (180 – A) = 0
RHS = sin D – sin B
= sin (180 – B) – sin B
= sin B – sin B = 0
LHS = RHS

b) LHS cos A + cos B + cos C + cos D
= cos A + cos B + cos (180 – A) + cos (180 – B)
= cos A + cos B – cos A – cos B = 0
= RHS

Question 4.
If a cos θ – b sin θ = c, then show that a sin θ + b sin θ = ±\(\sqrt{a^2+b^2-c^2}\)
Answer:
Given a cos θ – b sin θ = c
and let a sin θ + b cos θ = x
squaring and adding, we get
⇒ (a cos θ – b sin θ)² + (a sin θ + b cos θ)²
= c² + x²
a² (cos² θ + sin² θ)² + b² (sin² θ + cos² θ)
= c² + x²
⇒ a² + b² + c² + x² ⇒ x² = a² + b² + c²
⇒ x = ±\(\sqrt{a^2+b^2-c^2}\)

(ii) If 3 sin A + 5 cos A = 5, then show that 5 sin A – 3 cos A = ± 3
Answer:
Given that 3 sin A + 5 cos A = 5
Let 5 sin A – 3 cos A = x
squaring and adding, we get
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)²
= 5² + x²
⇒ 9 (sin² A + cos² A) + 25 (cos² A + sin² A)
⇒ 34 = 25 + x² ± ⇒ x² = 9 ⇒ x = ±3
∴ 5 sin A – 3 cos A = ± 3

(iii) If tan² θ = (1 – e²), show that sec θ + tan³ θ. cosec θ = (2 – e²)^3/2.
Answer:
Given tan²θ = 1 – e²
⇒ sec² θ= 1 + tan² θ = 1
LHS = sec θ + tan³ θ. cosec θ
= sec θ + \(\frac{\sin ^3 \theta}{\cos ^3 \theta} \cdot \frac{1}{\sin \theta}\)
= sec θ + tan² θ sec θ = ( 1 + tan² θ) sec θ
= sec² θ sec θ
= (2 – e²) \(\sqrt{2-\mathrm{e}^2}\)
= (2 – e²)^3/2 = RHS

III.
Question 1.
Prove that following
(i) \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\)
Answer:

(ii) prove that
(1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2
Answer:
(1 + cot θ – cosec θ) (1 + tan θ + sec θ)

(iii) 3 (sin θ – cos θ)⁴ + 6 (sin θ + cos θ)² + 4 (sin⁶ θ + cos⁶ θ) = 13
Answer:
(sin θ – cos θ)² = sin² θ + cos² θ – 2 sin θ cos θ
= 1 – 2sin θ cos θ (sin θ – cos θ)⁴
= (1 – 2 sin θ cos θ)²
= 1 – 4 sin θ cos θ + 4 sin² θ cos² θ (sin θ + cos θ)²
= sin² θ + cos² θ + 2 sin θ cos θ
= 1 + 2 sin θ cos θ
sin⁶ θ + cos⁶ θ = (sin² θ)³ + (cos² θ)³
= (sin² θ + cos² θ) ( sin⁴ θ + cos⁴ θ + sin² θ cos² θ)
= 1 [(sin²θ + cos²θ)² – 2 sin²θ cos²θ + sin²θ cos²θ]
= [1 – sin² θ cos² θ]
LHS = 3 (sin θ – cos θ)⁴ + 6 (sin θ + cos θ)² + 4(sin⁶θ + cos⁶θ)
= 3 [ 1 – 4 sin θ cos θ + 4 sin² θ cos² θ] + 6 [1 + 2sin θ cos θ] + 4 [ 1 – sin² θ cos² θ]
= 3 + 6 + 4 = 13 = RHS

Question 2.
(i) Prove that (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan² θ + cot² θ) = 7
Answer:
(sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ)
= sin² θ + 2 + cosec² θ + cos² θ + 2 + sec² θ – tan² θ cot² θ
= sin² θ + 2 + 1 + cot² θ + cos² θ+ 2 + 1 + tan² θ – tan² θ – cot² θ
= (sin² θ + cos² θ) + 2 + 1 + 2 + 1
= 1 + 2 + 1 + 2 + 1 = 7

(ii) cos⁴α + 2 cos²α(1 – \(\frac{1}{\sec ^2 \alpha}\)) = 1 – sin²α
Answer:
cos⁴α + 2 cos²α(1 – cos²α)
= cos⁴α + 2 cos²α sin²α
= cos²α[cos²α + 2sin²α]
= (1 – sin²α)[cos²α + sin²α + sin²α]
= (1 – sin²α)(1 + sin²α) = 1 – sin⁴α

(iii) \(\frac{(1+\sin \theta-\cos \theta)^2}{(1+\sin \theta+\cos \theta)^2}=\frac{1-\cos \theta}{1+\cos \theta}\)
Answer:

(iv) If \(\frac{2 \sin \theta}{(1+\cos \theta+\sin \theta)}\) = x, then find the value of \(\frac{1-\cos \theta+\sin \theta}{1+\sin \theta}\)
Answer:

Question 3.
Eliminate θ from the following
(i) x = a cos³ θ, y = b sin³ θ
Answer:

(ii) x = a cos⁴ θ, y = b sin⁴ θ
Answer:

(iii) x = a (sec θ + tan θ), y = b(sec θ – tan θ)
Answer:
\(\frac{x}{a}\) = sec θ + tan θ, \(\frac{y}{b}\) = sec θ – tan θ
⇒ \(\left(\frac{x}{a}\right)\left(\frac{y}{b}\right)\) = (sec θ + tan θ)(sec θ – tan θ)
= sec²θ – tan²θ = 1
⇒ xy = ab

(iv) x = cot θ + tan θ, y = sec θ – cos θ
Answer:
x = cot θ + tan θ
⇒ x² = (cot θ + tan θ)²
= cot²θ + tan²θ + 2
= (1 + cot²θ) + (1 + tan²θ)
= cosec²θ + sec²θ
= \(\frac{1}{\sin ^2 \theta}+\frac{1}{\cos ^2 \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin ^2 \theta \cos ^2 \theta}=\frac{1}{\sin ^2 \theta \cos ^2 \theta}\)
∴ x² = sec²θ cosec²θ …………..(1)
y = sec θ – cos θ
⇒ y² = sec² θ + cos² θ – 2
= -1 + sec² θ – 1 + cos² θ
= tan² θ – sin² θ

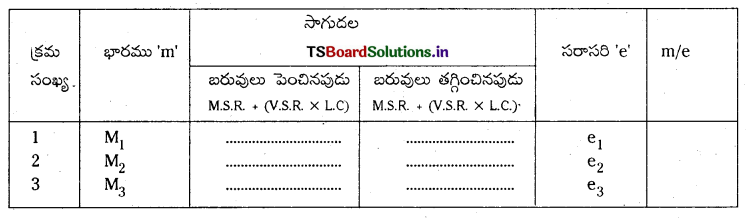
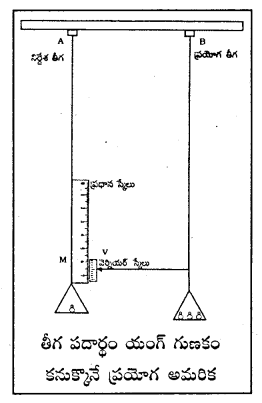
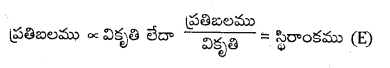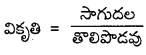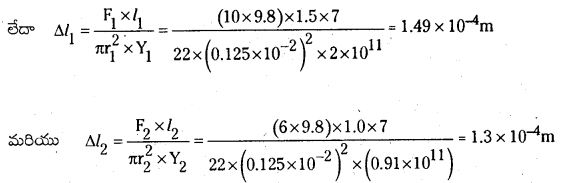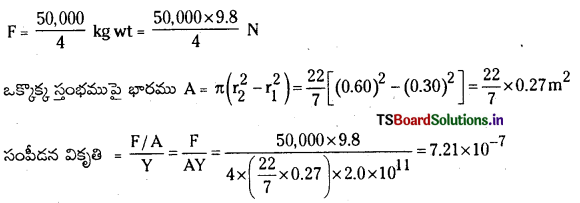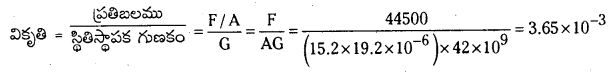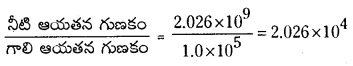Telangana TSBIE TS Inter 1st Year Physics Study Material 12th Lesson పదార్ధ ఉష్ణ ధర్మాలు Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 12th Lesson పదార్ధ ఉష్ణ ధర్మాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణం, ఉష్ణోగ్రతల మధ్య భేదాలను పేర్కొనండి.
జవాబు:
ఉష్ణము మరియు ఉష్ణోగ్రతల మధ్య భేదాలు :
ఉష్ణము

1. ఉష్ణము శక్తి స్వరూపము. దీనికి ప్రమాణాలు జౌల్ లేదా ఉష్ణోగ్రత
2. మనం వస్తువుకు నేరుగా ఉష్ణశక్తిని అందించగలము.
3. వస్తువు ఉష్ణోగ్రతను పెంచడానికి ఉష్ణశక్తిని మనం అందించాలి.
4. వస్తువుకు అందజేసిన ఉష్ణరాశి Q = mSt.

ఉష్ణోగ్రతల

1. ఉష్ణోగ్రత ఒక పదార్థము యొక్క వేడిమి లేదా చల్లదనాన్ని తెలిపే కొలమానము. ప్రమాణము °F లేదా °C.
2. వస్తువుకు ఉష్ణశక్తిని అందించడంవల్ల దాని ఉష్ణోగ్రత పెరుగుతుంది. మనం వస్తువుకు ఉష్ణోగ్రతను నేరుగా అందించలేము.
3. వస్తువుల మధ్య ఉష్ణోగ్రతాభేదం ఉంటేనే ఉష్ణరాశి ఒక వస్తువు నుండి మరొక వస్తువుకు ప్రవహిస్తుంది.
4. వస్తువు ఉష్ణోగ్రతలో మార్పు ∆t = \(\frac{\mathrm{Q}}{\mathrm{mS}}\)

ప్రశ్న 2.
సెల్సియస్, ఫారన్ హీట్ ఉష్ణోగ్రతా మానాలలో అధో, ఊర్ధ్వ స్థిర విలువలను తెలపండి. (మే 2014)
జవాబు:
సెల్సియస్ మానంలో నీటి త్రిక బిందు ఉష్ణోగ్రతను నిమ్న స్థిర బిందువు (°C అని వ్యవహరిస్తారు. సాధారణ వాతావరణ దగ్గర నీరు మరుగు స్థానాన్ని ఊర్ధ్వ స్థిర బిందువు 100°C అంటారు.
ఫారన్హీట్ మానంలో నీటి త్రిక బిందువును నిమ్న స్థిర బిందువు 32°F గా వ్యవహరిస్తారు. సాధారణ వాతావరణ పీడనం వద్ద నీరు మరుగు స్థానాన్ని ఊర్ధ్వ స్థిర బిందువు 212°F అంటారు.

ప్రశ్న 3.
ఉష్ణోగ్రతలను సెల్సియస్ లేదా ఫారస్వీట్ మానాలలో కొలిస్తే, వ్యాకోచ గుణకాల విలువలు మారతాయా ?
జవాబు:
వ్యాకోచ గుణకాలు ఉష్ణోగ్రతామానంపై ఆధారపడతాయి. ఉష్ణోగ్రతామానం మారితే ఉష్ణోగ్రతను కొలిచే ప్రమాణం విలువ మారుతుంది. α, β మరియు γ ను 1°C ఉష్ణోగ్రతా భేదానికి నిర్వచించటం వల్ల సెల్సియస్ మానంలో α, β, γ లు ఫారెన్హీట్ మానంలోని α, β మరియు γ విలువల కన్న 1.8 రెట్లు పెద్దవి.

ప్రశ్న 4
వేడిచేస్తే పదార్థాలు సంకోచిస్తాయా ? ఒక ఉదాహరణ ఇవ్వండి.
జవాబు:
కొన్ని రకాలైన పదార్థాలు వేడిచేస్తే సంకోచిస్తాయి.
ఉదా : రబ్బరు, తోలు, పోత ఇనుము మరియు టైపు మెటల్ వంటివి.

ప్రశ్న 5.
రైల్వే ట్రాక్పై రెండు వరస రైలు పట్టాల మధ్య ఖాళీ ప్రదేశం ఎందుకు వదులుతారు ?
జవాబు:
వేసవికాలంలో రైలు పట్టాలలోని వ్యాకోచ ప్రభావాన్ని తొలగించడానికి వీలుగా రైలు పట్టాల మధ్య ఖాళీని వదులుతారు. ఖాళీని వదలకపోతే రైలు పట్టాల వ్యాకోచం వల్ల రై. పటాలు వంకర చెంది ప్రమాదాలను కలగజేస్తాయి.

ప్రశ్న 6.
ద్రవాలకు దైర్ఘ్య, విస్తీర్ణ వ్యాకోచ గుణకాలు ఎందుకు లేవు ?
జవాబు:
ద్రవాలకు స్వతంత్ర ఆకారం లేదు. అందువల్ల వాటికి దైర్ఘ్య వ్యాకోచ గుణకము, విస్తీర్ణ వ్యాకోచ గుణకాలు ఉండవు. వీటిని పాత్రలలో తీసుకోవటం వల్ల కేవలం ఘనపరిమాణమును మాత్రమే లెక్కలోకి తీసుకుంటారు. అందుకని ద్రవాలకు ఘనపరిమాణ వ్యాకోచ గుణకం మాత్రమే చెపుతారు.

ప్రశ్న 7.
ద్రవీభవన గుప్తోష్ణం అంటే ఏమిటి ?
జవాబు:
ద్రవీభవన గుప్తోష్ణము : ప్రమాణ ద్రవ్యరాశి గల పదార్థము ఘనస్థితి నుండి ద్రవస్థితికి లేదా ద్రవస్థితి నుండి ఘనస్థితికి మార్పుచెందునపుడు గ్రహించిన లేక కోల్పోయిన ఉష్ణరాశిని ద్రవీభవన గుప్తోష్ణముగా నిర్వచించినారు.

ప్రశ్న 8.
బాష్పీభవన గుప్తోష్టం అంటే ఏమిటి ?
జవాబు:
బాష్పీభవన గుప్తోష్ణం : ప్రమాణ ద్రవ్యరాశి గల పదార్థము ద్రవస్థితి నుండి బాష్పస్థితికి లేదా బాష్పస్థితి నుండి ద్రవస్థితికి మారునపుడు అది గ్రహించిన లేక కోల్పోయిన ఉష్ణరాశిని బాష్పీభవన గుప్తోష్ఠముగా నిర్వచించినారు.

ప్రశ్న 9.
వంట పాత్రలకు నల్లటి రంగు ఎందుకు పూస్తారు ? వంట పాత్రల అడుగు భాగాన్ని రాగితో ఎందుకు తయారుచేస్తారు?
జవాబు:
వంట పాత్రల అడుగు భాగం నల్లని పూత వేయటానికి ముఖ్య కారణము నల్లని వస్తువులు ఉత్తమ శోషకాలు. కావున అవి ఎక్కువ మొత్తంలో ఉష్ణాన్ని శోషిస్తాయి. రాగి ఉత్తమ ఉష్ణవాహకం కావున వంట పాత్రల అడుగు భాగంలో రాగిని ఉపయోగిస్తారు.

ప్రశ్న 10.
వీన్ స్థానభ్రంశ నియమాన్ని తెలపండి.
జవాబు:
కృష్ణ వస్తువు గరిష్ట వికిరణం జరిగే తరంగదైర్ఘ్యం, ఆ కృష్ణ వస్తువు పరమ ఉష్ణోగ్రతకు విలోమానుపాతంలో ఉంటుంది.
అనగా λ_m = \(\frac{1}{T}\) లేదా λ_m = \(\frac{b}{T}\)
ఇచ్చట ‘b’ ను వీన్ స్థిరాంకం అని అందురు.

ప్రశ్న 11.
వెంటిలేటర్లను గదిలోని ఇంటిపై కప్పుకు కొద్దిగా కిందకి అమరుస్తారు. ఎందుకు ? (మార్చి 2014)
జవాబు:
వేడిగాలికి సాంద్రత తక్కువ. ఇది వాతావరణంలో పై పొరలను ఆక్రమిస్తుంది. గదిలో వేడిగాలి పైకప్పుకు దగ్గరగా చేరుతుంది. అందువల్ల వెంటిలేటర్లను కప్పుకు దగ్గరగా అమర్చితే వేడిగాలి తొందరగా బయటకు పోతుంది. ఫలితంగా గదిలోకి చల్లని గాలి ధారాళంగా క్రింది భాగాల గుండా రావటం జరుగుతుంది.

ప్రశ్న 12.
0 K వద్ద మానవ దేహం ఉష్ణాన్ని వికిరణం చేస్తుందా ? 0°C వద్ద కూడా అది వికిరణం చేస్తుందా ?
జవాబు:
ప్రివోస్ట్ సిద్ధాంత ప్రకారము ‘సున్న’ కెల్విన్ కన్న ఎక్కువ ఉష్ణోగ్రత వద్ద గల ప్రతి వస్తువు పరిసరాలలో ఉష్ణ వినిమయాన్ని కలిగి ఉంటుంది. కావున

1. ‘సున్న’ కెల్విన్ వద్ద గల వస్తువు నుండి ఏ విధమైన ఉష్ణవికిరణ శక్తి వెలువడదు. అనగా ఉష్ణ వికిరణం సాధ్యం కాదు.
2. 0 K అనగా 273 K కావున 0°C వద్ద గల వస్తువు ఉష్ణశక్తి వికిరణం వెలువడును. అనగా ఉష్ణ వికిరణం సాధ్యపడును.

ప్రశ్న 13.
ఉష్ణ బదిలీకి సంబంధించి వివిధ విధానాలను తెలపండి. వీటిలో ఏ విధానాలకు యానకం అవసరం ?
జవాబు:
ఉష్ణ ప్రసారము మూడు రకాలుగా జరుగుతుంది.

1. ఉష్ణ వహనము
2. ఉష్ణ సంవహనము
3. ఉష్ణ వికిరణము.

ఉష్ణ ప్రసారంలో ఉష్ణ వహనము మరియు ఉష్ణ సంవహనము అన్న పద్ధతుల ద్వారా ఉష్ణము ప్రసరించడానికి యానకం అవసరము.

ప్రశ్న 14.
ఉష్ణ వాహకత్వ గుణకం, ఉష్ణోగ్రత ప్రవణతలను నిర్వచించండి.
జవాబు:
పదార్థం ఏకాంక అడ్డుకోత వైశాల్యానికి లంబంగా, ఏకాంక ఉష్ణోగ్రతా ప్రవణత ఉన్నపుడు సెకనుకు జరిగిన ఉష్ణరాశి ప్రసారాన్నే ఉష్ణ వహన గుణకంగా నిర్వచించినారు.
ఉష్ణ వహన గుణకం K = \(\frac{\mathrm{Q} \cdot \mathrm{d}}{\mathrm{A}\left(\theta_2-\theta_1\right) \cdot \mathrm{t}}\)

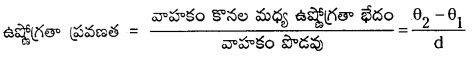
ప్రశ్న 15.
ఉద్గార సామర్థ్యం, ఉద్గారతలను నిర్వచించండి.
జవాబు:
ఉద్గార సామర్థ్యము (E_λ) : ఏదైనా ఉష్ణోగ్రత వద్ద ఏకాంక వైశాల్యం గల వస్తువు నుండి తరంగదైర్ఘ్యము . మరియు λ + dλ. అవధులలో వస్తువు ప్రమాణ కాలంలో వికిరణం చెందించిన ఉష్ణరాశిని ఆ వస్తువు ఉద్గార సామర్థ్యంగా నిర్వచించినారు.
ఉద్గార సామర్థ్యము E_λ = \(\frac{\mathrm{dQ}}{\mathrm{d} \lambda}\); ప్రమాణము : వాట్ / మీ².
ఉద్గారత (e_λ) : ఒక వస్తువు ఉద్గార సామర్థ్యానికి అదే ఉష్ణోగ్రత వద్ద పరిపూర్ణ కృష్ణ వస్తువు ఉద్గార సామర్థ్యానికి గల నిష్పత్తినే ఆ వస్తువు ఉద్గారత e_λ గా నిర్వచించినారు.

ప్రశ్న 16.
హరితగృహ ప్రభావం అంటే ఏమిటి ? గ్లోబల్ వార్మింగ్ గురించి వివరించండి.
జవాబు:
హరితగృహ ప్రభావము : భూమి నుండి శూన్యంలోకి వికిరణం చెందే ఉష్ణశక్తి తరంగదైర్ఘ్యం ఎక్కువ. ఈ ఉష్ణశక్తిని కార్బన్ డై ఆక్సైడ్ (CO₂), మీథేన్ (CH₄), క్లోరోఫ్లోరో కార్బన్ (CF_x Cl_x) వంటి వాయువులు గ్రహించి భూమి వాతావరణాన్ని వేడెక్కిస్తాయి. ఈ ప్రక్రియను హరితగృహ ప్రభావము అంటారు.

గ్లోబల్ వార్మింగ్ :
మానవుల చర్యల వల్ల హరితగృహ వాయువుల (CO₂, CH₄, N₂O మొ॥) గాఢత అధికమై భూమి వేడిగా తయారవుతుంది. భూమి ఉష్ణోగ్రత పెరుగుదలను గ్లోబల్ వార్మింగ్ అందురు. దీనివల్ల మంచు పర్వతాలు త్వరగా ద్రవీభవించడం, సముద్రమట్టం పెరగడం, వాతావరణం విధానం మార్పు చెందడం జరుగుతుంది.

ప్రశ్న 17.
ఒక వస్తువు శోషణ సామర్థ్యాన్ని నిర్వచించండి. పరిపూర్ణ కృష్ణ వస్తువు శోషణ సామర్థ్యం ఎంత ?(మార్చి 2014)
జవాబు:
శోషణ సామర్థ్యము (a_λ) : ఏదైనా వస్తువు యొక్క నియమిత వైశాల్యం మీద నియమిత కాలంలో dλ) తరంగ వ్యవధిలో పతనమైన వికిరణ శక్తి తరంగ అభివాహం (dΦ_λ) మరియు అదే కాలవ్యవధిలో అదే వైశాల్యం గల తలం శోషణం చేసుకున్న అభివాహానికి (dΦ_λ) గల నిష్పత్తి నిశోషణ సామర్థ్యము (a_λ) గా నిర్వచించినారు.

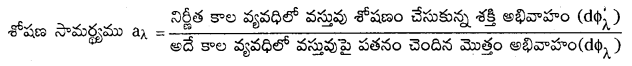
ఉత్తమ కృష్ణ వస్తువు శోషణ సామర్థ్యం ఒకటి (1).

ప్రశ్న 18.
న్యూటన్ శీతలీకరణ నియమాన్ని తెలపండి.
జవాబు:
న్యూటన్ శీతలీకరణ నియమము : వస్తువుకు, పరిసరాలకు మధ్య ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు ఆ వస్తువు కోల్పోయే ఉష్ణ శక్తి రేటు వస్తువుకూ, పరిసరాలకు మధ్య గల ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో ఉంటుంది.
వస్తువు కోల్పోయే ఉష్ణశక్తి రేటు \(\frac{\mathrm{dE}}{\mathrm{dt}}\) ∝ (T – T_s) లేదా
శీతలీకరణ రేటు \(\frac{\mathrm{dT}}{\mathrm{dt}}\) = – \(\frac{\mathrm{b}}{\mathrm{mc}}\) (T – T_s) ఇందులో T_s పరిసరాల ఉష్ణోగ్రత, T వస్తువు ఉష్ణోగ్రత.

ప్రశ్న 19.
న్యూటన్ శీతలీకరణ నియమం అనువర్తించడానికి కావలసిన పరిస్థితులను తెలపండి.
జవాబు:
న్యూటన్ శీతలీకరణ నియమం అనువర్తింపచేయడానికి అనువైన పరిస్థితులు :

1. వహనం ద్వారా ఉష్ణ నష్టం విస్మరించ దగినంత తక్కువగా ఉండి కేవలం సంవహనం ద్వారానే ఉష్ణ నష్టం జరిగినపుడు,
2. లేదా బలాత్కృత సంవహనం వలన ఉష్ణ నష్టం జరిగినపుడు,
3. వస్తువుకు, పరిసరాలకు గల ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు అనగా సుమారు 30 K ఉన్నపుడు,
4. వస్తువుపై ఉష్ణోగ్రత ఏకరీతి వితరణలో ఉన్నపుడు.

ప్రశ్న 20.
వేసవి కాలంలో భవనాలపై పై కప్పుకు తరచుగా తెలుపు రంగును పూతగా పూస్తారు. ఎందుకు ?
జవాబు:
భవనాల పైభాగాన తెల్లని రంగు పూయటం వల్ల ఎండాకాలంలో భవనం లోపలి భాగం చల్లగా ఉంటుంది.
ఎందుకనగా తెల్లని వస్తువులకు శోషణ గుణకము తక్కువ. కావున తెల్లని భాగాలు వాటిపై పడిన ఉష్ణశక్తిలో తక్కువ భాగాన్ని శోషణం చేసుకొని ఎక్కువ ఉష్ణశక్తిని పరావర్తనం చెందిస్తాయి. ఫలితంగా ఆ వస్తువు తక్కువ వేడెక్కును. అనగా ఇంటి పైకప్పు ఇంటి లోపలికి తక్కువ ఉష్ణశక్తిని ప్రసారం చేస్తుంది.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సెల్సియస్, ఫారన్హీట్ ఉష్ణోగ్రతా మానాలను వివరించండి. సెల్సియస్, ఫారన్హీట్ ఉష్ణోగ్రతా మానాల మధ్య సంబంధాన్ని రాబట్టండి.
జవాబు:
సెంటిగ్రేడ్ లేదా సెల్సియస్ ఉష్ణమానము : సెంటీగ్రేడ్ ఉష్ణమానంలో సాధారణ వాతావరణ పీడనం వద్ద నీరు ఘనీభవించు స్థానాన్ని అధోస్థిరస్థానంగా తీసుకున్నారు. దీనిని 0°C గా వ్యవహరిస్తారు.

సాధారణ వాతావరణ పీడనం వద్ద నీరు మరుగు స్థానాన్ని ఊర్ధ్వ స్థిరస్థానంగా తీసుకున్నారు. దీనిని 100°C గా వ్యవహరిస్తారు.

ఊర్ధ్వ, అధో స్థిరస్థానాల మధ్య భేదాన్ని (100 – 0 = 100) వంద సమాన భాగాలుగా చేసి ఒక్కొక్క భాగాన్ని 1°C గా పిలుస్తారు.

ఫారన్హీట్ ఉష్ణోగ్రతామానము : ఫారెన్హీట్ ఉష్ణోగ్రతామానంలో సాధారణ వాతావరణ పీడనం వద్ద నీరు ఘనీభవించు ఉష్ణోగ్రతను అధో స్థిరస్థానంగా తీసుకున్నారు. దీనిని 32°F గా నిర్వచించారు.

సాధారణ వాతావరణ పీడనం వద్ద నీరు మరుగుస్థానాన్ని ఊర్ధ్వ స్థిరస్థానంగా నిర్ణయించారు. దీనిని 212°F గా తీసుకున్నారు.

ఊర్ధ్వ, అధో స్థిరస్థానాల మధ్య భేదాన్ని (212 – 32 = 180) 180 సమాన భాగాలుగా చేసి ఒక్కొక్క భాగాన్ని 1°C గా పిలుస్తారు.

సెంటీగ్రేడ్ మరియు ఫారెన్హీట్ ఉష్ణోగ్రతల మధ్య సంబంధము : సెంటీగ్రేడ్ మరియు ఫారెన్హీట్ మానములలో ప్రామాణికంగా తీసుకున్న ఊర్ధ్వ స్థిరబిందువు మరియు అధో స్థిర బిందువులు ఒక్కటే.
కావున \(\frac{\mathrm{t}_{\mathrm{F}}-32}{180}=\frac{\mathrm{t}_{\mathrm{C}}}{100}\) (లేదా) \(\frac{9}{5}\) C = F – 32 (లేదా) 1.8 C = F – 32
C = సెల్సియస్ మానంలో ఉష్ణోగ్రత, F = ఫారెన్హీట్ మానంలో ఉష్ణోగ్రత.

ప్రశ్న 2.
రాగి, స్టీల్తో చేసిన రెండు సర్వసమాన లోహ పట్టీలను ఒకదానితో ఒకటి కలిపి సంయోగ పట్టీగా తయారుచేశారు. ఆ సంయోగ పట్టీని వేడిచేస్తే ఏమవుతుంది ?
జవాబు:
రెండు భిన్నజాతిలోహపు బద్దలను (రాగి మరియు ఇనుము అనుకోండి) రివిట్ల సహాయంతో అతికితే ఆ అమరికను ద్విలోహపు పట్టి అంటారు. ఇటువంటి ద్విలోహపు పట్టీని వేడిచేస్తే అది ఒక లోహపు ముక్కవలె సంకోచ వ్యాకోచాలను పొందుతుంది.

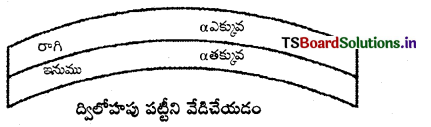
ద్విలోహాత్మక పట్టీని వేడిచేసినపుడు వృత్త చాపము వలె వంగుతుంది. ఈ చాపంపైభాగంలో ఎక్కువ వ్యాకోచ గుణకం గల పదార్థము, క్రింది భాగంలో తక్కువ వ్యాకోచ గుణకం గల పదార్థము ఉంటాయి.
ఈ స్థిరాంకమును స్థితిస్థాపక గుణకము అంటారు.

ప్రశ్న 3.
లోలక గడియారాలు సాధారణంగా శీతాకాలంలో అధిక కాలాన్ని చూపుతాయి. వేసవిలో తక్కువ కాలాన్ని చూపుతాయి. ఎందుకు ?
జవాబు:
సాధారణంగా లోలకంతో పనిచేసే గడియారాలను తయారుచేసేటప్పుడు అవి రోజుకు ఒక నిర్దిష్ట సంఖ్యలో (0 డోలనాలు చేసే విధంగా తయారుచేస్తారు).

ఎండాకాలంలో వాతావరణంలో ఉష్ణోగ్రత పెరగడం వల్ల ఘనపదార్థాలు వ్యాకోచిస్తాయి. అనగా లోలకం పొడవు పెరుగును. లోలకం పొడవు l₁ = l (l + α ∆t)

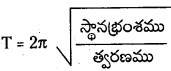
లోలకం ఆవర్తన కాలము T = 2π\(\sqrt{\frac{l}{g}}\) లేదా T ∝ \(\sqrt{l}\) అనగా లోలకం పొడవు పెరిగితే దాని ఆవర్తనకాలం పెరగడం వల్ల అది ఒకరోజులో చేసే డోలనాల సంఖ్య తగ్గుతుంది. అనగా గడియారం నెమ్మదిగా నడుస్తుంది.

చలికాలంలో వాతావరణ ఉష్ణోగ్రత తగ్గటం వల్ల లోలక పదార్థం సంకోచిస్తుంది. అనగా లోలకం పొడవు తగ్గుతుంది. ఫలితంగా డోలనావర్తన కాలం తగ్గుతుంది. అనగా లోలకం ఒకరోజులో చేసిన డోలనాల సంఖ్య పెరుగును. అంటే చలికాలంలో గడియారాలు వేగంగా చలిస్తాయి.

ప్రశ్న 4.
నీటి అసంగత వ్యాకోచం ఏ విధంగా జలచర సంబంధమైన జంతువులకు లాభం చేకూరుస్తుంది ? (March 2014 / May 2014)
జవాబు:
చలి దేశాలలో ముఖ్యంగా ధృవ ప్రాంతాలలో చలికాలంలో వాతావరణంలో ఉష్ణోగ్రతలు 0°C కన్న చాలా తక్కువకు పడిపోతాయి. ఫలితంగా నదులు, సరస్సులు మరియు సముద్రాల పైభాగాలు గడ్డ కడతాయి. కాని మంచు అధమ ఉష్ణవాహకం కావడం వల్ల మంచు పొరలలో లోతుకు పోయిన కొలది మనం నీరు 1°C, 2°C లేదా 3°C వంటి వివిధ పొరల రూపంలో ఉంటుంది. కాని సముద్రం అడుగు భాగం వద్ద నీరు 4°C వద్ద ఉంటుంది. దీనికి కారణము నీటికి 4°C వద్ద గరిష్ఠ సాంద్రత ఉండుట.

ప్రాముఖ్యత : సముద్ర జలాలు ఉపరితలం వద్ద గడ్డ కట్టినప్పటికి లోపలి భాగం 4°C వద్ద ఉండటం వల్ల జలచరాలు జీవించగలుగుతున్నాయి.

ప్రశ్న 5.
వహనం, సంవహనం, వికిరణాలను ఉదాహరణలతో వివరించండి.
జవాబు:
వహనం : వస్తువులోని కణాలు స్థానాంతరం చెందకుండా, వస్తువులో ఎక్కువ ఉష్ణోగ్రత గల ప్రదేశం నుండి తక్కువ ఉష్ణోగ్రత గల ప్రదేశానికి జరుగు ఉష్ణ ప్రసారాన్ని ఉష్ణ వహనం అంటారు.
ఉదా : ఒక పొడవైన లోహపు కడ్డీని ఒక చివర చేతితో పట్టుకొని రెండవ కొన మంటలో ఉంచితే, ఉష్ణం వాహనం ద్వారా కడ్డీ ఒక కొన నుండి మరొక కొనకు ప్రసరిస్తుంది.

సంవహనం : వస్తువులోని కణాలు స్థానాంతరం చెందుతూ, వస్తువులో ఎక్కువ ఉష్ణోగ్రత గల ప్రదేశం నుండి తక్కువ ఉష్ణోగ్రత గల ప్రదేశానికి ఉష్ణ ప్రసారాన్ని ఉష్ణ సంవహనం అంటారు.
ఉదా : సముద్రగాలి, భూగాలి

వికిరణం : యానకం నిమిత్తం లేకుండా ఒకచోట నుండి మరొక చోటుకు జరుగు ఉష్ణ ప్రసారాన్ని ఉష్ణ వికిరణం అంటారు.
ఉదా : సూర్యుని నుండి భూమికి ఉష్ణం వికిరణం ద్వారా చేరుతుంది..

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణవాహకత్వం, ఉష్ణవాహకత్వ గుణకాన్ని వివరించండి. 0.10 m పొడవు, 1.0 × 10⁶ m^-2 మధ్యచ్ఛేద వైశాల్యం ఉన్న ఒక రాగి కడ్డీ ఉష్ణ వాహకత్వం 401 W/(mK). కడ్డీ ఒక కొన 104°C వద్ద, మరొక కొన 24° C వద్ద కలవు. కడ్డీ వెంబడి ఉష్ణ ప్రవాహ రేటు ఎంత ?
జవాబు:
ఉష్ణవహనము : ఈ పద్ధతిలో ఉష్ణము ఒకచోటు నుండి మరొక చోటికి యానకంలోని అణువులను స్థానభ్రంశము చెందించకుండా ప్రయాణం చేస్తుంది.

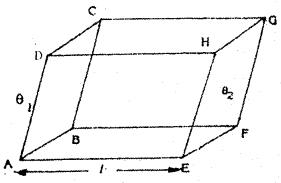
ఉష్ణవహనము ద్వారా ఉష్ణము ఘనపదార్థాలలో ప్రసరిస్తుంది.

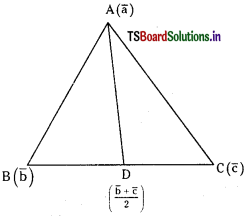
పటంలో చూపిన విధంగా ఒక దీర్ఘ ఘనమును తీసుకొనుము. దీని ఎదురెదురు సమాంతర తలాలు ABCD మరియు EFGH అనుకొనుము. ఈ తలాలను θ₁ మరియు θ₂ ఉష్ణోగ్రతల మధ్య ఉంచినామనుకొనుము. దీని అడ్డుకోత వైశాల్యము A మరియు పొడవు l అనుకొనుము.

ఒక పదార్థం గుండా ప్రవహించు ఉష్ణరాశి (Q) ఈ క్రింది నియమాలను పాటిస్తుంది అని ప్రయోగపూర్వకంగా కనుగొన్నారు.

1. ఇచ్చిన వాహకం గుండా ప్రవహించు ఉష్ణరాశి వాహకం అడ్డుకోత వైశాల్యము (A) కి అనులోమానుపాతంలో ఉంటుంది.
   ∴ Q∝ A ……………. (1)
2. వాహకం గుండా ప్రవహించిన ఉష్ణరాశి (Q) వాహకపు కొనల మధ్య గల ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో
   ఉంటుంది.
   ∴ Q ∝ (θ₂ – θ₁) …………….. (2)
3. వాహకం గుండా ప్రవహించిన ఉష్ణరాశి (Q) ఉష్ణము ప్రవహించిన కాలము (t) నకు అనులోమానుపాతంలో ఉంటుంది.
   Q ∝ t …………. (3)
4. వాహకం గుండా ప్రవహించిన ఉష్ణరాశి (Q) వాహకము పొడవు (l) కు విలోమానుపాతంలో ఉంటుంది.
   Q ∝ \(\frac{1}{l}\) ……………….. (4)

పై నాలుగు నియమాల నుండి Q ∝ \(\frac{\mathrm{A}\left(\theta_2-\theta_1\right) \mathrm{t}}{l}\) (లేదా) Q = \(\frac{{KA}\left(\theta_2-\theta_1\right) \mathrm{t}}{l}\)
ఇందులో K స్థిరాంకము. దీనిని ఉష్ణవహన గుణకము అంటారు.

ఉష్ణవహన గుణకము (K) : ప్రమాణ అడ్డుకోత వైశాల్యం గల పదార్థపు ఎదురెదురు సమాంతర తలముల మధ్య ఏకాంక ఉష్ణోగ్రతా అతిక్రమం ఉన్నపుడు ప్రమాణ కాలంలో ఆ తలముల మధ్య ప్రవహించిన ఉష్ణరాశిని ఆ పదార్థం ఉష్ణవహన గుణకంగా నిర్వచించినారు.
ఉష్ణవహన గుణకము K = \(\frac{\mathrm{Q} . l}{\mathrm{~A}\left(\theta_2-\theta_1\right) \mathrm{t}}\)
ఉష్ణవహన గుణకానికి ప్రమాణాలు వాట్ మీటర్^-1 కెల్విన్^-1 లేదా జౌల్సకన్^-1 మీటర్^-1 కెల్విన్^-1
మితి ఫార్ములా = [ M¹L¹T^-3θ^-1]

సమస్య :
రాగి ఉష్ణవహన గుణకము K_c = 401 W/m-k
ఒక కొన వద్ద ఉష్ణోగ్రత θ₂ = 104°C
రెండవ కొన వద్ద ఉష్ణోగ్రత θ₁ = 24°C
రాగి దండం పొడవు l = 0.1m; వైశాల్యము = A = 1.0 × 10^-6 m²
ఉష్ణవహన రేటు \(\frac{\mathrm{Q}}{\mathrm{t}}=\frac{{KA}\left(\theta_2-\theta_1\right)}{l}=\frac{401 \times 1 \times 10^{-6}(104-24)}{0.1}\) = 401 × 80 × 10^-5 = 0.3208 J/S

ప్రశ్న 2.
న్యూటన్ శీతలీకరణ నియమాన్ని తెలిపి, వివరించండి. న్యూటన్ శీతలీకరణ నియమం అనువర్తించడానికి కావలసిన పరిస్థితులను తెలపండి.
ఒక వస్తువు 60°Cనుంచి 50°C కు చల్లబడటానికి 5 నిమిషాల కాలం పట్టింది. తరువాత 40°C కు చల్లబడటానికి మరొక 8 నిమిషాలు పట్టింది. పరిసరాల ఉష్ణోగ్రతను కనుక్కోండి.
జవాబు:
న్యూటన్ శీతలీకరణ నియమము : వస్తువుకు, పరిసరాలకు మధ్య ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు ఆ వస్తువు కోల్పోయే ఉష్ణ శక్తి రేటు వస్తువుకూ, పరిసరాలకు మధ్య గల ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో ఉంటుంది.

వస్తువు కోల్పోయే ఉష్ణశక్తి రేటు \(\frac{\mathrm{dE}}{\mathrm{dt}}\) ∝ (T – T_s) లేదా
శీతలీకరణ రేటు \(\frac{\mathrm{dT}}{\mathrm{dt}}\) = – \(\frac{\mathrm{b}}{\mathrm{mc}}\) (T – T_s). ఇందులో T_s పరిసరాల ఉష్ణోగ్రత, T వస్తువు ఉష్ణోగ్రత.
ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నప్పుడు మాత్రమే ఈ నియమం వర్తిస్తుంది. వికిరణం ద్వారా నష్టపోయే ఉష్ణం, వస్తువు ఉపరితల స్వభావం మీద, ప్రత్యక్షీకరణం అయ్యే ఉపరితల వైశాల్యంపై ఆధారపడి ఉంటుంది.
– \(\frac{\mathrm{dQ}}{\mathrm{dt}}\) = k (T₂ – T₁) (రుణ గుర్తు నష్టాన్ని సూచిస్తుంది) ………………. (1)
ఇక్కడ k ధనాత్మక స్థిరాంకం. దీని విలువ వస్తువు ఉపరితల స్వభావం, వైశాల్యంపై ఆధారపడి ఉంటుంది. s విశిష్టోష్ణ సామర్థ్యం, mద్రవ్యరాశి ఉన్న వస్తువు, T₂ ఉష్ణోగ్రత వద్ద ఉందనుకోండి. పరిసరాల ఉష్ణోగ్రత T₁ అనుకోండి. dtకాలంలో స్వల్ప పరిమాణంలో ఉష్ణోగ్రతలో తగ్గుదల dT₂ అనుకొంటే, నష్టపోయిన ఉష్ణ పరిమాణం
dQ = ms dT₂
∴ నష్టపోయిన ఉష్ణ రేటును కింది విధంగా ఇవ్వచ్చు.
\(\frac{\mathrm{dQ}}{\mathrm{dt}}\) = ms \(\frac{\mathrm{dT}_2}{\mathrm{dt}}\) ………….. (2)
సమీకరణాలు (1), (2) ల నుంచి
-ms \(\frac{\mathrm{dT}_2}{\mathrm{dt}}\) = k (T₂ – T₁)
\(\frac{\mathrm{dT}_2}{\mathrm{~T}_2-\mathrm{T}_1}\) = – \(\frac{\mathrm{k}}{\mathrm{ms}}\) dt = -Kdt …………….. (3)
ఇక్కడ K = k/ms
సమాకలనం చేయగా,
loge (T₂ – T₁) = – Kt + c …………….. (4)
(T₂ – T₂) = e^{-Kt + c}
లేదా T₂ = T₁ + C’ e^-Kt; ఇక్కడ C’ = e^c ……………. (5)
ప్రత్యేకమైన ఉష్ణోగ్రత అవధిలో ఒక వస్తువు శీతలీకరణానికి పట్టే కాలాన్ని సమీకరణం (5) ఉపయోగించి లెక్కించవచ్చు.

స్వల్ప ఉష్ణోగ్రతా భేదాలకు, ఉష్ణ వహనం, సంవహనం, వికిరణాల కలయిక వల్ల శీతలీకరణ రేటు ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో ఉంటుంది. ఒక వికిరణకం నుంచి గదిలోకి బదిలీ అయ్యే ఉష్ణం, గదిలోని గోడల ద్వారా నష్టపోయే ఉష్ణం లేదా టేబుల్పై అమర్చిన కప్పులోని వేడి టీ శీతలీకరణం చెందే సందర్భాలలో ఈ నియమం ఉజ్జాయింపుగా చెల్లుబాటు అవుతుంది.

న్యూటన్ శీతలీకరణ నియమం అనువర్తింపచేయడానికి అనువైన పరిస్థితులు :

1. వహనం ద్వారా ఉష్ణ నష్టం విస్మరించదగినంత తక్కువగా ఉండి కేవలం సంవహనం ద్వారానే ఉష్ణ నష్టం జరిగినపుడు,
2. లేదా బలాత్కృత సంవహనం వలన ఉష్ణ నష్టం జరిగినపుడు,
3. వస్తువుకు, పరిసరాలకు గల ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు అనగా సుమారు 30K ఉన్నపుడు,
4. వస్తువుపై ఉష్ణోగ్రత ఏకరీతి వితరణలో ఉన్నపుడు.

సమస్య :
తొలి ఉష్ణోత్ర θ₁ = 60 C;
తుది ఉష్ణోగ్రత θ₂ = 50°C
పట్టిన కాలము t = 5 ని॥ = 300 సె॥; గది ఉష్ణోగ్రత = θ₀ అనుకొనుము.
న్యూటన్ శీతలీకరణ నియమం నుండి \(\frac{\mathrm{d} \theta}{\mathrm{dt}}=K\left[\frac{\theta_1+\theta_2}{2}-\theta_0\right]\)
⇒ \(\frac{60-50}{300}\) = K \(\left[\frac{60+50}{2}-\theta_0\right]\) ⇒ \(\frac{10}{300}\) = K [55 – θ₀] (లేదా) ⇒ \(\frac{1}{30}\) = K[55 – θ₀] ….. (1)
రెండవ సందర్భంలో వస్తువు 50 C నుండి 40°C కు 8 నిమిషాలలో చల్లారింది.
న్యూటన్ నియమం నుండి \(\frac{50-40}{8 \times 60}\) = K \(\left[\frac{50+40}{2}-\theta_0\right]\)
⇒ \(\frac{10}{480}\) = K[45 – θ₀] ⇒ 1 = 48K (45 – θ₀)
1 మరియు 2 సమీకరణముల నుండి 30 K (55 – θ₀) = 48K (45 – θ₀)
275 – 5θ₀ = 360 – 8θ₀ ⇒ 3θ₀ = 360 – 275
∴ θ₀ = \(\frac{85}{3}\) = 28.33°C

లెక్కలు

ప్రశ్న 1.
ఏ ఉష్ణోగ్రత వద్ద కెల్విన్ మానంలోని రీడింగ్, ఫారన్హీట్ మానంలోని రీడింగ్లు సమానం అవుతాయి ?
సాధన:
కెల్విన్, ఫారన్ హీట్ మానాలలో \(\frac{\mathrm{K}-273.15}{100}\) = \(\frac{F-32}{180}\)
ఇక్కడ K = F కావున
\(\frac{\mathrm{F}-273.15}{100}=\frac{\mathrm{F}-32}{180}\)
⇒ F – 273.15 = \(\frac{5}{9}\) F – \(\frac{160}{9}\)
\(\frac{4}{9}\) F – 273.15 – 17.77
⇒ F = \(\frac{9}{4}\) (255.38) = 574.6
∴ 574.6K = 574.6°F.

ప్రశ్న 2.
ఒక అల్యూమినియం కడ్డీ పొడవును 1% పెంచాలంటే దాని ఉష్ణోగ్రతలో కలిగే పెరుగుదల కనుక్కోండి. (అల్యూమినియం విలువ = 25 × 10^-6 / °C)
సాధన:
అల్యూమినియం దైర్ఘ్య వ్యాకోచ గుణకము, α = 25 × 10^-6 / °C

ప్రశ్న 3.
20°C ఉష్ణోగ్రత, 100 g ద్రవ్యరాశి ఉన్న నీటి ఉష్ణోగ్రతను 5°C పెంచడానికి 100°C ఉష్ణోగ్రత వద్ద ఉన్న ఎంత ఆవిరిని ఆ నీటిలోకి పంపించాలి ? (నీటి ఆవిరి గుప్తోష్ణం 510 cal / g, నీటి విశిష్టోష్ణం 1 cal / g°C)
సాధన:
నీటి బాష్పీభవన గుప్తోష్ణం, L_s = 540 cal / g; నీటి విశిష్టోష్ణం, S_w = 1 cal / g°C
నీటి ద్రవ్యరాశి, m_w = 100g
మిశ్రమ పద్ధతి సూత్రం ప్రకారం
నీటి ఆవిరి కోల్పోయిన ఉష్ణరాశి = నీరు గ్రహించిన ఉష్ణరాశి
i.e., m_sL_s + m_sS_w (100 – t) = m_wS_w (t – 20)
⇒ m_s × 540 + m_s × 1(100 – 25) = 100 × 1 × (25 – 20)
⇒ 615m_s = 500 (or)m_s = \(\frac{500}{615}\) = 0.813 g

ప్రశ్న 4.
2 kg ల గాలిని స్థిర ఘనపరిమాణం వద్ద వేడిచేశారు. గాలి ఉష్ణోగ్రత 293 K నుంచి 313 K కు పెరిగింది. స్థిర ఘనపరిమాణం వద్ద గాలి విశిష్టోష్ణం 0.718kJ/kg K. అది శోషించుకొనే ఉష్ణ పరిమాణాన్ని kJ లలో, kcalలలో కనుక్కోండి. (J = 4.2 kJ/kcal.)
సాధన:
గాలి సాంద్రత m = 2 kg;
ఉష్ణోగ్రతలో మార్పు ∆T = 313 – 293 20K.
స్థిర ఘనపరిమాణ విశిష్టోష్ణము C_v = 0.718 k. J/kg – K.
ఉష్ణ యాంత్రిక తుల్యాంకము = J. = 4.2 kJ/k.cal.
C_v = \(\frac{1}{\mathrm{~m}} \frac{\mathrm{dQ}}{\mathrm{dT}}\) ⇒ dQ = mC_vdT (లేదా) dQ = \(\frac{\mathrm{mC}_{\mathrm{v}} \mathrm{dT}}{\mathrm{J}}\) cal.
∴ గాలి శోషించుకొనిన ఉష్ణరాశి Q = 2 × 0.718 × 10³ × 20 = 28.72 kJ = 6.838 k calories.

ప్రశ్న 5.
ఇత్తడి లోలకం కలిగిన ఒక గడియారం 20°C వద్ద సరియైన కాలాన్ని చూపుతుంది. ఉష్ణోగ్రత 30°C కు పెరిగినప్పుడు ఆ గడియారం రోజుకు 8.212 సెకనుల కాలం తక్కువ చూపుతుంది. ఇత్తడి దైర్ఘ్య వ్యాకోచ గుణకం కనుక్కోండి.
సాధన:
సరియైన కాలం వద్ద ఉష్ణోగ్రత t = 20°C;
ఒక రోజులో నష్టపోయిన లేక లాభపడిన కాలము = 8.212 sec.
తుది ఉష్ణోగ్రత t₂ = 30 C ∴ ∆t = 30 – 20 = 10;
లోలకం చేయబడిన పదార్థం α = ?
లోలకంలో ఒక రోజుకు నష్టపోయిన లేదా లాభపడిన సెకండ్ల సంఖ్య = 43,200. α ∆t
∴ α = \(\frac{8.212}{43.200 \times 10}\) = 19 × 10^-6 / C.

ప్రశ్న 6.
ఒక వస్తువు 7 నిమిషాలలో 60°C నుంచి 40°C కు చల్లబడుతుంది. పరిసరాల ఉష్ణోగ్రత 10°C అయితే, తదుపరి 7 నిమిషాల తరువాత అది ఎంత ఉష్ణోగ్రతకు చేరుకొంటుంది ?
సాధన:
మొదటి సందర్భము :
తొలి’ ఉష్ణోగ్రత, θ₁ = 60°C;
తుది ఉష్ణోగ్రత, θ₂ = 40°C
చల్లబడటానికి పట్టిన కాలము, t₁ = 7 నిమిషాలు = 7 × 60 = 420s ;
పరిసరాల ఉష్ణోగ్రత, θ₀ = 10°C
న్యూటన్ శీతలీకరణ నియమం ప్రకారం,
\(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) = k \(\left[\frac{\theta_1+\theta_2}{2}-\theta_0\right]\) ⇒ \(\frac{60-40}{420}\) = k \(\left[\frac{60+40}{2}-10\right]\)
⇒ \(\frac{20}{420}\) = k × 40 …………….. (1)
రెండవ సందర్భము :
తొలి ఉష్ణోగ్రత, θ₁ = 40°C
చల్లబడటానికి పట్టిన కాలము, t₂ = 7 నిమిషాలు = 7 × 60 = 420s
న్యూటన్ శీతలీకరణ నియమం ప్రకారం,
\(\frac{50-\theta}{420}\) = k\(\left[\frac{50+\theta}{2}-10\right]\)
సమీకరణాలు (1) మరియు (2) లను సాధించగా, θ = 34°C

ప్రశ్న 7.
ఒక కృష్ణ వస్తువు గరిష్ఠ వికిరణ తీవ్రత 2.65 µ m వద్ద కనుక్కోవడమైంది. వికిరణాన్ని ఉద్గారం చేసే వస్తువు ఉష్ణోగ్రత ఎంత ? (వీన్ స్థిరాంకం = 2.9 × 10^-3 mK)
సాధన:
గరిష్ట తీవ్రత పద్ధతి తరంగదైర్ఘ్యం λ_max = 2.65 µm = 2.65 × 10^-6 m.
వస్తువు ఉష్ణోగ్రత T = ? వీన్ స్థిరాంకము b = 2.90 × 10^-3 mK.
వీస్ నియమం నుండి T = \(\frac{b}{\lambda_m}\) = \(\frac{2.90 \times 10^{-3}}{2.65 \times 10^{-6}}\) = 1094 K.

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
నియాన్, కార్బన్-డై-ఆక్సైడ్ త్రిక బిందువులు వరుసగా 24.57 K, 216.55 K. ఈ ఉష్ణోగ్రతలను సెల్సియస్, ఫారన్హీట్ మానాలలో తెలియచేయండి.
సాధన:
కెల్విన్ మానము మరియు సెల్సియస్ మానముల మధ్య సంబంధము T_C = T_K – 273.15
ఇక్కడ T_C, T_K లు సెల్సియస్ మరియు కెల్విన్ మానాలలో ఉష్ణోగ్రతలు
నియాను, T_C = 24.57 – 273.15 = – 248.58°C
CO₂, T_C = 216.55 – 273.15 = – 56.60°C.
ఫారన్హీట్ మానము మరియు కెల్విన్ మానంల మధ్య గల సంబంధము = \(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}=\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\)
T_F = \(\frac{180}{100}\) (T_K – 273.15) + 12
నియాను, T_F = \(\frac{180}{100}\) (24.57 – 273.15) + 32 = -415.44°F
CO₂, T_F = \(\frac{180}{100}\) (216.55 – 273.15) + 32 = -69.88°F

ప్రశ్న 2.
A, B అనే రెండు పరమ ఉష్ణోగ్రతా మానాలు నీటి త్రిక బిందువును 200 A, 350 B గా నిర్వచించాయి. T_A, T_B మధ్య ఉన్న సంబంధం ఏమిటి ?
సాధన:
దత్తాంశం ప్రకారం, ఉష్ణోగ్రతా మానం A లో నీటి త్రిక బిందువు = 200A
ఉష్ణోగ్రతా మానం Bలో నీటి త్రిక బిందువు = 350 B.
మన ప్రశ్నను బట్టి, 200A = 350 B = 273.16 లేదా 1A = \(\frac{273.16}{200}\)K మరియు 1B = \(\frac{273.16}{350}\) K
T_A మరియు T_B అనునవి వరుసగా నీటి త్రిక బిందువులుగా మానము A మరియు మానము B లలో సూచిస్తే
\(\frac{273.16}{200}\) T_A = \(\frac{273.16}{350}\) T_B (లేదా) \(\frac{\mathrm{T}_{\mathrm{A}}}{\mathrm{T}_{\mathrm{B}}}\) = \(\frac{200}{350}\) = \(\frac{4}{7}\) (లేదా) T_A = \(\frac{4}{7}\) T_B

ప్రశ్న 3.
ఒక థర్మామీటర్ విద్యుత్ నిరోధం ఓమ్లలో ఉష్ణోగ్రతతో ఉజ్జాయింపు నియమం ప్రకారం క్రింది విధంగా మారుతుంది. R = R₀ [1 + α (T – T₀)]
నీటి త్రిక బిందువు 273.16 K వద్ద నిరోధం 101.6 Ω, సీసం ప్రమాణ ద్రవీభవన స్థానం 600.5 Ω వద్ద నిరోధం 165.5 Ω. ఏ ఉష్ణోగ్రత వద్ద నిరోధం 123.4 Ω అవుతుంది ?
సాధన:
దత్తాంశము నుండి R₀ = 101.6 Ω; T₀ = 273.16 K
సందర్భం (i) R₁ = 165.5 Ω; T₁ = 600.5 K
సందర్భం (ii) R₂ = 123.4 Ω; T₂ = ?
R = R₀ [1 + α (T – T₀)] నకు సందర్భము (i) ఉపయోగించిన
165.5 = 101.6 [1 + α (600.5 – 273.16)]
α = \(\frac{165.5-101.6}{101.6 \times(600.5-273.16)}=\frac{63.9}{101.6 \times 327.34}\)
సందర్భం (ii) నుండి 123.4 = 101.6 [1+ α(T₂ – 273.16)]
(లేదా) 123.4 = 101.6 [1 + \(\frac{63.9}{101.6 \times 327.34}\) (T₂ – 273.16)] = 101.6 + \(\frac{63.9}{327.34}\) (T₂ – 273.16)
(లేదా) T₂ = \(\frac{(123.4-101.6) \times 327.34}{63.9}\) + 273.16 = 111.67 + 273.16 = 384.83K

ప్రశ్న 4.
క్రింది వాటికి సమాధానాలు ఇవ్వండి :
(a) ఆధునిక ఉష్ణమితిలో నీటి త్రిక బిందువు ప్రమాణ స్థిర బిందువు. ఎందుకు ? మంచు ద్రవీభవన స్థానాన్ని, నీటి బాష్పీభవన స్థానాన్ని ప్రమాణ స్థిర బిందువులుగా తీసుకొంటే కలిగే తప్పు ఏమిటి ? (సెల్సియస్ మానంలో అదే విధంగా తీసుకోవడమైంది)
(b) సెల్సియస్ మానంలో పై ప్రశ్నలో తెలిపిన విధంగా రెండు స్థిర బిందువులు కలవు. వాటికి వరుసగా 0°C, 100°C సంఖ్యలను కేటాయించడమైంది. పరమమానంలో రెండు స్థిర బిందువుల్లో ఒకటి నీటి త్రిక బిందువుగా తీసుకొని కెల్విన్ మానంలో 273.16 K సంఖ్యను కేటాయించడమైంది. ఈ (కెల్విన్) మానంలో మరొక స్థిర బిందువు ఏమిటి ?
(c) పరమ ఉష్ణోగ్రత (కెల్విన్ మానం) T, సెల్సియస్ మానంపై ఉష్ణోగ్రత t_c కి మధ్య సంబంధం t_c = T – 273.15
ఈ సంబంధంలో 273.16 కాకుండా, 273.15 ను తీసుకోవడానికి కారణం ఏమిటి ?
(d) పరమ ఉష్ణోగ్రతా మానంలో యూనిట్ అంతరం ఫారన్హీట్ మానంలో యూనిట్ అంతరానికి సమానం అయితే పరమ ఉష్ణోగ్రత మానంపై నీటి త్రిక బిందువు ఉష్ణోగ్రత ఎంత ?
సాధన:
(a) నీటి త్రిక బిందువుకు ఒకే ఒక విలువ 273.16 K. ఒకే ఒక బిందువు వుండుట ఒక సత్యం. అక్కడ పీడనానికి మరియు ఘనపరిమాణానికి ఒకే ఒక విలువ కలిగి వుంటుంది. వేరే విధంగా తెలిపిన, పీడనము మరియు ఘనపరిమాణములో మార్పు వచ్చునప్పుడు, నీరు మరుగు స్థానము, బాష్పీభవన స్థానములకు ఒకే విలువ వుండక మార్పు చెందుతూ ఉంటాయి.

(b) కెల్విన్ మానం లేదా కెల్విన్ సంపూర్ణ మానం నందు నిర్దేశ బిందువే దాని సంపూర్ణ లేదా పరమ శూన్య బిందువు.

(c) సెల్సియస్ మానంలో ‘C అనునది సాధారణ పీడనం వద్ద మంచు మరుగు బిందువు. దానికి అనుగుణమైన పరమ ఉష్ణోగ్రత 273.15 K, 273.16 K అనే ఉష్ణోగ్రత నీటి త్రిక బిందువును సూచిస్తుంది. ఈ సంబంధంను బట్టి నీటి త్రిక బిందువు సెల్సియస్ మానం నందు = 273.16 – 273.15 = 0.01°C.

(d) ఫారన్ హీట్ మానం మరియు పరమ ఉష్ణోగ్రతల మధ్య సంబంధము

నీటి త్రిక బిందువు ఉష్ణోగ్రత 273.16 K అనునది కొత్త ఉష్ణోగ్రత మానంలో
= 273.16 × \(\frac{9}{5}\) = 491.69

ప్రశ్న 5.
A, B అనే ఆదర్శవాయు థర్మామీటర్లలో వరుసగా ఆక్సిజన్, హైడ్రోజన్ వాయువులను ఉపయోగించారు. కింది పరిశీలనలు చేయడమైంది.

(a) A, B థర్మామీటర్లు సూచించే సల్ఫర్ సాధారణ ద్రవీభవన స్థానం పరమ ఉష్ణోగ్రత ఎంత ?
(b) A, B థర్మామీటర్ల జవాబులో స్వల్పంగా తేడా ఉండటానికి గల కారణాన్ని మీరు ఏమని ఊహిస్తున్నారు ? (థర్మామీటర్లలో ఎలాంటి దోషం లేదు) రెండింటి రీడింగ్ల మధ్య ఉన్న తేడాను తగ్గించడానికి పై ప్రయోగంలో ఇంకా ఏ పద్ధతి అవసరం ?
సాధన:
సల్ఫర్ ద్రవీభవన స్థానంను “T” అనుకొనుము.
(a) థర్మామీటర్ A లో T = \(\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{tr}}}\) × 273.16 = \(\frac{1.797 \times 10^5}{1.250 \times 10^5}\) × 273.16 = 392.69K
థర్మామీటర్ B లో T = \(\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{tr}}}\) × 273.16 = \(\frac{0.287 \times 10^5}{0.200 \times 10^5}\) × 273.16 = 391.98 K

(b) థర్మామీటర్ A మరియు B ల సమాధానముల యందు స్వల్ప తేడా వచ్చుటకు కారణం ఆక్సిజన్ మరియు హైడ్రోజన్ వాయువులు కచ్చితమైన ఆదర్శవాయువులు కావు.

ఇలాంటి అసమానతను తగ్గించాలంటే, అతి తక్కువ పీడనం వద్ద పరిశీలనలను తీసుకోవాలి. ఇలాంటి సందర్భము నందు వాయువులు ఆదర్శ వాయు ప్రవర్తనకు దగ్గరగా వుండగలవు.

ప్రశ్న 6.
1m పొడవు ఉన్న ఉక్కు కొలబద్ద 27.0°C ఉష్ణోగ్రత వద్ద సరియైన కొలతను ఇచ్చే విధంగా క్రమాంకనం చేశారు. బాగా వేడిగా ఉన్న రోజు, అంటే 45.0°C ఉష్ణోగ్రత ఉన్నప్పుడు ఈ కొలబద్ద ఉక్కు కడ్డీ పొడవును 63.0 cm గా కొలిచింది. ఆ రోజున ఉక్కు కడ్డీ అసలు పొడవు ఎంత ? 27.0°C ఉష్ణోగ్రత ఉన్న రోజున అదే ఉక్కు కడ్డీ పొడవు ఎంత ? ఉక్కు దైర్ఘ్య వ్యాకోచ గుణకం = 1.20 × 10^-5°K^-1
సాధన:
27°C వద్ద ఉక్కు కొలబద్ద పొడవు 100 cm. i.e., L = 100 cm మరియు T = 27°C
45°C వద్ద ఉక్కు కొలబద్ద పొడవు L’ = L + ∆L = L + αL∆T
= 100 + (1.20 × 10^-5°) × 100 × (45° – 27°) = 100.0216 cm.
27°C వద్ద కొలబద్దపై 1 భాగము పొడవు 45°C = 100.0216/100 cm.
63 cm ల ఉక్కు కడ్డీని కొలచిన పొడవు 45°C = \(\frac{100.0216}{100}\) × 63 = 63.0136 cm
27°C ఉష్ణోగ్రత ఉన్న రోజున అదే ఉక్కు కడ్డీ పొడవు = 63 × 1 = 63 cm.

ప్రశ్న 7.
ఒక పెద్ద ఉక్కు చక్రాన్ని అదే పదార్థంతో చేసిన కమ్మీపై 27°C ఉష్ణోగ్రత వద్ద బిగించాలి. ఆ కమ్మీ వెలుపల వ్యాసం 8.70 cm, చక్రం మధ్య ఉన్న రంధ్రం వ్యాసం 8.69 cm. కమ్మీని పొడి మంచు ఉపయోగించి చల్లబరచారు. కమ్మీ ఏ ఉష్ణోగ్రత వద్ద చక్రాన్ని కమ్మీపై బిగించవచ్చు. మనకు కావలసిన ఉష్ణోగ్రత అవధిలో ఉక్కు దైర్ఘ్య వ్యాకోచ గుణకం స్థిరంగా ఉంటుంది అని అనుకోండి. α_{ఉక్కు} 1.20 × 10^-5 K^-1.
సాధన:
ఇచ్చట T₁ = 27°C = 27 + 273 = 300 K.
T₁K ఉష్ణోగ్రత వద్ద పొడవు = l_T1 = 8.70 cm;
T₂ K ఉష్ణోగ్రత వద్ద పొడవు = l_T2 = 8.69 cm
పొడవులో మార్పు = l_T2 – l_T1 = l_T1 α (T₂ – T₁) (లేదా) 8.69 – 8.70 = 8.70 × (1.20 × 10^-5) (T₂ – 300)
(లేదా) T₂ – 300 = – \(\frac{0.01}{8.70 \times 1.2 \times 10^{-5}}\) = -95.8 (లేదా) T₂ = 300 – 95.8 = 204.2 K = – 68.8°C.

ప్రశ్న 8.
ఒక రాగి పలకలో రంధ్రం చేశారు. 27°C వద్ద ఆ రంధ్రం వ్యాసం 4.24 cm. ఆ పలకను 227°C కు వేడిచేసినప్పుడు ఆ రంధ్రం వ్యాసంలో కలిగే మార్పు ఎంత ? రాగి దైర్ఘ్య వ్యాకోచ గుణకం = 1.70 × 10^-5 K^-1
సాధన:
ఈ లెక్కలో వేడిచేసినపుడు రాగి రేకు విస్తీర్ణ వ్యాకోచము ఇమిడి ఉంటుంది.
27°C వద్ద రంధ్రం వైశాల్యం, S₁ = \(\frac{\pi \mathrm{D}_1^2}{4}=\frac{\pi}{4}\) × (4.24)² cm²
227°C వద్ద రంధ్రం వ్యాసార్ధం, D₂ cm అయిన
227°C వద్ద రంధ్రం వైశాల్యం, S₂ = \(\frac{\pi \mathrm{D}_2^2}{4}\) cm².
రాగి విస్తీర్ణ వ్యాకోచ గుణకం β = 2 α = 2 × 1.70 × 10^-5 = 3.4 × 10^-5 °C^-1
వైశాల్యంలో పెరుగుదల = S₂ – S₁ = βS₁∆T (లేదా) S₂ = S₁ + βS₁∆T = S₁ (1 + β∆T)
\(\frac{\pi \mathrm{D}_2^2}{4}=\frac{\pi}{4}\) (4.24)² [1 + 3.4 × 10^-5 (228 – 27)] (లేదా) D₂² = (4.24)² × 1.0068
D₂ = 4.2544 cm
వ్యాసంలో మార్పు = D₂ – D₁ = 4.2544 – 4.24 = 0.0144 cm

ప్రశ్న 9.
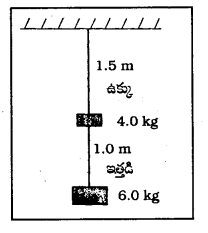
1.8 m పొడవు, 20 mm వ్యాసం ఉన్న ఒక ఇత్తడి తీగను 27°C వద్ద రెండు దృఢమైన ఆధారాల మధ్య తీగలో స్వల్ప తన్యత ఉండేటట్లు బిగించారు. ఒకవేళ తీగను -39°C ఉష్ణోగ్రతకు చల్లబరిస్తే, తీగలో ఏర్పడే తన్యత ఎంత ? తీగ వ్యాసం 2.0 mm. ఇత్తడి దైర్ఘ్య వ్యాకోచ గుణకం 2.0 × 10^-5 K^-1; ఇత్తడి యంగ్ గుణకం = 0.91 × 10¹¹ Pa.
సాధన:
ఇచ్చట L = 1.8 m, T₁ = 27°C, T₂ = -39°C, F = ?, r = 1 mm = 10^-3 m,
α = 2 × 10^-5 °K^-1, Y = 0.91 × 10¹¹ N/m²
Y = \(\frac{F \cdot L}{a \Delta L}\) . ∆L = \(\frac{F L}{a Y}\) నుండి
ఇంకా ∆L = α L ∆T ∴ \(\frac{F L}{a Y}\) = α L ∆T (లేదా) F = α∆TaY = α(T₂ – T₁) πr²Y
= 2 × 10^-5 × (39 – 27) × \(\frac{22}{7}\) (10^-3)² × 0.91 × 10¹¹ = -3.77 × 10² N
తీగ సంకోచం చెందునపుడు బలం లోపలి వైపు పనిచేయును అని ఋణగుర్తు తెలుపుతున్నది.

ప్రశ్న 10.
50 cm పొడవు, 3.0 mm వ్యాసం ఉన్న ఒక ఇత్తడి కడ్డీని అంతే పొడవు, వ్యాసం ఉన్న మరొక ఉక్కు కడ్డీతో జతపరచారు. వాటి తొలి పొడవులు 40°C వద్ద ఉంటే, 250°C ఉష్ణోగ్రత వద్ద ఆ సంయోగ కడ్డీ పొడవులో కలిగే మార్పు ఎంత ? ఆ రెండు కడ్డీలు కలిసే సంధి వద్ద ఉష్ణప్రతిబలం ఏర్పడుతుందా ? కడ్డీ ఛివరి కొనలు స్వేచ్ఛగా వ్యాకోచించగలవు. (ఇత్తడి, ఉక్కు కడ్డీల దైర్ఘ్య వ్యాకోచ గుణకాలు వరుసగా 2.0 × 10^-5K^-1, 1.2 × 10^-5 K^-1).
సాధన:
∆L₁ =L₁α₁∆T= 50 × (2.10 × 10^-5 )(250 – 40) = 0.2205 cm
∆L₂ = L₂α₂∆T = 50(1.2 × 10^-5) (250 – 40) = 0.126 cm
∴ సంయోగ కడ్డీలో మార్పు = ∆L₁ + ∆L₂ = 0.220 + 0.126 = 0.346 cm

ప్రశ్న 11.
గ్లిసరిన్ ఘనపరిమాణ వ్యాకోచ గుణకం 49 × 10^-5K^-1. ఉష్ణోగ్రతను 30°C కు పెంచితే దాని సాంద్రతలో కలిగే అంశిక మార్పు ఎంత ?
సాధన:
ఇచ్చట γ = 49 × 10^-5K^-1,
∆T = 30°C
V’ = V + ∆V = V(1 + γ∆T)
∴ V’ =V(1 + 49 × 10^-5 × 30) = 1.0147 V
ρ = కనుక ρ’ = \(\frac{\mathrm{m}}{\mathrm{V}^{\prime}}=\frac{\mathrm{m}}{1.0147 \mathrm{~V}}\) = 0.9855p
సాంద్రతలో కలిగే అంశిక మార్పు = \(\frac{\rho-\rho^{\prime}}{\rho}=\frac{\rho-0.9855 \rho}{\rho}\) = 0.0145

ప్రశ్న 12.
8.0 kg ద్రవ్యరాశి ఉన్న ఒక చిన్న అల్యూమినియం దిమ్మెలో రంధ్రం వేయడానికి 10kW (రంధ్రాలు చేసే) యంత్రాన్ని ఉపయోగించారు. 50% యంత్రం సామర్థ్యం యంత్రం వేడెక్కడానికి లేదా పరిసరాలలోకి ఉష్ణ నష్టం జరగడానికి ఉపయోగపడింది అనుకొంటే 2.5 నిమిషాలలో దిమ్మె ఉష్ణోగ్రతలో కలిగే పెరుగుదల ఎంత ? అల్యూమినియం విశిష్ట గుప్తోష్ణం = 0.91 Jg^-1 °K^-1,
సాధన:
ఇచ్చట P = 10 k W = 10⁴W, ద్రవ్యరాశి,m = 8.0 kg = 8 × 10³ g
ఉష్ణోగ్రతలో తగ్గుదల AT = ?, కాలం t = 2.5 నిమిషాలు = 2.5 × 60 = 150s
రాగి విశిష్టోష్టం, C = 0.91 Jg^-1 K^-1
మొత్తం శక్తి Q = P × t = 10⁴ × 150 = 15 × 10⁵ J
50% శక్తి నష్టపోయిన ఉపయోగించుటకు వీలుగా వున్న శక్తి ∆Q = \(\frac{1}{2}\) × 15 × 10⁵ = 7.5 × 10⁵ J
As, ∆Q = m c ∆T
∴ ∆T = \(\frac{\Delta Q}{\mathrm{mc}}=\frac{7.5 \times 10^5}{8 \times 10^3 \times 0.91}\) = 103°C

ప్రశ్న 13.
2.5 kg ద్రవ్యరాశి ఉన్న ఒక రాగి దిమ్మెను కొలిమిలో 500°C ఉష్ణోగ్రతకు వేడిచేసి ఒక పెద్ద మంచు దిమ్మెపై ఉంచారు. అప్పుడు గరిష్ఠంగా కరిగే మంచు పరిమాణం ఎంత ? (రాగి విశిష్టోష్ణం = 0.39 Jg^-1 K^-1 నీటి ద్రవీభవన గుప్తోష్ణం = 335 Jg^-1 ).
సాధన:
రాగి దిమ్మె ద్రవ్యరాశి m = 2.5 kg = 2500 g ;
రాగి విశిష్టోష్ణం c = 0.39 J g^-1 K^-1;
ఉష్ణోగ్రతలో తగ్గుదల ∆T = 500 – 0 = 500°C
ద్రవీభవన గుప్తోష్ణం L = 335 J g^-1
కరుగుచున్న మంచు ద్రవ్యరాశిని m’ అని అనుకొనుము.
మంచు గ్రహించిన ఉష్ణరాశి = రాగి కోల్పోయిన ఉష్ణరాశి
∴ m’L = mc ∆T
m’ = \(\frac{\mathrm{mc} \Delta \mathrm{T}}{\mathrm{L}}=\frac{2500 \times 0.39 \times 500}{335}\) = 1500g = 1.5kg

ప్రశ్న 14.
ఒక పదార్థం విశిష్టోష్ణం కనుక్కొనే ప్రయోగంలో 150°C వద్ద ఉన్న 0.20 kg ల ఒక లోహపు దిమ్మెను 27°C వద్ద 150 cm3 నీరు ఉన్న కెలోరిమీటరు (జల తుల్యాంకం 0.025 kg) లోకి జారవిడిచారు. తుది ఉష్ణోగ్రత 40°C. లోహపు దిమ్మె విశిష్టోష్ణం గణన చేయండి. పరిసరాలలోకి నష్టపోయిన ఉష్ణం విస్మరించదగినంత కాకపోతే మీ సమాధానం ఆ పదార్థం విశిష్టోష్టం అసలు విలువ కంటే ఎక్కువగా ఉంటుందా లేదా తక్కువగా ఉంటుందా ?
సాధన:
లోహం ద్రవ్యరాశి m = 0.20 kg = 200 g
లోహం ఉష్ణోగ్రతలో తగ్గుదల ∆T = 150 – 40 = 110°C
‘C’ అనునది లోహం విశిష్టోష్టం అయిన లోహం కోల్పోయిన ఉష్ణరాశి
∆Q = mC∆T = 200 × c × 110 ………………. (i)
నీటి ఘనపరిమాణం = 150 c.c.
∴ నీటి ద్రవ్యరాశి m’. = 150 g
కైలోరి మీటరు నీటి తుల్యాంకం w = 0.025 kg = 25 g
నీటి మరియు కెలోరీ మీటరు ఉష్ణోగ్రతలో పెరుగుదల ∆T’ = 40 – 27 = 13°C
నీరు మరియు కెలోరీ మీటరు గ్రహించిన ఉష్ణరాశి
∆Q’ = (m’ + w)∆T’ = (150 + 25) × 13 = 175 × 13 …………….. (ii)
∆Q = ∆Q’ కావున
∴ (i) మరియు (ii) సమీకరణముల నుంచి 200 × c × 110 = 175 × 13 (లేదా) c = \(\frac{175 \times 13}{200 \times 110}\) ≈ 0.1.
పరిసరాలకు కొంత ఉష్ణం నష్టపోవడం వలన నిజ విలువ కన్నా సాధించిన c విలువ తక్కువగా ఉంటుంది.

ప్రశ్న 15.
గది ఉష్ణోగ్రత వద్ద కొన్ని సాధారణ వాయువుల మోలార్ విశిష్టోష్టాలపై చేసిన పరిశీలనలు కింద ఇవ్వడమైంది.

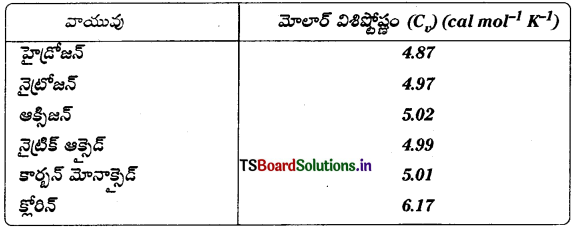
ఈ విధంగా కొలచిన వాయువుల మోలార్ విశిష్టోష్ట విలువలు ఏక పరమాణు వాయువుల విలువల కంటె విశేషంగా భిన్నమైనవి. ఉదాహరణకు, ఏక పరమాణుక వాయువు మోలార్ విశిష్టోష్ణం 2.92 cal/mol K. ఈ వ్యత్యాసం ఎందుకో వివరించండి. క్లోరిన్ విలువ కొంత వరకు అధికంగా (మిగతా వాటి కంటే) ఉండటాన్ని బట్టి ఏమి చెప్పవచ్చు ?
సాధన:
పైన పట్టికలో ఇవ్వబడిన వాయువుల ద్వి పరమాణు వాయువులు, ఏక పరమాణు వాయువులు కావు. ద్విపరమాణువు వాయువుల మోలార్ విశిష్టోష్ణం = \(\frac{1}{2}\)R = \(\frac{5}{2}\) × 1.98=4 .95 ఈ పట్టిక నందు ఇచ్చిన పరిశీలనల దృష్ట్యా క్లోరిన్ మినహాయించి మిగిలిన వాయువులు అన్నియూ నియమానుసారం ఉన్నట్లుగా ఆమోదించవచ్చును. ఏక పరమాణు వాయువులలో β అణువులకు స్థానాంతర చలనం మాత్రమే ఉంటుంది.

ద్వి పరమాణువు వాయువులో β అణువులు స్థానాంతర చలనంతో పాటు కంపన మరియు భ్రమణ చలనాలను కూడా కలిగి ఉంటాయి. అందువలన 1 మోల్ ద్విపరమాణు వాయువు ఉష్ణోగ్రతను 1°C పెంచుటకు, స్థానాంతర శక్తితో పాటుగా, భ్రమణ మరియు కంపన శక్తులను పెంచుటకు కావలసిన ఉష్ణరాశిని సరఫరా చేయవలెను. అందువల్ల మోలార్ విశిష్టోష్టం ఏక పరమాణు వాయువుల కన్నా ద్వి పరమాణు వాయువులకు ఎక్కువ.

గది ఉష్ణోగ్రత వద్ద క్లోరిన్ మోలార్ విశిష్టోష్ణం విలువ మిగిలిన ద్విపరమాణు వాయువులు హైడ్రోజన్, నైట్రోజన్, ఆక్సిజన్ మొ॥ కన్నా అధికముగా ఉండటాన్ని బట్టి క్లోరిన్క స్థానాంతర, భ్రమణ చలనాలతో పాటు కంపన చలనాలు కూడా ఉంటాయి. మిగిలిన వాయువులకు స్థానాంతర మరియు భ్రమణ చలనాలు మాత్రమే ఉంటాయి. ఈ కారణం వలన క్లోరిన్ వాయువు కొంత అధిక మోలార్ విశిష్టోష్ణం విలువను కలిగి ఉంటుంది.

ప్రశ్న 16.
కార్బన్ డై ఆక్సైడ్ P-T ప్రావస్థా పటం ఆధారంగా కింది ప్రశ్నలకు సమాధానాలను ఇవ్వండి.
(a) ఏ ఉష్ణోగ్రతా పీడనాల వద్ద సమతాస్థితిలో CO₂ ఘన, ద్రవ, బాష్ప స్థితులు కలిసి ఉంటాయి ?
(b) CO₂ ఘనీభవన, బాష్పీభవన స్థానాలపై పీడన తగ్గుదల ప్రభావమేమిటి ?
(c) CO₂ సందిగ్ధ ఉష్ణోగ్రత, పీడన విలువలు ఏమిటి ? వాటి ప్రాముఖ్యత ఏమిటి ?
(d) క్రింది వివిధ సందర్భాలలో CO₂ ఘనమా, ద్రవమా లేదా వాయువా తెలపండి. a) 1atm, – 70°C వద్ద b) 10atm, -60°C వద్ద c) 56 atm, 15°C వద్ద ?

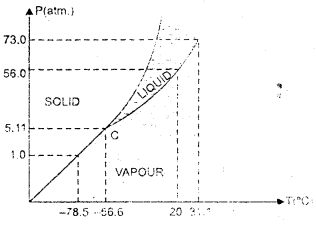
సాధప:
(a) -56.6° C ఉష్ణోగ్రత, 5.11 వాతావరణ పీడనం (త్రిక బిందువు) ల వద్ద CO₂, ఘన, ద్రవ మరియు బాష్ప స్థితులు కలసి ఉంటాయి.

(b)పీడనాన్ని తగ్గిస్తూ ఉంటే, CO₂ యొక్క ఘనీభవన మరియు బాష్పీభవన స్థానాలు తగ్గుతాయి.

(c) CO₂ సందిగ్ధ ఉష్ణోగ్రత విలువ 31.1°C మరియు సందిగ్ధ పీడనము విలువ 73 వాతావరణ పీడనము. CO₂ ఉష్ణోగ్రత 31.1°C కన్నా పెంచినపుడు ఎంత ఎక్కువ పీడనాన్ని ప్రయోగించిన అది ద్రవంగా మారదు.

(d) (a) 1 atm, -70° C వద్ద CO₂ వాయువు వాయు స్థితిలో ఉంటుంది.
(b) 1 atm, -60°C వద్ద CO₂ ఘన స్థితిలో ఉంటుంది.
(c) 56 atm, 150°C వద్ద CO₂ ద్రవ స్థితిలో ఉంటుంది.

ప్రశ్న 17.
CO₂ P-T ప్రావస్థా పటం ఆధారంగా క్రింది ప్రశ్నలకు సమాధానాలు ఇవ్వండి.
(a) 1 atm పీడనం, -60°C ఉష్ణోగ్రత వద్ద CO₂ ను సమోష్ణోగ్రతా ప్రక్రియలో సంపీడనం చెందిస్తే దానిలో మార్పు ద్రవ ప్రావస్థ ద్వారా జరుగుతుందా ?
(b) 4 atm పీడనం వద్ద ఉన్న CO₂ను స్థిర పీడనం వద్ద గది ఉష్ణోగ్రత నుంచి చల్లబరిస్తే ఏమవుతుంది ?
(c) 10 atm పీడనం, -65°C ఉష్ణోగ్రత వద్ద నిర్దిష్ట ద్రవ్యరాశి ఉన్న ఘన CO₂ ను స్థిర పీడనం వద్ద గది ఉష్ణోగ్రతకు వేడిచేస్తే, దానిలో కలిగే మార్పులను గుణాత్మకంగా వివరించండి.
(d) CO₂ను 70°C ఉష్ణోగ్రతకు వేడిచేసి సమోష్ణోగ్రతా ప్రక్రియలో సంపీడనం చెందించారు. దాని ధర్మాలలో ఎలాంటి మార్పులు కలుగుతాయో మీరు ఊహించగలరా ?
సాధన:
(a) 60°C ఉష్ణోగ్రత వక్రంలో 56.6°C కు ఎడమవైపు ఉన్నది. అనగా ఇది ఘన మరియు బాష్ప ప్రదేశాలలో ఉంటుంది. కావున CO₂ ద్రవ ప్రావస్థను చేరకుండా బాష్ప ప్రావస్థ నుండి ఘన ప్రావస్థను చేరుతుంది.

(b) CO₂ పీడనం 4 atm విలువ 5.11 atm ల కన్నా తక్కువగా ఉన్నది కావున, అది ద్రవ ప్రావస్థను పొందకుండా నేరుగా ఘనీభవిస్తుంది.

(c) 10 atm పీడనం, -65°C ఉష్ణోగ్రత వద్ద నిర్దిష్ట ద్రవ్యరాశి ఉన్న ఘన CO₂ ను స్థిర పీడనం వద్ద వేడిచేస్తే ఘన స్థితి నుండి ద్రవ స్థితికి మారి ఆ తరువాత బాష్ప స్థితికి చేరుతుంది. P-T పటంలో క్షితిజ సమాంతర రేఖ 10 atm స్థిర పీడనం వద్ద ఘనీభవన, బాష్పీభవన వక్రాలను ఖండించే బిందువులు ఘనీభవన, బాష్పీభవన బిందువులను ఇస్తాయి.

(d) CO₂ ను 70°C ఉష్ణోగ్రతకే వేడిచేసి సమ ఉష్ణోగ్రతా ప్రక్రియలో సంపీడనం చెందించిన ద్రవస్థితికి పరివర్తనను విస్పష్టంగా ప్రదర్శించదు. ఎందుకనగా వాయువు ఉష్ణోగ్రత, సందిగ్ధ ఉష్ణోగ్రత కన్నా ఎక్కువ. కాని పీడనం అధికమయ్యే కొలదీ ఆదర్శ వాయు ప్రవర్తన నుంచి విచలనము పెరుగుతుంది.

ప్రశ్న 18.
ఒక బాలుడు 101°F ఉష్ణోగ్రత జ్వరంతో ఉన్నాడు. అతడు జ్వరాన్ని తగ్గించే ఆంటీసైరిన్ మాత్ర తీసుకొన్నప్పుడు ఆ మాత్ర కారణంగా అతని దేహం నుంచి వెలువడే చెమట ఆవిరయ్యే రేటు పెరుగుతుంది. 20 నిమిషాలలో బాలుడి జ్వరాన్ని 98°Fకు తగ్గిస్తే, ఆ మాత్ర వల్ల కలిగే ఆదనపు ఆవిరయ్యే రేటు ఎంత ? ఆవిరిగా మారే క్రియ వల్లనే ఉష్ణ నష్టం జరుగుతుంది అనుకోండి. బాలుడి ద్రవ్యరాశి 30 kg. మానవ దేహం విశిష్టోష్ణం ఉజ్జాయింపుగా నీటి విశిష్టోష్ణానికి సమానం. ఆ ఉష్ణోగ్రత వద్ద నీటి ఆవిరి గుప్తోష్టం సుమారుగా 580 cal g^-1,
సాధన:
ఉష్ణోగ్రతలో తగ్గుదల, ∆T = 101 – 98 = 3°F = 3 × \(\frac{5}{9}\)°C = 5/3°C
బాలుడు ద్రవ్యరాశి, m = 30 kg
మానవ శరీరం విశిష్టోష్ణం = నీటి విశిష్టోష్ణం c = 1000 cal. kg^-1 °C^-1
∴ బాలుడు నష్టపోయిన ఉష్ణరాశి, ∆Q = mc∆T = 30 × 1000 × \(\frac{5}{3}\) = 50000 cals
20 నిమిషాలలో ఆవిరి అయిన నీటి ద్రవ్యరాశి m’ అయిన m’L = ∆Q (లేదా) m’ = \(\frac{\Delta Q}{L}\) = \(\frac{50000}{580}\) = 86.2g
∴ అధికంగా ఆవిరి కాబడిన నీటి సగటు రేటు = \(\frac{86.2}{20}\) = 4.31 g min^-1

ప్రశ్న 19.
ప్రత్యేకంగా వేసవి కాలంలో తక్కువ పరిమాణంలో వండిన ఆహారాన్ని నిల్వ చేయడానికి చౌకయిన, సమర్థవంతమైన పద్ధతి థర్మోకోల్ మంచుపెట్టె. 30 cm పొడవు గల ఘన మంచు పెట్టె మందం 5.0 cm. ఆ పెట్టెలో 4.0 kg ల మంచును ఉంచారు. 6 గంటల తరువాత మిగిలి ఉండే మంచు పరిమాణాన్ని అంచనా వేయండి. వెలుపలి ఉష్ణోగ్రత 45°C, థర్మోకోల్ ఉష్ణ వాహకత్వ గుణకం 0.01 J s^-1 m^-1K^-1 [నీటి ద్రవీభవన ఉష్ణం = 335 × 10^-3 J kg^-1]
సాధన:
మంచు పెట్టె పొడవు, l = 30 cm = 0.3 m;
మందం, ∆x = 5 cm = 0.05 m
మొత్తం ఉపరితల వైశాల్యం, A = 6l² = 6 × 0.3 × 0.3 = 0.54 m²
ఉష్ణోగ్రతలో వ్యత్యాసము, ∆T = 45 – 0 = 45°C, K = 0.01 Js^-1 m^-1 K^-1
కాలం = ∆t = 6hrs = 6 × 60 × 60s
ద్రవీభవన గుప్తోష్టం, L = 335 × 10³ J / kg
ఈ కాలంలో కరిగిన మంచు ద్రవ్యరాశిని ‘m’ అనుకొనిన ∆Q = mL = KA\(\left(\frac{\Delta \mathrm{T}}{\Delta \mathrm{x}}\right)\)ΔΤ
m = KA \(\left(\frac{\Delta \mathrm{T}}{\Delta \mathrm{x}}\right) \frac{\Delta \mathrm{t}}{\mathrm{L}}\) = 0.01 × 0.54 × \(\frac{45}{0.05}\) × \(\frac{6 \times 60 \times 60}{335 \times 10^3}\) = 0.313kg
∴ మిగిలిన మంచు ద్రవ్యరాశి = 4 – 0.313 = 3.687 kg.

ప్రశ్న 20.
ఒక ఇత్తడి బాయిలర్ అడుగు భాగం వైశాల్యం 0.15 m², మందం 1.0 cm. దీనిని ఒక గ్యాస్ స్టవ్ పై పెట్టినప్పుడు 6.0 kg/min రేటున నీటిని మరిగిస్తుంది. బాయిలర్తో స్పర్శలో ఉన్న మంటలోని కొంత భాగం ఉష్ణోగ్రతను అంచనా వేయండి. ఇత్తడి-ఉష్ణవాహకత్వం = 109 J s^-1 m^-1 K^-1; నీటి బాష్పీభవన ఉష్ణం = 2256 × 10³ J kg^-1.
సాధన:
ఇచ్చట A = 0.15 m², ∆x = 1.0 cm = 10^-2 m.
\(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{t}}=\frac{6 \times 10^3 \times 2256}{60}\) Js^-1 = 2256 × 10² Js^-1
K = 609 J s^-1 m^-1 °C^-1, ∆T = (t-100)
\(\frac{\Delta Q}{\Delta t}\) = KA \(\left(\frac{\Delta T}{\Delta \mathrm{x}}\right)\) నుండి 2256 × 10² = 609 × 0.15\(\frac{(\mathrm{t}-100)}{10^{-2}}\)
t – 100 = \(\frac{2256}{609 \times 0.15}\) = 24.70
⇒ t = 124.70°C

ప్రశ్న 21.
ఎందుకో వివరించండి :
(a) అధిక పరావర్తకత ఉన్న వస్తువు అధమ ఉద్గారకం.
(b) అతి శీతలంగా ఉన్న రోజు చెక్క పళ్ళెం కంటే ఇత్తడి పాత్ర చాలా చల్లగా ఉంటుంది.
(c) పరిపూర్ణ కృష్ణ వస్తువు వికిరణానికి క్రమాంకనం చేసిన దృశా పైరామీటరు (అధిక ఉష్ణోగ్రత కొలవడానికి) బాహ్య ప్రదేశంలో ఉన్న బాగా ఎర్రగా వేడెక్కిన ఇనుప కడ్డీ ఉష్ణోగ్రతను చాలా తక్కువ విలువగా చూపుతుంది. కాని, అదే కడ్డీని కొలిమిలో అమర్చినప్పుడు ఆ ఉష్ణోగ్రత వద్ద సరైన విలువను చూపుతుంది.
(d) భూమిపై భూ వాతావరణం లేకుంటే జీవకోటి ఉండటానికి వీలులేనంత చల్లగా ఉండేది.
(e) వేడి నీటిని ప్రవహింపచేయడంపై ఆధారపడ్డ తాపన వ్యవస్థ కంటే ఆవిరిని ప్రవహింప చేయడంపై ఆధారపడ్డ తాపన వ్యవస్థ చాలా సమర్థవంతంగా భవంతిని వేడి చేయగలదు.
సాధన:
(a) అధిక పరావర్తకత కలిగిన వస్తువు ఉష్ణాన్ని అధమంగా శోషించుకుంటుంది. ప్రివోస్ట్ సిద్ధాంతము ప్రకారము అధమ శోషకాలు, అధమ ఉద్గారకాలు.

(b) అతిశీతలంగా ఉన్న రోజున ఇత్తడి పాత్రను తాకిన, ఉష్ణం మనిషి శరీరం నుండి ఇత్తడి పాత్రకు ప్రవర్తిస్తుంది. అందువల్ల ఇత్తడి పలక చల్లగా ఉంటుంది. చెక్క పళ్ళెంను తాకిన, ఉష్ణం మనిషి శరీరం నుండి పళ్ళెంనకు ప్రసరించదు.

(c) కొలమిలో అమర్చి బాగా ఎర్రగా వేడిచేసిన ఇనుపకడ్డీ ఉష్ణోగ్రత TK ను E = σT^-1 అను సంబంధము ద్వారా రాబట్టవచ్చు. T_o ఉష్ణోగ్రత కలిగిన బాహ్య ప్రదేశంలో ఉంచిన బాగా ఎర్రగా వేడెక్కిన ఇనుప కడ్డీ విడుదల చేసే శక్తిని, E = σ(T⁴ – T_o^4-) అను సంబంధము ద్వారా కనుగొనవచ్చు.

దృశ్యా పైరోమీటరు అను పరికరము వస్తువు యొక్క ప్రకాశం, దాని ఉష్ణోగ్రతపై ఆధారపడి ఉంటుందనే సూత్రముపై పనిచేస్తుంది. అందువల్ల బాహ్య ప్రదేశంలో ఉంచిన ఇనుప కడ్డీ ఉష్ణోగ్రతను చాలా తక్కువగా చూపుతుంది.

(d) సూర్యుని నుంచి భూమికి వచ్చే ఉష్ణ వికిరణాలలో పరారుణ వికిరణాలను భూవాతావరణంలోని పొరలు పరావర్తనం చెందించి భూఉపరితలానికి చేరుస్తాయి. దీని ఫలితంగా భూవాతావరణం వెచ్చగా ఉంటుంది. భూమిపై భూవాతావరణం లేకుంటే, పరారుణ వికిరణాలు పరావర్తనం జరగక జీవకోటి ఉండటానికి వీలు లేనంత చల్లగా ఉంటుంది.

(e) 100°C ఉష్ణోగ్రత వద్ద ఉన్న బాష్పం, 100°C ఉష్ణోగ్రత వద్ద ఉన్న అంతే ద్రవ్యరాశి కలిగిన వేడి నీటికన్నా ఎక్కువ ఉష్ణరాశిని కలిగియుంటుంది. 100°C వద్ద ఉన్న 1 గ్రామ్ నీటి ఉష్ణం కన్నా, 100°C వద్ద ఉన్న 1 గ్రామ్ బాష్పం 540 కెలరీల ఎక్కువ ఉష్ణరాశిని కలిగియుంటుంది. కావున వేడినీటిని ప్రవహింపచేయడంపై ఆధారపడ్డ తాపన వ్యవస్థ కంటే ఆవిరిని ప్రవహింపచేయటంపై ఆధారపడ్డ తాపన వ్యవస్థ చాలా సమర్థవంతంగా భవంతిని వేడి చేయగలదు.

ప్రశ్న 22.
ఒక వస్తువు 5 నిమిషాలలో 80°C నుంచి 50°C కు చల్లబడుతుంది. 60°C నుంచి 30°C కు చల్లబడటానికి పట్టే కాలం కనుక్కోండి. పరిసరాల ఉష్ణోగ్రత 20°C.
సాధన:
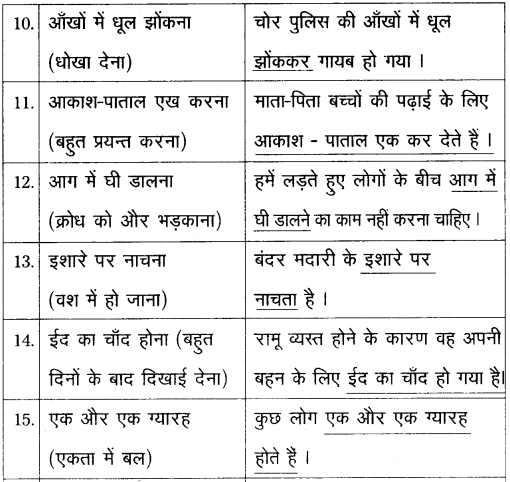
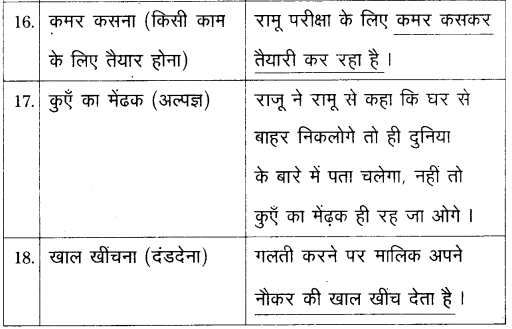
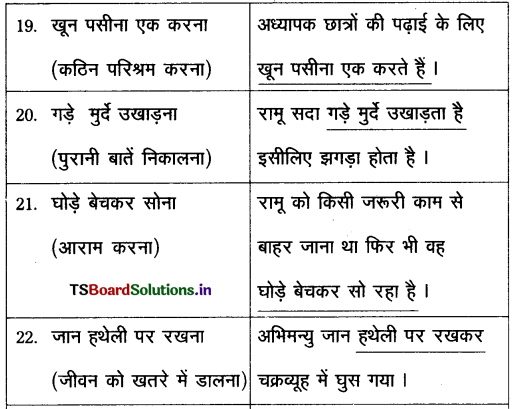
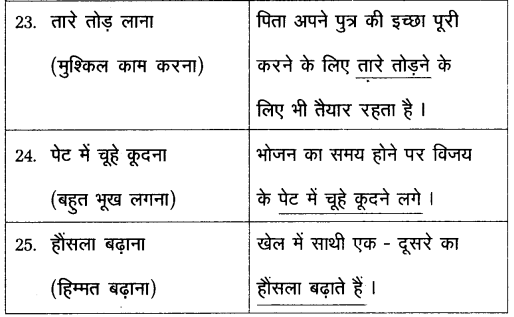
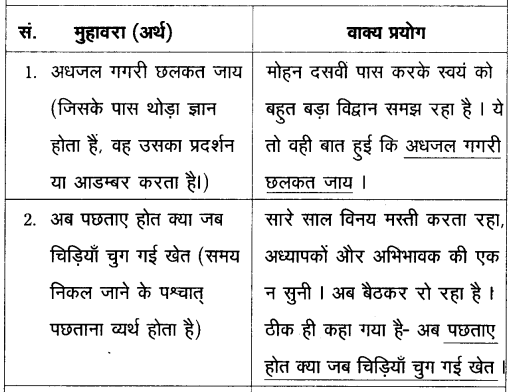
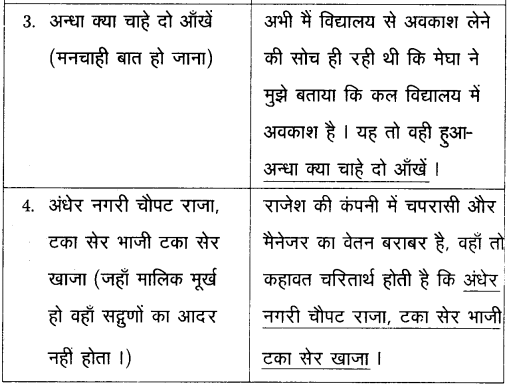
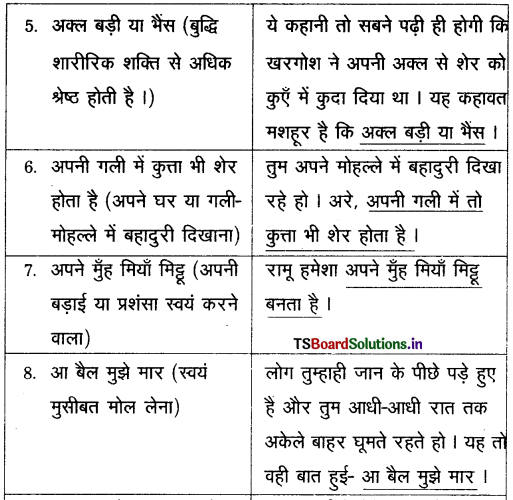
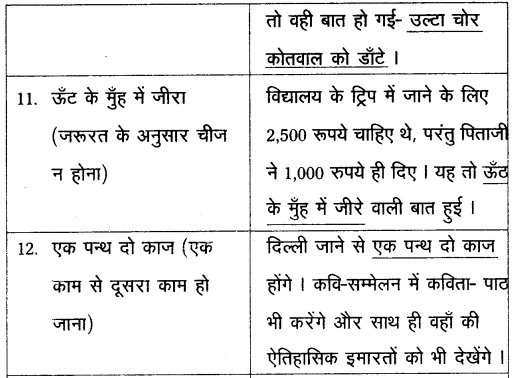
వస్తువు ఉష్ణోగ్రత మరియు పరిసరాల ఉష్ణోగ్రతలు వరుసగా T మరియు T_o అయిన న్యూటన్ శీతలీకరణ సిద్ధాంతము ప్రకారము
\(\frac{\mathrm{dT}}{\mathrm{dt}}\) = -K(T – T_o) (లేదా) \(\frac{\mathrm{dT}}{\mathrm{T}-\mathrm{T}_0}\) = -K dt
వస్తువు ఉష్ణోగ్రత T₁ నుంచి T₂ వరకు t అనే కాలంలో తగ్గిన పై సంబంధాన్ని సమాకలనం చేయగా

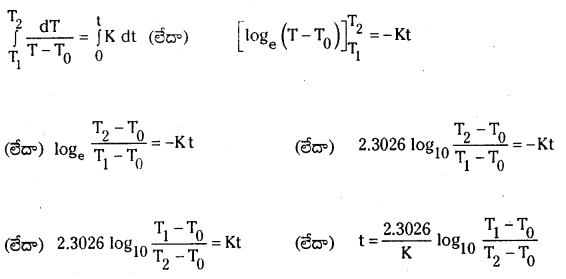
ప్రశ్నలోని మొదటి సందర్భమునకు,
T₁ = 80°C,
T₂ = 50°C,
T₀ = 20°C,
t = 5 min. = 5 × 60s

(లేదా) t = 5 × 60 × 2 = 10 × 60s = 10 min.

Students must practice these TS Intermediate Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(b)

I.
Question 1.
If |p̅| = 2, |q̅| = 3 and (p, q) = \(\frac{\pi}{6}\), then find |p̅ × q̅|².
Answer:
p̅ × q̅ = |p̅| |q̅| sinθn̂
Given p̅ = 2, q̅ = 3 and (p̅. q̅) = \(\frac{\pi}{6}\)
|p̅ × q̅| = (2) (3)sin\(\frac{\pi}{6}\) = 3
∴ |p̅ × q̅|² = 9

Question 2.
If a̅ = 2i̅ – j̅ + k̅ and b̅ = i̅ – 3j̅ – 5k̅, then find |a̅ × b̅|. (March 2013)
Answer:
a̅ = 2 i̅ – j̅ + k̅ and b̅ = i̅ – 3 j̅ – 5k̅

Question 3.
If a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅, then find (a̅ + b̅) × (a̅ – b̅).
Answer:
Given a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅
Then a̅ + b̅ = 3 i̅ + j̅ – k̅ and a̅ – b̅ = i̅ – 7j̅ + 3k̅
(a + b) × (a – b) = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -1 \\
1 & -7 & 3
\end{array}\right|\)
= i̅(3 – 7) – j̅(9 + l) + k̅ (- 21 – 1)
= -4i̅ – 10j̅ – 22k̅
= -2 (2i̅ + 5j̅ + 11k̅)

Question 4.
If 4i̅ + \(\frac{2 p}{3}\) j̅ + pk̅ is parallel to the vector 3 i̅ + 2j̅ + 3k̅, find p.
Answer:
Given 4i̅ + \(\frac{2 p}{3}\) j̅ + pk̅ is parallel to
i̅ + 2j̅ + 3k̅
∴ \(\frac{4}{1}=\frac{\frac{2 p}{3}}{2}=\frac{p}{3}\)
⇒ \(\frac{2 p}{3}\) = -4 ⇒ p = 12

Question 5.
Compute
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
Sol.
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) + (b̅ × a̅) + (c̅ × a̅) + (c̅ × b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) – (a̅ × b̅) – (a̅ × c̅) – (b̅ × c̅)
= 0

Question 6.
If p̅ = xi̅ + yj̅ + zk̅, then find |p̅ × k̅|².
Answer:
p̅ × k̅ = (xi̅ + yj̅ + zk̅) × k̅
= x(i̅ × k̅) + y(j̅ × k̅) + z(k̅ × k̅)
= -xj̅ + yi̅ + z(0)
= yi̅ – xj̅
|p̅ × k̅|² = x² + y²

Question 7.
Compute 2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
Sol.
2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
= 6(j̅ × i̅) – 8(j̅ × k̅) + (i̅ × k̅) + 2(j̅ × k̅)
= -6k̅ – 8i̅ – j̅ + 2i̅
= -6i̅ – j̅ – 6k̅

Question 8.
Find unit vector perpendicular to both i̅ + j̅ + k̅ and 2i̅ + j̅ + 3k̅.
Answer:
Given a̅ = i̅ + j̅ + k̅ and b̅ = 2i̅ + j̅ + 3k̅
then a̅ × b̅ = \(\left|\begin{array}{lll}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
2 & 1 & 3
\end{array}\right|\)
= i̅(3 – 1) – j̅(3 – 2) + k̅(1 – 2)
= 2i̅ – j̅ – k̅
|a̅ × b̅| = \(\sqrt{4+1+1}=\sqrt{6}\)
Unit vector perpendicular to both a̅ and b̅
= ±\(\frac{\overline{\mathrm{a}} \times \overline{\mathrm{b}}}{|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}=\pm\left(\frac{2 \overline{\mathrm{i}}-\overline{\mathrm{j}}-\overline{\mathrm{k}}}{\sqrt{6}}\right)\)

Question 9.
If θ is the angle between the vectors i̅ + j̅ and j̅ + k̅, then find sin θ.
Answer:
Let a̅ = i̅ + j̅ and b̅ = j̅ + k̅

Question 10.
Find the area of the parallelogram having a̅ = 2j̅ – k̅ and b̅ = – i̅ + k̅ as adjacent sides.
Answer:
Vector area of the parallelogram having
a̅ = 2j̅ – k̅ and b̅ = -i̅ + k̅ as adjacent sides = a̅ × b̅
= \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
0 & 2 & -1 \\
-1 & 0 & 1
\end{array}\right|\) = 2 i̅ + j̅ + 2k̅
Area of the parallelogram
= |a̅ × b̅| = \(\sqrt{4+1+4}\) = 3 sq. units.

Question 11.
Find the area of the parallelogram whose diagonals are 3i̅ + j̅ – 2k̅ and i̅ – 3j̅ + 4k̅.
Answer:
Let a̅ = 3i̅ + j̅ – 2k̅ and b̅ = i̅ – 3j̅ + 4k̅ be the diagonals of a parallelogram then its vector area = \(\frac{1}{2}\)(a̅ × b̅) and area |\(\frac{1}{2}\)(a̅ × b̅)|
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -2 \\
1 & -3 & 4
\end{array}\right|\)
= i̅ [4 – 6] – j̅ [12 + 2] + k̅ [-9 – 1]
= -2i̅ – 14j̅ – 10k̅
= 2(-i̅ – 7j̅ – 5k̅)
Vector area of parallelogram = |\(\frac{1}{2}\)(a̅ × b̅)|
= |[2(-i̅ – 7j̅ – 5k̅)]
= (-i̅ – 7j̅ – 5k̅)
Area of the parallelogram = |- i̅ – 7 j̅ – 5k̅|
= \(\sqrt{1+49+25}=\sqrt{75}\) = 5√3 sq. units.

Question 12.
Find the area of the triangle having 3 i̅ + 4j̅ and – 5 i̅ + 7j̅ as two of its sides.
Answer:
Area of the triangle = \(\frac{1}{2}\) \(|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (3i̅ + 4j̅) × (-5i̅ + 7j̅)
= -15(i̅ × i̅) – 20(j̅ × i̅) + 21(i̅ × j̅) + 28 (j̅ × j̅)
= 20k̅ + 21k̅ = 41k̅
Area of the ΔABC = \(\frac{1}{2}\) \((41) = 20.5 sq. units

Question 13.
Find unit vector perpendicular to the plane determined by the vectors a̅ = 4i + 3j – k and b̅ = 2 i – 6 j 3k .
Answer:
Here a̅ = 4 i̅ + 3 j̅ – k̅ and b̅ = 2 i̅ – 6 j̅ – 3k̅
then a̅ × b̅

= i̅(-15) – j̅(-10) + k̅(-30)
= -15i̅ +10j̅ – 30k̅
= -5(3i̅ – 2j̅ + 6k̅)
|a̅ × b̅| = 5[latex]\sqrt{9+4+36}\) = 5(7) = 35
∴ Unit vector perpendicular to the plane
= \(\pm \frac{5(3 \bar{i}-2 \bar{j}+6 \bar{k})}{35}\)
= \(\frac{\pm(3 \bar{i}-2 \bar{j}+6 \bar{k})}{7}\)

Question 14.
Find the area of the triangle whose vertices are A (1, 2, 3), B (2, 3, 1) and C (3, 1, 2). (Mar. ’14, ’06)
Answer:
Suppose i̅, j̅, k̅ are unit vectors along the coordinate axes.
Position vectors of A, B, C are i̅ + 2j̅ + 3k̅, 2i̅ + 3j̅ + k̅, 3i̅ + j̅ + 2k̅
\(\overline{\mathrm{AB}}\) = (2i̅ + 3j̅ + k̅) – (i̅ + 2j̅ + 3k̅)
= i̅ + j̅ – 2k̅
\(\overline{\mathrm{AC}}\) = (3 i̅ + j̅ + 2k̅) – (i̅ + 2 j̅ + 3k̅)
= 2i̅ – j̅ + k̅

\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}=\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -2 \\
2 & -1 & -1
\end{array}\right|\)
= i̅(-1 – 2) – j̅(-1 + 4) + k̅(-1 – 2)
= -3i̅ – 3 j̅ – 3k̅ = -3(i̅ + j̅ + k̅)
Area of the ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
= \(\frac{3}{2} \sqrt{1+1+1}=\frac{3 \sqrt{3}}{2}\)sq.units

II.
Question 1.
If a̅ + b̅ + c̅ = 0, then prove that a̅ × b̅ = b̅ × c̅ = c̅ × a̅.
Answer:
Given a̅ + b̅ + c̅ = 0
⇒ a̅ = -b̅ – c̅
∴ a̅ × b̅ = -(b̅ × b̅) – (c̅ × b̅)
= 0 + (b̅ × c̅) = (b̅ × c̅) …………(1)
Again a̅ + b̅ + c̅ = 0
⇒ c = -a̅ – b̅
⇒ c̅ × a̅ = (-a̅ – b̅) × a̅
= -(a̅ × a̅) – (b̅ × a̅)
= 0 + (a̅ × b̅)
∴ (c̅ × a̅) = (a̅ × b̅) …………..(2)
From (1) and (2), a̅ × b̅ = b̅ × c̅ – c̅ × a̅

Question 2.
If a̅ = 2i̅ + j̅ – k̅, b̅ = -i̅ + 2j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅, then find (a̅ × b̅) – (b̅ × c̅). (March 2015-A.P)
Answer:
Given a̅ = 2i̅ + j̅ – k̅, b̅ = – i̅ + 2 j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅
Then a̅ × b̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 1 & -1 \\
-1 & 2 & -4
\end{array}\right|\)
= i̅ (-4 + 2) – j̅ (-8 – 1) + k̅(4 + 1)
= -2i̅ + 9 j̅ + 5k̅
b̅ × c̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
-1 & 2 & -4 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (2 + 4) – j̅ (-1 + 4) + k̅(-1 – 2)
= 6i̅ – 3j̅ – 3k̅
(a̅ × b̅) – (b̅ × c̅) = (-2i̅ + 9j̅ + 5k̅) – (6i̅ – 3j̅ – 3k̅)
= -12 – 27 – 15
= -54

Question 3.
Find the vector area and the area of the parallelogram having a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅ as adjacent sides.
Answer:
Given a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅
Then the vector area of parallelogram = a̅ × b̅
∴ (a̅ x b̅) = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
1 & 2 & -1 \\
2 & -1 & 2
\end{array}\right|\)
= i̅ (4 – 1)- j̅ (2 + 2) + k̅(-1 – 4)
= 3i̅ – 4j̅ – 5k̅

Magnitude of the area = \(\sqrt{9+16+25}\)
= \(\sqrt{50}\) = 5√2 sq. units

Question 4.
If a̅ × b̅ = b̅ × c̅ ≠ 0, then show that a̅ + c̅ = pb̅, where p is some scalar.
Answer:
Consider (a̅ + c̅ – pb̅) × b̅
= (a̅ × b̅) + (c̅ × b̅) – p(b̅ × b̅)
= (b̅ × c̅) – (b̅ × c̅) – p(0) = 0
∴ a̅ + c̅ – pb̅ = 0 ⇒ a̅ + c̅ = pb̅

Question 5.
Let a and b be vectors, satisfying |a̅| = |b̅| = 5 and (a̅, b̅) = 45°. Find the area of the triangle having a̅ – 2b̅ and 3a̅ + 2b̅ as two of its sides. [March 2007]
Answer:
Area of the triangle = \(\frac{1}{2}\) |(a̅ – 2b̅) × (3a̅ + 2b̅)|
Now |(a̅ – 2b̅) × (3a̅ + 2b̅)|
= 13(a̅ × a̅) – 2(b̅ × a̅) – 6(b̅ × a̅) – 4(b̅ × b̅)|
= 12(a̅ × b̅) + 6(a̅ × b̅)| = 18(a̅ × b̅)|
= 8|a̅| |b̅| sin45°
= 8(5)(5)\(\frac{1}{\sqrt{2}}\)n̂
= 100√2n̂
From (1)
Area of the triangle = \(\frac{1}{2}\)(100)√2
= 50√2 sq. units

Question 6.
Find die vector having magnitude √6 units and perpendicular to both 2j̅ – k̅ and 3j̅ – i̅ – k̅.
Answer:
Let a̅ = 2 i̅ – k̅ and b̅ = 3i̅ – j̅ – k̅
Then a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{j} & \bar{i} & \bar{k} \\
2 & 0 & -1 \\
3 & -1 & -1
\end{array}\right|\)
= i̅(-1) – j̅(-2 + 3) + k̅(-2)
= – i̅ – j̅ – 2k̅
= -(i̅ + j̅ + 2k̅)
|a̅ × b̅| = \(\sqrt{1+1+4}=\sqrt{6}\)
Vector perpendicular to a̅ and b̅ and having magnitude √6 units is = -(i̅ + j̅ + 2k̅)
Unit vector perpendicular to a and b and having magnitude √6 units is ±\(\left(\frac{\bar{a} \times \bar{b}}{|\bar{a} \times \bar{b}|}\right)\)

Question 7.
Find unit vector perpendicular to the plane determined by the points P (1, – 1, 2), Q (2, 0, – 1) and R (0, 2, 1).
Answer:
Let O be the origin.
\(\overline{\mathrm{OP}}\) = i̅ – j̅ + 2k̅
\(\overline{\mathrm{OQ}}\) = 2i̅ – k̅
\(\overline{\mathrm{OR}}\) = 2j̅ + k̅
\(\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}-\overline{\mathrm{OP}}\) = (2i̅ – k̅) – (i̅ – j̅ + 2k̅)
= i̅ + j̅ – 3k̅
\(\overline{\mathrm{PR}}=\overline{\mathrm{OR}}-\overline{\mathrm{OP}}\) = (2j̅ + k̅) – (i̅ – j̅ + 2k̅)
= – i̅ + 3 j̅ – k̅

Now \(\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}=\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -3 \\
-1 & 3 & -1
\end{array}\right|\)
= i̅ (-1 + 9) – j̅ (-1 – 3) + k̅(3 + 1)
= 8i̅ + 4j̅ + 4k̅
= 4(2i̅ + j̅ + k̅)
\(|\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}|=4 \sqrt{4+1+1}=4 \sqrt{6}\)

∴ Unit vector perpendicular to the plane determined by the points P, Q and R is

Question 8.
If a̅. b̅ = a̅. c̅ and a̅ × b̅ = a̅ × c̅, a ≠ 0, then show that b̅ = c̅.
Answer:
a̅ . b̅ = a̅. c̅
⇒ a̅.b̅ – a̅.c̅ = 0
⇒ a̅ . (b̅ – c̅) = 0
⇒ b̅ – c̅ = 0 (or) a̅ is perpendicular to
b̅ – c̅ ……… (1) (∵ a̅ ≠ 0)
Again a̅ × b̅ = a̅ × c̅ = 0
⇒ a̅ × b̅ – a̅ × c̅
⇒ a̅ × (b̅ – c̅) = 0 (∵ a ≠ 0)
⇒ b̅ – c̅ = 0 (or) a is parallel to
b̅ – c̅ ………(2)
From (1) and (2);
b̅ – c̅ = 0 ⇒ b̅ = c

Question 9.
Find a vector of magnitude 3 and perpendicular to both the vectors b̅ = 2 i̅ – 2j̅ + k̅ and c̅ = 2i̅ + 2j̅ + 3k̅.
Answer:
b̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \vec{j} & \bar{k} \\
2 & -2 & 1 \\
2 & 2 & 3
\end{array}\right|\)
= i̅ [-6 – 2] – j̅ [6 – 2] + k̅ [4 + 4]
= -8i̅ – 4j̅ + 8k̅ = -4(2i̅ + j̅ – 2k̅)
∴ A vector of magnitude 3 and perpendicular to both the vectors b̅ and c̅ is = ± 3\(\frac{\bar{b} \times \bar{c}}{|\bar{b} \times \bar{c}|}\)
= 3\(\left[\frac{-4(2 \bar{i}+\bar{j}-2 \bar{k})}{12}\right]\)
= ± (2i̅ + j̅ – 2k̅)

Question 10.
If |a̅|=13, |b̅| = 5 and a̅. b̅ = 60, then find |a̅ × b̅|.
Answer:
We have |a̅ × b̅| = |a̅|² |b̅|² – (a̅. b̅)²
= (13)² (5)² – (60)²
= (169) 25 – 3600
= 4224 – 3600 = 625
|a̅ × b̅| = \(\sqrt{625}\) = 25

Question 11.
Find unit vector perpendicular to the plane passing through the points (1, 2, 3), (2,-1, 1) and (1,2,- 4). (March 2005)
Answer:
Let O’ be the origin and let A (1, 2, 3), B (2, – 1, 1) and C (1, 2,-4) be the given points.
Then \(\overline{\mathrm{OA}}\) = i̅ + 2 j̅ + 3k̅
\(\overline{\mathrm{OB}}\) = 2 i̅ – j̅ + k̅
\(\overline{\mathrm{OC}}\) = i̅ + 2j̅ – 4k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\)
= (2i̅ – j̅ + k̅) – (i̅ + 2j̅ + 3k̅)
= i̅ – 3 j̅ – 2k̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\)
= (i̅ + 2j̅ – 4k̅) – (i̅ + 2j̅ + 3k̅)
= -7k̅
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}=\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & -3 & -2 \\
0 & 0 & -7
\end{array}\right|\)
= i̅(21) – j̅(-7) + k̅(0)
= 7(3i̅ + j̅)
\(|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|=7 \sqrt{9+1}=7 \sqrt{10}\)

Unit vector perpendicular to the plane

III.
Question 1.
If a̅, b̅ and c̅ represent the vertices A, B and C respectively of ΔABC, then prove that |(a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)| is twice the area of ΔABC.
Answer:
Let ‘O’ be the origin and
\(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OC}}\) = c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = b – a
and \(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = c – a
∴ Area of ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\) ………(1)
Here \(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (b̅ – a̅) × (c̅ – a̅)
= (b̅ × c̅) – (a̅ × c̅) – (b̅ × a̅) + (a̅ × a̅)
= (b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅) (v a̅ × a̅ = 0)
∴ Area of ΔABC = \(\frac{1}{2}\)|b̅ × c̅ + c̅ × a̅ + a̅ × b̅|
⇒ |b̅ × c̅ + c̅ × a̅ + a̅ × b̅| = 2 (area of ΔABC)
⇒ |(a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)|
= 2 (area of ΔABC)

Question 2.
If a̅ = 2i̅ + 3j̅ + 4k̅, b̅ = i̅ + j̅ – k̅ and c̅ = i̅ – j̅ + k̅, then compute a̅ × (b̅ × c̅) and verify that it is perpendicular to a̅.
Answer:
b̅ × c̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -1 \\
1 & -1 & 1
\end{array}\right|\)
= i̅(1 – 1) – j̅(1 + 1) + k̅(-1 – 1)
= -2j̅ – 2k̅

a̅ × (b̅ × c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 3 & 4 \\
0 & -2 & -2
\end{array}\right|\)
= i̅(-6 + 8)- j̅(-4) + k̅(-4)
= 2i̅ + 4j̅ – 4k̅
Now [a̅ × (b̅ × c̅)].a̅
= (2i̅ + 4j̅ – 4k̅)(2i̅ + 3j̅ + 4k̅)
= 4 + 12 – 16 = 0
a̅ × (b̅ × c̅) is perpendicular to a̅.

Question 3.
If a̅ = 7i̅ – 2j̅ + 3k̅, b̅ = 2i̅ + 8k̅ and c̅ = i̅ + j̅ + k̅, then compute a̅ × b̅, a̅ × c̅ and a̅ × (b̅ + c̅), Verify whether the cross product is distributive over vector addition.
Answer:
a̅ × b̅ = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
7 & -2 & 3 \\
2 & 0 & 8
\end{array}\right|\)
= i̅ (-16 – 0) – j̅ (56 – 6) + k̅(4)
= -16 i̅ – 50 j̅ + 4k̅

a̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
7 & -2 & 3 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (-2 – 3) – j̅ (7 – 3) + k̅(7 + 2)
= -5i̅ – 4 j̅ + 9k̅

b̅ + c̅ = 2i̅ + 8k̅ + i̅ + j̅ + k̅
= 3 i̅ + j̅ + 9k̅

a̅ × (b̅ + c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
7 & -2 & 3 \\
3 & 1 & 9
\end{array}\right|\)
= i̅ (-18 – 3) – j̅ (63 – 9) + k̅(7 + 6)
= -21i̅ – 54j̅+ 13k̅ …………..(1)
Now (a̅ × b̅) + (a̅ × c̅)
= -16i̅ – 50j̅ + 4k̅ – 5i̅ – 4j̅ + 9k̅
= -21i̅ – 54j̅ + 13k̅ …………(2)
From (1) and (2);
a̅ × (b̅ + c̅) = (a̅ × b̅) + (a̅ × c̅)
∴ Vector product is distributive over vector addition.

Question 4.
If a̅ = i̅ + j̅ + k̅, c = j̅ – k̅, then find vector b such that a̅ × b̅ = c̅ and a̅. b̅ = 3
Answer:
Let b̅ = b₁i̅ + b₂j̅ + b₃k̅
Given a̅. b̅ = 3
⇒ b₁ + b₂ + b₃ = 3 ………..(1)
and a̅ × b̅ = c̅
\(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
\mathrm{~b}_1 & \mathrm{~b}_2 & \mathrm{~b}_3
\end{array}\right|\) = j̅ – k̅
⇒ i̅(b₃ – b₂) – j̅(b₃ – b₁) + k̅(b₂ -b₁) = j̅ – k̅
∴ b₃ – b₁ = – 1 ……………(2)
and b₂ – b₁ = – 1 ……………(3)

∴ b₃ – b₂ = 0 ⇒ b₃ = b₂
∴ From (1), b₁ + 2b₂ = 3 ………(4)
∴ From (3), – b₁ + b₂ = – 1
∴ 3b₂ = 2 ⇒ b₂ = \(\frac{2}{3}\) ……..(5)
∴ b₂ = b₃ = \(\frac{2}{3}\)
b₁ = 3 – 2b₂ = 3 – \(\frac{4}{3}=\frac{5}{3}\) ………(6)

b = b₁ i̅ + b₂ j̅ + b₃k̅
= \(\frac{5}{2}\)i̅ + \(\frac{2}{3}\) j̅ + \(\frac{2}{3}\)k̅
= \(\frac{1}{3}\) (5i̅ + 2 j̅ + 2k̅)

Question 5.
a̅, b̅, c̅ are three vectors of equal magnitudes and each of them is inclined at an angle of 60° to the others. If |a̅ + b̅ + c̅| = √6(5 then find |a̅|.
Answer:
Given |a̅| = |b̅| = |c̅| = k(suppose)
and (a̅,b̅) = (b̅, c̅) = (c̅, a̅) = 60°
Also
(a̅ + b̅ + c̅) = |a̅|² + |b̅|² + |c̅|² + 2(a̅.b̅ + b̅.c̅ + c̅.a̅)
= k² + k² + k² + 2 [|a̅| |b̅| cos60° + |b̅| |c̅| cos60° + |c̅||a̅|cos60°]
= 3k² + \(\frac{2}{2}\)[k² + k² + k²] = 6k²
∴ 6 = 6k² (∵ |a̅ + b̅ + c̅| = √6)
⇒ k = 1
∴ |a̅| = 1

Question 6.
For any two vectors a and b, show that (1 + |a̅|²)(1 + |b̅|²) = |1 – a̅.b̅|² + |a̅ + b̅ + a̅ × b̅|²
Answer:

Question 7.
If a̅, b̅, c̅ are unit vectors such that a is perpendicular to the plane of b̅, c̅ and the angle between b̅ and c̅ is \(\frac{\pi}{3}\), then find |a̅ + b̅ + c̅|.
Answer:
Given that |a̅| = |b̅| = |c̅| = 1
Since a is perpendicular to the plane of b̅, c̅
⇒ We have a̅ . b̅ = 0 and a̅ . c̅ = 0
and given (b̅, c̅) = \(\frac{\pi}{3}\)
Now (a̅ + b̅ + c̅)² = |a̅|² + |b̅|² + |c̅|² + 2[(a̅. b̅) + (b̅. c̅) + (c̅. a̅)]
= 1 + 1 + 1 + 2|b̅||c̅|cos \(\frac{\pi}{3}\)
= 3 + 2\(\left(\frac{1}{2}\right)\) = 4
∴ |a + b + c| = 2

Question 8.
If a̅ = 3i̅ – j̅ + 2k̅, b̅ = – i̅ + 3j̅ + 2k̅, c̅ = 4i̅ + 5j̅ – 2k̅ and d̅ = i̅ + 3j̅ + 5k̅. then compute the following
i) (a̅ × b̅) × (c̅ × d̅)
Answer:
a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
3 & -1 & 2 \\
-1 & 3 & 2
\end{array}\right|\)
= i̅ (-2 – 6) – j̅ (6 + 2) + k̅(9 – 1)
= -8i̅ – 8j̅ + 8k̅ = 8(-i̅ – j̅ + k̅)

c̅ × d̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
4 & 5 & -2 \\
1 & 3 & 5
\end{array}\right|\)
= i̅(25 + 6) – j̅(20 + 2) + k̅(12 – 5)
= 31i̅ – 22j̅ + 7k̅

(a̅ × b̅) × (c̅ × d̅) = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
-8 & -8 & 8 \\
31 & -22 & 7
\end{array}\right|\)
= i̅ (-56 +176) – j̅ (-56 – 248) + k̅(176 + 248)
= i̅(120) + j̅(304) + 424 k̅
= 8[15i̅ + 38j̅ + 53k̅]

ii) (a̅ × b̅) . c̅ – (a̅ × d̅), b̅
Answer:
a̅ × b̅ = -8i̅ – 8j̅ + 8k̅
c̅ = 4 i̅ + 5 j̅ – 2k̅
∴ (a̅ × b̅). c̅ = -32 – 40 – 16 = -88 ………(1)
a̅ × d̅ = \(\left|\begin{array}{rrr}
\overline{\mathbf{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & -1 & 2 \\
1 & 3 & 5
\end{array}\right|\)
= i̅ (-5 – 6) – j̅ (15 – 2) + k̅(9 + 1)
= -11i̅ – 13j̅ + 10k̅
(a̅ × d̅) . b̅ = (-11i̅ – 13 j̅ + 10k̅) – (-i̅ + 3j̅ + 2k̅)
= 11 – 39 + 20 = -8 ……….(2)
(a̅ × b̅).c̅ – (a̅ × d̅).b̅ = – 88 + 8 = – 80

Students must practice these TS Intermediate Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a)

Question 1.
Find the angle between the vectors i̅ + 2j̅ + 3k̅ and 3i̅ – j̅ + 2k̅. (Mar. ’14)
Answer:
Let a̅ = i̅ + 2j̅ + 3k̅ and b̅ = 3i̅ – j̅ + 2k̅ and θ be the angle between them. Then

Question 2.
If the vectors 2i̅ + λ j̅ – k̅ and 4i̅ – 2j̅+ 2k̅ are perpendicular to each other then find λ. [March, May 2005]
Answer:
Let a̅ = 2i̅ + λ j̅ – k̅ and b̅ = 4i̅ – 2j̅+ 2k̅ and If a̅ is perpendicular to b̅ then a̅.b̅ = o
⇒ (2i̅ + λ j̅ – k̅).(4i̅ – 2j̅+ 2k̅) = o
⇒ 8 – 2λ – 2 = 0 ⇒ 6 – 2λ = 0 ⇒ λ = 3

Question 3.
For what values of , the vectors i̅ – j̅ + 2k̅ and 8i̅ + 6j̅ – k̅ are at right angles?
Answer:
Let a̅ = i̅ – j̅ + 2k̅ and b̅ = 8i̅ + 6j̅ – k̅
If a̅, b̅ are right angles then a̅.b̅ = o
⇒ 8 – 6λ – 2 = 0
⇒ -6λ + 6 = 0
⇒ λ = 1

Question 4.
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅. Find the vector c such that a, b and c form the sides of a triangle.
Answer:
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅
∵ a̅, b̅, c̅ form the sides of a triangle a̅ + b̅ + c̅ = 0

∴ c̅ = -a̅ – b̅
= -(2i̅ – j̅ + k̅) – (i̅ – 3 j̅ – 5k̅)
= -3i̅ + 4j̅ + 4k̅

Question 5.
Find the angle between the planes r̅ . (2i̅ – j̅ + 2k̅) = 3 and r̅ .(3i̅ + 6j̅ + k̅) =4 (March 2015-T.S)
Answer:
If the angle between planes

Question 6.
Let \(\overline{\mathrm{e}}_1\) and \(\overline{\mathrm{e}}_{\mathbf{2}}\) be unit vectors making angle θ. If \(\frac{1}{2}\left|\overline{\mathrm{e}}_1-\overline{\mathrm{e}}_2\right|\) = sin λθ, then find λ.
Answer:

Question 7.
Let a̅ = i̅ + j̅ + k̅ and b̅ = 2 i̅ + 3j̅ + k̅. Find
(i) the projection vector of bona and its magnitude
(ii) The vector components of b̅ in the direction of a̅ and perpendicular to a̅. [May 2006]
Answer:
Orthogonal projection of a vector b̅ on a̅ is

(ii) The component vector b in the direction of –

Question 8.
Find the equation of the plane through the point (3, – 2, 1) and perpendicular to the vector (4, 7, – 4).
Answer:
The equation of the plane passing through a̅ and perpendicular to the vector n̅ is r̅. n̅ = a̅. n̅
Given n̅ = 4i̅ + 7j̅ – 4k̅ and a̅ = 3i̅ – 2j̅ + k̅
r̅ . (4i̅ + 7j̅ – 4k̅) – (3i̅ – 2j̅ + k̅) . (4i̅ + 7j̅ – 4k̅)
r . (4i̅ + 7j̅ – 4k̅) = 12 – 14 – 4 = – 6
⇒ r̅ . (-4i̅ – 7j̅ + 4k̅) = 6

Question 9.
If a̅ = 2i̅ + 2j̅ – 3k̅, b = 3i̅ – j̅ + 2k̅, then find the euigle between 2a̅ + b̅ and a̅ + 2b̅.
Answer:
Given a̅ = 2i̅ + 2j̅ – 3k̅ and b̅ = 3i̅ – j̅ + 2k̅
We have
2a̅ + b = 4i + 4j̅ – 6k̅ + 3i̅ – j̅ + 2k̅ = 7i̅ + 3j̅ – 4k̅
and a̅ + 2b̅ = (2i̅ + 2 j̅ – 3k̅) + 2(31-7 + 2k) = 8i̅ + k̅
Let ‘θ’ be the angle between the vectors 2a̅ + b̅ and a̅ + 2b̅

II.
Question 1.
Find the unit vector parallel to the XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅.
Answer:
Any vector parallel to XOY plane will be of the form xi̅ + yj̅.
The vector parallel to the XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅ is 3i̅ + 4j̅
Its magnitudes |3i̅ + 4j̅| = \(\sqrt{9+16}\) = 5
Unit vector parallel to XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅ is
\(\pm\left(\frac{3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}}}{\sqrt{9+16}}\right)=\pm\left(\frac{3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}}}{5}\right)\)

Question 2.
If a̅ + b̅ + c̅ = 0, |a̅I|= 3, |b̅| = 5 and |c̅| = 5 then find the angle between a̅ and b̅.
Answer:
Given a̅ + b̅ + c̅ = 0
c̅ = -(a̅ + b̅)
⇒ |c̅|² = (a̅ + b̅)² = a̅² + b̅² + 2(a̅. b̅)
⇒ 49 = 9 + 25 + 2( .6)

Question 3.
If |a̅| = 2, |b̅| = 3 and |c̅| = 4 juid each of a̅, b̅, c̅ is perpendicular to the sum of the other two vectors, then find the magnitude of a̅ + b̅ + c̅.
Answer:
Given |a̅| = 2, |b̅| = 3 and |c̅| = 4
Since each of a̅, b̅, c̅ is perpendicular to the sum of other two vectors i.e., a̅ is perpendicular to b̅ + c̅
a̅ . (b̅ + c̅) = 0 ⇒ a̅ . b̅ + a̅ . c̅ = 0
Similarly
b̅.(c̅ + a̅) = 0 ⇒ b̅.c̅ + b̅.a̅ = 0
and c-(a + b) = 0 ⇒ c̅. a̅ + c̅. b̅ = 0 Adding we get
2 [(a̅ . b̅) + (b̅ . c̅) + (c̅ . a̅)] = 0 …….(1)
Also (a̅ + b̅ + c̅)
= |a̅|² + |b̅|² + |c̅|² + 2(a̅.b̅ + b̅.c̅ + c̅.a̅)
= 4 + 9 + 16 + 2(a̅.b̅ + b̅. c̅ + c̅.a̅)
= 4 + 9 + 16 + 2 (0) = 29
∴ |a̅ + b̅ + c̅| = \(\sqrt{29}\)

Question 4.
Find the equation of the plane passing through the point a̅ = 2i̅ + 3j̅ – k̅ and perpendicular to the vector 3i̅ – 2j̅ – 2k̅ and the distance of this plane from the origin.
Answer:
Equation of the plane passing through the point a, and perpendicular to the vector n̅ is (r̅ – a̅) . n̅ = 0
⇒ 7 . n̅ = a̅ . n̅
(liven a̅ = 2i̅ + 3 j̅ – k̅ and n̅ = 3i̅ – 2j̅ – 2k̅
We have r̅ . (3 i̅ – 2 j̅ – 2k̅)
= (2i̅ + 3j̅ – k̅) . (3i̅ – 2j̅ – 2k̅)
= 6 – 6 + 2 = 2
⇒ r̅ . (3i̅ – 2j̅ – 2k̅) = 2
The distance from origin to this plane is

Question 5.
a̅, b̅, c̅ and d̅ are the position vectors of four coplanar points such that (a̅ – d̅) . (b̅ – c̅) = (b̅ – d̅) . (c̅ – a̅) = 0. Show that the point d represents the orthocentre of the triangle with a̅, b̅ and c̅ as its vertices.
Answer:

Position vectors of A, B, C, D are a̅, b̅, c̅, d̅ respectively.
\(\overline{\mathrm{DA}}=\overline{\mathrm{OA}}-\overline{\mathrm{OD}}\) = a̅ – d̅
\(\overline{\mathrm{CB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OC}}\) = b̅ – c̅
\(\overline{\mathrm{DB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OD}}\) = b̅ – d̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = c̅ – a̅
Given (a̅ – d̅) . (b̅ – c̅) = 0
⇒ \(\overline{\mathrm{DA}} \cdot \overline{\mathrm{CB}}\) = 0
⇒ \(\overline{\mathrm{DA}}\) is perpendicular to \(\overline{\mathrm{BC}}\)
∴ \(\overline{\mathrm{AD}}\) is an altitude of ΔABC
and (b̅ – d̅) . (c̅ – a̅) = 0
⇒ \(\overline{\mathrm{DB}} \cdot \overline{\mathrm{AC}}\) = 0
⇒ \(\overline{\mathrm{DB}}\) is perpendicular to \(\overline{\mathrm{AC}}\)
\(\overline{\mathrm{DB}}\) another altitude ΔABC
Altitudes AD and BD intersect at D
D(d) is the orthocentre of ΔABC.

III.
Question 1.
Show that the points (5, – 1, 1), (7, – 4, 7), (1,-6, 10) and (- 1, – 3, 4) are the vertices of a rhombus. (March 2013)
Answer:
Let A (5,-1, 1), B (7,-4, 7), C (1,-6, 10) and D (- 1, – 3, 4) are the given points.

∴ AB = BC = CD = DA = 7 units and AC ≠ BD
∴ A, B, C, D are the points which are the vertices of a rhombus.

Question 2.
Let a̅ = 4i̅ + 5j̅ – k̅, b̅ = i̅ – 4j̅ + 5k̅ and c̅ = 3i̅ + j̅ – k̅. Find the vector which is perpendicular to both a and b and whose magnitude is twenty one times the magnitude of c̅.
Answer:
Given a̅ = 4 i̅ + 5 j̅ – k̅
b̅ = i̅ – 4 j̅ + 5k̅
and c̅ = 3 i̅ + j̅ – k̅
Let r̅ = xi̅ + yj̅ + zk̅ be the vector which is perpendicular to both a and b.
Then r̅. a̅ = 0 and r̅.b̅ = 0
⇒ 4x + 5y – z = 0 …………..(1)
and x – 4y + 5z = 0 ……….(2)

⇒ x = λ, y = -λ, z = -λ
∴ The vector which is perpendicular to both a̅ and b̅ is r̅ = λ(i̅ – j̅ – k̅)
Magnitude of c = \(\sqrt{9+1+1}=\sqrt{11}\)
∴ The vector which is perpendicular to both a̅ and b̅ whose magnitude is 21 times the
magnitude of c̅ is = ± \(\frac{21 \sqrt{11}(\bar{i}-\bar{j}-\bar{k})}{|\bar{i}-\bar{j}-\bar{k}|}\)
= ± 7\(\sqrt{33}\) (i̅ – j̅ – k̅)

Question 3.
G is the centroid of ΔABC and a̅, b̅, c̅ are the lengths of the sides \(\overline{\mathrm{B C}}, \overline{\mathrm{C A}}\) and \(\overline{\mathrm{AB}}\) respectively. Prove that \(\bar{a}^2+\bar{b}^2+\bar{c}^2=3\left(\overline{\mathrm{OA}}^2+\overline{\mathrm{OB}}^2+\overline{\mathrm{OC}}^2\right)-9(\overline{\mathrm{OG}})^2\). where ‘O’ is any point.

Answer:
Given that \(\overline{\mathrm{BC}}=\overline{\mathrm{a}}, \overline{\mathrm{CA}}=\overline{\mathrm{b}}\) and \(\overline{\mathrm{AB}}=\overline{\mathrm{c}}\).
Let O’ be the origin and let p.q.r be the position vectors of A, B, C then \(\overline{\mathrm{OA}}=\overline{\mathrm{p}}\), \(\overline{\mathrm{OB}}=\overline{\mathrm{q}}, \quad \overline{\mathrm{OC}}=\overline{\mathrm{r}}\) respectively.
Then the position vector of centroid

Question 4.
A line makes angles θ₁, θ₂, θ₃, and θ₄ with the diagonals of a cube. Show that cos²θ₁ + cos²θ₂ + cos²θ₃ + cos²θ₄ = \(\frac{4}{3}\).
Answer:

Let ‘O’ be the origin and ‘a’ be the length of the side of a cube.
i̅, j̅, k̅ are unit vectors along X, Y and Z axes respectively.

Let r̅ = xi̅ + yj̅ + zk̅ be the line makes angles θ₁, θ₂, θ₃, θ₄ with diagonals of a cube

Telangana TSBIE TS Inter 1st Year Physics Study Material 10th Lesson ఘనపదార్ధాల యాంత్రిక ధర్మాలు Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 10th Lesson ఘనపదార్ధాల యాంత్రిక ధర్మాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
స్థితిస్థాపకతలో హుక్ నియమాన్ని తెలపండి.
జవాబు:
స్థితిస్థాపక అవధిలో ప్రతిబలము వికృతికి అనులోమానుపాతంలో ఉండును.

ఈ స్థిరాంకమును స్థితిస్థాపకతా గుణకము అందురు.

ప్రశ్న 2.
ప్రతిబలానికి మితులు, ప్రమాణాలు తెలపండి.
జవాబు:

S.I. పద్ధతిలో ప్రమాణము : న్యూ/మీ² లేదా పాస్కల్. మితిఫార్ములా : ML^-1T^-2

ప్రశ్న 3.
స్థితిస్థాపక గుణకానికి ప్రమాణాలు, మితులను తెలపండి.
జవాబు:

S.I. ప్రమాణము : న్యూ/మీ² లేదా పాస్కల్. మితిఫార్ములా : ML^-1T^-2

ప్రశ్న 4.
యంగ్ గుణకం ప్రమాణాలు, మితులను తెలపండి.
జవాబు:

మితిఫార్ములా : ML^-1T^-2
ప్రమాణము : న్యూటన్/మీ² లేదా పాస్కల్

ప్రశ్న 5.
దృఢతా గుణకం ప్రమాణాలు, మితులను తెలపండి.
జవాబు:

మితిఫార్ములా : ML^-1T^-2
ప్రమాణము : న్యూటన్/మీ2 లేదా పాస్కల్

ప్రశ్న 6.
ఆయత గుణకం ప్రమాణాలు, మితులను తెలపండి.
జవాబు:

మితిఫార్ములా : ML^-1T^-2
ప్రమాణము : న్యూటన్/మీ² లేదా పాస్కల్

ప్రశ్న 7.
సంపూర్ణ స్థితిస్థాపక, ప్లాస్టిక్ కు సమీపంగా ఉండే వస్తువులకు ఉదాహరణలు ఇవ్వండి.
జవాబు:
సమ సర్పిలాకార స్ప్రింగు సంపూర్ణ స్థితిస్థాపక వస్తువులకు ఉదాహరణ. పిండి లేదా మట్టి ముద్ద ప్లాస్టిక్ వస్తువులకు ఉదాహరణ.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
హుక్ నియమం, అనుపాత అవధి, శాశ్వత స్థితి, విచ్ఛేదన ప్రతిబలం పదాలను నిర్వచించండి.
జవాబు:
హుక్ నియమము : స్థితిస్థాపక అవధులలో ప్రతిబలము వికృతికి అనులోమానుపాతంలో ఉంటుంది.

ఈ స్థిరాంకమును స్థితిస్థాపక గుణకము అంటారు.

అనుపాత అవధి : ప్రతిబలము – వికృతి వక్రరేఖపై OA బిందువుల మధ్య భాగం సరళరేఖ ఈ ప్రాంతంలో ప్రతిబలం వికృతికి అనులోమానుపాతంలో ఉంటుంది. బాహ్య బలం తొలగించగానే వస్తువు సంపూర్ణంగా యథాస్థితి పొందుతుంది. అందువల్ల ‘A’ బిందువును అనుపాత అవధి అంటారు.

శాశ్వత స్థితి : ప్రతిబలం – వికృతి వక్రంలో బాహ్యబలాన్ని ‘C’ బిందువు వరకు పెంచి తొలగిస్తే వస్తువు తన పూర్వ స్థితిని సంపూర్ణంగా పొందలేదు. వస్తువులో కొంత వికృతి శాశ్వతంగా మిగిలిపోతుంది. అందువల్ల ‘C’ బిందువును శాశ్వత స్థితి బిందువు అంటారు.

విచ్ఛేదన ప్రతిబలము : ప్రతిబలం-వికృతి వక్రంలో వస్తువుపై ప్రతిబలాన్ని ఈగే బిందువు దాటి ప్రయోగిస్తే (E బిందువు వరకు) ప్రతిబలంలో స్వల్ప మార్పుకే వికృతి విపరీతంగా పెరిగి E అను బిందువు వద్ద తీగ సన్నబడి తెగిపోతుంది. తీగ తెగిపోవడానికి అవసరమైన E బిందువు వద్ద గల ప్రతిబలాన్ని విచ్ఛేదన ప్రతిబలం అంటారు.

ప్రశ్న 2.
స్థితిస్థాపక గుణకం, ప్రతిబలం, వికృతి, స్వాజూన్ నిష్పత్తులను నిర్వచించండి.
జవాబు:

ఈ స్థిరాంకమును స్థితిస్థాపక గుణకము అంటారు.

ప్రతిబలము (σ) : ఏకాంక వైశాల్యంపై పనిచేసే పునఃస్థాపక బలాన్ని ప్రతిబలం అంటారు.

ప్రమాణము Nm^-2 లేదా పాస్కల్ మితి ఫార్ములా = ML^-1T^-2

వికృతి : ప్రమాణ పరిమాణం గల వస్తువు ఆకారంలో వచ్చిన మార్పును వికృతి అంటారు.

ఇది నిష్పత్తి. కావున ప్రమాణాలు, మితులు లేవు.

ప్వాజూన్ నిష్పత్తి (σ) : సాగదీసిన తీగలో పార్శ వికృతి మరియు అనుదైర్ఘ్య వికృతుల నిష్పత్తిని ప్వాజూన్ నిష్పత్తి అంటారు.
ప్వాజూన్ నిష్పత్తి (σ) = \(\frac{\Delta \mathrm{d} / \mathrm{d}}{\Delta l / l}\) దీనికి మితులు, ప్రమాణాలు లేవు.

ప్రశ్న 3.
యంగ్ గుణకం, ఆయత గుణకం, ద్రుఢతా గుణకాలను నిర్వచించండి.
జవాబు:
యంగ్ గుణకము : అనుదైర్ఘ్య ప్రతిబలము, అనుదైర్ఘ్య వికృతిల నిష్పత్తిని యంగ్ గుణకమందురు.

అనుదైర్ఘ్య ప్రతిబలము = \(\frac{\mathrm{F}}{\mathrm{A}}\); అనుదైర్ఘ్య వికృతి = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\)
∴ Y = \(\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{F}}{\mathrm{A}} \frac{\mathrm{l}}{\Delta \mathrm{L}}\)
ఆయత గుణకము (B) : ఘనపరిమాణాత్మక ప్రతిబలము మరియు ఘనపరిమాణాత్మక వికృతిల నిష్పత్తిని ఆయత గుణకము అందురు.

విమోటనా గుణకము లేదా దృఢతా గుణకము (G) :
స్పర్శీయ ప్రతిబలము మరియు విరూపణా వికృతిలో నిష్పత్తిని విమోటనా గుణకము అందురు.

ప్రశ్న 4.
ప్రతిబలం నిర్వచనం తెలిపి వివిధ రకాల ప్రతిబలాలను వివరించండి.
జవాబు:
ప్రతిబలము (σ) : ఏకాంక వైశాల్యంపై పనిచేసే పునఃస్థాపక బలాన్ని ప్రతిబలం అంటారు.

ప్రమాణము Nm^-2 లేదా
పాస్కల్ మితి ఫార్ములా = ML^-1T^-2
ప్రతిబలమునందలి రకాలు : 1) అనుదైర్ఘ్య ప్రతిబలము 2) స్పర్శియ ప్రతిబలము 3) ఘనపరిమాణాత్మక ప్రతిబలము

అనుదైర్ఘ్య ప్రతిబలము లేదా తన్యజ ప్రతిబలం : వస్తువుపై దాని పొడవు పెరుగునట్లు బలమును ప్రయోగించిన ప్రమాణ వైశాల్యములోని పునఃస్థాపక బలమును అనుదైర్ఘ్య ప్రతిబలము అంటారు.

స్పర్శీయ లేదా విమోటన ప్రతిబలము : తలానికి సమాంతరముగా దాని ఉపరితల పొరలో స్థానభ్రంశము కలుగునట్లు బలమును ప్రయోగించిన ప్రమాణ వైశాల్యములోని పునఃస్థాపక బలమును స్పర్శియ ప్రతిబలము అందురు.

ఘనపరిమాణాత్మక ప్రతిబలము : ఒక వస్తువుపై అన్ని వైపులా లేదా వస్తువు ఘనపరిమాణమంతటా బలమును ప్రయోగించిన ప్రమాణ. వైశాల్యములోని పునఃస్థాపక బలమును ఘనపరిమాణాత్మక ప్రతిబలము అందురు.

ప్రశ్న 5.
వికృతిని నిర్వచించి, వివిధ రకాల వికృతులను వివరించండి.
జవాబు:
వికృతి : ప్రమాణ పరిమాణం గల వస్తువు ఆకారంలో వచ్చిన మార్పును వికృతి అంటారు.

ఇది నిష్పత్తి. కావున ప్రమాణాలు, మితులు లేవు.
వికృతి నందలి రకాలు : వికృతి మూడు రకములు.
1) అనుదైర్ఘ్య వికృతి 2) స్పర్శీయ లేదా విరూపణ వికృతి 3) ఘనపరిమాణ వికృతి.

1) అనుదైర్ఘ్య వికృతి (ε) : వస్తువు పొడవులో మార్పు (∆l) మరియు తొలి పొడవు (l) లకు గల నిష్పత్తిని అనుదైర్ఘ్య వికృతి అంటారు.
అనుదైర్ఘ్య వికృతి (ε) = \(\frac{\Delta l}{l}\)

2) విరూపణ వికృతి : ఒక వస్తువు తలముపై స్పర్శరేఖ దిశలో బలమును ప్రయోగించిన, దాని ఉపరితలము పొందిన స్థానభ్రంశపు మరియు మొదటి లంబ తలముల మధ్య గల కోణమును విరూపణ వికృతి అంటారు.
విరూపణ వికృతి = θ = \(\left(\frac{\Delta l}{l}\right)\) = tan θ (కోణము చిన్న విలువలకు tan θ = θ)

3) ఘనపరిమాణాత్మక వికృతి : వస్తువు ఘనపరిమాణంలో మార్పు కలుగునట్లు బలమును ప్రయోగించిన ఘనపరిమాణంలో మార్పుకు తొలి ఘనపరిమాణ మార్పుకు గల నిష్పత్తిని ఘనపరిమాణాత్మక వికృతి అందురు.

ప్రశ్న 6.
వికృతి శక్తి అంటే ఏమిటో తెలిపి, దానికి సమీకరణాన్ని ఉత్పాదించండి. (మార్చి 2014, మే 2014)
జవాబు:
వికృతిశక్తి : తీగలో వికృతి కలుగునట్లు బలమును ప్రయోగించినపుడు జరిగిన పని తీగలో స్థితిశక్తిగా నిల్వయుండును. దీనిని వికృతిశక్తి అందురు.
తీగపై ప్రయోగించిన విరూపణ బలమును తొలగించిన వికృతిశక్తి ఉష్ణశక్తిగా మారును.

సమీకరణ ఉత్పాదన : L పొడవు గల ఏకరీతి తీగ ఒక చివరను స్థిర ఆధారము నుండి వ్రేలాడదీసి దానిపై F బలమును . ప్రయోగించిన దానిలో సాగుదల dl అనుకొనుము.
∴ జరిగిన పని = dW = Fdl
తీగను దాని పొడవులో మార్పు ‘0’ నుండి / ను పొందుటలో జరిగిన పని
W = \(\int\) dW కాని \(\int_o^l \mathrm{Fd} l=\int_0^l \frac{\mathrm{YA} l}{\mathrm{~L}}=\frac{\mathrm{YA}}{\mathrm{L}}\left(\frac{l^2}{2}\right)_0^l \mathrm{~d} l\)
∴ \(\frac{\mathrm{YA}}{\mathrm{L}}\left(\frac{l^2}{2}\right)=\frac{\mathrm{YA}}{\mathrm{L}}\left(\frac{l^2}{2}\right) \frac{1}{2} \frac{\mathrm{Ya} l}{\mathrm{~L}} \cdot l\)
W = \(\frac{1}{2}\) × బలము × సాగుదల. ఈ పని తీగలో వికృతిశక్తికి సమానము.
∴ వికృతి శక్తి = \(\frac{1}{2}\) × బలము × సాగుదల.
ప్రమాణ ఘనపరిమాణంలో వికృతి శక్తి

ప్రమాణ ఘనపరిమాణంలో శక్తి = \(\frac{1}{2}\) × ప్రతిబలము × వికృతి

ప్రశ్న 7.
భారీ పని యంత్రాలలోనూ, నిర్మాణరంగ రూపకల్పనలోనూ రాగి, ఇత్తడి, అల్యూమినియంతో పోల్చితే ఉక్కును ఎందుకు వాడతారు ?
జవాబు:
ఉక్కుకు యంగ్ గుణకము మరియు దృఢతా గుణకములు రాగి, ఇత్తడి మరియు అల్యూమినియంల కన్న చాలా ఎక్కువ. అందువల్ల ఉక్కు కడ్డీలను సాగదీయడానికి మరియు వంచడానికి చాలా ఎక్కువ ప్రతిబలం కావాలి.

సుమారు 0.1 సెం.మీ2 వైశాల్యం గల ఉక్కు తీగను 0.1% సాగదీయటానికి సుమారు 2000 న్యూటన్ల బలం అవసరము. ఇదే సాగుదలకు అల్యూమినియంకు 690 న్యూ, రాగికి 900 న్యూ మరియు ఇత్తడికి 1100 న్యూటన్ల బలం అవసరము. అంటే ఉక్కు స్థితిస్థాపక గుణకము అల్యూమినియం, రాగి, ఇత్తడిల కన్నా ఎక్కువ కాబట్టి ఉక్కుతో కట్టిన కట్టడాలు ఎక్కువ బరువును మోయగల సామర్థ్యాన్ని, దృఢత్వాన్ని కలిగి ఉండటం వల్ల భవన నిర్మాణంలో, భారీ కట్టడాలు కట్టడంలోను ఉక్కును వాడతారు.

ప్రశ్న 8.
క్రమంగా భారం పెంచుతూ పోయినప్పుడు తీగ ప్రవర్తన ఏ విధంగా ఉంటుందో విశదీకరించండి.
జవాబు:
ఏకరీతి అడ్డుకోత వైశాల్యము గల తీగ ఒక చివరను స్థిరమైన ఆధారానికి బిగించి రెండవ చివర భారమును క్రమంగా పెంచినామనుకొనుము. వస్తువుపై ప్రయోగించిన ప్రతిబలము మరియు వస్తువులోని వికృతికి రేఖాపటం గీయగా అది పటంలో చూపినట్లు ఉంటుంది. ఈ రేఖాపటం నుండి తీగ ప్రవర్తనను వివిధ బిందువుల వద్ద వివరించవచ్చు.

అనుపాత అవధి : ప్రతిబలము వికృతి వక్రరేఖపై OA బిందువుల మధ్య భాగం సరళరేఖ ఈ ప్రాంతంలో ప్రతిబలం వికృతికి అనులోమానుపాతంలో ఉంటుంది. బాహ్య బలం తొలగించగానే వస్తువు సంపూర్ణంగా యథాస్థితి పొందుతుంది. అందువల్ల ‘A’ బిందువును అనుపాత అవధి అంటారు.

స్థితిస్థాపక అవధి : ప్రతిబలము – వికృతి వక్రంలోని AB ప్రాంతము వక్రరేఖ. ఈ ప్రాంతంలో ప్రతిబలము, వికృతికి రేఖీయ సంబంధం కలిగి ఉండదు. కాని బాహ్యబలాన్ని తొలగించగానే వస్తువు తన యథాస్థితిని సంపూర్ణంగా పొందుతుంది. అందువల్ల B బిందువును ఈగే బిందువు లేదా స్థితిస్థాపక అవధి అంటారు.
ఈగే బిందువును చేరడానికి ప్రయోగించిన బాహ్యబలాన్ని ఈగుడుబలం అంటారు.

శాశ్వత స్థితి : ప్రతిబలం – వికృతి వక్రంలో బాహ్యబలాన్ని ‘C’ బిందువు వరకు పెంచి తొలగిస్తే వస్తువు తన పూర్వ స్థితిని సంపూర్ణంగా పొందలేదు. వస్తువులో కొంత వికృతి శాశ్వతంగా మిగిలిపోతుంది. అందువల్ల ‘C’ బిందువును శాశ్వత స్థితి బిందువు అంటారు.

విచ్ఛేదన ప్రతిబలము : ప్రతిబలం-వికృతి వక్రంలో వస్తువుపై ప్రతిబలాన్ని ఈగే బిందువు దాటి ప్రయోగిస్తే (E బిందువు వరకు) ప్రతిబలంలో స్వల్ప మార్పుకే వికృతి విపరీతంగా పెరిగి E అను బిందువు వద్ద తీగ సన్నబడి తెగిపోతుంది. తీగ తెగిపోవడానికి అవసరమైన E బిందువు వద్ద గల ప్రతిబలాన్ని విచ్ఛేదన ప్రతిబలం అంటారు.

ప్రశ్న 9.
ఏనుగు దంతంతో, బంక మట్టితో చేసిన రెండు సర్వసమాన బంతులను కొంత ఎత్తు నుంచి కిందికి వేసినారు. నేలను తాకిన తరువాత రెండింటిలో ఏది ఎక్కువ ఎత్తుకు లేస్తుంది ? ఎందువల్ల ?
జవాబు:
ఏనుగు దంతంతోను మరియు బంకమట్టితోను తయారుచేసిన రెండు సర్వసమానమైన బంతులను ఒకే ఎత్తు నుంచి జారవిడిచితే ఏనుగు దంతంతో చేసిన బంతి ఎక్కువ ఎత్తుకు లేస్తుంది.

వివరణ : 1) బంకమట్టి ప్లాస్టిక్ పదార్థము. అనగా దీని మీద బాహ్యబలం ప్రయోగిస్తే దాని ఆకారం మారుతుంది. పైనుండి క్రింద పడి నేలను తాకగానే వస్తువుకు గల శక్తి దానిలో విరూపణ కలిగించడానికి సరిపోవడం వల్ల బంకమట్టి ముద్ద దాదాపు సంపూర్ణ అస్థితిస్థాపక అభిఘాతానికి లోనుగావడం వల్ల పైకి లేవదు.

2) ఏనుగు దంతము దృఢమైన నిర్మాణం గల పదార్థంతో చేయబడటం వల్ల ఎక్కువ స్థితిస్థాపకతను కలిగి ఉంటుంది. ఫలితంగా నేలను తాకినపుడు దాని ఆకారంలో విరూపణ అతిస్వల్పంగా ఉండి దంతపు బంతి స్థితిస్థాపక అభిఘాతానికి లోనై ఎక్కువ ఎత్తు పైకి లేస్తుంది.

ప్రశ్న 10.
వంతెనలు, భవనాల నిర్మాణంలో భారం వితరణ చెందని స్తంభాల కంటే వితరిత స్తంభాలను వాడతారు. ఎందుకు ?
జవాబు:
భవనాలు, వంతెనలు వంటి కట్టడాలకు ఆధారంగా ఉండవలసిన దూలాలవంటివి నిర్మించేటపుడు నిర్మాణంలో వాడిన పదార్థాల స్థితిస్థాపక ధర్మాలతో పాటు నిర్మాణపు ఆకారం వల్ల కూడా దృఢత్వం సంతరించు కుంటుంది. స్థంభాలు లేదా కాలమ్స్ విషయంలో కొనలు ఉన్న స్తంభాలు (వితరిత స్తంభాలు), కొనలు లేని (వితరితం చెందని) స్థంభాల కన్నా ఎక్కువ భారం మోయగలుగుతాయి. అందువల్ల పెద్ద పెద్ద నిర్మాణాలలో భార వితరిత కొనలు ఉన్న స్థంభాలను ఎక్కువగా వాడతారు.

ప్రశ్న 11.
భూమిపై పర్వతాల గరిష్ఠ ఎత్తు సుమారు 10 కి.మీ. మాత్రమే ఎందుకు ఉంటుందో వివరించండి.
జవాబు:
రాళ్ళ స్థితి స్థాపక ధర్మాలను పరిగణనలోకి తీసుకొని భూమిపై పర్వతాల గరిష్ఠ ఎత్తు సుమారు 10 కి.మీ. దాటదు అని వివరించవచ్చు.

రాయి స్థితిస్థాపక అవధి సుమారు 30 × 10⁷ న్యూ/మీ³ మరియు రాయి తయారుచేయబడిన పదార్థ సాంద్రత ρ = 3 × 10³ కి.గ్రా./మీ³.
కావున h ఎత్తు గల రాళ్ళ పర్వతాల వల్ల పర్వతం అడుగున ఉన్న రాయిపై ప్రతిబలము ప్రతిబలము = hρg న్యూ/మీ². ఈ ప్రతిబలము రాయి స్థితిస్థాపక హద్దులలో గల ప్రతిబలము దాటరాదు. ఒకవేళ దాటితే రాయి స్థితిస్థాపక ధర్మాలు కోల్పోయి పూర్తిగా విరూపణం చెందే అవకాశం ఎక్కువ.
∴ 30 × 10⁷ = hpg లేదా 30 × 10⁷ = h . 3 × 10³ × 10
∴ h = 10⁴ = 10 కి.మీ.
అందువల్ల భూమిపై పర్వతాల ఎత్తు గరిష్ఠంగా 10 కి.మీ.కు మించదు.

ప్రశ్న 12.
సాగదీసిన తీగలో స్థితిస్థాపక స్థితిజశక్తి భావనను వివరించి దానికి సమాసాన్ని రాబట్టండి.
జవాబు:
తీగపై తన్యజ ప్రతిబలం పనిచేసినపుడు అంతరపరమాణు బలాలకు వ్యతిరేకంగా పని జరుగుతుంది. ఈ పని తీగలో స్థితిస్థాపక స్థితిజశక్తిగా మిగిలిపోతుంది.
‘l’ పొడవు గల, A మధ్యచ్ఛేద వైశాల్యం గల తీగపై F బలం ప్రయోగించామనుకోండి. తీగ యంగ్ గుణకము Y అనుకొనుము.
Y = \(\frac{\mathrm{F} / \mathrm{A}}{l / \mathrm{L}}\) సమీకరణం నుండి F = \(\frac{\text { YAl }}{\text { L }}\)
తీగలో ∆l పొడవులో వృద్ధి కలిగించడానికి చేసిన పని ∆W అనుకుంటే తీగను ‘l’ పొడవు సాగదీయడానికి చేసిన పని
∴ W = \(\int \mathrm{dw}=\int_0^l \mathrm{~F} \cdot \Delta l=\int_0^l \frac{\mathrm{YA} l}{\mathrm{~L}} \mathrm{~d} l=\frac{1}{2} \mathrm{YA} \frac{l^2}{\mathrm{~L}}\)
∴ W = \(\frac{1}{2}\) Y . AL . \(\frac{l^2}{\mathrm{~L}}\) = \(\frac{1}{2}\) × యంగ్ గుణకము × తీగ ఘ.ప. × (వికృతి)² ……………. (1)
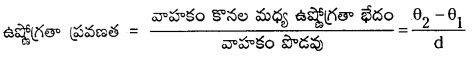
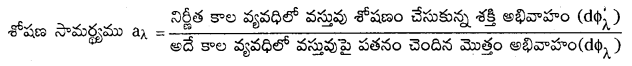
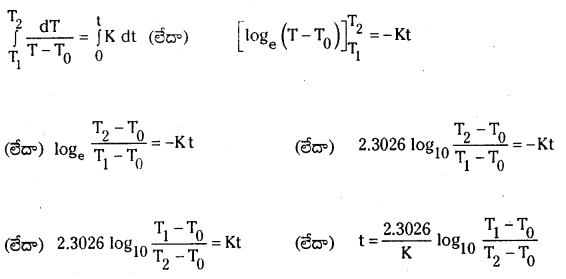
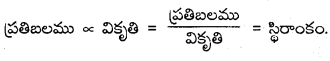
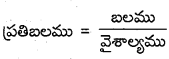
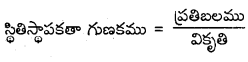
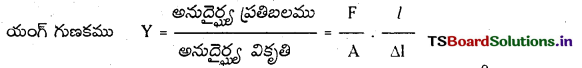
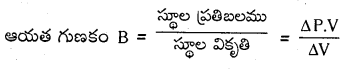
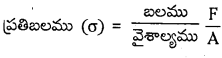
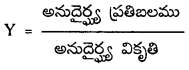
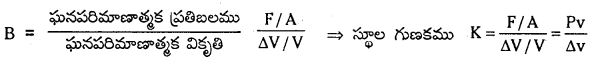
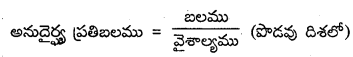
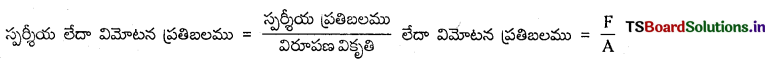
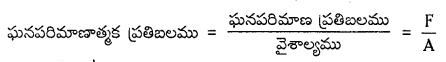
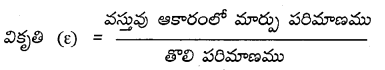
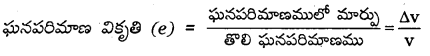
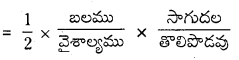
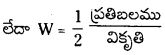× ఘ.ప. × (వికృతి)² = \(\frac{1}{2}\) ప్రతిబలము × వికృతి × ఘ.ప.
ప్రమాణ ఘనపరిమాణానికి వికృతి శక్తి = W/ఘ.ప. = \(\frac{1}{2}\) ప్రతిబలము (σ) × వికృతి (ε) …………. (2)
పై సమీకరణాలలో తీగను సాగదీయడానికి జరిపిన పని W వస్తువులో గల స్థితిస్థాపక శక్తికి సమానము.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
స్థితిస్థాపకతలోని హుక్ నియమాన్ని నిర్వచించి, తీగ పదార్థపు యంగ్ గుణకాన్ని కనుక్కొనే ప్రయోగాన్ని వివరించండి.
జవాబు:
హుక్ సూత్రము :
స్థితిస్థాపక అవధిలో ప్రతిబలము వికృతికి అనులోమానుపాతంలో ఉండును.

E అనుపాత స్థిరాంకము. దీనిని పదార్థము యొక్క స్థితిస్థాపకతా గుణకము అందురు.

పరికరం వర్ణన : యంగ్ గుణకాన్ని కనుగొనే ప్రయోగం అమరికలో సమాన పొడవు, వ్యాసార్థం గల రెండు తీగలను (A, B) దృఢమైన ఆధారం నుండి వ్రేలాడదీసి వాటి చివర ఒక వెర్నియర్ మాపకాన్ని కలుపుతారు. తీగ A ను మాపకం ప్రధాన స్కేలు (M) కు కలిపి దాని క్రింద భాగంలో ఒక స్థిరమైన బరువును కలిపి తీగ A లో నొక్కులు లేకుండా స్థిరంగా ఉండేటట్లు చేస్తారు. తీగ B ని వెర్నియర్ స్కేలుకు కలుపుతారు.. ఈ తీగకు గల పళ్ళెంలో కావలసిన విధంగా బరువులను మార్చవచ్చు. ఈ ప్రయోగంలో ప్రతిసారి ప్రధాన స్కేలు రీడింగు (M.S.R.) మరియు వెర్నియర్ స్కేలు రీడింగు (V.S.R.) లను కొలుస్తారు.

చేయు విధానము : ప్రయోగపు తీగ నొక్కులు లేకుండా ఉండటానికి తగినంత బరువును కొంకి తీగకు తగిలిస్తారు. వెర్నియర్ మాపకం రీడింగులు కొలుస్తారు. కొంకి బరువులను ప్రతిసారి 1/2 కిలో చొప్పున పెంచుతూ సుమారు 3 కి.గ్రా. వరకు బరువు పెంచుతారు. బరువు పెంచేటప్పుడు ప్రతిసారి ప్రధాన స్కేలు రీడింగు (M.S.R) మరియు వెర్నియర్ స్కేలు రీడింగు (V.S.R) లను కొలుస్తారు.

బరువు 3 కి.గ్రా. వరకు పెంచిన తరువాత క్రమంగా ప్రతిసారి 1/2 కి.గ్రా. చొప్పున తగ్గిస్తారు. బరువు తగ్గించిన ప్రతిసారి ప్రధాన స్కేలు (M.S.R.) మరియు వెర్నియర్ స్కేలు (V.S.R.) రీడింగులు కొలుస్తారు. ఈ విలువలు పట్టికలో పొందుపరుస్తారు.

మొదటి రీడింగును (M₁ మరియు e₁) లను ఆధారంగా తీసుకొని ప్రతి విలువ (M₂, M₃ మరియు e₂, e₃ వంటివి) నుండి తొలి విలువ (M₁, e₁) లను తీసివేయడం ద్వారా ద్రవ్యరాశిలో మార్పు ‘m’ మరియు దానికి సంబంధించిన సాగుదల ‘e’ లను లెక్కగడతారు.
ద్రవ్యరాశిలో మార్పు m = m₂ – m₁; తీగలో సాగుదల e = e₂ – e₁

సరాసరి = m/e; తీగపై బలము = mg
తీగ అడ్డుకోత వైశాల్యము = πr²
r = తీగ వ్యాసార్ధము
సాగుదల = e,
తీగ తొలి పొడవు = l
ప్రతిబలము = \(\left(\frac{\mathrm{F}}{\mathrm{a}}\right)=\frac{\mathrm{mg}}{\pi r^2}\)
వికృతి = \(\left(\frac{\mathrm{e}}{l}\right)\)
యంగ్ గుణకము Y = \(\left(\frac{g l}{\pi r^2}\right)\left(\frac{m}{e}\right)\)

ప్రయోగపూర్వకంగా కనుగొనిన విలువలు l, r, e, m లను ఈ సమీకరణంలో ప్రతిక్షేపించి Y విలువ కనుగొంటారు.
జాగ్రత్తలు :

1. వ్రేలాడదీయు బరువులు స్థితిస్థాపక అవధి కన్న చాలా తక్కువగా ఉండవలెను.
2. ఏకీభవించు వెర్నియర్ స్థానమును పారలాక్సు దోషము లేకుండా కొలవవలెను.

లెక్కలు

ప్రశ్న 1.
1 mmవ్యాసం ఉన్న రాగి తీగను 10 N బలం అనువర్తించి సాగదీశారు. ఆ తీగలోని ప్రతిబలం కనుక్కోండి.
సాధన:
వ్యాసము d = 1 mm;
బలము F = 10N;
∴ వ్యాసార్ధము r = 0.5 mm = = 0.5 × 10^-3 m
∴ ప్రతిబలము = \(\frac{\mathrm{F}}{\pi \mathrm{r}^2}=\frac{10}{3.141 \times 0.5 \times 0.5 \times 10^{-6}}=\frac{40 \times 10^6}{3.141}\) = 1.273 × 10⁷ Pa

ప్రశ్న 2.
20 cm పొడవు వున్న టంగ్స్టన్ తీగను 0.1 cm అదనంగా సాగదీశారు. తీగలోని వికృతిని కనుక్కోండి.
సాధన:
తీగ పొడవు l = 20cm = 0.2m;
సాగుదల e = 0.1cm = 1 × 10^-3 m

= \(\frac{1 \times 10^{-3}}{0.2}\) = 5 × 10^-3 = 0.005

ప్రశ్న 3.
ఇనుప తీగను 1% సాగదీసినట్లయితే దానిలో వచ్చిన వికృతి ఎంత ?
సాధన:
పొడవులో పెరుగుదల = e = 1% = \(\frac{1}{100}\) l

= \(\frac{\mathrm{e}}{l}=\frac{1}{100 \times l}=\frac{1}{100}\) = 0.01

ప్రశ్న 4.
1 mm వ్యాసం, 2m పొడవు ఉన్న ఇత్తడి తీగపై 20 N బలం ప్రయోగించి సాగదీశారు. పొడవులో పెరుగుదల 0.51 mm అయితే, 1) తీగ ప్రతిబలం, 2) వికృతి, 3) యంగ్ గుణకాలను కనుక్కోండి.
సాధన:
తీగ పొడవు l = 2m;
బలము F = 20N;
వ్యాసము d = 1mm = 10^-3 m
పొడవులో పెరుగుదల e = 0.51mm = 0.51 × 10^-3 m

ప్రశ్న 5.
రాగి, అల్యూమినియం తీగల పొడవుల నిష్పత్తి 3: 2, వ్యాసాల నిష్పత్తి 2: 3, వీటిపై అనువర్తిత బలాల నిష్పత్తి 4:5గా ఉన్నాయి. రెండు తీగల పొడవుల పెరుగుదల నిష్పత్తిని కనుక్కోండి. (Y_Cu = 1.1 × 10¹¹ Nm^-2, Y_Al = 0.7 × 10¹¹ Nm^-2)
సాధన:
పొడవుల నిష్పత్తి l₁ : l₂ = 3 : 2 ;
వ్యాసముల నిష్పత్తి d₁ : d₂ = 2 : 3
బలాల నిష్పత్తి F₁ : F₂ = 4:5
Y₁ = రాగి యంగ్ గుణకము : 1.1 × 10¹¹
Y₂ = అల్యూమినియం యంగ్ గుణకము = 0.7 × 10¹¹
సాగుదల నిష్పత్తి e₁ : e₂ = ?
e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}=\frac{4 \mathrm{~F} l}{\pi \mathrm{d}^2 \mathrm{Y}}\)
∴ \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{4 \mathrm{~F}_1 l_1}{\pi \mathrm{d}_1^2 \mathrm{Y}_1} \times \frac{\pi \mathrm{d}_2^2 \mathrm{Y}_2}{4 \mathrm{~F}_2 l_2}\)
⇒ \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{\mathrm{F}_1 l_1 \mathrm{~d}_2^2 \mathrm{Y}_2}{\mathrm{~F}_2 l_2 \mathrm{~d}_1^2 \mathrm{Y}_1}=\frac{4 \times 3 \times 3^2 \times 0.7 \times 10^{11}}{5 \times 2 \times 2^2 \times 1.1 \times 10^{11}}=\frac{189}{110}\)
∴ e₁ : e₂ = 189 : 110

ప్రశ్న 6.
2 mm² మధ్యచ్ఛేద వైశాల్యం ఉన్న ఇత్తడి తీగ ఒక కొనను ద్రుఢ ఆధారానికి బిగించి రెండో కొనకు 100 cm³ ఘనపరిమాణం ఉన్న వస్తువును కట్టారు. వస్తువును నీటిలో పూర్తిగా ముంచినప్పుడు తీగ పొడవు 0.11 mm తగ్గింది. తీగ సహజ పొడవును కనుక్కోండి. (Y_{ఇత్తడి} : 0.91 × 10¹¹ Nm^-2, ρ_నీరు = 10³ kg m^-3)
సాధన:
అడ్డుకోత వైశాల్యము A = 2mm² = 2 × 10^-6 m²
వస్తువు ఘనపరిమాణము V = 100cc = 100 × 10^-6 m³
పొడవులో తగ్గుదల e’ = 0.11mm = 0.11 × 10^-3 m
ఇత్తడి యంగ్ గుణకము Y = 0.91 × 10¹¹ N/m²
నీరు సాంద్రత ρ = 1000 kg / m³; వికృతి e’ = \(\frac{\mathrm{V} \rho \mathrm{g} l}{\mathrm{AY}}\) ని ఉపయోగించగా
తీగ సహజ పొడవు l = \(\frac{\mathrm{e}^{\prime} \mathrm{AY}}{\mathrm{V} \rho \mathrm{g}}=\frac{0.11 \times 10^{-3} \times 2 \times 10^{-6} \times 0.91 \times 10^{11}}{100 \times 10^{-6} \times 1000 \times 9.8}\)
∴ l = \(\frac{0.2002 \times 10^2}{9.8}=\frac{20.02}{9.8}\) = 2.043 m

ప్రశ్న 7.
ఒకే పదార్థంతో చేసిన రెండు తీగల వ్యాసార్ధాల, పొడవుల నిష్పత్తులు ఒకే విధంగా ఉన్నాయి. ఆ నిష్పత్తి 1 : 2 రెండింటిలోనూ వచ్చిన దైర్ఘ్యవృద్ధి సమంగా ఉంటే, వాటిపై వేసిన భారాల నిష్పత్తి ఎంత ?
సాధన:
పొడవుల నిష్పత్తి l₁ : l₂ = 1 : 2; .
తీగలలో సాగుదలలు సమానము ⇒ e₁ = e₂;
వ్యాసార్ధముల నిష్పత్తి r₁ : r₂ = 1 : 2
రెండు తీగలు ఒకే పదార్థముతో చేయబడినవి ⇒ Y₁ = Y₂
వ్రేలాడదీసిన ద్రవ్యరాశుల నిష్పత్తి m₁ : m₂ = ?
Y = \(\frac{\mathrm{mg}}{\pi \mathrm{r}^2} \frac{\mathrm{l}}{\mathrm{e}}\) ని ఉపయోగించగా
\(\frac{\mathrm{m}_1}{\mathrm{~m}_2}=\frac{\mathrm{Y}_1 \mathrm{r}_1^2 l_2}{l_1 \mathrm{Y}_2 \mathrm{r}_2^2}=\frac{1 \times 2}{1 \times 2^2}=\frac{1}{2}\)
∴ m₁ : m₂ = 1 : 2

ప్రశ్న 8.
వేరు వేరు పదార్థాలతో చేసిన రెండు తీగలు ఒకే పొడవు, మధ్యచ్ఛేదాన్ని కలిగి ఉన్నాయి. వీటిపై సమానమైన బలాలను అనువర్తించినప్పుడు రెండింటి పొడవుల పెరుగుదల నిష్పత్తి ఎంత ?
(Y₁ = 0.9 × 10¹¹ Nm^-2, Y₂ = 3.60 × 10¹¹ Nm^-2)
సాధన:
రెండు తీగల పొడవులు సమానము ⇒ l₁ = l₂; తీగల అడ్డుకోత వైశాల్యములు సమానము A₁ = A₂
Y₁ = 0.9 × 10¹¹ Nm^-2
Y₂ = 3.60 × 10¹¹ Nm^-2
సాగుదల e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}\)
∴ \(\frac{e_1}{e_2}=\frac{F_1 l_1}{A_1 Y_1} \cdot \frac{A_2 Y_2}{F_2 l_2}\) (∵ ఇందులో F, I మరియు A లు సమానము)
∴ \(\frac{e_1}{e_2}=\frac{Y_2}{Y_1}\)
∴ \(\frac{e_1}{e_2}=\frac{3.60 \times 10^{11}}{0.9 \times 10^{11}}=\frac{4}{1}\) (లేదా) e₁ : e₂ = 4 : 1

ప్రశ్న 9.
2.5 m పొడవు, 1.5 × 10⁶ m² మధ్యచ్ఛేద వైశాల్యం ఉన్న లోహతీగను 2 mm సాగదీశారు. తీగ యంగ్ గుణకం 1.25 × 10¹¹ Nm^-2 అయితే దానిలో ఉండే తన్యతను కనుక్కోండి.
సాధన:
తీగ పొడవు l = 2.5m
సాగుదల e = 2 m.m = 2 × 10^-3 m
అడ్డుకోత వైశాల్యము A = 1.5 × 10^-6 m²
Y = 1.25 × 10²² N/m²
తన్యత T = mg = F = ?
Y = \(\frac{\mathrm{Fl}}{\mathrm{Ae}}\) ⇒ F = \(\frac{\mathrm{YAe}}{l}\)
∴ T = \(\frac{1.25 \times 10^{11} \times 1.5 \times 10^{-6} \times 2 \times 10^{-3}}{2.5}\) = \(\frac{3.75 \times 10^2}{2.5}\) = 150 N

ప్రశ్న 10.
ఒకే పొడవు, మధ్యచ్ఛేదం ఉన్న అల్యూమినియం, ఉక్కు తీగల కొనలను కలిపారు. ఈ మిశ్రమ తీగ ఒక కొనను ద్రుఢ ఆధారానికి బిగించి రెండో కొనకు భారాన్ని వేలాడదీశారు. మిశ్రమ తీగ పొడవులో పెరుగుదల 1.35mm ఉంటే 1) రెండు తీగలపై పనిచేసే ప్రతిబలాల 2) రెండు తీగలలో వచ్చే వికృతుల నిష్పత్తులను కనుక్కోండి.
(Y_AL = 0.7 × 10¹¹ Nm^-2, Y_steel = 2 × 10¹¹ Nm^-2)
సాధన:
i) రెండు తీగల పొడవులు సమానము ⇒ l₁ = l₂ ;
అడ్డుకోత వైశాల్యములు సమానము ⇒ A₁ = A₂
సంయోగ తీగలో రెండు తీగలపై ఒకే బలము పనిచేయును;
∴ ప్రతిబలాల నిష్పత్తి = 1 : 1

ii) మొత్తము సాగుదల e = 1.35mm = e_Al + e_s
అల్యూమినియం యంగ్ గుణకము 7 × 10¹¹ N/m²,
స్టీలు తీగ యంగ్ గుణకము, Y = 2 × 10¹¹ N/m²
సాగుదల e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}\) కాని F, I మరియు A లు సమానము.
∴ e ∝ \(\frac{1}{\mathrm{Y}}\) లేదా \(\frac{\mathrm{e}_{\mathrm{A} l}}{\mathrm{e}_{\mathrm{S}}}=\frac{\mathrm{Y}_{\mathrm{S}}}{\mathrm{Y}_{\mathrm{A} l}}=\frac{20 \times 10^{10}}{7 \times 10^{10}}=\frac{20}{7}\) లేదా 20 : 7
∴ తీగలలో వికృతిల నిష్పత్తి 20 : 7.

ప్రశ్న 11.
ఒక పదార్థంతో చేసిన 2 cm భుజం కలిగిన ఘనంపై ప్రయోగించిన 0.3 N స్పర్శాబలం దాని పై తలాన్ని 0.15 cm స్థానభ్రంశం చెందించింది. ఘనం కింది తలాన్ని స్థిరంగా ఉంచారు. పదార్థం విమోటన గుణకం కనుక్కోండి.
జవాబు:
ఘనము యొక్క ఒక భుజము పొడవు a = 2.0cm = 2 × 10² m
∴ ఘనము యొక్క ఒక తలము వైశాల్యము A = 4 × 10^-4 m²
ఉపరితల పొర స్థాన భ్రంశం = 0.15cm = 0.15 × 10^-2m
స్పర్శీయ బలము F = 0.30N
విమోటనా గుణకము η = \(\frac{\mathrm{F}}{\mathrm{A}} \cdot \frac{\mathrm{x}}{\Delta \mathrm{x}}=\frac{0.30}{4 \times 10^{-4}} \frac{2 \times 10^{-2}}{0.15 \times 10^{-2}}\)
∴ η = \(\frac{0.60 \times 10^4}{0.60}\) = 1 × 10⁴ N/m²

ప్రశ్న 12.
1000 cm³ ఘనపరిమాణం ఉన్న గోళాకార బంతిపై 10 atm పీడనాన్ని ప్రయోగించారు. ఘనపరిమాణంలో వచ్చిన మార్పు 10^-2 cm³. బంతిని ఇనుముతో తయారుచేసినట్లైతే దాని యంగ్ గుణకాన్ని కనుక్కోండి. (1 atm = 1 × 10⁵ Nm^-2)
సాధన:
గోళాకార బంతి ఘనపరిమాణము V = 1000 cm³ = 10^-3 m³ (∵ 1M³ = 10⁶ cm³)
పీడనము P = 10 అట్మాస్పియర్లు = 10 × 10⁵ పాస్కల్ ( ∵ 1 atm = 10⁵ cm)
ఘనపరిమాణములో మార్పు ∆V = 10^-8 cm³ స్థూల గుణకము K ?
K = \(\frac{\mathrm{PV}}{\Delta \mathrm{V}}=\frac{10^6 \times 10^{-3}}{10^{-8}}\) = 1 × 10¹¹ N/m²

ప్రశ్న 13.
1 cm భుజం ఉన్న రాగి ఘనాన్ని 100 atm పీడనానికి గురిచేశారు. రాగి ఆయత గుణకం 1.4 × 10¹¹ Nm^-2 అయితే ఘనపరిమాణంలో వచ్చే మార్పును కనుక్కోండి. (1 atm = 1 × 10⁵ Nm^-2)
సాధన:
ఒక రాగి ఘనము ఒక్కొక్క భుజము పొడవు ‘a’ 1 సెం.మీ. = 10^-2 m
∴ ఘనము ఘనపరిమాణము = 10^-6m
పీడనము P = 100 అట్మాస్పియర్లు = 100 × 10⁵ = 10⁷ పాస్కల్లు
స్థూల గుణకము K = 1.4 × 10¹¹ N/m²;
ఘనపరిమాణములో మార్పు ∆V = \(\frac{P . V}{K}=\frac{10^7 \times 10^{-6}}{1.4 \times 10^{11}}=\frac{10^{-10}}{1.4}\)
= 0.7143 × 10^-10 m³

ప్రశ్న 14.
ఇచ్చిన నీటి ఘనపరిమాణాన్ని 2% తగ్గించడానికి ఎంత పీడనం అవసరమవుతుంది ? నీటి ఆయత గుణకం 2.2 × 10⁹ Nm^-2.
సాధన:
స్థూల వికృతి = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) = 2% ⇒ ∆V = \(\frac{2}{100}\) V
స్థూల గుణకము _ K = 2.2 × 10⁹ Nm^-2
∴ కావలసిన పీడనము P = \(\frac{\mathrm{K} \Delta \mathrm{V}}{\mathrm{V}}=\frac{2.2 \times 10^9 \times 2 \mathrm{~V}}{\mathrm{~V} \times 100}\) = 4.4 × 10⁷ పాస్కల్

ప్రశ్న 15.
20 cm పొడవు ఉన్న ఉక్కు తీగను సాగదీసి దాని పొడవును 0.2 cm పెంచారు. ఉక్కు ప్వాజూన్ నిష్పత్తి 0.19 అయితే, తీగలో వచ్చే పార్శ్వ వికృతి ఎంత ?
సాధన:
తీగ పొడవు l = 20cm = 0.20m, ప్వాజూన్ నిష్పత్తి σ = 0.19
పొడవులో సాగుదల ∆l = 0.2cm = 2 × 10³ m;
పార్శ్వీయ వికృతి = ?
పార్శ్వ వికృతి = σ × అనుదైర్ఘ్య వికృతి ‘e’;
కాని e = \(\)
∴ పార్శ్వీయ వికృతి = σ \(\frac{\Delta l}{l}\) = \(\frac{0.19 \times 2 \times 10^{-3}}{0.20}\) = 1.9 × 10^-3 = 0.0019m.

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
4.7 m పొడవు, 3.0 × 10^-5 m² మధ్యచ్ఛేద వైశాల్యం ఉన్న ఉక్కు తీగ, 3.5 m పొడవు, 4.0 × 10^-5 m² తీగ రెండూ ఇచ్చిన భారం వల్ల సమానంగా సాగాయి. ఉక్కు రాగి యంగ్ గుణకాల మధ్యచ్ఛేద వైశాల్యం ఉన్న రాగి నిష్పత్తి ఎంత ?
సాధన:
ఉక్కు తీగకు a₁ = 3.0 × 10^-5 m²; l₁ = 4.7 m; ∆l₁ = ∆l ; F₁ = F
రాగి తీగకు a₂ = 4.0 × 10^-5 m²; l₂ = 3.5 m; ∆l₂ = ∆l ; F₂ = F
Y₁, Y₂ లను వరుసగా ఉక్కు, కాపర్ల యంగ్ గుణకాలు అనుకొనుము.

ప్రశ్న 2.
పటంలో ఒక పదార్థం వికృతి-ప్రతిబలం వక్రం చూపించడమైనది. ఈ పదార్థం ఎ) యంగ్ గుణకం, బి) ఉజ్జాయింపు ఈగే సామర్థ్యం ఎంత ?
సాధన:
ఎ) గ్రాఫ్ నుండి ప్రతిబలము = 150 × 10⁶ Nm^-2,
వికృతి = 0.002

= 7.5 × 10¹⁰ Nm^-2

బి) ఉజ్జాయింపుగా ఊగే సామర్థ్యము అది భరించగల అత్యధిక ప్రతిబలానికి సమానము.
∴ ఉజ్జాయింపుగా ఊగే సామర్థ్యము
= 300 × 10⁶ Nm^-2 = 3 × 10⁸ Nm^-2

ప్రశ్న 3.
రెండు పదార్థాలు A, B ప్రతిబలం – వికృతి వక్రాలను పటంలో ఇవ్వడమైంది. రెండు వక్రాలను ఒకే స్కేలు ప్రకారం గీశారు.
ఎ) రెండు పదార్థాల్లో ఏ పదార్థం యంగ్ గుణకం ఎక్కువ ?
బి) రెండు పదార్థాల్లో ఏది బలమైనది ?

సాధన:
ఎ) ఇచ్చిన రెండు ప్రతిబలము – వికృతి రేఖాపటాలలో A గ్రాఫ్ ప్రతిబలము B కన్న ఎక్కువ కావున A కి యంగ్ గుణకము ఎక్కువ. (Y = ప్రతిబలము/వికృతి కావున)
బి) ఒక వస్తువు యొక్క దృఢత్వము దానిని తెంపటానికి కావలసిన ప్రతిబలంపై ఆధారపడును. A కి ప్రతిబలం ఎక్కువ కావున కన్న A దృఢమైనది.

ప్రశ్న 4.
కింద ఇచ్చిన రెండు ప్రవచనాలను జాగ్రత్తగా చదివి అది తప్పా, ఒప్పా కారణాలతో వివరించండి.
ఎ) రబ్బరు యంగ్ గుణకం ఉక్కు కంటే ఎక్కువ.
బి) తీగ చుట్ట సాగుదలను దాని విమోటన గుణకం ఆధారంగా నిర్ణయించవచ్చు.
సాధన:
ఎ) ఈ వాక్యము అబద్ధము. ఒకే ప్రతిబలానికి స్టీలు కన్న రబ్బరుకు వికృతి ఎక్కువ. స్థితిస్థాపక గుణకము వికృతికి విలోమానుపాతంలో ఉండును. yo : 1/వికృతి

బి) ఈ వాక్యము నిజము. స్ప్రింగ్ను సాగదీస్తే మనం వాడిన బలం తీగ పొడవు మారకుండా స్ప్రింగ్ ఆకారాన్ని మారుస్తుంది. అందువల్ల ఈ ప్రక్రియలో దృఢతా గుణకము లెక్కలోనికి వస్తుంది.

ప్రశ్న 5.
పటంలో చూపించినట్లు 0.25 cm వ్యాసం ఉన్న ఉక్కు, ఇత్తడి తీగలను భారయుతం చేశారు. భారరహిత స్థితిలో ఉక్కుతీగ పొడవు 1.5 m, ఇత్తడి తీగ పొడవు 1.0 m. ఉక్కు, ఇత్తడి తీగలలో వచ్చే దైర్ఘ్యవృద్ధి లెక్కించండి.

సాధన:
ఉక్కుతీగకు, ఉక్కు తీగపై మొత్తం బలము
F₁ = 4 + 6 = 10 kg f = 10 × 9.8 N;
l₁ = 1.5 m, ∆l₁ = ?; 2r₁ = 0.25 cm
లేదా r₁ = (0.25/2) cm = 0.125 × 10^-2 m;
Y₁ = 2.0 × 10¹¹ Pa
ఇత్తడి తీగకు F₂ = 6.0 kg, f = 6 × 9.8 N; 2r₂ = 0.25 cm
లేదా r₂ = (0.25/2) cm = 0.125 × 10^-2 m;
Y₂ = 0.91 × 10¹¹ Pa, l₂ = 1.0 m, ∆l₂= ?
Y₁ = \(\frac{\mathrm{F}_1 \times l_1}{\mathrm{a}_1 \times \Delta l_1}=\frac{\mathrm{F}_1 \times l_1}{\pi \mathrm{r}_1^2 \times \Delta l_1}\)

ప్రశ్న 6.
అల్యూమినియం ఘనం అంచు పొడవు 10 cm. ఘనం ఒక తలాన్ని నిలువు గోడకు గట్టిగా బిగించారు. ఘనం ఎదురు తలానికి 100 kg ద్రవ్యరాశిని తగిలించారు. అల్యూమినియం విమోటన గుణకం 25 GPa. ఈ తలం నిట్టనిలువు అపవర్తనం ఎంత ?
సాధన:
A = 0.10 × 0.10 = 10^-2 m²; F = mg = 100 × 10 N
విమోటన వికృతి = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\) = \(\frac{(\mathrm{F} / \mathrm{A})}{\mathrm{G}}\) or ∆L = \(\frac{\mathrm{FL}}{\mathrm{AG}}\) = \(\frac{(100 \times 10) \times 0.10}{10^{-2} \times\left(25 \times 10^9\right)}\) = 4 × 10^-7 m.

ప్రశ్న 7.
50,000 kg ద్రవ్యరాశి ఉన్న భారీ కట్టడానికి ఆధారంగా నాలుగు బోలు స్థూపాకార, మృదు ఉక్కుస్తంభాలు ఉన్నాయి. ప్రతీ స్తంభం లోపలి, బాహ్య వాసార్ధాలు వరుసగా 30, 60 cm గా ఉన్నాయి. భార వితరణ ఏకరీతిగా ఉన్నదనుకొని ప్రతీ స్తంభంలో వచ్చే సంపీడన వికృతిని కనుక్కోండి.
సాధన:

ప్రశ్న 8.
15.2 mm × 19.1 mm కొలతలు ఉన్న దీర్ఘచతురస్రాకార రాగి ముక్కను 44,500 N తన్యత బలంతో కేవలం స్థితిస్థాపక విరూపణ కలిగే విధంగా లాగారు. దాని మూలంగా కలిగే ఫలిత వికృతిని గణించండి.
సాధన:
దత్తాంశం నుండి A = 15.2 × 19.2 × 10^-6 m²; F = 44,500 N; G = 42 × 10⁹ Nm^-2

ప్రశ్న 9.
స్కీయింగ్ ప్రాంతంలో ఉన్న చైర్ లిఫ్ట్ను మోసే ఉక్కు కేబుల్ వ్యాసార్ధం 1.5cm. గరిష్ట ప్రతిబలం విలువ 10⁸ Nm^-2 ను దాటకూడదు. అంటే, కేబుల్ గరిష్ఠంగా ఎంత బరువును మోయగలదు ?
సాధన:
గరిష్ఠ భారము = గరిష్ఠ ప్రతిబలము × అడ్డుకోత వైశాల్యము
= 10⁸ × πr² = 10⁸ × (22/7) × (1.5 × 10^-2)² = 7.07 × 10⁴ N

ప్రశ్న 10.
15 kg ద్రవ్యరాశి ఉన్న ద్రుఢమైన కడ్డీని సౌష్ఠవంగా అమర్చి ఉన్న మూడు తీగలు మోస్తున్నాయి. ప్రతి తీగ పొడవు 2.0 m. రెండు చివరల ఉన్న తీగలు రాగికి కాగా, మధ్యలో తీగ ఇనుముతో తయారయింది. అన్ని సమాన తన్యతను కలిగి ఉండాలంటే, వాటి వ్యాసాల నిష్పత్తులు ఎలా ఉండాలి ?
సాధన:
ప్రతీ తీగ ఒకే తన్యత 1 ను కల్గి ఉన్నందున, అవి ద్రుఢమైన కడ్డీ ద్రవ్యరాశి కారణంగా ఒకే విధమైన సాగుదలను కలిగి ఉంటాయి. ప్రతీ తీగ ఒకే పొడవు కలిగి ఉన్నందున వాటికి సమాన వికృతి ఉంటుంది. తీగ వ్యాసం D అయితే
Y = \(\frac{4 \mathrm{~F} / \pi \mathrm{D}^2}{\text { వికృతి }}\) (లేదా) D² ∝ 1/Y
∴ \(\frac{D_{\mathrm{cu}}}{\mathrm{D}_{\mathrm{iron}}}\) = \(\sqrt{\frac{Y_{\text {iron }}}{Y_{\mathrm{Cu}}}}\) = \(\sqrt{\frac{190 \times 10^9}{110 \times 10^9}}\) = \(\sqrt{\frac{19}{11}}\) = 1.31

ప్రశ్న 11.
1.0 m సహజ పొడవు ఉన్న ఉక్కు తీగ ఒక చివర 14.5 kg ద్రవ్యరాశిని కట్టి నిలువు తలంలో వృత్తాకారంగా తిప్పారు. దాని కనిష్ఠ బిందువు వద్ద కోణీయ వేగం 2 reu/s. తీగ మధ్యచ్ఛేద వైశాల్యం 0.065 cm². ద్రవ్యరాశి వృత్తాకార పథంలో కనిష్ఠ బిందువు వద్ద ఉన్నప్పుడు తీగలో వచ్చే దైర్ఘ్యవృద్ధిని లెక్కించండి.
సాధన:
దత్తాంశం నుండి m = 14.5 kg; l = r = 1 m; v = 2 rps; A = 0.065 × 10^-4 m²
నిలువు వృత్తంలో కనిష్ఠ బిందువు వద్ద మొత్తము బలము
F = mg + mr ω² = mg + mr 4 π² v² = 14.5 × 9.8 + 14.5 × 1 × 4 × (22/7)² × 2²
= 142.1+ 2291.6 = 2433.7 N
Y =\(\frac{\mathrm{F}}{\mathrm{A}} \times \frac{l}{\Delta l}\) or ∆l = \(\frac{\mathrm{Fl}}{\mathrm{AY}}=\frac{2433.7 \times 1}{\left(0.065 \times 10^{-4}\right) \times\left(2 \times 10^{11}\right)}\) = 1.87 × 10^-3 m = 1.87mm

ప్రశ్న 12.
క్రింద ఇచ్చిన దత్తాంశం సహాయంతో నీటి ఆయత గుణకాన్ని కనుక్కోండి. తొలి ఘనపరిమాణం = 100.0 litre, పీడనం పెరుగుదల = 100.0 atm (1 atm = 1,013 × 10⁵ Pa), తుది ఘనపరిమాణం = 100,5 litre. నీటి ఆయతన గుణకాన్ని గాలి (స్థిర ఉష్ణోగ్రత వద్ద) ఆయత గుణకంతో పోల్చండి. ఈ నిష్పత్తి ఎందుకు చాలా అధికంగా ఉంటుందో సులభరీతిలో వివరించండి.
సాధన:
దత్తాంశం నుండి V = 100 litre = 100 × 10^-3 m³; p = 100 atm = 100 × 1.013 10⁵ Pa.
V + ∆V = 100.5 లీటర్లు (లేదా) ∆V = (V + ∆V) – V = 100.5 – 100 = 0.5 litre = 0.5 ×10^-3 m³.
ఆయతన గుణకము, B = \(\frac{\mathrm{pV}}{\Delta \mathrm{V}}\) = \(\frac{100 \times 1.013 \times 10^5 \times 100 \times 10^{-3}}{0.5 \times 10^{-3}}\) = 2.026 × 10⁹ Pa
గాలి ఆయతన గుణకము 1.0 × 10⁵ Pa

వాయువులలో అణువుల మధ్య దూరము చాలా ఎక్కువ. వాటి మధ్య గల బంధాలు చాలా బలహీనమైనవి. అందువల్ల ద్రవాల కన్నా వాయువుల ఆయతన గుణకం చాలా తక్కువ.

ప్రశ్న 13.
ఉపరితలంపై నీటి సాంద్రత 1.03 × 10³ kg m^-3 గా ఉన్నట్లయితే, 80.00 atm పీడనం ఉండే లోతులో నీటి సాంద్రత ఎంత ఉంటుంది ?
సాధన:
దత్తాంశం నుండి_p = 80.00 atm = 80.0 × 1.013 × 10⁵ Pa; సంపీడ్యత \(\frac{1}{B}\) = 45.8 × 10^-11 Pa^-1
ఉపరితలం వద్ద నీటి సాంద్రత ρ = 1.03 × 10³ kg m^-3
M ద్రవ్యరాశి గల నీటికి ఉపరితలం వద్ద మరియు ఇచ్చిన లోతు వద్ద నీటి ఘనపరిమాణాలు
V = \(\frac{M}{\rho}\) మరియు V’ = \(\frac{\mathrm{M}}{\rho^{\prime}}\)

ప్రశ్న 14.
10 atm హైడ్రాలిక్ పీడనానికి గురిచేసిన గాజు పలక ఘనపరిమాణంలో వచ్చే అంశిక మార్పు కనుక్కోండి.
సాధన:
దత్తాంశం నుండి p = 10 atm = 10 × 1.013 × 10⁵ Pa; B = 37 × 10⁹ Nm^-2
ఘనపరిమాణ వికృతి = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{\mathrm{p}}{\mathrm{B}}=\frac{10 \times 1.013 \times 10^5}{37 \times 10^9}\) = 2.74 × 10^-5
∴ ఘనపరిమాణంలో అంశిక మార్పు = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) = 2.74 × 10^-5

ప్రశ్న 15.
7.0 × 10⁶ Pa హైడ్రాలిక్ పీడనానికి గురయిన 10 cm భుజం ఉన్న ఘన రాగి ఘనం ఏర్పడే ఘనపరిమాణ సంకోచాన్ని నిర్ణయించండి.
సాధన:
దత్తాంశం నుండి L = 10 cm = 0.10 m; p = 7 × 10⁶ Pa; B = 140 GPa = 140 × 10⁹ Pa
B = \(\frac{\mathrm{pV}}{\Delta \mathrm{V}}=\frac{\mathrm{p} L^3}{\Delta \mathrm{V}}\) or ∆V = \(\frac{\mathrm{pL}^3}{\mathrm{~B}}=\frac{\left(7 \times 10^6\right) \times(0.10)^3}{140 \times 10^9}\) = 5 × 10^-8; m³ = 5 × 10^-2 mm³

ప్రశ్న 16.
ఒక లీటరు నీటిని 0.10% సంపీడనం చెందించడానికి ఎంత పీడనం అవసరం ?
సాధన:
దత్తాంశం నుండి V = 1 లీటరు = 10^-3 m³; ∆V/V = 0.10/100 = 10^-3
B = \(\frac{\mathrm{pV}}{\Delta \mathrm{V}}\) (లేదా) p = B\(\frac{\Delta V}{V}\) = (2.2 × 10⁹) × 10^-3 = 2.2 × 10⁶ Pa

ప్రశ్న 17.
అధిక పీడనాల వద్ద పదార్థాల ప్రవర్తనను తెలుసుకోవడానికి పటంలో చూపిన ఆకృతిలో ఉన్న ఏక స్పటిక వజ్రం (స్వర్ణకారులు వాడేది) దాగిలి (Anvil) ని వాడతారు. సన్నకొన వద్ద ఉండే సమతలం వ్యాసం 0.50mm. వెడల్పు కొనను 50,000 N సంపీడ్యత బలానికి గురిచేశారు. దాగిలి మొన (tip) పై పనిచేసే పీడనం ఎంత ?

సాధన:
దత్తాంశం నుండి D = 0.5 mm = 0.5 × 10^-3 m = 5 × 10^-4 m
F = 50,000 N = 5 × 10⁴ N
దాగిలి మొనపై పీడనము, P = \(\frac{\mathrm{F}}{\pi \mathrm{D}^2 / 4}=\frac{4 \mathrm{~F}}{\pi \mathrm{D}^2}\)
∴ P = \(\frac{4 \times\left(5 \times 10^4\right)}{(22 / 7) \times\left(5 \times 10^{-4}\right)^2}\) = 2.5 × 10¹¹ Pa

ప్రశ్న 18.
రెండు లోహ పలకలను ఒకదానితో ఒకటి చివరల నాలుగు రివెట్లనుపయోగించి బిగించారు. ప్రతి రివెట్ వ్యాసం 6.0 mm. ప్రతి రివెట్పై విమోటన బలం 6.9 × 10⁷ Pa దాటకూడదు. రివెట్లు కట్టిన లోహ పలకల వల్ల కలిగే గరిష్ఠ తన్యత ఎంత ? ప్రతి రివెట్ భారంలో నాలుగో వంతును భరిస్తుందనుకోండి.
సాధన:
దత్తాంశం నుండి = : 6/2 = 3 mm = 3 × 10^-3 m; గరిష్ఠ ప్రతిబలము = 6.9 × 10⁷ Pa;
రివెట్ పై గరిష్ఠ భారము = గరిష్ఠ ప్రతిబలము × అడ్డుకోత వైశాల్యము = 6.9 × 10⁷ × (22/7) × (3 × 10^-3)²
∴ గరిష్ఠ తన్యత = 4[6.9 × 10⁷ × \(\frac{22}{7}\) × 9 × 10^-6] = 7.8 × 10³ N

ప్రశ్న 19.
పసిఫిక్ మహాసముద్రంలో ఉన్న మరీనా అగాధం లోతు ఒక చోట ఉపరితలం నుంచి 11 km ఉంటుంది. అగాధం అడుగు భాగంలో ద్రవ పీడనం సుమారు 1.1 × 10⁸ Pa గా ఉంటుంది. సముద్రంలో 0.32 m³ తొలి ఘనపరిమాణం ఉన్న ఉక్కు బంతిని వదిలినప్పుడు అది అగాధం అడుగుకు చేరుకొంది. అక్కడ బంతి ఘనపరిమాణంలో వచ్చే మార్పు ఎంత ?
సాధన:
దత్తాంశం నుండి p = 1.1 × 10⁸ pa; V = 0.32 m³; B = 1.6 × 10¹¹ Pa
∆V = \(\frac{\mathrm{pV}}{\mathrm{B}}\) = \(\frac{\left(1.1 \times 10^8\right) \times 0.32}{1.6 \times 10^{11}}\) = 2.2 × 10^-4 m³.

Students must practice these TS Intermediate Maths 1A Solutions Chapter 4 Addition of Vectors Ex 4(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b)

I.
Question 1.
Find the vector equation of the line passing through the point 2i̅ + 3j̅ + k̅ and parallel to the vector 4i̅ – 2j̅ + 3k̅.(March 2015-A.P) (May, March ’01) (V.S.A)
Answer:
Let a = 2i̅ + 3j̅ + k̅ and b = 4i̅ – 2 j̅ + 3k̅
The vector equation of the line passing through the point a̅ and parallel to the vector b̅ is
r̅ = a̅ + tb̅ where t is a scalar.
r̅ = (2i̅ + 3j̅ + k̅) + t (4i̅ – 2j̅ + 3k̅)
⇒ r̅ = (2 + 4t) i̅ + (3 – 2t) j̅ + (1 + 3t) k̅

Question 2.
OABC is a parallelogram. If \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}\) and \(\overline{\mathrm{OC}}=\overline{\mathrm{c}}\). Find the vector equation of the side BC. (March 2015-T.S) (V.S.A)
Answer:
OABC is a parallelogram.

∴ The vector equation of side BC is r̅ = (1 – t)c̅ + t(a̅ + c̅)
= (1 – t + t)c̅ + ta̅
= c̅ + t a̅ where t ∈ R.

Question 3.
If a̅, b̅, c̅ are the position vectors of the vertices A, B and C respectively of a ΔABC, then find the vector equation of the median through the vertex A. (March 2013) (V.S.A)
Answer:

Let \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}, \overline{\mathrm{OB}}=\overline{\mathrm{b}}\), and \(\overline{\mathrm{OC}}=\overline{\mathrm{c}}\)
Vector equation of the median AD is (1 – t)
a̅ + tb̅ = r̅
r̅ = (1 – t)a̅ + t\(\left(\frac{\overline{\mathrm{b}}+\overline{\mathrm{c}}}{2}\right)\)

Question 4.
Find the vector equation of the line joining the points 2i̅ + j̅ + 3k̅ and – 4i̅ + 3j̅ – k̅.(V.S.A)
Answer:
Let a = 2i̅ + j̅ + 3k̅ and b = -4i̅ + 3 j̅ – k̅
The vector equation of the line passing through the points a,b is
r̅ = (1 – t)a̅ + tb̅, t ∈ R
= a̅ + t (b̅ – a̅)
= (2i̅ + j̅ + 3k̅) + t (-4i̅ + 3j̅ – k̅ – 2i̅ – j̅ – 3k̅)
= (2i̅ + j̅ + 3k̅) +t(-6i̅ + 2j̅ – 4k̅)

Question 5.
Find the vector equation of the plane passing through the points i̅ – 2j̅ + 5k̅, – 5j̅ – k̅ and -3 i̅ + 5j̅. (V.S.A)
Answer:
Let a̅ = i̅ – 2 j̅ + 5k̅, b̅ = -5 j̅ – k̅, c = -3i̅ + 5j̅. (May 2014)
The vector equation of the plane passing through the points a̅, b̅, c̅ is r = (1 – s – t)a̅ + sb̅ + tc̅ where s, t ∈ R
= a̅ + s(b̅ – a̅) + t(c̅ – a̅)
= (i̅ – 2j̅ + 5k̅) + s(-5j̅ – k̅ – i̅ + 2j̅ – 5k̅) + t(-3i̅ + 5j̅ – i̅ + 2j̅ – 5k̅)
= i̅ – 2j̅ + 5k̅ + s(-i̅ – 3j̅ – 6k̅) + t(-4i̅ + 7j̅ – 5k̅)

Question 6.
Find the vector equation of the plane passing through the points (0,0, 0), (0, 5, 0) and (2, 0, 1). (V.S.A)
Answer:
The vector equation of the plane through a, b,c is
r̅ = (1 – s – t)a̅ + sb̅ + tc̅ where s, t ∈ R
⇒ r̅ = (1 – s – t) 0 + s(5j̅) + t(2i̅ + k̅)
= (5s) j̅ + t(2i̅ + k̅);s, t ∈ R

II.
Question 1.
If a, b, c are noncoplanar find the point of intersection of the line passing through the points 2a̅ + 3b̅ – c̅, 3a̅ + 4b̅ – 2c̅ with the line joining points a̅ – 2b̅ + 3c̅, a̅ – 6b̅ + 6c̅. (S.A)
Answer:
The vector equation of the straight line passing through the points 2a̅ + 3b̅ – c̅ and 3a̅ + 4b̅ – 2c̅ is
r̅ = (1 – t) (2a̅ + 3b̅ – c̅) + t(3a̅ + 4b̅ – 2c̅) where t ∈ 1
⇒ r̅ = (2 + t)a̅ + (3 + t) b̅ + (-1 – t)c̅
= (2a̅ + 3b̅ – c̅) + t (a̅ + b̅ – c̅) ……………(1)
The vector equation of the straight line passing through the points a̅ – 2b̅ + 3c̅ and a̅ – 6b̅ + 6c̅ is
r̅ = (a̅ – 2b̅ + 3c̅) (1 – s) + s (a̅ – 6b̅ + 6c̅) where s ∈ R
⇒ r̅ = a̅ + (-2 – 4s) b̅ + (3 + 3s)c̅
= (a̅ – 2b̅ + 3c̅) + s (-4b̅ + 3c̅) …………..(2)
Equating coefficients a̅, b̅, c̅ in (1) and (2) we have
2 + t = 1 ………..(3)
3 + t = – 2 – 4s ……….(4)
and – 1 – t = 3 + 3s ………..(5)
Solving equations (3), (4) and (5) we get t = – 1, and s = – 1
Hence from (1) and (2) the point of intersection of lines (1) and (2) is a̅ + 2b̅
Also line (1) is parallel to a + b – c ancl (2) is parallel to -4b̅ + 3c̅
If a̅ + b̅ – c̅ and 3c̅ – 4b̅ are parallel then two lines are same since they have common point otherwise they have only one point of intersection a̅ + 2b̅

Question 2.
ABCD is a trapezium in which AB and CD are parallel. Prove by vector methods that the mid points of the sides AB, CD and the intersection of the diagonals are collinear. (E.Q)
Answer:
Let A be the origin and \(\overline{\mathrm{AB}}\) = b̅
∴ \(\overline{\mathrm{DC}}\) = sb̅ (∵ \(\overline{\mathrm{DC}} \| \overline{\mathrm{AB}}\))
\(\overline{\mathrm{DC}}\) = c̅ – d̅ = sb
⇒ d̅ = c̅ – sb̅
⇒ c̅ – d̅ = sb̅

Equation of diagonal AC is
r̅ = (1 – t)o + tc̅
= tc̅ for t ∈ R …………..(2)
Equation of diagonal BD is
r̅ = (1 – s)b̅ + sd̅ for s ∈ R …………(3)

Let R be the point of intersection of diagonals AC and BD.
From (2) and (3) t c = (1 – s) b̅ + s d̅
⇒ t c̅ = (1 – s) b̅ + s (c – sb̅) from (1)
⇒ tc̅ = (1 – s)λ (c – d̅) + sd̅
= (1 – s) λc̅ – [λ(1 – s) – s]d̅
Equating coefficients of c̅ and d̅ on both sides
t = (1 – s) λ and λ (1 – s) – s = 0
⇒ s = λ (1 – s)
⇒ s(1 + λ) = λ
⇒ s = \(\frac{\lambda}{1+\lambda}\)
∴ t = (1 – s)λ = (1 – \(\frac{\lambda}{1+\lambda}\))λ
= \(\frac{\lambda}{1+\lambda}\)
Position vector of the point of intersection ‘R’ is

From (4) and (5)
\(\overline{\mathrm{RM}}\) = λ \(\overline{\mathrm{NR}}\)
⇒ M, R, N are collinear.
So the mid points of parallel sides of a trapezium and the point of intersection of the diagonals are collinear.

Question 3.
In a quadrilateral ABCD, if the midpoints of one pair of opposite sides and the point of intersection of the diagonals are collinear, using vector methods, prove that the quadrilateral ABCD is a trapezium. (S.A)
Answer:

\(\overline{\mathrm{AB}}=\overline{\mathrm{b}}, \overline{\mathrm{AC}}=\overline{\mathrm{c}}\) and \(\overline{\mathrm{AD}}=\overline{\mathrm{d}}\)
Let M, N be the mid points of one pair of opposite sides AB and CD of a quadrilateral ABCD.
\(\overline{\mathrm{AM}}=\frac{\overline{\mathrm{b}}}{2}\)
\(\overline{\mathrm{AN}}=\frac{\overline{\mathrm{c}}+\overline{\mathrm{d}}}{2}\)
Let P be the point of intersection of mid points of sides AB, CD and pair of diagonals AC, BD respectively.
Let \(\overline{\mathrm{AP}}=\overline{\mathrm{r}}\). Then equation of \(\overline{\mathrm{AC}}\) is
r̅ = t c̅ where t is a scalar ………….(1)
Equation of BD is
r̅ = (1 – s)b̅ + sd̅ for some scalars ………..(2)
and equation of line MN is
r̅ = (1 – α)\(\frac{\bar{b}}{2}\) + α\(\left(\frac{\bar{c}+\bar{d}}{2}\right)\)
where α is a scalar
⇒ 2r̅ = (1 – α)b̅ + a(c̅ + d̅)
⇒ r̅ + r̅ = (1 – α)b̅ + a(c̅ + d̅)
From (1) and (2)
tc̅ + (1 – s)b̅ + sd̅ = (1 – α)b̅ + α(c̅ + d̅)
Equating coefficients of b, c, d we get
1 – s = 1 – oc ⇒ s = a and .
t = a ⇒ s = t = a
From (1) and (2),
t c̅ = (1 – s) b̅ + s d̅
⇒ sc̅ = (1 – s) b̅ + s d̅ (‘- t = s)
⇒ (1 -s) b̅ =s(c̅ – d̅)
⇒ b is parallel to c̅ – d̅
⇒ AB is parallel to CD
∴ ABCD is a trapezium.

III.
Question 1.
Find the vector equation of the plane which passes through the points 2i̅ + 4j̅ + 2k̅, 2i̅ + 3j̅ + 5k̅ and parallel to the vector 3 i̅ – 2 j̅ + k̅. Also find the point where this plane meets the line joining the points 2 i̅ + j̅ + 3k̅ and 4 i̅ – 2 j̅ + 3k̅. (March 2012) (E.Q)
Answer:
Vector equation of the plane which passes through the points a̅ = 2i̅ + 4j̅ + 2k̅, b̅ = 2i̅ + 3j̅ + 5k̅ and parallel to vector c̅ = 3i̅ – 2j̅ + k̅ is
r̅ = (1 – t)a̅ + tb̅ + sc̅ where t, s e R
⇒ r̅ = (1 – t) (2i̅ + 4j̅ + 2k̅) + t(2i̅ + 3j̅ + 5k̅) + s(3i̅ – 2j̅ + k̅)
⇒ r̅ = (2 – 2t + 2t + 3s) i̅ + (4 – 4t + 3t – 2s) j̅ + (2 – 2t + 5t + s) k̅
⇒ r̅ = (2 – 2t + 2t + 3s) i̅ + (4 – 4t + 3t – 2s) j̅ + (2 – 2t + 5t + s) k̅
⇒ r̅ = (2 + 3s) i̅ + (4 – t – 2s) j̅ + (2 + 3t + s)k̅ …………(1)
Vector equation of the line passing through the points c̅ = 2i̅ + j̅ + 3k̅ and d̅ = 4 i̅ – 2 j̅ + 3k̅ is r̅ = (1 – a)d̅ + ac̅ where a e R
⇒ r̅ = (1 – α)(2i̅ + j̅ + 3k̅) + α(4i̅ – 2j̅ + 3k̅)
⇒ r̅ = (2 – 2α + 4α) i̅ + (1 – α – 2α) j̅ + (3 – 3α + 3α)k̅
⇒ r̅ = (2 + 2α) i̅ + (1 – 3α) j̅ + 3k̅ (2)
Let 7 be the point of intersection of (1) and (2)
(2 + 3s)i̅ + (4 – t – 2s) j̅ + (2 + 3t + s) k̅
= (2 + 2α) i̅ + (1 – 3α) j̅ + 3k̅
v Since i̅, j̅, k̅ are non coplanar,
2 + 3s = 2 + 2α ⇒ 2α – 3s = 0 ………………(3)
4 – 1 – 2s = 1 – 3α ⇒ 3α – 2s -1 = – 3 …………(4)
2 + 3t + s = 3 ⇒ s + 3t = 1 ………………(5)
From (5), t = \(\frac{1-\mathrm{s}}{3}\)
∴ From (4) 3α – 2s – \(\left(\frac{1-s}{3}\right)\) = -3
⇒ 9α – 6s – 1 + s = -9
9α – 5s + 8 = 0 (6)
Solving (6) & (3) equations

Question 2.
Find the vector equation of the plane passing through the points 4 i̅ – 3 j̅ – k̅ , 3i̅ + 7j̅ – 10k̅ and 2i̅ + 5j̅ – 7k̅ and show that the point i̅ + 2 j̅ – 3k̅ lies in the plane. (March 2013) (S.A.Q.)
Answer:
Vector equation of the plane passing through
A(4i̅ – 3j̅ – k̅ ), B (3i̅ + 7j̅ – 10k̅ ) and C(2i̅ + 5j̅ – 7k̅ ) is
r̅ = (1 – s – t) (4i̅ – 3 j̅ – k̅ ) + s(3i̅ + 7j̅ – 10k̅ ) + t(2i̅ + 5j̅ – 7k̅ )
Let D (i̅ + 2j̅ – 3k̅ ) lies on the plane, then
(i̅ + 2j̅ – 3k̅ ) = (1 – s – t)(4i̅ – 3j̅ – k̅ ) + s (3i̅ + 7j̅ – 10k̅ ) + t (2i̅ + 5j̅ – 7k̅ )
Since i̅ , j̅ ,k̅ are non coplanar, equating coefficients of i̅ , j̅ , k̅ both sides.
4(1 – s – t) + 3s + 2t = 1
⇒ 4 – 4s – 4t + 3s + 2t = 1
⇒ s + 2t = 3 …………(1)
– 3 (1 – s – t) + 7s + 5t = 2
⇒ -3 + 3s + 3t + 7s + 5t = 2
⇒ 10s + 8t = 5
Also – (1 – s – t) – 10s – 7t = – 3
⇒ – 1 + s + t – 10s – 7t = – 3
⇒ 9s + 6t = 2
From (1), 3s + 6t = 9
Solving (1) & (3) equations 6s = – 7
⇒ s = – 7/6

s = \(\frac{-7}{6}\) t = \(\frac{25}{12}\). satisfy (1), (2), (3).
and D lies on the plane passing through A, B, C.

Students must practice these TS Intermediate Maths 1A Solutions Chapter 4 Addition of Vectors Ex 4(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(a)

I.
Question 1.
ABCD is a parallelogram. If L and M are the middle points of BC CD respectively then find
i) \(\overline{\mathrm{A L}}\) and \(\overline{\mathrm{A M}}\) in terms of \(\overline{\mathrm{A B}}\) and \(\overline{\mathrm{A D}}\)
ii) λ, if \(\overline{\mathrm{A M}}\) = λ \(\overline{\mathrm{A C}}-\overline{\mathrm{A L}}\) (V.S.A)
Answer:

ABCD is a parallelogram and hence \(\overline{\mathrm{AB}}=\overline{\mathrm{DC}}\) and \(\overline{\mathrm{BC}}=\overline{\mathrm{AD}}\)
We have \(\overline{\mathrm{BC}}\) = \(\frac{1}{2} \overline{\mathrm{BC}}\)
(∵ L is the mid point of BC)
= \(\frac{1}{2} \overline{\mathrm{AD}}\) (∵ BC = AD)

Question 2.
In AABC, P, Q and R are the mid points of the sides AB, BC and CA respectively. If D is any point
i) Then express \(\overline{\mathrm{DA}}+\overline{\mathrm{DB}}+\overline{\mathrm{DC}}\) in terms of \(\overline{\mathrm{DP}}, \overline{\mathrm{DQ}}\) and \(\overline{\mathrm{DR}}\).
ii) If \(\overline{\mathrm{P A}}+\overline{\mathrm{Q B}}+\overline{\mathrm{R C}}=\bar{\alpha}\), then find a.(V.S.A)
Answer:
Let D be the origin.

and \(\overline{\mathrm{DA}}=\overline{\mathrm{a}}\) , \(\overline{\mathrm{DB}}=\overline{\mathrm{b}}\) and \(\overline{\mathrm{DC}}=\overline{\mathrm{c}}\)
P.V. of P is mid point of \(\overline{\mathrm{AB}}=\overline{\mathrm{DP}}=\frac{\overline{\mathrm{a}}+\overline{\mathrm{b}}}{2}\)
P.V. of Q is mid point of \(\overline{\mathrm{BC}}=\overline{\mathrm{DQ}}=\frac{\overline{\mathrm{b}}+\overline{\mathrm{c}}}{2}\)
P.V. of R is mid point of \(\overline{\mathrm{AC}}=\overline{\mathrm{DR}}=\frac{\overline{\mathrm{c}}+\overline{\mathrm{a}}}{2}\)

Question 3.
Let a̅ = i̅ + 2 j̅ + 3k̅ and b̅ = 3 i̅ + j̅. Find the unit vector in the direction of \(\bar{a}+\bar{b}\). (V.S.A)
Answer:
Unit vector in the direction of \(\bar{a}+\bar{b}\) is

Question 4.
If the vectors -3i̅ + 4j̅ + λk̅ and μi̅ + 8j̅ + 6k̅ are collinear vectors then find λ and μ. (May 2014, ’12, Mar. ’14)
Answer:
If the vectors a₁ i̅ + b₁ j̅ + c₁k̅ and a₂ i̅ + b₂ j̅ + c₂k̅ are collinear then

Question 5.
ABCDE is a pentagon. If the sum of the vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AE}}, \overline{\mathrm{BC}}, \overline{\mathrm{DC}}, \overline{\mathrm{ED}}\) and \(\overline{\mathrm{A C}}\) is λ \(\overline{\mathrm{A C}}\) , then find the value of λ. (S.A)
Answer:

Given ABCDE is a pentagon and

Question 6.
If the position vectors of the points A, B and C are -2i̅ + j̅ – k̅, -4i̅ + 2j̅ + 2k̅ and 6i̅ – 3j̅ – 13k̅ respectively and \(\overline{\mathrm{AB}}\) = λ\(\overline{\mathrm{A C}}\) then find the value of λ. (March 2011) (S.A)
Answer:
Let O be the origin and given

Question 7.
If \(\overline{\mathrm{OA}}=\overline{\mathrm{i}}+\overline{\mathrm{j}}+\overline{\mathrm{k}}\); \(\overline{\mathrm{AB}}=3 \overline{\mathrm{i}}-2 \overline{\mathrm{j}}+\overline{\mathrm{k}}\), \(\overline{\mathrm{BC}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}-2 \overline{\mathrm{k}}\) and \(\overline{\mathrm{CD}}=2 \overline{\mathrm{i}}+\overline{\mathrm{j}}+3 \overline{\mathrm{k}}\) then find the vector \(\overline{\mathrm{OD}}\). (March 2013) (V.S.A)
Answer:
Since \(\overline{\mathrm{OA}}+\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CD}}=\overline{\mathrm{OD}}\)
⇒ \(\overline{\mathrm{OD}}\) = (i̅ + j̅ + k̅) + (3i̅ – 2j̅ + k̅) + (i̅ + 2 j̅ – 2k̅) + (2 i̅ + j̅ + 3k̅)
= 7i̅ + 2j̅ + 3k̅

Question 8.
If a̅ = 2i̅ + 5j̅ + k̅ and b̅ = 4i̅ + mj̅ + nk̅ are collinear vectors then find m and n. (May 2011) (V.S.A)
Answer:
Since a̅ = 2i̅ + 5j̅ + k̅ and
b̅ = 4i̅ + mj̅ + nk̅ are collinear
⇒ \(\frac{2}{4}=\frac{5}{m}=\frac{1}{n}\)
⇒ \(\frac{1}{2}=\frac{5}{m}\) and \(\frac{1}{2}=\frac{1}{n}\) ⇒ m = 10 and n = 2

Question 9.
Let a̅ = 2i̅ + 4j̅ – 5k̅, b̅ = i̅ + j̅ + k̅ and c̅ = i̅ + 2k̅. Find the unit vector in the opposite direction of a̅ + b̅ + c̅. (March 2015-A.P)(May 2012; Mar. ’04, ’12; Board Model Paper) (V.S.A)
Answer:

Question 10.
Is the triangle formed by the vectors 3i̅ + 5j̅ + 2k̅, 2i̅ – 3j̅ – 5k̅ and -5i̅ – 2 j̅ + 3k̅ equilateral ? (V.S.A)
Answer:
Let ABC be the triangle with AB = 3i̅ + 5 j̅ + 2k̅
BC = 2i̅ – 3 j̅ – 5k̅
CA = -5i̅ – 2j̅ + 3k̅

∴ The given vectors formed on equilateral triangle.

Question 11.
If α, β and γ are the angles made by the vector 3i̅ – 6j̅ + 2k̅ with the positive directions of the coordinate axes then find cos α, cos β, cos γ. (S.A)
Answer:
Unit vectors along the coordinate axes are respectively i̅, j̅, k̅
Let p̅ = 3i̅ – 6j̅ + 2k̅

Question 12.
Find the angles made by the straight line passing through the points (1, -3, 2) and (3, -5, 1) with the coordinate axes. (S.A)
Answer:
Let the vectors along the coordinate axes be i̅, j̅, k̅ respectively. Let O be the origin and the points A(1, -3, 2) and B(3, -5, 1).
i. e. \(\overline{\mathrm{OA}}\) = i̅ – 3 j̅ + 2k̅, \(\overline{\mathrm{OB}}\) = 3 i̅ – 5 j̅ + k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = (3i̅ – 5j̅ + k̅) – (i̅ – 3j̅ + 2k̅) = 2i̅ – 2j̅ – k̅
Let α be the angle between \(\overline{\mathrm{AB}}\) and i̅ then
cos α = \(\frac{\overline{\mathrm{AB}} \cdot \overline{\mathrm{i}}}{|\overline{\mathrm{AB}}||\overline{\mathrm{i}}|}=\frac{2}{\sqrt{4+4+1} \cdot(1)}=\frac{2}{3}\)

Similarly if β, γ be the angles between \(\overline{\mathrm{AB}}\) and j and \(\overline{\mathrm{AB}}\) and k̅ then

∴ The angles made by the straight line AB with X, Y, Z axes are
α = cos^-1\(\left(\frac{2}{3}\right)\)
β = cos^-1\(\left(\frac{2}{3}\right)\)
γ = cos^-1\(\left(\frac{2}{3}\right)\)

II.
Question 1.
If a̅ + b̅ + c̅ = αd̅, b̅ + c̅ + d̅ = βa̅ and a̅, b̅, c̅ are non-coplanar vectors, then show that a̅ + b̅ + c̅ + d̅ = 0̅. (S.A)
Answer:
Given a̅ + b̅ + c̅ = αd̅ ……………. (1)
b̅ + c̅ + d̅ = βa̅ …………….. (2)
From (2), d̅ = pa̅ – b̅ – c̅
From (1), a̅ + b̅ + c̅ = a, (pa̅ – b̅ – c̅)
⇒ (1 – αβ)a̅ + (1 + a)b̅ + (1 + a)c̅ = 0
∴ a̅, b̅, c̅ are non coplanar vectors
1 – αβ = 0 ⇒ αβ = 1 and
1 + α = 0 ⇒ α = -l β = -1
Hence from (1); a̅ + b̅ + c̅ = -d̅
⇒ a̅ + b̅ + c̅ + d̅ = 0

Question 2.
a̅, b̅, c̅ are non coplanar vectors. Prove that the following four points are coplanar.
i) -a̅ + 4b̅ – 3c̅, 3a̅ + 2b̅ – 5c̅ (May,’14,’12)
-3a̅ + 8b̅ – 5c̅, – 3a̅ + 2b̅ + c̅
Answer:
Let 0 be the origin and A, B, C, D are the four points given by
OA = -a̅ + 4b̅ – 3c̅, OB = 3a̅ + 2b̅ – 5c̅
OC = -3a̅ + 8b̅ – 5c̅, OD = -3a̅ + 2b̅ + c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = (3a̅ + 2b̅ – 5c̅) – (-a̅ + 4b̅ – 3c̅)
= 4a̅ – 2b̅ – 2c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = (-3a̅ + 2b̅ – 5c̅) – (3a̅ + 2b̅ – 5c̅)
= -6a̅ – 4b̅ + 3c̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = (-3a̅ + 8b̅ – 5c̅) – (-a̅ + 4b̅ – 3c̅) = -2a̅ + 4b̅ – 2c̅
\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\) = (3a̅ + 2b̅ + c̅) – (-a̅ + 4b̅ – 3c̅) = -2a̅ – 2b̅ + 4c̅
Let a vector be expressed as a linear combination of other two.
Suppose \(\overline{\mathrm{AB}}\) = x(\(\overline{\mathrm{AC}}\)) + y (\(\overline{\mathrm{AD}}\)) where x, y are scalars.
∴ 4a̅ – 2b̅ – 2c̅ = x (-2a̅ + 4b̅ – 2c̅) + y(-2a̅ – 2b̅ + 4c̅)

Comparing coefficients of a̅, b̅, c̅ we get
(∵ a̅, b̅, c̅ are non coplanar vectors)
-2x – 2y = 4 ……………(1)
4x – 2y = -2 ……………(2)
-2x + 4y = -2 ………….(3)
Solving (1) and (2) we get 2x + 2y = – 4 and 4x – 2y = – 2
6x = – 6 ⇒ x = -1
x + y = -2 ⇒ y = -1
x = – 1 and y = -1 satisfy equation (3).
⇒ A, B, C, D are coplanar and
\(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}, \overline{\mathrm{AD}}\) are coplanar.
and \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}, \overline{\mathrm{AD}}\) are coplanar.
∴ The given points A, B, C, D are coplanar.

ii) 6a̅ + 2b̅ – c̅, 2a̅ – b̅ + 3c̅, -a̅ + 2b̅ – 4c̅, -12a̅ – b̅ – 3c̅
Answer:
Let O be the origin and A, B, C, D be the given points.
\(\overline{\mathrm{OA}}\) = 6a̅ + 2b̅ – c̅, \(\overline{\mathrm{OB}}\) = 2a̅ – b̅ + 3c̅
\(\overline{\mathrm{OC}}\) = -a̅ + 2b̅ – 4c̅, \(\overline{\mathrm{OD}}\) = -12a̅ – b̅ – 3c̅
∴ \(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\)
= (2a̅ – b̅ + 3c̅) – (6a̅ + 2b̅ – c̅)
= – 4a̅ – 3b̅ + 4c̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = (-a̅ + 2b̅ – 4c̅) – (6a̅ + 2b̅ – c̅) = -7a̅ – 3c̅
\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\) = (-12a̅ – b̅ – 3c̅) – (6a̅ + 2b̅ – c̅)= -18a̅ – 3b̅ – 2c̅
∴ Let a vector be expressed as a linear combination of other two.
Suppose \(\overline{\mathrm{AB}}\) = x\(\overline{\mathrm{AC}}\) + y\(\overline{\mathrm{AD}}\)
⇒ -4a̅ – 3b̅ + 4c̅ = x(-7a̅ – 3c̅) + y(-18a̅ – 3b̅ – 2c̅)

Comparing coefficients of a̅, b̅, c̅ since a̅, b̅, c̅ are non coplanar,
-7x – 18y = – 4 …………(1)
-3y = -3 ⇒ y = 1 ……….(2)
∴ -7x – 18 = – 4 ⇒ – 7x = 14 ⇒ x = -2
Comparing coefficient of c,
-3x – 2y = 4 ………..(3)
x = – 2 and y = 1 satisfy equation (3)
and hence A, B, C, D are coplanar.

Alternate Method For Above Problem :
Use scalar triple product of vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}\) and \(\overline{\mathrm{AD}}\) show that this
\(\overline{\mathrm{AB}} \cdot(\overline{\mathrm{AC}} \times \overline{\mathrm{AD}})\) = 0
\([\overline{\mathrm{AB}} \overline{\mathrm{AC}} \overline{\mathrm{AD}}]=\left|\begin{array}{rrr}
-4 & -3 & 4 \\
-7 & 0 & -3 \\
-18 & -3 & -2
\end{array}\right|\)
= -4 (-9) + 3 (14 – 54) + 4 (21)
= 36- 120 + 84 = 0
∴ Vectors AB, AC, AD are coplanar
⇒ The given points A, B, C, D are coplanar.

Question 3.
If i̅, j̅, k̅ are unit vectors along the positive directions of the co-ordinate axes, then show that the four points 4i̅ + 5j̅ + k̅, – j̅ – k̅ , 3i̅ + 9j̅ + 4k̅ and -4i̅ +4j̅ +4k̅ are coplanar. (Mar. ’14)
Answer:
Let O be the origin and let A, B, C, D be the given points. Then \(\overline{\mathrm{OA}}\) = 4i̅ + 5j̅ + k̅,
\(\overline{\mathrm{OB}}\) = – j̅ – k̅, \(\overline{\mathrm{OC}}\) = 3i̅ + 9 j̅ + 4k̅,
\(\overline{\mathrm{OD}}\) = -4 i̅, + 4 j̅, + 4k̅,
Now AB = OB — OA = (-j̅ – k̅) – (4i̅ + 5j̅ + k̅) – 4i̅ – 6j̅ – 2k̅
AC = OC – OD = -i̅ + 4j̅ + 3k̅,
AD = OD – OA = -8i̅ – j̅ + 3k̅
Let \(\overline{\mathrm{AB}}\) = x(\(\overline{\mathrm{AC}}\)) + y(\(\overline{\mathrm{AD}}\)) for some values of x and y
⇒ – 4i̅ – 6j̅ – 2k̅ = x(- i̅ + 4j̅ + 3k̅) + y(-8i̅ – j̅ + 3k̅)
⇒ (x + 8y – 4) i̅ + (-4x + y – 6)j̅ + (-3x – 3y – 2)k̅ = 0
∴ i̅, j̅, k̅ are non coplanar
x + 8y – 4 = 0 …………..(1)
4x – y + 6 = 0 …………..(2)
3x + 3y + 2 = 0 ………….(3)
Solving (1) and (2) we get

Hence the vectors AB, AC and AD are coplanar
⇒ The given points A, B, C, D are coplanar.

Second method :
\(\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]=\left|\begin{array}{rrr}
-4 & -6 & -2 \\
-1 & 4 & 3 \\
-8 & -1 & 3
\end{array}\right|\)
= – 4 (12 + 3) + 6 (- 3 + 24) – 2 (1 + 32)
= – 60 + 126 – 66 = 0
The vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}, \overline{\mathrm{AD}}\) are coplanar.
⇒ The given points A, B, C, D are coplanar.

Question 4.
If a̅, b̅, c̅ are non coplanar vectors, then test for the collinearity of the following points whose position vectors are given by
(i) a̅ – 2b̅ + 3c̅, 2a̅ + 3b̅ – 4c̅, – 7b̅ + 10c̅ (S.A)
Answer:
Given a, b, c are the non coplanar vectors
Let \(\overline{\mathrm{OA}}\) = a̅ – 2b̅ + 3c̅. \(\overline{\mathrm{OB}}\) = 2a̅ + 3b̅ – 4c̅
and \(\overline{\mathrm{OC}}\) = -7b̅ + 10c̅ be the points with respect to specific origin O’.
Then \(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = a̅ + 5b̅ – 7c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = -2a̅ – 10b̅ + 14c̅
and \(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = -a̅ – 5b̅ + 7c̅
∴ \(\overline{\mathrm{BC}}=-2(\overline{\mathrm{AB}}) \Rightarrow \overline{\mathrm{BC}}=2 \overline{\mathrm{BA}}\)
∴ The points A, B, C are collinear.
(∵ \(\overline{\mathrm{BC}}=\lambda \overline{\mathrm{BA}}\) where λ = 2)

ii) 3a̅ – 4b̅ + 3c̅, – 4a̅ + 5b̅ – 6c̅, 4a̅ – 7b̅ + 6c̅
Answer:
Let \(\overline{\mathrm{OA}}\) = 3a̅ – 4b̅ + 3c̅,
\(\overline{\mathrm{OB}}\) = -4a̅ + 5b̅ – 6c̅,
\(\overline{\mathrm{OC}}\) = 4a̅ – 7b̅ + 6c̅
∴ \(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = -7a̅ + 9b̅ – 9c̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = a̅ – 3b̅ + 3c̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = 8a̅ – 12b̅ + 12c̅
∴ \(\overline{\mathrm{AB}} \neq \lambda \overline{\mathrm{BC}}\), λ is a scalar.
⇒ The points A, B, C are non collinear.

iii) 2a̅ + 5b̅ – 4c̅, a̅ + 4b̅ – 3c̅, 4a̅ + 7b̅ – 6c̅
Answer:
Let O be the origin and A, B, C be the given points.
Then \(\overline{\mathrm{OA}}\) = 2a̅ + 5b̅ – 4c̅.
\(\overline{\mathrm{OB}}\) = a̅ + 4b̅ – 3c̅.
and \(\overline{\mathrm{OC}}\) = 4a̅ + 7b̅ – 6c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = (a̅ + 4b̅ – 3c̅) – (2a̅ + 5b̅ – 4c̅)
= -a̅ – b̅ + c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = (4a̅ + 7b̅ – 6c̅) – (a̅ + 4b̅ – 3c̅)
= 3a̅ + 3b̅ – 3c̅ = -3(a̅ – b̅ + c̅)
\(\overline{\mathrm{BC}}=-3(\overline{\mathrm{AB}})\)
⇒ \(\overline{\mathrm{BC}}=3(\overline{\mathrm{BA}})\) where λ = 3
∴ The points A, B, C are collinear.

III.
Question 1.
In the cartesian plane, O is the origin of the coordinate axes. A person starts at O and walks a distance of 3 units in the North-East direction and reaches the point P. From P he walks 4 units of distance parallel to North-West direction and reaches the point
Q. Express the vector \(\overline{\mathrm{OQ}}\) in terms of i̅ and j̅ (observe that (∠XOP=45°) (S.A)
Answer:

O is the origin and ∠XOP = 45°
The person starts at 0 and walks a distance of 3 units in North-East direction.
∴ \(\overline{\mathrm{OP}}\) = (3cos45°) i̅ + (3sin45°) j̅
= \(\frac{3}{\sqrt{2}}\)i̅ + \(\frac{3}{\sqrt{2}}\)j̅
PQ = 4 units
and pp is parallel to X axis
∴ ∠RPQ = 135°
PQ is parallel to North-West direction

Question 2.
The points O, A, B, X and Y are such that \(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OX}}\) = 3a̅ and \(\overline{\mathrm{OY}}\) = 3b̅. Find \(\overline{\mathrm{BX}}\) and \(\overline{\mathrm{AY}}\) interms of a and 5. Further, if the point P divides AY in the ratio 1 : 3, then express \(\overline{\mathrm{BP}}\) in terms of a and b. (S.A)
Answer:
Given \(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OX}}\) = 3a̅ \(\overline{\mathrm{OY}}\) = 3b̅
\(\overline{\mathrm{BX}}=\overline{\mathrm{OX}}-\overline{\mathrm{OB}}\) = 3a̅ – b̅
\(\overline{\mathrm{AY}}=\overline{\mathrm{OY}}-\overline{\mathrm{OA}}\) = 3b̅ – a̅
If P divides \(\overline{\mathrm{AY}}\) in the ratio 1 : 3 then the position vector of P is \(\overline{\mathrm{OP}}\)

Question 3.
In ΔOAB, E is the midpoint of AB and F Is a point on OA such that OF = 2 FA. If C Is the point of intersection of \(\overline{\mathrm{OE}}\) and \(\overline{\mathrm{BF}}\) then find the ratios OC : CE and BC : CF. (S.A)
Answer:

Let O be the origin and \(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅
Since E is the midpoint of AB,
\(\overline{\mathrm{OE}}\) = \(\frac{\overline{\mathrm{a}}+\overline{\mathrm{b}}}{2}\)

and OF = 2 FA ⇒ F divides OA in the ratio 2 : 1
\(\overline{\mathrm{OF}}\) = \(\frac{2 \bar{a}+1(0)}{2+1}=\frac{2}{3} \bar{a}\)

C is the point of intersection of \(\overline{\mathrm{OE}}\) and \(\overline{\mathrm{BF}}\).
let C divides \(\overline{\mathrm{OE}}\) in the ratio 1 : λ then the position vector of C is
\(\overline{\mathrm{OC}}\) = \(\frac{1(\overline{\mathrm{OE}})+\lambda(0)}{1+\lambda}=\frac{\overline{\mathrm{OE}}}{\lambda+1}=\frac{\bar{a}+\bar{b}}{2(\lambda+1)}\) ………..(1)

Let C divides \(\overline{\mathrm{BF}}\) in the ratio μ : 1 then the position vector of C is

⇒ 4(λ + 1) = 5
⇒ 4λ = 1 ⇒ λ = \(\frac{1}{4}\)

C divides OE in the ratio 1 : \(\frac{1}{4}\) = 4 : 1
∴ OC : CE = 4 : 1
C divides BF in the ratio μ : 1 = \(\frac{3}{2}\) : 1
= 3 : 2
∴ BC : CF = 3 : 2

Question 4.
The point E divides the segment PQ internally in the ratio 1 : 2 and R is any point not on the line PQ. If F is a point on QR such that QF: FR = 2 : 1, then show that EF is parallel to PR. (S.A)
Answer:

Let O be the origin and \(\overline{\mathrm{OP}}=\overline{\mathrm{a}}, \overline{\mathrm{OQ}}=\overline{\mathrm{b}}\) and \(\overline{\mathrm{OP}}=\overline{\mathrm{a}}, \overline{\mathrm{OQ}}=\overline{\mathrm{b}}\)
E divides PQ in the ratio 1: 2

Telangana TSBIE TS Inter 1st Year Physics Study Material 8th Lesson డోలనాలు Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 8th Lesson డోలనాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
డోలనాత్మకం కాని ఆవర్తన చలనాలకు రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:

1. గడియారములో సెకనుల ముల్లు చలనము.
2. స్థిరకోణీయ వడితో తిరుగుతూ ఉన్న ఫ్యాన్ రెక్కలు.

ఈ రెండు సందర్భాలలో అవి స్థిర కోణీయ వడితో తిరుగుచున్నవి. అవి ఆవర్తన చలనాలు. వీటి కంపన పరిమితి కాలంతో మారదు. కావున వీటిని సరళహరాత్మక చలనముగా తీసుకొనబడవు.

ప్రశ్న 2.
సరళ హరాత్మక చలన స్థానభ్రంశాన్ని y = a sin (20t + 4) తో సూచించారు. కాలాన్ని \(\frac{2 \pi}{\omega}\) పెంచితే దాని స్థానభ్రంశం ఎంత ?
జవాబు:
సరళ హరాత్మక చలన స్థానభ్రంశం y = a sin (20t + 4) తో సూచిస్తే అందులోని sin ప్రమేయంలో గల ఆర్గ్యుమెంట్ 20t. ఇది \(\frac{2 \pi}{\omega}\) అనగా ఆవర్తనకాలము (T) తో ఆవర్తనం చెందితే దాని స్థానభ్రంశంలో మార్పు ఉండదు.
వివరణ : (20t + 4) ను θ అనుకోండి. \(\frac{2 \pi}{\omega}\) = T. Tకాలంలో స్థానభ్రంశము 2π (ఆవర్తన చలనానికి)
y = sin θ మరియు Ꭹ₁ = sin (θ + 2π) అవుతాయి. కాని sin θ = sin (θ + 2π) కావున y₁ = y అవుతుంది.

ప్రశ్న 3.
ఒక బాలిక ఊయలలో కూర్చొని ఊగుతుంది. బాలిక ఊయలలో నిలబడితే దాని డోలన పౌనఃపున్యం ఏవిధంగా మారుతుంది ?
జవాబు:
బాలిక ఊయలలో నిలబడితే ఆమె ద్రవ్యరాశి కేంద్రం ఆధారానికి దగ్గరగా జరగడంవల్ల లోలకం పొడవు తగ్గును.
ఫలితంగా ఆవర్తన కాలము (T = 2π \(\sqrt{\frac{l}{g}}\)) తగ్గుతుంది.
కాబట్టి ఊయల పౌనఃపున్యం పెరుగును.

ప్రశ్న 4.
లఘులోలకం గుండు నీటితో నిండిన ఒక బోలు గోళం. గోళం నుంచి నీరు కారిపోతుంటే దాని డోలనావర్తన కాలం ఏవిధంగా మారుతుంది ?
జవాబు:
బోలు గోళం నుండి నీరు కారిపోతుంటే ద్రవ్యరాశి కేంద్రం గోళ కేంద్రం నుండి కిందికి జరుగును. కావున లోలకం పొడవు పెరిగి ఆవర్తన కాలం తగ్గును. ఈ ప్రక్రియ ద్రవం గోళంలో సగం వరకు కారేదాకా జరుగును.
గోళంలో ద్రవం సగాని కన్న కిందికి దిగునపుడు మరల ద్రవ్యరాశి కేంద్రం పైకి జరుగును. అంటే లోలకం పొడవు తగ్గడం మొదలై ఆవర్తనకాలం ‘T’ పెరుగును.
గోళం పూర్తిగా ఖాళీ అయితే డోలనావర్తనకాలంలో తొలి విలువను చేరును.

ప్రశ్న 5.
లఘులోలకానికి కట్టిన చెక్క గుండుకు బదులు దాన్ని పోలి ఉండే అల్యూమినియం గుండును ఉపయోగిస్తే దాని ఆవర్తన కాలం ఏవిధంగా మారుతుంది ?
జవాబు:
లోలకంలో చెక్క గుండుకు బదులుగా దానిని పోలిన అల్యూమినియం గుండును వాడితే దాని డోలనావర్తనకాలం మారదు.
డోలనావర్తనకాలం గోళం ద్రవ్యరాశిపై ఆధారపడదు.

ప్రశ్న 6.
లోలక గడియారాన్ని పర్వతంపైకి తీసుకొని వెళితే అది సమయాన్ని పొందుతుందా ? కోల్పోతుందా ?
జవాబు:
పర్వతం పైన g విలువ తక్కువ. లోలక గడియారాన్ని పర్వతం పైకి తీసుకొనిపోతే ఆవర్తనకాలం పెరుగుతుంది. లోలకం ఆవర్తనకాలము T = 2π\(\sqrt{\frac{l}{g}}\) కావున ‘g’ తగ్గితే T పెరుగును.

ప్రశ్న 7.
భూమధ్యరేఖ వద్ద సరైన సమయాన్ని చూపే లోలక గడియారాన్ని ధ్రువాల వద్దకు తీసుకొనిపోతే అది సమయాన్ని పొందుతుందా ? కోల్పోతుందా ? అయితే ఎందుకు ?
జవాబు:
భూమధ్యరేఖ వద్ద సరియైన కాలము చూపు లోలక గడియారమును ధృవాల వద్దకు తీసుకొనిపోయిన ఇది కాలంలో ‘g’ పెరిగిన యెడల T లాభం పొందును. ధృవాల వద్ద గురుత్వ త్వరణము అధికము. ఆవర్తనకాలము T = 2π\(\sqrt{\frac{l}{g}}\). ‘g’ తగ్గును. కావున ఇచ్చిన సమయములో అది చేయు డోలనాల సంఖ్య పెరుగును. కావున గడియారము వేగంగా కదలటం వల్ల కాలాన్ని ఎక్కువగా చూపిస్తుంది.

ప్రశ్న 8.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం కంపన పరిమితిలో సగానికి సమానమైనప్పుడు, దాని మొత్తం శక్తిలో K.E, వంతు ఎంత ?
జవాబు:
సరళ హరాత్మక డోలకం మొత్తం శక్తి E = \(\frac{1}{2}\) mω²A²
స్థానభ్రంశం X = \(\frac{\mathrm{A}}{2}\) అయితే P.E. = \(\frac{1}{2}\) mω²x² = \(\frac{1}{2}\) mω² \(\frac{A^2}{4}\)
∴ గతిజశక్తి KE =\(\frac{1}{2}\) mω²A² – \(\frac{1}{2}\) mω²\(\frac{A^2}{4}\) = \(\frac{3}{4}\) \(\frac{1}{2}\) mω²A²
గతిజశక్తి KE = మొత్తం శక్తి × \(\frac{3}{4}\) = మొత్తం శక్తిలో 75%

ప్రశ్న 9.
సరళ హరాత్మక డోలకం కంపన పరిమితిని రెట్టింపు చేస్తే దాని శక్తి ఏవిధంగా మారుతుంది ?
జవాబు:
స.హ.చ. డోలకం మొత్తము శక్తి E = \(\frac{1}{2}\) mω²A²; కొత్త కంపన పరిమితి A₁ = 2A
∴ E₁ = \(\frac{1}{2}\) mω² (2A)² = 4 . \(\frac{1}{2}\) mω²A² ⇒ E₁ = 4E
కంపన పరిమితిని రెట్టింపు చేసిన మొత్తము శక్తి నాలుగు రెట్లు అగును.

ప్రశ్న 10.
కృత్రిమ ఉపగ్రహంలో లఘులోలకాన్ని ఉపయోగించవచ్చా ?
జవాబు:
కృత్రిమ ఉపగ్రహాలలో లఘులోలకాన్ని ఉపయోగించరాదు. కృత్రిమ ఉపగ్రహాలు భారరహిత స్థితిలో ఉంటాయి. అనగా g = 0. ఈ స్థితిలో లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ τ = L mg sin 6 = θ కావున లోలకం కదలదు.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సరళ హరాత్మక చలనాన్ని నిర్వచించండి. రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:
సరళ హరాత్మక చలనం : డోలన చలనం యొక్క సరళమైన రూపాన్ని సరళ హరాత్మక చలనం అంటారు. ఈ చలనం కాల ప్రమేయము (f(t)) తో ఆవర్తనంగా ఉంటుంది.
సరళ హరాత్మక చలనాన్ని f(t) = A cos ωt లేదా A sin ωt వంటి అతిసరళమైన సమీకరణంతో సూచిస్తారు.
ఉదా :

1. సమవృత్తాకార గమనములోని వస్తువు లంబపాదము దాని వ్యాసముపై చలనము.
2. తక్కువ కంపన పరిమితితో చేయు కంపనాలు.
3. భారగ్రస్త స్ప్రింగ్ చేయు కంపనాలు.
4. గొట్టములోని ద్రవము చేయు కంపనాలు.

ప్రశ్న 2.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం, వేగం, త్వరణాలు కాలం దృష్ట్యా మారే విధానాన్ని గ్రాఫ్ ద్వారా సూచించండి.
జవాబు:
S.H.M లో ఉన్న కణం స్థానభ్రంశం X = A cos (ωt + Φ)
వేగము v = Aω sin (ωt + Φ)
త్వరణము a = – ω²A cos (ωt + Φ) అను ప్రమేయాలతో సూచిస్తారు. కాలము (t) ని x – అక్షం మీద స్థానభ్రంశము (X), వేగము (v) మరియు త్వరణము (a) లను y – అక్షం మీద తీసుకొని గీసిన రేఖాపటాలు ఈ క్రింది విధంగా ఉంటాయి.

a) స్థానభ్రంశ కాలవక్రము cosine ప్రమేయపు జ్యా వక్రీయ రేఖ. దీని విలువ t = 0 వద్ద గరిష్ఠంగా మొదలవుతుంది. కంపన పరిమితి – A నుండి A వరకు మారును.

b) వేగము ‘v’ sine ప్రమేయంగా మారుతుంది. t = 0 వద్ద వేగము సున్నగా ఉంటూ దీని విలువ -ωA నుండి + ωA వరకు మారును.

c) త్వరణము ‘a’ cosine ప్రమేయంగా మారుతుంది. t = 0 వద్ద – ω²A వద్ద ప్రారంభమై -ω²A నుండి ω²A వరకు మారుతుంది. ఇది స్థానభ్రంశ కాల వక్రాన్ని పోలి ఉండి \(\frac{\pi}{2}\) స్థిర దశాభేదంతో ఉంటుంది.

ప్రశ్న 3.
దశ అంటే ఏమిటి ? సరళ హరాత్మక చలనంలో స్థానభ్రంశం, వేగం, త్వరణాల మధ్య దశా సంబంధాన్ని చర్చించండి.
జవాబు:
స.హ.చ. లో ఉన్న కణము ఏదైనా సమయములో మాధ్యమిక బిందువు నుండి దాని ప్రయాణదిశను, దాని స్థానమును తెలుపు భౌతికరాశిని దశ అందురు.
ప్రావస్థ లేక దశ (Φ) : ఆవర్తన చలన ప్రారంభంలో t = 0 వద్ద ωt + Φ = Φ అవుతుంది. t = 0 వద్ద గల స్థానభ్రంశాన్ని ప్రావస్థ లేదా దశ ”Φ’ అంటారు.
ఆరంభదశ : స.హ.చ. లో ఉన్న కణము స్థానభ్రంశము Y = A cos (ωt – Φ)
వేగము V = A sin (ωt – Φ)
స్థానభ్రంశము మరియు వేగముల మధ్య దశాభేదము 90° ఉండును.
స్థానభ్రంశము, త్వరణముల మధ్య దశాకోణము :
స.హ.చ.లో త్వరణము ‘a’ = -ω² Y లేదా Y = A cos ωt మరియు a = -ω²A cos ωt
– ఋణగుర్తు స్థానభ్రంశము, త్వరణము వ్యతిరేకదిశలలో ఉండుటను సూచించును. వాటి మధ్య దశాభేదము 180° .

ప్రశ్న 4.
k బలస్థిరాంకం గల స్ప్రింగ్కు m ద్రవ్యరాశిని తగిలించారు. స్ప్రింగ్ వ్యవస్థ చేసే దోలన పౌనఃపున్యానికి సమీకరణం రాబట్టండి.
జవాబు:
భారగ్రస్త స్ప్రింగ్ డోలనావర్తనకాలం :
విస్మరించతగినంత తక్కువ ద్రవ్యరాశి గల స్ప్రింగుని ఒక చివర దృఢమైన ఆధారం నుండి వ్రేలాడదీశామనుకుందాము. దాని రెండవ చివర m ద్రవ్యరాశి గల వస్తువు ఉంది. ఈ వస్తువుని నిలువుగా క్రిందికి X దూరం లాగి వదిలామనుకోండి. అపుడు ఆ వస్తువు నిలువు తలంలో డోలనాలు చేస్తుంది.

ఇక్కడ X = మాధ్యమిక స్థానం నుండి వస్తువు స్థానంశం. వస్తువుపై పనిచేసే పునఃస్థాపక బలం స్థానభ్రంశంకి వ్యతిరేక దిశలో ఉంటూ, స్థానభ్రంశంకి అనులోమానుపాతంలో ఉంటుంది.

∴ F ∝ – x లేదా F = -kx. ఇక్కడ k, స్ప్రింగు యొక్క స్ప్రింగు స్థిరాంకం. (- గుర్తు వ్యతిరేక దిశను తెలియజేయును)
∴ వస్తువు త్వరణం = \(\frac{\mathrm{F}}{\mathrm{m}}=-\frac{\mathrm{kx}}{\mathrm{m}}\) = a
త్వరణం, స్థానభ్రంశంకి అనులోమానుపాతంలో ఉంది కనుక వస్తువు సరళ హరాత్మక చలనంలో ఉంటుంది.
సరళహరాత్మక చలనంలో గల వస్తువు ఆవర్తనకాలము

కనుక T = 2π \(\sqrt{\frac{x}{a}}\)
కాని స్ప్రింగ్లలో \(\frac{x}{a}=\frac{m}{y}\)
∴ స్ప్రింగ్ ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)

ప్రశ్న 5.
సరళ హరాత్మక డోలకానికి గతిజ, స్థితిజ శక్తులకు సమీకరణాలను రాబట్టండి.
జవాబు:
గతిజశక్తికి సమీకరణమును ఉత్పాదించుట :
సరళహరాత్మక చలనంలో గల వస్తువు స్థానభ్రంశమును x = A cos ωt తో సూచింపవచ్చును. ఇందులో A = కంపన పరిమితి; ωt = θ = కోణీయ స్థానభ్రంశము. స్థానభ్రంశములోని మార్పురేటును వేగం(v)గా నిర్వచించినారు.
వేగం = v = \(\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\) (A cos ωt) = – Aω sin ωt
∴ గతిజశక్తి = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) mA² ω²sin² ωt = \(\frac{1}{2}\) mA²ω² (1 – cos² ωt) = \(\frac{1}{2}\)mω² (A² – x²)
∴ ఏదైనా స్థానంలో గతిజశక్తి = \(\frac{1}{2}\) mω² (A² – x²
స్థానభ్రంశం x = 0 వద్ద K.E_max = \(\frac{1}{2}\) mω² A²

స్థితిజశక్తికి సమీకరణమును ఉత్పాదించుట :
m ద్రవ్యరాశి గల ఒక వస్తువు ‘O’ అను మధ్యబిందువు ఆధారంగా సరళహరాత్మక చలనంలో ఉన్నది అనుకొనుము. దీని కంపన పరిమితి ‘A’ అనుకొనుము.
సరళ హరాత్మక చలనంలో గల వస్తువు చలనాన్ని y = a cos ωt అను సమీకరణం సూచిస్తుంది.
S.H.M లో గల వస్తువుకు త్వరణము a = – ω²x;
∴ బలము F = mω²x
వస్తువును దాని స్థానం (x) నుండి కొంచెం దూరము dx ప్రక్కకు జరుపుటకు చేసిన పని = dw = F:dx = ఈ పని వస్తువులో స్థితిశక్తి రూపంలో నిలవ ఉంటుంది.
∴ స్థితిశక్తి P.E. = mω²x.dx
మొత్తం పని w = \(\int d w=\int_0^x m \omega^2 x \cdot d x\) దీనిని సమాకలనం చేయగా
మొత్తం పని = స్థితిశక్తి P.E. = \(\frac{1}{2}\) mω²x² …………… (5)

ప్రశ్న 6.
డోలనాలు చేసే లఘులోలకం ఒక అంత్యస్థానం నుంచి మరో అంత్యస్థానానికి చలించే సమయంలో శక్తి ఏవిధంగా మారుతుంది ?
జవాబు:
లఘు లోలకము : సాగదీయడానికి వీలులేని ద్రవ్యరాశి లేనటువంటి పొడవు గల దారానికి ఒక చిన్న లోహపు గుండును తగిలించి దృఢమైన ఆ దారానికి కడితే దానిని లఘు లోలకము అంటారు.
కంపన పరిమితి తక్కువగా గల లఘు లోలకం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.
లోలకం పొడవు వెంబడి నికర వ్యాసార్ధము బలం mg cos θ.
ఇది దారంతో తన్యత T ని తుల్యం చేస్తుంది.
లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ τ ను
స్పర్శీయ బలం mg sin θ ఇస్తుంది.
లోలకం డోలనాలకు కావలసిన టార్క్ τ = – L mg sin θ
లోలకం కోణీయ త్వరణము α = \(\frac{-\mathrm{mgL}}{\mathrm{I}}\) θ
లోలకం జడత్వ భ్రామకం I = mL²
లోలకం ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{I}}{\mathrm{ms} \mathrm{L}}}=2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
లఘు లోలకంలో T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{L}{g}}\) అనగా ω = \(\sqrt{\frac{g}{L}}\)
లఘు లోలకం మొత్తం శక్తి E = \(\frac{1}{2}\) mω²A² = \(\frac{1}{2}\) Iω² = \(\frac{1}{2} \mathrm{I} \frac{\mathrm{g}}{\mathrm{L}}\)

S.H.M లో గల వస్తువుకు సగటు స్థానం వద్ద గతిజశక్తి గరిష్ఠంగాను, గరిష్ఠ స్థానభ్రంశ బిందువువద్ద స్థితిశక్తి గరిష్ఠంగాను ఉంటుంది. కావున లోలకం ఒక అంత్య స్థానం నుండి మరొక అంత్య స్థానానికి మారులోపల సగటు స్థానం వద్ద దాని శక్తి స్థితిజశక్తి నుండి మొత్తం గతిజశక్తి మారుతుంది. సగటు స్థానం నుండి మరల అంత్య బిందువు చేరేసరికి మొత్తం గతిజశక్తి, స్థితిజశక్తిగా మారుతుంది. కాని లఘులోలకం మొత్తం శక్తి విలువ మారదు.

ప్రశ్న 7.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం, వేగం, త్వరణాలకు సమాసాలను ఉత్పాదించండి.
జవాబు:
సరళ హరాత్మక చలనంలో గల వస్తువు స్థానభ్రంశము X = A cos (ωt + Φ) అన్న సమీకరణంతో సూచిస్తారు.
a) t = 0 వద్ద స్థానభ్రంశము ‘A’, ωt + Φ = 90° అయిన చోట స్థానభ్రంశము X = 0. ఏదైనా కాలము t వద్ద స్థానభ్రంశము
x = A cos (ωt + Φ) అవుతుంది.

b) S.H.M లో గల వస్తువు వేగము V = \(\frac{\mathrm{d}}{\mathrm{dt}}\) A cos (ωt + Φ) = -ω \(\sqrt{A^2-x^2}\)
= – Aw sin (ωt + Φ)
t = 0 వద్ద వస్తువు వేగము ‘0’ ; (ωt + Φ) = 90° అయినచోట వేగము గరిష్ఠంగా – ωA ను చేరుతుంది.

c) త్వరణము a = \(\frac{d v}{d t}=\frac{d}{d t}\) [- Aw sin (ωt + Φ)] = – Aω² cos ωt + Φ) = -ω²x
గరిష్ఠ త్వరణము a_max = -ω²A

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సరళ హరాత్మక చలనాన్ని నిర్వచించండి. ఏకరీతి వృత్తాకార చలనం చేసే కణం విక్షేపం (ఏదైనా) వ్యాసంపై సరళ హరాత్మక చలనం చేస్తుందని చూపండి. (మే 2014)
జవాబు:
సరళ హరాత్మక చలనం : డోలన చలనం యొక్క సరళమైన రూపాన్ని సరళ హరాత్మక చలనం అంటారు. ఈ చలనం కాల ప్రమేయము (f(t)) తో ఆవర్తనంగా ఉంటుంది.
సరళ హరాత్మక చలనాన్ని f(t) = A cos ωt లేదా A sin ωt వంటి అతిసరళమైన సమీకరణంతో సూచిస్తారు.

సమవృత్తాకార చలనము మరియు సరళ హరాత్మక చలనముల మధ్య సంబంధము :
‘O’ కేంద్రము, ‘ వ్యాసార్ధం గల ఒక వృత్త పరిధి పై P అను ఒక వస్తువు లేదా కణము అపసవ్యదిశలో ”’ అను సమకోణీఁ వేగంతో చలిస్తున్నది అనుకొనుము. t అను స్వల్ప కాలము తరువాత వస్తువు స్థానము ‘P’ అనుకొనుము.

P నుండి X – – అక్షము మరియు y – అక్షముల మీదకు లంబములను గీయగా ON మరియు OM లు x, y అక్షమ విూద లంబపాదములను సూచించును.
t కాలంలో వస్తువు కోణీయ స్థానభ్రంశము θ = ωt
OPM త్రిభుజం నుండి x అక్షము మీద లంబపాదము
ON = OP cos θ కాని OP = కంపన పరిమితి = OY = r వ్యాసార్ధము
θ = ωt
∴ ఇచ్చిన క్షణంలో X అక్షంపై స్థానభ్రంశము = r cos ωt …………….. (1)

ఇదే విధంగా OPM లంబకోణ త్రిభుజం నుండి y అక్షము మీద లంబపాదము OM = OP sin θ (కాని OP = వ్యాసార్ధము, = కంపన పరిమితి, θ = ωt)
∴ ఇచ్చిన క్షణంలో y – అక్షము మీద స్థానభ్రంశము y = r sin ωt …………… (2)
వస్తువు వృత్తము ఒక భ్రమణము పూర్తిచేయుసరికి లంబపాదములు
ON, OM లు xox’ మరియు yoy’ ల మధ్య ఒక కంపనాన్ని పూర్తిచేస్తాయి.
ఏ క్షణంలోనైనా P బిందువు స్థానభ్రంశాన్ని OP² = ON² + OM² ద్వారా లెక్కగట్టవచ్చును. ఇందులో (ON = r cos ωt, OM = r sin ωt)
కావున సమవృత్తాకారచలనాన్ని పరస్పర లంబదిశలలో గల రెండు సరళ హరాత్మక చలనముల కలయికగా భావించవచ్చును.

ప్రశ్న 2.
లఘులోలకం చలనం సరళ హరాత్మకం అని చూపి, దాని డోలనావర్తన కాలానికి సమీకరణం ఉత్పాదించండి. సెకండ్ల లోలకం అంటే ఏమిటి ? (మార్చి 2014)
జవాబు:
లఘు లోలకము : సాగదీయడానికి వీలులేని ద్రవ్యరాశి లేనటువంటి ఓ పొడవు గల దారానికి ఒక చిన్న లోహపు గుండును తగిలించి దృఢమైన ఆధారానికి కడితే దానిని లఘు లోలకము అంటారు.
కంపన పరిమితి తక్కువగా గల లఘు లోలకం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.

లోలకం పొడవు వెంబడి నికర వ్యాసార్ధియ బలం mg cos θ.
ఇది దారంతో తన్యత Tని తుల్యం చేస్తుంది.
లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ τ ను
స్పర్శీయ బలం mg sin θ ఇస్తుంది.
లోలకం డోలనాలకు కావలసిన టార్క్ τ = – L mg sin θ
లోలకం కోణీయ త్వరణము α = \(\frac{-m g L}{I} \theta \Rightarrow \frac{\theta}{\alpha}=\frac{I}{m g L}\)
లోలకం జడత్వ భ్రామకం I = mL²
లోలకం ఆవర్తన కాలము T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{mgL}}}=2 \pi \sqrt{\frac{\mathrm{ML}^2}{\mathrm{mgL}}}=2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
లఘు లోలకంలో కోణీయ త్వరణము α = \(\frac{-\mathrm{mgL}}{\mathrm{I}}\) θ
అనగా త్వరణము α ∝ – θ (కోణీయ స్థానభ్రంశము) మరియు ఆవర్తన కాలము T = 2π\(\sqrt{\frac{L}{g}}\) ఈ రెండు లక్షణాలు వస్తువు సరళ హరాత్మక చలనంలో ఉండటానికి కావలసిన నిబంధనలు. కావున లఘులోలకం చలనం సరళ హరాత్మక చలనము.
సెకండ్ల లోలకం : డోలనావర్తన కాలం రెండు సెకనులు గల లోలకాన్ని సెకండ్ల లోలకం అంటారు. సెకన్ల లోలకం ఆవర్తన కాలము T = 2సెకనులు.

ప్రశ్న 3.
సరళ హరాత్మక డోలకం గతిజ, స్థితిజ శక్తులకు సమీకరణాలను ఉత్పాదించండి. సరళ హరాత్మక చలనంలోని కణం పథంపై అన్ని బిందువుల వద్ద మొత్తం శక్తి స్థిరం అని చూపండి.
జవాబు:
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశాన్ని x = A cos (ωt + Φ) అని రాస్తారు.

లేదా స్ప్రింగ్ పై బలం F = – Kx. ఇది కాలంతో పాటు మారే నిత్యత్వ బలం కాబట్టి స్థితిశక్తి
U = –\(\frac{1}{2}\) Kx . x = – \(\frac{1}{2}\) Kx²
∴ స్థితిశక్తి U = – \(\frac{1}{2}\) K.A² cos² (ωt + Φ)
S.H.M లో గల వస్తువుకు లేదా కణంకు ఏదైనా బిందువు వద్ద గల మొత్తం శక్తి KE + PE
∴ మొత్తం శక్తి E = \(\frac{1}{2}\) mω² (A² – x²) + \(\frac{1}{2}\) mω² x² (సమీకరణములు 1, 2 ల నుండి)
∴ E = \(\frac{1}{2}\) ω² A² S.H.M లో గల వస్తువుపై పనిచేయు బలాలు నిత్యత్వ బలాలు. ఇవి శక్తి నిత్యత్వ నియమం పాటిస్తాయి. అందువల్ల S.H.M లో గల వస్తువుకు అన్ని బిందువుల వద్ద మొత్తం శక్తి స్థిరము.

లెక్కలు

ప్రశ్న 1.
బోలుగా ఉండే ఇత్తడి గోళంతో ఒక లోలకం గుండును తయారుచేశారు. దాన్ని పూర్తిగా నీటితో నింపితే దాని డోలనావర్తన కాలం ఏమవుతుంది ? ఎందువల్ల ?
జవాబు:
బోలుగా ఉన్న ఇత్తడి గోళంలో పూర్తిగా నీటిని నింపితే దాని ద్రవ్యరాశి కేంద్రస్థానంలో మార్పురాదు. కావున డోలనా వర్తనకాలం మారదు. లోలకం డోలనావర్తన కాలం గోళం ద్రవ్యరాశిపై ఆధారపడదు.

ప్రశ్న 2.
k బల స్థిరాంకం గల రెండు సర్వసమానమైన స్ప్రింగ్లను శ్రేణిలో (ఒకదాని కొనకు మరొకటి) కలిపితే సంయుక్త స్ప్రింగ్ ప్రభావాత్మక బల స్థిరాంకం ఎంత ?
జవాబు:
స్ప్రింగులను శ్రేణిలో కలిపిన ఫలిత స్ప్రింగ్ స్థిరాంకము k_s = \(\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_1+\mathrm{k}_2}\)
k₁ = k₂ = k అయిన k_s = \(\frac{k k}{k+k}=\frac{k^2}{2 k}=\frac{k}{2}\)
శ్రేణిసంధానములో ఫలితస్ప్రింగ్ స్థిరాంకము తగ్గును.

ప్రశ్న 3.
సరళ హరాత్మక చలనంలో మాధ్యమిక స్థానం వద్ద ఏయే భౌతికరాశులు గరిష్ఠ విలువను కలిగి ఉంటాయి ?
జవాబు:
సరళ హరాత్మక చలనంలో మాధ్యమిక స్థానం వద్ద వేగము గరిష్ఠము. కావున గతిజశక్తి కూడా గరిష్ఠము.

ప్రశ్న 4.
సరళ హరాత్మక చలనంలో ఉన్న కణం గరిష్ఠ వేగం, గరిష్ఠ త్వరణంలో సంఖ్యాత్మకంగా సగం ఉంది. దాని డోలనావర్తన కాలం ఎంత?
జవాబు:
గరిష్ఠవేగము V_max = \(\frac{1}{2}\) గరిష్ఠ త్వరణము (a_max) ; కాని V_max = Aω మరియు a_max = ω²A
∴ Aω = \(\frac{1}{2}\) Aω² = ω = 2
∴ ఆవర్తన కాలము T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{2}\) = π సెకనులు.

ప్రశ్న 5.
బల స్థిరాంకం 260 Nm^-1 గల స్ప్రింగ్కు 2 kg ద్రవ్యరాశిని వేలాడదీశారు. అది 100 డోలనాలు చేయడానికి పట్టే కాలం ఎంత ?
జవాబు:
వ్రేలాడదీసిన ద్రవ్యరాశి m = 2 kg
బలస్థిరాంకము k = 260 N/m
∴ T = 2 × 3.142 × 0.0877 = 0.551 sec
100 డోలనాలకు పట్టుకాలము = 100 × 0.551 = 55.1 sec

ప్రశ్న 6.
నిశ్చలంగా ఉన్న లిఫ్ట్లోని లఘులోలకం డోలనావర్తన కాలం T. లిఫ్ట్ (1) సమవేగంతో పైకి వెళుతున్నప్పుడు (ii) సమవేగంతో కిందికి వెళుతున్నప్పుడు (iii) సమత్వరణం a తో పైకి వెళుతున్నప్పుడు (iv) సమత్వరణం 4 తో కిందికి వెళుతున్నప్పుడు (v) గురుత్వం వల్ల స్వేచ్ఛగా కిందికి పడుతున్నప్పుడు లోలకం డోలనావర్తన కాలం ఏవిధంగా మారుతుంది ?
జవాబు:
i) లిఫ్ట్ సమవేగంతో పైకి వెళుతుంటే దాని త్వరణము a = 0. లోలకంపై ఫలిత త్వరణము = g కావున లోలకం డోలనా వర్తన కాలము మారదు.

ii) సమవేగంతో కిందికి దిగునపుడు దాని త్వరణము a = 0 లోలకంపై ఫలిత త్వరణము a = g కావున దాని ఆవర్తన కాలం మారదు.

iii) లిఫ్ట్ ‘a’ సమత్వరణముతో పైకి పోతుంటే లోలకంపై ఫలిత త్వరణము = (a + g),
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{l}{(g+a)}}\) కావున ఆవర్తన కాలం తగ్గును.

iv) లిఫ్ట్ ‘a’ అను సమత్వరణంతో కిందికి దిగుతుంటే లోలకంపై ఫలిత త్వరణము = g – a కావున లోలకం ఆవర్తన కాలం పెరుగును.

v) లిఫ్ట్ స్వేచ్ఛగా కిందికి పడుతుంటే a = g. లోలకంపై ఫలిత త్వరణం = 0. ∴ ఆవర్తన కాలము అనంతము.

ప్రశ్న 7.
సరళ హరాత్మక చలనంలో ఉండే కణం కంపన పరిమితి 4 సెం.మీ. అది మాధ్యమిక స్థానం నుంచి 1 సెం.మీ. దూరంలో ఉన్నప్పుడు త్వరణం 3 cm s^-2. మాధ్యమిక స్థానం నుంచి 2 సెం.మీ. దూరంలో ఉన్నప్పుడు దాని వేగం ఎంత ?
జవాబు:
కంపన పరిమితి A = 4 cm = 4 × 10^-2m
త్వరణము a = 3cm/s² = 3 × 10^-2 m/s² ; స్థానభ్రంశము Y = 1cm = 10^-2m
∴ కోణీయ వేగం ω = \(\sqrt{\frac{a}{Y}}=\sqrt{\frac{3}{1}}=\sqrt{3}\)
స్థానభ్రంశము 2 సెం.మీ. వద్ద వేగము V = ω \(\sqrt{A^2-Y^2}\), y = 2 సెం.మీ. కావున
∴ V = \(\sqrt{3} \sqrt{(16-4) 10^{-4}}=\sqrt{3} \times \sqrt{12} \cdot 10^{-2}=\sqrt{3} 2 \sqrt{3} \times 10^{-2}=\) = 6 × 10^-2 m/sec = 6 cm/sec

ప్రశ్న 8.
సరళ హరాత్మక డోలకం డోలనావర్తనం కాలం 2s. డోలకం మాధ్యమిక స్థానాన్ని దాటిన 0.25s తరువాత దాని దశలో కలిగే మార్పు ఎంత ?
జవాబు:
ఆవర్తన కాలము T = 2 sec
కాలము t = 0.25 sec
దశాభేదము = Φ = \(\frac{\mathrm{t}}{\mathrm{T}}\) × 2π = \(\frac{0.25}{2}\) × 2π = \(\frac{\pi}{4}\) = 45°
అది మాధ్యమిక బిందువు నుండి \(\frac{\pi}{4}\) దూరములో ఉండును. అనగా దశలో మార్పు \(\frac{\pi}{4}\) రేడియ

ప్రశ్న 9.
సరళ హరాత్మక చలనం చేసే వస్తువు కంపన పరిమితి 5 cm, డోలనావర్తన కాలం 0.2s. వస్తువు స్థానభ్రంశం
(a) 5 cm (b) 3 cm (c) 0 cm వద్ద దాని త్వరణం, వేగాలను కనుక్కోండి.
జవాబు:
కంపన పరిమితి A = 5 సెం.మీ. ; డోలనా వర్తనకాలం T = 0.2 సె
a) స్థానభ్రంశం x = 5 సెం.మీ. అనగా x = A గరిష్ఠము
గరిష్ఠ త్వరణము a = – ω²A కాని ω = \(\frac{2 \pi}{T}=\frac{2 \pi}{0.2}\) = 2π
∴ a = (-10π)² × 5 = 500π² m/s = 5π² మీ/సె
వేగము V = 0 (గరిష్ఠ స్థానభ్రంశం వద్ద V = 0 కావున)

b) స్థానభ్రంశం 3 సెం.మీ. వద్ద
త్వరణం a = – ω²x = – (- 10π)² × 3 = – 100π² × 3
= -30π² సెం.మీ./సె²
= – 3π² మీ/సె
వేగము V = – ω\(\sqrt{A^2-x^2}\) = – 10π\(\sqrt{25-9}\) = 10π\(\sqrt{16}\) సెం.మీ./సె
= 40π సెం.మీ./సె’ = 0.4π మీ/సె

c) స్థానభ్రంశము x = 0 అయిన అనగా మధ్య బిందువు వద్ద
త్వరణము a = -ω²x = 0
వేగము V = – ω\(\sqrt{A^2-x^2}\) = – ωA = 10π × 5 = 50π సెం.మీ./సె
= 0.5π మీ/సె

ప్రశ్న 10.
ఒక గ్రహం ద్రవ్యరాశి, వ్యాసార్థాలు భూమి ద్రవ్యరాశి, వ్యాసార్థాల కంటే రెట్టింపు. భూమిపై లఘులోలకం డోలనావర్తన కాలం T అయితే గ్రహంపై లోలకం డోలనావర్తన కాలం ఎంత ?
జవాబు:
గ్రహము ద్రవ్యరాశి M_p = 2 M_e;
గ్రహము వ్యాసార్ధము R_p = 2 R_e
భూమిపై లోలకము ఆవర్తన కాలము = T
గ్రహముపై ఆవర్తన కాలము T’ = ? g_e = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
g_p = \(\frac{\mathrm{G} \cdot 2 \mathrm{M}}{(2 \mathrm{R})^2}=\frac{\mathrm{GM}}{2 \mathrm{R}^2}=\frac{\mathrm{g}_{\mathrm{e}}}{2}\) ; భూమి మీద, T = 2π \(\sqrt{\frac{l}{\mathrm{~g}_{\mathrm{e}}}}\) ; గ్రహము మీద T’ = 2π \(\sqrt{\frac{l}{\mathrm{~g}_{\mathrm{p}}}}\)
∴ \(\frac{T^{\prime}}{T}=\sqrt{\frac{g_e}{g_p}}=\sqrt{2}\) T = \(\sqrt{2}\)T

ప్రశ్న 11.
1 m పొడవు ఉండే లఘులోలకం డోలనావర్తన కాలం 2s నుండి 1.5s కు మారితే పొడవులో వచ్చే మార్పును లెక్కించండి.
జవాబు:
సెకండ్ల లోలకమునకు T₁ = 2 sec; పొడవు l₁ = 1 m.
కొత్త ఆవర్తన కాలము T₂ = 1.5 sec; పొడవు 1₂ = ?
T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\); సెకండ్ల లోలకమునకు 2 = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\)
2వ సందర్భంలో 1.5 = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\)
∴ \(\frac{2}{1.5}=\frac{1}{\sqrt{l}}=\frac{4}{3}\) ⇒ l = \(\frac{9}{16}\) m
∴ పొడవులో తగ్గుదల = 1 – \(\frac{9}{16}\) = \(\frac{7}{16}\) m = 0.4375 m

ప్రశ్న 12.
ఒక గ్రహంపై 8m ఎత్తు నుంచి వస్తువు స్వేచ్ఛగా కిందికి పడేందుకు 2s తీసుకొంటుంది. ఆ గ్రహంపై లోలకం డోలనావర్తన కాలం 7TS అయితే లోలకం పొడవును లెక్కించండి.
జవాబు:
ఎత్తు, h = 8m ; గ్రహతలమును చేరుటకు పట్టుకాలము t = 2 sec
స్వేచ్ఛగా వదలిన వస్తువుకు t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\) ⇒ 2 = \(\sqrt{\frac{16}{\mathrm{~g}}}\)
∴ గ్రహముపైన g = \(\frac{16}{4}\) = 4m/s²
లోలకము డోలనావర్తన కాలము T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\) = π ⇒ 2 \(\sqrt{\frac{l}{\mathrm{~g}}}\) = 1 లేదా \(\frac{l}{g}=\frac{1}{4}\) ⇒ l = \(\frac{g}{4}\)
ఆ గ్రహముపైన లోలకము పొడవు = \(\frac{4}{4}\) = 1m = 100 సెం.మీ.

ప్రశ్న 13.
ఒక లఘులోలకం పొడవును 0.6m పెంచినప్పుడు, డోలనావర్తన కాలం 50% పెరగడాన్ని గమనించడమైనది. g = 9.8 ms^-2 ఉన్న ప్రదేశంలో దాని తొలి పొడవు, తొలి డోలనావర్తన కాలాలను లెక్కించండి.
జవాబు:
a) లోలకము పొడవులో పెరుగుదల = 0.6m ; ఆవర్తన కాలములో పెరుగుదల = 50% = 1.5T
లోలకము యథార్థ పొడవు = l అనుకొనుము;
యథార్థ ఆవర్తన కాలము = T;
గురుత్వ త్వరణము g = 9.8 m/s²
మొదటి సందర్భానికి 9.8 = 4π² \(\frac{l}{\mathrm{~T}^2}\) ……………… (1)
రెండవ సందర్భానికి l₁ = (l + 0.6), T₁ = 1.5 T; ∴ 9.8 = 4π² \(\frac{l_1}{\mathrm{~T}_1^2}\) …………….. (2)
2ని 1చే భాగించగా 1 = \(\frac{l_1}{l} \cdot \frac{\mathrm{T}^2}{\mathrm{~T}_1^2} \Rightarrow \frac{l_1}{l}=\frac{\mathrm{T}_1^2}{\mathrm{~T}^2}\) 2.25 ⇒ l₁ = 2.25 1; కాని l₁ = l + 0.6;
∴ l + 0.6 = 2.25 l ⇒ 0.6 = 1.25 l ;
∴ లోలకము పొడవు l = \(\frac{0.6}{1.25}\) = 0.48 m

b) ఆవర్తన కాలము T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\) = 2 × 3.142 \(\sqrt{\frac{0.48}{9.8}}\) = 6.284 × 0.2213 = 1.391 sec.

ప్రశ్న 14.
సెకండ్ల లోలకంతో నియంత్రితమైన (regulated) ఒక గడియారం సరైన సమయాన్ని చూపిస్తూ ఉంది. ‘వేసవి కాలంలో లోలకం పొడవు 1.02 m లకు పెరిగినట్లైతే గడియారం ఒక రోజులో ఎంత కాలాన్ని పొందుతుంది లేదా కోల్పోతుంది ?
జవాబు:
సెకండ్ల లోలకము ఆవర్తనకాలము, T = 2 sec
సెకండ్ల లోలకము పొడవు, l = g² / 4π² = 0.9927 m
వేసవిలో సెకండ్ల లోలకము పొడవు = 1.02 m
∴ పొడవులో దోషము = ∆l = 1.02 – 1 = 0.0273
లోలకమునందు T ∝ \(\sqrt{\mathrm{l}}\). దోషముల వ్యాపన నియమము నుండి \(\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{2} \frac{\Delta l}{l}=\frac{1}{2} \quad \frac{0.0273}{0.9927}\)
∴ ఒక దినమునకు కాలములో దోషము = 86,400 × \(\frac{1}{2} \frac{0.0273}{0.9927}\) = 1188 sec.

ప్రశ్న 15.
స్ప్రింగ్కు వేలాడదీసిన వస్తువు ఆవర్తన కాలం T. ఆ స్ప్రింగ్ను రెండు సమాన భాగాలుగా చేసి (i) వస్తువును ఒక భాగానికి వేలాడదీసినప్పుడు (ii) రెండు భాగాలకు (సమాంతరంగా) ఒకేసారి వస్తువును వేలాడదీసినప్పుడు డోలనావర్తన కాలాలను లెక్కించండి.
జవాబు:
స్ప్రింగ్ ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)
స్ప్రింగు రెండు సమానభాగాలుగా కత్తిరించిన ఒక్కొక్క భాగము
స్ప్రింగ్ స్థిరాంకము K₁ = 2K

i) ఇచ్చిన ప్రదేశమునకు T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{K}_1}}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}} \frac{1}{\sqrt{2}}=\frac{\mathrm{T}}{\sqrt{2}}\)

ii) రెండు స్ప్రింగులను సమాంతరముగా కలిపి వాటికి ఒకేసారి ద్రవ్యరాశిని వ్రేలాడదీసిన ఫలిత స్ప్రింగ్ స్థిరాంకము
K_p = K₁ + K₂ = 4K
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{m}{K_p}}=2 \pi \sqrt{\frac{m}{4 \cdot K}}=2 \pi \sqrt{\frac{m}{K}} \cdot \frac{1}{2}=\frac{T}{2}\)

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
మానవ గుండె, సగటు స్పందన రేటు నిమిషానికి 75. గుండె పౌనఃపున్యం, ఆవర్తన కాలాలను లెక్కించండి.
జవాబు:
గుండె స్పందన పౌనఃపున్యం = 75 / (1 min) = 75/(60s) = 1.25 s^-1 = 1.25 Hz = 75 min
ఆవర్తన కాలం, T = 1/(1.25s^-1) = 0.8s

ప్రశ్న 2.
కింది కాల ప్రమేయాల్లో ఏది (a) సరళ హరాత్మక చలనం (b) ఆవర్తన చలనమే కాని సరళ హరాత్మక చలనం కాదు. రెండు సందర్భాల్లో ఆవర్తన కాలాలను తెలపండి.
a) sin ωt – cot ωt
b) sin² ωt
జవాబు:
a) sin ωt – cos ωt = sin ωt – sin (π/2 – ωt)
= 2 cos (π/4) sin (ωt – π/4)
= \(\sqrt{2}\) sin (ωt – π/4)
పై సమీకరణం ఆవర్తన కాలం T = 2 π/ω, దశా కోణం (−π/4) లేదా (π/4) తో ఉండే సరళ హరాత్మక చలనాన్ని సూచిస్తుంది.

b) sin²ωt = 1/2 – 1/2 cos 2ωt
ఇది ఆవర్తన కాలం T = π/ω తో ఉండే ఆవర్తన చలనాన్ని సూచిస్తుంది. ఇది 0 వద్ద కాక 1/2 వద్ద సమతాస్థితి స్థానాన్ని కలిగి ఉండే హరాత్మక చలనాన్ని కూడా సూచిస్తుంది.

ప్రశ్న 3.
కింద ఇచ్చిన సమీకరణా (SI ప్రమాణాలలో) నికి అనుగుణంగా ఒక వస్తువు సరళ హరాత్మక చలనం చేస్తుంది.
x = 5 cos [2πt + π/4]
t = 1.58 వద్ద వస్తువు (a) స్థానభ్రంశం, (b) వడి, (c) త్వరణాలను లెక్కించండి.
జవాబు:
వస్తువు కోణీయ పౌనఃపున్యం ω = 2πs^-1,
ఆవర్తన కాలం T = 1s
t = 1.5s వద్ద
a) స్థానభ్రంశం = (5.0m) cos [(2πs^-1) × 1.5s + π/4]
= (5.0 m) cos [(3π + π/4)]
= – 5.0 × 0.707 m = – 3.535 m

b) సమీకరణం v(t) = – ωA sin (ωt + Φ) ని ఉపయోగించి, వస్తువు వడి
= – (5.0m) (2πs^-1) sin ((2πs^-1) × 1.5s + π/4]
= – (5.0m) (2πs^-1) sin [(3π + π/4]
= 10π × 0.707 ms^-1 = 22 ms^-1

c) సమీకరణం v(t) = \(\frac{\mathrm{d}}{\mathrm{dt}}\) x(t) = \(\frac{\mathrm{d}}{\mathrm{dt}}\) [A cos (ωt + Φ)] ని ఉపయోగించి, వస్తువు త్వరణం
= – (2πs^-1)² × స్థానభ్రంశం
= – (2πs^-1)² × (-3.535 m) = 140 ms^-2

ప్రశ్న 4.
500 Nm^-1 బల స్థిరాంకం గల స్ప్రింగ్కు 5kg ద్రవ్యరాశి గల లోహ కంకణాన్ని (ring) బిగించారు. క్షితిజ సమాంతరంగా ఉండే కడ్డీపై ఘర్షణ లేకుండా కంకణం జారుతుంది. మాధ్యమిక స్థానం నుంచి కంకణాన్ని 10.0 cm లాగి వదిలారు. అయితే కంకణం a) డోలనావర్తన కాలం 5) గరిష్ఠ వడి c) గరిష్ఠ త్వరణాలను లెక్కించండి.
జవాబు:
a) సమీకరణం T = 2π \(\) నుంచి డోలనావర్తన కాలం
T = 2π \(\sqrt{\frac{5.0 \mathrm{~kg}}{500 \mathrm{Nm}^{-1}}}\)
= (2π/10)s = 0.63s

b) సరళ హరాత్మక చలనం చేసే కంకణం వేగం v(t) = – Aω sin (ωt + Φ)
గరిష్ఠ వడి
v_m = Αω
= 0.1 × \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\)
= 0.1 × \(\sqrt{\frac{500 \mathrm{Nm}^{-1}}{5 \mathrm{~kg}}}\) = 1 ms^-1
x = 0 వద్ద గరిష్ఠ వడి ఉంటుంది.

c) మాధ్యమిక స్థానం నుంచి x(t) స్థానభ్రంశం వద్ద కంకణం త్వరణం
a(t) = -ω²x(t)
= – \(\frac{\mathrm{k}}{\mathrm{m}}\) x(t)
గరిష్ఠ త్వరణం, a_max = ω²A
= \(\frac{500 \mathrm{Nm}^{-1}}{5 \mathrm{~kg}}\) × 0.1 m = 10 ms^-2
ఇది అంత్య స్థానాల వద్ద ఉంటుంది.

ప్రశ్న 5.
సెకండులను టిక్చేసే లఘులోలకం పొడవు ఎంత ?
జవాబు:
లఘులోలకం డోలనావర్తన కాలం
T = 2π \(\sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
దీని నుంచి కింది విధంగా రాయవచ్చు.
L = \(\frac{\mathrm{g} \mathrm{T}^2}{4 \pi^2}\)
సెకండ్లను టిక్ చేసే లఘులోలకం డోలనావర్తన కాలం 2s.
∴ g = 9.8 ms^-2, T = 2s విలువలకు
L = \(\frac{9.8\left(\mathrm{~ms}^{-2}\right) \times 4\left(\mathrm{~s}^2\right)}{4 \pi^2}\) = 1 m

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
కింది వాటిలో ఏవి ఆవర్తన చలనాలను సూచిస్తాయి ?
a) చెరువు ఒక ఒడ్డు నుంచి అవతలి ఒడ్డుకు, తిరిగి అవతలి ఒడ్డు నుంచి మొదటి ఒడ్డుకు ఒక ఈతగాడు పూర్తి చేసే ట్రిప్.
b) స్వేచ్ఛగా వేలాడదీసిన దండాయస్కాంతాన్ని NS దిశ నుంచి కదిల్చి వదిలితే అది చేసే చలనం.
c) తన ద్రవ్యరాశి కేంద్రం చుట్టూ భ్రమణం చెందే హైడ్రోజన్ అణువు.
d) ధనుస్సు (విల్లు) నుంచి విడుదలైన బాణం.
జవాబు:
a) ఈతగాడు ఈ ఒడ్డు నుండి ఆ ఒడ్డుకు మరల మొదటి వైపుకు వస్తే అది సంవృత చలనమే గాని ఆవృత చలనం కాదు. కారణం ఈ చలనము నియమిత కాలవ్యవధిలో పునరావృతం కాదు.
b) స్వేచ్ఛగా వేలాడదీసిన దండాయస్కాంత కంపనాలు ఆవృత చలనాలు.
c) ఇది ఆవృత చలనము. కారణం వస్తువు పరిభ్రమణంలో ఉంది.
d) విల్లు నుంచి వచ్చిన బాణం ఒకే దిశలో ముందుకు పోతుంది. ఇది ఆవృత చలనం కాదు.

ప్రశ్న 2.
కింది ఉదాహరణలలో ఏవి దాదాపు సరళ హరాత్మక చలనాలు, ఏవి సరళ హరాత్మకం కాని ఆవర్తన చలనాలను సూచిస్తాయి ?
a) తన అక్షం పరంగా భూమి చేసే భ్రమణ చలనం
b) U – గొట్టంలో డోలనం చేసే పాదరస స్తంభం చలనం
c) నునుపైన వక్రత గల లోతు గిన్నెలో సమతాస్థితి స్థానం కంటే కొద్దిగా ఎగువన వదిలిన ఇనుప గుండు చలనం
d) తన సమతాస్థితి స్థానం పరంగా బహుపరమాణుక అణువు చేసే సాధారణ కంపనాలు
జవాబు:
a) భూమి తన అక్షం చుట్టూ చేసే భ్రమణం ఆవృత చలనము. ఇది S.H.M కాదు.
b) U – గొట్టంలో ద్రవం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.
c) సమతాస్థితి నుంచి ఇనుప గుండును స్థానభ్రంశం చెందిస్తే అది నునుపు తలంపై సరళ హరాత్మక చలనం చేస్తుంది.
d) సగటు స్థానం నుండి బహుపరమాణుక అణువు కంపనాలు ఆవర్తన చలనాలు కావు.

ప్రశ్న 3.
దిగువన ఇవ్వబడిన పటం కణం రేఖీయ చలనానికి x – t ల మధ్య గీచిన గ్రాఫ్లను సూచిస్తుంది. వీటిలో ఏవి ఆవర్తన చలనాన్ని సూచిస్తాయి ? సూచిస్తే వాటి డోలనావర్తన కాలం ఎంత ?

జవాబు:
a) ఈ రేఖాపటము కాలంతో పాటు ఒకే దిశలో స్థానభ్రంశంలో మార్పు సూచిస్తుంది. కావున ఆవృత చలనం కాదు.
b) ఇది ఆవృత చలనాన్ని సూచిస్తుంది. దీని ఆవర్తన కాలము 2 సెకనులు.
c) ఈ చలన వక్రంలోని ఆకారం నియమిత కాలం తరువాత పునరావృతం కాలేదు. అందువల్ల ఇది ఆవృత చలనం కాదు.
d) ఇది ఆవృత చలనము. ఆవర్తన కాలము 2 సెకనులు.

ప్రశ్న 4.
కింది వాటిలో ఏ కాల ప్రమేయాలు a) సరళ హరాత్మక, b) ఆవర్తనమే కానీ సరళ హరాత్మకం కాని, c) ఆవర్తనం కాని చలనాలను సూచిస్తాయి. ప్రతి ఆవర్తన చలనం సందర్భంలో ఆవర్తన కాలాన్ని తెలియచేయండి. (ఎ ఏదైనా ధన స్థిరాంకం)
a) sin ωt – cos ωt
(b) sin³ ωt
(c) 3 cos\(\left(\frac{\pi}{4}-2 \omega t\right)\)
(d) cos ωt + cos 3ωt + cos 5ωt
(e) exp (- ω²t²)
(f) 1 + ωt + ω²t².
జవాబు:

1. ఒక చలనం ఆవృత చలనం కావాలంటే దాని చలనం ఒకే విధంగా ఉండి నిర్ణీత కాలవ్యవధి తరువాత పునరావృతం కావాలి.
2. వస్తువు చలనం S.H.M కావాలంటే దాని చలనం cos (ωt + Φ) లేదా sin (ωt + Φ) వంటి రూపంలో ఉండాలి.

a) sin ωt – cos ωt = \(\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin \omega \mathrm{t}-\frac{1}{\sqrt{2}} \cos \omega \mathrm{t}\right]=\sqrt{2}\left[\cos \frac{\pi}{4} \sin \omega \mathrm{t}-\sin \frac{\pi}{4} \cos \omega \mathrm{t}\right]\)
= \(\sqrt{2} \sin \left(\omega t-\frac{\pi}{4}\right)\)
ఇది S.H.M లో గల వస్తువు సమీకరణాన్ని సూచిస్తుంది. కావున సరళ హరాత్మక చలనము.

b) sin³ ωt = \(\frac{1}{4}\) [3 sin ωt – sin 3ωt]
ఇందులో sin ωt మరియు sin 3ωt లు ఆవృత చలనాలు. ఆవర్తన కాలము 2π/ω. కాని ఈ రెంటి కలయిక సరళ హరాత్మక చలనం కాదు. కేవలం ఆవృత చలనం మాత్రమే.

c) 3 cos \(\left(\frac{\pi}{4}-2 \omega t\right)\) = 3 cos (2ωt – \(\frac{\pi}{4}\)); [∵ cos – θ = cos θ]
కావున ఇది సరళ హరాత్మక చలనము.

d) cos ωt + cos 3ωt + cos 5ωt లలో ప్రతి పదము ఆవర్తన చలనాన్ని కలిగి ఉంది. వీటి అన్నింటి ఫలితంగా వచ్చిన చలనం సరళ హరాత్మక చలనం కాదు.

e) e^-ω2t2 వంటి ఘాతాంక ప్రమేయాలు ఒకే దిశలో పెరుగుతాయి. వీటి ప్రవర్తన పునరావృతం కాదు. అందువల్ల ఇవి ఆవృత చలనాలు లేదా S.H.M లు కావు.

f) 1 + ωt + ω²t² వంటి సమీకరణాల పరిమాణాలు కాలంతో పాటు పునరావృతం కావు. అందువల్ల ఇవి ఆవృత చలనాలు లేదా S.H.M లు కావు.

ప్రశ్న 5.
10 cm ఎడంతో ఉండే రెండు బిందువులు A, B ల మధ్య ఒక కణం రేఖీయ సరళ హరాత్మక చలనం చేస్తుంది. A నుంచి B కి దిశను ధన దిశగా తీసుకొని, కింద ఇచ్చిన స్థానాల వద్ద కణం ఉన్నప్పుడు వేగం, త్వరణం, బలం
దిశలను తెలపండి.
a) A
b) B
c) A, B ల మధ్య బిందువు వద్ద A వైపు వెళ్ళేటప్పుడు,
d) B నుంచి 2 cm దూరంలో, A వైపు వెళ్ళేటప్పుడు,
e) A నుంచి 3 cm దూరంలో, B వైపు వెళ్ళేటప్పుడు,
f) B నుంచి 4 cm దూరంలో, A వైపు వెళ్ళేటప్పుడు.
జవాబు:
a) A బిందువు వద్ద స్థానభ్రంశం గరిష్ఠము. కావున వేగం V = 0 త్వరణము, బలము గరిష్ఠము. వీటి దిశ A నుండి B వైపు ఉంటుంది.

b) B బిందువు వద్ద స్థానభ్రంశం గరిష్ఠము కావున V త్వరణము, బలము గరిష్ఠము. వీటి దిశ B నుండి A వైపు ఉంటుంది.

c) మధ్యబిందువు ‘C’ వద్ద స్థానభ్రంశము సున్న వేగము గరిష్ఠము. ఇది x -ve దిశలో ఉంటుంది. త్వరణము, బలముల పరిమాణము సున్న.

d) B నుండి 2 cm దూరంలో A వైపు చలిస్తే ఇవి x -ve వైపు చలించే ప్రవృత్తి కలిగి ఉన్నాయి. కావున వేగము, త్వరణము, బలం అన్నీ ఋణాత్మకమే.

e) A నుండి 3 cm దూరంలో B వైపు చలిస్తుంటే కణం గమన దిశ x ‘+ve’ వైపు ఉంది. కావున వేగం, త్వరణము మరియు బలముల దిశ ధనాత్మకము.

f) B నుండి 4 cm దూరంలో A వైపు చలిస్తుంటే వేగం x -ve వైపు ఉంది కావున ఋణాత్మకము, త్వరణము మధ్య బిందువు వైపు ఉంది. కావున త్వరణము, బలము ధనాత్మకము.

ప్రశ్న 6.
కణం త్వరణం a, స్థానభ్రంశం x ల మధ్య సంబంధాన్ని తెలిపే కింది సమీకరణాల్లో ఏవి సరళ హరాత్మక చలనాన్ని కలిగి ఉన్నాయి ?
a) a = 0.7 x
b) a = – 200 x²
c) a = – 10x
d) a = 100 x³
జవాబు:
a) ఇది S.H.M కాదు
b) S.H.M కాదు
c) a = – 10x ఇది a = – ω²y రూపంలో ఉంది కావున సరళ హరాత్మక చలనం (S.H.M) ను సూచిస్తుంది.
d) ఇది S.H.M కాదు.
గమనిక : S.H.M లో గల వస్తువు త్వరణము a = – ω²y రూపంలో ఉండాలి. ω = స్థిరపదము (విలువ స్థిరము).

ప్రశ్న 7.
స్ప్రింగ్ త్రాసు స్కేలుపై 0 నుంచి 50 kg వరకు రీడింగ్లు కలవు. స్కేలు పొడవు 20 cm. ఈ త్రాసుకు వేలాడదీసిన వస్తువును లాగి వదిలితే అది 0.6s డోలనావర్తన కాలంతో డోలనాలు చేస్తుంది. అయితే వేలాడదీసిన వస్తువు భారం ఎంత ?
జవాబు:
దత్తాంశం నుండి m₁ = 50 కి.గ్రా లకు సాగుదల y = 20 సెం.మీ. = 0.2 మీ; కాలము T = 0.6 సె
గరిష్ఠ బలం F = mg = 50 × 9.8 = 490 N
బలస్థిరాంకము K = \(\frac{\mathrm{F}}{\mathrm{y}}=\frac{490}{0.2}\) = 2450 న్యూ
ఆవర్తన కాలము T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\) ⇒ m = \(\frac{\mathrm{KT}^2}{4 \pi^2}\)
m = \(\frac{2450 \times 0.6 \times 0.6}{4 \times(3.14)^2}\) = = 22.56 kg
వస్తువు భారము w = mg = 22.56 × 9.8 = 221.1 న్యూ

ప్రశ్న 8.
పటంలో చూపిన విధంగా 1200 Nm^-1 స్ప్రింగ్ స్థిరాంకం గల స్ప్రింగ్ను క్షితిజ సమాంతరంగా ఉండే బల్లపై అమర్చారు. స్ప్రింగ్ స్వేచ్ఛా చివరకు 3 kg ద్రవ్యరాశిని తగిలించారు. ద్రవ్యరాశిని 2.0 cm దూరం పక్కకు లాగి వదిలారు. i) డోలనాల పౌనఃపున్యం, ii) ద్రవ్యరాశి గరిష్ఠ త్వరణం, iii) ద్రవ్యరాశి గరిష్ఠ వేగాలను కనుక్కోండి.
జవాబు:
దత్తాంశం నుండి k = 1200 Nm^-1; m = 3.0 kg; a = 2 cm = 0.02 m

ప్రశ్న 9.
పై అభ్యాసంలో స్ప్రింగ్ సాగదీయనప్పుడు ద్రవ్యరాశి స్థానం x = 0 అని, ఎడమ నుంచి కుడికి ధనాత్మక x – అక్షం అని తీసుకోండి. t = 0 వద్ద స్టాప్ వాచ్ను మొదలు పెట్టినట్లైతే, డోలనాలు చేస్తున్న ద్రవ్యరాశి కింది స్థానాల వద్ద ఉన్నప్పుడు t ప్రమేయంగా x విలువను తెలపండి.
a) మాధ్యమిక స్థానం
b) గరిష్టంగా సాగిన స్థానం
c) గరిష్ఠంగా సంపీడనం (నొక్కిన) చెందిన స్థానం
పై సరళ హరాత్మక చలన ప్రమేయాలు పౌనఃపున్యం, కంపన పరిమితి, తొలి దశల్లో ఒకదానితో ఒకటి ఏవిధంగా విభేదిస్తాయో తెలపండి.
జవాబు:
కంపన పరిమితి A = 2 సెం.మీ; ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}=\sqrt{\frac{1200}{3}}\) = 20 రే/సె
a) మాధ్యమిక స్థానం వద్ద x = A sin ωt నుండి x = 2 sin 2ω t

b) గరిష్ఠంగా సాగిన స్థానం వద్ద x = A అనగా Φ = \(\frac{\pi}{2}\) మూల సమీకరణం నుండి
x = A sin (ωt + Φ) నుండి x = 2 sin (20t + \(\frac{\pi}{2}\)) = 2 cos (20t)

c) గరిష్ఠ సంపీడన స్థానం వద్ద x = – A. కావున Φ = \(\frac{3\pi}{2}\) మూల సమీకరణం
x = A sin (ωt + Φ) నుండి x = – 2 sin (20t + \(\frac{3\pi}{2}\)) = -2 cos 20t.

ప్రశ్న 10.
పటం రెండు వృత్తాకార చలనాలను సూచిస్తుంది. వృత్త వ్యాసార్ధం, భ్రమణ కాలం, తొలిస్థానం, తిరిగే దిశ (సవ్య లేదా అపసవ్య) మొదలైన అంశాలు పటంలో చూపించడమైంది.

పై రెండు సందర్భాలలో భ్రమణం చెందే కణం P యొక్క వ్యాసార్ధ సదిశ x – అక్ష విక్షేపం యొక్క సహచలనాలను రాబట్టండి.
జవాబు:
పటము (a) నుండి T = 2సె; కంపన పరిమితి A = 3 సెం.మీ. ;
t = 0 వద్ద ‘OP’ x – అక్షంతో చేసిన కోణము \(\frac{\pi}{2}\) = 90° సవ్యదిశ
∴ S.H.M లో గల వస్తుసమీకరణం x = A cos \(\left(\frac{2 \pi \mathrm{t}}{\mathrm{T}}+\phi\right)\) = 3 cos \(\left(\frac{2 \pi \mathrm{t}}{2}+\frac{\pi}{2}\right)\) = 3 cos \(\left(\pi \mathrm{t}+\frac{\pi}{2}\right)\) సెం.మీ.

b) పటము (b) నుండి కాలము T = 4 సె ; కంపన పరిమితి A = 2 మీ.
t = 0 వద్ద x – అక్షంతో P చేయు కోణము Φ = π. (సవ్యదిశలో)
∴ S.H.M లో గల వస్తు సమీకరణం
x = A cos \(\left(\frac{2 \pi t}{T}+\phi\right)\) = 2 cos \(\left(\frac{2 \pi \mathrm{t}}{4}+\pi\right)\) = -2 cos \(\left(\frac{\pi}{2} t\right)\)

ప్రశ్న 11.
పటం (a)లో చూపించిన విధంగా బల స్థిరాంకం గల స్ప్రింగ్ ఒక చివరను దృఢంగా బిగించి, రెండో స్వేచ్ఛా చివరకు ద్రవ్యరాశి m ని బిగించారు. స్వేచ్ఛా చివర ప్రయోగించిన బలం Fవల్ల స్ప్రింగ్ కొంత సాగుతుంది. పటం (b)లో చూపించిన విధంగా అదే స్ప్రింగ్ రెండు స్వేచ్ఛా చివరలను m ద్రవ్యరాశి గల రెండు దిమ్మెలకు అనుసంధానం చేసి, రెండు చివరలా అంతే బలం F ప్రయోగించి స్ప్రింగ్ను సాగదీశారు.

(a) రెండు సందర్భాల్లో స్ప్రింగ్ పొందే గరిష్ఠ సాగుదల ఎంత ?
(b) పటం (a) లో ద్రవ్యరాశిని, పటం (b) లో రెండు ద్రవ్యరాశులను వదిలిపెడితే ప్రతి సందర్భంలో స్ప్రింగ్ చేసే డోలనావర్తన కాలం ఎంత ?
జవాబు:
రెండు సందర్భాలలోను స్ప్రింగ్లో గరిష్ఠ సాగుదల_x = F/k
పటం ‘a’ నుండి స్ప్రింగ్ను సాగదీసిన స్థానం వద్ద బరువును వదలివేస్తే పునఃస్థాపక బలం F = – kx లేదా F ∝ x
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\) స్ప్రింగ్లలో
m = తగిలించిన ద్రవ్యరాశి ; k = స్ప్రింగ్ స్థిరాంకము
పటము ‘b’ నుండి రెండు ద్రవ్యరాశులను శ్రేణి పద్ధతిలో కలిపితే స్ప్రింగ్ స్థిరాంకము k అయినపుడు ఫలిత ద్రవ్యరాశి
μ = \(\frac{\mathrm{m} \times \mathrm{m}}{\mathrm{m}+\mathrm{m}}=\frac{\mathrm{m}}{2}\)
ఆవర్తన కాలము T= 2π \(\sqrt{\frac{\mu}{k}}\) = 2π \(\sqrt{\frac{\mathrm{m}}{2 \mathrm{k}}}\)

ప్రశ్న 12.
ఒక వాహన ఇంజన్లోని సిలిండర్లో గల ముషలకం 1.0m (కంపన పరిమితికి రెట్టింపు) ఘాతం (stroke) ను ఇస్తుంది. ఒకవేళ ముషలకం 200 rad/min పౌనఃపున్యంతో సరళ హరాత్మక చలనం చేస్తున్నట్లైతే, దాని గరిష్ఠ వడి ఎంత ?
జవాబు:
కంపన పరిమితి A = \(\frac{1}{2}\) మీ.,
ω = 200 R.P.M
గరిష్ఠ వేగము V_max = A . ω = \(\frac{1}{2}\) × 200 = 100 మీ/నిమిషము

ప్రశ్న 13.
చంద్రుడిపై గురుత్వ త్వరణము విలువ 1.7 ms^-2. భూమిపై 3.58 డోలనావర్తన కాలం గల లఘులోలకాన్ని చంద్రుడిపైకి తీసుకొనిపోతే అక్కడ దాని డోలనావర్తన కాలం ఎంత ? (భూమిపై g విలువ 9.8 ms^-2)
జవాబు:
చంద్రునిపై గురుత్వ త్వరణము g_m = 1.7 మీ/సె^-2 ; భూమిపై g = 9.8 మీ/సె²
భూమిపై లోలకం ఆవర్తన కాలము T_e = 3.5 సె ;
చంద్రునిపై ఆవర్తన కాలం T_m = ?
T_e = 2π \(\sqrt{\frac{l}{g_e}}\)
T_m = 2π \(\sqrt{\frac{l}{g_m}}\)
∴ \(\frac{T_m}{T_e}=\sqrt{\frac{g_e}{g_m}\)
చంద్రునిపై ఆవర్తన కాలం T_m = T_e \(\sqrt{\frac{9.8}{1.7}}\) = 8.4 s

ప్రశ్న 14.
Mద్రవ్యరాశి గల గుండును కలిగి ఉన్న ! పొడవు గల లఘులోలకాన్ని కారులో వేలాడదీశారు. కారు R వ్యాసార్ధం గల వృత్తాకార మార్గంపై సమవడితో చలిస్తోంది. లోలకం వ్యాసార్ధ దిశలో సమతాస్థితి స్థానం పరంగా స్వల్ప డోలనాలను చేస్తే, దాని ఆవర్తన కాలం ఎంత ?
జవాబు:
అభిలంబ త్వరణము a_c = \(\frac{v^2}{\mathrm{R}}\) ఇది క్షితిజ సమాంతరంగా పనిచేస్తుంది.
గురుత్వ త్వరణము ‘g’ క్షితిజ లంబంగా పనిచేస్తుంది.
ఫలిత గురుత్వ త్వరణము g’ = \(\sqrt{g^2+a_c^2}=\sqrt{g^2+\frac{v^4}{R^2}}\)
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{l}{g^{\prime}}}\) = 2π \(\sqrt{\frac{l}{g^2 \quad v^4 / R^2}}\)

ప్రశ్న 15.
10 kg ద్రవ్యరాశి గల వృత్తాకార లోహపలక కేంద్రం వద్ద తీగతో కట్టి పలకను వేలాడదీశారు. తీగను మెలి తిప్పి వదిలితే పలక చేసే విమోటన డోలనాల ఆవర్తన కాలం 1.58 పలక వ్యాసార్ధం 15 cm అయితే తీగ విమోటన స్ప్రింగ్ స్థిరాంకం విలువను కనుక్కోండి. (విమోటన స్ప్రింగ్ స్థిరాంకం aను J = – α θ తో నిర్వచిస్తారు. ఇక్కడ J పునఃస్థాపక టార్క్, θ పురి తిప్పిన కోణం).
జవాబు:
దత్తాంశం నుండి m = 10 కి.గ్రా; R = 15 సెం.మీ. = 0.15 మీ; T = 1.5 సె
బిళ్ళ జడత్వ భ్రామకము I = \(\frac{\mathrm{MR}^2}{2}\) = \(\frac{1}{2}\) × 10 × (0.15)² = 0.1125 kg m²
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{I}}{\alpha}}\)
లేదా α = \(\frac{4 \pi^2 \mathrm{I}}{\mathrm{T}^2}\) = 4 × (3.14)² × \(\frac{1}{2}\) × \(\frac{0.1125}{(1.5)^2}\) = 1.97 Nm/Rad

ప్రశ్న 16.
5 cm కంపన పరిమితి, 0.2s డోలనావర్తన కాలంతో ఒక వస్తువు సహచ చేస్తుంది. వస్తువు స్థానభ్రంశాలు (a) 5 cm (b) 3 cm (c) 0 cm అయినప్పుడు దాని త్వరణం, వేగాలను కనుక్కోండి.
జవాబు:
దత్తాంశం నుండి A = 5 సెం.మీ. = 0.05 మీ; T = 0.2 సె
కోణీయ వేగము ω = \(\frac{2 \pi}{T}=\frac{2 \times 3.14}{0.2}\) = 10π
a) స్థానభ్రంశము x = 5 cm ⇒ x = A వద్ద
త్వరణము A = – ω²A = 10π × 10π × \(\frac{5}{100}\) = 5π² = 49.3 మీ/సె²
వేగము V = 0 (x = A అయినపుడు)

b) స్థానభ్రంశము x = 3 సెం.మీ.= \(\frac{3}{100}\) మీ.
త్వరణము a = – ω²x = 10π × 10π × \(\frac{3}{100}\) = 29.58 మీ/సె²
వేగము V = ω \(\sqrt{\mathrm{A}^2-\mathrm{x}^2}=10 \pi \sqrt{\left(\frac{5}{100}\right)^2-\left(\frac{3}{100}\right)^2}=\frac{10 \pi}{100} \sqrt{25-9}\)
= \(\frac{\pi}{10} \cdot \sqrt{16}=\frac{4 \pi}{10}\) = 1.256 మీ/సె

c) స్థానభ్రంశము x = 0 వద్ద, త్వరణము a = ω²x = 0
వేగము V గరిష్ఠము
∴ V_max = Aω = \(\frac{5}{100}\) × 10π = \(\frac{\pi}{2}\) = 1.57 మీ/సె

ప్రశ్న 17.
క్షితిజ సమాంతరంగా ఉండే స్ప్రింగ్ స్వేచ్ఛా చివరన కట్టిన ద్రవ్యరాశి, తలంపై ఎలాంటి ఘర్షణ లేదా అవరోధం లేనప్పుడు » కోణీయ వేగంతో డోలనాలు చేస్తుంది. t = 0 కాలం వద్ద ద్రవ్యరాశిని x₀ దూరం లాగి కేంద్రం వైపు V₀ వేగంతో నెట్టినప్పుడు కలిగే ఫలిత డోలనాల కంపన పరిమితిని ω, x₀, V₀ పదాలలో కనుక్కోండి.
(సూచన : x = a cos (ωt + θ) సమీకరణంతో ప్రారంభించండి. తొలి వేగం రుణాత్మకం అని గమనించండి.)
జవాబు:
దత్తాంశం నుండి కాలము t = 0 వద్ద x = x₀ మరియు \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = -V₀
S.H.M సమీకరణం x = A cos (ωt + Φ) నుండి x₀ = A cos ωt …………….. (1)
కాని \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = V₀ = -ω A sin ωt
⇒ A sin ωt = \(\frac{V_0}{\omega}\) ………………. (2)
1, 2 సమీకరణాలను వర్గీకరించి కలుపగా
x₀² + \(\frac{\mathrm{V}_0^2}{\omega^2}\) = A² (sin²ωt + cos²ωt) లేదా A² = x₀² + \(\frac{\mathrm{V}_0^2}{\omega^2}\)
∴ కంపన పరిమితి A = \(\sqrt{\mathrm{x}_0^2+\frac{\mathrm{V}_0^2}{\omega^2}}\)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 3 Matrices Ex 3(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(e)

I.
Question 1.
Find the adjoint and inverse of the following matrices. (March 2002)
i) \(\left[\begin{array}{rr}
2 & -3 \\
4 & 6
\end{array}\right]\)
Answer:
If A = \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) then adj A = \(\left[\begin{array}{rr}
\mathrm{d} & -\mathrm{b} \\
-\mathrm{c} & \mathrm{a}
\end{array}\right]\)

ii) \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)
Answer:

iii) Find the adjoint and inverse of the matrix \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 1 & 0 \\
3 & 2 & 1
\end{array}\right]\).
Answer:
Find cofactors of elements in the matrix as

iv) \(\left|\begin{array}{lll}
2 & 1 & 2 \\
1 & 0 & 1 \\
2 & 2 & 1
\end{array}\right|\)
Answer:

Question 2.
If A = \(\left[\begin{array}{cc}
\mathrm{a}+\mathrm{i b} & \mathrm{c}+\mathrm{i d} \\
-\mathrm{c}+\mathrm{i d} & \mathrm{a}-\mathrm{i b}
\end{array}\right]\), a² + b² + c² + d² = 1
Answer:
det A = (a + ib) (a – ib) – (c + id) (- c + id)
= (a² – i² b²) – (- c² + i²d²)
= a² + b² + c² + d² (∵ i² = -1)
= 1
Adj A = \(\left[\begin{array}{cc}
a-i b & -c-i d \\
c-i d & a+i b
\end{array}\right]\)
A^-1 = \(\frac{{Adj} A}{{det} A}=\left[\begin{array}{cc}
a-i b & -c-i d \\
c-i d & a+i b
\end{array}\right]\)

Question 3.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), then find (A’)^-1. (Board Model Paper)
Answer:

Question 4.
If A = \(\left[\begin{array}{rrr}
-1 & -2 & -2 \\
2 & 1 & -2 \\
2 & -2 & 1
\end{array}\right]\), then show that the adjoint of A = 3A, find A^-1
Answer:

Question 5.
If abc ≠ 0; find the inverse of \(\left[\begin{array}{lll}
\mathrm{a} & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right]\) (May 2006)
Answer:

II.
Question 1.
If A = \(\left[\begin{array}{lll}
\mathrm{b}+\mathrm{c} & \mathrm{c}-\mathrm{a} & \mathrm{b}-\mathrm{a} \\
\mathrm{c}-\mathrm{b} & \mathrm{c}+\mathrm{a} & \mathrm{a}-\mathrm{b} \\
\mathrm{b}-\mathrm{c} & \mathrm{a}-\mathrm{c} & \mathrm{a}+\mathrm{b}
\end{array}\right]\) and B = \(\frac{1}{2}\left[\begin{array}{lll}
\mathrm{b}+\mathrm{c} & \mathrm{c}-\mathrm{a} & \mathrm{b}-\mathrm{a} \\
\mathrm{c}-\mathrm{b} & \mathrm{c}+\mathrm{a} & \mathrm{a}-\mathrm{b} \\
\mathrm{b}-\mathrm{c} & \mathrm{a}-\mathrm{c} & \mathrm{a}+\mathrm{b}
\end{array}\right]\), then show that ABA^-1 is a diagonal matrix.
Answer:

Question 2.
If 3A = \(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
-2 & 2 & -1
\end{array}\right]\), then show that A^-I = A’.
Answer:

∴ A.A’ = I and by definition A’ = A^-1
similarly A’.A = I

Question 3.
If A = \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\), then show that A^-1 = A³
Answer:

So, the multiplicative inverse of A exists and it is A³.
∴ A^-1 = A³

Question 4.
If AB = I or BA = I, then prove that A is invertible and B = A^-1.
Answer:
Given AB = I
⇒ |AB| = |I|
⇒ |A| |B| = 1
⇒ |A| ≠ 0
∴ A is a non-singular matrix.
Also BA = I
⇒ |B| |A| = |I|
⇒ |A| |B| = 1
⇒ |A| *0
∴ A is a non-singular matrix.
⇒ A is invertible
⇒ A^-1 exists AB = I
⇒ A^-1 AB = A^-1I
⇒ (A^-1 A) B = A^-1I
⇒ IB = A^-1I
⇒ B = A^-1.

Telangana TSBIE TS Inter 1st Year Physics Study Material 6th Lesson పని, శక్తి, సామర్ధ్యం Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 6th Lesson పని, శక్తి, సామర్ధ్యం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బలం వల్ల పని జరగని పరిస్థితులను తెలపండి.
జవాబు:
1) టగ్ ఆఫ్ వార్ పోటీలో ఇద్దరు వ్యక్తులు తాడు మీద సమాన బలం F ప్రయోగిస్తే తాడులోని తన్యత T = F కు సమానము. ఎందుకనగా ఒక వ్యక్తి ప్రయోగించిన బలాన్ని తాడుకు కట్టిన ఆధారంగా భావించాలి. ఆధారం లేని తాడులో మనం తన్యత కలిగించలేము. ఈ స్థితిలో స్థానభ్రంశము S = 0, కావున జరిగిన పని సున్న.

2) బలము F మరియు స్థానభ్రంశము \(\bar{S}\) లు పరస్పర లంబాలైతే ఆ బలం జరిపిన పని W = 0 ఎందుకనగా W = F. \(\bar{S}=|\bar{F}||\bar{S}|\) cos θ. ఇందులో cos 90° = 0.

ప్రశ్న 2.
పని, సామర్థ్యం, శక్తులను నిర్వచించండి. వాటి SI ప్రమాణాలు తెలియచేయండి.
జవాబు:
పని : ఏదైనా బలం వస్తువు మీద పనిచేసి బలప్రయోగ దిశలో దానిని స్థానభ్రంశం చెందించితే బలం పనిచేసింది అంటారు.
పని W = F.S. (F, S లు ఒకే దిశలో ఉంటే) ; లేదా పని W = FS cos θ
శక్తి : పని చేయుటకు కావలసిన దారుఢ్యము లేదా స్థోమతను శక్తి అంటారు. ప్రమాణము జౌల్.
సామర్థ్యము (P) : పని జరిగే రేటును సామర్థ్యము అంటారు.

ప్రశ్న 3.
గతిజ శక్తి, ద్రవ్యవేగాల మధ్య సంబంధాన్ని తెలియచేయండి.
జవాబు:
గతిజశక్తి, ద్రవ్యవేగాల మధ్య సంబంధము :
గతిజశక్తి KE = \(\frac{1}{2}\) mv² ,
ద్రవ్యవేగము P = mv
∴ KE = \(\frac{1}{2} m v^2=\frac{1}{2} \frac{m^2 v^2}{m}=\frac{p^2}{2 m}\)

ప్రశ్న 4.
కింది సందర్భాల్లో బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
ఎ) బకెటు బిగించిన తాడు సహాయంతో బావిలో నుంచి బకెట్ను తీసే సందర్భంలో మనిషి చేసిన పని
బి) పై సందర్భంలో గురుత్వ బలం చేసిన పని
జవాబు:
ఎ) బావి నుండి నీటిని పైకి తోడడంలో మనిషి చేసిన పని ధనాత్మకము. ఎందుకనగా బలం, స్థానభ్రంశము ఒకే దిశలో ఉన్నాయి కావున.

బి) బకెట్ను పైకి లాగునపుడు గురుత్వాకర్షణ బలం చేసిన పని ఋణాత్మకము. ఎందుకనగా గురుత్వాకర్షణ బలం, స్థానభ్రంశం వ్యతిరేక దిశలో ఉన్నాయి కావున.

ప్రశ్న 5.
కింది సందర్భాల్లో ఒక బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
ఎ) ఒక వస్తువు వాలు తలంపై కిందికి జారుతున్నప్పుడు ఘర్షణ చేసిన పని
బి) పై సందర్భంలో గురుత్వ బలం చేసిన పని
జవాబు:
ఎ) వస్తువు క్రిందికి జారునపుడు ఘర్షణ చేసిన పని ఋణాత్మకము. కారణము ఘర్షణ బలం ఎల్లప్పుడూ స్థానభ్రంశానికి వ్యతిరేకము.

బి) కంపిస్తున్న లోలకాన్ని విరామస్థితికి తేవడానికి గాలి నిరోధక బలం చేసిన పని ఋణాత్మకము. కారణం నిరోధక బలం స్థానభ్రంశానికి వ్యతిరేకము.

ప్రశ్న 6.
కింది సందర్భాల్లో ఒక బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
ఎ) ఒక వస్తువు సమవేగంతో ఘర్షణ ఉన్న క్షితిజ సమాంతర తలంపై చలిస్తూ ఉంటే అనువర్తించిన బలం చేసిన పని
బి) కంపిస్తున్న లోలకాన్ని విరామస్థితిలోకి తేవడానికి గాలి నిరోధక బలం చేసే పని
జవాబు:
ఎ) ఘర్షణ బలాన్ని ఎదిరిస్తూ స్థిర వేగంతో వస్తువు చలించడానికి అనువర్తన బలం జరిపిన పని దిశ ధనాత్మకము.
కారణం : అనువర్తిత బలం, వస్తువు స్థానభ్రంశం ఒకే దిశలో ఉన్నాయి.

బి) కంపిస్తున్న లోలకాన్ని సమతాస్థితికి తేవడానికి గాలి నిరోధకబలం చేసిన పని ధనాత్మకము.
కారణం : లోలకంలో F ∝ -x. గాలి నిరోధక బలం బాహ్య బలానికి వ్యతిరేకము కావున గాలి నిరోధక బలం, లోలకం స్థానభ్రంశం ఒకే దిశలో ఉన్నాయి.

ప్రశ్న 7.
కింద ఇచ్చిన వివరణలు సరియైనవా ? కాదా ? మీ సమాధానాలకు కారణాలు ఇవ్వండి.
ఎ) ఏ అంతర్బలాలు, బాహ్య బలాలు పనిచేస్తున్నప్పటికి ఒక వ్యవస్థ మొత్తం శక్తి నిత్యత్వంగా ఉంటుంది.
బి) చంద్రుడు భూమి చుట్టూ ఒక భ్రమణం చేయడానికి భూమి గురుత్వ బలం చేసిన పని శూన్యం.
జవాబు:
ఎ) నిజమే, శక్తినిత్యత్వ నియమము బాహ్య బలాలు మరియు అంతర బలాలకు కూడా వర్తిస్తుంది.
బి) నిజమే, గురుత్వాకర్షణ బలాలు నిత్యత్వ బలాలు కావున ఒక సంవృత పథంలో జరిపిన పని సున్న.

ప్రశ్న 8.
కింది సందర్భాల్లో ఏ భౌతికరాశి స్థిరంగా ఉంటుంది ?
ఎ) స్థితిస్థాపక అభిఘాతంలో
బి) అస్థితిస్థాపక అభిఘాతంలో
జవాబు:
ఎ) స్థితిస్థాపక అభిఘాతాలలో వ్యవస్థ యొక్క మొత్తం, ద్రవ్యవేగము, వ్యవస్థ మొత్తం శక్తి స్థిరము.
బి) అస్థితిస్థాపక అభిఘాతాలలో వ్యవస్థ యొక్క మొత్తం ద్రవ్యవేగము స్థిరము.

ప్రశ్న 9.
‘h’ ఎత్తు నుంచి స్వేచ్ఛగా కిందకు పడిన ఒక వస్తువు చదునైన నేలను తాకిన తరువాత h/2 ఎత్తుకు పైకి లేస్తే ఆ వస్తువుకు, నేలకు మధ్య ప్రత్యావస్థాన గుణకం ఎంత ?
జవాబు:
వస్తువు h, ఎత్తు నుండి కిందపడి h, ఎత్తు పైకి లేస్తే ప్రత్యవస్థాన గుణకం
e = \(\sqrt{\frac{\mathrm{h}_2}{\mathrm{~h}_1}}\) కాని h₂ = \(\frac{\mathrm{h}_1}{2}\)
∴ e = \(\sqrt{\frac{1}{1 / 2}}=\frac{1}{\sqrt{2}}\)

ప్రశ్న 10.
స్వేచ్ఛగా కొంత ఎత్తు నుంచి భూమిపై పడ్డ వస్తువు అనేకసార్లు అదేచోట పడి లేచిన తరువాత అభిఘాతాలు ఆగిపోయే లోపు దాని మొత్తం స్థానభ్రంశం ఎంత ? వస్తువుకు, భూమికి మధ్య ప్రత్యావస్థాన గుణకం ‘e’ అనుకోండి.
జవాబు:
కొంత ఎత్తు (h) నుండి జారవిడిచిన వస్తువు అనేకసార్లు భూమితో అభిఘాతాలు జరిపి పైకి లేచి మరల, మరల క్రింద పడి ఆగిపోవు లోపల దాని మొత్తం స్థానభ్రంశం దాని తొలి ఎత్తు (h) కి సమానము.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
స్థితిజ శక్తి అంటే ఏమిటి ? గురుత్వ స్థితిజ శక్తికి సమాసాన్ని రాబట్టండి.
జవాబు:
స్థితిజశక్తి : ఏదైనా వస్తువుకు దాని స్థానం వలన కొంత శక్తి సంప్రాప్తిస్తే దానిని స్థితిశక్తి అంటారు.
ఉదా : కొంత ఎత్తులో గల వస్తువులు, చుట్టబడిన గడియారపు స్ప్రింగ్.

స్థితిశక్తికి సమీకరణం ఉత్పాదించుట : m ద్రవ్యరాశి గల ఒక వస్తువును గురుత్వాకర్షణ బలానికి వ్యతిరేకంగా h ఎత్తు పైకి జరిపినామనుకొనుము. వస్తువును పైకి జరుపుటలో చేసిన పని
W = F.S = maS.
కాని a = – g కావున W =-mgh (- గుర్తు వ్యతిరేక దిశ వల్ల) వస్తువును పైకి ఎత్తుటలో జరిపిన పని వస్తువులో స్థితిశక్తిగా నిలువ ఉంటుంది.

∴ వస్తువులో గల స్థితిశక్తి_P.E. = mgh.

ప్రశ్న 2.
ఒకే ద్రవ్యవేగం కలిగి ఉన్న ఒక లారీ, కార్లను విరామస్థితికి తీసుకొని రావడానికి ఒకే బ్రేక్ బలాన్ని ఉపయోగించారు. ఏ వాహనం తక్కువ కాలంలో విరామ స్థితికి వస్తుంది ? ఏ వాహనం తక్కువ దూరంలో ఆగుతుంది ?
జవాబు:
ద్రవ్యవేగము : P = mv. ఇది లారీ మరియు కారులకు సమానము.
గతిశక్తి K.E. మరియు ద్రవ్యవేగము P ల మధ్య సంబంధము : K.E. = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)
వస్తువును ఆపుటలో జరిపిన పని W = గతిజ శక్తులలోని భేదము
∴ F.S.= \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\) లేదా ఆగుటకు ముందు వస్తువు కదిలిన దూరము S = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)
ఈ సందర్భంలో \(\overline{\mathrm{P}}\) మరియు \(\overline{\mathrm{F}}\) లు సమానము కావున ms స్థిరము అనగా తక్కువ బరువు గల వస్తువు ఎక్కువ దూరం వెళ్ళి ఆగుతుంది.
∴ లారీ తక్కువ దూరం ప్రయాణించి ఆగుతుంది. కారు ఎక్కువ దూరం ప్రయాణించి ఆగుతుంది.

ప్రశ్న 3.
నిత్యత్వ, అనిత్యత్వ బలాల మధ్య తేడాలను రాయండి. వాటికి ఒక్కొక్క ఉదాహరణ కూడా రాయండి.
జవాబు:
నిత్యత్వ బలాలు (Conservative forces) : ఏ సంవృతపథం వెంబడి ఐనా వస్తువు మీడ బలం చేసిన పని మొత్తం విలువ సున్న ఐతే అటువంటి బలాలను నిత్యత్వ బలాలు అంటారు.

ఉదా :

1. ఏదైనా వస్తువును నిట్టనిలువుగా పైకి విసిరినపుడు అది తిరిగి విసిరిన బిందువును చేరేసరికి దాని గతిజశక్తిలో మార్పు సున్న. కావున పని-శక్తి సిద్ధాంతం ప్రకారము జరిగిన పని సున్న.
2. విద్యుత్ క్షేత్రంలో Q అను ఆవేశాన్ని ఒక సంవృత పథంలో జరిపితే దానిపై చేసిన మొత్తం పని సున్న.

అనిత్యత్వ బలాలు (Non-conservative forces) : ఏదైనా సంవృత పథం వెంబడి వస్తువు మీద బలం చేసిన మొత్తం పని విలువ సున్న కాకపోతే అటువంటి బలాలను అనిత్యత్వ బలాలు అంటారు. అనిత్యత్వ బలాల వల్ల వస్తువును సంవృత పథంలో జరిపినప్పటికి మొత్తం పని సున్న కాదు.

ఉదా : వస్తువుల చలనానికి వ్యతిరేకంగా ఘర్షణ బలాలు జరిపిన పని. అనిత్యత్వ బలం వల్ల వస్తువుపై జరిపిన పని వస్తువు ప్రయాణించిన మార్గంపై ఆధారపడుతుంది. వస్తువును ఏ దిశలో కదిల్చినప్పటికి ఘర్షణ బలం వల్ల కొంత పని వ్యర్థమవుతుంది. వస్తువును ఘర్షణ బలానికి వ్యతిరేకంగా సంవృతపథంలో జరిపినప్పటికి మొత్తం పని సున్న కాదు. కావున ఘర్షణ బలాలు అనిత్యత్వ బలాలు.

ప్రశ్న 4.
ఏకమితీయ స్థితిస్థాపక అభిఘాతంలో అభిఘాతానికి ముందు రెండు వస్తువుల అభిగమన సాపేక్ష వేగం అభిఘాతం తరువాత వాటి నిగమన సాపేక్ష వేగానికి సమానం అని చూపండి.
జవాబు:
m₁, m₂ ద్రవ్యరాశులు గల రెండు వస్తువులు u₁, u₂. అను వేగాలతో ఒకే సరళరేఖ వెంబడి చలిస్తూ ముఖాముఖి స్థితిస్థాపక అభిఘాతం చెందినవనుకొనుము.
అభిఘాతం పిమ్మట వాటి వేగాలు v₁, v₂ అనుకొనుము.
స్థితిస్థాపక అభిఘాతాలు ద్రవ్యవేగ నిత్యత్వనియమాన్ని, గతిజశక్తి నిత్యత్వనియమాన్ని పాటిస్తాయి.

ద్రవ్యవేగ నిత్యత్వనియమం ప్రకారము
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ లేదా m₁ (u₁ – v₁) = m₂ ( v₂ – u₂) …………… (1)
శక్తి నిత్యత్వనియమం ప్రకారము
\(\frac{1}{2}\)m₁u₁² + \(\frac{1}{2}\) m₂u₂² = \(\frac{1}{2}\)m₁v₁² + \(\frac{1}{2}\)m₂v₂² లేదా m₁ (u₁² – v₁²) = m₂ (v₂² – u₂²) …………. (2)
2వ సమీకరణాన్ని 1వ సమీకరణంచే భాగించగా
\(\frac{u_1^2-v_1^2}{u_1-v_1}=\frac{v_2^2-u_2^2}{v_2-u_2}\) లేదా \(\frac{\left(u_1-v_1\right)\left(u_1+v_1\right)}{\left(u_1-v_1\right)}=\frac{\left(v_2-u_2\right)\left(v_2+u_2\right)}{\left(v_2-u_2\right)}\)
u₁ + v₁ = v₂ + u₂ లేదా u₁ – u₂ = v₂ – v₁ …………….. (3)
అనగా అభిఘాతానికి ముందు వస్తువులు సమీపించు సాపేక్ష వేగము, అభిఘాతం పిమ్మట వస్తువులు విడిపోవు సాపేక్ష వేగమునకు సమానము అని నిరూపించబడినది.

ప్రశ్న 5.
రెండు సమాన ద్రవ్యరాశులు ఏటవాలు స్థితిస్థాపక అభిఘాతం చెందినప్పుడు అభిఘాతం తరువాత అవి ఒకదానికొకటి లంబంగా చలిస్తాయని చూపండి.
జవాబు:
రెండు సమాన ద్రవ్యరాశులు (m, m) కల వస్తువులు ఏటవాలు స్థితిస్థాపక అభిఘాతం చెందాయి అనుకోండి. మొదట వస్తువు ‘u’ అను తొలివేగంతో చలిస్తూ నిశ్చల స్థితిలో ఉన్న రెండవ వస్తువును ఢీకొన్నది అనుకోండి. అభిఘాతం పిమ్మట ఆ రెండు వస్తువులు X – అక్షంతో θ₁ మరియు θ₂ కోణాలతో చలిస్తే స్థితిస్థాపక అభిఘాతాలు ద్రవ్యవేగ నిత్యత్వనియమాన్ని పాటిస్తాయి. కావున X – అక్షం వెంబడి

mu = mv₁ cos θ₁ + mv₂ cos θ₂ లేదా
u= v₁ cos θ₁ + v₂ cos θ₂ …………….. (1)
ఇదే విధంగా y-అక్షం వెంబడి
0 = v₁ sin θ₁ – v₂ sin θ₂ ………… (2) (ఎందుకనగా y దిశలో తొలివేగం సున్న)
సమీ. (1) మరియు (2) లను వర్గీకరించి కలుపగా
u² = v₁² + v₂² + 2v₁v₂ cos (θ₁ + θ₂) ……….. (3)
స్థితిస్థాపక అభిఘాతాలు శక్తి నిత్యత్వనియమాన్ని పాటిస్తాయి.
∴ \(\frac{1}{2}\)mu² = \(\frac{1}{2}\)mv₁² + \(\frac{1}{2}\)mv₂² లేదా . u² = v₁² + v₂² ……………… (4)
3, 4 సమీకరణాల నుండి 2 v₁, v₂ cos (θ₁ + θ₂) = 0
కాని v₁, v₂ లు సున్న కాదు కావున cos (θ₁ + θ₂) = 0
cos (θ₁ + θ₂) = 0 అనగా θ₁ + θ₂ = 90°
కావున సమాన ద్రవ్యరాశులు గల వస్తువులు కొంత కోణంతో అభిఘాతం చెందితే అభిఘాతం పిమ్మట అవి పరస్పర లంబ దిశలలో విడిపోతాయి.

ప్రశ్న 6.
కొంత ఎత్తు నుంచి స్వేచ్ఛగా కిందికి పడిన వస్తువు భూమితో ‘n’ అభిఘాతాలు చెందిన తరువాత అది పొందిన ఎత్తుకు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
ఏదైనా బంతిని ‘h’ ఎత్తు నుండి భూమి మీదకు జారవిడిచినామనుకొనుము. భూమిని ఢీకొన్న తరువాత అది మరల ‘h₁‘ అన్న ఎత్తు పైకి లేచినది అనుకొనుము.
భూమిని తాకుటకు ముందు వేగము u₁ = \(\sqrt{2 \mathrm{gh}}\)
మొదటి అభిఘాతం తరువాత విడిపోవు వేగము v₁ = \(\sqrt{2 \mathrm{gh}_1}\)
అభిఘాతం ముందు, అభిఘాతం తరువాత భూమి వేగము సున్న.
కావున u₂ = 0 మరియు v₂ = 0

∴ h₁ = e²h
∴ మొదటిసారి అభిఘాతం వల్ల పైకి లేచిన ఎత్తు h₁ = e²h
2వ సారి అభిఘాతం వల్ల పైకి లేచిన ఎత్తు h₂ = e²h₁ = e²e²h = e⁴h
3వ సారి అభిఘాతం వల్ల పైకి లేచిన ఎత్తు h₃ = e²h₂ = e²e⁴h = e⁶h
∴ nవ సారి అభిఘాతం వల్ల పైకి లేచిన ఎత్తు h_n = e²ⁿh.

ప్రశ్న 7.
శక్తి నిత్యత్వ నియమాన్ని వివరించండి.
జవాబు:
“ఏదైనా వ్యవస్థపై పనిచేసే బలాలు నిత్యత్వ బలాలు ఐతే వ్యవస్థకు గల మొత్తం శక్తి (స్థితిజ శక్తి + గతిజ శక్తి) స్థిరము. దీనిని సృష్టించడం కాని, నాశనం చేయడంగాని సాధ్యపడదు.”

వివరణ : ఒక వస్తువు నిత్యత్వ బలాల వల్ల ∆x అను స్వల్ప దూరం స్థానభ్రంశం పొందింది అనుకోండి. పని-శక్తి సిద్ధాంతం ప్రకారము KE లో మార్పు = జరిగిన పని
∴ ∆KE = F(x). ∆x ……………….. (1) కాని స్థితిజ శక్తిలో మార్పు
∆V = – F(x) . ∆x ………………… (2)
1, 2 సమీకరణాల నుండి ∆K – ∆V లేదా
∆K + ∆V = 0. అనగా మొత్తం శక్తిలో మార్పు సున్న.
కావున వ్యవస్థకు గల మొత్తం గతిజశక్తి KE మరియు స్థితిజశక్తి PE స్థిరము. కావున శక్తి నిత్యత్వ నియమము నిరూపించబడినది.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1
పని, గతిజశక్తి భావనలను అభివృద్ధి పరచి ఇది పని శక్తి సిద్ధాంతానికి దారితీస్తుందని చూపండి. (మార్చి 2014)
జవాబు:
స్థితిజశక్తి:
పని : ఏదైనా బలం వస్తువు మీద పనిచేసి బలప్రయోగ దిశలో దానిని స్థానభ్రంశం చెందించితే బలం పనిచేసింది అంటారు.
పని W = F.S. (F. S లు ఒకే దిశలో ఉంటే)
లేదా పని W = FS cos θ (‘θ’ బలము F మరియు స్థానభ్రంశము S ల మధ్యకోణము. సదిశలలో పనిని
W = \(\overline{\mathrm{F}} . \overline{\mathrm{S}}\) = FS cos θ గా చెపుతారు. పని అదిశరాశి ప్రమాణము కి.గ్రా.మీ²/సె² దీనిని జౌల్ (J) అంటారు.
గతిజశక్తి : వస్తువులు చలనంలో ఉండటం వల్ల వాటికి సంప్రాప్తించే శక్తిని గతిజశక్తి అంటారు. గతిజశక్తి KE = \(\frac{1}{2}\) mv²
ఉదా : గమనంలో ఉన్న అన్ని వస్తువులకు గతిజశక్తి ఉంటుంది.

ఎ) గతిజశక్తి = \(\frac{1}{2}\) mv² ఉత్పాదన :
m ద్రవ్యరాశి గల వస్తువు వేగంతో గమనంలో ఉందనుకుందాము. గమనానికి వ్యతిరేకంగా F బలం వస్తువుపై ప్రయోగించినపుడు ఆ వస్తువు S దూరం ప్రయాణం చేసి విరామస్థితికి వచ్చిందనుకుందాము.
తొలివేగము u = v, తుది వేగము V = 0, ప్రయాణించిన దూరము = S

v² – u² = 2aS అను సమీకరణం నుండి
∴ 0 – v² = 2as
∴ త్వరణము a = \(\frac{-v^2}{2 s}\)
∴ నిరోధక బలం F = ma = \(\frac{m v^2}{2 \mathrm{~s}}\)
∴ వస్తువును విరామస్థితికి తేవడానికి జరిగిన పని W = FS
∴ W = \(\frac{m v^2}{2 s} \times \mathrm{S}=\frac{1}{2} m v^2\)
వస్తువును ఆపడానికి చేసిన పని ఆ వస్తువులో గల గతిజశక్తికి సమానము.
∴ గతిజశక్తి = \(\frac{1}{2}\) mv²
పని-శక్తి సిద్ధాంతం: “ఒక నిత్యత్వ ఫలితబలం వస్తువుపై పనిచేయునపుడు ఆ వస్తువుపై జరిగిన పని దాని గతిజశక్తిలోని మార్పునకు సమానం.”

నిరూపణ : m ద్రవ్యరాశి గల వస్తువుపై F బలం ప్రయోగించినపుడు దాని వేగం u నుంచి v కి మారిందనుకుందాము. వేగం U నుండి V కి మారునంతలో వస్తువు స్థానభ్రంశం S అనుకుందాము.
తొలివేగము = u, తుదివేగము = v, స్థానభ్రంశము = S కాని స్థానభ్రంశము = S = సగటు వేగం × కాలం
∴ S = \(\frac{(u+v)}{2}\)t, త్వరణం = \(\frac{v-u}{t}\) = a
వస్తువుపై బలం, F= = ma = m\(\left(\frac{v-u}{t}\right)\)
∴ వస్తువుపై జరిగిన పని W = FS
∴ W = m\(\frac{(v-u)}{t} \cdot \frac{(u+v)}{2} t=m \frac{\left(v^2-u^2\right)}{2}=\frac{1}{2} m v^2-\frac{1}{2} m u^2\) = KE₂ – KE₁
అంటే, వస్తువుపై జరిగిన పని వస్తువు గతిజశక్తిలోని మార్పుకి సమానం.

ప్రశ్న 2.
అభిఘాతాలు అంటే ఏమిటి ? వాటిలో సాధ్యమయ్యే రకాలను వివరించండి. ఏకమితీయ స్థితిస్థాపక అభిఘాతాల సిద్ధాంతాన్ని వివరించండి. (మే 2014)
జవాబు:
అభిఘాతాలు (Collisions) : గమనంలో ఉన్న వస్తువు మరొక వస్తువును ఢీకొన్నపుడు దాని శక్తిలో మార్పులు సంభవిస్తాయి. ఈ రకమైన భౌతిక ప్రక్రియను అభిఘాతాలు అంటారు. ఇవి రెండు రకాలు. 1) స్థితిస్థాపక అభిఘాతము 2) అస్థితిస్థాపక అభిఘాతము.

స్థితిస్థాపక అభిఘాతాలు : స్థితిస్థాపక అభిఘాతాలు 1) ద్రవ్యవేగ నిత్యత్వ నియమాన్ని 2) శక్తి నిత్యత్వ నియమాన్ని పాటిస్తాయి. ఇటువంటి అభిఘాతాలలో శక్తి నష్టము ఉండదు.

అస్థితిస్థాపక అభిఘాతాలు: ఈ రకమైన అభిఘాతాలు ద్రవ్యవేగ నిత్యత్వ నియమాన్ని మాత్రమే పాటిస్తాయి. ఈ విధమైన అభిఘాతాలలో శక్తి నష్టం ఉంటుంది.

స్థితిస్థాపక అభిఘాతానికి గురైన రెండు వస్తువుల తుది వేగాలకు సమీకరణాలు :
m₁, m₂ ద్రవ్యరాశులు గల రెండు వస్తువులు u₁, u₂ అను వేగాలతో ఒకే సరళరేఖ వెంబడి చలిస్తూ ముఖాముఖి స్థితిస్థాపక అభిఘాతం చెందినవనుకొనుము.
అభిఘాతం పిమ్మట వాటి వేగాలు v₁, v₂ అనుకొనుము.
స్థితిస్థాపక అభిఘాతాలు ద్రవ్యవేగ నిత్యత్వనియమాన్ని, గతిజశక్తి నిత్యత్వనియమాన్ని పాటిస్తాయి.

ద్రవ్యవేగ నిత్యత్వనియమం ప్రకారము
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ లేదా m₁ (u₁ – v₁) = m₂ (v₂ – u₂) ……………….. (1)
శక్తి నిత్యత్వనియమం ప్రకారము
\(\frac{1}{2}\)m₁u₁² + \(\frac{1}{2}\) m₂u₂² = \(\frac{1}{2}\)m₁v₁² + \(\frac{1}{2}\)m₂v₂² లేదా m₁ (u₁² – v₁²) = m₂ (v₂² – u₂²) …………. (2)
2వ సమీకరణాన్ని 1వ సమీకరణంచే భాగించగా
\(\frac{u_1^2-v_1^2}{u_1-v_1}=\frac{v_2^2-u_2^2}{v_2-u_2}\) లేదా \(\frac{\left(u_1-v_1\right)\left(u_1+v_1\right)}{\left(u_1-v_1\right)}=\frac{\left(v_2-u_2\right)\left(v_2+u_2\right)}{\left(v_2-u_2\right)}\)
u₁ + v₁ = v₂ + u₂ లేదా u₁ – u₂ = v₂ – v₁ …………….. (3)
అనగా అభిఘాతానికి ముందు వస్తువులు సమీపించు సాపేక్ష వేగము, అభిఘాతం పిమ్మట వస్తువులు విడిపోవు సాపేక్ష వేగమునకు సమానము. అనగా వాటి ప్రత్యవస్థాన గుణకము e = 1 కి సమానము.
v₁ విలువ కనుక్కోవడానికి v₂ = u₁ – u₂ + v₁ ను సమీకరణం (1) లో ప్రతిక్షేపించగా
m₁u₁ + m₂u₂ = m₁v₁ + m₂( u₁ – u₂ + v₁)
∴ m₁u₁ + m₂u₁ = m₁v₁ + m₂u₁ – m₂u₂ + m₂v₁
m₁u₁ + m₂u₂ – m₂u₁ + m₂u₂ = v₁ (m₁ + m₂ )
∴ u₁ ( m₁ – m₂) + 2 m₂u₂ = v₁ (m₁ + m₂ )
∴ మొదటి వస్తువు తుదివేగము v₁ = \(\frac{\mathrm{u}_1\left(\mathrm{~m}_1-\mathrm{m}_2\right)}{\mathrm{m}_1+\mathrm{m}_2}+\frac{2 \mathrm{~m}_2 \mathrm{u}_2}{\mathrm{~m}_1+\mathrm{m}_2}\) ……………… (4)
ఇదేవిధంగా v₂ కనుక్కోవడానికి v₁ = v₂ – u₁ + u₂ ను సమీకరణం (1) లో ప్రతిక్షేపించగా
రెండవ వస్తువు తుదివేగము v₂ = \(\frac{\mathrm{u}_2\left(\mathrm{~m}_2-\mathrm{m}_1\right)}{\mathrm{m}_1+\mathrm{m}_2}+\frac{2 \mathrm{~m}_1 \mathrm{u}_1}{\mathrm{~m}_1+\mathrm{m}_2}\) …………….. (5)

ప్రశ్న 3.
శక్తినిత్యత్వ నియమాన్ని తెలిపి, స్వేచ్ఛగా కిందికి పడే వస్తువు విషయంలో దీనిని నిరూపించండి.
గమనిక : ఈ ప్రశ్న తెలుగుమీడియం టెక్స్ట్బుక్లో లేదు. కాని ఇంగ్లీషు మీడియంలో ఉంది. అందువలన ఈ ప్రశ్నను అదనంగా ఇవ్వడం జరిగింది. సౌలభ్యం కోసం పాత టెక్స్ట్బుక్ విధానంలో వివరించటం జరిగింది.
జవాబు:
శక్తినిత్యత్వ నియమము : శక్తిని సృష్టించడము కాని, నాశనం చేయడము కాని చేయలేము. కాని శక్తిని ఒక రూపం నుండి మరొక రూపానికి మార్చవచ్చును.

స్వేచ్ఛగా క్రిందికి పడుచున్న వస్తువు విషయంలో శక్తి నిత్యత్వ సూత్రం నిరూపించుట :
m ద్రవ్యరాశి గల వస్తువు h ఎత్తులో ఉన్న A బిందువు నుండి
స్వేచ్ఛగా జారవిడచినామనుకొనుము.
1) A బిందువు వద్ద అనగా వస్తువును జారవిడచిన క్షణంలో
A వద్ద భూమి నుండి ఎత్తు = h; ∴ స్థితిశక్తి = mgh
వేగము u = 0 గతిజశక్తి = 0 (u = 0 కనుక)
∴ A వద్ద మొత్తం శక్తి = స్థితిశక్తి + గతిజశక్తి
= mgh + 0 = mgh ……………….. (1)

2) B బిందువు వద్ద అనగా భూమి నుండి ‘x’ ఎత్తులో ఉన్నపుడు
B వద్ద, వేగం v₁ అనుకుందాము. A నుండి B కి క్రిందకి పడిన దూరం = x.
v² – u² = 2as కనుక v₁² – 0 = 2gx; . v₁² = 2gx
∴ B వద్ద గతిజశక్తి = \(\frac{1}{2}\) mv₁² = \(\frac{1}{2}\) m 2gx = mgx
B నేలనుండి (h – x) ఎత్తులో ఉంది. ∴ B వద్ద స్థితిశక్తి = mg(h-x)
∴ B వద్ద మొత్తం శక్తి = స్థితిశక్తి + గతిజశక్తి = mg (h – x) + mgx
= mgh ……………… (2)

3) C బిందువు వద్ద అనగా భూమిని తాకబోవు క్షణంలో C వద్ద, అది నేలను చేరింది కనుక h = 0
∴ స్థితిశక్తి = mg (h) = 0;
C వద్ద వేగం V అనుకుంటే, v² – u² = 2 as నుండి
v² – 0 = 2gh; ∴ v² = 2gh;
∴ గతిజశక్తి = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) m (2gh) = mgh
∴ C వద్ద మొత్తం శక్తి = స్థితిశక్తి + గతిజశక్తి = 0 + mgh = mgh ……………….. (3)
పై సమీకరణముల నుండి వస్తువు ఏ స్థానంలో ఉన్నా మొత్తం శక్తి స్థిరంగా ఉంటుంది. కాని తొలి స్థితిశక్తి అంతా నేలను చేరునపుడు గతిజశక్తిగా మారింది. మార్గమధ్యంలో వస్తువుకు కొంత స్థితిశక్తి, కొంత గతిశక్తి ఉంది కాని మొత్తం శక్తి స్థిరము. అనగా శక్తి నిత్యత్వనియమం నిరూపించబడినది.

లెక్కలు

ప్రశ్న 1.
10 గ్రా. ద్రవ్యరాశి కలిగిన పరీక్ష నాళికలో కొంత ఈథర్ ఉంది. ఈ పరీక్షనాళికను 1 గ్రా. ద్రవ్యరాశి కలిగిన కార్లో మూయడమైంది. పరీక్షనాళికను వేడిచేసినప్పుడు ఈథర్ వాయువు కలిగించే పీడనం వల్ల కార్క్ ఎగిరిపోతుంది. 5 సెం.మీ. పొడవు ఉన్న దృఢమైన భారరహిత కడ్డీ నుంచి ఈ పరీక్ష నాళికను క్షితిజ సమాంతరంగా వేలాడదీశారు. పరీక్షనాళిక ౧ బిందువు పరంగా నిలువు వృత్తంలో తిరగాలంటే ఎంత కనీస వేగంతో కార్క్ పరీక్షనాళిక నుంచి ఎగిరిపోవాలి ? (ఈథర్ ద్రవ్యరాశిని పరిగణనలోనికి తీసుకోవద్దు)
సాధన:
కడ్డీ పొడవు ! = 5 సెం.మీ. = \(\frac{5}{100}\) మీ.;
g = 10 మీ/సె²
పరీక్ష నాళిక నుండి కార్క్ బయటకు రాకూడదు అంటే అపకేంద్ర బలం పూర్తిగా అభికేంద్రబలం వల్ల రద్దు కావాలి. ఈ స్థితిలో నిమ్నతమ బిందువు వద్ద కనీస వేగము v = \(\sqrt{5 g l}\) . ఇది కార్క్ బయటకు రాకుండా ఉండగల గరిష్ఠ వేగము
∴ V = \(\sqrt{5 \times \frac{5}{100} \times 10}=\frac{5}{10} \sqrt{10} \mathrm{~m} / \mathrm{s}=0.5 \sqrt{10}\) మీ/సె.

ప్రశ్న 2.
ఒక మర తుపాకి నిమిషానికి 360 బుల్లెట్లు పేల్చగలదు. వెలువడే ప్రతి బుల్లెట్ వేగం 600 మీ/సె^-1. ప్రతి బుల్లెట్ ద్రవ్యరాశి 5 గ్రా. అయితే మరతుపాకి సామర్థ్యం ఎంత ? (మార్చి 2014)
సాధన:
బుల్లెట్ల సంఖ్య n = 360;
కాలము = t = 1 ని = 60 సె.
బుల్లెట్ వేగము v = 600 మీ/సె ;
బుల్లెట్ ద్రవ్యరాశి m = 5 గ్రా= 5 × 10^-3 కి.గ్రా.

ప్రశ్న 3.
8 మీ. లోతు ఉన్న బావి నుంచి గంటకు 3425 మీ” నీటిని పైకి తోడుతున్నప్పుడు అశ్వసామర్థ్యంలో 40% వృధా అయితే ఇంజను సామర్ధ్యాన్ని అశ్వసామర్థ్యాలలో రాబట్టండి.
సాధన:
తోడబడిన నీటి ఘనపరిమాణము v = 3425 మీ³
∴ పైకి తోడిన నీటి ద్రవ్యరాశి m = 3425 × 10³ కి.గ్రా.
(1m³ నీటి ద్రవ్యరాశి = 10³ కి.గ్రా.)
బావిలోతు d = 8 మీ.; కాలము t = 1 గం = 60 × 60 = 3600 సె.
వ్యర్థమైన సామర్థ్యము = 40%
∴ ఉపయోగపడిన సామర్థ్యము η = 60%
వాస్తవంగా జరిగిన పని W = mgh = 3425 × 10³ × 10 × 8 = 897000 జౌల్
యంత్రము మొత్తం సామర్థ్యము = \(\frac{\mathrm{W}}{\mathrm{t}} \times \frac{100}{\eta}=\frac{897000 \times 100}{3600 \times 60}\)
= 124315 వాట్, కాని 1 అశ్వ సామర్థ్యము = 746 వాట్
∴ P = \(\frac{124315}{746}\) = 166.6 H.P

ప్రశ్న 4.
ఒక పంపు 25 మీ. లోతు ఉన్న బావి నుంచి నిమిషానికి 600 కి.గ్రా.ల నీటిని పైకి తోడి 50 మీ/సె^-1 వడితో బయటకు వదలాలి. దీనికి అవసరమయ్యే సామర్థ్యాన్ని లెక్కించండి.
సాధన:
ద్రవ్యరాశి m = 600 కి.గ్రా.
కాలము t = 1ని = 60 సె.
లోతు d = 25 మీ.
నీటి వేగము v = 50 మీ/సె

నీటి గతిజశక్తి KE = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) 600 × 50 × 50 = 750000
స్థితిశక్తిలో మార్పు = నీటిని తోడడంలో జరిగినప పని = mgh
= 600 × 9.8 × 25 = 147000
మొత్తం పని W = 147000 + 75000 = 897000 జౌల్
యంత్రం సామర్థ్యము P = \(\frac{\mathrm{W}}{\mathrm{t}}=\frac{897000}{60}\) = 14950 = 14.95 కి.వా.

ప్రశ్న 5.
తొలుత నిశ్చల స్థితిలో ఉండి మూల బిందువు నుంచి బయలుదేరిన 5 కి.గ్రా. ద్రవ్యరాశి ఉన్న దిమ్మెపై ధన X-అక్షఁ వెంట F = (20 + 5x) N అనే బలం పనిచేస్తుంది. దిమ్మె x = 0 నుంచి x = 4m కు స్థానభ్రంశం చెందినపుడు ఆ బలఁ చేసిన పనిని లెక్కించండి.
సాధన:
దిమ్మె ద్రవ్యరాశి m = 5 కి.గ్రా.;
దిమ్మెపై బలం F = (20 + 5x) న్యూ
వస్తువును ‘0’ నుండి ‘4’ మీటర్ల వరకు స్థానభ్రంశం చెందించడంలో జరిగిన పని
W = \(\int \mathrm{dW}=\int_{\mathrm{x}=0}^{\mathrm{x}=4} \mathrm{~F}(\mathrm{x}) \cdot \mathrm{dx}=\int_{\mathrm{x}=0}^4(20+5 \mathrm{x}) \mathrm{dx}=\left[20 \mathrm{x}+\frac{5 \mathrm{x}^2}{2}\right]_0^4=80+\frac{5 \times 4 \times 4}{2}\)
= 80 + 40 = 120 జౌల్

ప్రశ్న 6.
పటంలో చూపినట్లు 5 కి.గ్రా. ద్రవ్యరాశి ఉన్న దిమ్మె ఘర్షణ లేని వాలుతలంపై నుంచి జారుతుంది. వాలు తలం అడుగు భాగాన 600 N/m బల స్థిరాంకం కలిగిన స్ప్రింగ్ను ఏర్పాటు చేశారు. దిమ్మె వేగం గరిష్ఠమయిన క్షణంలో స్ప్రింగ్లో కలిగే సంపీడనాన్ని కనుక్కోండి.

సాధన:
దిమ్మె ద్రవ్యరాశి m = 5 కి.గ్రా. ;
బల స్థిరాంకము K = 600 న్యూ.
పటం నుండి sin θ = \(\frac{3}{5}\)
వాలుతలం వెంబడి బలం F = mg sinθ
∴ F = 5 × 10 × \(\frac{3}{5}\)
= 30 న్యూ
బల స్థిరాంకము K \(\frac{\mathrm{F}}{\mathrm{K}}\)
x = \(\frac{\mathrm{F}}{\mathrm{K}}=\frac{30}{600}\) = 0.05 మీ. = 5 సెం.మీ.

ప్రశ్న 7.
X-అక్షం వెంట ఒక కణంపై F = –\(\frac{K}{x^2}\) (x ≠ 0) బలం పనిచేస్తుంది. కణం x = +a నుంచి x = + 2a కి స్థానభ్రంశం చెందినప్పుడు బలం చేసిన పనిని కనుక్కోండి. K ని ధన స్థిరాంకంగా తీసుకోండి.
సాధన:
ఇచ్చిన కణంపై బలము F = \(\frac{K}{x^2}\)
వస్తువు స్థానభ్రంశము = + a నుండి + 2a వరకు

ప్రశ్న 8.
ఒక కణంపై పనిచేసే బలం F, కణ స్థానం x తో గ్రాఫ్లో చూపించిన విధంగా మారుతుంది. x = -4 నుంచి x = + 2 కి కణం స్థానభ్రంశం చెందినపుడు బలం చేసిన పనిని కనుక్కోండి.

సాధన:
ఇచ్చిన కణంపై పనిచేయు సగటు బలము F = \(\frac{-\mathrm{b}+2 \mathrm{~b}}{2}=\frac{\mathrm{b}}{2}\)
వస్తువు స్థానభ్రంశము = – a నుండి + 2a వరకు
జరిగిన పని W = \(\int\) F dx
= \(\int_{x=-a}^{x=2 a} \frac{b}{2} d x=\frac{b}{2}[x]_{-a}^{2 a}\)
∴ W = \(\frac{\mathrm{b}}{2}\)(2a – (-a) = \(\frac{\mathrm{b}}{2}\) (3a) = \(\frac{3}{2}\) ab

ప్రశ్న 9.
ఒక బంతిని 20 మీ. ఎత్తు నుంచి క్షితిజ సమాంతర నేల మీదకు 20 మీ/సె తొలి వేగంతో కిందికి విసిరారు. నేలను తాకిన తరువాత బంతి అంతే ఎత్తుకు పైకిలేచింది. ఈ అభిఘాతంలో బంతికి, నేలకు మధ్య ప్రత్యావస్థాన గుణకం కనుక్కోండి. (g = 10 మీ/సె²)
సాధన:
తొలి వేగము u₁ = 20 మీ/సె. ;
ఎత్తు h = 20 మీ. ;
g = 10 మీ/సె²
నేలను సమీపించు వేగము u² = u₁² + 2gh
= 202 + 2 × 20 × 10
= 400 + 400
∴ u = \(\sqrt{800}\) = 20\(\sqrt{2}\)
పైకి లేచిన ఎత్తు h = 20 మీ.
∴ నేలను విడిపోవు వేగము v = \(\sqrt{2 \mathrm{gh}}=\sqrt{2 \times 10 \times 20}=\sqrt{400}\) = 20 మీ/సె.
ప్రత్యవస్థాన గుణకము

ప్రశ్న 10.
స్వేచ్ఛగా 10 మీ. ఎత్తు నుంచి దృఢమైన క్షితిజ సమాంతర తలంపై పడిన బంతి అనేకసార్లు అదేచోట పడిలేచిన తరువాత నిశ్చల స్థితికి వచ్చేలోగా బంతి ప్రయాణించిన మొత్తం దూరం ఎంత ? బంతికి, తలానికి మధ్య ప్రత్యావస్థాన గుణకం \(\frac{1}{\sqrt{2}}\) అనుకోండి.
సాధన:
బంతిని జారవిడచిన స్థానం ఎత్తు h = 20 మీ.
బంతి ప్రత్యవస్థాన గుణకము e = \(\frac{1}{\sqrt{2}}\)
బంతి ఆగిపోవు లోపల దాని మొత్తం స్థానభ్రంశము d
d = h \(\left[\frac{\left(1+\mathrm{e}^2\right)}{\left(1-\mathrm{e}^2\right)}\right] \frac{\mathrm{h}\left(1+\frac{1}{2}\right)}{\left(1-\frac{1}{2}\right)}=10\left(\frac{1.5}{0.5}\right)\)
= 30 మీ.

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
F = \((3 \hat{i}+4 \hat{j}-5 \hat{k})\) ప్రమాణాలు. స్థానభ్రంశం d = \((5 \hat{i}+4 \hat{j}+3 \hat{k})\) ప్రమాణాలు అయితే వాటి మధ్య కోణాన్ని, d సదిశ దిశలో F విక్షేపాన్ని కనుక్కోండి.
సాధన:
F.d = F_xd_x = F_yd_y + F_zd_z
= 3(5) + 4(4) + (-5) (3) = 16 ప్రమాణాలు
∴ F.d = F d cos.θ = 16 ప్రమాణాలు
ఇప్పుడు r.F = F² = F_x² + F_y² + F_z²
= 9 + 16 + 25 = 50 ప్రమాణాలు
d.d = d² = d_x² + d_y² + d_z²
= 25 + 16 + 9 = 50 ప్రమాణాలు
∴ cos θ = \(\frac{16}{\sqrt{50} \sqrt{50}}=\frac{16}{50}\) = 0.32,
∴ θ = cos^-1 0.32
d దిశలో F విక్షేపం = F cos θ
= 50 × \(\frac{16}{50}\) = 16 ప్రమాణాలు

ప్రశ్న 2.
వాన నీటి బిందువులు పడేటప్పుడు కిందకు పనిచేసే గురుత్వాకర్షణ బలం, దీన్ని వ్యతిరేకించే నిరోధక బలాల ప్రభావం ఉంటుందని మనకు బాగా తెలుసు. నిరోధక బలం వాన నీటి బిందువు వేగానికి అనులోమానుపాతంలో ఉంటుంది. దీని గురించి నిర్ధారించవలసి ఉంది. 1.00 గ్రా. ద్రవ్యరాశి ఉన్న నీటి బిందువు 1.00 కి.మీ. ఎత్తు నుంచి కిందకు పడుతుందనుకోండి. అది 50.0 మీ/సె^-1 వడితో నేలను తాకింది. దానిపై ఎ) గురుత్వాకర్షణ బలం వల్ల జరిగిన పని ఎంత ? బి) తెలియని నిరోధక బలం వల్ల జరిగిన పని ఎంత ?
సాధన:
ఎ) నీటి బిందువు గతిజశక్తిలో మార్పు
∆K = \(\frac{1}{2}\)mv² – 0
= \(\frac{1}{2}\) × 10^-3 × 50 × 50 = 1.25 జౌల్
ఇక్కడ నీటి బిందువు ప్రారంభంలో నిశ్చలస్థితిలో ఉందని ఊహించడమైంది.
g విలువ 10 మీ/సె² తో స్థిరంగా ఉంటుందని ఊహిస్తే, గురుత్వాకర్షణ బలం వల్ల జరిగిన పని
W_g = mgh
= 10^-3 × 10 × 10³ = 10.0 జౌల్

బి) పని-శక్తి సిద్ధాంతం నుంచి
∆K = W_g + W_r
ఇక్కడ W_r అనేది వాన నీటి బిందువుపై నిరోధక బలం వల్ల జరిగిన పని
W_r = ∆K – W_g = 1.25 – 10 = – 8.75 జౌల్
W_r విలువ రుణాత్మకం.

ప్రశ్న 3.
సైకిల్పై ప్రయాణిస్తున్న వ్యక్తి, బ్రేకు వేసినప్పుడు 10 మీ. దూరం జారుతూ ఆగాడు. ఈ ప్రక్రియలో రోడ్డు వల్ల సైకిల్ గమనానికి వ్యతిరేక దిశలో, సైకిల్పై పనిచేసే బలం 200 N.
ఎ) సైకిల్పై రోడ్డు ఎంత పనిచేస్తుంది ?
బి) రోడ్డుపై సైకిల్ ఎంత పని చేస్తుంది ?
సాధన:
రోడ్డు సైకిల్పై చేసిన పని అంటే రోడ్డు వల్ల కలిగే నిరోధక బలం (ఘర్షణ బలం) చేసిన పని అవుతుంది.
ఎ) నిరోధక బలం, స్థానభ్రంశాలు ఒకదానితో ఒకటి చేసే కోణం 180° (π రేడియన్లు) కాబట్టి రోడ్డు వల్ల జరిగిన పని,
W_r = Fd cos θ
200 × 10 × cоs л = -2000 J
ఈ రుణ పనివల్లనే పని-శక్తి సిద్ధాంతం ప్రకారం సైకిల్ ఆగుతుంది.

బి) న్యూటన్ మూడవ గమన నియమం ప్రకారం సైకిల్ వల్ల సమానం, వ్యతిరేక బలం రోడ్డుపై పనిచేస్తుంది. దీని పరిమాణం 200 N. కాని రోడ్డు ఎటువంటి స్థానభ్రంశం పొందలేదు కాబట్టి రోడ్డుపై సైకిల్ చేసే పని శూన్యం అవుతుంది.

ఉదాహరణ నుంచి తెలిసే అంశమేమంటే A పై B కలగచేసే బలానికి సమానం, వ్యతిరేక దిశలో B పై A కలగచేసే బలం ఉన్నప్పటికీ (న్యూటన్ మూడవ గమన నియమం) B వల్ల A పై జరిగిన పనికి, B పై A వల్ల జరిగే పని సమానం, వ్యతిరేక దిశలో ఉండనవసరం లేదు.

ప్రశ్న 4.
ప్రక్షేపణాల ప్రదర్శనలో ఒక పోలీసు అధికారి 50.0 గ్రా. ద్రవ్యరాశి ఉన్న బుల్లెట్ను 200 మీ/సె^-1 వడితో 2.00 సెం.మీ. మందం ఉన్న ప్లైవుడ్లోకి పేల్చాడు. తొలి గతిజశక్తిలో కేవలం 10% తో మాత్రమే బుల్లెట్ బయటకు వెలువడింది. బయటకు వెలువడిన బుల్లెట్ వడి ఎంత ?
సాధన:
బుల్లెట్ తొలి గతిజశక్తి = mv²/2 = 1000 J. దాని తుది గతిజశక్తి 0.1 × 1000 = 100 J.
బయటకు వెలువడిన బుల్లెట్ వడి v_f అయితే,
\(\frac{1}{2}\) mv₁² = 100J
v_f = \(\sqrt{\frac{2 \times 100 \mathrm{~J}}{0.05 \mathrm{~kg}}}\) = 63.2 ms^-1
వడి దాదాపు 68% తగ్గింది (90% కాదు).

ప్రశ్న 5.
ద్రవ్యరాశి m = 1కి.గ్రా. ఉన్న దిమ్మె క్షితిజ సమాంతర తలంపై v_i = 2 ms^-1 వడితో కదులుతూ x = 0.10 m నుంచి x = 2.01 m వరకు విస్తరించి ఉన్న గరుకు ప్రదేశంలోకి ప్రవేశించింది. ఈ వ్యాప్తిలో చలనానికి వ్యతిరేకంగా పనిచేసే బలం F_r, x కు విలోమానుపాతంలో ఉంటుంది.
F_r = \(\frac{-k}{x}\) 0.1 < x < 2.01 m వద్ద
= 0 x < 0.1m, x > 2.01 m వద్ద
ఇక్కడ k = 0.5 J గరుకు ప్రదేశాన్ని దాటిన తరువాత దిమ్మె తుది గతిజశక్తి, వడి v_f ఎంత ?.
సాధన:

ఇక్కడ ln, e ఆధారం కలిగిన సహజ సంవర్గమానం. అంతేకాని 10 ఆధారం కలిగిన సంవర్గమానం కాదు అని గుర్తించాలి. [ln X = log_e X = 2.303 log₁₀ X].

ప్రశ్న 6.
కారు ప్రమాదాలను పోలి ఉండే విధంగా కారు తయారీదార్లు వివిధ స్ప్రింగ్ స్థిరాంకాలు కలిగిన స్ప్రింగ్ తో గమనంలో ఉన్న కార్ల అభిఘాతాలను అధ్యయనం చేస్తారు. అలాంటి ఒక పోలికను పరిగణిద్దాం. 1000 కి.గ్రా. ద్రవ్యరాశి కలిగిన కారు 18.0 km/h వడితో నున్నటి రోడ్డుపై చలిస్తూ 6.25 × 10³ Nm^-1 స్ప్రింగ్ స్థిరాంకం ఉన్న క్షితిజ సమాంతరంగా తగిలించిన స్ప్రింగ్ను ఢీకొంది. స్ప్రింగ్ చెందే గరిష్ఠ సంపీడనం ఎంత ?
సాధన:
స్ప్రింగ్ గరిష్ఠ సంపీడనం చెందినప్పుడు కారు గతిజశక్తి పూర్తిగా స్ప్రింగ్ స్థితిజ శక్తిగా మారుతుంది.
గమనంతో ఉన్న కారు గతిజ శక్తి
K = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) × 10³ × 5 × 5
K = 1.25 × 10^-4 J
ఇక్కడ 18 km h^-1ను 5 ms^-1 గా మార్చడమైంది. (36kmh^-1 = 10ms^-1 అని గుర్తుంచుకోవడం ఉపయోగకరం). యాంత్రిక శక్తి నిత్యత్వ నియమం ప్రకారం స్ప్రింగ్ గరిష్ఠ సంపీడనం x_m వద్ద స్ప్రింగ్ స్థితిజ శక్తి V గమనంలో ఉన్న కారు గతిజశక్తి K కి సమానం.
V = \(\frac{1}{2}\) kx_m² = 1.25 × 10⁴ J
దీని నుంచి
x_m = 2.00 m వస్తుంది.
ఇక్కడ మనం స్ప్రింగ్ను ద్రవ్యరాశి లేనిదిగా, తలానికి ఉపేక్షించదగిన ఘర్షణ ఉందని పరిగణించడమైంది. ఇది ఒక ఆదర్శ పరిస్థితి అని గమనించవచ్చు.

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
వస్తువుపై బలం చేసిన పని సంజ్ఞ గురించి అర్థం చేసుకోవడం చాలా ముఖ్యమైంది. కింది భౌతికరాశులు, ధనాత్మకమా? రుణాత్మకమా ? జాగ్రత్తగా తెలియచేయండి.
ఎ) బకెటు బిగించిన తాడు సహాయంతో బావి నుంచి బకెట్ను తీసే సందర్భంలో మనిషి చేసిన పని
బి) పై సందర్భానికి గురుత్వ బలం చేసిన పని
సి) ఒక వస్తువు వాలు తలంపై జారుతున్నప్పుడు ఘర్షణ బలం చేసిన పని
డి) ఘర్షణ ఉన్న (గరుకు) క్షితిజ సమాంతర తలంపై వస్తువు సమవేగంతో చలిస్తున్నప్పుడు అనువర్తించిన బలం చేసిన పని
ఇ) కంపిస్తున్న లోలకాన్ని విరామస్థితిలోకి తేవడానికి గాలి నిరోధక బలం చేసే పని
సాధన:ఎ
ఎ) బకెట్ను పైకి లాగడానికి దాని భారమునకు సమానమైన బలం ప్రయోగించాలి. ఈ సందర్భంలో బలం, స్థానభ్రంశము ఒకే దిశలో ఉండటం వలన పని ధనాత్మకము.

బి) బకెట్ పైకి పోతున్నపుడు గురుత్వ బలం చేసిన పని ఋణాత్మకము. కారణం స్థానభ్రంశము మరియు గురుత్వ బలాలు వ్యతిరేకదిశలలో ఉండటము.

సి) ఘర్షణ బలం వస్తువు కదిలే దిశకు వ్యతిరేకము కావున ఘర్షణ బలం చేసిన పని ఋణాత్మకము.

డి) వస్తువు సమవేగంతో గరుకు తలంపై బలం ప్రయోగిస్తే బలం మరియు స్థానభ్రంశం ఒకే దిశలో ఉంటాయి. కావున పని ధనాత్మకము.

ఇ) గాలి నిరోధక బలం గమన దిశకు వ్యతిరేకంగా ఉండటం వల్ల పని ఋణాత్మకము.
గమనిక : పని W = \(\overline{\mathrm{F}} \cdot \overline{\mathrm{S}}\) = F.S. cos θ ఇది అదిశరాశి. పని ఎల్లపుడూ ధనాత్మకమే. \(\overline{\mathrm{F}} \cdot \overline{\mathrm{S}}\) లు ఒకే దిశలో ఉంటే పనిని ధనాత్మకంగాను, \(\overline{\mathrm{F}} \cdot \overline{\mathrm{S}}\) లు వ్యతిరేక దిశలలో ఉంటే ఋణాత్మకంగాను భావిస్తారు. అంతేగాని పని ఋణాత్మకం కాదు.

ప్రశ్న 2.
గతిక ఘర్షణ గుణకం 0.1 కలిగిన బల్లపై నిశ్చల స్థితిలో ఉన్న 2కి.గ్రా. ద్రవ్యరాశి ఉన్న వస్తువు 7 న్యూ క్షితిజ సమాంతర బలం వల్ల చలిస్తూ ఉంది. కింది రాశులను లెక్కించండి.
ఎ) 10 సె. కాలంలో అనువర్తిత బలం చేసిన పని
బి) 10 సె. కాలంలో ఘర్షణ బలం చేసిన పని
సి) 10 సె. కాలంలో నికర బలం చేసిన పని
డి) 10 సె. కాలంలో వస్తువు గతిజ శక్తిలోని మార్పు
మీ ఫలితాలను వివరించండి.
సాధన:
ద్రవ్యరాశి m = 2 కి.గ్రా. ; తొలి వేగము u = 0; బలము F = 7 న్యూ ; ఘర్షణ గుణకము μ = 0.1
ఎ) 10 సెకనులలో బలం చేసిన పని W = μF.S.
త్వరణము a₁ = \(\frac{\mathrm{F}}{\mathrm{m}}=\frac{7}{2}\) = 3.5 మీ/సె²
ఘర్షణ బలం వలన వ్యతిరేక దిశలో త్వరణము

a₂ = \(\frac{\mu \mathrm{mg}}{\mathrm{m}}\) = 0.1 × 9.8 = 0.98 మీ/సె²
ఫలిత త్వరణము a = a₁ – a₂ = 3.5 – 0.98 = 2.52 మీ/సె²
వస్తువు కదిలిన దూరము s = ut + \(\frac{1}{2}\) at² = 0 + \(\frac{1}{2}\) × 2.52 × 10 × 10 = 126 మీ.
బలం జరిపిన పని W₁ = F.S. = 7 × 126 = 882 J

బి) ఘర్షణ బలం జరిపిన పని W₂ = F_s × S = -1.96 × 126 = -246.9 J

సి) ఫలితబలం చేసిన పని W₃ = (F – F_s) S = (7 – 1.96) 126 = 635 J

డి) v = u + at నుండి V = 0 + 2.52 × 10 = 25.2 మీ/సె.
∴ తుది గతిజశక్తి \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) × 2 × (25.2)² = 635.J
తొలి గతిజశక్తి = \(\frac{1}{2}\) mu²
∴ గతిజశక్తిలో మార్పు = 635 – 0 = 635 J

ప్రశ్న 3.
పటంలో కొన్ని ఏకమితీయ స్థితిజ శక్తి ప్రమేయాలకు ఉదాహరణలు ఇవ్వడమైంది. కణం మొత్తం శక్తిని ద్వితీయ నిరూపక అక్షం (y – అక్షం) పై క్రాస్ సూచించడమైంది. ఇచ్చిన శక్తికి, కణాన్ని కనుక్కోలేని ప్రాంతం ఏదైనా ఉంటే ఆ ప్రాంతాన్ని ప్రతి సందర్భానికి వివరించండి. ప్రతి సందర్భంలో కణానికి ఉండవలసిన మొత్తం కనీస శక్తిని కూడా సూచించండి. ఈ స్థితిజ శక్తి ఆకారాలకు సంబంధించిన సరళమైన భౌతిక సందర్భాలను ఆలోచించండి.

సాధన:
మొత్తం శక్తి E = P.E. + K.E. లేదా K.E. = E-P.E. ఇందులో K.E. విలువ ఋణాత్మకం కాదు.

1. x > a ఐతే P.E. (V₀) > E అనగా K.E. ఋణాత్మకం కావలెను. ఇది సాధ్యం కాదు కాబట్టి వస్తువు x > a ప్రాంతంలో ఉండదు.
2. x < a మరియు x > b ప్రాంతంలో P.E. (V₀) > E.
   అనగా KE ఋణాత్మకము. ఇది సాధ్యం కాదు. కాబట్టి వస్తువు X < a మరియు x > b ప్రాంతంలో ఉండదు.
3. ఈ పటంలోని ఏ ప్రాంతంలోను మనం కణాన్ని కనుక్కోలేము. ఎందుకనగా దాని P.E. > E (మొత్తం శక్తి)
4. వస్తువుకు – b/2 < x < a/2 మరియు a/2 < x < b/2 ప్రాంతంలో వస్తువు P.E.7 మొత్తం శక్తి E కావున KE ఋణాత్మకంగా ఉండాలి. అనగా ఈ ప్రాంతంలో ఇచ్చిన కణం ఉండే అవకాశం లేదు.

ప్రశ్న 4.
రేఖీయ సరళహరాత్మక చలనం చేస్తున్న కణం స్థితిజ శక్తి ప్రమేయం V(x) = kx² / 2 గా ఇవ్వడమైంది. ఇక్కడ k డోలకం బల స్థిరాంకం. k = 0.5 N m^-1 విలువకు V(x), ౫ ల మధ్య గ్రాఫ్ పటంలో చూపించడమైంది. ఈ పొటెన్షియల్లో చలించే 1J మొత్తం శక్తి కలిగిన కణం x = ± 2m కే చేరినపుడు అది వెనుకకు మరలుతుందని చూపండి.

సాధన:
ఏదైనా క్షణంలో సరళ హరాత్మక చలనం చేస్తున్న కణం మొత్తం శక్తి = KE + PE = \(\frac{1}{2}\) mu² + \(\frac{1}{2}\) kx²
వస్తువు వేగము u = (0 వద్ద వెనుకకు మరలుతుంది. అనగా గరిష్ఠ స్థానభ్రంశ బిందువు వద్ద u = 0 ⇒ KE = 0
∴ మొత్తం శక్తి E = \(\frac{1}{2}\) kx² కాని E = 1, k = \(\frac{1}{2}\)
∴ 1 = \(\frac{1}{2}\) kx² కావున 1 = \(\frac{1}{2}\) × \(\frac{1}{2}\) x² లేదా x² = 4 ⇒ x = ± 2 మీ.

ప్రశ్న 5.
క్రింది వాటికి సమాధానాలివ్వండి:
ఎ) రాకెట్ గమనంలో ఉన్నపుడు దాని చుట్టూ ఉన్న కప్పు ఘర్షణ వల్ల కాలిపోతుంది. కాలిపోవడానికి అవసరమయ్యే ఉష్ణ శక్తి రాకెట్ నుంచి లభ్యమవుతుందా ? లేదా వాతావరణం నుంచి లభ్యమవుతుందా ?
బి) అధిక దీర్ఘాక్ష దీర్ఘ వృత్తాకార కక్ష్యల్లో తోకచుక్కలు సూర్యుని చుట్టూ తిరుగుతూ ఉంటాయి. సూర్యుని వల్ల తోకచుక్కపై పనిచేసే గురుత్వ బలం సాధారణంగా తోకచుక్క వేగానికి లంబంగా ఉండదు. కాని తోకచుక్క ప్రతి పూర్తి భ్రమణానికి గురుత్వ బలం చేసిన పని శూన్యమవుతుంది. ఎందుకు ?
సి) పలుచని వాతావరణంలో భూమి చుట్టూ తిరుగుతున్న కృత్రిమ ఉపగ్రహం వాతావరణ నిరోధం వల్ల క్రమంగా చాలా స్వల్ప మోతాదులో శక్తిని కోల్పోతుంది. అయితే అది భూమిని దగ్గరగా సమీపిస్తున్న కొద్దీ దాని వడి ఎందుకు క్రమంగా పెరుగుతుంది ?

డి) పటం (i) లో ఒక మనిషి 15 కి.గ్రా. ద్రవ్యరాశిని తన చేతులతో తీసుకొని వెళ్తూ 2 మీ. దూరం నడిచాడు. పటం (ii) లో అతను తన వెనుక ఉన్న తాడును లాగుతూ అంతే దూరాన్ని నడిచాడు. కప్పీ మీదగా వెళ్తున్న తాడుకు రెండవ చివర 15 కి.గ్రా. ద్రవ్యరాశి వేలాడదీయడమైంది. ఏ సందర్భంలో జరిగిన పని ఎక్కువ ?
సాధన:
ఎ) రాకెట్ పై భాగం కాలడానికి అవసరమైన శక్తి రాకెట్ నుండి లభ్యమవుతుంది. వాతావరణం నుండి కాదు. రాకెట్ మొత్తం శక్తి E = P.E. + K.E. = mgh + \(\frac{1}{2}\) mv². రాకెట్ పైకి పోవు కొలది దాని ద్రవ్యరాశి తగ్గుతుంది. (ఇంధనం మండటంవల్ల) ఫలితంగా దాని శక్తి తగ్గుతుంది. ఈ తగ్గిన శక్తి రాకెట్ పైభాగం కాలిపోవడానికి ఉపయోగపడుతుంది.
బి) గురుత్వాకర్షణ బలాలు నిత్యత్వ బలాలు. కావున ఒక సంవృత వలయంలో జరిగిన పని సున్నకు సమానము అనగా తోకచుక్క ప్రతి పరిభ్రమణంలో జరిగిన పని = 0.

సి) ఉపగ్రహం భూమిని సమీపిస్తుంటే దాని ఎత్తు తగ్గుతుంది. కాబట్టి స్థితిశక్తి PE తగ్గును. మొత్తంశక్తి PE + KE స్థిరముగా ఉండడంవల్ల స్థితిశక్తి తగ్గితే ఉపగ్రహం వేగం పెరుగుతుంది. ఈ ప్రక్రియలో వాతావరణంలో రాపిడి వల్ల అతి స్వల్ప మొత్తంలో శక్తి నష్టం ఉంటుంది.

డి) (i) పటంలో మనిషి ప్రయోగించిన బలం మరియు వస్తువు స్థానభ్రంశం పరస్పరం లంబంగా ఉన్నాయి.
∴ θ = 90°
జరిగిన పని W = F s cos θ

(ii) ఈ పటంలో బలము, స్థానభ్రంశం ఒకే దిశలో ఉన్నాయి. ∴ θ = 0
జరిగిన పని W = F s cos θ = mg s cos θ
దత్తాంశం నుండి m = = 15 కి.గ్రా. ; స్థానభ్రంశం = 2మీ.
W = 15 × 9.8 × 2 = 294 జౌల్

ప్రశ్న 6.
సరైన ప్రత్యామ్నాయం కింద గీత గీయండి.
ఎ) వస్తువుపై నిత్యత్వ బలం చేసిన పని ధనాత్మకమయితే, వస్తువు స్థితిజ శక్తి పెరుగుతుంది/తగ్గుతుంది/మారకుండా ఉంటుంది.
బి) ఘర్షణకు వ్యతిరేకంగా వస్తువు పనిచేయడం వల్ల ఎప్పుడు గతిజ/స్థితిజ శక్తి నష్టం జరుగుతుంది.
సి) అనేక కణ వ్యవస్థ యొక్క మొత్తం ద్రవ్యవేగంలోని మార్పురేటు బాహ్యబలం / వ్యవస్థలోని అంతర బలాల మొత్తానికి అనులోమానుపాతంలో ఉంటుంది.
డి) రెండు వస్తువుల మధ్య జరిగిన అస్థితి స్థాపక అభిఘాతంలో, అభిఘాతం తరువాత వ్యవస్థ మొత్తం గతిజశక్తి / మొత్తం రేఖీయ ద్రవ్యవేగం / మొత్తం శక్తి మారకుండా స్థిరంగా ఉంటుంది.
సాధన:
ఎ) నిత్యత్వ బలాలు పనిచేస్తే వస్తువు స్థితిజశక్తి తగ్గుతుంది. ఎందుకనగా స్థితిజశక్తి వస్తువులో దాచిపెట్టబడిన పని.

బి) ఘర్షణకు వ్యతిరేకంగా పని జరిగినపుడు వస్తువు గతిజశక్తి తగ్గుతుంది. కారణం ఘర్షణకు వ్యతిరేకంగా జరిపిన పని గతిజశక్తి నుండి సమకూరడమే.

సి) ద్రవ్యవేగంలోని మార్పు బాహ్యబలం నుండీ సమకూరుతుంది. కారణం అంతర్గత మార్చలేవు.

డి) అస్థితి స్థాపక అభిఘాతాలలో వ్యవస్థ ద్రవ్యవేగం స్థిరము. బలాలు వ్యవస్థ ద్రవ్య వేగాన్ని

ప్రశ్న 7.
క్రింద ఇచ్చిన ప్రతిపాదనలు సరి అయినవా ? కావా ? మీ సమాధానాలకు కారణాలు రాయండి.
ఎ) రెండు వస్తువుల మధ్య జరిగే స్థితిస్థాపక అభిఘాతంలో ప్రతి వస్తువు యొక్క ద్రవ్యవేగం, శక్తి నిత్యత్వంగా ఉంటుంది.
బి) వస్తువుపై ఎటువంటి అంతర, బాహ్యబలాలు పనిచేసినప్పటికీ వ్యవస్థ మొత్తం శక్తి ఎప్పుడూ నిత్యత్వంగా ఉంటుంది.
సి) ఒక సంవృత ఉచ్చు వెంబడి చలనంలో ఉన్న వస్తువుపై ప్రకృతిలోని ప్రతి బలం చేసే పని శూన్యం.
డి) అస్ధితిస్థాపక అభిఘాతంలో వ్యవస్థ తొలి గతిజ శక్తి కంటె తుది గతిజ శక్తి ఎప్పుడూ తక్కువగా ఉంటుంది.
సాధన:
ఎ) ప్రతిపాదన సరియైనది కాదు. స్థితిస్థాపక అభిఘాతాలలో వ్యవస్థ మొత్తం శక్తి, ద్రవ్యవేగాలు స్థిరము. విడివిడిగా ప్రతి వస్తువుకు ఈ నియమం వర్తించదు.

బి) ప్రతిపాదన సరియైనది కాదు. బాహ్యబలం వల్ల వ్యవస్థ మొత్తం శక్తి మారవచ్చు.

సి) ప్రతిపాదన సరియైనది కాదు. నిత్యత్వ బలాలకు మాత్రమే సంవృత మార్గంలో జరిపిన మొత్తం పని సున్న. అనిత్యత్వ బలాలకు ఈ నియమం వర్తించదు.

డి) నిజమే. అస్థితిస్థాపక అభిఘాతాలలో కొంత శక్తి నష్టం జరుగుతుంది.

ప్రశ్న 8.
తగిన కారణాలతో జాగ్రత్తగా సమాధానమివ్వండి :
ఎ) రెండు బిలియర్డ్ బంతుల స్థితిస్థాపక అభిఘాతంలో బంతుల మధ్య అభిఘాతం జరుగుతున్న స్వల్ప కాలంలో (ఒక దానితో ఒకటి స్పర్శించుకొన్నప్పుడు) మొత్తం గతిజ శక్తి నిత్యత్వంగా ఉంటుందా ?
బి) స్వల్ప కాలవ్యవధిలో రెండు బంతుల మద్య జరిగిన స్థితిస్థాపక అభిఘాతంలో రేఖీయ ద్రవ్యవేగం మొత్తం నిత్యత్వంగా ఉంటుందా ?
సి) అస్ధితిస్థాపక అభిఘాతానికి (ఎ), (బి) లకు సమాధానాలు ఏమిటి ?
డి) రెండు బిలియర్డ్ బంతుల స్థితిజ శక్తి, వాటి కేంద్రాల మధ్య దూరంపై మాత్రమే ఆధారపడితే ఆ అభిఘాతం స్థితిస్థాపకమా లేదా అస్థితిస్థాపకమా ? (సూచన : అభిఘాత సమయమప్పుడు ఉండే బలానికి సంబంధించిన స్థితిజ శక్తి గురించి మాట్లాడుతున్నాం కాని గురుత్వ స్థితిజ శక్తిని గురించి కాదు.)
సాధన:
ఎ) ప్రతిపాదన సరియైనది కాదు. అస్థితిస్థాపక అభిఘాతాలలో అభిఘాతానికి ముందు వ్యవస్థ KE అభిఘాతం తరువాత వ్యవస్థ KE కి సమానము. వాస్తవంగా జరిగేది ఏమిటంటే అభిఘాత సమయంలో గతిజశక్తి స్థితిజశక్తిగా మారుతుంది.

బి) నిజమే. స్థితిస్థాపక అభిఘాతాలలో వస్తువులు కలిసి ఉన్న స్వల్ప వ్యవధిలో వాటి మధ్య ద్రవ్యవేగ వినిమయం జరుగుతుంది.

సి) అస్థితిస్థాపక ఏక అభిఘాతాలలో గతిజశక్తి స్థిరంగా ఉండదు. కాని వ్యవస్థకు గల ద్రవ్యవేగము స్థిరము.

డి) ఈ అభిఘాతం స్థితిస్థాపక అభిఘాతం. ఎందుకనగా ఇందులో పాల్గొనిన బలాలు నిత్యత్వ బలాలు.

ప్రశ్న 9.
నిశ్చల స్థితి నుంచి బయలుదేరిన ఒక వస్తువు స్థిర త్వరణంతో ఏకమితీయ చలనం కలిగి ఉంది. t కాలంలో దానికి అందచేసిన సామర్థ్యం కింది వాటికి అనులోమానుపాతంలో ఉంటుంది.
(i) t^1/2
(ii) t
(iii) t^3/2
(iv) t²
సాధన:
v = u + at నుండి v = 0 + at = సామర్థ్యము P = F × v
∴ P = mav = m.a.a.t = ma²t
m, a లు స్థిరం కావున p ∝ t

ప్రశ్న 10.
స్థిర సామర్థ్యాన్ని అందించే జనకం ప్రభావం వల్ల ఒక వస్తువు ఏక దిశాత్మకంగా చలిస్తుంది. t కాలంలో కలిగిన స్థానభ్రంశం కింది వాటికి అనులోమానుపాతంలో ఉంటుంది.
(i) t^1/2
(ii) t
(iii) t^3/2
(iv) t²
సాధన:
సామర్థ్యము P = బలం × వేగము
∴ P = [MLT^-2][LT^-1] = [ML²T^-3]
వస్తువు స్థిర సామర్థ్యముతో కదులుతున్నపుడు m, p లు స్థిరము
కావున L²T^-3 స్థిరము లేదా \(\frac{\mathrm{L}^2}{\mathrm{~T}^3}\) = స్థిరరాశి
అనగా L² ∝ T³ లేదా L ∝ T^3/2

ప్రశ్న 11.
ఒక నిరూపక వ్యవస్థలో Z- అక్షం వెంట చలనానికి పరిమితం అయిన వస్తువుపై
\(\overrightarrow{\mathrm{F}}=-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}\)N
అనే స్థిర బలం పనిచేస్తుంది. ఇక్కడ X-, Y-, Z- అక్షాల వెంట ప్రమాణ సదిశలు వరుసగా \(\hat{\mathrm{i}}, \hat{\mathrm{j}}, \hat{\mathrm{k}}\). Z- అక్షంపై 4 మీ. దూరం చలించడానికి ఈ బలం చేసిన పని ఎంత ?
సాధన:
దత్తాంశం నుండి \(\overrightarrow{\mathrm{F}}=-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}\) న్యూ, \(\overrightarrow{\mathrm{s}}=4 \hat{\mathrm{k}}\) మీ.
జరిగిన పని _ W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{S}}\)
= \((-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}) \cdot(4 \hat{\mathrm{k}})=12 \hat{\mathrm{k}} \cdot \hat{\mathrm{k}}\) = 12J

ప్రశ్న 12.
విశ్వకిరణాల ప్రయోగంలో 10 keV, 100 keV శక్తి గల ఎలక్ట్రాన్, ప్రోటాన్లను కనుక్కొన్నారు. వీటిలో వేగవంతం అయినది ఏది ? ఎలక్ట్రాన్ లేదా ప్రోటాన్ ? వాటి వడుల నిష్పత్తిని రాబట్టండి. (ఎలక్ట్రాన్ ద్రవ్యరాశి = 9.11 × 10^-31 = కి.గ్రా., ప్రోటాన్ ద్రవ్యరాశి 1.67 × 10^-27 కి.గ్రా., 1 eV = 1.60 × 10^-19 J).
సాధన:
ఎలక్ట్రాన్ గతిజశక్తి KE₁ = 10 KeV = 10 × 1.6 × 10^-16 J
ఫోటాన్ గతిజశక్తి KE₂ = 100 KeV = 100 × 1.6 × 10^-16 J
ఎలక్ట్రాన్ ద్రవ్యరాశి m_e = 9.11 × 10^-31 ; ప్రోటాన్ ద్రవ్యరాశి m_p = 1.67 × 10^-27
\(\frac{1}{2}\) m_ev_e² : \(\frac{1}{2}\) m_pv_p² = 10 : 100 = 1 : 10 ⇒ \(\frac{v_{\mathrm{e}}}{\mathrm{v}_{\mathrm{p}}}=\sqrt{\frac{1}{10} \frac{\mathrm{m}_{\mathrm{p}}}{\mathrm{m}_{\mathrm{e}}}}\)
∴ \(\frac{\mathrm{v}_{\mathrm{e}}}{\mathrm{v}_{\mathrm{p}}}=\frac{1}{10} \sqrt{\frac{1.67 \times 10^{-27}}{10 \times 9.11 \times 10^{-31}}}=10^2 \sqrt{\frac{1.67}{91.1}}\) = 13.53

ప్రశ్న 13.
500 మీ. ఎత్తు నుంచి 2 మి.మీ. వ్యాసార్ధం ఉన్న వాన నీటి బిందువు నేలపై పడుతుంది. సగం ఎత్తువరకు తగ్గుతున్న త్వరణం (గాలి స్నిగ్ధతా నిరోధం వల్ల) కలిగి గరిష్ఠ (అంత్య) వడిని పొందుతుంది. ఆ తరువాత అది ఏకరీతి వడితో కిందికి చలిస్తుంది. వాన నీటి బిందువు ప్రయాణంలో, మొదటి, రెండవ సగంలో గురుత్వ బలం చేసిన పని ఎంత ? 10 మీ/సె^-1 వడితో నేలను చేరినట్లైతే దాని పూర్తి ప్రయాణంలో నిరోధక బలం చేసిన పని ఎంత ?
సాధన:
నీటి బిందువు వ్యాసార్ధము r = 2 మి.మీ. = 2 × 10^-3 మీ.
మొత్తం ప్రయాణించిన దూరము = 500 మీ.
సగం దూరము = 250 మీ.
నీటిసాంద్రత ρ = 10³ కి.గ్రా./మీ³ ; నీటి బిందువు ద్రవ్యరాశి = v × ρ
∴ m = v.ρ = \(\frac{4}{3}\) πr³ × ρ = \(\frac{4}{3}\) × \(\frac{22}{7}\) (2 × 10^-3)³ × 10³ = 3.35 × 10^-5 కి.గ్రా.
నిరోధక బలం పనిచేసినా చేయకపోయినా వస్తువు స్థితిశక్తిలో మార్పు
E₁ = mgh = 3.35 × 10^-5 × 10 × 500 = 0.164J
నేలను తాకినపుడు నీటి బిందువు వేగము v = 10 మీ/సె.
∴ గతిజశక్తి E₂ = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 3.35 × 10^-5 (10)² = 1.675 × 10^-3 J.
నిరోధక బలం జరిపిన పని W = మొత్తం శక్తి – గతిజశక్తి
= 0.164 – 1.675 × 10^-3 = 0.1623 J

ప్రశ్న 14.
పాత్రలో ఉన్న వాయువులోని అణువు, 200 మీ/సె^-1 వడితో, లంబంతో 30 కోణం చేస్తున్న దిశలో క్షితిజ సమాంతర (పాత్ర) గోడను ఢీకొని అంతే వడితో వెనుకకు మరలింది. ఈ అభిఘాతంలో ద్రవ్యవేగం నిత్యత్వంగా ఉంటుందా ? ఈ అభిఘాతం స్థితిస్థాపకమా లేదా అస్థితిస్థాపకమా ?
సాధన:
అభిఘాతాలలో ద్రవ్యవేగం స్థిరము; వాయు అణువు తొలి వేగము V₁ = 200 మీ/సె;
తొలి గతిజశక్తి పరిశీలిస్తే వాయు అణువుకు KE = \(\frac{1}{2}\) mv₁² = \(\frac{1}{2}\) m(200)² …………….. (1)

గోడకు K.E. = \(\frac{1}{2}\) mv₁² = 0 (కదలలేదు కావున)
అభిఘాతం పిమ్మట గోడ గతిజశక్తి = \(\frac{1}{2}\) m(0)² = 0
తుది వేగము V₂ = 200 మీ/సె.
∴ KE = \(\frac{1}{2}\) m(200)² …………….. (2)
సమీ. (1), (2) నుండి అభిఘాతం ముందు గతిజశక్తి = అభిఘాతం తరువాత గతిజశక్తి
అనగా ఈ అభిఘాతంలో శక్తి నిత్యత్వం జరిగింది.

ప్రశ్న 15.
భవనం నేల అంతస్తుపై ఉన్న పంప్ (మోటార్) 300 మీ³ ఘనపరిమాణం ఉన్న టాంకును 15 నిమిషాలలో నింపగలదు. పంప్ దక్షత 30% కలిగి ఉండి, టాంక్ నేలపై నుంచి 40 మీ. ఎత్తులో ఉంటే పంప్ ఎంత విద్యుత్ సామర్థ్యం వినియోగించుకొంటుంది ?
సాధన:
నీటి ఘనపరిమాణము V = 30 m³;
1 m³ నీటి ద్రవ్యరాశి = 1000 కి.గ్రా.
కాలము t = 15 ని. = 15 × 60 = 900 సె.; ఎత్తు h = 40 మీ
దక్షత η = 30%;
నీటి ద్రవ్యరాశి = 30 × 10³ కి.గ్రా.
వాస్తవంగా జరిగిన పని W = mgh = 30 × 10³ × 9.8 × 40
వాస్తవ సామర్థ్యము = \(\frac{\mathrm{P}}{\mathrm{t}}==\frac{30 \times 10^3 \times 9.8 \times 40}{900}\) = 13070 వాట్
యంత్రం మొత్తం సామర్థ్యము p_t = \(\frac{P \times 100}{\eta}=\frac{13070 \times 100}{30}\) = 43.567 కి.వాట్

ప్రశ్న 16.
ఘర్షణ లేని బల్లపై రెండు సర్వసమాన బాలే బేరింగ్లు ఒకదానితో ఒకటి స్పర్శించుకొంటూ నిశ్చలంగా ఉన్నాయి. అంతే ద్రవ్యరాశి ఉన్న వేరొక బాల్బేరింగు, V తొలి వడితో వీటిని సూటిగా ఢీకొంది. ఇది స్థితిస్థాపక అభిఘాతమయితే, అభిఘాతం తరువాత పక్క వాటిలో (పటంలో) ఏది సాధ్యమయ్యే ఫలితమవుతుంది ?

సాధన:
ప్రతి బంతి ద్రవ్యరాశి m అనుకోండి. మూడవ బంతి వేగము = v; ద్రవ్యరాశి = m
అభిఘాతం ముందు వ్యవస్థ మొత్తం K.E. = \(\frac{1}{2}\)mv² + 0
(మిగిలిన బంతులు నిశ్చలంగా ఉన్నవి కావున)
అభిఘాతం పిమ్మట 1వ సందర్భములో v₁ = v₂. (బొమ్మ నుండి)
∴ KE₁ = \(\frac{1}{2}\) (2m) \(\left(\frac{\mathrm{V}}{2}\right)^2\) = \(\frac{1}{4}\) mv²
2వ సందర్భంలో తుదివేగము = v, ద్రవ్యరాశి = m,
∴ KE₂ = \(\frac{1}{2}\) mv²
3వ సందర్భంలో ద్రవ్యరాశి = 3m, వేగము \(\frac{\mathrm{v}}{3}\)
KE₃ = \(\frac{1}{2}\) = (3m)(v/3)² = \(\frac{1}{6}\) mv²
పై సందర్భాలలో కేవలం 2వ సందర్భంలోనే గతిశక్తి నిత్యత్వం పాటించబడును.

ప్రశ్న 17.
క్షితిజ లంబానికి 30° కోణం చేస్తూ ఉన్న లోలక గోళం A ని వదిలితే అది బల్లపై నిశ్చలస్థితిలో ఉన్న అంతే ద్రవ్యరాశి కలిగిన B గోళాన్ని పటంలో చూపినట్లు ఢీకొంది. అభిఘాతం తరువాత A గోళం ఎంత ఎత్తుకు లేస్తుంది ? అభిఘాతం స్థితిస్థాపకం అని ఊహించి, గోళాల పరిమాణాలను ఉపేక్షించండి.

సాధన:
రెండు సమాన ద్రవ్యరాశులు గల వస్తువుల మధ్య అభిఘాతం జరిగితే అవి వాటి వేగాలను పరస్పరం మార్చుకుంటాయి.
B గోళం నిశ్చలంగా ఉంది కావున అబిఘాతం పిమ్మట A గోళం నిశ్చలస్థితికి వస్తుంది. పైకి లేవదు.

ప్రశ్న 18.
ఒక లోలక గోళాన్ని క్షితిజ సమాంతర స్థానం నుంచి విడిచిపెట్టారు. గాలి నిరోధం వల్ల తొలి శక్తిలో 5% దుర్వ్యయమయితే గోళం అత్యంత నిమ్నతమ బిందువును ఎంత వడితో చేరుతుంది ? లోలకం పొడవు 1.5 మీ.

సాధన:
ఎత్తు = h, శక్తి నష్టము = 5%, తుది పొడవు l = 1.5 మీ.
క్షితిజ సమాంతర బిందువు నుండి వదిలితే PEW లో మార్పు = mgl = mgh
B పొందిన గతిజశక్తి = mgh లో 95% = \(\frac{95}{100}\) mgh = \(\frac{1}{2}\) mv²
∴ v = \(\sqrt{\frac{95}{100} \times \mathrm{gh}}=\sqrt{\frac{19}{20} \times 9.8 \times 1.5}\)
= 5.28 మీ/సె.

ప్రశ్న 19.
25 కి.గ్రా. ద్రవ్యరాశి ఉన్న ఇసుక సంచిని మోస్తున్న 300 కి.గ్రా. ద్రవ్యరాశి కలిగిన ట్రాలీ ఘర్షణ లేని బాటలో 27 km/h ఏకరీతి వడితో చలిస్తూ ఉంది. కొంతసేపటి తరువాత సంచికి కలిగిన రంధ్రం ద్వారా 0.05కి.గ్రా./సె. రేటుతో ఇసుక ట్రాలీ తలంపై లీకు అవుతూ ఉంది. ఇసుక సంచి ఖాళీ అయిన తరువాత ట్రాలీ వడి ఎంత ?
సాధన:
ఏకరీతి వడితో చలిస్తున్నది. అనగా త్వరణము a = 0
∴ వ్యవస్థపై బాహ్య బలము F = ma = (0)
ట్రాలీ నుంచి కారుతున్న ఇసుక వ్యవస్థ అంతర్గత బలము కావున ఇది ట్రాలీ వడిని మార్చజాలదు.

ప్రశ్న 20.
0.5 కి.గ్రా. ద్రవ్యరాశి ఉన్న వస్తువు సరళరేఖా మార్గంలో v = ax^3/2 వేగంతో ప్రయాణిస్తుంది. ఇక్కడ a = 5m^-1/2 s^-1. అది x = 0 నుంచి x = 2 m కి స్థానభ్రంశం చెందినపుడు ఫలిత బలం చేసిన పని ఎంత ?
సాధన:
దత్తాంశం నుండి m = 0.5కి.గ్రా.;
వేగము V = ax^3/2,
a = 5 మీ/సె²;
తొలి వేగము అనగా x = 0 వద్ద, v₁ = 0
x = 2 వద్ద తుదివేగము v₁ = 5 × 2^3/2
జరిగిన పని W = \(\frac{1}{2}\) m (v₂² – v₁²) = \(\frac{1}{2}\) × 0.5 [(5 × 2^3/2)²]
∴ W = \(\frac{0.5 \times 5 \times 5 \times 2 \times 2 \times 2}{2}\) = 50 J

ప్రశ్న 21.
ఒక గాలిమర రెక్కలు A వైశాల్యం ఉన్న వృత్తాన్ని చిమ్ముతున్నాయి. (ఎ) ఈ వృత్తానికి లంబంగా v వేగంతో గాలి ప్రవహిస్తుంటే, దీని ద్వారా ! కాలంలో వెళ్ళే గాలి ద్రవ్యరాశి ఎంత ? (బి) గాలి గతిజశక్తి ఎంత ? (సి) గాలి మర, గాలి శక్తిలో 25% శక్తిని విద్యుత్ శక్తిగా మారుస్తుందని ఊహించండి. A = 30 m², u = 36 km/h, గాలి సాంద్రత 1.2kg m^-3, ఉత్పత్తి అయ్యే విద్యుత్ సామర్థ్యం ఎంత ?
సాధన:
a) ఒక సెకనులో వీచిన గాలి ఘ.ప. = A v
గాలి ద్రవ్యరాశి / సె. = A v ρ
(ρ = గాలి సాంద్రత)
t సెకనులలో వీచిన గాలి ద్రవ్యరాశి = Avρt

b) గాలి గతిజశక్తి K.E = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) Avρtv² = \(\frac{1}{2}\) Av³ρt

c) ఉత్పత్తి అయిన విద్యుచ్ఛక్తి = దక్షత × గాలి గతిజశక్తి
దక్షత η = 25%
∴ ఉత్పత్తి అయిన విద్యుచ్ఛక్తి = \(\left(\frac{25}{100}\right) \times \frac{1}{2}\) Av³ρt
విద్యుదుత్పాదక యంత్ర సామర్థ్యము

దత్తాంశం నుండి A = 30 మీ², v = 36 kmph = \(\frac{36 \times 5}{18}\) = 10 మీ/సె
గాలి సాంద్రత ρ = 1.2 కి.గ్రా/మీ³
∴ P = \(\frac{1}{8}\) × 30 × 10³ × 1.2 = 4500 వాట్ = 4.5 కి.వాట్

ప్రశ్న 22.
బరువు తగ్గాలనుకొనే వ్యక్తి (dieter) 10 కి.గ్రా. ద్రవ్యరాశిని ప్రతిసారి 0.5 మీ. ఎత్తుకు లేపుతూ వెయ్యిసార్లు పైకి ఎత్తాడు. అతడు ప్రతిసారి ద్రవ్యరాశిని కిందకు దించేటప్పుడు నష్టపోయిన స్థితిజ శక్తి దుర్వ్యయమవుతుందని ఊహించండి. ఎ) గురుత్వ బలానికి వ్యతిరేకంగా అతడు చేసిన పని ఎంత ? బి) ప్రతి కిలోగ్రాముకు 3.8 × 10⁷ జౌల్ శక్తిని కొవ్వు అందిస్తుంది. ఇది, 20% దక్షతతో యాంత్రిక శక్తిగా మారుతుంది. బరువు తగ్గాలనుకొనే వ్యక్తి ఎంత కొవ్వును ఉపయోగించినట్లు ?
సాధన:
దత్తాంశం నుండి m = 10 కి.గ్రా., h = 0.5 మీ., n = 1000; η = 20%
ఎ) గురుత్వ త్వరణానికి వ్యతిరేకంగా జరిగిన పని W = n (mgh)
W = 1000 (10 × 9.8 × 0.5) = 49000 J

బి) ఒక కిలో కొవ్వు అందించిన యాంత్రిక శక్తి = వాస్తవంగా కొవ్వు అందించిన శక్తి × దక్షత
దేహానికి 1 కిలో కొవ్వు ఇచ్చిన వాస్తవ శక్తి = 3.8 × 10⁷ × \(\frac{20}{100}\) = 0.76 × 10⁷ జౌల్/కి.గ్రా.
బరువు తగ్గాలనుకున్న వ్యక్తి వాడిన కొవ్వు = \(\frac{1}{0.76 \times 10^7}\) × 49000 = 6.45 × 10^-2 కి.గ్రా.

ప్రశ్న 23.
ఒక కుటుంబం 8 కి. వాట్ విద్యుత్ సామర్థ్యాన్ని ఉపయోగిస్తుంది. ఎ) సౌరశక్తి నేరుగా క్షితిజ సమాంతర తలంపై సగటున ప్రతి చదరపు మీటరుకు 200 వాట్ రేటున పతనమవుతుంది. ఈ శక్తిలో 20% విద్యుత్ శక్తిగా ఉపయోగపడితే, 8 కి.వాటిని సరఫరా చేయడానికి ఎంత పెద్ద వైశాల్యం ఉన్న తలం అవసరమవుతుంది ? (బి) దీన్ని ఒక మాదిరి ఇంటి పై కప్పు వైశాల్యంతో పోల్చండి.
సాధన:
ఉపరితల వైశాల్యము A అనుకుంటే దానిపై పతనం చెందిన సౌరశక్తి E = 200 A జౌల్ ; దక్షత = 20%
అవసరమైన విద్యుత్ శక్తి = 8 KW = 8000 W
ఒక సెకనుకు ఉత్పత్తి అయిన ఉపయోగపడిన విద్యుత్ శక్తి = 200A × η
= 200 A . \(\frac{20}{100}\) = 40 A

A = \(\frac{8000}{40}\) = 200 చ.మీ.
ఇది దాదాపు ఒక పెద్ద ఇంటి పై కప్పు వైశాల్యానికి సమానము.