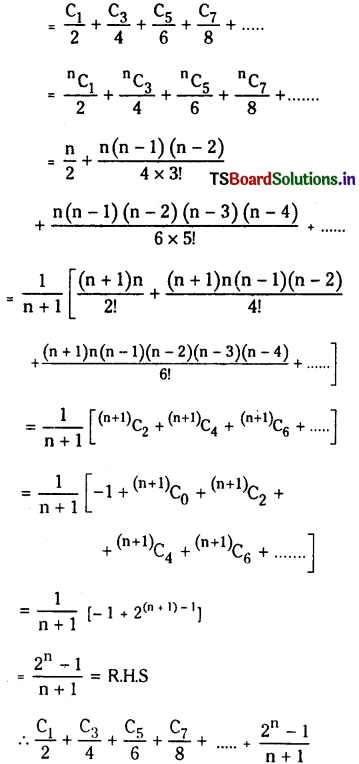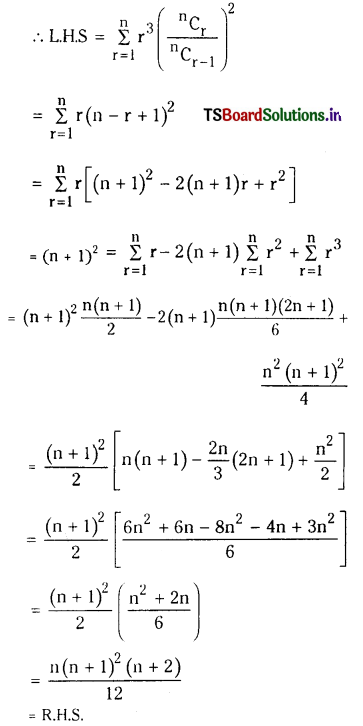Srinivas – Page 48 – TS Board Solutions

TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions

February 28, 2024February 27, 2024 by Srinivas

Students must practice these TS Inter 1st Year Maths 1A Important Questions Chapter 7 Trigonometric Equations to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions

Question 1.
Solve 2cos²θ – \(\sqrt{3}\) sin θ+1 = 0
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 1

Question 2.
Solve 1 +sin²θ = 3 sinθ cosθ
Solution:
Dividing by cos² θ we get
⇒ sec² θ + tan² θ = 3 tanθ
⇒ 1 + 2 tan² θ = 3 tanθ
⇒ 2tan² θ – 3tan θ +1 = θ
⇒ 2 tan² θ – 2tan θ – tanθ + 1 = θ
⇒ (tanθ – 1)(2tan θ – 1) = θ
⇒ tanθ = 1 or tanθ = \(\frac{1}{2}\)
If tan θ = 1 then principal solution is α =\( \frac{\pi}{4}\)
General solution is θ = nπ + \(\frac{\pi}{4}\) n ∈ Z
Let a be the principal solution of tan θ = \(\frac{1}{2}\)
Then the general solution is
θ = nπ+α,n∈ Z

Question 3.
Solve \(\sqrt{2}(\sin x+\cos x)=\sqrt{3}\)
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 3

Question 4.
Solve tanθ+3 cotθ = 5 secθ
Solution:
The given equation is
tanθ + 3 cotθ = 5 secθ
⇒ \(\frac{\sin \theta}{\cos \theta}+\frac{3 \cos \theta}{\sin \theta}=\frac{5}{\cos \theta}\)
⇒ sin² θ + 3cos²θ= 5 sinθ
⇒ sin² θ + 3(1 – sin² θ) = 5 sinθ
⇒ sin² θ + 3 – 3 sin² θ = 5 sinθ
⇒ -2 sin θ – 5 sinθ + 3 = 0
⇒ 2 sin θ+ 5 sinθ – 3 = θ
⇒ 2 sin θ + 6 sinθ – sinθ – 3 = θ
⇒ 2 sin θ(sin θ + 3) – 1(sinθ + 3) = θ
⇒ (2sinθ – 1)(sinθ + 3)= θ
⇒ sin θ = \(\frac{1}{2}\) or sinθ = – 3.
sinθ =-3 is not admissible but for sinθ = \(\frac{1}{2}\) general solution is
θ=nπ+(-n)ⁿ ,n∈Z
Since the principal solution is α = \(\frac{1}{2}\)

Question 5.
If acos²θ + bsin²θ =c has θ₁,θ₂ as its solutions then show that tan θ₁ + tan θ₁ = \(\frac{2 b}{c+a}\)
Solution:
Given equation is acos2θ + bsin2θ = c
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 4
This is a quadratic equation in an θ.
Given θ₁,θ₂ are the solutions of θ.
tan θ₁, tanθ₂are the roots of equation (1)
∴ Sum of the roots tan θ₁ + tan θ₂ = \(\frac{2 b}{a+c}\) and product of the roots
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 5

Question 6.
Find all values of x in (-π, π) satisfying the equation g¹+cosx+cos² x +……………….. = 4³
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 6

Question 7.
Solve sin x = \(\frac{1}{\sqrt{2}}\)
Solution:
Principal solution is α = \(\frac{\pi}{4}\)
General solution is
\(\mathrm{x}=\mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{\pi}{4}, \mathrm{n} \in \mathrm{Z}\)

Question 8.
Solve sin 2θ \(=\frac{\sqrt{5}-1}{4}\)
Solution:
The principal solution is α = 18°
∴ General solution is
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 7
Question 9.
Solve tan²θ = 3.
Solution:

Question 10.
Solve 3cosec x = 4sinx.
Solution:
Given 3 cosec x = 4 sin x

Question 11.
If x is acute and sin(x+10°) = cos(3x – 68°) find x in degrees.
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 10
When k = 0 we get x = 37°
If we take k = 1, 2 the value of x is not acute.
Hence the value of x is 37°.

Question 12.
Solve cos 3θ = sin 2θ.
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 11

Question 13.
Solve 7 sin²θ+3cos² θ= 4.
Solution:
Given 7 sin²θ+3cos² θ= 4.
⇒ 7 sin 2θ + 3(1 -sin² θ) = 4
⇒ 4 sin 2θ = 1
⇒ sinθ = ± \(\frac{1}{2}\)
Principal solutions are \(\alpha=\pm \frac{\pi}{6}\) and general solution is given by general solution is given by
θ = nπ ± ,\(\alpha=\pm \frac{\pi}{6}\),n∈Z

Question 14.
Find general solution of θ which satisfies both the equations sinθ = \(-\frac{1}{2}\) and cosθ = \(-\frac{\sqrt{3}}{2}\)
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 12

Question 15.
Solve 4 sin x. sin 2x sin 4x = sin 3x
Solution:
Given sin 3x = 4 sinx sin 2x sin 4x
= 2sinx (2sin2x – sin4x)
⇒ 2 sin x (cos 2x – cos 6x)
⇒ sin3x = 2cos 2x sinx – 2 cos 6x sin x
⇒ sin 3x = sin 3x – sin x – 2 cos 6xsinx
⇒ 2cos 6x sinx + sinx= 0
⇒ sinx(2 cos 6x + 1)=0
⇒ sinx = 0 or cos 6x \(-\frac{1}{2}\)

Case (i): sin x = 0, x= nπ, n∈Z is the general solution.
Case (ii) : cos 6x = \(-\frac{1}{2}\)
Principal solution is α \( =\frac{2 \pi}{3}\)
∴ General solution is 6x = 2πr ± \(\frac{2 \pi}{3}\)
\(x=\frac{n \pi}{3} \pm \frac{\pi}{9}, n \in Z\)

Question 16.
If 0<θ<π solve cosθ cos2θ cos3θ = \(\frac{1}{4}\)
Solution:
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 12

Question 18.
Solve sin2x – cos2x = sinx – cosx
Solution:
The given equation can be written as
sin 2x – sin x = cos 2x – cos x
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 14

Question 19.
Solve cos 3x + cos 2x = sin + sin = \(\sin \frac{3 x}{2}+\sin \frac{x}{2} 0 \leq x \leq 2 \pi\)
Solution:
Given cos 3x + cos 2x = sin + sin = \(\sin \frac{3 x}{2}+\sin \frac{x}{2} 0 \leq x \leq 2 \pi\)
TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions 15

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions

February 27, 2024February 26, 2024 by Srinivas

Students must practice these TS Inter 1st Year Maths 1A Important Questions Chapter 8 Inverse Trigonometric Functions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions

Question 1.
Prove that
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 14
Solution:

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 2.
Find the values of the following.

(i) \(\sin ^{-1}\left(-\frac{1}{2}\right)\)
Solution:
\(\sin ^{-1}\left(-\frac{1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)=-\frac{\pi}{6}\)

(ii) \(\cos ^{-1}\left(-\frac{\sqrt{3}}{2}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 2

(iii) \(\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)
Solution:
\(\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=\tan ^{-1}\left(\tan \frac{\pi}{6}\right)=\frac{\pi}{6}\)

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

(iv) cot^-1 (-1)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 3

(v) sec ^-1 \((-\sqrt{2})\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 4

(vi) Cosec ^-1 \(\left(\frac{2}{\sqrt{3}}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 15

Question 3.
Find the values of the following.

(i) sin^-1 \(\left(\sin \frac{4 \pi}{3}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 6

(ii) \(\tan ^{-1}\left(\tan \frac{4 \pi}{3}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 7

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 4.
Find the values of the following.

(i) \(\sin \left(\cos ^{-1} \frac{5}{13}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 8

(ii) \(\tan \left(\sec ^{-1} \frac{25}{7}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 9

(iii) \(\cos \left(\tan ^{-1} \frac{24}{7}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 10

Question 5.
Find the values of the following.

(i) \(\sin ^2\left(\tan ^{-1} \frac{3}{4}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 11

(ii) \(\sin \left(\frac{\pi}{2}-\sin ^{-1}\left(-\frac{4}{5}\right)\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 12

(iii) \(\cos \left(\cos ^{-1}\left(-\frac{2}{3}\right)-\sin ^{-1}\left(\frac{2}{3}\right)\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 13

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

(iv) sec² (cot^-13) + cosec² (tan^-1 2)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 16

Question 6.
Find the value of \(\cot ^{-1}\left(\frac{1}{2}\right)+\cot ^{-1}\left(\frac{1}{3}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 17

Question 7.
Prove that
\(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{7}{25}\right)=\sin ^{-1}\left(\frac{117}{125}\right)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 18

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 8.
If x ∈(-1, 1) prove that 2 tan^-1 x = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\)
Solution:
Given x ∈ (-1,1) and it tan^-1 x = a then tan α = x and
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 19

Question 9.
Prove that \(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{5}{13}\right) +\sin ^{-1}\left(\frac{16}{65}\right)=\frac{\pi}{2}\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 20

Question 10.
Prove that cot^-1 9+ cosec^-1 \( \frac{\sqrt{41}}{4}=\frac{\pi}{4}\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 21

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 11.
Show that cot \(\begin{aligned} \cot \left(\operatorname{Sin}^{-1} \sqrt{\frac{13}{17}}\right) \\ = \sin \left(\operatorname{Tan}^{-1}\left(\frac{2}{3}\right)\right) \end{aligned}\)
Solution:

Question 12.
Find the value of \(tan \left[2 \operatorname{Tan}^{-1}\left(\frac{1}{5}\right)-\frac{\pi}{4}\right]\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 23

Question 13.
Prove that \(\operatorname{Sin}^{-1}\left(\frac{4}{5}\right)+2 \operatorname{Tan}^{-1}\left(\frac{1}{3}\right)=\frac{\pi}{2}\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 24

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 14.
If sin^-1x + sin^-1 y + sin^-1 z = π, then prove that x⁴ + y⁴ + z⁴ + 4x²y²z²= 2 (x²y² + y²z²+ z²x²)
Solution:
Let sin^-1 x = A, sin^-1 y = B and sin^-1z = C
then A+B+C = π …………………..(1)
and sinA = x, sin B = y, sin C = z
Now A+B = π – c
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 25

Question 15.
If \(\operatorname{Cos}^{-1}\left(\frac{p}{a}\right)+\operatorname{Cos}^{-1}\left(\frac{q}{b}\right)\) =α the prove that
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 36
Solution:

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 16.
Solve \(\sin ^{-1}\left(\frac{5}{x}\right)+\sin ^{-1}\left(\frac{12}{x}\right)=\frac{\pi}{2},(x>0)\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 28

Question 17.
Solve
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 35
Solution:

Question 18.
Solve \(\operatorname{Sin}^{-1} x+\operatorname{Sin}^{-1} 2 x=\frac{\pi}{3}\)
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 31
when \(x=-\frac{\sqrt{3}}{2 \sqrt{7}}\) value is not admissible
Since sin^-1 x and sin^-1 2x are negative
Hence \(x=-\frac{\sqrt{3}}{2 \sqrt{7}}\)

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 19.
If sin [2 Cos^-1 (cot (2 Tan^-1x)}] = 0 find x.
Solution:
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 32

Question 20.
Prove that
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions 34
Solution:
Let cot^-1x=θ then cot θ = x and θ <x<π
∴ sin (cot^-1x) = sinθ = \(\frac{1}{\operatorname{cosec} \theta}\)

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions width=

Question 21.
Show that sec² (tan^-1) + cosec² (cot^-1 2) = 10.
Solution:
[1 + tan² (tan^-1(2)] + [1+ cot² (cot^-1(2))]
= 1 + 4 + 1 + 4 = 10

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions

February 28, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions

Do This

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 1

Question 1.
Draw a circle with any radius. Draw four tangents at different points. How many tangents can you draw to this circle ? (AS₃, AS₅) (Page No. 226)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 2
Let ‘O’ be the centre of the circle with radius ‘OA’. l, m, n, p and q be the tangents to the circle at A, B, C, D and E. We can draw a tangent at each point on the circle, i.e., infintely many tangents can be drawn to a circle.

Question 2.
How many tangents you can draw to circle from a point away from it ? (AS₃) (Page No. 226)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 3
We can draw only two tangents from an exterior point.

Question 3.
In the below figure which are tangents to the circles ? (AS₃) (Page No. 226)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 4
P and M are the tangents to the circles.

Question 4.
Draw a circle and a secant PQ of the circle on a paper as shown below. Draw various lines parallel to the secant on both sides of it. What happens to the length of chord coming closer and closer to the center of the circle ?
What is the longest chord ? How many tangents can you draw to a circle, which are parallel to each other. (Page No. 227)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 5
The length of the chord increases as it comes closer to the centre of the circle.

i) What is the longest chord ? (Page No. 227)
Solution:
Diameter is the longest of all chords.

ii) How many tangents can you draw to a circle which are parallel to each other ? (Page No. 227)
Solution:
Only one tangent can be drawn parallel to a given tangent. To a circle, we can draw infinetely pairs of parallel tangents.

Try This

Question 1.
How can you prove the converse of the above theorem. “If a line in the plane of a circle is perpendicular to the radius at its end point on the circle, then the line is tangent to the circle”. (Page No. 228)
Solution:
Given : Circle with centre ‘O’, a point ‘A’ on the circle and the line AT’ perpendicular to OA’.
RTP : ‘AT’ is a tangent to the circle at A.
Construction :
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 6
Suppose ‘AT’ is not a tangent then ‘AT’ produced either way if necessary, will meet the circle again. Let it do so at R join OR

Proof : Since OA = OP (radii)
∴ ∠OAP = ∠OPA
But ∠OPA = 90°
∴ Two angles of a triangle are right angles which is impossible.
∴ Our supposition is false, hence AT is a tangent.

We can find some more results using the above theorem.

Since there can be only one perpendicular OP at the point R it follows that one and only are tangent can be drawn to a circle at a given point on the circumference.
Since there can be only one perpendicular to XY at the point R it follows that the perpendicular to a tangent at its point of contact passes through the centre.

Question 2.
How can you draw the tangent to a circle at a given point when the centre of the circle is not known ? (Page No. 229) Hint : Draw equal angles ∠QPX and ∠PRQ. Explain the construction.
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 7
Steps of construction :

Take a point ‘P’ and draw a chord PR through P
Construct ∠PRQ and measure it.
Construct ∠QPX at P equal to ∠PRQ.
Extend PX on otherside. XY is the required tangent at R

Note : Angle between a tangent and chord is equal to angle in the alternate segment.

Try This

Question 1.
Use pythagorus theorem and write proof for the statement “the lengths of tangents drawn from an external point to a circle are equal”. (Page No. 231)
Solution:
Given : Two tangents PA and PB to a circle with centre ‘O’, from an exterior point P.
R.T.P : PA = PB
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 8
Proof : In ∆OAP; ∠OAP = 90°
∴ AP² = OP² – OA² [∵ square of the hypotenuse is equal to the sum of squares on the other 2 sides → Pythagoras theorem]
⇒ (AP)² = (OP)² – (OB)²
[∵ OA = OB, radii of the same circle]
⇒ AP² = BP²
[∴ In a ∆OBP; OB² + BP² = OP²
⇒ BP² = OP² – OB²]
⇒ AP² = BP²
∴ PA = PB (CPCT)
Hence proved.

Question 2.
Draw a pair of radii OA and OB such that ∠BOA = 120°. Draw the bisector of ∠BOA and draw lines perpendicular to OA and OB at A and B. These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and justify. (Page No. 235)
Solution:
Justification :
OA ⊥ PA
OB ⊥ PB
Also in ∆OAP, ∆OBP
OA = OB
∠OAP = ∠OBP
OP = OP
∴ ∆OAP ≅ ∆OBP
∴ PA = PB [Q.E.D]
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 9

Do This

Question 1.
Shankar made the following pictures also
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 10
What shapes can they be broken into that we can find area easily ? (Page No. 237)
Solution:

Into two rectangles.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 12
A rectangle and a circle

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 13
A cone and a secant

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 14
A rectangle and 2 segments

Make some more pictures and think of the shapes they can be divided into different parts.
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 15
A cone and segment

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 16
A rectangle and a segment

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 17
A square and four segments

A cone and segment
A rectangle and a segment A square and four segments.

Do This

Question 1.
Find the area of sector, whose radius is 7 cm with the given angle : (Page No. 239)
(i) 60°
(ii) 30°
(iii) 72°
(iv) 90°
(v) 120°
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 18

Question 2.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 10 minutes. (Page No. 239)
Solution:
Angle made by minute hand in 360°
1 min = \(\frac{360^{\circ}}{60^{\circ}}\) = 6°
Angle made by minute hand in
10 min = 10 × 6° = 60°
The area swept by minute hand is in the shape of a sector with radius.
r = 14 cm and angle x° = 60°
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 19
Area (A) = \(\frac{x^{\circ}}{360^{\circ}}\) × πr²
= \(\frac{60^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 14 × 14
= \(\frac{616}{6}\) ⇒ 102.66 cm²
∴ Area swept by the minute hand in 10 minutes = 102.66 cm²

Try This

Question 1.
How can you find the area of major seg¬ment using are a of minor segment ?
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions 20
Area of the major segment = (Area of the circle) – (Area of the minor segment)

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise

February 28, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise

Question 1.
Prove that the angle between the two tan-gents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
PA and PB are tangents to the circle with centre ‘0’ from and external point P.
Join OA, OB and OR The angle between the tangents is ∠APB.
We have to prove that ∠AOB + ∠APB = 180°
PA is a tangent to the circle with centre ‘O’.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 1
A is the point of contact. AO is the radius drawn through the point of contact i.e., A
∴ ∠PAO = 90°
PB is a tangent to the circle with centre ‘O’.
B is the point of contact. BO is the radius drawn through the point of contact i.e., B
∴ ∠PBO = 90°
OAPB is a quadrilateral.
The sum of the angles of a quadrilateral is 360°
∠APB + ∠PBO + ∠AOB + ∠PAO = 360°
∠APB + ∠AOB + ∠PAO + ∠PBO = 360°
∠APB + ∠AOB + 90° + 90° = 360°
∴ ∠APB + ∠AOB = 360° – 90° – 90°
= 360° – 180° = 180°
∠APB and ∠AOB are supplementary.

Question 2.
PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T (See figure). Find the length of TP.
Solution:
PQ is a chord of length 8cm of a circle with centre ‘O’.
Radius of the circle = 5 cm.
⇒ OP = OQ = 5cm
The tangents at P and Q meet at T. Join OT.
OT is the perpendicular bisector of PQ.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 2
In triangle OPT, ∠OPT = 90°
∴ PT² = OT² – OP² …………….. (1)
In ∆ PRO, ∠R = 90°
∴ OP² = OR² + PR²
⇒ OR² = OP² – PR²
= 5² – 4²
= 25 – 16 = 9
∴ OR = \(\sqrt{9}\) = 3 cm
In the right triangle OPT,
PR is perpendicular to the hypotenuse OT.
∴ PR² = TR. RO
4² = TR × 3 ⇒ TR = \(\frac{4^2}{3}\) = \(\frac{16}{3}\)
OT = OR + TR = \(\frac{3}{1}\) + \(\frac{16}{3}\) = \(\frac{25}{3}\)
From (1), PT² = \(\left(\frac{25}{3}\right)^2\) – (5)²
= \(\frac{625}{9}\) – \(\frac{25}{1}\)
= \(\frac{625-225}{9}\) = \(\frac{400}{9}\)
∴ PT = \(\sqrt{\frac{400}{9}}\) = \(\frac{20}{3}\) cm

Question 3.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
ABCD is a quadrilateral, circumscribing a circle whose centre is O.
The opposite sides AB and CD are subtend angles ∠AOB and ∠COD at the centre.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 3
Similarly, the other pair of opposite sides AD and BC subtend angles ∠AOD and ∠BOC at the centre.
We have to prove that
∠AOB + ∠COD = 180°
and ∠AOD + ∠BOC = 180°
Join OR OQ, OR and OS.
We know that the tangents drawn from an ex¬ternal point to a circle subtend equal angles at the centre.
AP and AS are the tangents to the circle from A.
∴ ∠AOP = ∠AOS ……………. (1)
BP and BQ are the tangents to the circle from B.
∴ ∠BOP = ∠BOQ …………….. (2)
CQ and CR are the tangents to the circle from C.
∴ ∠COQ = ∠COR ………………. (3)
DR and DS are the tangents to the circle from D.
∴ ∠DOR = ∠DOS …………………. (4)
Adding (1), (2), (3) and (4), we get
∠AOP + ∠BOP + ∠COQ + ∠DOR + ∠AOS + ∠BOQ + ∠COR + ∠DOS = 360°
(∵ Sum of the angles formed at’O’is equal to 360°)
(∠AOP + ∠BOP) + (∠COR + ∠DOR) + (∠BOQ + ∠COQ) + (∠AOS + ∠DOS) = 360° 2∠AOP + 2∠COR + 2 ∠BOQ + 2 ∠DOS = 360°
⇒ ∠AOP + ∠COR + ∠BOQ + ∠DOS = 180°
⇒∠AOP + ∠BOQ + ∠COR + ∠DOS = 180°
⇒ ∠AOP + ∠BOP + ∠COR + ∠DOR = 180°
(∵ ∠BOQ = ∠BOP and ∠DOS = ∠DOR
⇒ ∠AOB + ∠COD = 180°
In ∆^les BOP & BOQ)
Similarly, we can prove that
∠BOC + ∠AOD = 180°

Question 4.
Draw a line segment AB of length 8cm. Taking A as centre, draw a circle of radius 4cm and taking B as centre, draw another circle of radius 3cm. Construct tangents to each circle from the centre of the other circle.
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 4

Draw a line segment AB = 8 cm.
Take A as centre and draw a circle (C₁) of radius 4cm.
Take B as centre and draw a circle (C₂) of radius 3 cm.
Draw the perpendicular bisector PQ of AB.
Draw a circle with AB as diameter (C₃). This circle intersects the circle with A as centre in T₁ and T₂. Join BT₁ and BT₂. These are the tangents to the circle C₁.
The circle with AB as diameter (C₃) intersects the circle with B as centre (C₂) in R₁ and R₂. Join AR₁ and AR₂. These are the tangents to the circle C₂.

Question 5.
Let ABC be a right angled triangle in which AB = 6cm, BC = 8cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
Construction :
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 5

Draw a line segment AB = 6cm.
Make ∠ABX = 90°.
Mark a point C on \(\overrightarrow{\mathrm{BX}}\) such that BC = 8cm. Join AC.
Draw BD ⊥ AC intersecting AC in D.
Draw the perpendicular bisectors of BC and CD. Let them intersect at ‘O’.
Take ‘O’ as centre and OB = OD = OC as radius, draw a circle passing through B, D and C
Join AO. Find M the mid point of AO.
Take M as centre and radius as (AM = MO) draw a circle passing through A and C, intersecting the first circle at T₁ and T₂.
Join AT₁ and AT₂.
AT₁ and AT₂ are the required tangents.

Question 6.
Find the area of the shaded region in the figure, given in which two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 6
Solution:
AC denotes the radius of the bigger circle.
AC = 8cm. (Given)
AB denotes the distance between the centres of two circles.
AB = 3cm (Given)
∴ BC denotes the radius of the smaller circle
BC = AC – AB = 8 – 3 = 5 cm
The Area of the shaded region = Area of the bigger circle – Area of the smaller circle =
= π(8)² – π(5)²
= π[8² – 5²]
= π[64 – 25]
= \(\frac{22}{7}\) × 39
= \(\frac{858}{7}\)
= 122.57 cm²

Question 7.
ABCD is a rectangle with AB = 14 cm and BC = 7cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise 7
Solution:
ABCD is a rectangle.
Length of the rectangle AB = CD = 14 cm
Breadth of the rectangle AD = BC = 7cm
Area of the rectangle ABCD
= length × breadth
= 14 × 7
= 98 cm²
Two semi-circles are drawn on AD and BC clearly, They are of the same diameters.
Hence, Area of two semi-circles becomes area of one complete circle with diameter 7 cm.
So, radius of the circle (r) = \(\frac{7}{2}\) cm
Area of the circle = πr²
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\)
= 38.5 cm² ……………….. (1)
Area a of the semi-circle whose diameter is 14 cm = \(\frac{1}{2}\)πr² ; Here, r = 7cm
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7
= 77 cm²
Area of the shaded region in the rectangle
= Area of the rectangle – Area of the semicircle
= 98 – 77
= 21 cm² ……………… (2)
Area of the total shaded region
= Area of the circle (shaded) + Area of the shaded region in the rectangle.
= (38.5 + 21) cm²
= 59.5 cm²

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a)

February 27, 2024February 26, 2024 by Srinivas

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a)

I.
Question 1.
Expand the following using binomial theorem.
i) (4x + 5y)⁵
ii) \(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\)
iii) \(\left(\frac{2 p}{5}-\frac{3 q}{7}\right)^6\)
iv) (3x + x – x²)⁴
Solution:
i) we know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)
∴ (4x + 5y)⁷ = \({ }^7 \mathrm{C}_0\) (4x)⁷ + \({ }^7 \mathrm{C}_1\) (4x)⁶ (5y) + \({ }^7 \mathrm{C}_2\) (4x)⁵ (5y)² + \({ }^7 \mathrm{C}_3\) (4x)⁴ (5y)³ + \({ }^7 \mathrm{C}_4\) (4x)³ (5y)⁴ + \({ }^7 \mathrm{C}_5\) (4x)² (5y)⁵ + \({ }^7 \mathrm{C}_6\) (4x) (5y)⁶ + \({ }^7 \mathrm{C}_7\) (5y)⁷
= \(\sum_{r=0}^7{ }^7 C_r\) . (4x)^7-r . (5y)^r.

ii) We know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)

\(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\) = \({ }^5 C_0\left(\frac{2}{3} x\right)^5+{ }^5 C_1\left(\frac{2}{3} x\right)^4\left(\frac{7}{4} y\right)+{ }^5 C_2\left(\frac{2}{3} x\right)^3\left(\frac{7}{4} y\right)^2 +{ }^5 C_3\left(\frac{2}{3} x\right)^3\left(\frac{7}{4} y\right)^3\) + \({ }^5 C_4\left(\frac{2}{3} x\right)\left(\frac{7}{4} y\right)^4+{ }^5 C_5\left(\frac{7}{4} y\right)^5\)

= \(\sum_{r=0}^5{ }^5 C_r \cdot\left(\frac{2}{3} x\right)^{5-r} \cdot\left(\frac{7}{4} y\right)^r\)

iii) We know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 1

iv) We know that
(3 + x – x²)⁴ = [3 + x (1 – x)]⁴
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)
∴ [3 + x (1 – x)]⁴ = \({ }^4 C_0\) 3⁴ + \({ }^4 C_1\)3³x (1 – x + \({ }^4 C_2\) 3²x² (1 – x)² + \({ }^4 C_3\) 3x³ (1 – x)³ + \({ }^4 C_4\) x⁴ (1 – x)⁴
= 81 + 108x (1 – x) + 54x² (1 – 2x + x²) + 12x³ (1 – 3x + 3x² – x³) + x⁴ (1 – 4x + 6x² – 4x³ + x⁵
= 81 + 108x – 54x² – 96x³ + 19x⁴ + 32x⁵ – 6x⁶ – 4x⁷ + x⁸.

Question 2.
Write down and simplify
i) 6th term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^y\)
ii) 7th term in (3x – 4y)¹⁰
iii) 10th term \(\left(\frac{3 p}{4}-5 q\right)^{14}\)
iv) rth term in \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) (1 ≤ r ≤ 9).
Solution:
i) r + 1th term n the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
∴ 6th term in the expansion of \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) is given by
T₆ = \({ }^9 C_5 \cdot\left(\frac{2 x}{3}\right)^4 \cdot\left(\frac{3 y}{2}\right)^5\)
= 189 . x⁴ . y⁵

ii) (r + 1)th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
7th term In the expansion of (3x – 4y)¹⁰ is given by
T₇ = \({ }^{10} \mathrm{C}_6\) (3x)⁴ (- 4y)⁶
= 280 . 12⁵ x⁴ y⁶.

iii) (r + 1)th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
10th term in the expansion of \(\left(\frac{3 p}{4}-5 q\right)^{14}\) is given by
T₁₀ = \({ }^{14} \mathrm{C}_9\left(\frac{3 p}{4}\right)^5\) (- 5q)⁹
= \(\frac{-(2002) \cdot 3^5 \cdot 5^9}{4^5}\) . p⁵ . q⁹.

iv) (r + )th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
∴ rth term in the expansion of \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) is given by
T_r = \({ }^8 C_{r-1}\left(\frac{3 a}{5}\right)^{9-r}\left(\frac{5 b}{7}\right)^{r-1}\).

Question 3.
Find the number of terms in the expansion of
i) \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\)
ii) (3p + 4q)¹⁴
iii) (2x + 3y + z)⁷
Solution:
1) The expansion of (x + a)ⁿ contains (n + 1) terms.
∴ Expansion of \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\) contains 10 terms.

ii) The expansion of (x + a)ⁿ contains (n + 1) terms.
∴ Expansion of (3p + 4q)¹⁴ contains 15 terms.

iii) Number of terms in the expansion of
(a + b + c)ⁿ = \(\frac{(n+1)(n+2)}{2}\)
∴ Expansion oF (2x + + z)⁷ contains \(\frac{(7+1)(7+2)}{2}\) = 36 terms.

Question 4.
Find the numerically greatest term(s) in the expansion of coefficients in (4x – 7y)⁴⁹ + (4x + 7y)⁴⁹.
Solution:
We know that
(4x – 7y)⁴⁹ = \({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ – \({ }^{49} \mathrm{C}_1\)(4x)⁴⁸ (7y) + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² – \({ }^{49} \mathrm{C}_3\) (4x)⁴⁶ (7y)³ + ……………. + \({ }^{49} \mathrm{C}_49\) (7y)⁴⁹ ………….(1)

(4x + 7y)⁴⁹ = \({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ + \({ }^{49} \mathrm{C}_1\)(4x)⁴⁸ (7y) + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² + \({ }^{49} \mathrm{C}_3\) (4x)⁴⁶ (7y)³ + ……………. + \({ }^{49} \mathrm{C}_49\) (7y)⁴⁹ ………….(2)

(1) + (2)
(4x – 7y)⁴⁹ + (4x + 7y)⁴⁹ = 2[\({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² + \({ }^{49} \mathrm{C}_4\) (4x)⁴⁵ (7y)⁴ + ………….. + \({ }^{49} \mathrm{C}_48\) (4x) (7y)⁴⁸]
which contains 25 non-zero coefficients.

Question 5.
Find the sum of last 20 coefficients in the expansion of (1 + x)³⁹.
Solution:
The last 20 coeffIcients in the expansion of (1 + x)³⁹ are \({ }^{39} \mathrm{C}_{20},{ }^{39} \mathrm{C}_{21}, \ldots \ldots \ldots,{ }^{39} \mathrm{C}_{39}\)
We know that

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 2

∴ The sum of last 20 coefficients in expansion of (1 + x)³⁹ is 2³⁸.

Question 6.
If A and B are coefficients of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^{2n – 1} respectively, then find the value of \(\frac{A}{B}\).
Solution:
Coefficient of xⁿ in the expansion of (1 + x)²ⁿ is \({ }^{2 n} C_n\).
Coefficient of xⁿ in the expansion of (1 + x)^{2n – 1} is \({ }^{2 n – 1} C_n\)
∴ A = \({ }^{2 n} C_n\) and B = \({ }^{2 n – 1} C_n\).
∴ \(\frac{A}{B}=\frac{{ }^{2 n} C_n}{2 n-1}=\frac{\frac{2 n !}{n ! n !}}{\frac{(2 n-1) !}{(n-1) ! \cdot n !}}\)
\(\frac{2 n !}{(2 n-1) ! n !} \cdot(n-1) !=\frac{2 n}{n}\)
\(\frac{A}{B}\) = 2.

II.
Question 1.
Find the coefficient of
i) x^-6 in \(\left(3 x-\frac{4}{x}\right)^{10}\)
ii) x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\)
iii) x² in \(\left(7 x^3-\frac{2}{x^2}\right)^9\)
iv) x^-7 in \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\)
Solution:
i) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
(r + 1)th term in the expansion of \(\left(3 x-\frac{4}{x}\right)^{10}\) is
T_r+1 = \({ }^{10} \mathrm{C}_{\mathrm{r}}\) . (3x)^10-r . (\(\frac{-4}{x}\))^r
T_r+1 = \({ }^{10} \mathrm{C}_{\mathrm{r}}\) . (3)^10-r . (- 4)^r . x^10-2r.
for coefficient of x^-6, 10 – 2r = – 6
⇒ 2r = 16
⇒ r = 8.
∴ Coefficient of x^-6 is \({ }^{10} \mathrm{C}_8\) . 3^10-8 . (- 4)⁸ = 405 × 4⁸.

ii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
(r + 1)th term in the expansion of \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) is
T_r+1 = \({ }^{13} C_r \cdot\left(2 x^2\right)^{13-r} \cdot\left(\frac{3}{x^3}\right)^r\)
T_r+1 = \({ }^{13} C_r \) . 2^13-r . 3^r . x^26-5r
For coefficients of x¹¹, 26 – 5r = 11
⇒ 5r = 15
⇒ r = 3.
Coefficient of x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) is \({ }^{13} C_3 \) . 2^13-3 . 3³
= 286 . 2¹⁰ . 3³.

iii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
∴ General term in the expansion of \(\left(7 x^3-\frac{2}{x^2}\right)^9\) is
T_r+1 = \({ }^9 C_r \cdot\left(7 x^3\right)^{9-r}\left(\frac{-2}{x^2}\right)^r\)
= \({ }^9 C_r\) 7^9-r (- 2)^r . x^27-5r
for coefficient of x², 27 – 5r = 2
⇒ 5r = 25
⇒ r = 5.
∴ Coefficient of x² is \({ }^9 \mathrm{C}_5\) . 7⁴ . (- 2)⁵
= – 126 . 7⁴ . 2⁵.

iv) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)\) is
T_r+1 = \(={ }^7 C_r \cdot\left(\frac{2}{3} x^2\right)^{7-r} \cdot\left(\frac{-5}{4 x^5}\right)^r\)
= \({ }^7 \mathrm{C}_{\mathrm{r}} \cdot\left(\frac{2}{3}\right)^{7-\mathrm{r}}\left(\frac{-5}{4}\right)^{\mathrm{r}} \mathrm{x}^{14-7 \mathrm{r}}\)
For coefficient of x^-7, 14 – 7r = – 7
⇒ 7r = 21
⇒ r = 3
∴ Coefficient of x^-7 is \({ }^7 C_3 \cdot\left(\frac{2}{3}\right)^4 \cdot \frac{(-5)^3}{4^3}\)
= \(-\frac{35 \times 16 \times 125}{81 \times 64}=\frac{-4375}{324}\).

Question 2.
Find the term independent of x in the expansion of
i) \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\)
ii) \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
iii) \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\)
iv) \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\)
Solution:
i) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\) is
T_r+1 = \({ }^{10} C_r \cdot\left(\frac{\sqrt{x}}{3}\right)^{10-r} \cdot\left(\frac{-4}{x^2}\right)^r\)
= \({ }^{10} C_r \cdot \frac{x^{\frac{10-r}{2}}}{3^{10-r}} \cdot \frac{(-4)^r}{x^{2 r}}\)
= \({ }^{10} C_r \cdot \frac{(-4)^r}{3^{10-r}} \cdot x^{\frac{10-5 r}{2}}\)
For the independent term (i.e., the coefficient of x⁰)
put \(\frac{10-5 r}{2}\) = 0
⇒ r = 2.
∴ Term independent of ‘x’ in the expansion is
T3 = \({ }^{10} C_2 \frac{(-4)^2}{3^8} \times x^0=\frac{80}{729}\).

ii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\) is
T_r+1 = \({ }^{25} C_r\left(\frac{3}{\sqrt[3]{x}}\right)^{25-r} \cdot(5 \sqrt{x})^r\)
= \({ }^{25} C_r\) . 3^25-r . 5^r . x^{(5r – 50)/6}
For the independent term,
(i.e., coefficient of x⁰)
Put \(\frac{5 r-50}{6}\) = 0
⇒ r = 10.
∴ Term independent of ‘x’ in the expansion is T₁₁ = \({ }^{25} \mathrm{C}_{10}\) . 3¹⁵ . 5¹⁰.

iii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\) is
T_r+1 = \({ }^{14} C_r \cdot\left(4 x^3\right)^{14-r} \cdot\left(\frac{7}{x^2}\right)^r\)
= \({ }^{14} C_r\) . 4^14-r . 7^r . x^42-5r.
For the independent term, (i.e., coefficient of x⁰)
Put 42 – 5r = 0
which is impossible as ‘r’ is integer.
∴ Term independent of ‘x in the expansion is ‘0’.

iv) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\) is
T_r+1 = \({ }^9 C_r\left(\frac{2 x^2}{5}\right)^{9-r} \cdot\left(\frac{15}{4 x}\right)^r\)
= \({ }^9 \mathrm{C}_{\mathrm{r}}\left(\frac{2}{5}\right)^{9-\mathrm{r}} \cdot\left(\frac{15}{4}\right)^{\mathrm{r}} \cdot \mathrm{x}^{18-3 \mathrm{r}}\)
For the independent term, (i.e. coefficient of x⁰)
Put 18 – 3r = 0
⇒ r = 6
Term independent of ‘x’ in the expansion is
T₇ = \({ }^9 \mathrm{C}_6 \cdot\left(\frac{2}{5}\right)^3 \cdot\left(\frac{15}{4}\right)^6\)
= \(\frac{3^7 \cdot 5^3 \cdot 7}{2^7}\).

Question 3.
Find the middle term(s) in the expansion of
i) \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
ii) \(\left(4 a+\frac{3}{2} b\right)^{11}\)
iii) (4x² + 5x³)¹⁷
iv) \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\)
Solution:
i) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3 x}{7}-2 y\right)^{10}\) is
T_r+1 = \({ }^{10} C_{\mathrm{r}} \cdot\left(\frac{3 \mathrm{x}}{7}\right)^{10-\mathrm{r}}(-2 \mathrm{y})^{\mathrm{r}}\)
The expansion has 11 (odd number) terms.
Hence T₆ is the only middle term.
Thus r = 5
∴ Middle term in the expansion is
T₆ = \(-10 C_5\left(\frac{6}{7}\right)^5\) . x⁵ . y⁵.

ii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion \(\left(4 a+\frac{3}{2} b\right)^{11}\) is
T_r+1 = \(\)
The expansion has 12 (even numbers) terms.
Hence T₆ and T₇ are the middle terms.
Thus r = 5 and r = 6
when r = 5,
T₆ = \({ }^{11} C_5 \cdot(4 a)^6 \cdot\left(\frac{3}{2} b\right)^5\)
= 77 × 2⁸ . 3⁶ . a⁶ . b⁵.
when r = 6,
T₇ = \({ }^{11} C_6(4 a)^5 \cdot\left(\frac{3}{2} b\right)^6\)
= 77 × 2⁵ . 3⁷ . a⁵ . b⁶.

iii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of (4x² + 5x³)¹⁷ is
T_r+1 = \({ }^{17} \mathrm{C}_r\) . (4x²)^17-r . (5x³)^r.
The expansion has 18 (even number) terms.
Hence T₉ and T₁₀ are the middle terms.
Thus r = 8 and r = 9
When r = 8.
T₉ = \({ }^{17} \mathrm{C}_8\) . (4x²)⁹ . (5x³)⁸
= \({ }^{17} \mathrm{C}_8\) . 4⁹ . 5⁸ . x⁴²
When r = 9,
T10 = \({ }^{17} \mathrm{C}_9\) (4x²)⁸ (3)⁹
= \({ }^{17} \mathrm{C}_9\) . 4⁸ . 5⁹ . x⁴³

iv) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\) is
T_r+1 = \({ }^{20} C_r \cdot\left(\frac{3}{a^3}\right)^{20-r} \cdot\left(5 a^4\right)^r\)
The expansion has 21 (odd number) terms. Hence, T₁₁ is the only middle term
Thus r = 10
∴ Middle term in the expansion is
T₁₁ = \({ }^{20} C_{10} \cdot\left(\frac{3}{a^3}\right)^{10} \cdot\left(5 a^4\right)^{10}\)
= \({ }^{20} C_{10}\) . 15¹⁰ . a¹⁰.

Question 4.
Find the numerically greatest term(s) in the expansion of
i) (4 + 3x)¹⁵ when x = \(\frac{7}{2}\).
ii) (3x + 5y)¹² when x = \(\frac{1}{2}\), y = \(\frac{4}{3}\)
iii) (4a – 6b)¹³ when a = 3, b = 5.
iv) (3 + 7x)ⁿ when x = \(\frac{4}{5}\), n = 5.
Solution:
i) We know that (4 + 3x)¹⁵ = 4¹⁵ \(\left(1+\frac{3 x}{4}\right)^{15}\)
First we find the numerically greatest term in the expansion of \(\left(1+\frac{3 x}{4}\right)^{15}\)
Let X = \(\frac{3 x}{4}\)
x = \(\frac{7}{2}\), |X| = \(\left|\frac{3}{4} \times \frac{7}{2}\right|=\frac{21}{8}\)
Now \(\frac{(n+1)|X|}{1+|X|}=\frac{16 \times \frac{21}{8}}{1+\frac{21}{8}}=\frac{336}{29}\)
not an integer.
Its integral part m = \(\left[\frac{336}{29}\right]\) = 11.
∴ T_m+1, i.e., T₁₂ is the numerically greatest term in the binomial expansion of \(\left(1+\frac{3 x}{4}\right)^{15}\)
∴ T₁₂ = \({ }^{15} C_{11}\left(\frac{3 x}{4}\right)^{11}\)
= \({ }^{15} \mathrm{C}_{11}\left(\frac{21}{8}\right)^{11}\)
∴ Numerically greatest term in the expansion 01(4 + 3x)¹⁵ = \({ }^{15} C_{11}\left(4^{15}\right) \frac{21^{11}}{8^{11}}\)
= \({ }^{15} C_{11} \cdot \frac{21^{11}}{2^3}\).

ii) We know that
(3x + 5y)¹² = (3x)¹² . (1 + \(\frac{5 y}{3 x}\))¹²
First we find the numerically greatest term in the expansion of (1 + \(\frac{5 y}{3 x}\))¹²

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 3

iii) We know that
(4a – 6b)¹³ = (4a)¹³ (1 – \(\frac{6 b}{4 a}\))¹³
First we find the numerically greatest term in the expansion of (1 – \(\frac{6 b}{4 a}\))¹³
Let X = – \(\frac{6 b}{4 a}\)
As a = 3 and b = 5, |X| = \(\frac{5}{2}\)

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 4

∴ The numerically greatest terms in the expansion of (4a – 6b)¹³ are T₁₀ and T₁₁.
T₁₀ = – 12¹³ . ¹³C₉ . \(\left(\frac{5}{2}\right)^9\)
= – ¹³C₉ . (12)⁴ . (30)⁹
and T₁₁ = 12¹⁰ . ¹³C₁₀ . \(\left(\frac{5}{2}\right)^10\)
= 143 . 2¹⁷ . 3¹³ . 5¹⁰.

iv) We know that (3 + 7x)ⁿ = 3ⁿ (1 + \(\frac{7}{3}\) x)ⁿ
First we find numerically greatest term in the expansion of (1 + \(\frac{7}{3}\) x)ⁿ
Let X = \(\frac{7}{3}\) x
As x = \(\frac{4}{5}\), |X| = \(\frac{28}{15}\) and
\(\frac{(n+1)|X|}{1+|X|}=\frac{56}{5}\) and n = 15.

Its integral part,
m = \(\left[\frac{(\mathrm{n}+1)|\mathrm{X}|}{1+|\mathrm{X}|}\right]\) = 11
∴ T_m+1 i.e., T₁₂ is numerically greatest term in the expansion of (1 + \(\frac{7}{3}\) x)ⁿ
T₁₂ = ¹⁵C₁₁ . \(\left(\frac{28}{15}\right)^{11}\)
∴ The numerically greatest terms in the expansion of (3 + 7x)ⁿ is
T₁₂ = 3¹⁵ . ¹⁵C₁₁ . \(\left(\frac{28}{15}\right)^{11}\)
= ¹⁵C₁₁ . \(\left(\frac{28}{5}\right)^{11}\) . 3⁴.

Question 5.
Prove the following:
i) 2 . C₀ + 5 . C₁ + 8. C₂ + ……………. + (3n + 2) C_n = (3n + 4) 2^n-1
ii) C₀ – 4 C₁ + 7 . C₂ – 10 . C₃ + ……………. = 0,
if n is an even positive Integer.
iii) \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\)
iv) \(C_0+\frac{3}{2} \cdot C_1+\frac{9}{3} \cdot C_2+\frac{27}{4} \cdot C_3+\ldots \ldots+\frac{3^n}{n+1} C_n=\frac{4^{n+1}-1}{3(n+1)}\)
v) C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ………….. + 2ⁿ . C_n = 3ⁿ
Solution:
i) We know that
C₀ = C_n, C₁ = C_n-1, ………… C_r = C_n-r
Let S = 2 . C₀ + 5 . C₁ + 8 . C₂ + ………….. + (3n – 1) . C_n-1 + (3n + 2) C_n ………….(1)
∴ S = (3n + 2) C₀ + (3n – 1)C₁ + (3n – 4)C₂ + …………. + 5 . C_n-1 + 2 . C_n ………….(2)
(1) + (2) ⇒ 2S = (3n + 4) . C₀ + (3n + 4) . C₁ + (3n + 4) . C₂ + …………… (3n + 4) . C_n
= (3n + 4) (C₀ + C₁ + C₂ + …………… + C_n)
⇒ 2S = (3n + 4) . 2ⁿ
⇒ S = (3n + 4) . 2^n-1
∴ 2 . C₀ + 5 . C₁ + 8 . C₂ + ………… + (3n + 2) . C_n = (3n + 4) . 2^n-1

ii) We know that 1, 4, 7, 10, ………… are in A.P.
(n + 1)th term,
T_n+1 = 1 + (n)3 = 3n + 1
∴ C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……….. (n + 1) terms.
= \(\sum_{r=0}^n(-1)^r(3 r+1) C_r\)
= \(3 \sum_{r=0}^n(-1)^r r \cdot C_r+\sum_{r=0}^n(-1)^r \cdot C_r\)
= 3 (0) + 0 = 0
∴ C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……….. = 0.

iii) Given L.H.S

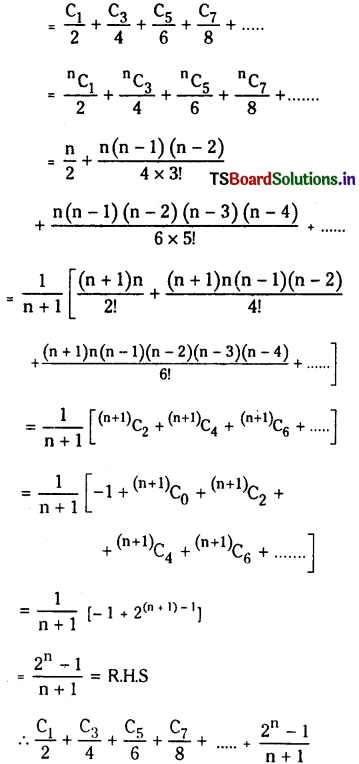
TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 5

iv) Given L.H.S

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 6

v) L.HS = C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ……….. + 2ⁿ . C_n
= C₀ + C₁ . 2 + C₂ . 2² + C₃ . 2³ + ………. + C_n 2ⁿ
= (1 + 2)ⁿ
= 3ⁿ = R.H.S
∴C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ……….. + 2ⁿ . C_n = 3ⁿ.

Question 6.
Find the sum of the following:
i) \(\frac{{ }^{15} C_1}{{ }^{15} C_0}+2 \frac{{ }^{15} C_2}{{ }^{15} C_1}+3 \frac{{ }^{15} C_3}{{ }^{15} C_2}+\ldots+15 \frac{{ }^{15} C_{15}}{{ }^{15} C_{14}}\)
ii) C_n . C₃ + C₁ .C₄ + C₂ . C₅ + + …………… + C_n-3 . C_n
iii) 2² C₀ + 3² C₁ + 4² C₂ + …………. + (n + 2)² C_n
iv) 3C₀ + 6C₁ + 12C₂ + ……………. + 3 . 2ⁿ C_n
Solution:
i) We know that

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 7

ii) (1 + x)ⁿ = C₀ + C₁x + C₂x² + …………. + C_nxⁿ …………..(1)
(x + 1)ⁿ = C₀xⁿ + C₁x^{n – 1} + C₂₃x^n-2 + …………… + C_n …………….. (2)
(1) x (2) = (1 + x)²ⁿ
= (C₀ + C₁x + C₂x² + ……….. + C_nxⁿ) (C₀x + C₁x^n-1 + C₂x^n-2 + C₃x^n-3 + ………….. + C_n]
Comparing coefficients of x^n-3 on bothsides,
²ⁿC_n-3 = C₀ . C₃ + C₁ . C₄ + C₂ . C₅ + …………. + C_n-3 . C_n
i.e., C₀. C₃ + C₁ . C₄ + C₂. C₅ + …………… + C_n-3 . C_n = ²ⁿC_n-3 = ²ⁿC_n+3
[∵ ⁿC_r = ⁿC_n-r].

iii) 2² C₀ + 3² C₁ + 4² C₂ + …………. + (n + 2)² C_n

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 8

= n (n – 1) 2^n-2 + 5 n 2^n-1 + 4 (2ⁿ)
= 2^n-2 [n (n – 1) + 10n + 16]
= (n² + 9n . 16) 2^n-2.

iv) 3 . C₀ + 6 . C₁ + 12 . C₂ + ……………. + 3 . 2ⁿ C_n
= \(\sum_{r=0}^n 3 \cdot 2^r \cdot C_r\)
= \(3 \sum_{r=0}^n 2^r \cdot C_r\)
= 3 [1 + C₁ (2) + C₂ (2²) + C₃ (2³) + …………. + C_n 2ⁿ]
= 3 [1 + 2]ⁿ
= 3 . 3ⁿ
= 3ⁿ⁺¹.

Question 7.
Using binomial theorem prove that 50ⁿ – 49n – 1 is divisible by 49² for all positive integers n.
Solution:
We know that,
50ⁿ – 49n – 1
= (1 + 49)ⁿ – 49n – 1
= [1 + ⁿC₁ . 49 + ⁿC₂ . 49² + ⁿC₃ . 49³ + ………… + 49ⁿ] – 49n – 1
= ⁿC₂ . 49² + ⁿC₃ . 49³ + …………… + ⁿC_n . 49ⁿ
= 49² [ⁿC₂ + ⁿC₃ . 49 + ……….. + ⁿC_n . 49^n-2]
= 49² (a positive integer)
Hence 50ⁿ 49n – 1 is divisible by 49² ∀n ∈ N.

Question 8.
Using binomial theorem prove that 5⁴ⁿ + 52n – 1 is divisible by 676 for all positive integers n.
Solution:
We know that, 5⁴ⁿ + 52n – 1
= (5²)²ⁿ + 52n – 1
= (25)²ⁿ+ 52n – 1
= (26 – 1)²ⁿ+ 52n – 1
= ²ⁿC₀ (26)²ⁿ – ²ⁿC₁ (26)^2n-1 + ²ⁿC₂ (26)^2n-2 + …………. + ²ⁿC_2n-2(26)² – ²ⁿC_2n-1 (26) + ²ⁿC_2n + 52n – 1
= 26²ⁿ + ²ⁿC₁ (26)^2n-1 + ²ⁿC₂ (26)^2n-2 + …………….. + ²ⁿC_2n-2 (26)²
= 26² [26^2n-2 – ²ⁿC₁ 26^2n-3 + ²ⁿC₂ 26^2n-4 + ……… + ²ⁿC_2n-2]
= 676 (some integer)
∴ 5⁴ⁿ + 52n – 1 is divisible by 676, ∀n ∈ N.

Question 9.
If (1 + x + x²)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_2nx²ⁿ, then prove that
i) a₀ + a₁ + a₂ + ……….. + a_2n = 3ⁿ
ii) a₀ + a₂ + a₄ + ………… + a_2n = \(\frac{3^n+1}{2}\)
iii) a₁ + a₃ + a₅ + ……………. + a_2n-1 = \(\frac{3^n-1}{2}\)
iv) a₀ + a₃ + a₆ + a₉ + ………… = 3^n-1
Solution:
Given (1 + x + x²)^{n/sup> = a₀ + a₁x + a₂x² + ………….. + a_2nx²ⁿ
i) Subtituting x = 1 in (I), we have
a₀ + a₁ + a₂ + ……….. + a_2n = 3ⁿ …………. (1)
Substituting x = – 1 in (I), we have
a₀ – a₁ + a₂ + ……….. + a_2n = 1 …………….(2)}

ii) (1) + (2)
⇒ 2a₀ + 2a₂ + 2a₄ + ……….. + 2a_2n = 3ⁿ + 1
⇒ a₀ + a₂ + a₄ + ……….. + a_2n = \(\frac{3^n+1}{2}\)

iii) (1) – (2)
⇒ 2a₁ + 2a₃ + 2a₅ + ……….. + 2a_2n-1 = 3ⁿ – 1
⇒ a₁ + a₃ + a₅ + ……….. + a_2n-1 = \(\frac{3^n-1}{2}\)

iv) Substituting x = ω, in (1), we have
a₀ + a₁ω + a₂ω² + ……….. + a_2nω²ⁿ = 0
(∵ 1 + ω + ω² = 0)

Substituting x = ω² in (1), we have
a₀ + a₁ω² + a₂ω⁴ + a₃ω⁶ + ……….. + a_2nω⁴ⁿ = 0 …………… (4)
(1) + (3) +(4):
3a₀ + a₁ (1 + ω + ω²) + a₂ (1 + ω + ω²) + a₃ (1 + ω³ + ω⁶) + ………… + a_2n (1 + ω²ⁿ + ω⁴ⁿ) = 3ⁿ
⇒ 3a₀ + 3a₃ + 3a₆ + 3a₉ + …………. = 3ⁿ
(∵ 1 + ω + ω² = 0 and ω³ = 1)
⇒ a₀ + a₃ + a₆ + a₉ + ……….. = 3^n-1

Question 10.
If (1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……………+ b₂₁ x²¹, then find the value of
i) b₀ + b₂ + b₄ + ……………. + b₂₀
ii) b₁ + b₃ + b₅ + ……………. + b₂₁
Solution:
Given
(1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……………+ b₂₁ x²¹ ……………(1)
Substituting x = 1 in (1),
we get b₀ + b₁ + b₂ + ……………. + b₂₁ = 4⁷ ……….(2)
Substituting x = – 1 in (1),
we get b₀ – b₁ + b₂ + ……………. – b₂₁ = 0 …………… (3)
i) (2) + (3)
⇒ 2b₀ + 2b₂ + 2b₄ + ……………. + b₂₀ = 4⁷
⇒ b₀ + b₂ + b₄ + ……………. + b₂₀ = 2¹³.

ii) (2) – (3)
⇒ 2b₁ + 2b₃ + 2b₅ + ……………. + 2b₂₁ = 4⁷
⇒ b₁ + b₃ + b₅ + ……………. + b₂₁ = 2¹³.

Question 11.
If the coefficients of x¹¹ and x¹² in the binomial expansion of \(\left(2+\frac{8 x}{3}\right)^n\) are equal, find n.
Solution:
We know that \(\left(2+\frac{8 x}{3}\right)^n=2^n\left(1+\frac{4 x}{3}\right)^n\)
Coefficient of x¹¹ in the expansion of \(\left(2+\frac{8 x}{3}\right)^n\) is ⁿC₁₁ . 2ⁿ . (\(\frac{4}{3}\))¹¹
Coefficient of x¹² in the expansion of \(\left(2+\frac{8 x}{3}\right)^n\) is ⁿC₁₂ . 2ⁿ . (\(\frac{4}{3}\))¹²
Given coefficients of x¹¹ and x¹² are same
⇒ ⁿC₁₁ . 2ⁿ . (\(\frac{4}{3}\))¹¹ = ⁿC₁₂ . 2ⁿ . (\(\frac{4}{3}\))¹²
⇒ \(\frac{n !}{(n-11) ! 11 !}=\frac{n !}{(n-12) ! 12 !}\left(\frac{4}{3}\right)\)
⇒ 12 = (n – 11) \(\frac{4}{3}\)
⇒ 9 = n – 11
⇒ n = 11 + 9 = 20.

Question 12.
Find the remainder when 2²⁰¹³ is divided by 17.
Solution:
We have 2²⁰¹³
= 2 (2²⁰¹²)
= 2 (2⁴)²⁰³
= 2 (16)⁵⁰³
= 2 (17 – 1)²⁰³
= 2 [⁵⁰³C₀ 17⁵⁰³ – ⁵⁰³C₁ 17⁵⁰² + ⁵⁰³C₂ 17⁵⁰¹ – ……….. + ⁵⁰³C₅₀₂ 17 – ⁵⁰³C₅₀₃]
= 2 [⁵⁰³C₀ 17⁵⁰³ – ⁵⁰³C₁ 17⁵⁰² + ⁵⁰³C₂ 17⁵⁰¹ – ……….. + ⁵⁰³C₅₀₂ 17 – ⁵⁰³C₅₀₃] – 2
= 17m – 2 where ‘m is some integer
∴ 2²⁰¹³ = 17m – 2 (or) 17k + 15
∴ The remainder is – 2 or 15.

Question 13.
If the coefficient of (2r + 4)th term and (3r + 4)th term in the expansion of (1 + x)²¹ are equal, find r.
Solution:
We know that coefficient of (r + 1)th term of (1 + x)ⁿ is ⁿC_r.
∴ Coefficient of (2r + 4)th term 0f (1 + x)²¹ is ²¹C_2r+3
Also coefficient of (3r + 4)th term of (1 +x)²¹ is ²¹C_3r+3.
Given coefficient of (2r + 4)th term and (3r + 4)th terms in the expansion of (1 + x)²¹ are equal.
∴ ²¹C_2r+3 = ²¹C_3r+4
∴ Either 2r + 3 = 3r + 3 0r 2r + 3 + 3 = 21
If 2r + 3 = 3r + 3 then r = 0,
If 2r + 3 + 3r = 21 then r = 3.
∴ r = 0 or r = 3.

III.
Question 1.
If the coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in AP. then prove that n² – 4m + 398 = 0.
Solution:
Coefficient of x^r in the expansion of (1 + x)ⁿ is ⁿC_r.
Given coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in A.P., then
2(ⁿC₁₀) = ⁿC₉ + ⁿC₁₁
⇒ \(2 \frac{n !}{(n-10) ! 10 !}=\frac{n !}{(n-9) ! 9 !}+\frac{n !}{(n-11) !+11 !}\)
⇒ \(\frac{2}{10(n-10)}=\frac{1}{(n-9)(n-10)}+\frac{1}{11 \times 10}\)
⇒ \(\frac{2}{(n-10) 10}=\frac{110+(n-9)(n-10)}{110(n-9)(n-10)}\)
⇒ 22 (n – 9) = 110 + n² – 19n + 90
⇒ n² – 41n + 398 = 0.

Question 2.
If 36, 84, 126 are three successive binomial coefficients in the expansion of (1 + then find n.
Solution:
Let us consider ⁿC_r-1, ⁿC_r and ⁿC_r+1 as three successive binomial coefficients of (1 + xy)ⁿ.
i.e., ⁿC_r-1 = 36; ⁿC_r-1 = 84 and ⁿC_r-1 = 126
Consider \(\frac{{ }^{n_C} C_r}{{ }^n C_{r-1}}=\frac{84}{36}\)
⇒ \(\frac{n-r+1}{r}=\frac{7}{3}\)
⇒ 3n + 3 = 10r …………..(1)
Similarly,
\(\frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{126}{84}\)
⇒ \(\frac{\mathrm{n}-\mathrm{r}}{\mathrm{r}+1}=\frac{3}{2}\)
⇒ 2n = 5r + 3 ………….(2)
⇒ 2n = 5 \(\left(\frac{3 \mathrm{n}+3}{10}\right)\) + 3 (∵ from (1))
⇒ n = 9.

Question 3.
If the 2nd, 3rd and 4th terms in the expansion of (a + x)ⁿ are respectively 240, 720, 1080. find a, x, n.
Solution:
General term in the expansion of (a + x)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
∴ 2nd term,T₂ = ⁿC₁ . a^n-1 . x …………..(1)
3rd term, T₃ = ⁿC₂ . a^n-2 . x² ………..(2)
4th term, T₄ = ⁿC₃ . a^n-3 . x³ …………(3)
Given T₂ = 240, T₃ = 720, T₃ = 1080
From (1) and (2),

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 9

Sub. n = 5 in (1), we get
5 . a⁴ . x = 240 ………..(6)
Substituting n = 5 in (4), we get x = \(\frac{3 a}{2}\) ………….(7)
Substituting x = \(\frac{3 a}{2}\) in (6),
we get 5 . a⁴ = 240
⇒ a⁵ = 32
⇒ a = 2
Substituting in (7), we get x = 3
∴ a = 2; x = 3 and n = 5.

Question 4.
If the coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are in A.P., then show that n² – (4r + 1)n + 4r² – 2 = 0.
Solution:
We know that, the general term, (r + 1)th term in the expansion of (1 + x)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r
∴ The coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are ⁿC_r-1, ⁿC_r and ⁿC_r+1
Given ⁿC_r-1, ⁿC_r & ⁿC_r+1 are in A.P.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 10

⇒ 2(n – r + 1) (r + 1) = r (r + 1) + (n – r) (n – r + 1)
⇒ 2nr + 2n – 2r² – 2r + 2r + 2 = r² + r + n² – nr + n – nr + r² + r
⇒ n² – n (4r + 1) + 4r² – 2 = 0.

Question 5.
Find the sum of the coefficients of x³² and x^-18 in the expansion of (2x³ – \(\frac{3}{x^2}\))¹⁴.
Solution:
The general term in (2x³ – \(\frac{3}{x^2}\))¹⁴ is
T_r+1 = ¹⁴C_r (2x³)^14-r (\(\frac{-3}{x^2}\))^r
T_r+1 = (- 1)^r . ¹⁴C_r . 2^14-r . 3^r . x^42-5r ………….(1)
For coefficient of x³², put
42 – 5r = 32
⇒ r = 2
Substituting r = 2 in (1), we get
T₃ = ¹⁴C₂ . 2¹² . 3² . x³²
∴ Coefficient of x³² is ¹⁴C₂ . 2¹² . 3² ………(2)
For coefficient of x^-18, put
42 – 5r = 18
⇒ r=12
Substituting r = 12 in (1), we get
T₁₃ = ¹⁴C₂ . 2² . 3¹² . x^-18
∴ Coefficient of x^-18 is ¹⁴C₁₂ . 2² . 3¹² ………….(3)
Hence sum of the coefficients of x³² and x^-18 is
¹⁴C₂ . 2¹² . 3² + ¹⁴C₁₂ . 2² . 3¹²
= ¹⁴C₂ . 2² . 3² (2¹⁰ + 3¹⁰)
= 91 × 36(2¹⁰ + 3¹⁰).

Question 6.
If P and Q are the sum of odd terms and the sum of even terms respectively in the expansion of (x + a)ⁿ then prove that
i) P² – Q² = (x² – a²)ⁿ
ii) 4PQ (x + a)²ⁿ – (x – a)²ⁿ
Solution:
We know that,
(x + a)ⁿ = ⁿC₀ xⁿ + ⁿC₁ x^n-1 . a + ⁿC₂ x^n-2 . a² + ………….. + ⁿC_n-1 x a^n-1 + ⁿC_n aⁿ
= (ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………) + (ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..)
∴ (x + a)ⁿ = P + Q
∴ Sum of odd terms,
P = ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………
Sum of even terms,
Q = ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..
∴ (x + a)ⁿ = P + Q
We know that
(x – a)ⁿ = ⁿC₀ xⁿ a – ⁿC₁ x^n-1 a + ⁿC₂ x^n-2 a¹² – ⁿC₃ x^n-3 a³ + ……………. + ⁿC_n (- 1)ⁿ aⁿ
= (ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………) – (ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..)
⇒ (x – a)ⁿ = P – Q

i) P² – Q² = (P + Q) (P – Q)
= (x + a)ⁿ (x – a)ⁿ
⇒ P² – Q² = (x² – a²)ⁿ

ii) 4PQ = (P + Q)² – (P – Q)²
= [(x + a)ⁿ]² – [(x – a)ⁿ]²
⇒ 4PQ = (x + a)²ⁿ – (x – a)²ⁿ

Question 7.
If the coefficients of 4 consecutive terms in the expansion of (1 + x)ⁿ are a₁, a₂, a₃, a₄ respectively, then show that \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\)
Solution:
Given a₁, a₂, a₃, a₄ are the coefficients of 4 consecutive terms in (1 + x)ⁿ respectively.
Let a₁ = ⁿC_r-1
a₂ = ⁿC_r
a₃ = ⁿC_r+1
a₄ = ⁿC_r+2

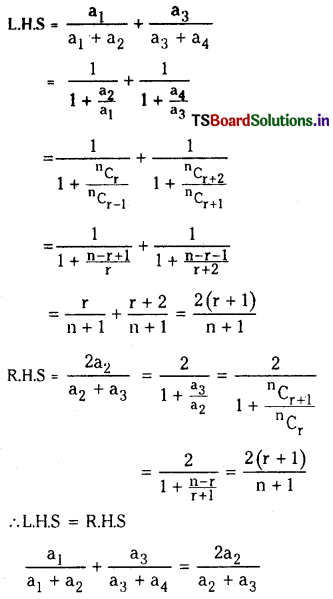
TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 11

Question 8.
Prove that (²ⁿC₀)² – (²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ……….. + (²ⁿC_2n)² = (- 1)ⁿ ²ⁿC_n.
Solution:
We know that
(x + 1)²ⁿ = ²ⁿC₀ x²ⁿ + ²ⁿC₁ x^2n-1 + ²ⁿC₂ x^2n-2 + …………… + ²ⁿC_2n ……………(1)
(1 – x)²ⁿ = ²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² – …………… + ²ⁿC_2n x²ⁿ ……………(2)
From (1) and (2),
(1 – x)²ⁿ (1 + x)²ⁿ = (²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² + ……………… + ²ⁿC_2n x²ⁿ)
⇒ (1 – x²)²ⁿ = [²ⁿC₀ x²ⁿ + ²ⁿC₁ x^2n-1 + ²ⁿC₂ x^2n-2 + …………… + ²ⁿC_2n] . [²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² + …………… + ²ⁿC_2n x²ⁿ]
Equating coefficient of x²ⁿ on both sides, we get
(- 1)ⁿ . ²ⁿC_n = (²ⁿC₀)² + ((²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ………….. + (²ⁿC_2n)²

Question 9.
Prove that
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n) = \(\frac{(\mathbf{n}+1)^{\mathbf{n}}}{\mathbf{n} !}\) . C₀ . C₁ . C₂ ………….. C_n.
Solution:
Given L.H.S
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n)

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 12

= R.H.S
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n) = \(\frac{(\mathbf{n}+1)^{\mathbf{n}}}{\mathbf{n} !}\) . C₀ . C₁ . C₂ ………….. C_n.

Question 10.
Find the term independent of x in (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ.
Solution:
We know that (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ = (\(\frac{1}{3 x}\))ⁿ (1 + 3x)²ⁿ
= \(\frac{1}{3^n \cdot x^n} \sum_{r=0}^{2 n}\left({ }^{2 n} C_r\right)(3 x)^r\)
For the term, independent of x put r = n.
∴ The term independent of x in (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ is \(\frac{1}{3^n}\) ²ⁿC_n . 3ⁿ.

Question 11.
Show that the middle term In the expansion of (1 + x)²ⁿ is \(\frac{1 \cdot 3 \cdot 5 \ldots \ldots(2 n-1)}{n !}\) (2x)ⁿ.
Solution:
The expansion of (1 + x)²ⁿ contains 2n + 1 terms.
∴ Middle term is (n + 1)th term

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 13

Question 12.
If (1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² …………… + a₂₀x²⁰, then prove that
i) a₀ + a₁ + a₂ + …………… + a₂₀ = 2¹⁰
ii) a₀ – a₁ + a₂ – a₃ + …………. + a₂₀ = 4¹⁰
Solution:
Given
(1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² …………… + a₂₀x²⁰ …………….(1)
i) Put x = 1, in (1), we get
(1 + 3 – 2)¹⁰ = a₀ + a₁ + a₂ + …………… + a₂₀
⇒ a₀ + a₁ + a₂ + …………… + a₂₀ = 2¹⁰.

ii) Put x – 1 in (1), we get
(1 – 3 – 2)¹⁰ = a₀ – a₁ + a₂ – a₃ + …………. + a₂₀
a₀ – a₁ + a₂ – a₃ + …………. + a₂₀ = 4¹⁰.

Question 13.
If (3√3 + 5)^{2n + 1} = x and f = x – [x] (where [x] the integral part of x), find the value of x.f.
Solution:
Given (3√3 + 5)^{2n + 1} = x
and f = x – [x]
∴ 0 < f < 1
Let us consider F = (3√3 + 5)^{2n + 1}
We know that
5 < 3√3 < 6 = 0 < 3√3 – 5 < 1
⇒ 0 < (3√3 – 5)^{2n + 1} < 1
⇒ 0 < F < 1
⇒ – 1 < – F < 0
Let x = I + f (where E is an integer)
Now
i + f – F = (3√3 + 5)^{2n + 1} + (3√3 – 5)^{2n + 1}
= [^{2n + 1}C₀ (3√3)²ⁿ⁺¹ + ^{2n + 1}C₁ (3√3)²ⁿ . 5 + ^{2n + 1}C₂ (3√3) . 5² + …………..] – [^{2n + 1}C (3√3)²ⁿ⁺¹ – ^{2n + 1}C₁ (3√3)²ⁿ . 5 + ^{2n + 1}C₂ (3√3)^2n-1 . 5² – …………]
= 2 [^{2n + 1}C₁ (3√3) 5 + ^{2n + 1}C₃ (3√3)^2n-2 5³ + …………. + ^{(2n + 1)}C_(2n+1) (5)²ⁿ⁺¹]
= 2k, where k is an integer
∴ I + f – F is an even integer
⇒ f – F is also integer.
∴ (1) + (2)
⇒ – 1 < f – F < 1
⇒ f – F = 0
⇒ f = F
∴ x . f = x . F
= (3√3 + 5)^{2n + 1} . (3√3 – 5)^{2n + 1}
= (27 – 25)^{2n + 1}
= 2^{2n + 1}.

Question 14.
If R, n are posilve integers, n is odd, 0< F < 1 and if (5√5 + 11) = R + F, then prove that
i) R is an even integer and
ii) (R + F). F = 4ⁿ
Solution:
Given R, n are positive integers, 0 < F < 1 and
(5√5 + 11)ⁿ = R + F …………….(1)
i) Consider (5√5 – 11)ⁿ = f …………….(2)
We know that 11 < 5√5 < 12
⇒ 0 < 5√5 – 11 < 1
⇒0 < (5√5 – 11)ⁿ < 1
⇒ 0 < f < 1
⇒ – 1 < – f < 0 ………….(3)
From (1) and (3)
– 1 < F -f < 1 ……………(4)
Also R + F – f
= (5√5 + 11)ⁿ – (5√5 – 11)ⁿ
= [ⁿC₀ (5√5)ⁿ + ⁿC₁ (5√5)^n-1 (11) + ⁿC₂ (5√5)^n-2 . 11² + ⁿC₃ (5√5)^n-3 . 11³ + ………… + ⁿC_n (11)ⁿ] – [ⁿC₀ (5√5)ⁿ – ⁿC₁ (5√5)^n-1 (11) + ⁿC₂ (5√5)^n-2 . 11² – ⁿC₃ (5√5)^n-3 . 11³ + ………….. + (- 1)ⁿC_n (11)ⁿ]
= 2 [ⁿC₁ (5√5)^n-1 (11) + ⁿC₃ (5√5)^n-3 (11)³ + ……………]
= 2k, where k is an integer (∵ f is odd)
∴ R + F – f is an even Integer.
⇒ F – f is also an interger. (∵ R is integer)
From (4), we have F – f = 0
⇒ F = f
∴ R is an even Integer.

ii) Now (R + F) . F
= (5√5 + 11)ⁿ (5√5 + 11)ⁿ
= ((5√5)² – 11²)ⁿ = 4ⁿ
∴ (R + F) . F = 4ⁿ.

Question 15.
If I, n are positive Integers, 0 < f < 1 and if (7 + 4√3) = I + f, then show that
i) I is an odd integer and
ii) (I + f) (I – f) =
Solution:
Given I and n are positve integers.
0 < f < I and (7 + 4√3)ⁿ = I + f ………….(1)

i) Let us consider (7 – 4√3)ⁿ = F
We know that 6 < 4√3 < 7
⇒ – 7 < – 4√3 < – 6
⇒ 0 < 7 – 4√3 < 1
⇒ 0 < (7 – 4√3)ⁿ < 1
⇒ 0 < F < 1
we have 0 < F + f < 2 …………(2)
Now I + f + F = (7 + 4√3)ⁿ + (7 – 4√3)ⁿ
= [ⁿC₀ 7ⁿ + ⁿC₁ 7^n-1 (4√3) + ⁿC₂ 7^n-2 (4√3)² + ………….. + ⁿC_n (4√3)ⁿ] + [ⁿC₀ 7ⁿ – ⁿC₁ 7^n-1 (4√3) + ⁿC₂ 7^n-2 (4√3)² – ………….. + ⁿC_n (- 1)ⁿ (4√3)ⁿ]]
= 2[ⁿC₀ 7ⁿ + ⁿC₂ 7^n-2 (4√3)² + ⁿC₄ 7^n-4 (4√3)⁴ + ……………]
= 2k, where k is an integer.
∴ I + f + F is an even integer.
∴ f + F is also an integer. (∵ I is an integer)
from (2) we have f + F = I ………..(3)
∴ I + I is an even integer
⇒ I is an odd integer.

ii) Also (I + f) (I – f) = (I + f) F
= (7 + 4√3)ⁿ (7 – 4√3)ⁿ
= (7² – (4√3)²)ⁿ = 1.

Question 16.
If n is a Positive integer, prove that \(\sum_{r=1}^n \mathbf{r}^3 \cdot\left(\frac{{ }^n C_r}{{ }^n C_{r-1}}\right)^2=\frac{n(n+1)^2(n+2)}{12}\).
Solution:
We know that \(\frac{{ }^{{ }^r} C_r}{{ }^n C_{r-1}}=\frac{n-r+1}{r}\)

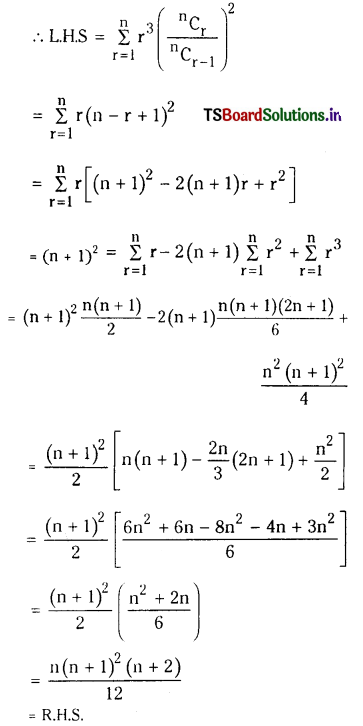
TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) 14

Question 17.
Find the number of irrational terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰.
Solution:
Number of terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰ are 101.
General term in the expansion of (x + y)ⁿ is
T_r+1 = ⁿC_r x^n-r . y^r
∴ General term in the expansion of (5^1/6 + 2^1/8)¹⁰⁰
T_r+1 = ¹⁰⁰C_r . \(\left(5^{\frac{1}{6}}\right)^{100-r} \cdot\left(2^{\frac{1}{8}}\right)^r\)
= ¹⁰⁰C_r . \(\cdot 5^{\frac{100-r}{6}} \cdot 2^{\frac{r}{8}}\)
For T_r+1 to be a rational.
Clearly ‘r’ is a multiple of 8 and 100 – r is a multiple of 6
∴ r = 16, 40, 64. 88.
Number of rational terms are 4.
∴ Number of irrational terms are 101 – 4 = 97.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3

February 28, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Ex 9.3 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Exercise 9.3

Question 1.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding : (use π = 3.14)
(i) Minor segment
(ii) Major segment. (A.P. Mar. ’16, June ’15)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 1
Given :
Angle subtended by the chord = 90°
Radius of the circle = 10 cm
Area of the minor segment = Area of the sector POQ – Area of ∆POQ
Area of the sector = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × πr²
= \(\frac{90}{360}\) × 3.14 × 10 × 10 = 78.5
Area of the triangle POQ
= \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × 10 × 10 = 50
∴ Area of the minor segement
⇒ 78.5 – 50 = 28.5 cm²
Area of the major segment = Area of the circle – Area of the minor segment
⇒ 3.14 × 10 × 10 – 28.5
⇒ 314 – 28.5 cm²
⇒ 285.5 cm²

Question 2.
A chord of a circle of radius 12 cm. subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle, (use π = 3.14 and \(\sqrt{3}\) = 1.732).
Solution:
Radius of the circle r = 12 cm
Area of the sector = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) πr²
Here x = 120°
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 2
= \(\frac{120^{\circ}}{360^{\circ}}\) × 3.14 × 12 × 12
= 150.72
Drop a perpendicular from ‘O’ to the chord ‘PQ’
∆OPM = ∆OQM [∵ OP = OQ, ∠P = ∠Q; angles opposite to equal sides OP & OQ, ∠OMP = ∠OMQ by A.A.S]
∴ ∆OPQ = ∆OPM + ∆OQM
= 2(∆OPM)
Area of ∆OPM = \(\frac{1}{2}\) × PM × OM
But cos 30° = \(\frac{\mathrm{PM}}{\mathrm{OP}}\)
[∴ In ∆OPQ ∠POQ = 120° ∠OPQ = ∠OQP = \(\frac{180-120^{\circ}}{2}\) = 120°]
∴ PM = \(\frac{12 \times \sqrt{3}}{2}\) = 6\(\sqrt{3}\)
Also sin 30° = \(\frac{\mathrm{OM}}{\mathrm{OP}}\)
⇒ \(\frac{1}{2}\) = \(\frac{\mathrm{OM}}{12}\) ⇒ OM = \(\frac{12}{2}\) = 6
∴ ∆OPM = \(\frac{1}{2}\) × 6\(\sqrt{3}\) × 6
= 18 × 1.732 = 31.176 cm²
∴ ∆OPQ = 2 × 31.176 = 62.352 cm²
Area of the minor segment PQ = (Area of the sector) – (Area of the ∆OPQ)
= 150.72 – 62.352 = 88.368 cm²

Question 3.
A car has two wipers which do not overlap. Each wiper has a blade of length 25cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades (use π = \(\frac{22}{7}\))
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 3
Angle made by the each blade = 115°
It is evident that each wiper sweeps a sector of a circle of radius 25cm and sector angle 115°.
Area of a sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr²
Total area cleaned at each sweep of the blades
= 2 × \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr²
= 2 × \(\frac{115^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 25 × 25
= 2 × \(\frac{23}{72}\) × \(\frac{22}{7}\) × 25 × 25
= \(\frac{23}{36}\) × \(\frac{22}{7}\) × 25 × 25
= 1254.96 cm²

Question 4.
Find the area of the shaded region in the figure, where ABCD is a square of side 10cm and semicircles are drawn with each side of the square as diameter. (use π = 3.14).
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 4
Solution:
Let us mark the four unshaded regions as I, II, III and IV.

Area of I + Area of III = Area of ABCD – Areas of 2 semicircles with radius 5 cm.
= 10 × 10 – 2 × \(\frac{1}{2}\) × 7π × 5²
= 100 – 3.14 × 25
⇒ 100 – 78.5 ⇒ 21.5 cm²
Similarly, Area of II + Area of IV = 21.5 cm²
So, area of the shaded region
= are a of ABCD – Area of unshaded region
⇒ 100 – 2 × 21.5
= 100 – 43 = 57 cm²

Question 5.
Find the area of the shaded region in the figure, if ABCD is a square of side 7cm and APD and BPC are semi-circles. (use π = \(\frac{22}{7}\))
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 6
Solution:
Given,
ABCD is a square of side 7 cm
Area of the shaded region
= Area of ABCD – Area of 2 semi-circles with 7 radius (\(\frac{7}{2}\) = 3.5 cm)
APD and BPC are semi-circles 1 22
= 7 × 7 – 2 × \(\frac{1}{2}\) × \(\frac{22}{7}\) × 3.5 × 3.5
= 49 – 38.5 = 10.5 cm²
∴ Area of shaded region = 10.5 cm²

Question 6.
In figure, OACB is a quadrant of a circle with centre ‘O’ and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region, (use π = \(\frac{22}{7}\)).
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 7
Solution:
Given OACB is a quadrant of a circle radius 3.5 cm OD = 2 cm
Area of the shaded region = Area of the sector – Area of ABOD
= \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × πr² – \(\frac{1}{2}\) OB . OD
= \(\frac{99^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 3.5 × 3.5 – \(\frac{1}{2}\) × 3.5 × 2
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × 3.5 × 3.5 – 3.5
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × 12.25 – 3.5
= 9.625 – 3.5 = 6.125 cm²
Area of shaded region = 6.125 cm²

Question 7.
AB and CD are respectively arcs of two concentric circles of radii 21cm and 7cm with centre ‘O’ (see figure) If ∠AOB = 30°, find the area of the shaded region. (Use π = \(\frac{22}{7}\))
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 8
Solution:
Area of the shaded region
= Area of sector OAB – Area of the sector COD
= \(\frac{30^{\circ}}{360^{\circ}} \) × \(\frac{22}{7}\) × 21 × 21 – \(\frac{30^{\circ}}{360^{\circ}} \) × \(\frac{22}{7}\) × 7 × 7
= \(\frac{30^{\circ}}{360^{\circ}} \) × \(\frac{22}{7}\) (21 × 21 – 7 × 7)
= \(\frac{1}{12}\) × \(\frac{22}{7}\) (441 – 49)
= \(\frac{1}{6}\) × \(\frac{11}{7}\) × 392
= \(\frac{1}{6}\) × 11 × 56
= \(\frac{11 \times 28}{3}\)
= 102.67 cm²

Question 8.
Calculate the area of the designed region in figure, common between the two quadrants of the circles of radius 10 cm. each, (use π = 3.14)
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 9
Solution:
Radius of the circle (r) = 10 cm
Area of the designed region
= 2 [Area of quadrant ABYD – Area of ∆ABD]
= 2 [\(\frac{1}{4}\) × πr² – \(\frac{1}{2}\) × Base × Height]
= 2 [(\(\frac{1}{4}\) × 3.14 × 10 × 10) – (\(\frac{1}{2}\) × 10 × 10)]
= 2 [78.5 – 50]
⇒ 2 × 28.5
= 57 cm²

TS 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise

February 27, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 10 Mensuration Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise

Question 1.
A golf ball has diameter equal to 4.1cm. Its surface has 150 dimples each of radius 2mm. Calculate total surface area which is exposed to the surroundings (Assume that the dimples are all hemispherical) [π = \(\frac{22}{7}\)]
Solution:
Area exposed = surface area of the ball – total area of 150 dimples with radius 2 mm
= 4πr² – 150 × πr²
= 4 × \(\frac{22}{7}\) × \(\frac{4.1}{2}\) × \(\frac{4.1}{2}\) – 150 × \(\frac{22}{7}\) × \(\frac{2}{10}\) × \(\frac{2}{10}\)
[∵ 2 mm = \(\frac{2}{10}\) cm]
= 52.831 – 18.85 = 33.972 cm²

Question 2.
A cylinder of radius 12 cm. contains water to a depth of 20 cm. when a spherical iron ball is dropped in to the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. [π = \(\frac{22}{7}\)]
Solution:
Rise in the water level is seen as a cylinder of radius ‘r’ = r₁ = 12 cm
Height, h = 6.75 cm
Volume of the rise = Volume of the spherical iron ball dropped
πr₁²h = \(\frac{4}{3}\) πr₂³
r₁²h = \(\frac{4}{3}\) π₂³
12 × 12 × 6.75 cm³ = \(\frac{4}{3}\) × r₂³ cm³
r₂³ = \(\frac{3}{4}\) × 12 × 12 × 6.75
= 9 × 12 × 6.75
= 108 × 5.75
r₂³ = 729
r₂³ = 9 × 9 × 9
∴ 729 = (3 × 3) × (3 × 3) × (3 × 3)
∴ Radius of the ball r = r₂ = 9 cm.
TS 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise 1

Question 3.
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm. and height of the cylindrical and conical portion are 12 cm. and 7 cm. respectively. Find the volume of the solid toy. [π = \(\frac{22}{7}\)]
Solution:
TS 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise 2
Volume of the toy
= volume of the hemisphere + volume of the cylinder + volume of the cone.
= \(\frac{2}{3}\) πr³ + πr²h₁ + \(\frac{1}{3}\) πr²h₂
= πr²(\(\frac{2}{3}\)r + h₁ + \(\frac{\mathrm{h}_2}{3}\))
= \(\frac{22}{7}\) × \(\frac{4.2}{2}\) × \(\frac{4.2}{2}\)[\(\frac{2}{3}\) × \(\frac{4.2}{2}\) + 12 + \(\frac{7}{3}\)]
= 11 × 0.6 × 2.1 [1.4 + 12 + \(\frac{7}{3}\)]
= 13.86[13.4 + \(\frac{7}{3}\)]
= 13.86 × \(\left[\frac{40.2+7}{3}\right]\)
= \(\frac{13.86 \times 47.2}{3}\) = 218.064 cm³

(or)

Hemisphere :
Radius = \(\frac{\text { diameter }}{2}\) = \(\frac{4.2}{2}\) = 2.1 cm
V = \(\frac{2}{3}\) πr³ = \(\frac{2}{3}\) × \(\frac{22}{7}\) × 2.1 × 2.1 × 2.1
= 19.404 cm³

Cylinder :
Radius, r = \(\frac{\mathrm{d}}{2}\) = \(\frac{4.2}{2}\) = 2.1 cm
height, h = 12 cm
V = πr²h = \(\frac{22}{7}\) × 2.1 × 2.1 × 12
= 166.32 cm³

Cone :
Radius, r = \(\frac{\mathrm{d}}{2}\) = \(\frac{4.2}{2}\) = 2.1cm
Height, h = 7 cm
V = \(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 2.1 × 2.1 × 7
= 32.34 cm³
∴ Total volume = 19.404 + 166.32 + 32.34
= 218.064 cm³.

Question 4.
Three metal cubes with edges 15 cm., 12 cm. and 9 cm. respectively are melted together and formed into a single cube. Find the diagonal of this cube.
Solution:
Edges l₁ = 15 cm, l₂ = 12 cm, l₁₃ = 9 cm.
TS 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise 3
Volume of the resulting cube = Sum of the volumes of the three given cubes
L³ = l³₁h
L³ = l₁³ + l₂³ + l₃³
L³ = 15³ + 12³ + 9³
L³ = 3375 + 1728 + 729
L³ = 5832 = 18 × 18 × 18
∴ Edge of the new cube l = 18 cm
Diagonal = \(\sqrt{3 l^2}\) = \(\sqrt{3 \times 18^2}\)
= \(\sqrt{3 \times 324}\) = \(\sqrt{972}\) = 31.176 cm.

Question 5.
A hemi-spherical bowl of internal diameter 36 cm. contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3 cm. and height 6 cm. How many bottles are required to empty the bowl ?
Solution:
Let the number of bottles required = n.
Then total valume of a ’n’ bottles = volume of the hemispherical bowl.
n. πr₁²h = \(\frac{2}{3}\) πr₂²h
Bottle :
Radius, r₁ = 3 cm
Height, h = 6 cm
Volume, V = πr₁²h
= \(\frac{22}{7}\) × 3 × 3 × 6 = \(\frac{1188}{7}\)
∴ Total volume of n bottles = n × \(\frac{1188}{7}\) cm³.
Bowl :
TS 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise 4
∴ 72 bottles are required to empty the bowl.

TS 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.4

February 27, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 10 Mensuration Ex 10.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 10 Mensuration Exercise 10.4

Question 1.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of cylinder. (AS4)
Solution:
Radius of the sphere(r) = 4.2 cm
Volume of the sphere = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 4.2 × 4.2 × 4.2
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × \(\frac{42}{10}\) × \(\frac{42}{10}\) × \(\frac{42}{10}\) cm³
Radius of the cylinder (r) = 6 cm
Height of the cylinder (h) = ?
Volume of the cylinder = πr²h
= \(\frac{22}{7}\) × 6 × 6 × h cm³
By problem, volume of the metallic sphere = volume of the cylinder
∴ \(\frac{22}{7}\) × 6 × 6 × h = \(\frac{4}{3}\) × \(\frac{22}{7}\) × \(\frac{42}{10}\) × \(\frac{42}{10}\) × \(\frac{42}{10}\)
∴ h = \(\frac{4}{3}\) × \(\frac{22}{7}\) × \(\frac{42}{10}\) × \(\frac{42}{10}\) × \(\frac{42}{10}\) × \(\frac{7}{22}\) × \(\frac{1}{6 \times 6}\) = 2.74 cm
Height of the cylinder = 2.74 cm.

Question 2.
Three metallic spheres of radii 6 cm; 8 cm. and 10 cm respectively are melted to from a single solid sphere. Find the radius of resulting sphere. (AS₁)
Solution:
Given : Radii of the three spheres
r₁ = 6 cm
r₂ = 8 cm
r₃ = 10 cm
These three are melted to form a single sphere. Let the radius of the resulting sphere be V Then volume of the resultant sphere = sum of the the volumes of the three small spheres.
⇒ \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)πr₁³ + \(\frac{4}{3}\)πr₂³ + \(\frac{4}{3}\)πr₃³
⇒ \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)π(r₁³ + r₂³ + r₃³)
r³ = r₁³ + r₂³ + r₃³
= 6³ + 8³ + 10³
= 216 + 512 + 1000 = 1728.
∴ 1728 = (2 × 2 × 3) × (2 × 2 × 3) × (2 × 2 × 3)
r³ = 12 × 12 × 12
r³ = 12³
∴ r = 12
Thus the radius of the resultant sphere = 12 cm.

Question 3.
A 20m deep well of diameter 7m is dug and the earth got by digging is evenly spread out to form a platform 22 m of base 14 m. Find the height of the platform. (AS₄)
Solution:
Diameter of the well (d) = 7 m
Radius the well (r) = \(\frac{7}{2}\) m
Depth of the well (h) = 20 m
Quantity of the earth dig out = Volume of the cylindrical well
= πr²h = \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 20
= 770 cm³
Area of the platform on which the earth is spread out = 22 × 14 = 308 cm²
Let the height of the platform be = x cm
∴ 308 × x = 770
⇒ x = \(\frac{770}{308}\) = 2.5 m
Hence, the height of the platform = 2.5m

Question 4.
A well of diameter 14 m. is dug 15m. deep. The earth taken out of it has been spread evenly to form circular embankment of width 7m. Find the height of the embankment. (AS₄)
Solution:
Diameter of the well (d) = 14m
Radius of the well = \(\frac{\mathrm{d}}{2}\) = \(\frac{14}{2}\) = 7m
Depth of the well (h) = 15m
TS 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.4 1
Quantity of the earth dug out = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 15
Area of circular embankment = π(R + r) (R – r)
= 7(14 + 7)(14 – 7)
= \(\frac{22}{7}\) × 21 × 7 = 462 m²
Let the height of the embankment be ‘x’ m.
462 × x = \(\frac{22}{7}\) × 7 × 7 × 15
∴ x = \(\frac{22}{7}\) × 7 × 7 × 15 × \(\frac{1}{462}\)
Hence, the height of the embankment = 5m.

Question 5.
A Container shaped like a right circular cylinder having diameter 12 cm. and height 15cm. is full of ice cream. The ice cream is to be filled into cones of height 12 cm. and diameter 6 cm. having a hemispherical shape on the top. Find die number of such cones which can be filled with the ice cream. (AS₄)
Solution:
Diameter of the container (d) = 12 km
Radius of the cylindrical container (r) = 6 cm
Height of the cylindrical container (h) = 15 cm
TS 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.4 2
Volume of the cylinder = πr²h
= \(\frac{22}{7}\) × 6 × 6 × 15 cm³ = \(\frac{11880}{7}\) cm³
Diameter of the base of the cone(d) = 6 cm
Radius of the base of the cone (r) = \(\frac{\mathrm{d}}{2}\) = \(\frac{6}{2}\) = 3 cm
Volume of the conical part = \(\frac{1}{3}\) × πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 12
= \(\frac{792}{7}\) cm³
Radius of the hemisphere(r) = 3 cm
TS 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.4 3
Radius of the hemisphere (r) = 3 cm
Volume of the hemi-sphere = \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 3 = \(\frac{396}{7}\) cm³
Total volume of the conical part and hemispherical part
= \(\frac{792}{7}\) + \(\frac{396}{7}\) = \(\frac{1188}{7}\) cm³
Number of cones which can be filled with ice cream = \(\frac{11880}{7}\) + \(\frac{1188}{7}\)
(Q Number of icecream cones = \(\frac{\text { Volume of the cylinder }}{\text { Total volume of ice – cream cone }} \)
= \(\frac{11880}{7}\) × \(\frac{7}{1188}\) = 10

Question 6.
How many silver coins, 1.75 cm in diameter and thickness 2mm, need to be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm ? (AS₄)
Solution:
Let the number of silver coins needed to melt = n
then total volume of n coins = volume of the cuboid.
n × πr²h = lbh
[∵ The shape of the coins is a cylinder then v = πr²h]
n × \(\frac{22}{7}\) × \(\left[\frac{1.75}{2}\right]^2\) × \(\frac{2}{10}\) = 5.5 × 10 × 3.5
[∵ 2mm = \(\frac{2}{10}\) cm, r = \(\frac{\mathrm{d}}{2}\)]
n × \(\frac{22}{7}\) × \(\frac{1.75}{2}\) × \(\frac{1.75}{2}\) × \(\frac{2}{10}\) = 55 × 3.5
n = 55 × 3.5 × \(\frac{7 \times 2 \times 2 \times 10}{22 \times 1.75 \times 1.75 \times 2}\)
= \(\frac{55 \times 35 \times 7 \times 4}{22 \times 2 \times 1.75 \times 1.75}\) = \(\frac{5 \times 35 \times 7}{1.75 \times 1.75}\)
= \(\frac{175 \times 7}{1.75 \times 1.75}\) = \(\frac{100 \times 1}{0.25}\) = 400
∴ 400 Silver coins are needed.

Question 7.
A vessel is in the form of an inverted cone. Its height is 8 cm. and the radius of its top is 5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, \(\frac{1}{4}\) of the water flows out. Find the number of lead shots dropped into the vessel. (AS₄)
Solution:
Let the number of lead shots dropped = n
then the total volume of n – lead shots
= \(\frac{1}{4}\) volume of the conical vessel
TS 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.4 4
Leadshots : Radius (r) = 0.5 cm
Volume (V) = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 0.5 × 0.5 × 0.5
Total volume of n-shots
= n × \(\frac{4}{3}\) × \(\frac{22}{7}\) × 0.125
Cone : Radius (r) = 5 cm
height (h) = 8 cm
Volume (V) = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 5 × 5 × 8
= \(\frac{1}{3}\) × \(\frac{1}{3}\) × 200
\(\frac{1}{4}\)th volume = \(\frac{1}{4}\) × \(\frac{1}{3}\) × \(\frac{22}{7}\) × 200
∴ n × \(\frac{4}{3}\) × \(\frac{22}{7}\) × 0.125 = \(\frac{1}{4}\) × \(\frac{1}{3}\) × \(\frac{22}{7}\) × 200
n = \(\frac{1}{4}\) × \(\frac{1}{3}\) × \(\frac{22}{7}\) × 200 × \(\frac{3}{4}\) × \(\frac{7}{22}\) × \(\frac{1}{0.125}\)
= \(\frac{200 \times 1}{4 \times 4 \times 0.125}\) = \(\frac{200}{2}\) = 100
∴ Number of lead shots = 100

Question 8.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4\(\frac{2}{3}\) cm and height 3 cm. Find the number of cones so formed. (AS₄)
Solution:
Diameter of the solid metallic sphere (d) = 28 cm
∴ Radius of the sphere (r) = \(\frac{\mathrm{d}}{2}\) = \(\frac{2 r}{2}\) = 14 cm
Volume of the sphere = \(\frac{4}{3}\) pr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 14 × 14 × 14
= \(\frac{176 \times 196}{3}\) cm³
Cone : Diameter of the cone = 4\(\frac{2}{3}\) cm
= \(\frac{14}{3}\) cm
∴ Radius of the cone (r) = \(\frac{14}{3}\) × \(\frac{1}{2}\) = \(\frac{7}{3}\) cm
Height of the cone (h) = 3 cm
Volume of the cone = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{7}{3}\) × \(\frac{7}{3}\) × 3
= \(\frac{154}{9}\) cm³
Metallic sphere is recast into smaller cones.
Therefore, the number of cones formed
= \(\frac{176 \times 196}{3}\) ÷ \(\frac{154}{9}\)
= \(\frac{176 \times 196}{3}\) × \(\frac{9}{154}\) = 672
Hence, 672 smaller cones are formed.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2

February 27, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Ex 9.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Exercise 9.2

Question 1.
Choose the correct answer and give justification for each.
(i) The angle between a tangent to a circle and the radius drawn at the point of contact is ______
(a) 60°
(b) 30°
(c) 45°
(d) 90°
Solution:
[ d ]
According to theorem (The tangent at any point of a circle is perpendicular to the radius through the point of contact) tangent is perpendicular to the radius at the point of contact.
Therefore, the correct answer is option
(d) i.e – 90°

(ii) From a point Q, the length of the tangent to a circle is 24cm, and the distance of Q from the centre is 25cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
[ a ]
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 1
In the figure, PQ is the tangent to the circle with centre ‘O’, from an external point Q. P is the point of contact. PO is the radius drawn throught the point of contact P.
∴ ∠OPQ = 90°
In the right triangle OPQ,
OQ² = OP² + PQ²(By pythagoras theorem)
Here, OQ = 25 cm; PQ = 24 cm
⇒ OP² = OQ² – PQ²
= 25² – 24²
= 625 – 576 = 49
∴ OP = \(\sqrt{49}\) = 7 cm.
The radius of the circle is 7cm
The correct answer is option (a), i.e 7 cm.

(iii) If AP and AQ are the two tangents of a circle with centre ‘O’ so that ∠POQ = 110°, then ∠PAQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
Solution:
[ b ]
AP is a tangent to the circle with centre ‘O’. P is the point of contact. PO is the radius drawn through R
∴ ∠OPA = 90°
Similarly, AQ is a tangent. Q is the point of contact. QO is the radius drawn through Q.
∴ ∠OQA = 90°
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 2
In the quadrilateral OQAR the sum of the interior angles is equal to 360°.
⇒ ∠OPA + ∠PAQ + ∠OQA + ∠POQ = 360°
⇒ 90° + ∠PAQ + 90° + 110° = 360°
⇒ 290° + ∠PAQ = 360°
⇒ ∠PAQ = 360° – 290° = 70°
The correct answer is option (b) i.e. 70°

(iv) If tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at an angle of 80°, then ZPOA is equal to
a) 50°
b) 60°
c) 70°
d) 80°
Solution:
[ None ]
PA is a tangent to the circle with centre ‘O’ from an external point R A is the point of contact.
AO is the radius drawn through A.
∴ ∠OAP = 90°
The centre of the circle ‘O’ lies on the bisector of the angle between the two tangents.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 3
∴ ∠OPA = \(\frac{1}{2}\) ∠APB = \(\frac{1}{2}\) × 80° = 40°
Now, in ∆ OAP, ∠OAP = 90°, ∠OPA = 40°
The sum of the angles in a triangle = 180°
∴ ∠OAP + ∠OPA + ∠POA = 180°
90° + 40° + ∠POA = 180°
130° + ∠POA = 180°
∴ ∠POA = 180° – 130° = 50°.
The correct answer is option (a), i.e 50°

(v) In the figure XY and X1Y1 are two parallel tangents to a circle with centre ‘O’ and another tangent AB with point of contact C intersecting XY at ‘A’ and X¹Y¹ at B then ∠AOB =
a) 80°
b) 100°
c) 90°
d) 60°
Solution:
[ C ]
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 4

Question 2.
Two concentric circles of radii 5 cm and 3 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle. (A.P. Mar. ’15)
Solution:
Given : Two circles of radii 3 cm and 5 cm with common centre.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 5
Let AB be a tangent to the inner / small circle and chord to the larger circle.
Let ‘P’ be the point of contact.
Construction : Join OP and OB.
In ∆OPB, ∠OPB = 90°
(radius is perpendicular to the tangent)
OP = 3 cm
OB = 5 cm
Now, (OB)² = (OP)² + (PB)²
[(Hypotenuse)² = (side)² + (side)², pythagorus theorem]
5² = 3² + (PB)²
(PB)² = 25 – 9 = 16
PB = \(\sqrt{16}\) = 4 cm
Now, AB = 2 × PB [∵ The perpendicular drawn from the cnetre of the circle to a chord, bisect it]
AB = 2 × 4 = 8 cm
∴ The length of the chord of the large circle which touches the smaller circle is 8 cm.

Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus. (A.P. Mar. ’16)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 6
Given : A circle with centre O’. A parallelogram ABCD, circumscribing the given circle.
Let P Q, R, S be the points of contact.
Required to prove : ABCD is a rhombus
Proof : AP = AS …………… (1)
[∵ tangents drawn from an external point to a circle are equal]
BP = BQ ……………… (2)
CR = CQ ……………… (3)
DR = DS ……………… (4)
Adding (1), (2), (3) and (4) we get
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + DC = AD + BC
AB + AB = AD + AD
[∴ Opposite sides of a parallelogram all equal]
2AB = 2AD
AB = AD
Hence, AB = CD and AD = BC
[∴ Opposite sides of a parallelogram]
∴ AB = BC = CD = AD
Thus ◊ ABCD is a rhombus

Question 4.
A triangle ABC is drawn to circumscribe a circle of radius 3 cm. such that the segments BD and DC into which BC is divided by the point of contact D are of length 9 cm. and 3 cm. respectively. Find the sides AB and AC.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 7
Solution:
The given figure can also be drawn as

Given : Let ∆ABC be the given triangle circumscribing the given circle with centre ‘O’ and radius 3 cm
i.e., the circle touches the sides BC, CA and AB at D, E, F respectively.
It is given that BD = 9 cm
CD = 3 cm
∴ Length of 2 tangents drawn from an external point to circle are equal.
∴ BF = BD = 9 cm; AF = AE = x cm (say)
The sides of the triangle are 12 cm, (9 + x) cm, (3 + x) cm
Perimeter = 2S = 12 + 9 + x + 3 + x
⇒ 2S = 24 + 2x
S = 12 + x
⇒ S – a = 12 + x – 12 = x
⇒ S – b = 12 + x – 3 – x = 9
⇒ S – c = 12 + x – 9 – x = 3
∴ Area of the triangle ∆ABC
= \(\sqrt{S(S-a)(S-b)(S-c)}\)
= \(\sqrt{(12+x)(x)(9)(3)}\)
= \(\sqrt{27\left(x^2+12 x\right)}\) …………….. (1)
But ∆ABC = ∆OBC + ∆OCA + ∆OAB
= \(\frac{1}{2}\) × BC × OD + \(\frac{1}{2}\) × CA × OE + \(\frac{1}{2}\) AB × OF
= \(\frac{1}{2}\) (12 × 3) + \(\frac{1}{2}\) (3 + x) × 3 + \(\frac{1}{2}\) (9 + x) × 3
= \(\frac{1}{2}\) [36 + 9 + 3x + 27 + 3x]
= \(\frac{1}{2}\) [72 + 6x] ⇒ 36 + 3x ……………. (2)
From (1) and (2),
\(\sqrt{27\left(x^2+12 x\right)}\) = 36 + 3x
Squaring on both sides we get,
27(x² + 12x) = (36 + 3x)²
27x² + 324x = 1296 + 9x² + 216x
⇒ 18x² + 108x – 1296 = 0
⇒ x² + 6x – 72 = 0
⇒ x² + 12x – 6x – 72 = 0
x(x + 12) – 6(x + 12) = 0
(x – 6) (x + 12) = 0
x = 6 or -12
But ‘x’ can’t be negative hence, x = 6
AB = 9 + 6 = 15 cm
AC = 3 + 6 = 9 cm

Question 5.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Verify by using phythagorus theorem. (A.P. June ’15)
Solution:
Steps of construction :

Draw a circle with centre ‘O’ and radius = 6 cm
Take a point P outside the circle such that OP = 10 cm, join OP.
Draw the perpendicular bisector to OP which bisects it at M.
Taking M as centre and PM or MO as ra-dius draw a circle. Let the circle intersects the given circle at A and B.
Join P to A and B.
PA and PB are the required tangents of lengths 8 cm each.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 9
Proof : In ∆OAP
(OA)² + (AP)² = 6² + 8²
⇒ 36 + 64 = 100
(OP)² = 10² = 100
∴ (OA)² + (AP)² = (OP)²
Hence AP is a tangent.
Similarly, BP is a tangent.

Question 6.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 10
Construction :

Mark a point ‘O’ on the plane of the paper and draw a circle with ‘O’ as centre and 4 cm as radius
Taking ‘O’ as centre, draw another circle of radius 6 cm.
Mark a point B on the bigger circle. Join OB. Draw the perpendicular bisector of OB to intersect OB at C.
Now, Take ‘C’ as centre and CO = CB as radius, draw a circle which intersects the smaller circle at P and Q.
Join BP and BQ.
BP and BQ are the required tangents
By actual measurement, we find BP = BQ = 4.5 cm

Verification :
In ∆ BPO, ∠P = 90°
OP = 4cm, OB = 6cm By Pythagoras Theorem,
OB² = PB² + OP²
⇒ PB² = OB² – OP²
= 6² – 4² = 36 – 16 = 20
∴ PB = \(\sqrt{20}\) = 4.47 cm = 4.5 cm (approximately)

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle and measure them. Write conclusion.
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 11
Construction :

Draw a circle with the help of a bangle.
Take two non-parallel chords AB and CD of this circle.
Draw the perpendicular bisectors of AB and CD. Let these intersect at O. Then, O is the centre of the circle drawn.
Take a point P outside the circle. Join OR Draw the perpendicular bisector of OR Let M be its midpoint.
Draw a circle with M as centre and MO = MP as radius.
Join PQ and PR.
So, PQ and PR are the required tangents.

Conclusion : Tangents drawn from an external point to a circle are equal.

Question 8.
In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 12
Solution:
Let ABC be a right triangle, right angled at P.
Consider a circle with diameter AB.
From the figure, the tangent to the circle at B meets BC in Q.
Now QB and QP are 2 tangents to the circle from the same point P.
∴ QB = QP ……………. (1)
Also, ∠QPC = ∠QCP
∴ PQ = QC
From (1) and (2);
QB = QC.
Hence proved.

Question 9.
Draw a tangent to a given circle with center O from a point ‘R’ outside the circle. How many tangents can be drawn to the circle from that point ?
[Hint: The distance of two points to the point of contact is the same].
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 13
Only 2 tangents can be drawn from a given point outside the circle.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1

February 27, 2024February 26, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Ex 9.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Exercise 9.1

Question 1.
Fill in the blanks :
(i) A tangent to a circle intersects it in __________ points
Solution:
one

(ii) A line intersecting a circle in two points is called a _________
Solution:
secant

(iii) A circle can have _________ parallel tangents at the most,
Solution:
two

(iv) The common point of a tangent to a circle and the circle is called _______
Solution:
point of contact

(v) We can draw __________ tangents to a given circle
Solution:
infinite

Question 2.
A tangent PQ of a point P’ of a circle of radius 5 cm meets a line through the centre ‘O’ at a point Q so that OQ = 12 cm. Find the length of PQ.
Solution:
PQ is a tangent to a circle whose centre is ‘O’.
P is the point of contact. PO is the radius of the circle.
Hence ∠OPQ = 90°
Given that OP = 5 cm and OQ = 12 cm
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1 1
By pythagorus theorem.
(OP)² + (PQ)² = (OQ)²
(PQ)² = (OQ)² – (OP)²
(PQ)² = 12² – 5² = 119
PQ = \(\sqrt{119}\)
Hence, length of PQ = \(\sqrt{119}\) cm

Question 3.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
The adjacent figure is a circle with centre ‘O’
AB is the given line CD is a tangent to the circle of P parallel to AB.
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1 2
EF is a secant of the circle, drawn parallel to AB

Question 4.
Calculate the length of tangent from a point 15 cm. away from the centre of a circle of radius 9 cm. (A.P. Mar. ’16, 15)
Solution:
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1 3
In ∆OTR ∠OTP = 90°
OT = 9 cm
OP = 15 cm
By pythagorus theorem
(OP)² = (OT)² + (PT)²
⇒ 15² = 9² + (PT)²
⇒ PT² = 15² – 92 = 225 – 81
(PT)² = 144 ⇒ PT = \(\sqrt{144}\) = 12
Length of the required tangent = PT = 12 cm

Question 5.
Prove that the tangents to a circle at the end points of a diameter are parallel. (A.P. June ’15)
Solution:
PQ is the diameter of a circle with centre ‘O’. APB and CQD are tangents to the circle at P and Q respectively.
We have to prove that AB || CD
AB is a tangent to the circle ‘P’ is the point of contact and
PO is the radius drawn through P
∴ ∠APO = 90° ……………… (1)
CD is a tangent to the circle. Q is the point of contact and QO is the radius draw through Q.
∴ ∠DQO = 90°
From (1) and (2), we have
∠APO = ∠DQO
AB, CD are two lines. PQ is a transversal ∠APO and ∠DQO are a pair alternate angles. Since the alternate angles are equal AB || CD
TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1 4

TS 10th Class Maths Solutions Chapter 10 Mensuration InText Questions

February 26, 2024February 25, 2024 by Srinivas

Students can practice 10th Class Maths Study Material Telangana Chapter 10 Mensuration InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 10 Mensuration InText Questions

Try This

Question 1.
Consider the following situations. In each find out whether you need volume or area and why ? (Page No.245)

Quantity of water inside a bottle.
Canvas needed for making a tent.
Number of bags inside the lorry.
Gas filled in a cylinder.
Number of match sticks that can be put in match box.

Solution:

Volume : 3-d shape
Area : L.S.A. / T.S.A
Volume : 3-d shape
Volume : 3-d shape
Volume : 3-d shape

Question 2.
State 5 more such examples and ask your friends to choose what they need ? (AS₃) (Page No. 245)
Solution:

To paint a pillar in the shape of a cylinder.
To white wash the walls of a house.
To find the quantity of rich in a heap of rice.
An object is the form of a cone having a herispherical shape on its top. Quantity of ice-cream to be filled in it.
Later flowing through a cylindricalipipe.

Question 3.
Break the pictures in the previous figure into solids of known shapes. (AS₅) (Page No. 246)
Solution:
TS 10th Class Maths Solutions Chapter 10 Mensuration InText Questions 1

Question 4.
Think of 5 more objects around you that can be seen as a combination of shapes. Name the shapes that combined to make them. (AS₃) (Page No. 246)
Solution:
Student’s Activity.

Try This

Question 1.
Use known solid shapes and make as many objects (by combining more than two) as possible that you come across in
your daily life.
(Hint : Use clay, or balls, pip€s. paper cones, boxes like cube, cuboid etc.) (AS4, AS5) (Page No. 252)
Solution:
Student’s Activity.

Think – Discuss

Question 1.
A sphere is inscribed in a cylinder. Is the surface of the sphere equal to the curved surface of the cylinder ? If yes, explain how. (AS2, AS3) (Page No. 252)
TS 10th Class Maths Solutions Chapter 10 Mensuration InText Questions 2
Solution:
Yes, the surface area of the sphere is equal to the curved surface area of the cylinder.
Let the radius of this cylinder be ‘r’ and its height ‘h’
Then its curved surface area = 2πrh
= 2πr (r + r)
∴ height = diameter of the sphere
= diameter of the cylinder
= 2r
= 2πr(2r)
= 4πr²
And surface area of the sphere = 4πr²
∴ C.S.A of cylinder = Surface area of sphere.

Try This

Question 1.
If the diameter of the cross-section of a wire is decreased by 5% by what percentage should the length be increased so that the volume remains the same ? (AS4) (Page No. 257)
Solution:
Radius of wire r = r and length = h₁
diameter of cross – section of wire d₁ = 2r
decreased diameter 5%
= 2r × \(\frac{5}{100}\) = \(\frac{\mathrm{r}}{10}\)
∴ decreased radius r₂ = 2r – \(\frac{\mathrm{r}}{20}\)
= \(\frac{19\mathrm{r}}{10}\) × \(\frac{1}{2}\) = \(\frac{19 \mathrm{r}}{20}\)
volume of the wire V₁ = πr₁²h₁, length = h₂ (after increased) volume of the wire V₁ (after increased) = πr₂²h₂ volumes are equal. So v₁ = v₂
πr₁²h₁ = πr₂²h₂
πr²h₁ = π \(\left(\frac{19 r}{20}\right)^2\) × h₂
h₁ = \(\frac{361}{400}\) × h₂
h₁ = \(\frac{361}{400}\) h₂
h₂ = \(\frac{400 \mathrm{~h}_1}{361}\)
increased length = h₂ – h₁
= \(\frac{400 \mathrm{~h}_1}{361}\) – h₁
= \(\frac{400 \mathrm{~h}_1-361 \mathrm{~h}_1}{361}\) = \(\frac{39 \mathrm{~h}_1}{361}\)
increased percentage
= 100 × \(\frac{39 \mathrm{~h}_1}{361}\) × \(\frac{\mathrm{h}_1}{\mathrm{~h}_1}\)
= \(\frac{3900}{361}\) = 10.8%

Question 2.
Surface areas of a sphere and cube are equal then find the ratio of their volumes. (AS4)(Page No. 257)
Solution:
radius of sphere = r, and side of cube = a
surface area of sphere = 4πr²
surface area of cube = 6a²
surface area of sphere = surface area of cube (given)
4πr² = 6a² ⇒ 4 × \(\frac{22}{7}\) × π² = 6 × a²
TS 10th Class Maths Solutions Chapter 10 Mensuration InText Questions 3

Think – Discuss

Question 1.
Which barrel shown in the below figure can hold more water ? Discuss with your friends. (AS₂, AS₃) (Page No. 262)
TS 10th Class Maths Solutions Chapter 10 Mensuration InText Questions 4
Solution:
r₁ = \(\frac{1}{2}\) = 0.5 cm; h₁ = 4 cm
Volume of the 1^st barrel = πr²h
= \(\frac{22}{7}\) × 0.5 × 0.5 × 4 = 3.142 cm³

r₂ = \(\frac{4}{2}\) = 2 cm ; h = 1 cm
Volume of the 2^nd barrel
V = πr²h = \(\frac{22}{7}\) × 2 × 2 × 1
= 12.57 cm³
Hence, the volume of the 2^nd barrel is more than the first barrel.

Do This

Question 1.
A copper rod of diameter 1cm and length 8 cm is drawn into a wire of length 18m of uniform thickness. Find the thickness of wire. (AS₄) (Page No. 263)
Solution:
Volume of the copper rod(Cylinder) = πr²h
= \(\frac{22}{7}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × 8
= \(\frac{44}{7}\) cm²
If ‘r’ is the radius of the wire, then its volume = πr²h
∴ The volume of rod is equal to the volume of the wire. We have
⇒ \(\frac{22}{7}\) × r² × 18 m = \(\frac{44}{7}\) cm³
⇒ r² = \(\frac{44}{7}\) × \(\frac{7}{22}\) × \(\frac{1}{1800}\)
[∴ 18m = 18 × 100 cm]
⇒ r² = \(\frac{1}{900}\)
⇒ r = \(\frac{1}{30}\) cm = \(0.0 \overline{3}\) cm
∴ Thickness = d = 2 × 0.03 = 0.06 cm

Question 2.
Pravali house has a water tank in the shape of a cylinder on the roof. This is filled by pumping water from a sumpfan underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44m × 9.5 cm. The water tank has radius 60 cm. and height 95 cm. Find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water. Compare the ca¬pacity of the tank with that of the sump. (AS₄) (Page No. 263)
Solution:
Volume of the water in the sump = [v = lbh]
= 1.57 × 1.44 × 0.95
(∵ 9.5 cm = \(\frac{9.5}{100}\) m = 0.95 m).
= 2.14776 m³ = 2147160 cm³
Volume of the tank on the roof = πr²h
= 3.14 × 60 × 60 × 95 = 1073880 cm³
∴ Volume of the water left in the sump after filling the tank
= 2147760 – 1073880
= 1073880 cm³
Let the height of the water in the tank be h.
∴ 157 × 144 × h = 1073880
h = \(\frac{1073880}{157 \times 144}\) = 47.5 cm
∴ Ratio of the volume of the sump and tank
= 21447760 : 1073880 = 2 : 1
∴ Sump can hold two times the water that can be hold in the tank.