TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise

Question 1.
Prove that the angle between the two tan-gents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
PA and PB are tangents to the circle with centre ‘0’ from and external point P.
Join OA, OB and OR The angle between the tangents is ∠APB.
We have to prove that ∠AOB + ∠APB = 180°
PA is a tangent to the circle with centre ‘O’.

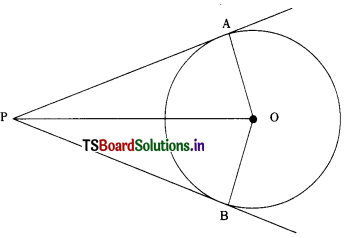
A is the point of contact. AO is the radius drawn through the point of contact i.e., A
∴ ∠PAO = 90°
PB is a tangent to the circle with centre ‘O’.
B is the point of contact. BO is the radius drawn through the point of contact i.e., B
∴ ∠PBO = 90°
OAPB is a quadrilateral.
The sum of the angles of a quadrilateral is 360°
∠APB + ∠PBO + ∠AOB + ∠PAO = 360°
∠APB + ∠AOB + ∠PAO + ∠PBO = 360°
∠APB + ∠AOB + 90° + 90° = 360°
∴ ∠APB + ∠AOB = 360° – 90° – 90°
= 360° – 180° = 180°
∠APB and ∠AOB are supplementary.

Question 2.
PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T (See figure). Find the length of TP.
Solution:
PQ is a chord of length 8cm of a circle with centre ‘O’.
Radius of the circle = 5 cm.
⇒ OP = OQ = 5cm
The tangents at P and Q meet at T. Join OT.
OT is the perpendicular bisector of PQ.

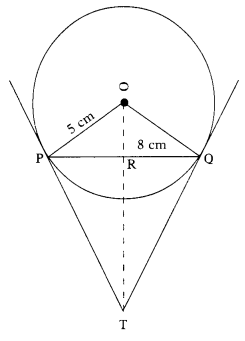
In triangle OPT, ∠OPT = 90°
∴ PT² = OT² – OP² …………….. (1)
In ∆ PRO, ∠R = 90°
∴ OP² = OR² + PR²
⇒ OR² = OP² – PR²
= 5² – 4²
= 25 – 16 = 9
∴ OR = \(\sqrt{9}\) = 3 cm
In the right triangle OPT,
PR is perpendicular to the hypotenuse OT.
∴ PR² = TR. RO
4² = TR × 3 ⇒ TR = \(\frac{4^2}{3}\) = \(\frac{16}{3}\)
OT = OR + TR = \(\frac{3}{1}\) + \(\frac{16}{3}\) = \(\frac{25}{3}\)
From (1), PT² = \(\left(\frac{25}{3}\right)^2\) – (5)²
= \(\frac{625}{9}\) – \(\frac{25}{1}\)
= \(\frac{625-225}{9}\) = \(\frac{400}{9}\)
∴ PT = \(\sqrt{\frac{400}{9}}\) = \(\frac{20}{3}\) cm

Question 3.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
ABCD is a quadrilateral, circumscribing a circle whose centre is O.
The opposite sides AB and CD are subtend angles ∠AOB and ∠COD at the centre.

Similarly, the other pair of opposite sides AD and BC subtend angles ∠AOD and ∠BOC at the centre.
We have to prove that
∠AOB + ∠COD = 180°
and ∠AOD + ∠BOC = 180°
Join OR OQ, OR and OS.
We know that the tangents drawn from an ex¬ternal point to a circle subtend equal angles at the centre.
AP and AS are the tangents to the circle from A.
∴ ∠AOP = ∠AOS ……………. (1)
BP and BQ are the tangents to the circle from B.
∴ ∠BOP = ∠BOQ …………….. (2)
CQ and CR are the tangents to the circle from C.
∴ ∠COQ = ∠COR ………………. (3)
DR and DS are the tangents to the circle from D.
∴ ∠DOR = ∠DOS …………………. (4)
Adding (1), (2), (3) and (4), we get
∠AOP + ∠BOP + ∠COQ + ∠DOR + ∠AOS + ∠BOQ + ∠COR + ∠DOS = 360°
(∵ Sum of the angles formed at’O’is equal to 360°)
(∠AOP + ∠BOP) + (∠COR + ∠DOR) + (∠BOQ + ∠COQ) + (∠AOS + ∠DOS) = 360° 2∠AOP + 2∠COR + 2 ∠BOQ + 2 ∠DOS = 360°
⇒ ∠AOP + ∠COR + ∠BOQ + ∠DOS = 180°
⇒∠AOP + ∠BOQ + ∠COR + ∠DOS = 180°
⇒ ∠AOP + ∠BOP + ∠COR + ∠DOR = 180°
(∵ ∠BOQ = ∠BOP and ∠DOS = ∠DOR
⇒ ∠AOB + ∠COD = 180°
In ∆^les BOP & BOQ)
Similarly, we can prove that
∠BOC + ∠AOD = 180°

Question 4.
Draw a line segment AB of length 8cm. Taking A as centre, draw a circle of radius 4cm and taking B as centre, draw another circle of radius 3cm. Construct tangents to each circle from the centre of the other circle.
Solution:

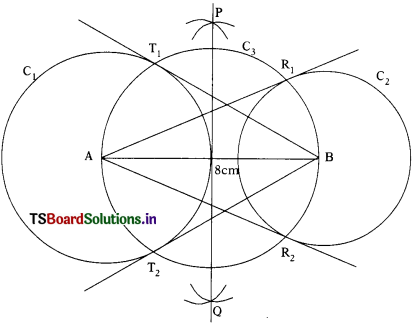
1. Draw a line segment AB = 8 cm.
2. Take A as centre and draw a circle (C₁) of radius 4cm.
3. Take B as centre and draw a circle (C₂) of radius 3 cm.
4. Draw the perpendicular bisector PQ of AB.
5. Draw a circle with AB as diameter (C₃). This circle intersects the circle with A as centre in T₁ and T₂. Join BT₁ and BT₂. These are the tangents to the circle C₁.
6. The circle with AB as diameter (C₃) intersects the circle with B as centre (C₂) in R₁ and R₂. Join AR₁ and AR₂. These are the tangents to the circle C₂.

Question 5.
Let ABC be a right angled triangle in which AB = 6cm, BC = 8cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
Construction :

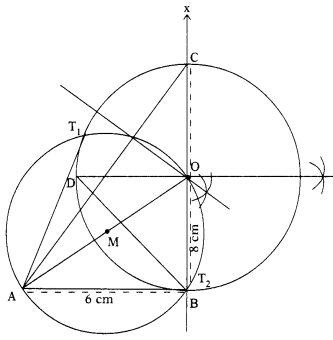
1. Draw a line segment AB = 6cm.
   Make ∠ABX = 90°.
   Mark a point C on \(\overrightarrow{\mathrm{BX}}\) such that BC = 8cm. Join AC.
2. Draw BD ⊥ AC intersecting AC in D.
3. Draw the perpendicular bisectors of BC and CD. Let them intersect at ‘O’.
4. Take ‘O’ as centre and OB = OD = OC as radius, draw a circle passing through B, D and C
5. Join AO. Find M the mid point of AO.
6. Take M as centre and radius as (AM = MO) draw a circle passing through A and C, intersecting the first circle at T₁ and T₂.
7. Join AT₁ and AT₂.
8. AT₁ and AT₂ are the required tangents.

Question 6.
Find the area of the shaded region in the figure, given in which two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm.

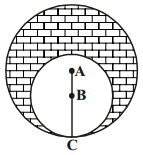
Solution:
AC denotes the radius of the bigger circle.
AC = 8cm. (Given)
AB denotes the distance between the centres of two circles.
AB = 3cm (Given)
∴ BC denotes the radius of the smaller circle
BC = AC – AB = 8 – 3 = 5 cm
The Area of the shaded region = Area of the bigger circle – Area of the smaller circle =
= π(8)² – π(5)²
= π[8² – 5²]
= π[64 – 25]
= \(\frac{22}{7}\) × 39
= \(\frac{858}{7}\)
= 122.57 cm²

Question 7.
ABCD is a rectangle with AB = 14 cm and BC = 7cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.

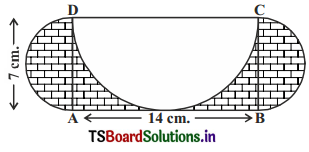
Solution:
ABCD is a rectangle.
Length of the rectangle AB = CD = 14 cm
Breadth of the rectangle AD = BC = 7cm
Area of the rectangle ABCD
= length × breadth
= 14 × 7
= 98 cm²
Two semi-circles are drawn on AD and BC clearly, They are of the same diameters.
Hence, Area of two semi-circles becomes area of one complete circle with diameter 7 cm.
So, radius of the circle (r) = \(\frac{7}{2}\) cm
Area of the circle = πr²
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\)
= 38.5 cm² ……………….. (1)
Area a of the semi-circle whose diameter is 14 cm = \(\frac{1}{2}\)πr² ; Here, r = 7cm
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7
= 77 cm²
Area of the shaded region in the rectangle
= Area of the rectangle – Area of the semicircle
= 98 – 77
= 21 cm² ……………… (2)
Area of the total shaded region
= Area of the circle (shaded) + Area of the shaded region in the rectangle.
= (38.5 + 21) cm²
= 59.5 cm²