TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions

Students must practice these TS Inter 1st Year Maths 1A Important Questions Chapter 8 Inverse Trigonometric Functions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions

Question 1.
Prove that

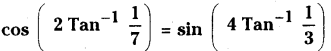
Solution:

Question 2.
Find the values of the following.

(i) \(\sin ^{-1}\left(-\frac{1}{2}\right)\)
Solution:
\(\sin ^{-1}\left(-\frac{1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)=-\frac{\pi}{6}\)

(ii) \(\cos ^{-1}\left(-\frac{\sqrt{3}}{2}\right)\)
Solution:

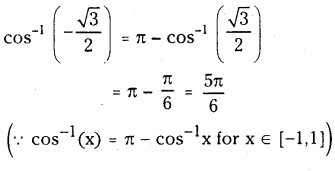
(iii) \(\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)
Solution:
\(\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=\tan ^{-1}\left(\tan \frac{\pi}{6}\right)=\frac{\pi}{6}\)

(iv) cot^-1 (-1)
Solution:

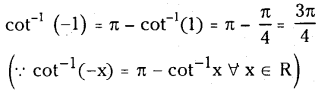
(v) sec ^-1  \((-\sqrt{2})\)
Solution:

(vi) Cosec ^-1  \(\left(\frac{2}{\sqrt{3}}\right)\)
Solution:

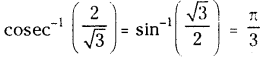
Question 3.
Find the values of the following.

(i) sin^-1 \(\left(\sin \frac{4 \pi}{3}\right)\)
Solution:

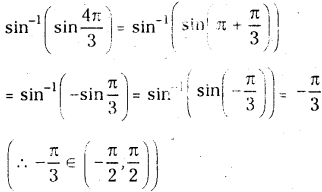
(ii) \(\tan ^{-1}\left(\tan \frac{4 \pi}{3}\right)\)
Solution:

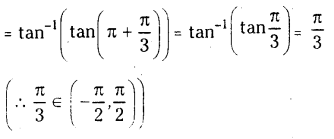
Question 4.
Find the values of the following.

(i) \(\sin \left(\cos ^{-1} \frac{5}{13}\right)\)
Solution:

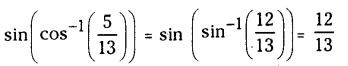
(ii) \(\tan \left(\sec ^{-1} \frac{25}{7}\right)\)
Solution:

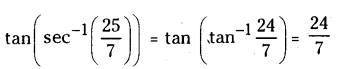
(iii) \(\cos \left(\tan ^{-1} \frac{24}{7}\right)\)
Solution:

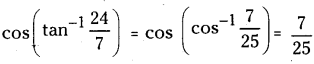
Question 5.
Find the values of the following.

(i) \(\sin ^2\left(\tan ^{-1} \frac{3}{4}\right)\)
Solution:

(ii) \(\sin \left(\frac{\pi}{2}-\sin ^{-1}\left(-\frac{4}{5}\right)\right)\)
Solution:

(iii) \(\cos \left(\cos ^{-1}\left(-\frac{2}{3}\right)-\sin ^{-1}\left(\frac{2}{3}\right)\right)\)
Solution:

(iv) sec² (cot^-1 3) + cosec² (tan^-1 2)
Solution:

Question 6.
Find the value of \(\cot ^{-1}\left(\frac{1}{2}\right)+\cot ^{-1}\left(\frac{1}{3}\right)\)
Solution:

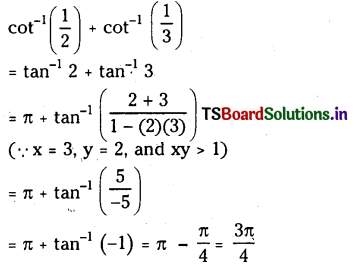
Question 7.
Prove that
\(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{7}{25}\right)=\sin ^{-1}\left(\frac{117}{125}\right)\)
Solution:

Question 8.
If x ∈(-1, 1) prove that 2 tan^-1 x = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\)
Solution:
Given x ∈ (-1,1) and it tan^-1 x = a then tan α = x and

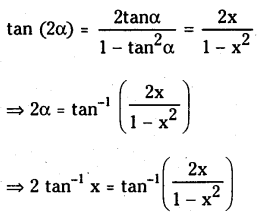
Question 9.
Prove that \(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{5}{13}\right) +\sin ^{-1}\left(\frac{16}{65}\right)=\frac{\pi}{2}\)
Solution:

Question 10.
Prove that cot^-1 9+ cosec^-1 \( \frac{\sqrt{41}}{4}=\frac{\pi}{4}\)
Solution:

Question 11.
Show that cot \(\begin{aligned} \cot \left(\operatorname{Sin}^{-1} \sqrt{\frac{13}{17}}\right) \\ = \sin \left(\operatorname{Tan}^{-1}\left(\frac{2}{3}\right)\right) \end{aligned}\)
Solution:

Question 12.
Find the value of \(tan \left[2 \operatorname{Tan}^{-1}\left(\frac{1}{5}\right)-\frac{\pi}{4}\right]\)
Solution:

Question 13.
Prove that \(\operatorname{Sin}^{-1}\left(\frac{4}{5}\right)+2 \operatorname{Tan}^{-1}\left(\frac{1}{3}\right)=\frac{\pi}{2}\)
Solution:

Question 14.
If sin^-1 x + sin^-1 y + sin^-1 z = π, then prove that x⁴ + y⁴ + z⁴ + 4x²y²z² = 2 (x²y² + y²z² + z²x²)
Solution:
Let sin^-1 x = A, sin^-1 y = B and sin^-1z = C
then A+B+C = π …………………..(1)
and sinA = x, sin B = y, sin C = z
Now A+B = π – c

Question 15.
If \(\operatorname{Cos}^{-1}\left(\frac{p}{a}\right)+\operatorname{Cos}^{-1}\left(\frac{q}{b}\right)\) =α the prove that

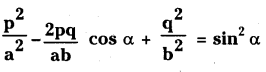
Solution:

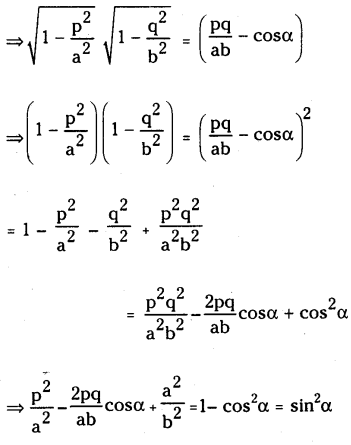
Question 16.
Solve \(\sin ^{-1}\left(\frac{5}{x}\right)+\sin ^{-1}\left(\frac{12}{x}\right)=\frac{\pi}{2},(x>0)\)
Solution:

Question 17.
Solve

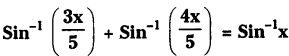
Solution:

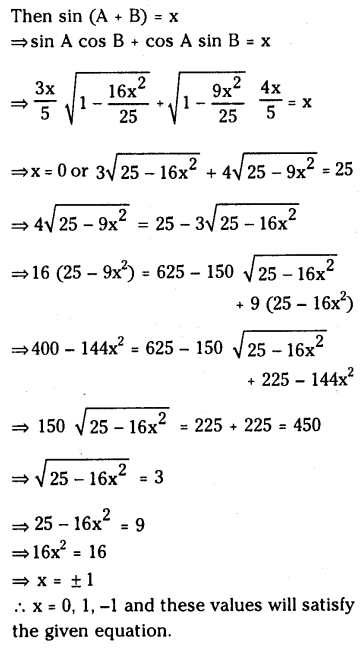
Question 18.
Solve \(\operatorname{Sin}^{-1} x+\operatorname{Sin}^{-1} 2 x=\frac{\pi}{3}\)
Solution:

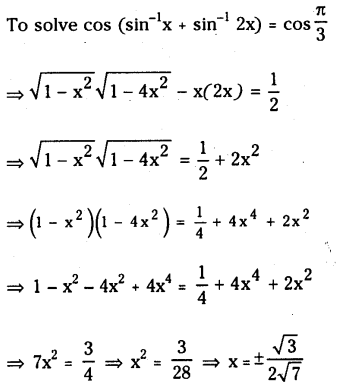
when \(x=-\frac{\sqrt{3}}{2 \sqrt{7}}\) value is not admissible
Since sin^-1 x and sin^-1 2x are negative
Hence \(x=-\frac{\sqrt{3}}{2 \sqrt{7}}\)

Question 19.
If sin [2 Cos^-1 (cot (2 Tan^-1x)}] = 0 find x.
Solution:

Question 20.
Prove that

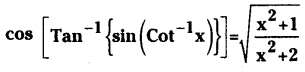
Solution:
Let cot^-1 x=θ then cot θ = x and θ <x<π
∴ sin (cot^-1x) = sinθ = \(\frac{1}{\operatorname{cosec} \theta}\)

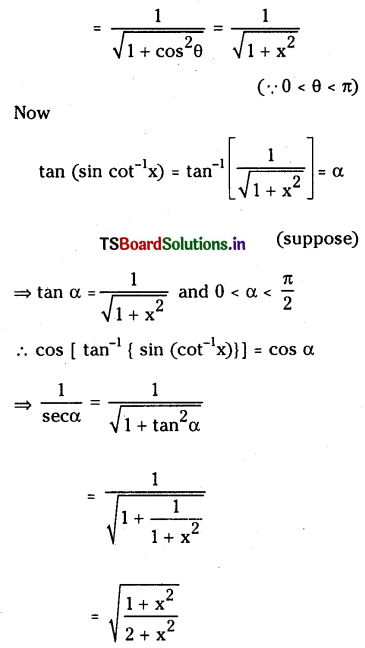
Question 21.
Show that sec² (tan^-1) + cosec² (cot^-1 2) = 10.
Solution:
[1 + tan² (tan^-1(2)] + [1+ cot² (cot^-1(2))]
= 1 + 4 + 1 + 4 = 10