TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Ex 9.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Exercise 9.1

Question 1.
Fill in the blanks :
(i) A tangent to a circle intersects it in __________ points
Solution:
one

(ii) A line intersecting a circle in two points is called a _________
Solution:
secant

(iii) A circle can have _________ parallel tangents at the most,
Solution:
two

(iv) The common point of a tangent to a circle and the circle is called _______
Solution:
point of contact

(v) We can draw __________ tangents to a given circle
Solution:
infinite

Question 2.
A tangent PQ of a point P’ of a circle of radius 5 cm meets a line through the centre ‘O’ at a point Q so that OQ = 12 cm. Find the length of PQ.
Solution:
PQ is a tangent to a circle whose centre is ‘O’.
P is the point of contact. PO is the radius of the circle.
Hence ∠OPQ = 90°
Given that OP = 5 cm and OQ = 12 cm

By pythagorus theorem.
(OP)² + (PQ)² = (OQ)²
(PQ)² = (OQ)² – (OP)²
(PQ)² = 12² – 5² = 119
PQ = \(\sqrt{119}\)
Hence, length of PQ = \(\sqrt{119}\) cm

Question 3.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
The adjacent figure is a circle with centre ‘O’
AB is the given line CD is a tangent to the circle of P parallel to AB.

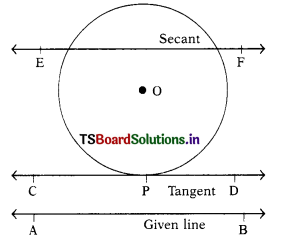
EF is a secant of the circle, drawn parallel to AB

Question 4.
Calculate the length of tangent from a point 15 cm. away from the centre of a circle of radius 9 cm. (A.P. Mar. ’16, 15)
Solution:

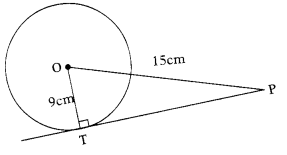
In ∆OTR ∠OTP = 90°
OT = 9 cm
OP = 15 cm
By pythagorus theorem
(OP)² = (OT)² + (PT)²
⇒ 15² = 9² + (PT)²
⇒ PT² = 15² – 92 = 225 – 81
(PT)² = 144 ⇒ PT = \(\sqrt{144}\) = 12
Length of the required tangent = PT = 12 cm

Question 5.
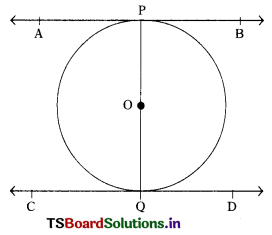
Prove that the tangents to a circle at the end points of a diameter are parallel. (A.P. June ’15)
Solution:
PQ is the diameter of a circle with centre ‘O’. APB and CQD are tangents to the circle at P and Q respectively.
We have to prove that AB || CD
AB is a tangent to the circle ‘P’ is the point of contact and
PO is the radius drawn through P
∴ ∠APO = 90° ……………… (1)
CD is a tangent to the circle. Q is the point of contact and QO is the radius draw through Q.
∴ ∠DQO = 90°
From (1) and (2), we have
∠APO = ∠DQO
AB, CD are two lines. PQ is a transversal ∠APO and ∠DQO are a pair alternate angles. Since the alternate angles are equal AB || CD