TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2

Students can practice 10th Class Maths Study Material Telangana Chapter 9 Tangents and Secants to a Circle Ex 9.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Exercise 9.2

Question 1.
Choose the correct answer and give justification for each.
(i) The angle between a tangent to a circle and the radius drawn at the point of contact is ______
(a) 60°
(b) 30°
(c) 45°
(d) 90°
Solution:
[ d ]
According to theorem (The tangent at any point of a circle is perpendicular to the radius through the point of contact) tangent is perpendicular to the radius at the point of contact.
Therefore, the correct answer is option
(d) i.e – 90°

(ii) From a point Q, the length of the tangent to a circle is 24cm, and the distance of Q from the centre is 25cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
[ a ]

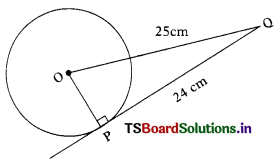
In the figure, PQ is the tangent to the circle with centre ‘O’, from an external point Q. P is the point of contact. PO is the radius drawn throught the point of contact P.
∴ ∠OPQ = 90°
In the right triangle OPQ,
OQ² = OP² + PQ²(By pythagoras theorem)
Here, OQ = 25 cm; PQ = 24 cm
⇒ OP² = OQ² – PQ²
= 25² – 24²
= 625 – 576 = 49
∴ OP = \(\sqrt{49}\) = 7 cm.
The radius of the circle is 7cm
The correct answer is option (a), i.e 7 cm.

(iii) If AP and AQ are the two tangents of a circle with centre ‘O’ so that ∠POQ = 110°, then ∠PAQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
Solution:
[ b ]
AP is a tangent to the circle with centre ‘O’. P is the point of contact. PO is the radius drawn through R
∴ ∠OPA = 90°
Similarly, AQ is a tangent. Q is the point of contact. QO is the radius drawn through Q.
∴ ∠OQA = 90°

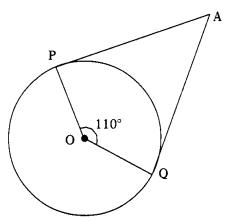
In the quadrilateral OQAR the sum of the interior angles is equal to 360°.
⇒ ∠OPA + ∠PAQ + ∠OQA + ∠POQ = 360°
⇒ 90° + ∠PAQ + 90° + 110° = 360°
⇒ 290° + ∠PAQ = 360°
⇒ ∠PAQ = 360° – 290° = 70°
The correct answer is option (b) i.e. 70°

(iv) If tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at an angle of 80°, then ZPOA is equal to
a) 50°
b) 60°
c) 70°
d) 80°
Solution:
[ None ]
PA is a tangent to the circle with centre ‘O’ from an external point R A is the point of contact.
AO is the radius drawn through A.
∴ ∠OAP = 90°
The centre of the circle ‘O’ lies on the bisector of the angle between the two tangents.

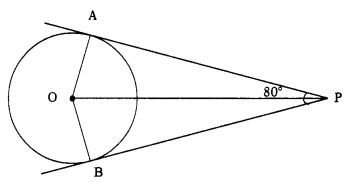
∴ ∠OPA = \(\frac{1}{2}\) ∠APB = \(\frac{1}{2}\) × 80° = 40°
Now, in ∆ OAP, ∠OAP = 90°, ∠OPA = 40°
The sum of the angles in a triangle = 180°
∴ ∠OAP + ∠OPA + ∠POA = 180°
90° + 40° + ∠POA = 180°
130° + ∠POA = 180°
∴ ∠POA = 180° – 130° = 50°.
The correct answer is option (a), i.e 50°

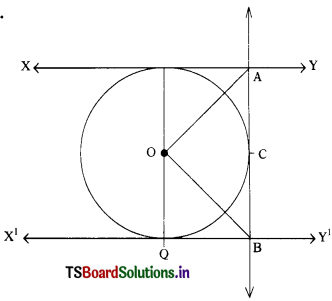
(v) In the figure XY and X1Y1 are two parallel tangents to a circle with centre ‘O’ and another tangent AB with point of contact C intersecting XY at ‘A’ and X¹Y¹ at B then ∠AOB =
a) 80°
b) 100°
c) 90°
d) 60°
Solution:
[ C ]

Question 2.
Two concentric circles of radii 5 cm and 3 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle. (A.P. Mar. ’15)
Solution:
Given : Two circles of radii 3 cm and 5 cm with common centre.

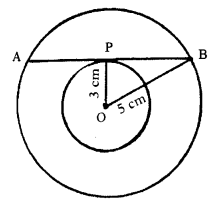
Let AB be a tangent to the inner / small circle and chord to the larger circle.
Let ‘P’ be the point of contact.
Construction : Join OP and OB.
In ∆OPB, ∠OPB = 90°
(radius is perpendicular to the tangent)
OP = 3 cm
OB = 5 cm
Now, (OB)² = (OP)² + (PB)²
[(Hypotenuse)² = (side)² + (side)², pythagorus theorem]
5² = 3² + (PB)²
(PB)² = 25 – 9 = 16
PB = \(\sqrt{16}\) = 4 cm
Now, AB = 2 × PB [∵ The perpendicular drawn from the cnetre of the circle to a chord, bisect it]
AB = 2 × 4 = 8 cm
∴ The length of the chord of the large circle which touches the smaller circle is 8 cm.

Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus. (A.P. Mar. ’16)
Solution:

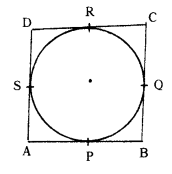
Given : A circle with centre O’. A parallelogram ABCD, circumscribing the given circle.
Let P Q, R, S be the points of contact.
Required to prove : ABCD is a rhombus
Proof : AP = AS …………… (1)
[∵ tangents drawn from an external point to a circle are equal]
BP = BQ ……………… (2)
CR = CQ ……………… (3)
DR = DS ……………… (4)
Adding (1), (2), (3) and (4) we get
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + DC = AD + BC
AB + AB = AD + AD
[∴ Opposite sides of a parallelogram all equal]
2AB = 2AD
AB = AD
Hence, AB = CD and AD = BC
[∴ Opposite sides of a parallelogram]
∴ AB = BC = CD = AD
Thus ◊ ABCD is a rhombus

Question 4.
A triangle ABC is drawn to circumscribe a circle of radius 3 cm. such that the segments BD and DC into which BC is divided by the point of contact D are of length 9 cm. and 3 cm. respectively. Find the sides AB and AC.

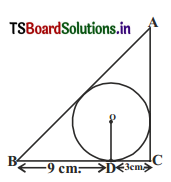
Solution:
The given figure can also be drawn as

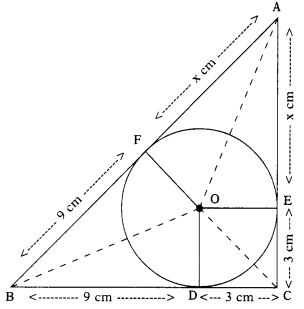
Given : Let ∆ABC be the given triangle circumscribing the given circle with centre ‘O’ and radius 3 cm
i.e., the circle touches the sides BC, CA and AB at D, E, F respectively.
It is given that BD = 9 cm
CD = 3 cm
∴ Length of 2 tangents drawn from an external point to circle are equal.
∴ BF = BD = 9 cm; AF = AE = x cm (say)
The sides of the triangle are 12 cm, (9 + x) cm, (3 + x) cm
Perimeter = 2S = 12 + 9 + x + 3 + x
⇒ 2S = 24 + 2x
S = 12 + x
⇒ S – a = 12 + x – 12 = x
⇒ S – b = 12 + x – 3 – x = 9
⇒ S – c = 12 + x – 9 – x = 3
∴ Area of the triangle ∆ABC
= \(\sqrt{S(S-a)(S-b)(S-c)}\)
= \(\sqrt{(12+x)(x)(9)(3)}\)
= \(\sqrt{27\left(x^2+12 x\right)}\) …………….. (1)
But ∆ABC = ∆OBC + ∆OCA + ∆OAB
= \(\frac{1}{2}\) × BC × OD + \(\frac{1}{2}\) × CA × OE + \(\frac{1}{2}\) AB × OF
= \(\frac{1}{2}\) (12 × 3) + \(\frac{1}{2}\) (3 + x) × 3 + \(\frac{1}{2}\) (9 + x) × 3
= \(\frac{1}{2}\) [36 + 9 + 3x + 27 + 3x]
= \(\frac{1}{2}\) [72 + 6x] ⇒ 36 + 3x ……………. (2)
From (1) and (2),
\(\sqrt{27\left(x^2+12 x\right)}\) = 36 + 3x
Squaring on both sides we get,
27(x² + 12x) = (36 + 3x)²
27x² + 324x = 1296 + 9x² + 216x
⇒ 18x² + 108x – 1296 = 0
⇒ x² + 6x – 72 = 0
⇒ x² + 12x – 6x – 72 = 0
x(x + 12) – 6(x + 12) = 0
(x – 6) (x + 12) = 0
x = 6 or -12
But ‘x’ can’t be negative hence, x = 6
AB = 9 + 6 = 15 cm
AC = 3 + 6 = 9 cm

Question 5.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Verify by using phythagorus theorem. (A.P. June ’15)
Solution:
Steps of construction :

1. Draw a circle with centre ‘O’ and radius = 6 cm
2. Take a point P outside the circle such that OP = 10 cm, join OP.
3. Draw the perpendicular bisector to OP which bisects it at M.
4. Taking M as centre and PM or MO as ra-dius draw a circle. Let the circle intersects the given circle at A and B.
5. Join P to A and B.
6. PA and PB are the required tangents of lengths 8 cm each.

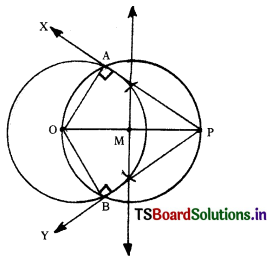
Proof : In ∆OAP
(OA)² + (AP)² = 6² + 8²
⇒ 36 + 64 = 100
(OP)² = 10² = 100
∴ (OA)² + (AP)² = (OP)²
Hence AP is a tangent.
Similarly, BP is a tangent.

Question 6.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:

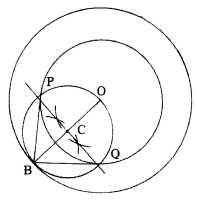
Construction :

1. Mark a point ‘O’ on the plane of the paper and draw a circle with ‘O’ as centre and 4 cm as radius
2. Taking ‘O’ as centre, draw another circle of radius 6 cm.
3. Mark a point B on the bigger circle. Join OB. Draw the perpendicular bisector of OB to intersect OB at C.
4. Now, Take ‘C’ as centre and CO = CB as radius, draw a circle which intersects the smaller circle at P and Q.
5. Join BP and BQ.
6. BP and BQ are the required tangents
7. By actual measurement, we find BP = BQ = 4.5 cm

Verification :
In ∆ BPO, ∠P = 90°
OP = 4cm, OB = 6cm By Pythagoras Theorem,
OB² = PB² + OP²
⇒ PB² = OB² – OP²
= 6² – 4² = 36 – 16 = 20
∴ PB = \(\sqrt{20}\) = 4.47 cm = 4.5 cm (approximately)

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle and measure them. Write conclusion.
Solution:

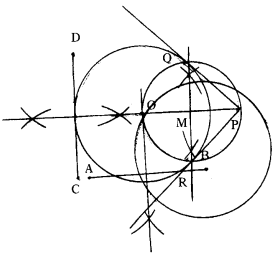
Construction :

1. Draw a circle with the help of a bangle.
2. Take two non-parallel chords AB and CD of this circle.
3. Draw the perpendicular bisectors of AB and CD. Let these intersect at O. Then, O is the centre of the circle drawn.
4. Take a point P outside the circle. Join OR Draw the perpendicular bisector of OR Let M be its midpoint.
5. Draw a circle with M as centre and MO = MP as radius.
6. Join PQ and PR.
7. So, PQ and PR are the required tangents.

Conclusion : Tangents drawn from an external point to a circle are equal.

Question 8.
In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.

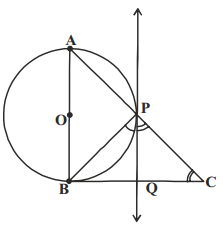
Solution:
Let ABC be a right triangle, right angled at P.
Consider a circle with diameter AB.
From the figure, the tangent to the circle at B meets BC in Q.
Now QB and QP are 2 tangents to the circle from the same point P.
∴ QB = QP ……………. (1)
Also, ∠QPC = ∠QCP
∴ PQ = QC
From (1) and (2);
QB = QC.
Hence proved.

Question 9.
Draw a tangent to a given circle with center O from a point ‘R’ outside the circle. How many tangents can be drawn to the circle from that point ?
[Hint: The distance of two points to the point of contact is the same].
Solution:

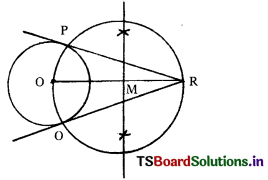
Only 2 tangents can be drawn from a given point outside the circle.