Srinivas

Students must practice this TS Intermediate Maths 2A Solutions Chapter 5 Permutations and Combinations Ex 5(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 5 Permutations and Combinations Ex 5(a)

I.
Question 1.
If \({ }^{\mathrm{n}} \mathrm{P}_3\) = 1320, find n.
Solution:
Given \({ }^{\mathrm{n}} \mathrm{P}_3\) = 1320
⇒ n(n – 1) (n – 2) = 12 × 11 × 10
On comparing, we have n = 12.

Question 2.
If \({ }^n P_7\) = 42 P5, find n.
Solution:
Given \({ }^n P_7\) = 42 . \({ }^n P_5\)
⇒ \(\frac{n !}{(n-7) !}=42 \cdot \frac{n !}{(n-5) !}\)
⇒ \(\frac{n !}{(n-7) !}=42 \cdot \frac{n !}{(n-5)(n-6)(n-7) !}\)
⇒ (n – 5) (n – 6) – 42
⇒ (n – 5) (n – 6) = 7 × 6
On comparing largest integers, we have n – 5 = 7
⇒ n = 12.

Question 3.
If \({ }^{(n+1)} P_5:{ }^n P_6\) = 2 : 7, find n.
Solution:
Given \({ }^{(n+1)} P_5:{ }^n P_6\) = 2 : 7
⇒ \(\frac{(n+1) !}{(n-4) !}: \frac{n !}{(n-6) !}\) = 2 : 7
⇒ \(7 \cdot \frac{(n+1) !}{(n-4) !}=2 \cdot \frac{n !}{(n-6) !}\)
⇒ \(\frac{7 \cdot(n+1) \cdot n !}{(n-4)(n-5)(n-6) !}=2 \cdot \frac{n !}{(n-6) !}\)
⇒ 7(n + 1) = 2 (n – 4) (n – 5)
⇒ 2n² – 25n + 33 = 0
⇒ (2n – 3) (n – 11) = 0
(∵ 2n – 3 ≠ 0 as an integer)
⇒ n – 11 = 0
⇒ n = 11.

Question 4.
If \({ }^{12} P_5+5 \cdot{ }^{12} P_4={ }^{13} P_t\) find r.
Solution:
Given, \({ }^{12} P_5+5 \cdot{ }^{12} P_4={ }^{13} P_t\)

Alternate method:
We know that
\({ }^n P_r={ }^{(n-1)} P_r+r \cdot{ }^{(n-1)} P_{r-1}\)
∴ \({ }^{12} \mathrm{P}_5+5 \cdot{ }^{12} \mathrm{P}_4={ }^{13} \mathrm{P}_{\mathrm{r}}\)
\({ }^{13} P_5={ }^{13} P_r\)
∴ r = 5.

Question 5.
If \({ }^{18} P_{(r-1)}{ }^{17} P_{(r-1)}\) = 9 : 7, find r.
Solution:
Given \({ }^{18} P_{(r-1)}{ }^{17} P_{(r-1)}\) = 9 : 7

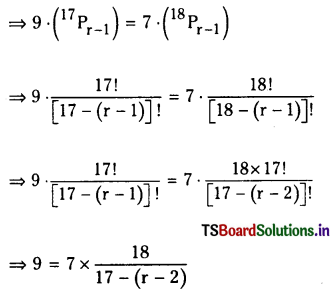
19 – r = 14
r = 5.

Question 6.
A man has 4 sons and there are 5 schools within his reach. In how many ways can he admit his sons In the schools so that no two of them will he in the same school.
Solution:
The first son can be admitted to any one of the 5 schools ¡n 5 ways.
The second son can be admitted to any one of the remaining 4 schools in 4 ways.
Proceeding like this, the number of ways can he admit his sons in the schools so that no two of them will be in same school = 5 × 4 × 3 × 2 = \({ }^5 \mathrm{P}_4\) (or) 120.

II.
Question 1.
If there are 25 railway stations on a railway line, how many types of single second class tickets must be printed, so as to enable a passenger to travel from one station to another.
Solution:
Let the ticket printed to enable a passenger to travel be from station ‘x’ to station ‘y’.
As there are 25 railway stations on a railway line, ‘x’ can be filled in 25 ways and ‘y’ can be filled in remaining 24 ways.
∴ The required number of tickets = 25 × 24
= \({ }^{25} \mathrm{P}_2\) or 600.

Question 2.
In a class there are 30 students. On the New year day, every student posts a greeting card to all his/her classmates. Find the total number of greeting cards posted by them.
Solution:
Number of students in a class = 30.
As every student posts a greeting card to all his/her classmates,
the total number of greeting cards = \({ }^{30} \mathrm{P}_2\) = 870.

Question 3.
Find the number of ways of arranging the letters of the word TRIANGLE so that the relative positions of the vowels and conso-nants are not disturbed.
Solution:
The given word TRIANGLE has 3 vowels and 5 consonants.
Since the relative positions of vowels and consonants are not to be disturbed.
3 vowels can be arranged in their relative positions in 3! ways.
Similarly, 5 consonants can be arranged in their relative position in 5! ways.
∴ By fundamental principle of counting, the required number of ways = 3! × 5! = 720.

Question 4.
Find the sum of all 4 digited numbers that can be formed using the digits 0, 2, 4, 7, 8, without repetition.
Solution:
Given digits are 0, 2, 4, 7, 8.
For a four digit number formed from given digits without repetition,
Thousand’s place can be filled by non-zero digit in 4 ways,
Hundred’s place can be filled by remaining 4 digits in 4 ways,
Ten’s place can be filled in 3 ways and units place can be filled in 2 ways.
∴ By fundamental principle of counting, the number of four digited numbers formed = 4 × 4 × 3 × 2 = 96
Out of these 96 numbers,
the numbers with ‘2’ in units place are 3 × 3 × 2 = 18
Similarly the numbers with ’2’ in ten s place are 18.
The numbers with ‘2’ in Hundred’s place are = 18.
The numberlrwith ‘2’ in thousands place are \({ }^4 \mathrm{P}_3\) = 24.
∴ The value obtained by adding ‘2’ in all the numbers = 18 (2) + 18 (20) + 18 (200) + 24 (2000)
= 18 × 2 (111) + 24 × 2 × 1000
Similarly the value obtained by adding ‘4’ is 18 × 4 (111) + 24 × 4 × 1000
The value obtained by adding ‘7’ is 18 (7) (111) + 24 × 7 × 1000
The value obtained by adding ‘8’ is 18 × 8 × 111 + 24 × 8 × 1000
∴ The sum of all numbers = 18 × 2 × 111 + 24 × 2 × 1000 + 18 × 4 × 111 + 24 × 4 × 1000 + 18 × 7 × 111 + 24 × 7 × 1000 + 18 × 8 × 111 + 24 × 8 × 1000
= 18 × 111 × (2 + 4 + 7 + 8) + 24 × 1000 × (2 + 4 + 7 + 8)
= 18 × 111 × 21 + 24 × 1000 × 21
= 3 × 6 × 111 × 21 +4 × 6 × 1000 × 21
= 21 × 6 (333 + 4000)
= 21 × 6 (4333) = 5,45,958.

Question 5.
Find the number of numbers that are greater than 4000 which can be formed using the digits 0, 2, 4, 6, 8 without repetition.
Solution:
Given digits are 0, 2, 4, 6, 8.
All the five digit numbers are greater than 4000.
In the case of four digit numbers, the numbers which start with 4 or 6 or 8 are greater than 4000.
The number of 4 digit numbers which starts with 4 or 6 or 8 using the given digits with out repetition are 3 × \({ }^4 P_3\) = 3 × 24 = 72.
The number of 5 digit numbers using the given digits with out repetition are 4 × 4! = 4 × 24 = 96
∴ The number of numbers which are greater than 4000 are 72 + 96 = 168.

Question 6.
Find the number of ways of arranging the letters of the word MONDAY so that no vowel occupies even place.
Solution:
Given word is MONDAY
Given word contains 2 vowels and 4 conso-nants.
Also given word contains 3 odd places and 3 even places.
. Since no vowel occupies even places, the two vowels in three odd places can be filled in \({ }^3 \mathrm{P}_2\) ways.
The four consonants can be filled in remain-ing four places in 4! ways.
∴ By fundamental principle of counting the required numbers of ways = \({ }^3 \mathrm{P}_2\) × 4! = 144.

Question 7.
Find the number of ways of arranging 5 different mathematics books, 4 different physics books and 3 different chemistry books such that the books of the same subject are together.
Solution:
Given number of Mathematics books = 5
Given number of Physics books = 4
Given number of Chemistry books = 3
Treat all Mathematics books as 1 unit, Phys¬ics books as 1 unit, Chemistry books as 1 unit.
The number of ways of arranging 3 units of books = 3!
5 different Mathematics books can be arranged in 5! ways.
4 different Physics books can be arranged in 4!
3 different Chemistry books can be arranged in 3! ways.
∴. By fundamental principle of counting, required number of ways of arranging books = 3! × 5! × 4! × 3!
= 6 × 120 × 24 × 6 = 1,03,680.

III.
Question 1.
Find the number of 5 letter words that can be formed using the letter of the word CONSIDER. How many of them begin with “C”, how many of them end with “R”, and how many of them begin with “C” and end with “R” ?
Solution:
Given word “CONSIDER” contains 8 different letters.
The number of 5 letter words that can be formed using the letters of word CONSIDER = \({ }^8 \mathrm{P}_5\)
Out of them,
i) If first place is filled by ‘C’, the remaining 4 places by remaining 7 letters can be filled in \({ }^7 \mathrm{P}_4\) ways.
Number of words begin which ‘C’ are P4.
ii) if last place is filled by ’R’, the remaining first four places by remaining 7 letters can be filled in \({ }^7 \mathrm{P}_4\) ways.
/. Number of words end with ’R’ are \({ }^7 \mathrm{P}_4\).
iii) If first place is filled with ‘C’ and last place is filled by ‘R’, the remaining 3 places between them by remaining 6 letters can be filled in \({ }^6 \mathrm{P}_3\) ways.
∴ Number of words begin with ‘C’ and end with ‘R’ are \({ }^6 \mathrm{P}_3\).

Question 2.
Find the number of ways of seating 10 students A₁, A₂, ………….., A₁₀ in a row such that
i) A₁, A₂, A₃ sit together
ii) A₁, A₂, A₃ sit in a specified order.
iii) A₁, A₂, A₃ sit together in a specified order.
Solution:
A₁, A₂, ……………., A₁₀ are the 10 students.
i) A₁, A₂, A₃ sit together :
Treat A₁, A₂, A₃ as 1 unit.
This unit with remaining 7 students can be arranged in 8! ways.
The students A₁, A₂, A₃ can be arranged in 3! ways.
∴ The number of ways of seating 10 students such that A₁, A₂, A₃ sit together = 8! × 3!.

ii) A₁, A₂, A₃ sit in a specified order :
In 10 positions remaining 7 students other than A₁, A₂, A₃ can be arranged in \({ }^{10} \mathrm{P}_7\)ways.
As A₁, A₂, A₃ sit in a specified order, they can be arranged in 3 gaps in only 1 way.
∴ The number of ways of A₁, A₂, A₂ sit in a 10 specified order = \({ }^{10} \mathrm{P}_7\).

iii) A₁, A₂, A₃ sit together in a specified order :
Treat A₁, A₂, A₃ as 1 unit and they are in a specified order.
This unit with remaining 7 students can be arranged in 8! ways.
∴ The number of ways of A₁, A₂, A₃ sit to-gether in specified order = 8!.

Question 3.
Find the number of ways in which 5 red balls, 4 black balls of different sizes can be arranged in a row so that
(i) no two balls of the same colour come together
(ii) the balls of the same colour come together.
Solution:
Given 5 red balls and 4 black balls are of different sizes.
i) No two balls of same colour come to-gether :
First arrange 4 black balls in row, which can be done in 4! ways × B × B × B × B ×
Then we find 5 gaps, to arrange 5 red balls. This arrangement can be done in 5! ways.
∴ By principle of counting total number of ways of arranging = 5! × 4!.

ii) The balls of same colour come together:
Treat all red balls as one unit and all black balls as another unit.
The number of ways of arranging these two units = 2!
The 5 red balls can be arranged in 5! ways while 4 black balls are arranged in 4! ways.
By fundamental principal of counting, the required number of ways = 2! × 4! × 5!.

Question 4.
Find the number of 4 – digit numbers that can be formed using the digits 1, 2, 5, 6, 7. How many of them are divisible by
i) 2
ii) 3
iii) 4
iv) 5
v) 25
Solution:
The number of 4 digit numbers that can be formed using the digits 1, 2, 5, 6, 7 with out repetition are \({ }^5 \mathrm{P}_4\) or 120.

i) Divisible by 2 :
A number with an even digit in its units place is divisible by ‘2’.
This can be done in 2 ways (with 2 or 6). The remaining 3 places can be filled with the remaining 4 digits in \({ }^4 P_3\) ways.
∴ The number of 4 digit numbers, divisible by 2 are 2 × \({ }^4 P_3\) = 48.

ii) Divisible by 3 :
A number is divisible by 3 only when the sum of digits in that number is a multiple of 3.
Sum of given 5 – digits is 21.
The only way to select 4 digits using digits such that their sum is a multiple of 3 is selecting 1, 2, 5, 7.
We can arrange then in 4! ways.
∴ The number of 4 digit numbers which are divisible by 3 are 4! = 24.

iii) Divisible by 4 :
A number is divisible by 4 only when the number in last two places (i.e., ten’s and units) is a multiple of 4.
∴ The last two places should be filled with one of the following.
12, 16, 52, 56, 72, 76.
i.e., this can be done in 6 ways.
The remaining 2 places can be filled with remaining 3 digits in \({ }^3 \mathrm{P}_2\) ways.
∴ The number of 4 digit numbers which are divisible by 4 are 6 × \({ }^3 \mathrm{P}_2\)= 36.

iv) Divisible by 5 :
A number is divisible by 5, if the units place is 0 or 5.
Hence the units place from given digits is filled with ‘5’ only.
The remaining 3 places by remaining 4 digits can be filled in \({ }^4 \mathrm{P}_3\) ways.
The number of 4 digit numbers which are divisible by 5 are \({ }^4 \mathrm{P}_3\) = 24.

v) Divisible by 25 :
A 4 digit number formed by using given digits is divisible by 25 if the number formed by ten’s and unit’s places is either 25 or 75. This can be done in 2 ways.
Now the remaining 2 places with remaining 3 digits can be filled in \({ }^3 \mathrm{P}_2\) ways.
∴ The number of 4 digit numbers which are divisible by 25 are 2 × \({ }^3 \mathrm{P}_2\) = 12.

Question 5.
If the letters of the word MASTER are permuted in all possible ways and the words thus formed are arranged in the dictionary order, then find the ranks of the words
i) REMAST
ii) MASTER.
Solution:
Given word is MASTER.
∴ The alphabetical order of the letters is A, E, M, R, S, T.
In the dictionary order, first we write all words beginning with ‘A’.
Filling first place with ‘A’, the remaining 5 places can be filled with the remaining 5 letters in 5! ways.
∴ The number of words begin with ‘A’ are 5! on proceeding like this, we get.

i) Rank of the word REMAST :
The number of words begin with A is 5! = 120
The number of words begin with E is 5! = 120
The number of words begin with M is 5! = 120
The number of words begin with RA is 4! = 24
The number of words begin with REA is 3! = 6
The next word is REMAST.
∴ Rank of word REMAST = (120) 3 + 24 + 6 + 1 = 391.

ii) Rank of the word MASTER :
The number of words begin with A is 5! = 120
The number of words begin with E is 5! = 120
The number of words begin with MAE is 3! = 6
The number of words begin with MAR is 3! = 6
The number of words begin with MASE is 2! = 2
The number of words begin with MASR is 2! = 2
The next word is MASTER.
∴ Rank of word MASTER = 2 (120) + 2 (6) + 2 (2) + 1 = 257.

Question 6.
If the letters of the word BRING are per-muted in all possible ways and the words thus formed are arranged in the dictionary order, then find the 59th word.
Solution:
Given word is BRING.
∴ The alphabetical order of the letters is B, G, I, N, R.
In the dictionary order, first we write all words beginning with B.
Clearly the number of words beginning with B are 4! = 24.
Similarly the number of words begin with G are 4! = 24.
Since the words begin with B and G sum to 48, the 59th word must start with I.
Number of words given with IB = 3! = 6
Hence the 59th word must start with IG.
Number of words begin with 1GB = 2! = 2
Number of words begin with IGN = 2! = 2
∴ Next word is 59th = IGRBN.

Question 7.
Find the sum of all 4 digited numbers that can be formed using the digits 1, 2, 4, 5, 6 without repetition.
Solution:
Given digits are 1, 2, 4, 5, 6.
Hence the number of four digit numbers formed using given digits with out repetition are \({ }^5 P_4\) = 120.
Out of these 120 numbers the numbers with 2 in unit’s place = \({ }^4 P_3\)
the numbers with 2 in ten’s place = \({ }^4 P_3\)
the numbers with 2 in Hundred’s place = \({ }^4 P_3\)
The numbers with 2 in thousands place = \({ }^4 P_3\)
∴ The value obtained by adding ‘2’ in all-the numbers = \({ }^4 P_3\) × 2 + \({ }^4 P_3\) × 20 + \({ }^4 P_3\) × 200 + \({ }^4 P_3\) × 2000
= \({ }^4 P_3\) × 2 × 1111
Similarly the value obtained by adding T in all the numbers is \({ }^4 P_3\) × 1 × 1111
The value obtained by adding 4 in all the numbers is \({ }^4 P_3\) × 4 × 1111
The value obtained by adding 5 in all the numbers is \({ }^4 P_3\) × 5 × 1111
The value obtained by adding 6 in all the numbers is \({ }^4 P_3\) × 6 × 1111
.\ The sum of all the numbers = \({ }^4 P_3\) × 1 × 1111 + \({ }^4 P_3\) × 2 × 1111 + \({ }^4 P_3\) × 4 × 1111 + \({ }^4 P_3\) × 5 × 1111 + \({ }^4 P_3\) × 6 × 1111
= \({ }^4 P_3\) × (1111) (1 + 2 + 4 + 5 + 6)
= 24 × 1111 × 18 = 4,79,952
The sum of all 4 digit numbers that can be formed with given digits is 4,79, 952.

Question 8.
There are 9 objects and 9 boxes. Out of 9 objects, 5 cannot fit in three small boxes. How many arrangements can be made such that each object can be put in one box only.
Solution:
Given that there are 9 objects and 9 boxes.
As 5 objects out of 9, cannot fit in 3 small boxes, these 5 objects should be arranged in . remaining 6 boxes.
This can be done in \({ }^6 \mathrm{P}_5\) ways.
∴ The remaining 4 blanks are to be filled with remaining 4 objects.
This can be done in 4! ways.
∴ The required number of ways = \({ }^6 \mathrm{P}_5\) × 4! = 17,280.

Students must practice this TS Intermediate Maths 2A Solutions Chapter 3 Quadratic Expressions Ex 3(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 3 Quadratic Expressions Exercise 3(a)

I.
Question 1.
Find the roots of the following equations.
i) x² – 7x + 12 = 0
ii) – x² + x + 2 = 0
iii) 2x² + 3x + 2 = 0
iv) √3x² + 10x – 8√3 = 0
v) 6√5x² – 9x – 3√5 = 0
Solution:
x² – 7x + 12 = 0
(x – 4) (x – 3) = 0
x = 4, 3.

ii) – x² + x + 2 = 0
x² – x – 2 = 0
(x – 2) (x + 1) = 0
x = 2, – 1

iii) 2x² + 3x + 2 = 0
x = \(\frac{-3 \pm \sqrt{9-16}}{4}\)
x = \(\frac{-3 \pm \sqrt{7} i}{4}\)

iv) √3x² + 10x – 8√3 = 0

v) 6√5x² – 9x – 3√5 = 0

Question 2.
Form quadratic equations whose roots are
i) 2, 5
ii) \(\frac{\mathbf{m}}{\mathbf{n}}, \frac{-\mathbf{n}}{\mathbf{m}}\) (m ≠ 0, n ≠ 0)
iii) \(\frac{\mathbf{p}-\mathbf{q}}{\mathbf{p}+\mathbf{q}}, \frac{-(\mathbf{p}+\mathbf{q})}{\mathbf{p}-\mathbf{q}}\) (p ≠ ± q)
iv) 7 ± 2√5
v) – 3 ± 5i
Solution:
i) α = 2, β = 5 → roots then quadratic equation be
(x – α) (x – β) = 0
(x – 2) (x – 5) = 0
x² – 7x + 10 = 0.

ii) α = \(\frac{\mathrm{m}}{\mathrm{n}}\), β = – \(\frac{\mathrm{n}}{\mathrm{m}}\)
(x – \(\frac{\mathrm{m}}{\mathrm{n}}\)) (x + \(\frac{\mathrm{n}}{\mathrm{m}}\)) = 0
x + x (\(\frac{\mathrm{n}}{\mathrm{m}}-\frac{\mathrm{m}}{\mathrm{n}}\)) – \(\frac{m}{n} \cdot \frac{n}{m}\) = 0
x² + x \(\frac{\left(n^2-m^2\right)}{n m}\) – 1 = 0
mnx² + x (n² – m²) – nnm = 0
x² – x(α + β) + αβ = 0.

iii) x² – \(\left(\frac{p-q}{p+q}-\frac{p+q}{p-q}\right)\) x – \(\left(\frac{p+q}{p-q}\right)\left(\frac{p-q}{p+q}\right)\) = 0
x – \(\left(\frac{(p-q)^2-(p+q)^2}{p^2-q^2}\right)\)x – 1 = 0
x + \(\frac{4 p q}{p^2-q^2}\)x – 1 = 0
(p² – q²)x² + 4px – (p² – q²) = 0.

iv) x² – x(7 + 2√5 + 7 – 2√5)+ (7 + 2√5) (7 – 2√5) = 0
x² – x(14) + (49 – 20) = 0
x² – 14x + 29 = 0.

v) x² – x (- 3 + 5i – 3 – 5i) + (- 3 + 5i) (- 3 – 5i) = 0
x² – x (- 6) + (9 + 25) = 0
x² + 6x + 34 = 0.

Question 3.
Find the nature of the roots of the following equations without finding the roots.
i) 2x² – 8x + 3 = 0
ii) 9x² – 30x + 25 = 0
iii) x² – 12x + 32 = 0
iv) 2x²2 – 7x + 10 = 0
Solution:
i) 2x² – 8x + 3 = 0
b² – 4ac = 64 – 24 > 0
roots are real and distinct.

ii) 9x² – 30x + 25
b² – 4ac = 900 – 4 × 9 × 25 = 0
Roots are real and equal.

iii) x² – 12x + 32 = 0
(12)² – 4 × 32 > 0
Roots are real and distinct.

iv) 2x² – 7x 10 = 0
(- 7)² – 4 × 2 × 10 < 0
Roots are imaginary.

Question 4.
If α, β are the roots of the equation ax² + bx + c = 0, find the value of following expressions in terms of a, b, c.
i) \(\frac{1}{\alpha}+\frac{1}{\beta}\)
ii) \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}\)
iii) α⁴β⁷ + α⁷β⁴
iv) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\), if c ≠ 0
v) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\), if c ≠ 0.
Solution:
i) α + β = \(\frac{-b}{a}\);
αβ = \(\frac{c}{a}\)
\(\frac{\alpha+\beta}{\alpha \beta}=\frac{\frac{-b}{a}}{\frac{c}{a}}=\frac{-b}{c}\)

ii) \(\frac{\alpha^2+\beta^2}{\alpha^2 \beta^2}=\frac{(\alpha+\beta)^2-2 \alpha \beta}{\alpha^2 \beta^2}\)
= \(\frac{\frac{b^2}{a^2}-\frac{2 c}{a}}{\frac{c^2}{a^2}}\)
= \(\frac{b^2-2 c a}{c^2}\)

iii) α⁴β⁷ + α⁷β⁴
= α⁴β⁴ (β³ + α³)
= (αβ)⁴ [(α + β)³ – 3αβ (α + β)]
= \(\frac{c^4}{a^4}\left[\frac{-b^3}{a^3}+\frac{3 c}{a} \cdot \frac{b}{a}\right]\)
= \(\frac{c^4}{a^4}\left[\frac{3 a b c-b^3}{a^3}\right]\)

iv) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\)

v) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\)
= α²β²
= \(\frac{c^2}{a^2}\).

Question 5.
Find the values of m for which the following equations have equal roots.
i) x² – m(2x – 8) – 15 = 0
ii) (m + 1) x² + 2 (m + 3) x + (m + 8) = 0
iii) x² + (m + 3) x + (m + 6) = 0
iv) (3m + 1) x² + 2 (m + 1) x + m = 0
v) (2m + 1) x² + 2 (m + 3) x + m + 5 = 0
Solution:
i) x² – 2xm + 8m – 15 = 0
b² – 4ac = 0
(- 2m)² – 4 (8m – 15) = 0
4m² – 32m + 60 = 0
m² – 8m + 15=0
(m – 5) (m – 3) = 0
m = 3, 5.

ii) (m + 1)x² + 2(m + 3)x + (m + 8) = 0
b² – 4ac = 0
4(m + 3)² – 4(m + 8) (m + 1) = 0
(m + 3)² (m² + 9m + 8) = 0
6m + 9 – 9m – 8 = 0
– 3m + 1 = 0
m = \(\frac{1}{3}\).

iii) x² + (m + 3) x + (m + 6) = 0
b² – 4ac = 0
(m + 3)² – 4 (m + 6) = 0
m² e 6m +9-4m-24-0
m² + 2m – 15 = 0
(m + 5) (m – 3) = 0
m = 3, – 5.

iv) (3m + 1)x² + 2(m + 1)x + m = 0
b² – 4ac = 0
4(m + 1)² – 4m(3m + 1) = 0
m² + 2m + 1 – 3m² – m = 0
– 2m² + m + 1 = 0
2m² – m – 1 = 0
2m² – 2m + m – 1 = 0
2m (m – 1) + (m – 1) = 0
(m – 1) (2m + 1)= 0
m = 1, m = – \(-\frac{1}{2}\)

v) (2m + 1)x² + 2(m + 3)x + (m + 5) = 0.
b² – 4ac = 0
4(m + 3)² – 4(2m + 1) (m + 5) = 0
m² + 6m + 9 – 2m² – 11m – 5 = 0
– m² – 5m + 4 = 0
m² + 5m – 4 = 0
m = \(\frac{-5 \pm \sqrt{25+16}}{2}\)
m = \(\frac{-5}{2}\).

Question 6.
If α and β are the roots of equation x² + px + q = 0, form a quadratic equation where roots are (α – β)² and (α + β)².
Solution:
α + β = \(\frac{-b}{a}\); αβ = \(\frac{c}{a}\)
x² – [(α – β)² + (α + β)²]x + [(α – β) (α + β)]² = 0
x² – [2(α² + β²)]x + [α + β]² [(α + β)² – 4αβ] = o
x² – 2[(α – β)² – 2αβ]x + (α + β)² [(α + β)² – 4αβ] = o
x² – 2 \(\left[\frac{b^2-2 a c}{a^2}\right]\) x + \(\frac{b^2}{a^2}\left[\frac{b^2-4 a c}{a^2}\right]\) = 0
Here b = p, c = q, a = 1
x² – 2 (p² – 2q) x + p² (p² – 4q) = 0

Question 7.
If x² + bx + c = 0, x² + cx + b = 0 (b ≠ c) have a common root, then show that b + c + 1 = 0.
Solution:
x² + bx + c = 0
x² + cx + b = 0
α² is common root.
α² + bα + c = 0
α² + cα + b = 0
α (b – c) + c – b = 0
α (b – c) = b – c
α = 1
∴ 1 + b + c = 0.

Question 8.
Prove that roots of (x – a) (x – b) = h² are always real.
Solution:
(x – a) (x – b) = h²
x² – x (a + b) + ab – h² = 0
Discriminant = (a + b)² – 4 (ab – h²)
= (a + b)² – 4ab + 4h²
= (a – b)² + 4h² > 0
∴ Roots are real.

Question 9.
Find the condition that one root of the quadratic equation ax² + bx + c = 0 shall be n times the other, where n is positive integer.
Solution:
α + nα = – b/a
α . nα = \(\frac{c}{a}\)
α = \(\frac{-b}{a(n+1)}\)
\(\frac{n b^2}{a^2(n+1)^2}=\frac{c}{a}\)
nb² = ac (n + 1)²

Question 10.
Find two consecutive potive even Integers, the sum of whose squares in 340.
Solution:
2n, 2n + 2
(2n)² + (2n + 2)² = 340
4n² + 4n² + 8n + 4 = 340
8n² + 8n + 4 = 340
2n² + 2n + 1 = 85
2n² + 2n – 84 = 0
n² + n – 42 = 0
(n + 7) (n – 6) = 0
n = 6
12, 14 are two numbers.

II.
Question 1.
If x₁, x₂ are the roots of equation ax² + bx + c = 0 and c ≠ 0. Find the value of (ax₁ + b)^-2 + (ax₂ + b)^-2 in terms of a, b, c.
Solution:
ax₁² + bx₁ + c = 0
x₁ (ax₁ + b) + c = 0
(ax₁ + b) = \(\frac{-\mathrm{c}}{\mathrm{x}_1}\)
Similarly (ax₂ + b) = \(\frac{-\mathrm{c}}{\mathrm{x}_2}\)
∴ (ax₁ + b)^-2 + (ax₂ + b)^-2 = \(\)
= \(\frac{1}{c^2}\) [(x₁ + x₂)² – 2x₁x₂]
= \(\frac{1}{c^2}\left[\frac{b^2-2 a c}{a^2}\right]\)
= \(\frac{b^2-2 a c}{a^2 c^2}\)

Question 2.
If α, β are the roots of equation ax² + bx + c = 0, find a quadratic equation whose roots are α² + β² and α^-2 + β^-2.
Solution:

Solve the following equations:

Question 3.
2x⁴ + x³ – 11x² + x + 2 = 0
Solution:
2x⁴ + x³ – 10x² – x² + x + 2 = 0
x² (2x² + x – 10) – (x² – x – 2) = 0
x² [(2x + 5) (x – 2) – [(x – 2) (x + 1)] = 0
(x – 2) [x² (2x + 5) – x – 1] = 0
(x – 2) [2x³ + 5x² – x – 1] = 0
(x – 2) [(2x – 1) (x² + 3x + 1)] = 0
x = 2, \(\frac{1}{2}\); x² + 3x + 1 = 0
x = \(\frac{-3 \pm \sqrt{9-4}}{2}\)
x = \(\frac{-3 \pm \sqrt{5}}{2}\).

Question 4.
3^1+x + 3^1-x = 10
Solution:
Let 3^x = t
3. t + \(\frac{3}{t}\) = 10
3t² + 3 – 10t = 0
3t² – 10t + 3 = 0
3t² – 9t – t + 3 = 0
3t (t – 3) – 1 (t – 3) = 0
(3t – 1) (t – 3) = 0
t = \(\frac{1}{3}\), t = 3
3^x = 3^-1, 3^x = 3¹
x = – 1, 1.

Question 5.
4^{x – 1} – 3 . 2^{x – 1} + 2 = 0.
Solution:
\(\frac{4^x}{4}-\frac{3 \cdot 2^x}{2}\) + 2 = 0
4^x – 6 . 2^x + 8 = 0
2^x = t
t² – 6t + 8 = 0
(t – 4) (t – 2) = 0
2^x = t
t² – 6t + 8 = 0
(t – 4) (t – 2) = 0
2^x = 2²; 2^x = 2¹
x = 1, 2.

Question 6.
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\) when x ≠ 0, x ≠ 3.
Solution:
\(\sqrt{\frac{x}{x-3}}\) = t
t + \(\frac{1}{t}=\frac{5}{2}\)
2t² – 5t + 2 = 0
2t² – 4t – t + 2 = 0
2t (t – 2) – 1 (t – 2) = 0
(2t – 1) (t – 2) = 0
t = \(\frac{1}{2}\); t = 2
\(\frac{x}{x-3}\) = 4
x = 4x – 12
12 = 3x
x = 4
(or)
\(\frac{x}{x-3}=\frac{1}{4}\)
4x = x – 3
3x = – 3
x = – 1.

Question 7.
\(\sqrt{\frac{3 x}{x+1}}+\sqrt{\frac{x+1}{3 x}}\) = 2 when x ≠ 0, x ≠ 1.
Solution:
Let \(\sqrt{\frac{3 x}{x+1}}\) = t
t + \(\frac{1}{t}\) = 2
t² – 2t + 1 = 0
(t – 1)² = 0
t = 1
\(\frac{3 x}{x+1}\) = 1
3x = x + 1
x = \(\frac{1}{2}\).

Question 8.
2 \(\left(x+\frac{1}{x}\right)^2\) – 7 \(\left(x+\frac{1}{x}\right)\) + 5 = 0, when x ≠ 0.
Solution:
x + \(\frac{1}{x}\) = t
2t² – 7t + 5 = 0
2t² – 5t – 2t + 5 = 0
2t (t – 1) – 5 (t – 1) = 0
t = \(\frac{5}{2}\), t = 1 but x + \(\frac{1}{x}\) ≥ 2 ∀ x ∈ R⁺
x + \(\frac{1}{x}\) = \(\frac{5}{2}\) only possible
2x² – 5x + 2 = 0
(2x – 1) (x – 2) = 0
x = \(\frac{1}{2}\), 2
Now if x + \(\frac{1}{x}\) = 1
x² – x + 1 = o
x = \(\frac{1 \pm \sqrt{1-4}}{2}\)
x = \(\frac{1 \pm \sqrt{3} i}{2}\).

Question 9.
\(\left(x^2+\frac{1}{x^2}\right)-5\left(x+\frac{1}{x}\right)\) + 6 = 0 when x ≠ o.
Solution:
\(\left(x^2+\frac{1}{x^2}\right)-5\left(x+\frac{1}{x}\right)\) + 6 = 0
x + \(\frac{1}{x}\) = t
t² – 5t + 4 = 0
(t – 4) (t – 1) = 0
t = 4, 1
x + \(\frac{1}{x}\) = 4
x² – 4x + 1 = 0
x = \(\frac{4 \pm \sqrt{16-4}}{2}\)
x = 2 ± √3
x + \(\frac{1}{x}\) = 1
x² – x + 1 = 0
x = \(\frac{1 \pm \sqrt{1-4}}{2}\)
x = \(\frac{1 \pm \sqrt{3} i}{2}\).

Question 10.
Find a quadratic equation for which the sum of the roots is 7 and the sum of the squares of the roots is 25.
Solution:
α + β = 7, α² + β² = 25
(α + β)² – 2αβ= 25
49 – 2αβ = 25
24 = 2αβ
αβ = 12
x² – (7)x + 12 = 0.

Students must practice this TS Intermediate Maths 2A Solutions Chapter 1 Complex Numbers Ex 1(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 1 Complex Numbers Exercise 1(b)

I.
Question 1.
Write the following complex numbers in the form A + iB.
i) (2 – 3i) (2 + 3i)
ii) (1 + 2i)³
iii) \(\frac{a-i b}{a+i b}\)
iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)
v) (- √3 + √-2) (2√3 – i)
vi) (- 5i) \(\frac{i}{8}\)
vii) (- i) (2i)
viii) i⁹
ix) i^-19
x) 3 (7 + 7i) + i (7 + 7i)
xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)
Solution:
i) z = (2 – 3i) (3 + 4i)
z = 6 + 8i – 9i + 12
z = 18 – i
= 18 + (- 1)i

ii) z = (1 + 2i)³
= 1³ + (2i)³ + 3 . 2i(1 + 2i)
= 1 – 8i + 6i (1 + 2i)
= (1 – 12) – 2i
= – 11 – 2i
= (- 11, – 2)

iii) z = \(\frac{a-i b}{a+i b}\)
z = \(\frac{(a-i b)(a-i b)}{(a+i b)(a-i b)}\)
= \(\frac{a^2-b^2-2 a b i}{a^2+b^2}\)
= \(\left(\frac{a^2-b^2}{a^2+b^2}, \frac{-2 a b}{a^2+b^2}\right)\)

iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)

v) (- √3 + √-2) (2√3 – i)
z = (- √3 + √2i) (2√3 – i)
= – 2 . 3 + √3i + 2√6i + √2
= (√2 – 6) + i (√3 + 2√6).

vi) z = (- 5i) (\(\frac{i}{8}\))
z = \(\) i²
z = \(\frac{5}{8}\) + 0i

vii) (- i) (2i)
z = (- i) (2i)
= 2 + 0i

viii) z = i⁹
z = (i²)⁴ . i
z = i = 0 + i . 1

ix) z = i^-19
z = \(\frac{1}{\left(\mathrm{i}^2\right)^9} \cdot \frac{1}{\mathrm{i}}\)
= \(\frac{-1}{i}=\frac{-1}{1^2}\)
z = i = 0 + 1 . i

x) z = 3 (7 + 7i) + i (7 + 7i)
= 21 + 21i + 7i + 7i²
= 21 – 7 + 28i
z = 14 + 28i

xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)

Question 2.
Write the conjugate of the following complex numbers.
i) (3 + 4i)
ii) (15 + 3i) – (4 – 20i)
iii) (2 + 5i) (- 4 + 6i)
iv) \(\frac{5 \mathbf{i}}{7+1}\)
Solution:
i) z = 3 + 4i
\(\overline{\mathbf{z}}\) = 3 – 4i

ii) z = (15 + 31) – (4 – 201)
z = 11 + 23i
z = 11 – 23i

iii) z = (2 + 5i) (- 4 + 6i)
z = – 8 + 12i – 20i + 30i2
z = – 38 – 8i
z = – 38 + 8i

iv) \(\frac{5 \mathbf{i}}{7+1}\)

Question 3.
Simplify
i) i² + i⁴ + i⁶ + ………… + (2n + 1) terms
ii) i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (- i)²⁶
Solution:
i) i² + i⁴ + i⁶ + …………… (2n + 1) terms
= i² + i⁴ + i⁶ + ……………. +
= -1 + 1+(-1) + 2n terms + i2
= 0 – 1 = – 1

ii) i¹⁸ – 3i⁷ + i² (1 + i⁴) (- i)²⁶
(i²)⁹ – 3i⁶i + i² (1 + i⁴) (i)²⁶ = – 1 + 3i + (- 1) (1 + 1) (- 1)¹³
= 3i – 1 + 2 = 3i + 1.

Question 4.
Find a square root for the following complex numbers.
i) 7 + 24i
ii) – 8 – 6i
iii) 3 + 4i
iv) – 47 + i 8√3
Solution:
i) z = 7 + 24i
Let square root of z be a + ib
a + ib = \(|\sqrt{7+24i}|\)
(a + ib)² = 7 + 24i
a² – b² + 2abi = 7 + 24i
a² – b² = 7, 2ab = 24 ……………..(1)
| a + ib | = \(|\sqrt{7+24i}|\)
Squaring on both sides,
| a + ib |2 = | 7 + 24i|
a² + b² = \(\sqrt{49+576}\)
a² + b² = \(\sqrt{625}\)

a² = 16
a = ± 4
2b² = 25 – 7
b² = 9
b = ± 3
a + ib = ± (4 + 3i)

ii) z = – 8 – 6i
Let square root of z be a + ib
a + ib = \(\sqrt{-8-6 \mathrm{i}}\)
Squaring on both sides,
(a + ib)² = – 8 – 61
a² – b² + 2abi = – 8 – 6i
a² – b² = – 8, 2ab = – 6 …………..(i)
| a + ib | = \(|\sqrt{-8-6 \mathbf{i}}|\)
Squaring on both sides,
| a + ib |² = \(|\sqrt{-8-6 \mathrm{i}}|^2\)
a² + b² = \(\sqrt{64+36}\)
a² + b² = 10 ………….(ii)
(i) + (ii)
2a² = 2
a² = 1 or a = ± 1
(ii) – (i)
2b² = 18
b² = 9
⇒ b = ± 3
a + ib = ± (1 – 3i).

iii) z = 3 + 4i
Let square root of z be a + ib
a + ib = \(\sqrt{3+4i}\)
Squaring on both sides,
(a + ib)² = 3 + 4i
a² – b² + 2abi = 3 + 4i
a² – b² = 3; 2ab = 4 …………..(i)
| a + ib | = \(|\sqrt{3+4 \mathrm{i}}|\)
Squaring on both sides,
| a + ib |² = | 3 + 4i |
a² + b² = \(\sqrt{9+16}\) …………..(ii)
a² – b² = 3

2a² = 8
a² = 4
⇒ a = ± 2
2b² = 2
⇒ b = ± 1
a + ib = ± (2 + i).

iv) z = – 47 + i 8√3
Let the square root of z be a + ib
(a + ib)² = – 47 + i 8√3
a² – b² = – 47, 2ab = 8√3
| a + ib | = \(|\sqrt{-47+i 8 \sqrt{3}}|\)
Squaring on bothsides,
a² + b² = \(\sqrt{(-47)^2+(8 \sqrt{3})^2}\)
= \(\sqrt{2209+192}=\sqrt{2401}\)

a² + b² = 49
a² – b² = – 47
2a² = 2
a² = 1
a = ± 1
2b² = 96
b² = 48
b = ± 4√3
a + ib = ± (1 + 4√3i).

Question 5.
Find the multiplicative inverse of the following complex numbers.
i) √5 + 3i
ii) – i
iii) i^-35
Solution:
i) z = √5 + 3i
Let a + ib be multiplicative inverse then (a + ib) . z = 1
z = \(\frac{1}{a+i b}\)
or a + ib = \(\frac{1}{\mathrm{z}}\)
a + ib = \(\frac{\overline{\mathbf{z}}}{(\mathrm{z} \overline{\mathrm{z}})}\)
a + ib = \(\frac{\bar{z}}{|z|^2}=\frac{\sqrt{5}-3 i}{5+9}\)
= \(\frac{1}{14}\) (√5 – 3i).

ii) z = – i
Let a + ib be multiplicative inverse then (a + ib) z = 1
a + ib = \(\frac{1}{\mathrm{z}}\)
= \(\frac{1}{-i}\)
= \(\frac{i}{-i \cdot i}\)
a + ib = i.

iii) z = i^-35
Let a + ib be multiplicative inverse then (a + ib) z = 1
a + ib = \(\frac{1}{\mathrm{z}}\)
= \(\frac{1}{i^{-35}}\) = i³⁵
(a + ib) = i³⁵
= (i²)¹⁷ i = – i.

II.
Question 1.
i) If (a + ib)² = x + iy, find x² + y².
ii) lf x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) then, show that x² + y² = 4x – 3.
iii) If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\) then, show that 4x² – 1 = 0.
iv)If u + iv = \(\frac{2+i}{z+3}\) and z = x + iy find u, v.
Solution:
i) (a + ib) = x + iy
a² – b² + 2abi = x + iy ,
a² – b² = x
2ab = y
Now x2 = (a² – b²)²
y² = 4a²b²
x² + y² = (a² – b²)² . 4a²b² = (a² + b²)²

ii) x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\)

iii) x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\)
x + iy = \(\frac{1+\cos \theta-i \sin \theta}{(1+\cos \theta)^2+\sin ^2 \theta}\)
x = \(\frac{1+\cos \theta}{2+2 \cos \theta}=\frac{(1+\cos \theta)}{2(1+\cos \theta)}\)
x = \(\frac{1}{2}\)
2x = 1
4x² = 1
4x² – 1 = 0.

iv) u + iv = \(\frac{2+i}{z+3}\)

Question 2.
i) If z = 3 + 5i then show that z³ – 10z² + 58z – 136 = 0
ii) If z = 2 – i√7 then show that 3z³ – 4z² + z + 88 = 0
iii) Show that \(\frac{2-i}{(1-2 i)^2}\) and \(\frac{-2-11 i}{25}\) are conjugate to each other.
Solution:
i) z = 3 + 5i
(z – 3)² = (5i)²
z² – 6z + 9 = 25i2
z² – 6z + 9 = – 25
z² – 6z + 34 = 0
z³ – 6z² + 34z = 0
(z³ – 10z² + 58z – 136) + 4z² – 24z + 136 = 0
(z³ – 10z² + 58z – 136) + 4 (z² – 6z + 34) = 0
(z³ – 10z² + 58z – 136) = 0

il) z = 2 – i√7
(z – 2)² = (- i – √7)²
z² – 4z + 4 = – 7
z² – 4z + 11 = 0
z³ – 4z² + 11z = 0
3z³ – 12z² + 33z = 0
(3z³ – 4z² + z + 88) + (- 8z² + 32z – 88) = 0
(3z³ – 4z² + z + 88) – 8 (z² – 4z + 11) = 0
3z³ – 4z² + z + 88 = 0.

iii) z = \(\frac{2-i}{(1-2 i)^2}\) (If z = a + ib, \(\overline{\mathbf{Z}}\) = a – ib)

Question 3.
i) If (x – iy)^1/3 = a – ib then show that \(\frac{x}{a}+\frac{y}{b}\) = 4(a² – b²)
ii) Write \(\left(\frac{a+i b}{a-i b}\right)^2-\left(\frac{a-i b}{a+i b}\right)^2\) in the form x + iy.
iii) If x and y are real numbers such that \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-i}\) determine the values of x and y.
Solution:
(x – iy)^1/3 = (a – ib)
x – iy = (a – ib)³
x – iy = a³ + ib³
x = a³ – 3ab²
– iy = ib³ – 3a²bi
\(\frac{x}{a}\) = a² – 3b²
y = b³ – 3a²b
\(\frac{x}{a}\) = a² – 3b²
\(\frac{y}{b}\) = b² – 3a²
\(\frac{x}{a}-\frac{y}{b}\) = 4(a² – b²).

ii) \(\left(\frac{a+i b}{a-i b}\right)^2-\left(\frac{a-i b}{a+i b}\right)^2\)

iii) \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-i}\)

4x + 9y – 3 = 0
2x – 7y – 3 = 10
Solving, we get
x = 3, y = – 1.

Question 4.
i) Find the least positive integer n, satisfying \(\left(\frac{1+1}{1-1}\right)^n\) = 1.
ii) If \(\left(\frac{1+i}{1-i}\right)^3-\left(\frac{1-i}{1+i}\right)^3\) = x + iy find x and y.
iii) Find the real values of θ in order that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is a
a) real number
b) purely imaginary number
iv) Find the real values of x and y if \(\frac{x-1}{3+i}+\frac{y-1}{3-i}\) = i.
Solution:
i) \(\left(\frac{1+i}{1-i}\right)^n\) = 1
\(\left(\frac{(1+i)(1+i)}{(1-i)(1+i)}\right)^n\) = 1
\(\left(\frac{2 \mathrm{i}}{2}\right)^{\mathrm{n}}\) = 1
iⁿ = 1
(∵ iⁿ = 1 = – 1 × – 1 = i² × i² = i⁴)
n = 4
i⁴ = 1
Least value of n = 4.

ii) \(\left(\frac{1+i}{1-i}\right)^3-\left(\frac{i-i}{1+i}\right)^3\) = x + iy
\(\left(\frac{(1+i)(1+i)}{(1+i)(1-i)}\right)^3-\left(\frac{(1-i)(1-i)}{(1+i)(1-i)}\right)^3\) = x + iy
\(\left(\frac{2 \mathrm{i}}{2}\right)^3-\left(\frac{-2 \mathrm{i}}{2}\right)^3\)
– i – i = x + iy
x = 0
y = – 2.

iii) z = \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\)
z = \(\frac{(3+2 i \sin \theta)(1+2 i \sin \theta)}{(1-2 i \sin \theta)(1+2 i \sin \theta)}\)
z = \(\frac{3-4 \sin ^2 \theta+8 i \sin \theta}{1+4 \sin ^2 \theta}\)
z is purely real ⇒ imaginary part = 0
\(\frac{8 \sin \theta}{1+4 \sin ^2 \theta}\) = 0
sin θ = 0
θ = nπ, n ∈ 1
z is purely imaginary ⇒ Real part zero
\(\frac{3-4 \sin ^2 \theta}{1+4 \sin ^2 \theta}\) = 0
sin θ = \(\frac{3}{4}\)
sin θ = \(\pm \frac{\sqrt{3}}{2}\)
sin θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ 1.

iv) \(\frac{x-1}{3+i}+\frac{y-1}{3-1}\) = 1
\(\frac{(x-1)(3-i)}{9+1}+\frac{(y-1)(3+i)}{9+1}\) = 1
\(\frac{3(x-1)+3(y-1)}{10}+\frac{i(1-x+y-1)}{10}\) = 1
3x + 3y – 6 = 0
y – x = 10
Solving we get
x = – 4, y = 6.

Students must practice this TS Intermediate Maths 2A Solutions Chapter 5 Permutations and Combinations Ex 5(e) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 5 Permutations and Combinations Ex 5(e)

I.
Question 1.
If \({ }^{\mathrm{n}} \mathrm{C}_4\) = 210, find n.
Solution:
Given \({ }^{\mathrm{n}} \mathrm{C}_4\) = 210
⇒ \(\frac{n(n-1)(n-2)(n-3)}{4 !}\) = 210
⇒ n (n – 1) (n – 2) (n – 3) = 41 × 210
= 24 × 210
= 7 × 8 × 9 × 10
On comparing largest integers, we get n = 10.

Question 2.
If \({ }^{12} \mathrm{C}_{\mathrm{r}}\) = 495, find the possible values of ‘r’.
Solution:
Given \({ }^{12} \mathrm{C}_{\mathrm{r}}\) = 495
= 11 × 9 × 5
= \(\frac{12 \times 11 \times 9 \times 10}{4 \times 3 \times 2 \times 1}\)
⇒ \({ }^{12} \mathrm{C}_{\mathrm{r}}={ }^{12} \mathrm{C}_4 \text { or }{ }^{12} \mathrm{C}_8\)
⇒ r = 4 or 8.

Question 3.
If 10 . \({ }^n \mathrm{C}_2\) = 3 . \({ }^{n+1} C_3\), find n.
Solution:
Given 10 . \({ }^n C_2\) = 3 . \({ }^{n+1} C_3\)
\(10 \times \frac{n(n-1)}{2}=3 \cdot \frac{(n+1) n(n-1)}{3 \times 2 \times 1}\)
⇒ 10 = n + 1
⇒ n = 9.

Question 4.
If \({ }^n P_r\) = 5040 and \({ }^n C_r\) = 210, find n and r.
Solution:
Given \({ }^n P_r\) = 5040 and \({ }^n C_r\) = 210, \({ }^n P_r=r !^n C_r\)
5040 = r! × 210
⇒ r! = 24
⇒ r! = 4!
∴ r = 4
∴ \({ }^n \mathrm{P}_4\) = 5040
⇒ n (n – 1) (n – 2) (n – 3) = 10 × 9 × 8 × 7
On comparing largest integers, we get n = 10
∴ n = 10 and r = 4.

Question 5.
If \({ }^n C_4={ }^n C_6\), find n.
Solution:
Given \({ }^n C_4={ }^n C_6\)
If \({ }^n C_r={ }^n C_s\), then either r = s or r + s = n.
Clearly, we have n = 4 + 6
⇒ n = 10.

Question 6.
If \({ }^{15} \mathrm{C}_{2 \mathrm{r}-1}={ }^{15} \mathrm{C}_{2 \mathrm{r}+4}\), find r.
Solution:
Given \({ }^{15} \mathrm{C}_{2 \mathrm{r}-1}={ }^{15} \mathrm{C}_{2 \mathrm{r}+4}\)
If \({ }^n C_r={ }^n C_s\) then either r = s or r + s = n.
∴ 2r – 1 = 2r + 4
Which is impossible.
or
2r – 1 + 2r + 4 = 15
⇒ 4r + 3 = 15
⇒ r = 3
∴ r = 3.

Question 7.
If \({ }^{17} C_{2 t+1}={ }^{17} C_{3 t-5}\), find t.
Solution:
Given \({ }^{17} C_{2 t+1}={ }^{17} C_{3 t-5}\)
If \({ }^n C_r={ }^n C_s\), then either r = s or n = r + s.
i.e., either
2t + 1 = 3t – 5
⇒ t = 6 = 17
2t + 1 + 3t – 5 = 17
⇒ 5t = 21
⇒ t = \(\frac{21}{5}\)
Since t’ is an integer, we have t = 6.

Question 8.
If \({ }^{12} C_{r+1}={ }^{12} C_{3 r-5}\), find r.
Solution:
Given \({ }^{12} C_{r+1}={ }^{12} C_{3 r-5}\).
If \({ }^n C_r={ }^n C_s\), then either r = s or n = r + s.
i.e., r + 1 = 3r – 5
or 12 = r + 1 + 3r – 5
⇒ r = 3 or r = 4.

Question 9.
If \({ }^9 C_3+{ }^9 C_5={ }^{10} C_r\), then find r.
Solution:
Given \({ }^9 C_3+{ }^9 C_5={ }^{10} C_r\)
⇒ \({ }^9 \mathrm{C}_3+{ }^9 \mathrm{C}_4={ }^{10} \mathrm{C}_r\) (∵ \({ }^n C_r={ }^n C_s\))
⇒ \({ }^{10} \mathrm{C}_4={ }^{10} \mathrm{C}_{\mathrm{r}}\) (or) \({ }^{10} \mathrm{C}_6={ }^{10} \mathrm{C}_{\mathrm{r}}\)
⇒ r = 4 or r = 6.

Question 10.
Find the number of ways of forming a com-mittee of 5 members from 6 men and 3 ladies.
Solution:
Selecting 5 members to form a commitee from 6 men and 3 ladies (i.e., 9 members) can be done in \({ }^9 \mathrm{C}_5\) = 126 ways.

Question 11.
In question 10, how many committees contain atleast two ladies.
Solution:
In selecting 5 members from 6 men and 3 ladies to form a committee containing atleast two ladies, two cases arises.

Case – (1):
(When committee contains exactly two ladies) :
Number of ways of selecting 2 ladies from 3 ladies is \({ }^3 \mathrm{C}_2\).
Now the remaining 3 members are selected from 6 men and this can be done in C3 ways
∴ Number of ways to form a committee with 2 ladies = \({ }^3 \mathrm{C}_2 \times{ }^6 \mathrm{C}_3\) = 60.

Case – (2)
(When committee contains 3 ladies) :
Selecting 3 ladies from 3 ladies can be done in \({ }^3 \mathrm{C}_3\) ways.
Selecting remaining 2 members from 6 men can be done in \({ }^6 \mathrm{C}_2\) ways.
∴ Number of ways to form a committee with 3 ladies = \({ }^3 \mathrm{C}_3 \times{ }^6 \mathrm{C}_2\) = 15
∴ Total number of ways = 60 + 15 = 75.

Question 12.
If \({ }^n C_5={ }^n C_6\), then \({ }^{13} \mathrm{C}_{\mathrm{n}}\).
Solution:
Given, \({ }^n C_5={ }^n C_6\)
⇒ n = 5 + 6
(If \({ }^n C_r={ }^n C_s\) then either n = r + s or r = s)
⇒ n = 11
Now, \({ }^{13} C_n={ }^{13} C_{11}={ }^{13} C_2\) = 78.

II.
Question 1.
Prove that 3 ≤ r ≤ n, \({ }^{(n-3)} C_r+3 \cdot{ }^{(n-3)} C_{(r-1)}+3 \cdot{ }^{(n-3)} C_{(r-2)}+{ }^{(n-3)} C_{(r-3)}={ }^n C_r\).
Solution:
Given 3 ≤ r ≤ n

Question 2.
Find the value of \({ }^{10} C_5+2 \cdot{ }^{10} C_4+{ }^{10} C_3\).
Solution:
\({ }^{10} C_5+2 \cdot{ }^{10} C_4+{ }^{10} C_3\)
= \({ }^{10} C_5+{ }^{10} C_4+{ }^{10} C_4+{ }^{10} C_3\)
= \({ }^{11} C_5+{ }^{11} C_4\) (∵ \({ }^n C_{r-1}+{ }^n C_r={ }^{n+1} C_r\))
= \({ }^{12} \mathrm{C}_5\) = 792.

Question 3.
Simplify \({ }^{34} C_5+\sum_{r=0}^4(38-r) C_4\).
Solution:

Question 4.
In a class there are 30 students. If each student plays a chess gaine with each of the other student, then find the total number of chess games played by them.
Solution:
Number of students in a class = 30.
Given each students plays a chess game with each of the other student.
∴ The total number of chess games played is equal to number of ways of selecting 2 students to play a game from 30 students.
This can be done in \({ }^{30} \mathrm{C}_2\) ways.
∴ The number of chess games played = \({ }^{30} \mathrm{C}_2\) = 435.

Question 5.
Find the number of ways of selectIng 3 girls and 3 boys out of 7 girls and 6 boys.
Solution:
Number of ways of selecting 3 girls out of 7 girls = \({ }^7 \mathrm{C}_3\)
Number of ways of selecting 3 boys ouf of 6 boys = \({ }^6 \mathrm{C}_3\)
∴ The total number of ways = \({ }^7 \mathrm{c}_3 \cdot{ }^6 \mathrm{c}_3\)
= 35 . 20 = 700.

Question 6.
Find the number of ways of selecting a committee of 6 members out of 10 mem bers always Including a specified member.
Solution:
A committee of 6 members is to be formed out of 10 members in which a specified member is always included.
So, remaining 5 members are to be selected from rest of 9 members.
This can be done in \({ }^9 \mathrm{C}_5\) ways.
∴ Required number of ways \({ }^9 \mathrm{C}_5\) = 126.

Question 7.
Find the number of ways of selecting 5 books from 9 different mathematics books such that a particular book ¡s not included.
Solution:
Given out of 9 different mathematics books a particular book is not included.
∴Number of book left are ‘8′.
∴ Number of ways of selecting 5 books out of 8 different books are \({ }^8 C_5\) = 56.

Question 8.
Find the number of ways of selecting 3 vowels and 2 consonants from the letters of the word EQUATION.
Solution:
The word EQUATION contains 5 vowels and 3 consonants.
Number of ways of selecting 3 vowels out of 5 = \({ }^5 \mathrm{C}_3\) = 10
Number of ways of selecting 2 consonants out of 3 = \({ }^3 \mathrm{C}_2\) = 3
∴ Total number of ways = 10 x 3 = 30.

Question 9.
Find the number of diagonals of a polygon with 12 sides.
Solution:
Number of sides of a polygon = 12
Number of diagonals of a n – sided polygon = \({ }^n C_2\) – n
∴ Number of diagonals of 12 sided polygon = \({ }^{12} C_2\) – 12 = 54.

Question 10.
If n persons are sitting in a row, find the number of ways of selecting two persons, who are sitting adjacent to each other.
Solution:
Number of ways of selecting 2 persons out of n persons sitting in a row, who are sitting adjacent to each other = n – 1.

Question 11.
Find the number of ways of giving away 4 similar coins to 5 boys if each boy can be given any number (less than or equal to 4) of coins.
Solution:
In distribution of 4 similar coins to 5 boys, the following cases arises.

Case – (i) :
Giving all 4 coins to one boys. This is done in \({ }^5 \mathrm{C}_1\) ways.

Case – (ii) :
Giving 4 coins to two boys so that one of them gets 1 and the other 3 coins.
This is done in 2 x \({ }^5 \mathrm{C}_2\) ways.

Case – (iii) :
Giving 4 coins to two boys so that each get 2 coins. This can be done in \({ }^5 \mathrm{C}_2\) ways.

Case – (iv) :
Giving 4 coins to three boys so that, two of them gets 1 coin and the other gets 2. This is done in \({ }^5 \mathrm{C}_3 \times \frac{3 !}{2 !}\) ways.

Case – (v):
Giving 4 coins to four boys so that each gets 1.
This is done in \({ }^5 \mathrm{C}_4\) ways.
∴ Total number of ways = \({ }^5 \mathrm{C}_1+2 \times{ }^5 \mathrm{C}_2+{ }^5 \mathrm{C}_2+\frac{3 !}{2 !}{ }^5 \mathrm{C}_3+{ }^5 \mathrm{C}_4\) = 70.

III .
Question 1.
Prove that \(\frac{{ }^{4 n} C_{2 n}}{{ }^{2 n} C_n}=\frac{1 \cdot 3 \cdot 5 \ldots \ldots(4 n-1)}{\{1 \cdot 3 \cdot 5 \ldots \ldots(2 n-1)\}^2}\).
Solution:

Question 2.
If a set A has 12 elements, find the number of subsets of A having
i) 4 elements
ii) Atleast 3 elements
iii) Atmost 3 elements.
Solution:
Given number of elements in set A are 12.

i) Subsets of A having 4 elements :
Number of subsets of A having 4 elements is equal to number of ways of selecting 4 elements from 12 elements in set ‘A’.
This can be done in \({ }^{12} C_4\) ways.
∴ Number of subsets of A having 4 elements = \({ }^{12} C_4\) = 495.

ii) Subset of A contains atleast 3 elements:
Number of subsets of A, having ‘r’ elements is equal to number of ways of selecting ‘r’ elements from 12 elements in set A’, i.e., \({ }^{12} \mathrm{C}_{\mathrm{r}}\) ways.
∴ Number of ways of selecting at least 3 elements from 12 elements in set A is \({ }^{12} \mathrm{C}_3+{ }^{12} \mathrm{C}_4+\ldots \ldots+{ }^{12} \mathrm{C}_{12}\)
Number of subsets of A having atleast 3 elements = \({ }^{12} \mathrm{C}_3+{ }^{12} \mathrm{C}_4+\ldots \ldots+{ }^{12} \mathrm{C}_{12}\)
= \(\left({ }^{12} \mathrm{C}_0+{ }^{12} \mathrm{C}_1+\ldots \ldots+{ }^{12} \mathrm{C}_{12}\right)-{ }^{12} \mathrm{C}_0-{ }^{12} \mathrm{C}_1-{ }^{12} \mathrm{C}_2\)
= 2¹² – \({ }^{12} \mathrm{C}_0+{ }^{12} \mathrm{C}_1+{ }^{12} \mathrm{C}_2\) = 4017.

iii) Number of subsets of ‘A’ having atmost 3 elements :
Number of subsets of A having ‘r’ elements is equal to number of ways of selecting r’ elements from 12 elements in set ‘A’ i.e., \({ }^{12} C_r\) ways.
∴ Number of ways of selecting atmost 3 elements from 12 elements in set A is \({ }^{12} \mathrm{C}_0+{ }^{12} \mathrm{C}_1+{ }^{12} \mathrm{C}_2+{ }^{12} \mathrm{C}_3\).
∴ Number of subsets of ‘A’ having atmost 3 elements = \({ }^{12} \mathrm{C}_0+{ }^{12} \mathrm{C}_1+{ }^{12} \mathrm{C}_2+{ }^{12} \mathrm{C}_3\) = 299.

Question 3.
Find the numbers of ways of selecting a cricket team of 11 players from 7 batsmen and 6 bowlers such that there will be atleast 5 bowlers in the team.
Solution:
Number of batsmen = 7
Number of bowlers = 6
In selecting 11 players in a team out of given 13 players so that the team contains atleast 5 bowlers, two cases arises.

Case (i) : (Selecting 5 bowlers) :
Number of ways of selecting 5 bowlers from 6 = \({ }^6 \mathrm{C}_5\)
The remaining 6 players are selected from 7 batsmen can be done in \({ }^7 \mathrm{C}_6\) ways.
Number of ways of selecting = \({ }^7 \mathrm{C}_6 \times{ }^6 \mathrm{C}_5\).

Case – (ii) (Selecting 6 bowlers) :
Number of ways of selecting 6 bowlers from 6 = \({ }^6 \mathrm{C}_6\)
The remaining 5 players to be selected from 7 batsmen can be done in \({ }^7 \mathrm{C}_5\) ways.
∴ Number of ways of selecting = \(\mathrm{C}_6 \times{ }^7 \mathrm{C}_5\)
Total number of ways of selecting = \({ }^7 \mathrm{C}_6 \times{ }^7 \mathrm{C}_5+{ }^7 \mathrm{C}_5 \times{ }^6 \mathrm{C}_6\) = 63.

Question 4.
In 5 vowels and 6 consonants are given, then how many 6 letter words can be formed with 3 vowels and 3 consonants.
Solution:
Given 5 vowels and 6 consonants.
6 letter word is formed with 3 vowels and 3 consonants.
Number of ways of selecting 3 vowels from 5 vowels is \({ }^5 \mathrm{C}_3\).
Number of ways of selecting 3 consonants from 6 consonants is \({ }^6 \mathrm{C}_3\).
∴ Total number of ways of selecting = \({ }^5 \mathrm{C}_3 \times{ }^6 \mathrm{C}_3\)
These letters can be arranged themselves in 6! ways.
∴ Number of 6 letter words formed = \({ }^5 \mathrm{C}_3 \times{ }^6 \mathrm{C}_3\) × 6!.

Question 5.
There are 8 railway stations along a rail-way line. In how many ways can a train be stopped at 3 of these stations such that no two of them are consecutive ?
Solution:
Let S₁, S₂, S₃ ……. S₈ be 8 railway stations along a railway line.
Train is to be stopped at 3 stations.
Number of ways of selecting 3 stations out of 8 stations is 8Cr
Number of ways of selecting 3 consecutive stations is 6.
(i.e., (S₁, S₂, S₃), (S₂, S₃, S₄), ………. (S₆, S₇, S₈)}
Number of ways of selecting only 2 consecu¬tive stations = 2 × 5 + 5 × 4 = 30
As no two stops are consecutive, number of ways of selecting = \({ }^8 \mathrm{C}_3\) – 6 – 30 = 20.

Question 6.
Find the number of ways of forming a com¬mittee of 5 members out of 6 Indians and 5 Americans so that always the Indians will be in majority in the committee.
Solution:
A committee of 5 members is to be formed out of 6 Indians and 5 Americans.
As committee contains the majority of Indians, 3 cases arises.

i) Selecting 3 Indians and 2 Americans :
Number of ways of selecting 3 Indians out of 6 Indians = \({ }^6 \mathrm{C}_3\)
Number of ways of selecting 2 Americans out of 3 Indians = \({ }^5 \mathrm{C}_2\)
Number of ways of selecting 3 Indians and 2 Americans = \({ }^6 \mathrm{C}_3 \times{ }^5 \mathrm{C}_2\).

ii) Selecting 4 Indians and 1 American :
Number of ways of selecting 4 Indians out of 6 Indians = \({ }^6 \mathrm{C}_4\)
Number of ways of selecting 1 American out of 5 Americans = \({ }^5 \mathrm{C}_1\)
Number of ways of selecting 4 Indians and 1 American = \({ }^6 \mathrm{C}_4 \times{ }^5 \mathrm{C}_1\).

iii) Selecting 5 Indians :
Number of ways of selecting all 5 members
Indians out of 6 Indians = \({ }^6 \mathrm{C}_5\).
∴ Total numbers of ways of forming a committee = \({ }^6 \mathrm{C}_3 \times{ }^5 \mathrm{C}_2+{ }^6 \mathrm{C}_4 \times{ }^5 \mathrm{C}_1+{ }^6 \mathrm{C}_5\) = 281.

Question 7.
A question paper is divided into 3 sections A, B, C containing 3, 4, 5 questions respectively, Find the number of ways of attempting 6 questions choosing atleast one from each section.
Solution:
A question paper contains 3 sections A, B, C containing 3, 4, 5 questions respectively.
Number of ways of selectng 6 questions out of these 12 questions = \({ }^{12} \mathrm{C}_6\)
Number of ways of selecting 6 questions from sections B and C (i.e., from 9 questions) = \({ }^{9} \mathrm{C}_6\)
Number of ways of selecting 6 questions from sections A and C (i.e., from 8 questions) = \({ }^{8} \mathrm{C}_6\)
Number of ways of selecting 6 questions from sections A and B (i.e., 7 questions) = \({ }^{7} \mathrm{C}_6\)
∴ Number of ways of selecting 6 questions choosing atleast one from each section = \({ }^{12} \mathrm{C}_6-{ }^7 \mathrm{C}_6-{ }^8 \mathrm{C}_6-{ }^9 \mathrm{C}_6\) = 805.

Question 8.
Find the number of ways in which 12 things be
(i) divided into 4 equal groups
(ii) distributed to 4 persons equally.
Solution:
i) Dividing 12 things in 4 equal groups :
Number of ways of dividing 12 things into 4 equal groups = \(\frac{12 !}{(3 !)^4 \cdot 4 !}\).

ii) Distributing 12 things to 4 persons equally
Number of ways of distributing 12 things to 4 persons equally = \(\frac{12 !}{(3 !)^4 \cdot 4 !}\).

Question 9.
A class contains 4 boys and g girls. Every Sunday, five students with atleast 3 boys go for a picnic. A different group is being sent every week. During the picnic, the class teacher gives each girl in the group a doll. If the total number of dolls distributed is 85, find g.
Solution:
A class contains 4 boys and ‘g’ girls,
In selecting 5 students with atleast 3 boys for picnic two cases arises.

i) Selecting 3 boys and 2 girls :
Number of ways of selecting 3 boys and 2 girls = \({ }^4 C_3 \times{ }^g C_2=4\left({ }^g C_2\right)\)
As each group contains 2 girls, number of dolls required = 8 \(8\left({ }^8 \mathrm{C}_2\right)\).

ii) Selecting 4 boys and 1 girl :
Number of ways of selecting 4 boys and 1 girl = \({ }^4 \mathrm{C}_4 \times{ }^{\mathrm{g}} \mathrm{C}_1\) = g
∴ As each group contains only 1 girl, number of dolls required = g
∴ Total number of dolls = 8 (\(\left({ }^g \mathrm{C}_2\right)\)) + g
i.e., 85 = \(\frac{g(g-1)}{2}\) + g
⇒ 85 = 4g² – 3g
⇒ 4g² – 3g – 85 = 0
⇒ (4g + 17) (g – 5) = 0
⇒ g = 5 (∵ ‘g’ is non-negative integer).

TS Inter 2nd Year Economics Study Material 9th Lesson పర్యావరణ అర్థశాస్త్రం

వ్యాసరూప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
వివిధ రకాల కాలుష్యాలను వివరించి, వాటి ప్రభావాలను పరిశీలించండి.
జవాబు.
కాలుష్యం (Pollution) :
గాలి, నీటితో కలసిన కాలుష్యకాలు కాలుష్యాన్ని సృష్టిస్తాయి. ఇవి వాతావరణాన్ని కలుషితం చేసి పరిసరాలకు నష్టాన్ని కలిగిస్తాయి. కాలుష్యం అన్ని జీవరాశులకు ప్రమాదాన్ని కలిగిస్తుంది. భౌతిక పర్యావరణ విచ్ఛేదనకు కూడా కాలుష్యం కారణమవుతుంది. కాలుష్యం ప్రధానంగా వాయు కాలుష్యం, జల కాలుష్యం, ధ్వని కాలుష్యం అనే మూడు రూపాలలో ఉంటుంది.

1. వాయు కాలుష్యం :
వాయు కాలుష్యానికి కారణాలు లేదా ఆధారాలు :

1. వ్యవసాయ కార్యకలాపాలు
2. పదార్థాల దహనం
3. యంత్రాల సహాయంతో జరిగే ఉత్పత్తి ప్రక్రియలు
4. ద్రావకం ఉపయోగిత
5. న్యూక్లియర్ శక్తి కార్యక్రమాల నిర్వహణ, మానవులు, జంతువులు, పక్షులు మొదలైన జీవరాశి శ్వాస వ్యవస్థపై వాయు కాలుష్యం తీవ్ర ప్రభావాన్ని చూపుతుంది.

ఆహార వస్తువులు, కూరగాయలు, పండ్లపై వాయు కాలుష్య ప్రభావం ఉంటుంది. మొక్కలు, పంటలు, పచ్చిక భూములపై దుమ్ము పొరలు ఏర్పడటంవల్ల భూమి ఉత్పాదక శక్తి తగ్గుతుంది. హరిత గృహంపై దీని ప్రభావంవల్ల భూమి మీది ఉష్ణోగ్రతలు ఎక్కువగా పెరిగి ధ్రువ ప్రాంతాలలోని మంచుగడ్డలు, హిమానీనదాలు కరిగిపోయే ప్రమాదం ఉంది. ఆమ్ల వర్షాలు, వాయు కాలుష్యం ద్వారా ఏర్పడి భూమి మీద భవనాలను, చెట్లను, మొక్కలను, అటవీ ప్రాంతాలను నష్టపరుస్తాయి.

2. జల కాలుష్యం (Water Pollution) :
నీటి స్వభావాన్ని మార్చి ఉపయోగానికి పనికి రాకుండా ప్రమాదకరమైన రీతిలో జల కాలుష్యం నీటిని పాడుచేస్తుంది. ప్రాణి కోటికి ప్రమాదకరమైన అదనపు పదార్థాలు నీటిలో కలవడమే జల కాలుష్యంగా నిర్వచించవచ్చు. కాలుష్యం వల్ల వీటి మధ్య సమతుల్యత దెబ్బతింటుంది.

1. మురుగు వ్యర్థ పదార్థాలు
2. అంటు వ్యాధుల ఏజెంట్లు
3. విదేశీ సేంద్రియ రసాయనాలు
4. రసాయనిక ఖనిజ పదార్థాలు, సమ్మేళనాలు మొదలైన వాటిని నీటి కాలుష్య కారకాలుగా చెప్పవచ్చు.

నీటి కాలుష్యం అనేక సమస్యలను సృష్టిస్తుంది. వాస్తవానికి ఎన్నో వ్యాధులకు ఇతర పర్యావరణ ప్రమాదాలకంటే నీటి కాలుష్యమే ప్రధానమైంది. కలరా, టైఫాయిడ్ అతి విరోచనాలవంటి వ్యాధులు నీటి కాలుష్యం ద్వారా వ్యాప్తి చెందుతాయి.

కొన్ని పరిశ్రమలు తమకు కావలసిన స్థాయిలో నీటిని శుభ్రపరచడంకోసం అధిక మొత్తాలలో వెచ్చించాల్సి రావడంవల్ల ఉత్పత్తి వ్యయాలు పెరుగుతున్నాయి. నీటి కాలుష్యం చేపలను చంపి జల ఆహార నిల్వలను నశింపచేస్తుంది.

3. ధ్వని కాలుష్యం (Noise Pollution) :
ధ్వని కాలుష్యం శరీర సంబంధమైన లేదా మానసిక సంబంధమైన హానిని కలగజేస్తుంది. రైల్వేలు, పరిశ్రమలు, నిర్మాణ రంగ కార్యకలాపాలు, ప్రజా సమూహాల కలయికల, లౌడ్ స్పీకర్లను ఉపయోగించడం `వంటి క్రియలు ధ్వనిని వ్యాప్తి చేస్తాయి.

చెవికి ఇబ్బంది కలిగించే ధ్వని కాలుష్యం తాత్కాలికంగా కాని, శాశ్వతంగా కాని వినికిడి సామర్థ్యాన్ని తగ్గిస్తుంది. కొంతకాలంపాటు ధ్వని కాలుష్యానికి లోనైతే చెవిటితనం వచ్చే ప్రమాదముంది. ధ్వని కాలుష్యంవల్ల మెదడు, నరాల వ్యవస్థ దెబ్బతిని, చికాకు స్వభావం పెరుగుతుంది. నిరంతర ధ్వని కాలుష్య ప్రభావంవల్ల శ్రామిక సామర్థ్యం, వారి వృత్తిపరమైన పనితీరు క్షీణిస్తుంది.

ప్రశ్న 2.
పర్యావరణ క్షీణత ఆర్థిక వ్యవస్థను ఏ విధంగా ప్రభావితం చేస్తుంది ? ఈ సమస్యను అధిగమించడానికి నివారణ చర్యలను సూచించండి.
జవాబు.
I. పర్యావరణ విచ్ఛేదన భావన :
పర్యావరణ విచ్ఛేదనం అంటే భూమిపై జరిగిన ఛిద్రత లేదా పర్యావరణంలోని సహజ వనరుల రూపంలో ఉన్న ఆస్తుల క్షీణత అనవచ్చు. ప్రకృతి ఉపరితలంలో రాకూడని మార్పులు లేదా తీవ్రతను పర్యావరణ విచ్ఛేదనంగా చెప్పవచ్చు. భూమిపైగల సహజ వనరులు క్రమంగా క్షీణించి కొన్ని జీవరాశులు అంతరించి పోవడం పర్యావరణ విచ్ఛేదనను కలుగజేస్తుంది. వాయు కాలుష్యం, జల కాలుష్యం, భూమిపై పొరలలో ఉన్న సహజ శక్తుల క్షీణతవంటి సమస్యలు ఈ విచ్ఛేదనంవల్ల సృష్టించబడతాయి.

II. పర్యావరణ విచ్ఛేదనకు కారణాలు :

1. భూసార క్షీణత :
పనికిరాని పిచ్చి మొక్కలు ప్రకృతిని, పరిసరాలను ఆవరించే సహజంగా ఉన్న హరిత ప్రదేశాలను క్రమంగా క్షీణింపచేస్తాయి. ఈ విధమైన వృక్ష సంబంధమైన జీవరాశులు భూమి, భూమిలోని పర్యావరణపరమైన ఆస్తులను నాశనం చేస్తాయి. అటవీ ప్రాంతాలలో, మైదాన ప్రాంతాలలో, పంట భూములలో పశువుల మేతకోసం తొక్కిడి అధికంగా ఉన్నప్పుడు సారవంతమైన భూమి ఉపరితలంలోని పొరలు దెబ్బతిని భూమి గట్టితనాన్ని సంతరించుకుంటుంది.

2. కాలుష్యం :
వాయు, జల, ధ్వని పరమైన కాలుష్యాలు పర్యావరణానికి ప్రమాదకరమైనవి. ఈ కాలుష్యాలు గాలి, నీరు, భూమి నాణ్యతలను క్షీణింప చేస్తాయి. ధ్వని కాలుష్యం చెవులకు కలిగించే నష్టంతోపాటు పక్షులకు, జంతువులకు భయాందోళనలను కలిగిస్తుంది. అమితమైన జనాభా పెరుగుదల సహజ వనరులపై ఒత్తిడిని పెంచి పర్యావరణ విచ్ఛేదనకు దారితీస్తుంది.

3. చెత్తా చెదారాల సమూహం (Landfills) :
చెత్తా చెదారాల కుప్పలు వాయు కాలుష్యాన్ని సృష్టిస్తాయి. ఇవి చెడు వాసనలు సృష్టించడంతోపాటు అధికస్థాయిలో పర్యావరణ విచ్ఛేదనకు కారణమవుతాయి. వ్యర్థ పదార్థాలు, అపరిశుభ్రమైన మురుగు నీటితో ఇవి నిండి ఉంటాయి.

4. వన నిర్మూలన:
గృహ నిర్మాణ కార్యకలాపాల దృష్ట్యా, పరిశ్రమల స్థాపన దృష్ట్యా అడవులను నరికివేయడాన్ని వన నిర్మూలన అంటారు. వ్యవసాయ భూమి విస్తరణకోసం, వంట చెరకు అవసరాలకోసం అడవులలోని వృక్షాలను నరికి వేస్తున్నారు. పెద్ద తరహా నీటిపారుదల ప్రాజెక్టులకోసం కొన్ని ప్రాంతాలలో వన నిర్మూలన జరుగుతుంది. ఇందువల్ల పర్యావరణంలోకి చేరే కార్బన్ పరిమాణం పెరిగి ప్రపంచవ్యాప్తంగా భూతాపం పెరుగుతూ ఉంది. వర్షాభావం కూడా ఏర్పడే ప్రమాదం ఉంది.

5. సహజ కారణాలు :
భూకంపాలు, సముద్ర కెరటాలు, ఉప్పెనలు, సునామీలు, వన దహనాలు, జంతువులను, వృక్ష సముదాయాలను నాశనం చేస్తాయి. వీటివల్ల వర్తమానంలోనూ మరియు దీర్ఘకాలంలోనూ పర్యావరణంపై ప్రభావాలు ఉంటాయి.

6. పారిశ్రామికీకరణ, అధికోత్పత్తి:
శాస్త్ర, సాంకేతిక రంగాల అభివృద్ధితో ప్రపంచదేశాలలో ఉత్పాదక సామర్థ్యాలు విస్తరించాయి. ఉత్పత్తిని విస్తరించడానికి సహజ వనరులు, ముడి పదార్థాలు విరివిగా వినియోగించబడుతున్నాయి. పరిశ్రమల పొగ, ధ్వని, వ్యర్థ పదార్థాల విసర్జకాల ద్వారా పర్యావరణ విచ్ఛేదనానికి కారణాలు అవుతున్నాయి.

III. పర్యావరణ విచ్ఛేదన ప్రభావాలు :

1. మానవాళి ఆరోగ్యంపై పర్యావరణ విచ్ఛేదన ప్రభావం తీవ్రంగా ఉంది. ఆస్తమా, క్షయ, న్యూమోనియా, అతి విరోచనాలు వంటి వ్యాధులు కాలుష్యంవల్ల పెరుగుతున్నాయి. వాయు, జల, ధ్వని కాలుష్యంవల్ల సంబంధిత సమస్యలు క్రమంగా పెరుగుతున్నాయి.
2. జీవావరణ వ్యవస్థ సమతుల్యంగా ఉండటానికి జీవ వైవిధ్యం అవసరం. పర్యావరణ క్షీణత జీవ వైవిధ్యాన్ని క్షీణింపచేస్తుంది. పర్యావరణ విచ్ఛేదన ఓజోన్ పొరను క్షీణింపచేస్తుంది. ఇందువల్ల హానికరమైన కాంతి కిరణాలు భూమిపైకి వస్తాయి.
3. పర్యాటకులు ఒకే దేశంలోని లేదా ప్రాంతంలోని ప్రకృతిని, జంతు జాలాన్ని పక్షులను పచ్చదనంతో కూడిన భూభాగాన్ని దర్శించి ఆనందించాలని భావిస్తారు. కానీ, పర్యావరణ విచ్ఛేదన పర్యాటక బృందాలను నిరుత్సాహపరుస్తుంది.
4. పర్యావరణ విచ్ఛేదన ప్రభుత్వాలపై అధిక ఆర్థిక భారాన్ని మోపుతుంది. అధిక మొత్తాలను పర్యావరణం పరిరక్షణపై వ్యయం చేయడం ప్రభుత్వాలకు తప్పనిసరి భారం అవుతుంది.
   పర్యావరణం విచ్ఛేదనను తగ్గించి పుడమి తల్లిని రక్షించుకోవలసిన బాధ్యత అందరిపైనా ఉంది. ఇందుకు ప్రజలను పర్యావరణపరమైన విద్య ద్వారా చైతన్య పరచవలసిన అవసరం ఎంతో ఉంది.

ప్రశ్న 3.
వివిధ రకాల కాలుష్యాలకు గల కారణాలను, వాటివల్ల ఏర్పడే ప్రభావాలను తెలియజేయండి.
జవాబు.
వ్యాసరూప సమాధాన ప్రశ్న – 1 చూడుము.

ప్రశ్న 4.
పర్యావరణ సుస్థిరత లక్ష్యాలు ఏవి ? సుస్థిర అభివృద్ధి ప్రాధాన్యతను వివరించండి.
జవాబు.
సుస్థిర అభివృద్ధి లక్ష్యాలు :

1.వృద్ధి లేదా ఆదాయాలలో పెరుగుదల :
సుస్థిర అభివృద్ధి అన్ని వర్గాల జీవన ప్రమాణాలను పెంపొందించే ఉద్దేశంలో ఉంటుంది. విద్య, ఆరోగ్య, ప్రజా జీవనంలో భాగస్వామ్యం, స్వచ్ఛమైన పర్యావరణం, సమ న్యాయం పెంపొందించడం భావి తరాల జీవన ప్రమాణాలను పెంపొందించడానికి, సుస్థిర అభివృద్ధిలో సమ్మేళనం చేయబడ్డాయి.

2. అభివృద్ధి కొనసాగింపు :
సుస్థిర అభివృద్ధిలో భౌతిక, మానవపరమైన, సహజ మూలధనాలు పరిరక్షించబడి నియమబద్ధంగా ఉపయోగించబడతాయి.

3. క్షీణత నియంత్రణ :
ఆర్థికాభివృద్ధి పర్యావరణ క్షీణతకు దారితీస్తూ, నాణ్యమైన జీవన విధానానికి హాని కలిగించే రీతిలో ఉండకూడదు. భూమి, నీరు, గాలి, భూసార నాణ్యతలను సుస్థిర అభివృద్ధికోసం కొనసాగించాలి. ఆర్థికాభివృద్ధికి సంబంధించిన ప్రస్తుత నిర్ణయాలు, భావితరాల జీవన ప్రమాణాలను దెబ్బతీయకూడదు.

4. జీవ వైవిధ్య రక్షణ :
సుస్థిర అభివృద్ధిలో జీవ వైవిధ్య రక్షణకు ప్రాధాన్యతను ఇస్తుంది. ఈ విధానంలో అన్ని ఉత్పాదక కార్యక్రమాలు జీవ వైవిధ్యంతో, జన్యు వైవిధ్యంతో జీవరాశుల వైవిధ్యంతో ఆవరణాత్మక వైవిధ్యంతో సంబంధాన్ని కలిగి ఉంటాయి. కాబట్టి ఈ వైవిధ్యాలను సుస్థిర అభివృద్ధి కోసం కొనసాగించవలసి ఉంటుంది.

సుస్థిర అభివృద్ధి ప్రాధాన్యత :
ప్రపంచ స్థాయిలో సుస్థిర అభివృద్ధి ప్రాధాన్యతను దృష్టిలో ఉంచుకొని ఐక్యరాజ్యసమితి 2005-15 దశాబ్దాన్ని సుస్థిర అభివృద్ధి కోసం విద్య’గా ప్రకటించింది. సుస్థిర అభివృద్ధి ప్రాధాన్యతలను కింది విధంగా సంక్షిప్తంగా వివరించడమైంది.

1. దృక్పథాలలో మార్పులు :
సుస్థిర అభివృద్ధి భావన ప్రజల దృక్పథాలను మారుస్తుంది. అత్యాశకు కాకుండా మన ‘అవసరాలకు మాత్రమే వనరులు ఉపయోగించినట్లయితే వినియోగాన్ని నియంత్రించే దృక్పథాన్ని పెంపొందిస్తుంది.

2. స్నేహపూర్వక నవకల్పనలు :
ఆర్థికాభివృద్ధికి పర్యావరణంతో స్నేహపూర్వకంగా ఉండే పద్ధతులను, నవ కల్పనలను ప్రోత్సాహిస్తుంది.

3. ఆర్థిక కార్యకలాపాలకు పరిమితి :
పర్యావరణానికిగల పోషక సామర్థ్యాన్ని దృష్టిలో ఉంచుకొని ఆర్థిక కార్యకలాపాలకు పరిమితులను విధిస్తుంది.

4. భవిష్యత్ అభివృద్ధి :
పర్యావరణాన్ని పరిరక్షిస్తూ భావితరాల ఆర్థిక బాగోగుల అభివృద్ధి తోడ్పడుతుంది.

5. ప్రభుత్వ చర్యల విస్తరణ :
సుస్థిర అభివృద్ధి పరిపాలనాపరమైన ప్రభుత్వ పాత్రను విస్తరింపచేస్తుంది. ఈ అభివృద్ధి దృష్ట్యా .ప్రభుత్వ కార్యకలపాల కింద

• సామాజిక భాగస్వామ్యం
• వికేంద్రీకరణ
• ధనాత్మక ప్రోత్సాహకాలు
• (నూతన విధానం, పాలనా యంత్రాంగాల సృష్టి
• పర్యావరణ కార్యక్రమాలకు స్వచ్ఛంధ సంస్థలకు NGO ప్రోత్సాహం’ వంటివి ఉంటాయి.

6. వృద్ధికి కొత్త నిర్వచనం :
నాణ్యమైన జీవన రూపంలో సుస్థిర అభివృద్ధి ఆర్థికాభివృద్ధికి ఒక కొత్త నిర్వచనాన్ని ఇస్తుంది.

7. వనరుల సంరక్షణ :
అభివృద్ధి. నిరంతరం సాగుతూ సమానత్వ స్వభావంతో ఉండటానికి వనరుల సంరక్షణ అవసరాన్ని పదే పదే గుర్తు చేస్తుంది. ఈ విధమైన వృద్ధి వనరుల పునఃసృష్టిని ప్రోత్సాహిస్తుంది.

8. జీవ వైవిధ్య పరిరక్షణ :
సుస్థిర అభివృద్ధి జీవ వైవిధ్య ప్రాధాన్యతను గుర్తిస్తుంది. జీవ వైవిధ్య పరిరక్షణ నిర్వాహణలకై మానవుడి మనుగడ ఆధారపడి ఉంది.

• పర్యావరణం
• కాలుష్యం
• సహజ వనరులను అతిగా వినియోగించడం
• వృక్ష, జంతు కోటి క్షీణత
• ప్రపంచ పర్యావరణ వ్యత్యాసాలు మొదలైన సమస్యల నియంత్రణకు అవసరమైన విధానాలను ప్రోత్సాహిస్తాయి.

9. అభివృద్ధిలో ఆర్థిక, సామాజిక, పర్యావరణ కోణాల సమతుల్యత :
దీనికి సంబంధించిన కింద పేర్కొన్న మూడు విభాగాలు పరస్పరం ఆధారపడి ఉంటాయి. దీనిని కింద పటంలో చూపడమైంది.

10. ప్రకృతికిగల ప్రాధాన్యతను గుర్తించడం:
సుస్థిర అభివృద్ధి ప్రకృతి ప్రాధాన్యతను అభివృద్ధితో సంబంధం కలిగిన భాగస్వాముల గుర్తించేటట్లు చేస్తుంది. మనందరం సమిష్టిగా భూమాతను సుస్థిరంగా ఆరోగ్యప్రదంగా పంచడానికి కృషి చేయవలసిన అవసరాన్ని సుస్థిర అభివృద్ధి గుర్తుచేస్తుంది. పర్యావరణాన్ని, అందులోని వనరులను పదిలపరచవలసిన, పరిరక్షించవలసిన అవసరాన్ని కూడా దృఢంగా తెలియజేస్తుంది.

స్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
సహజ వనరులు అంటే ఏమిటి ?
జవాబు.
ఒక నిర్ణీత ప్రదేశంలో, సమయంలో మానవ అవసరాలను తీర్చగలిగే సాధనాలే వనరులు. వివిధ రూపాలలో ఉన్న వనరుల సంపదనే ప్రకృతి కల్గి ఉంటుంది. సహజ వనరులు ఆర్థిక వ్యవస్థకు అతీతంగా కర్బనజనిత, మూలక లేదా అకర్బన పదార్థాల ద్వారా సమకూరుతాయి.

సహజ వనరుల లక్షణాలు :

1. సహజ వనరులు ప్రకృతి ఉచితంగా ప్రసాదించిన కానుకలు, మానవులు వాటిని అన్వేషించి ఉపయుక్తంగా మారుస్తారు.
2. ఒక నిర్ణీత కాలంలో సహజ వనరుల సంపద స్థిరంగా ఉంటుంది.
3. సహజ వనరులు ప్రకృతిలో నిక్షిప్తమై ఉంటాయి. మానవుడు సాంకేతిక విజ్ఞానం సహాయంతో పరిశోధనచేసి వీటిని కనుగొంటాడు.
4. సహజ వనరులు, సహజ, సజీవ భాగంలో మార్పులద్వారా కొంతకాలం పరిమితిలో సహజ వనరుల పరిమాణంలో మార్పులు సంభవిస్తాయి.
5. శాస్త్రీయ, సాంకేతిక విజ్ఞానాలు అభివృద్ధిచెందడంతో నూతన వనరులు ప్రకృతినుంచి కాలానుగుణంగా ఆవిర్భవిస్తాయి. తౌడు నుంచి నూనెను వెలికి తీయడం ఒక ఉదాహరణగా చెప్పవచ్చు.

సహజ వనరుల వర్గీకరణ :
మన్నిక, పునరుద్ధరణ వ్యూహం ప్రాతిపదికలపై సహజ వనరులను వర్గీకరిస్తారు. సహజ వనరుల వర్గీకరణ ఈ కింది విభాగాలలో ఉంటుంది.

ప్రశ్న 2.
సుస్థిర అభివృద్ధి అంటే ఏమిటి ?
జవాబు.
సుస్థిర అభివృద్ధి భావన :
పర్యావరణ విధ్వంసం లేకుండా జరిగే ఆర్థికాభివృద్ధిని సుస్థిర అభివృద్ధి అంటారు. ఈ విధమైన అభివృద్ధి ప్రక్రియలో పర్యావరణం విలీనం చేయబడుతుంది. వర్తమానంలో అవసరాలను తీర్చుకొంటూ భావి తరాల అవసరాలు తీర్చుకోవడంలో రాజీలేని అభివృద్ధిని సుస్థిర అభివృద్ధి అంటారు.

అంటే భావితరాల అవసరాలను సుస్థిర అభివృద్ధిలో దృష్టిలో ఉంచుకొంటుంది. వనరుల వినియోగం, పునఃకల్పనం మధ్య సమతుల్యతను ఏర్పరిచి అభివృద్ధి ప్రక్రియను కొనసాగిస్తే సుస్థిర వృద్ధి సాధ్యపడుతుంది. కాబట్టి ప్రస్తుతకాలంలో అభివృద్ధి వ్యూహాలు సహజం, ఆర్థిక వ్యవస్థ, పర్యావరణాలు సామూహిక అభివృద్ధికి ప్రాధాన్యత ఇస్తున్నాయి. సుస్థిర రూపంలో ఉన్న అభివృద్ధికి ప్రాధాన్యత ఇస్తున్నాయి. ‘సుస్థిర రూపంలో ఉన్న అభివృద్ధి నిరాటంకంగా కొనసాగుతుంది.

ప్రకృతి, సహజ వనరుల రక్షణకు సంబంధించిన అంతర్జాతీయ సంఘం (International Union for the Con- servation of Nature and Natural Resources) ప్రపంచ వ్యాప్తంగా సంరక్షణ వ్యూహంలో మొట్ట మొదట 1980లో సుస్థిర అభివృద్ధి భావనను తెలియజేసింది. ఈ పదం సాధారణ ఉపయోగంలోకి Brundtland నివేదిక ద్వారా క్రమంగా వచ్చింది. డాలీ 1990లో సుస్థిర అభివృద్ధికి మూడు నియమాలు తెలియచేశారు.

1. పునరుద్ధరించగల వనరులను పునఃకల్పన రేటులకు (regeneration rate) మించి ఉపయోగించరాదు.
2. పునరుద్ధరించడానికి వీలులేని వనరులు ప్రత్యామ్నాయ వనరులు లభించే రేటుకన్నా ఎక్కువ రేటులో ఉపయోగించకూడదు.
3. పర్యావరణం విలీనం చేసుకోగల్గిన సామర్థ్యంకంటే ఎక్కువ పరిమాణంలో కాలుష్య పదార్థాలు పర్యావరణంలోకి విసర్జించరాదు.

ప్రశ్న 3.
పర్యావరణాన్ని ఎందుకు సంరక్షించాలి ?
జవాబు.

1. భారతదేశంవంటి ఎన్నో అభివృద్ధి చెందుతున్న దేశాలు వ్యవసాయంపై ఆధారపడ్డాయి. మంచి వర్షపాతం, అనుకూల వాతావరణం, భూసారం నాణ్యమైన విత్తనాలు పర్యావరణం ద్వారా అందజేయబడతాయి. అయితే రసాయనిక ఎరువులు, క్రిమి సంహారక మందులు అధికంగా వినియోగించడంవల్ల పర్యావరణపు సమతుల్యత విచ్ఛిత్తి చెంది దీర్ఘకాలంలో భూమి యొక్క సహజ భూసారం క్షీణిస్తుంది.
2. అడవులు, వృక్ష సంపద సకాలంలో వర్షాలకు తోడ్పడి వాతావరణ సమతుల్యతను కాపాడతాయి. అందువల్ల క్షీణిస్తున్న అటవీ సంపదను అధికంగా మొక్కలు నాటడం ద్వారా పెంపొందించాలి.
3. ఖనిజాలు వెలికితీయడం, పాడి పరిశ్రమ, చేపల పెంపకం, పారిశ్రామిక కార్యకలాపాలవంటి ఆర్థిక కార్యకలాపాలకు పర్యావరణ పరిరక్షణ సహాయపడుతుంది.
4. పర్యావరణ పరిరక్షణ ఒకదేశ ప్రజల సంపదను, ఆరోగ్య జీవనాన్ని పెంపొందించడం ద్వారా సామాజిక అభివృద్ధికి దోహదపడుతుంది.
5. పర్యావరణ పరిరక్షణ మానవుల సుఖ సంతోషాలను పెంపొందిస్తుంది. పర్యావరణ అసమతుల్యత, వరదలు, భూకంపాలు, కరువులు, తుఫానులువంటి సమస్యలు సమాజాన్ని, ఆర్థిక వ్యవస్థను ఛిన్నాభిన్నం చేస్తాయి.
6. సహజ వనరులను ప్రస్తుతం ఎక్కువగా దుర్వినియోగంచేస్తే, భావితరాల సంక్షేమం దెబ్బతింటుంది. కాబట్టి సుస్థిర అభివృద్ధి ద్వారా పర్యావరణ పరిరక్షణ భావితరాల సంక్షేమానికి సహాయపడుతుంది.
7. పర్యావరణ పరిరక్షణ కాలుష్య రహిత జీవితాన్ని అందజేస్తుంది. కాలుష్యరహిత పరిస్థితులలో మానవాళి ఆరోగ్యకరమైన సుఖ సంతోషాలు మెరుగుపడతాయి.
8. జీవ వైవిధ్యాన్ని, ఆవరణ సంతులతను పెంపొందించడానికి పర్యావరణ పరిరక్షణ సహాయపడుతుంది. ఓజోన్ పొర, హిమానీ నదాలు ఇతర ప్రకృతిపరమైన అంశాలు సరైన క్రమంలో నిర్వహించడానికి పర్యావరణ పరిరక్షణ సహాయపడుతుంది.

ప్రశ్న 4.
కాలుష్యం రకాలను చర్చించండి..
జవాబు.

వివిధ రకాల కాలుష్యాలను వివరించి, వాటి ప్రభావాలను పరిశీలించండి.
జవాబు.
కాలుష్యం (Pollution) :
గాలి, నీటితో కలసిన కాలుష్యకాలు కాలుష్యాన్ని సృష్టిస్తాయి. ఇవి వాతావరణాన్ని కలుషితం చేసి పరిసరాలకు నష్టాన్ని కలిగిస్తాయి. కాలుష్యం అన్ని జీవరాశులకు ప్రమాదాన్ని కలిగిస్తుంది. భౌతిక పర్యావరణ విచ్ఛేదనకు కూడా కాలుష్యం కారణమవుతుంది. కాలుష్యం ప్రధానంగా వాయు కాలుష్యం, జల కాలుష్యం, ధ్వని కాలుష్యం అనే మూడు రూపాలలో ఉంటుంది.

1. వాయు కాలుష్యం :
వాయు కాలుష్యానికి కారణాలు లేదా ఆధారాలు :

1. వ్యవసాయ కార్యకలాపాలు
2. పదార్థాల దహనం
3. యంత్రాల సహాయంతో జరిగే ఉత్పత్తి ప్రక్రియలు
4. ద్రావకం ఉపయోగిత
5. న్యూక్లియర్ శక్తి కార్యక్రమాల నిర్వహణ, మానవులు, జంతువులు, పక్షులు మొదలైన జీవరాశి శ్వాస వ్యవస్థపై వాయు కాలుష్యం తీవ్ర ప్రభావాన్ని చూపుతుంది.

ఆహార వస్తువులు, కూరగాయలు, పండ్లపై వాయు కాలుష్య ప్రభావం ఉంటుంది. మొక్కలు, పంటలు, పచ్చిక భూములపై దుమ్ము పొరలు ఏర్పడటంవల్ల భూమి ఉత్పాదక శక్తి తగ్గుతుంది. హరిత గృహంపై దీని ప్రభావంవల్ల భూమి మీది ఉష్ణోగ్రతలు ఎక్కువగా పెరిగి ధ్రువ ప్రాంతాలలోని మంచుగడ్డలు, హిమానీనదాలు కరిగిపోయే ప్రమాదం ఉంది. ఆమ్ల వర్షాలు, వాయు కాలుష్యం ద్వారా ఏర్పడి భూమి మీద భవనాలను, చెట్లను, మొక్కలను, అటవీ ప్రాంతాలను నష్టపరుస్తాయి.

2. జల కాలుష్యం (Water Pollution) :
నీటి స్వభావాన్ని మార్చి ఉపయోగానికి పనికి రాకుండా ప్రమాదకరమైన రీతిలో జల కాలుష్యం నీటిని పాడుచేస్తుంది. ప్రాణి కోటికి ప్రమాదకరమైన అదనపు పదార్థాలు నీటిలో కలవడమే జల కాలుష్యంగా నిర్వచించవచ్చు. కాలుష్యం వల్ల వీటి మధ్య సమతుల్యత దెబ్బతింటుంది.

1. మురుగు వ్యర్థ పదార్థాలు
2. అంటు వ్యాధుల ఏజెంట్లు
3. విదేశీ సేంద్రియ రసాయనాలు
4. రసాయనిక ఖనిజ పదార్థాలు, సమ్మేళనాలు మొదలైన వాటిని నీటి కాలుష్య కారకాలుగా చెప్పవచ్చు.

నీటి కాలుష్యం అనేక సమస్యలను సృష్టిస్తుంది. వాస్తవానికి ఎన్నో వ్యాధులకు ఇతర పర్యావరణ ప్రమాదాలకంటే నీటి కాలుష్యమే ప్రధానమైంది. కలరా, టైఫాయిడ్ అతి విరోచనాలవంటి వ్యాధులు నీటి కాలుష్యం ద్వారా వ్యాప్తి చెందుతాయి.

కొన్ని పరిశ్రమలు తమకు కావలసిన స్థాయిలో నీటిని శుభ్రపరచడంకోసం అధిక మొత్తాలలో వెచ్చించాల్సి రావడంవల్ల ఉత్పత్తి వ్యయాలు పెరుగుతున్నాయి. నీటి కాలుష్యం చేపలను చంపి జల ఆహార నిల్వలను నశింపచేస్తుంది.

3. ధ్వని కాలుష్యం (Noise Pollution) :
ధ్వని కాలుష్యం శరీర సంబంధమైన లేదా మానసిక సంబంధమైన హానిని కలగజేస్తుంది. రైల్వేలు, పరిశ్రమలు, నిర్మాణ రంగ కార్యకలాపాలు, ప్రజా సమూహాల కలయికల, లౌడ్ స్పీకర్లను ఉపయోగించడం `వంటి క్రియలు ధ్వనిని వ్యాప్తి చేస్తాయి.

చెవికి ఇబ్బంది కలిగించే ధ్వని కాలుష్యం తాత్కాలికంగా కాని, శాశ్వతంగా కాని వినికిడి సామర్థ్యాన్ని తగ్గిస్తుంది. కొంతకాలంపాటు ధ్వని కాలుష్యానికి లోనైతే చెవిటితనం వచ్చే ప్రమాదముంది. ధ్వని కాలుష్యంవల్ల మెదడు, నరాల వ్యవస్థ దెబ్బతిని, చికాకు స్వభావం పెరుగుతుంది. నిరంతర ధ్వని కాలుష్య ప్రభావంవల్ల శ్రామిక సామర్థ్యం, వారి వృత్తిపరమైన పనితీరు క్షీణిస్తుంది.

ప్రశ్న 5.
పర్యావరణానికి, ఆర్థికాభివృద్ధికి మధ్యగల సంబంధాన్ని వివరించండి.
జవాబు.
అభివృద్ధిచెందుతున్న భారతదేశంలాంటి దేశాలలో పర్యావరణం వనరులపై ఒత్తిడి, స్వయం సమృద్ధి, ఆదాయ పంపిణీ, భవిష్యత్తులో ఆర్థికవృద్ధిపై తీవ్ర ప్రభావాలను సృష్టిస్తుంది. ఈ ప్రభావాలను జనాభాలో ఉన్న 22-30% పేద ప్రజలు ఎక్కువ భరించవలసి రావడం దురదృష్టకరం.

ఆర్థిక వృద్ధి ప్రక్రియలో పర్యావరణానికి సంబంధించిన అవగాహన చారిత్రాత్మకంగా లేకపోవడం దీనికి కారణం. భవిష్యత్లో ఆర్థిక కార్యకలాపాలు క్షీణించిన పర్యావరణంలోనే జరగవలసి ఉంటుంది.

బీహార్, ఒడిస్సా, మధ్యప్రదేశ్, గోవా వంటి రాష్ట్రాలు కొన్ని ప్రాజెక్టులను చేపట్టాయి. ఇవి సమాజంలో ప్రాబల్యం ఉన్న శక్తివంతమైన వర్గాల ప్రయోజనాలను కాపాడటానికి ఉద్దేశించబడ్డాయి. వీటివల్ల బలహీన వర్గాలు, ఆదిమ జాతులు, పేద వర్గాలు సమస్యలను ఎదుర్కోవలసి వస్తోంది. పర్యావరణ విచ్ఛేదన ప్రభావాలు ఆ ప్రాంతంలో నివసించే అధిక శాతం ప్రజలపై పడతాయి. సామాజిక, ఆర్థిక, సాంస్కృతిక, జనాభాపరమైన నష్టాలను ఎక్కువ శాతం అక్కడి ప్రజలు భరించాల్సి ఉంటుంది.

ఆర్థిక కార్యకలాపాలకు ముడి పదార్థాలను అందజేయడంతోపాటు అనువైన వాతావరణ పరిస్థితులను పర్యావరణం కల్పిస్తుంది. అంతేగాక, ఉత్పాదక సంస్థలు విడుదలచేసే వ్యర్థాలు పర్యావరణం ఇముడ్చుకొంటుంది. ఇందుమూలంగా పర్యావరణ సమతుల్యత దెబ్బతిని పర్యావరణ క్షీణతకు కారణభూతమవుతుంది.

కెన్నత్. ఇ. బౌల్డింగ్ వంటి ఆర్థికవేత్తలు ఈ దృష్టితో పర్యావరణ వనరులపై ఒత్తిడి ద్వారా ఏర్పడే ఫలితాల గురించి ప్రపంచానికి హెచ్చరికలు చేశారు. వర్తమాన, భవిష్యత్ తరాల శ్రేయస్సుకు ప్రపంచ దేశాలు పర్యావరణ వనరులను పరిమితంగా ఉపయోగించాలి.

ఇంకో విధంగా చెప్పాలంటే, వస్తువుల ఉత్పత్తికి ఉపయోగించే ఉత్పాదకాలు, వ్యర్థ పదార్థాల విడుదల మధ్య సమతుల్యత ఏర్పడాలి. వ్యర్థ పదార్థాల పరిమాణం, విసర్జకాల పరిమాణం తక్కువగా ఉన్నప్పుడు పర్యావరణం తేలికగా విలీనం చేసుకోగలుగుతుంది.

వాస్తవానికి ఆర్థికాభివృద్ధికి అవసరమైన వనరులన్నీ పర్యావరణంలో లభిస్తాయి. పునరుద్ధరించగలిగిన, పునరుద్ధరించలేని సహజ వనరులు పర్యావరణం నుంచి సేకరించబడతాయి. సరైన పర్యావరణం లేకుండా ఏ దేశం కూడా ఆర్థికాభివృద్ధి సాధించలేదు.

పర్యావరణానికి సంబంధించిన ఆర్థిక విధులను శ్రద్ధగా గమనించవలసిన అవసరం ఉంది. ఆర్థికాభివృద్ధి ప్రక్రియకు పర్యావరణానికి మధ్యగల అంతర్గత సంబంధాలను గుర్తించవలసిన అవసరం కూడా ఉంది.

ఆర్థికాభివృద్ధికి, పర్యావరణానికి మధ్య గల సంబంధం :
ప్రకృతి నుంచి ఆర్థికాభివృద్ధికి అవసరమైన అన్ని వనరులు లభిస్తాయి. ఈ భూగోళం మీద జీవకోటి పర్యావరణంలోనే మనుగడ సాగిస్తుంది. ఆర్థికాభివృద్ధిని కొనసాగిస్తూనే వనరుల సంరక్షణ ప్రత్యేక శ్రద్ధతో జరగాలి. ఆర్థిక లక్ష్యాలను రూపొందించేటప్పుడు వనరుల సంరక్షణ కార్యక్రమాలకు సంబంధించిన ప్రణాళికలను సిద్ధం చేసుకోవాలి.

ఆర్థికాభివృద్ధి సుస్థిరతను దృష్టిలో ఉంచుకోవాలి. సుస్థిర వృద్ధి భావితరాలను, పర్యావరణ మూలధనాన్ని రక్షించే లక్ష్యంతో పనిచేస్తుంది. ఒకదేశం వాయు, జల, ధ్వని కాలుష్యాలను అధిక ఉత్పత్తులను సృష్టిస్తాయి.

వ్యవసాయం, గ్రామీణాభివృద్ధికి సంబంధించిన ఆర్థిక విధానాలు పర్యావరణానికి స్నేహపూర్వకంగా ఉండాలి. సేద్య పద్ధతులు, జీవ వైవిధ్యం, రసాయనిక ఎరువులు పరిమితంగా ఉపయోగించడం, వర్షపు నీటిని సంరక్షించుకోవడం, మొక్కల పెంపకాన్ని అభివృద్ధి చేయడం మొదలైన అంశాలకు పర్యావరణ సంరక్షణ, సుస్థిర వృద్ధి లక్ష్యాల దృష్ట్యా ప్రాధాన్యతను ఇవ్వాలి.

పెరుగుతున్న పట్టణీకరణ పర్యావరణానికి సమస్యలను సృష్టిస్తుంది. అందువల్ల జల, వాయు, దృశ్య కాలుష్యాలు ఏర్పడే ప్రమాదం ఉంది. వేగవంతమైన పారిశ్రామికీకరణ పెరుగుతున్న ఆర్థిక కార్యకలాపాలు పట్టణ ప్రాంతాలలో పర్యావరణానికి నష్టాన్ని కలిగిస్తున్నాయి.

అభివృద్ధి ప్రక్రియలో భాగంగా వినియోగత్వం పెరుగుతూ ఉంటుంది. హరిత గృహ ప్రభావం, ఓజోన్ పొరను హరింపచేసే కాలుష్యం, భూతాప, అకాల వర్షాలు, వరదలు మొదలైనవి వనరులను అతిగా ఉపయోగించడం, అధిక ఉత్పత్తుల తయారీవల్ల ఏర్పడిన సమస్యలు.

ఆర్థికాభివృద్ధికి అవసరమైన అన్ని వనరులను పర్యావరణం అందచేస్తుంది. అదే సమయంలో ఆర్థికాభివృద్ధి కార్యకలాపాల వల్ల పర్యావరణ విచ్ఛేదన సమస్య ఏర్పడుతుంది. ఆర్థికాభివృద్ధి, పర్యావరణ విచ్ఛేదనాల మధ్య సమతుల్యత ఉండేలా ప్రపంప దేశాలన్నీ కృషి చేయాలి.

ప్రశ్న 6.
పర్యావరణ క్షీణత ఆర్థిక వ్యవస్థను ఏ విధంగా ప్రభావితం చేస్తుంది ? ఈ సమస్యను అధిగమించడానికి నివారణ చర్యలను సూచించండి.
జవాబు.
I. పర్యావరణ విచ్ఛేదన భావన :
పర్యావరణ విచ్ఛేదనం అంటే భూమిపై జరిగిన ఛిద్రత లేదా పర్యావరణంలోని సహజ వనరుల రూపంలో ఉన్న ఆస్తుల క్షీణత అనవచ్చు. ప్రకృతి ఉపరితలంలో రాకూడని మార్పులు లేదా తీవ్రతను పర్యావరణ విచ్ఛేదనంగా చెప్పవచ్చు. భూమిపైగల సహజ వనరులు క్రమంగా క్షీణించి కొన్ని జీవరాశులు అంతరించి పోవడం పర్యావరణ విచ్ఛేదనను కలుగజేస్తుంది. వాయు కాలుష్యం, జల కాలుష్యం, భూమిపై పొరలలో ఉన్న సహజ శక్తుల క్షీణతవంటి సమస్యలు ఈ విచ్ఛేదనంవల్ల సృష్టించబడతాయి.

II. పర్యావరణ విచ్ఛేదనకు కారణాలు :

1. భూసార క్షీణత :
పనికిరాని పిచ్చి మొక్కలు ప్రకృతిని, పరిసరాలను ఆవరించే సహజంగా ఉన్న హరిత ప్రదేశాలను క్రమంగా క్షీణింపచేస్తాయి. ఈ విధమైన వృక్ష సంబంధమైన జీవరాశులు భూమి, భూమిలోని పర్యావరణపరమైన ఆస్తులను నాశనం చేస్తాయి. ` అటవీ ప్రాంతాలలో, మైదాన ప్రాంతాలలో, పంట భూములలో పశువుల మేతకోసం తొక్కిడి అధికంగా ఉన్నప్పుడు సారవంతమైన భూమి ఉపరితలంలోని పొరలు దెబ్బతిని భూమి గట్టితనాన్ని సంతరించుకుంటుంది.

2. కాలుష్యం :
వాయు, జల, ధ్వని పరమైన కాలుష్యాలు పర్యావరణానికి ప్రమాదకరమైనవి. ఈ కాలుష్యాలు గాలి, నీరు, – భూమి నాణ్యతలను క్షీణింప చేస్తాయి. ధ్వని కాలుష్యం చెవులకు కలిగించే నష్టంతోపాటు పక్షులకు, జంతువులకు భయాందోళనలను కలిగిస్తుంది. అమితమైన జనాభా పెరుగుదల సహజ వనరులపై ఒత్తిడిని పెంచి పర్యావరణ విచ్ఛేదనకు దారితీస్తుంది.

3. చెత్తా చెదారాల సమూహం (Landfills) :
చెత్తా చెదారాల కుప్పలు వాయు కాలుష్యాన్ని సృష్టిస్తాయి. ఇవి చెడు వాసనలు సృష్టించడంతోపాటు అధికస్థాయిలో పర్యావరణ విచ్ఛేదనకు కారణమవుతాయి. వ్యర్థ పదార్థాలు, అపరిశుభ్రమైన మురుగు నీటితో నిండి ఉంటాయి.

4. వన నిర్మూలన :
గృహ నిర్మాణ కార్యకలాపాల దృష్ట్యా, పరిశ్రమల స్థాపన దృష్ట్యా అడవులను నరికివేయడాన్ని వన నిర్మూలన అంటారు. వ్యవసాయ భూమి విస్తరణకోసం, వంట చెరకు అవసరాలకోసం అడవులలోని వృక్షాలను నరికి వేస్తున్నారు. పెద్ద తరహా నీటిపారుదల ప్రాజెక్టులకోసం కొన్ని ప్రాంతాలలో వన నిర్మూలన జరుగుతుంది. ఇందువల్ల పర్యావరణంలోకి చేరే కార్భన్ పరిమాణం పెరిగి ప్రపంచవ్యాప్తంగా భూతాపం పెరుగుతూ ఉంది. వర్షాభావం కూడా ఏర్పడే ప్రమాదం ఉంది.

5. సహజ కారణాలు :
భూకంపాలు, సముద్ర కెరటాలు, ఉప్పెనలు, సునామీలు, వన దహనాలు, జంతువులను, వృక్ష సముదాయాలను నాశనం చేస్తాయి. వీటివల్ల వర్తమానంలోనూ మరియు దీర్ఘకాలంలోనూ పర్యావరణంపై ప్రభావాలు ఉంటాయి.

6. పారిశ్రామికీకరణ, అధికోత్పత్తి:
శాస్త్ర, సాంకేతిక రంగాల అభివృద్ధితో ప్రపంచదేశాలలో ఉత్పాదక సామర్థ్యాలు విస్తరించాయి. ఉత్పత్తిని విస్తరించడానికి సహజ వనరులు, ముడి పదార్థాలు విరివిగా వినియోగించబడుతున్నాయి. పరిశ్రమల పొగ, ధ్వని, వ్యర్థ పదార్థాల విసర్జకాల ద్వారా పర్యావరణ విచ్ఛేదనానికి కారణాలు అవుతున్నాయి.

అతిస్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
పర్యావరణ రకాలు.
జవాబు.
మనచుట్టూ ఆవరించి ఉన్న అన్ని అంశాలను పర్యావరణంగా చెప్పవచ్చు. ఈ పర్యావరణంలో సజీవ, నిర్జీవ నిర్మాణాలు పరస్పరం ఆధారపడి ఒకదానిని మరొకటి ప్రభావితం చేసుకొంటాయి. ఇవి ప్రధానంగా నాలుగు రకాలు.

• భౌతిక పర్యావరణం
• జీవ పర్యావరణం
• సామాజిక లేదా సాంస్కృతిపరమైన పర్యావరణం.

ప్రశ్న 2.
ఆవరణ వ్యవస్థ (Eco-System)
జవాబు.
మన చుట్టూ పర్యావరణం ఉంది. పర్యావరణంలో ఆవరణ వ్యవస్థలు (Eco-System) ఉంటాయి. ఆవరణ వ్యవస్థను వివిధ రూపాలలో నిర్వచించారు. ఈ నిర్వచనాలకు మూడు సాధారణ లక్షణాలు ఉన్నాయి. అవి :

1. జీవ అంశాలు (biotic)
2. నిర్జీవ అంశాలు (abiotic components)
3. ఈ రెండింటి పరస్పర ప్రభావాలు (their inetractions) పరస్పర ప్రభావాల ద్వారా వీటి మధ్య శక్తి (energy), పదార్థం (matter), సమాచారాలు (information)
   వాప్తి చెందుతుంటాయి.

ప్రశ్న 3.
వాయు కాలుష్యం.
జవాబు.
భూమి చుట్టూ ఉన్న వాతావరణంలోని అనేక వాయువులను అన్నింటిని ఉమ్మడిగా కలిపి వాయువు (గాలి) అని సామాన్య అర్థంగా చెబుతారు. గాలిలో ఇతర కాలుష్యకారక పదార్థాల గాఢత ఎక్కువైపోయి మానవుని శ్రేయస్సును, జీవకోటికి మరియు వివిధ రూపాలలోఉన్న ఆస్తులపై ప్రతికూల ప్రభావాన్ని చూపడాన్ని వాయు లేదా గాలి కాలుష్యం అంటారు.

ప్రశ్న 4.
జల కాలుష్యం.
జవాబు.
భూమి మీద ఉండే నీటిలో 97 శాతం వరకు సముద్రాల్లో ఉంటుంది. మిగతా 3 శాతం మాత్రమే స్వచ్ఛమైన నీరు. కొన్ని పదార్థాలుగాని, కారకాలు గాని నీటిలో ఎక్కువగా చేరిపోయి నీటి యొక్క స్వచ్ఛతను తగ్గించి వేసి, దానిని ఆరోగ్యానికి హానికరంగాను వాడుకోవడానికి పనికి రాకుండా మార్చివేస్తాయి. దానినే జలకాలుష్యం అంటారు.

ప్రశ్న 5.
భౌతిక కాలుష్యం.
జవాబు.
భౌతిక, రసాయన మరియు జీవ అంశాలు అయిన భూమి, వాతావరణం, వృక్షసంపద, వన్యమృగాలు, చుట్టుప్రక్కల ఉన్న భూమి మరియు దాని స్వభావం, అవస్థాపనా సౌకర్యాలు, గాలి మరియు శబ్ద కాలుష్య స్థాయి మొదలైన వాటిని కలిగి ఉంటుంది. వీటి నాణ్యత తగ్గడాన్ని భౌతిక కాలుష్యం అంటారు.

ప్రశ్న 6.
పర్యావరణ విచ్ఛేదన.
జవాబు.
పర్యావరణ విచ్ఛేదనం అంటే భూమిపై జరిగిన ఛిద్రత లేదా పర్యావరణంలోని సహజ వనరుల రూపంలో ఉన్న ఆస్తుల క్షీణత అనవచ్చు. ప్రకృతి ఉపరితలంలో రాకూడని మార్పులు లేదా తీవ్రతను పర్యావరణ విచ్ఛేదనంగా చెప్పవచ్చు.

భూమిపైగల సహజ వనరులు క్రమంగా క్షీణించి కొన్ని జీవరాశులు అంతరించి పోవడం పర్యావరణ విచ్ఛేదనను కలుగజేస్తుంది. వాయు కాలుష్యం, జల కాలుష్యం, భూమిపై పొరలలో ఉన్న సహజ శక్తుల క్షీణతవంటి సమస్యలు ఈ విచ్ఛేదనంవల్ల సృష్టించబడతాయి.

ప్రశ్న 7.
సుస్థిరమైన అభివృద్ధి.
జవాబు.
పర్యావరణ విధ్వంసం లేకుండా జరిగే ఆర్థికాభివృద్ధిని సుస్థిర అభివృద్ధి అంటారు. ఈ విధమైన అభివృద్ధి ప్రక్రియలో పర్యావరణం విలీనం చేయబడుతుంది. వర్తమానంలో అవసరాలను తీర్చుకొంటూ భావి తరాల అవసరాలు తీర్చుకోవడంలో రాజీలేని అభివృద్ధిని సుస్థిర అభివృద్ధి అంటారు.

ప్రశ్న 8.
పునరుద్ధరించగల, పునరుద్ధరించలేని సహజ వనరులు.
జవాబు.
తిరిగి సమకూర్చుకోగలిగిన లేదా సృష్టించుకోగలిగిన వనరులను పునరుద్ధరించగల సహజ వనరులు అని అంటారు. వీటినే ప్రవాహ వనరులు అని కూడా అంటారు.
ఉదా : నీరు, అడవులు, మత్స్య సంపద, సౌరశక్తి, తరంగ శక్తి.

పునరుద్ధరించలేని సహజ వనరులను అంతరించిపోయే స్వభావం గల వనరులు అని అంటారు. ఒక నిర్ణీత సమయంలో వీటి పరిమాణం స్థిరంగా ఉంటుంది.
ఉదా : బొగ్గు, ఖనిజాలు, పెట్రోలియం, గ్యాస్ నిల్వలు.

TS Inter 2nd Year Economics Study Material

Students must practice this TS Intermediate Maths 2A Solutions Chapter 2 De Moivre’s Theorem Ex 2(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 2 De Moivre’s Theorem Exercise 2(a)

I.
Question 1.
If n is an integer then show that (1 + i)²ⁿ + (1 – i)²ⁿ = 2^{n + 1} cos \(\frac{n \pi}{2}\)
Solution:
L.H.S = (1 + i)²ⁿ + (1 – i)²ⁿ

Question 2.
Find the values of the following:
i) (1 + √3)³
ii) (1 – i)⁸
iii) (1 + i)¹⁶
iv) \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5\)
Solution:
i) z = (1 + i√3)³
= (\(\left(\frac{1}{2}+\mathrm{i} \frac{\sqrt{3}}{2}\right)^3\))³ . 2³
= [cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\)]³ . 2³
=[cos \(\frac{\pi}{3}\) . 3 + i sin \(\frac{\pi}{3}\) . 3] . 2³
= 8 [cos π + i sin π]
∴ z = – 8.

ii) z = (1 – i)⁸
z = \(\left[(\sqrt{2})\left[\frac{1}{\sqrt{2}}-\frac{\mathrm{i}}{\sqrt{2}}\right]\right]^8\)
z = (2)⁴ [cos \(\frac{\pi}{2}\) – i sin \(\frac{\pi}{2}\)]⁸
z = 16 [cos 2π – i sin 2π]
z = 16.

iii) z = (1 + i)¹⁶
z = \(\left[(\sqrt{2})\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)\right]^{16}\)
z = 2⁸ [(cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))¹⁶]
z = 2⁸ [cos 4π + i sin 4π]
z = 256.

iv) \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5\)

II.
Question 1.
If α, β are roots of the equation x² – 2x + 4 = 0 then for any n ∈ N show that αⁿ + βⁿ = 2ⁿ⁺¹ cos \(\frac{n \pi}{3}\).
Solution:
x² – 2x + 4 = 0
x = \(\frac{2 \pm \sqrt{4-16}}{2}\)
x = \(\frac{2 \pm 2 \sqrt{3} i}{2}\)
x = 1 ± √3i
α = 1 + √3i ; β = 1 – √3i

Question 2.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ then show that
i) cos 3α + cos 3β + cos 3γ = 3cos (α + β + γ)
ii) sin 3α + sin 3β + sin 3γ = 3sin(α + β + γ)
iii) cos (α + β) + cos (β + γ) + cos (γ + α) = 0
Solution:
1) cos α + cos β + cos γ = 0
sin α + sin β + sin γ = 0
(cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ) = 0
A + B + C = 0
A³ + B³ + C³ = 3ABC
A = e^iα, B = e^iβ, C = e^iγ
A³ + B³ + C³ = e^3αi + e^3βi + e^3γi ……………(1)
= cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + isin 3γ …………..(1)
3ABC = 3e^{i(α + β + γ)}
= 3[cos (α + β + γ) + isin (α + β + γ)] …………..(2)
(1) = (2)
Comparing real and Imaginary parts
cos 3α + cos 3β . cos 3γ = 3 cos (α + β + γ)
sin3α. sin 3β + Sin 3γ = 3 sin (α + β + γ).

ii) cos (α + β) cos (β + γ) cos (γ + α) = 0
A + B + C = 0
\(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\) = 0
AB + BC + CA = 0
e^{i(α + β)} + e^{i(β + γ)} + e^{i(α + γ)} = o
cos (α + β) + i sin (α + β) + cos(β + γ) + isin(β + γ) + cos (α + γ) + isin (α + γ) = 0 + 0i
cos (α + β) cos (β + γ)) + cos (α + γ) = 0
sin (α + β) sin (β + γ)) + sin (α + γ) = 0.

Question 3.
If n is an integer and z = cis θ, (θ ≠ (2n + 1)\(\frac{\pi}{2}\)], then show that \(\frac{z^{2 n}-1}{z^{2 n}+1}\) = i tan nθ
Solution:
z = e^iθ
z²ⁿ = (e^iθ)²ⁿ
z²ⁿ = e^2nθi
z²ⁿ = cos 2nθ + isin2nθ – 1
z – 1 = cos 2nθ + isin 2nθ – 1
= – 2 sin²nθ + 2i sin nθ . cos nθ
= i 2 sin nθ [cos nθ + i sin nθ]
= 2i sin nθ [cos nθ + i sin nθ] …………..(1)
z²ⁿ + 1 = cos 2nθ + i sin 2nθ + 1
= 2 cos² nθ + 2 i sin nθ cos nθ
= 2 cos nθ [cos nθ + i sin bθ] ……………..(2)
\(\frac{z^{2 n}-1}{z^{2 n}+1}=\frac{2 i \sin n \theta}{2 \cos n \theta}\) = i tan nθ.

Question 4.
If (1 + x)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_nxⁿ, then show that
i) a₀ – a₂ + a₄ – a₆ + ………….. = 2^n/2 cos \(\frac{n \pi}{4}\)
ii) a₁ – a₃ + a₅ ……………. = 2^n/2 sin \(\frac{n \pi}{4}\)
Solution:
(1 + x)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_nxⁿ
(1 + i) = a₀ + a₁i + a₂i² + ………………… + a_niⁿ
(√2)ⁿ \(\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)\)ⁿ = (a₀ – a₂ + a₄ – ………….) + i(a₁ – a₃ …………………)
Equating Real parts both sides
(√2)ⁿ cos \(\frac{n \pi}{4}\) = a₀ – a₂ + a₄ ……………
Equating Imaginary parts
(√2)ⁿ sin \(\frac{n \pi}{4}\) = a₁ – a₃ + a₅ ………………

Students must practice this TS Intermediate Maths 2A Solutions Chapter 3 Quadratic Expressions Ex 3(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 3 Quadratic Expressions Exercise 3(c)

I.
Question 1.
Solve the following inequatlons by algebraic method.
i) 15x² – 4x – 4 ≤ 0
ii) x² – 2x + 1 < 0
iii) 2 – 3x – 2x² ≥ 0
iv) x² – 4x – 21 ≥ 0
Solution:
i) 15x² – 4x – 4 ≤ 0
15x² + 10x – 6x – 4 ≤ 0
5x (3x + 2) – 2 (3x + 2) ≤ 0
(3x + 2) (5x – 2) ≤ 0
\(\frac{-2}{3}\) ≤ x ≤ \(\frac{2}{5}\).

ii) x² – 2x + 1 < 0
(x- 1)² < 0
Not possible
∵ (x – 1)² ≥ 0
No solution.

iii) 2 – 3x – 2x² ≥ 0
2x² + 3x – 2 ≤ 0
2x² + 4x – x – 2 ≤ 0
2x (x + 2) – 1 (x + 2) ≤ 0
(2x – 1)(x + 2) ≤ 0
– 2 ≤ x ≤ \(\frac{1}{2}\)

iv) x² – 4x – 21 ≥ 0
x² – 7x + 3x – 21 ≥ 0
x (x – 7) + 3 (x – 7) ≥ 0
(x + 3) (x – 7) ≥ 0
x ≥ 7 or x ≤ – 3
(- ∞ < x ≤ – 3) ∪ (7 ≤ x < ∞).

II.
Question 1.
Solve the following inequations by graphical method.
i) x² – 7x + 6 > 0
ii) 4 – x² > o
iii) 15x² + 4x – 4 ≤ 0
iv) x² – 4x – 21 ≥ 0
Solution:
i) (x – 6) (x – 1) > 0

ii) 4 – x² > 0
x² – 4 > 0
(x – 2) (x + 2) > 0
– 2 < x < 2

iii) 15x² + 4x – 4 ≤ 0
15x² + 10x – 6x – 4 ≤ 0
5x (3x + 2) – 2 (3x + 2) ≤ 0
\(\frac{-2}{3} \leq x \leq \frac{2}{5}\)

iv) x² – 4x – 21 ≥ 0
(x – 7) (x + 3) ≥ 0
x ≥ 7 or x ≤ – 3

Question 2.
Solve the following Inequations.
i) \(\sqrt{3 x-8}\) < – 2
ii) \(\sqrt{-x^2+6 x-5}\) > 8 – 2x
Solution:
\(\sqrt{3 x-8}\) < – 2 Possible when 3x – 8 > 0
x > \(\frac{8}{3}\)
also \(\sqrt{3 x-8}\) ≥ 0
∴ Solution does not exist.

ii) \(\sqrt{-x^2+6 x-5}\) > 8 – 2x
Possible
– x² + 6x – 5 ≥ 0
x² – 6x + 5 ≤ 0
(x – 5) (x – 1) ≤ 0
1 ≤ x ≤ 5 …………….(1)
Squaring on both sides we get
– x² + 6x – 5 > 64 + 4x² – 32x
0 > 5x² – 38x + 64 + 5
or 5x² – 38x + 69 < 0
5x² – 23x – 15x + 69 < 0
5x (x – 3) – 23(x – 3)< 0
(x – 3) (5x – 23) < 0

Students must practice this TS Intermediate Maths 2A Solutions Chapter 1 Functions Ex 1(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 1 Complex Numbers Exercise 1(d)

I.
Question 1.
i) Find the equation of the perpendicular bisector of the line segment joining the points 7 + 7i, 7 – 7i.
ii) Find the equation of the straight line joining the points – 9 + 6i, 11 – 4i in the Argand plane.
Solution:
i) z₁ = 7 + 7i
z₂ = 7 – 71
A (7, 7) B (7, – 7)

M(7, 0)

Slope of AB = \(\frac{7+7}{7-7}\) → ∞
Line ⊥ to AB slope is zero,
y = 0 is line.

ii) A (- 9, 6) B (11, – 4)
Slope of AB = \(\frac{6+4}{-9-11}\)
= \(\frac{10}{-20}=\frac{-1}{2}\)
Equation of line AB,
y – 6 = \(\frac{- 1}{2}\) (x + 9)
2y – 12 = – x – 9
x + 2y = 3.

Question 2.
If z = x + ily and if the point Pin the Argand plane represents z, then describe geometrically the locus of z satisfying the equations
i) |z – 2 – 3i| = 5
ii) 2|z – 2| = |z – 1|
iii) im z² = 4
iv) Arg \(\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
Solution:
i) |z – 2 – 3i| = 5
|(x – 2) + (y – 3)i| = 5
(x – 2)² + (y – 3)² = 25
x² + y² – 4x – 6y + 4 + 9 – 25 = 0
x² + y² – 4x – 6y – 12 = 0

ii) 2|z – 2| = |z – 1|
4(z – 2) (- 2) = (z – 1) (\(\overline{\mathbf{z}}\) – 1)
4z\(\overline{\mathbf{z}}\) – 8z – 8\(\overline{\mathbf{z}}\) + 16 = z\(\overline{\mathbf{z}}\) – z – \(\overline{\mathbf{z}}\) + 1
3z\(\overline{\mathbf{z}}\) – 7z – 7\(\overline{\mathbf{z}}\) + 15 = 0
3(x² + y²) – 7(2x) + 15 = 0.

iii) Im (z²) = 4
Im (z²) = 4
z = x + iy
z² = (x + iy)²
z² = x² – y² + 2xyi
Im(z²) = 2xy
2xy = 4
xy = 2 rectangualr hyperbola

iv) Arg \(\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)

Question 3.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i, – 2 – 2i, – 2√3 + 2√3i are the vertices of an equilateral triangle..
Solution:
A(2, 2), B(- 2, – 2), C (- 2√3 + 2√3)
AB = \(\sqrt{(2+2)^2+(2+2)^2}\) = 4√2
BC = \(\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2}\)
BC = \(\sqrt{4+12-8 \sqrt{3}+4+12+8 \sqrt{3}}\)= 4√2
AC = \(\sqrt{\left(2+2 \sqrt{3}^2\right)+(2-2 \sqrt{3})^2}\) = 4√2
AB = AC = BC
∆ ABC is equilateral.

Question 4.
Find the eccentricity of the ellipse whose equtaion is | z – 4 | + |z – \(\frac{12}{5}\)| = 10
Solution:
SP + S’P = 2a
S (4, 0) S’(\(\frac{12}{5}\), 0)
2a = 10
a = 5
SS’ = 2ae
4 – \(\frac{12}{5}\) = 2 × 5e
\(\frac{8}{5}\) = 10e
e = \(\frac{4}{25}\).

II.
Question 1.
If \(\frac{z_3-z_1}{z_2-z_1}\) is a real number, show that the points represented by the complex numbers z₁, z₂, z₃ are collinear.
Solution:

Arg \(\left(\frac{z_1-z_3}{z_1-z_2}\right)\) = 0 then \(\frac{z_1-z_3}{z_1-z_2}\) is real θ = 0.
∴ z₁, z₂, z₃ are collinear.

Question 2.
Show that the four points in the Argand plane represented by the complex numbers 2 + i, 4 + 3i, 2 + 5i, 3i are vertices of a square.
Solution:
A (2, 1), B (4, 3), C (2, 5), D (0, 3)
AB = \(\sqrt{(4-2)^2+(3-1)^2}\) = 2√2
BC = \(\sqrt{(4-2)^2+(3-5)^2}\) = 2√2
CD = \(\sqrt{(2-0)^2+(5-3)^2}\) = 2√2
AD = \(\sqrt{(2-0)^2+(1-3)^2}\) = 2√2
Slope of AB = \(\frac{5-3}{2-4}\)= 1
Slope of BC = \(\frac{3-1}{4-2}\) = 1
AB ⊥ BC
BC ⊥ CD
⇒ ABCD is a square.

Question 3.
Show that die points in the Argand plane represented by the complex numbers – 2 + 7i, – \(\frac{-3}{2}\) + \(\frac{1}{2}\)i, 4 – 3i, \(\frac{7}{2}\) (1 + i) are the vertices of a rhombus.
Solution:

AC ⊥ BD
∴ ABCD is rhombus.

Question 4.
Show that the points in the Argand diagram represented by the complex numbers z₁, z₂, z₃ are collhitear if and only if there exists three real numbers p, q, r not all zero satisfying p + qz₂ + rz₃ = 0 and p + q + r = 0.
Solution:
pz₁ + qz₂ + rz₃ = 0
pz₁ + qz₂ = – rz₃
\(\left(\frac{p z_1+q z_2}{p+q}\right)\) (p + q) = – rz₃
Now p + q = – r
\(\left(\frac{p z_1+q z_2}{p+q}\right)\) = z₃
⇒ z₃ divides z₁ and z₂ is q : p ratio.
∴ z₁, z₂, z₃ are collinear.

Question 5.
The points P, Q denote the complex numbers z₁, z₂ in the Argand diagram. O is
origin. If z₁\(\overline{\mathbf{z}}_2\) + \(\overline{\mathbf{z}}_1\)z₂ = 0 tlien show that ∠POQ = 90°.
Solution:
z₁\(\overline{\mathbf{z}}_2\) + \(\overline{\mathbf{z}}_1\)z₂ = 0
\(\frac{\mathbf{z}_1 \overline{\mathbf{z}}_2+\overline{\mathbf{z}}_1 \mathbf{z}_2}{\mathbf{z}_2 \overline{\mathrm{z}}_2}\) = 0
⇒ Real of \(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = 0
\(\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}+\frac{\overline{\mathrm{z}}_1}{\mathrm{z}_2}\right)\)
Imaginary part of (\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\)) is k.
\(\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}\right)+\left(\frac{\overline{\mathrm{z}}_1}{\mathrm{z}_2}\right)\) = 0 or
\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) is purely imaginary.
\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = ki
⇒ Arg\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = \(\frac{\pi}{2}\).

Question 6.
The complex number z has argument θ 0 < θ < \(\frac{\pi}{2}\) and satisfy the equation |z – 3i| = 3. Then prove that (cot θ – \(\frac{6}{z}\)) = 1.
Solution:
(x²) + (y – 3)² = 9
x + y = 0
x + y = 6y