TS Inter 2nd Year Maths 2A Solutions Chapter 1 Complex Numbers Ex 1(b)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 1 Complex Numbers Ex 1(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 1 Complex Numbers Exercise 1(b)

I.
Question 1.
Write the following complex numbers in the form A + iB.
i) (2 – 3i) (2 + 3i)
ii) (1 + 2i)³
iii) \(\frac{a-i b}{a+i b}\)
iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)
v) (- √3 + √-2) (2√3 – i)
vi) (- 5i) \(\frac{i}{8}\)
vii) (- i) (2i)
viii) i⁹
ix) i^-19
x) 3 (7 + 7i) + i (7 + 7i)
xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)
Solution:
i) z = (2 – 3i) (3 + 4i)
z = 6 + 8i – 9i + 12
z = 18 – i
= 18 + (- 1)i

ii) z = (1 + 2i)³
= 1³ + (2i)³ + 3 . 2i(1 + 2i)
= 1 – 8i + 6i (1 + 2i)
= (1 – 12) – 2i
= – 11 – 2i
= (- 11, – 2)

iii) z = \(\frac{a-i b}{a+i b}\)
z = \(\frac{(a-i b)(a-i b)}{(a+i b)(a-i b)}\)
= \(\frac{a^2-b^2-2 a b i}{a^2+b^2}\)
= \(\left(\frac{a^2-b^2}{a^2+b^2}, \frac{-2 a b}{a^2+b^2}\right)\)

iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)

v) (- √3 + √-2) (2√3 – i)
z = (- √3 + √2i) (2√3 – i)
= – 2 . 3 + √3i + 2√6i + √2
= (√2 – 6) + i (√3 + 2√6).

vi) z = (- 5i) (\(\frac{i}{8}\))
z = \(\) i²
z = \(\frac{5}{8}\) + 0i

vii) (- i) (2i)
z = (- i) (2i)
= 2 + 0i

viii) z = i⁹
z = (i²)⁴ . i
z = i = 0 + i . 1

ix) z = i^-19
z = \(\frac{1}{\left(\mathrm{i}^2\right)^9} \cdot \frac{1}{\mathrm{i}}\)
= \(\frac{-1}{i}=\frac{-1}{1^2}\)
z = i = 0 + 1 . i

x) z = 3 (7 + 7i) + i (7 + 7i)
= 21 + 21i + 7i + 7i²
= 21 – 7 + 28i
z = 14 + 28i

xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)

Question 2.
Write the conjugate of the following complex numbers.
i) (3 + 4i)
ii) (15 + 3i) – (4 – 20i)
iii) (2 + 5i) (- 4 + 6i)
iv) \(\frac{5 \mathbf{i}}{7+1}\)
Solution:
i) z = 3 + 4i
\(\overline{\mathbf{z}}\) = 3 – 4i

ii) z = (15 + 31) – (4 – 201)
z = 11 + 23i
z = 11 – 23i

iii) z = (2 + 5i) (- 4 + 6i)
z = – 8 + 12i – 20i + 30i2
z = – 38 – 8i
z = – 38 + 8i

iv) \(\frac{5 \mathbf{i}}{7+1}\)

Question 3.
Simplify
i) i² + i⁴ + i⁶ + ………… + (2n + 1) terms
ii) i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (- i)²⁶
Solution:
i) i² + i⁴ + i⁶ + …………… (2n + 1) terms
= i² + i⁴ + i⁶ + ……………. +
= -1 + 1+(-1) + 2n terms + i2
= 0 – 1 = – 1

ii) i¹⁸ – 3i⁷ + i² (1 + i⁴) (- i)²⁶
(i²)⁹ – 3i⁶i + i² (1 + i⁴) (i)²⁶ = – 1 + 3i + (- 1) (1 + 1) (- 1)¹³
= 3i – 1 + 2 = 3i + 1.

Question 4.
Find a square root for the following complex numbers.
i) 7 + 24i
ii) – 8 – 6i
iii) 3 + 4i
iv) – 47 + i 8√3
Solution:
i) z = 7 + 24i
Let square root of z be a + ib
a + ib = \(|\sqrt{7+24i}|\)
(a + ib)² = 7 + 24i
a² – b² + 2abi = 7 + 24i
a² – b² = 7, 2ab = 24 ……………..(1)
| a + ib | = \(|\sqrt{7+24i}|\)
Squaring on both sides,
| a + ib |2 = | 7 + 24i|
a² + b² = \(\sqrt{49+576}\)
a² + b² = \(\sqrt{625}\)

a² = 16
a = ± 4
2b² = 25 – 7
b² = 9
b = ± 3
a + ib = ± (4 + 3i)

ii) z = – 8 – 6i
Let square root of z be a + ib
a + ib = \(\sqrt{-8-6 \mathrm{i}}\)
Squaring on both sides,
(a + ib)² = – 8 – 61
a² – b² + 2abi = – 8 – 6i
a² – b² = – 8, 2ab = – 6 …………..(i)
| a + ib | = \(|\sqrt{-8-6 \mathbf{i}}|\)
Squaring on both sides,
| a + ib |² = \(|\sqrt{-8-6 \mathrm{i}}|^2\)
a² + b² = \(\sqrt{64+36}\)
a² + b² = 10 ………….(ii)
(i) + (ii)
2a² = 2
a² = 1 or a = ± 1
(ii) – (i)
2b² = 18
b² = 9
⇒ b = ± 3
a + ib = ± (1 – 3i).

iii) z = 3 + 4i
Let square root of z be a + ib
a + ib = \(\sqrt{3+4i}\)
Squaring on both sides,
(a + ib)² = 3 + 4i
a² – b² + 2abi = 3 + 4i
a² – b² = 3; 2ab = 4 …………..(i)
| a + ib | = \(|\sqrt{3+4 \mathrm{i}}|\)
Squaring on both sides,
| a + ib |² = | 3 + 4i |
a² + b² = \(\sqrt{9+16}\) …………..(ii)
a² – b² = 3

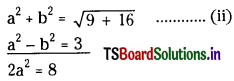
2a² = 8
a² = 4
⇒ a = ± 2
2b² = 2
⇒ b = ± 1
a + ib = ± (2 + i).

iv) z = – 47 + i 8√3
Let the square root of z be a + ib
(a + ib)² = – 47 + i 8√3
a² – b² = – 47, 2ab = 8√3
| a + ib | = \(|\sqrt{-47+i 8 \sqrt{3}}|\)
Squaring on bothsides,
a² + b² = \(\sqrt{(-47)^2+(8 \sqrt{3})^2}\)
= \(\sqrt{2209+192}=\sqrt{2401}\)

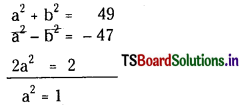
a² + b² = 49
a² – b² = – 47
2a² = 2
a² = 1
a = ± 1
2b² = 96
b² = 48
b = ± 4√3
a + ib = ± (1 + 4√3i).

Question 5.
Find the multiplicative inverse of the following complex numbers.
i) √5 + 3i
ii) – i
iii) i^-35
Solution:
i) z = √5 + 3i
Let a + ib be multiplicative inverse then (a + ib) . z = 1
z = \(\frac{1}{a+i b}\)
or a + ib = \(\frac{1}{\mathrm{z}}\)
a + ib = \(\frac{\overline{\mathbf{z}}}{(\mathrm{z} \overline{\mathrm{z}})}\)
a + ib = \(\frac{\bar{z}}{|z|^2}=\frac{\sqrt{5}-3 i}{5+9}\)
= \(\frac{1}{14}\) (√5 – 3i).

ii) z = – i
Let a + ib be multiplicative inverse then (a + ib) z = 1
a + ib = \(\frac{1}{\mathrm{z}}\)
= \(\frac{1}{-i}\)
= \(\frac{i}{-i \cdot i}\)
a + ib = i.

iii) z = i^-35
Let a + ib be multiplicative inverse then (a + ib) z = 1
a + ib = \(\frac{1}{\mathrm{z}}\)
= \(\frac{1}{i^{-35}}\) = i³⁵
(a + ib) = i³⁵
= (i²)¹⁷ i = – i.

II.
Question 1.
i) If (a + ib)² = x + iy, find x² + y².
ii) lf x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) then, show that x² + y² = 4x – 3.
iii) If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\) then, show that 4x² – 1 = 0.
iv)If u + iv = \(\frac{2+i}{z+3}\) and z = x + iy find u, v.
Solution:
i) (a + ib) = x + iy
a² – b² + 2abi = x + iy ,
a² – b² = x
2ab = y
Now x2 = (a² – b²)²
y² = 4a²b²
x² + y² = (a² – b²)² . 4a²b² = (a² + b²)²

ii) x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\)

iii) x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\)
x + iy = \(\frac{1+\cos \theta-i \sin \theta}{(1+\cos \theta)^2+\sin ^2 \theta}\)
x = \(\frac{1+\cos \theta}{2+2 \cos \theta}=\frac{(1+\cos \theta)}{2(1+\cos \theta)}\)
x = \(\frac{1}{2}\)
2x = 1
4x² = 1
4x² – 1 = 0.

iv) u + iv = \(\frac{2+i}{z+3}\)

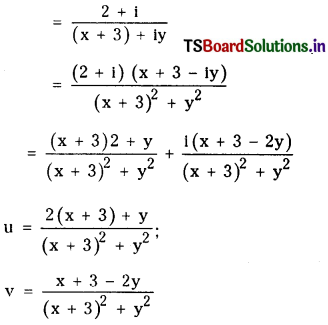
Question 2.
i) If z = 3 + 5i then show that z³ – 10z² + 58z – 136 = 0
ii) If z = 2 – i√7 then show that 3z³ – 4z² + z + 88 = 0
iii) Show that \(\frac{2-i}{(1-2 i)^2}\) and \(\frac{-2-11 i}{25}\) are conjugate to each other.
Solution:
i) z = 3 + 5i
(z – 3)² = (5i)²
z² – 6z + 9 = 25i2
z² – 6z + 9 = – 25
z² – 6z + 34 = 0
z³ – 6z² + 34z = 0
(z³ – 10z² + 58z – 136) + 4z² – 24z + 136 = 0
(z³ – 10z² + 58z – 136) + 4 (z² – 6z + 34) = 0
(z³ – 10z² + 58z – 136) = 0

il) z = 2 – i√7
(z – 2)² = (- i – √7)²
z² – 4z + 4 = – 7
z² – 4z + 11 = 0
z³ – 4z² + 11z = 0
3z³ – 12z² + 33z = 0
(3z³ – 4z² + z + 88) + (- 8z² + 32z – 88) = 0
(3z³ – 4z² + z + 88) – 8 (z² – 4z + 11) = 0
3z³ – 4z² + z + 88 = 0.

iii) z = \(\frac{2-i}{(1-2 i)^2}\) (If z = a + ib, \(\overline{\mathbf{Z}}\) = a – ib)

Question 3.
i) If (x – iy)^1/3 = a – ib then show that \(\frac{x}{a}+\frac{y}{b}\) = 4(a² – b²)
ii) Write \(\left(\frac{a+i b}{a-i b}\right)^2-\left(\frac{a-i b}{a+i b}\right)^2\) in the form x + iy.
iii) If x and y are real numbers such that \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-i}\) determine the values of x and y.
Solution:
(x – iy)^1/3 = (a – ib)
x – iy = (a – ib)³
x – iy = a³ + ib³
x = a³ – 3ab²
– iy = ib³ – 3a²bi
\(\frac{x}{a}\) = a² – 3b²
y = b³ – 3a²b
\(\frac{x}{a}\) = a² – 3b²
\(\frac{y}{b}\) = b² – 3a²
\(\frac{x}{a}-\frac{y}{b}\) = 4(a² – b²).

ii) \(\left(\frac{a+i b}{a-i b}\right)^2-\left(\frac{a-i b}{a+i b}\right)^2\)

iii) \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-i}\)

4x + 9y – 3 = 0
2x – 7y – 3 = 10
Solving, we get
x = 3, y = – 1.

Question 4.
i) Find the least positive integer n, satisfying \(\left(\frac{1+1}{1-1}\right)^n\) = 1.
ii) If \(\left(\frac{1+i}{1-i}\right)^3-\left(\frac{1-i}{1+i}\right)^3\) = x + iy find x and y.
iii) Find the real values of θ in order that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is a
a) real number
b) purely imaginary number
iv) Find the real values of x and y if \(\frac{x-1}{3+i}+\frac{y-1}{3-i}\) = i.
Solution:
i) \(\left(\frac{1+i}{1-i}\right)^n\) = 1
\(\left(\frac{(1+i)(1+i)}{(1-i)(1+i)}\right)^n\) = 1
\(\left(\frac{2 \mathrm{i}}{2}\right)^{\mathrm{n}}\) = 1
iⁿ = 1
(∵ iⁿ = 1 = – 1 × – 1 = i² × i² = i⁴)
n = 4
i⁴ = 1
Least value of n = 4.

ii) \(\left(\frac{1+i}{1-i}\right)^3-\left(\frac{i-i}{1+i}\right)^3\) = x + iy
\(\left(\frac{(1+i)(1+i)}{(1+i)(1-i)}\right)^3-\left(\frac{(1-i)(1-i)}{(1+i)(1-i)}\right)^3\) = x + iy
\(\left(\frac{2 \mathrm{i}}{2}\right)^3-\left(\frac{-2 \mathrm{i}}{2}\right)^3\)
– i – i = x + iy
x = 0
y = – 2.

iii) z = \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\)
z = \(\frac{(3+2 i \sin \theta)(1+2 i \sin \theta)}{(1-2 i \sin \theta)(1+2 i \sin \theta)}\)
z = \(\frac{3-4 \sin ^2 \theta+8 i \sin \theta}{1+4 \sin ^2 \theta}\)
z is purely real ⇒ imaginary part = 0
\(\frac{8 \sin \theta}{1+4 \sin ^2 \theta}\) = 0
sin θ = 0
θ = nπ, n ∈ 1
z is purely imaginary ⇒ Real part zero
\(\frac{3-4 \sin ^2 \theta}{1+4 \sin ^2 \theta}\) = 0
sin θ = \(\frac{3}{4}\)
sin θ = \(\pm \frac{\sqrt{3}}{2}\)
sin θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ 1.

iv) \(\frac{x-1}{3+i}+\frac{y-1}{3-1}\) = 1
\(\frac{(x-1)(3-i)}{9+1}+\frac{(y-1)(3+i)}{9+1}\) = 1
\(\frac{3(x-1)+3(y-1)}{10}+\frac{i(1-x+y-1)}{10}\) = 1
3x + 3y – 6 = 0
y – x = 10
Solving we get
x = – 4, y = 6.