TS Inter 2nd Year Maths 2A Solutions Chapter 2 De Moivre’s Theorem Exercise 2(a)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 2 De Moivre’s Theorem Ex 2(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 2 De Moivre’s Theorem Exercise 2(a)

I.
Question 1.
If n is an integer then show that (1 + i)²ⁿ + (1 – i)²ⁿ = 2^{n + 1} cos \(\frac{n \pi}{2}\)
Solution:
L.H.S = (1 + i)²ⁿ + (1 – i)²ⁿ

Question 2.
Find the values of the following:
i) (1 + √3)³
ii) (1 – i)⁸
iii) (1 + i)¹⁶
iv) \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5\)
Solution:
i) z = (1 + i√3)³
= (\(\left(\frac{1}{2}+\mathrm{i} \frac{\sqrt{3}}{2}\right)^3\))³ . 2³
= [cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\)]³ . 2³
=[cos \(\frac{\pi}{3}\) . 3 + i sin \(\frac{\pi}{3}\) . 3] . 2³
= 8 [cos π + i sin π]
∴ z = – 8.

ii) z = (1 – i)⁸
z = \(\left[(\sqrt{2})\left[\frac{1}{\sqrt{2}}-\frac{\mathrm{i}}{\sqrt{2}}\right]\right]^8\)
z = (2)⁴ [cos \(\frac{\pi}{2}\) – i sin \(\frac{\pi}{2}\)]⁸
z = 16 [cos 2π – i sin 2π]
z = 16.

iii) z = (1 + i)¹⁶
z = \(\left[(\sqrt{2})\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)\right]^{16}\)
z = 2⁸ [(cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))¹⁶]
z = 2⁸ [cos 4π + i sin 4π]
z = 256.

iv) \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5\)

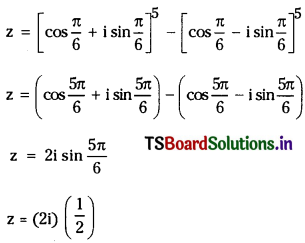
II.
Question 1.
If α, β are roots of the equation x² – 2x + 4 = 0 then for any n ∈ N show that αⁿ + βⁿ = 2ⁿ⁺¹ cos \(\frac{n \pi}{3}\).
Solution:
x² – 2x + 4 = 0
x = \(\frac{2 \pm \sqrt{4-16}}{2}\)
x = \(\frac{2 \pm 2 \sqrt{3} i}{2}\)
x = 1 ± √3i
α = 1 + √3i ; β = 1 – √3i

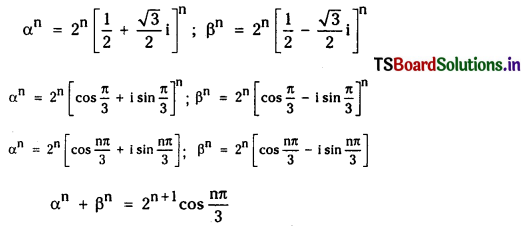
Question 2.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ then show that
i) cos 3α + cos 3β + cos 3γ = 3cos (α + β + γ)
ii) sin 3α + sin 3β + sin 3γ = 3sin(α + β + γ)
iii) cos (α + β) + cos (β + γ) + cos (γ + α) = 0
Solution:
1) cos α + cos β + cos γ = 0
sin α + sin β + sin γ = 0
(cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ) = 0
A + B + C = 0
A³ + B³ + C³ = 3ABC
A = e^iα, B = e^iβ, C = e^iγ
A³ + B³ + C³ = e^3αi + e^3βi + e^3γi ……………(1)
= cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + isin 3γ …………..(1)
3ABC = 3e^{i(α + β + γ)}
= 3[cos (α + β + γ) + isin (α + β + γ)] …………..(2)
(1) = (2)
Comparing real and Imaginary parts
cos 3α + cos 3β . cos 3γ = 3 cos (α + β + γ)
sin3α. sin 3β + Sin 3γ = 3 sin (α + β + γ).

ii) cos (α + β) cos (β + γ) cos (γ + α) = 0
A + B + C = 0
\(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\) = 0
AB + BC + CA = 0
e^{i(α + β)} + e^{i(β + γ)} + e^{i(α + γ)} = o
cos (α + β) + i sin (α + β) + cos(β + γ) + isin(β + γ) + cos (α + γ) + isin (α + γ) = 0 + 0i
cos (α + β) cos (β + γ)) + cos (α + γ) = 0
sin (α + β) sin (β + γ)) + sin (α + γ) = 0.

Question 3.
If n is an integer and z = cis θ, (θ ≠ (2n + 1)\(\frac{\pi}{2}\)], then show that \(\frac{z^{2 n}-1}{z^{2 n}+1}\) = i tan nθ
Solution:
z = e^iθ
z²ⁿ = (e^iθ)²ⁿ
z²ⁿ = e^2nθi
z²ⁿ = cos 2nθ + isin2nθ – 1
z – 1 = cos 2nθ + isin 2nθ – 1
= – 2 sin²nθ + 2i sin nθ . cos nθ
= i 2 sin nθ [cos nθ + i sin nθ]
= 2i sin nθ [cos nθ + i sin nθ] …………..(1)
z²ⁿ + 1 = cos 2nθ + i sin 2nθ + 1
= 2 cos² nθ + 2 i sin nθ cos nθ
= 2 cos nθ [cos nθ + i sin bθ] ……………..(2)
\(\frac{z^{2 n}-1}{z^{2 n}+1}=\frac{2 i \sin n \theta}{2 \cos n \theta}\) = i tan nθ.

Question 4.
If (1 + x)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_nxⁿ, then show that
i) a₀ – a₂ + a₄ – a₆ + ………….. = 2^n/2 cos \(\frac{n \pi}{4}\)
ii) a₁ – a₃ + a₅ ……………. = 2^n/2 sin \(\frac{n \pi}{4}\)
Solution:
(1 + x)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_nxⁿ
(1 + i) = a₀ + a₁i + a₂i² + ………………… + a_niⁿ
(√2)ⁿ \(\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)\)ⁿ = (a₀ – a₂ + a₄ – ………….) + i(a₁ – a₃ …………………)
Equating Real parts both sides
(√2)ⁿ cos \(\frac{n \pi}{4}\) = a₀ – a₂ + a₄ ……………
Equating Imaginary parts
(√2)ⁿ sin \(\frac{n \pi}{4}\) = a₁ – a₃ + a₅ ………………