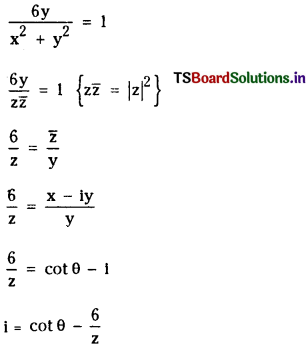TS Inter 2nd Year Maths 2A Solutions Chapter 1 Complex Numbers Ex 1(d)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 1 Functions Ex 1(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 1 Complex Numbers Exercise 1(d)

I.
Question 1.
i) Find the equation of the perpendicular bisector of the line segment joining the points 7 + 7i, 7 – 7i.
ii) Find the equation of the straight line joining the points – 9 + 6i, 11 – 4i in the Argand plane.
Solution:
i) z₁ = 7 + 7i
z₂ = 7 – 71
A (7, 7) B (7, – 7)

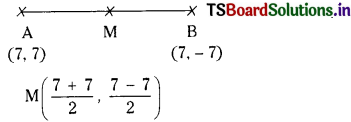
M(7, 0)

Slope of AB = \(\frac{7+7}{7-7}\) → ∞
Line ⊥ to AB slope is zero,
y = 0 is line.

ii) A (- 9, 6) B (11, – 4)
Slope of AB = \(\frac{6+4}{-9-11}\)
= \(\frac{10}{-20}=\frac{-1}{2}\)
Equation of line AB,
y – 6 = \(\frac{- 1}{2}\) (x + 9)
2y – 12 = – x – 9
x + 2y = 3.

Question 2.
If z = x + ily and if the point Pin the Argand plane represents z, then describe geometrically the locus of z satisfying the equations
i) |z – 2 – 3i| = 5
ii) 2|z – 2| = |z – 1|
iii) im z² = 4
iv) Arg \(\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
Solution:
i) |z – 2 – 3i| = 5
|(x – 2) + (y – 3)i| = 5
(x – 2)² + (y – 3)² = 25
x² + y² – 4x – 6y + 4 + 9 – 25 = 0
x² + y² – 4x – 6y – 12 = 0

ii) 2|z – 2| = |z – 1|
4(z – 2) (- 2) = (z – 1) (\(\overline{\mathbf{z}}\) – 1)
4z\(\overline{\mathbf{z}}\) – 8z – 8\(\overline{\mathbf{z}}\) + 16 = z\(\overline{\mathbf{z}}\) – z – \(\overline{\mathbf{z}}\) + 1
3z\(\overline{\mathbf{z}}\) – 7z – 7\(\overline{\mathbf{z}}\) + 15 = 0
3(x² + y²) – 7(2x) + 15 = 0.

iii) Im (z²) = 4
Im (z²) = 4
z = x + iy
z² = (x + iy)²
z² = x² – y² + 2xyi
Im(z²) = 2xy
2xy = 4
xy = 2 rectangualr hyperbola

iv) Arg \(\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)

Question 3.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i, – 2 – 2i, – 2√3 + 2√3i are the vertices of an equilateral triangle..
Solution:
A(2, 2), B(- 2, – 2), C (- 2√3 + 2√3)
AB = \(\sqrt{(2+2)^2+(2+2)^2}\) = 4√2
BC = \(\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2}\)
BC = \(\sqrt{4+12-8 \sqrt{3}+4+12+8 \sqrt{3}}\)= 4√2
AC = \(\sqrt{\left(2+2 \sqrt{3}^2\right)+(2-2 \sqrt{3})^2}\) = 4√2
AB = AC = BC
∆ ABC is equilateral.

Question 4.
Find the eccentricity of the ellipse whose equtaion is | z – 4 | + |z – \(\frac{12}{5}\)| = 10
Solution:
SP + S’P = 2a
S (4, 0) S’(\(\frac{12}{5}\), 0)
2a = 10
a = 5
SS’ = 2ae
4 – \(\frac{12}{5}\) = 2 × 5e
\(\frac{8}{5}\) = 10e
e = \(\frac{4}{25}\).

II.
Question 1.
If \(\frac{z_3-z_1}{z_2-z_1}\) is a real number, show that the points represented by the complex numbers z₁, z₂, z₃ are collinear.
Solution:

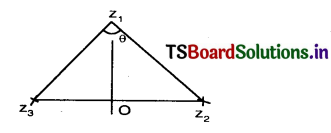
Arg \(\left(\frac{z_1-z_3}{z_1-z_2}\right)\) = 0 then \(\frac{z_1-z_3}{z_1-z_2}\) is real θ = 0.
∴ z₁, z₂, z₃ are collinear.

Question 2.
Show that the four points in the Argand plane represented by the complex numbers 2 + i, 4 + 3i, 2 + 5i, 3i are vertices of a square.
Solution:
A (2, 1), B (4, 3), C (2, 5), D (0, 3)
AB = \(\sqrt{(4-2)^2+(3-1)^2}\) = 2√2
BC = \(\sqrt{(4-2)^2+(3-5)^2}\) = 2√2
CD = \(\sqrt{(2-0)^2+(5-3)^2}\) = 2√2
AD = \(\sqrt{(2-0)^2+(1-3)^2}\) = 2√2
Slope of AB = \(\frac{5-3}{2-4}\)= 1
Slope of BC = \(\frac{3-1}{4-2}\) = 1
AB ⊥ BC
BC ⊥ CD
⇒ ABCD is a square.

Question 3.
Show that die points in the Argand plane represented by the complex numbers – 2 + 7i, – \(\frac{-3}{2}\) + \(\frac{1}{2}\)i, 4 – 3i, \(\frac{7}{2}\) (1 + i) are the vertices of a rhombus.
Solution:

AC ⊥ BD
∴ ABCD is rhombus.

Question 4.
Show that the points in the Argand diagram represented by the complex numbers z₁, z₂, z₃ are collhitear if and only if there exists three real numbers p, q, r not all zero satisfying p + qz₂ + rz₃ = 0 and p + q + r = 0.
Solution:
pz₁ + qz₂ + rz₃ = 0
pz₁ + qz₂ = – rz₃
\(\left(\frac{p z_1+q z_2}{p+q}\right)\) (p + q) = – rz₃
Now p + q = – r
\(\left(\frac{p z_1+q z_2}{p+q}\right)\) = z₃
⇒ z₃ divides z₁ and z₂ is q : p ratio.
∴ z₁, z₂, z₃ are collinear.

Question 5.
The points P, Q denote the complex numbers z₁, z₂ in the Argand diagram. O is
origin. If z₁\(\overline{\mathbf{z}}_2\) + \(\overline{\mathbf{z}}_1\)z₂ = 0 tlien show that ∠POQ = 90°.
Solution:
z₁\(\overline{\mathbf{z}}_2\) + \(\overline{\mathbf{z}}_1\)z₂ = 0
\(\frac{\mathbf{z}_1 \overline{\mathbf{z}}_2+\overline{\mathbf{z}}_1 \mathbf{z}_2}{\mathbf{z}_2 \overline{\mathrm{z}}_2}\) = 0
⇒ Real of \(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = 0
\(\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}+\frac{\overline{\mathrm{z}}_1}{\mathrm{z}_2}\right)\)
Imaginary part of (\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\)) is k.
\(\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}\right)+\left(\frac{\overline{\mathrm{z}}_1}{\mathrm{z}_2}\right)\) = 0 or
\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) is purely imaginary.
\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = ki
⇒ Arg\(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = \(\frac{\pi}{2}\).

Question 6.
The complex number z has argument θ 0 < θ < \(\frac{\pi}{2}\) and satisfy the equation |z – 3i| = 3. Then prove that (cot θ – \(\frac{6}{z}\)) = 1.
Solution:
(x²) + (y – 3)² = 9
x + y = 0
x + y = 6y