Students must practice this TS Intermediate Maths 2A Solutions Chapter 3 Quadratic Expressions Ex 3(c) to find a better approach to solving the problems.
TS Inter 2nd Year Maths 2A Solutions Chapter 3 Quadratic Expressions Exercise 3(c)
I.
Question 1.
Solve the following inequatlons by algebraic method.
i) 15x2 – 4x – 4 ≤ 0
ii) x2 – 2x + 1 < 0
iii) 2 – 3x – 2x2 ≥ 0
iv) x2 – 4x – 21 ≥ 0
Solution:
i) 15x2 – 4x – 4 ≤ 0
15x2 + 10x – 6x – 4 ≤ 0
5x (3x + 2) – 2 (3x + 2) ≤ 0
(3x + 2) (5x – 2) ≤ 0
\(\frac{-2}{3}\) ≤ x ≤ \(\frac{2}{5}\).
ii) x2 – 2x + 1 < 0
(x- 1)2 < 0
Not possible
∵ (x – 1)2 ≥ 0
No solution.
![]()
iii) 2 – 3x – 2x2 ≥ 0
2x2 + 3x – 2 ≤ 0
2x2 + 4x – x – 2 ≤ 0
2x (x + 2) – 1 (x + 2) ≤ 0
(2x – 1)(x + 2) ≤ 0
– 2 ≤ x ≤ \(\frac{1}{2}\)
iv) x2 – 4x – 21 ≥ 0
x2 – 7x + 3x – 21 ≥ 0
x (x – 7) + 3 (x – 7) ≥ 0
(x + 3) (x – 7) ≥ 0
x ≥ 7 or x ≤ – 3
(- ∞ < x ≤ – 3) ∪ (7 ≤ x < ∞).
![]()
II.
Question 1.
Solve the following inequations by graphical method.
i) x2 – 7x + 6 > 0
ii) 4 – x2 > o
iii) 15x2 + 4x – 4 ≤ 0
iv) x2 – 4x – 21 ≥ 0
Solution:
i) (x – 6) (x – 1) > 0
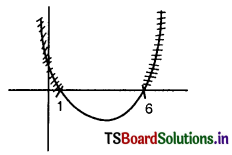
ii) 4 – x2 > 0
x2 – 4 > 0
(x – 2) (x + 2) > 0
– 2 < x < 2
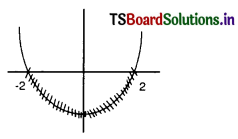
![]()
iii) 15x2 + 4x – 4 ≤ 0
15x2 + 10x – 6x – 4 ≤ 0
5x (3x + 2) – 2 (3x + 2) ≤ 0
\(\frac{-2}{3} \leq x \leq \frac{2}{5}\)
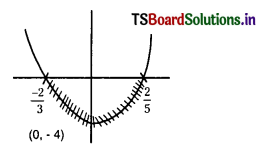
iv) x2 – 4x – 21 ≥ 0
(x – 7) (x + 3) ≥ 0
x ≥ 7 or x ≤ – 3
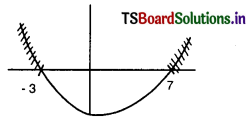
![]()
Question 2.
Solve the following Inequations.
i) \(\sqrt{3 x-8}\) < – 2
ii) \(\sqrt{-x^2+6 x-5}\) > 8 – 2x
Solution:
\(\sqrt{3 x-8}\) < – 2 Possible when 3x – 8 > 0
x > \(\frac{8}{3}\)
also \(\sqrt{3 x-8}\) ≥ 0
∴ Solution does not exist.
ii) \(\sqrt{-x^2+6 x-5}\) > 8 – 2x
Possible
– x2 + 6x – 5 ≥ 0
x2 – 6x + 5 ≤ 0
(x – 5) (x – 1) ≤ 0
1 ≤ x ≤ 5 …………….(1)
Squaring on both sides we get
– x2 + 6x – 5 > 64 + 4x2 – 32x
0 > 5x2 – 38x + 64 + 5
or 5x2 – 38x + 69 < 0
5x2 – 23x – 15x + 69 < 0
5x (x – 3) – 23(x – 3)< 0
(x – 3) (5x – 23) < 0