Srinivas

We are offering TS 10th Class Maths Notes Chapter 11 Trigonometry to learn maths more effectively.

TS 10th Class Maths Notes Chapter 11 Trigonometry

→ Trigonometry is the study of relationship between the sides and angle of a triangle.

→ Ratios of the sides of a right triangle with respect to its acute angle are called trigonometric ratios of the angle.

→ An equation involving trigonometric ratios of an angle is called a trigonometric identity. If it is true of all values of the angle.

→ Let us consider ΔABC in which ∠B = 90°, A and C are acute angles. Let us study the ratios of the sides of ΔABC with respect to the acute angle A.

sine of ∠A = sin A = \(\frac{\text { Side opposite to angle } \mathrm{A}}{\text { Hypotenuse }}=\frac{\mathrm{BC}}{\mathrm{AC}}\)
cosine of ∠A = cos A = \(\frac{\text { Side adjacent to angle } \mathrm{A}}{\text { Hypotenuse }}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
tangent of ∠A =tan A = \(\frac{\text { Side opposite to angle } A}{\text { Side adjacent to angle } A}=\frac{B C}{A B}\)

→ cosec A = \(\frac{1}{\sin A}\)
sec A = \(\frac{1}{\cos A}\)
cot A = \(\frac{1}{\tan A}\)

→ If one of trigonometric ratios of an acute angle is known the remaining trigonometric ratios of the angle can be easily determined.

→ Trigonometric ratios of 0°, 30°, 45°, 60° and 90°.

Note : From the above table we can observe that ∠A increases from 0° to 90°, sin A increases from 0 to 1 and cos A decreases from 1 to 0.

→ Trigonometric ratios of complementary angles : Two angles are said to be complementary angle if their sum equals to 90°.

• sin (90° – A) = cos A;
• cosec(90° – A) = sec A
• cos (90° – A) = sin A;
• sec(90°- A) = cosec A
• tan (90° – A) = cot A;
• cot(90° – A) = tan A

→ Trigonometric identities :

• sin²A + cos²A = 1
• sec²A – tan²A = 1 for 0°< A < 90°
• cosec²A – cot²A = 1 for 0° < A < 90°

Note : sin²θ = (sin θ)² but sinθ² ≠ (sin θ)²

Important Formula:

• sin(90° – A) = cos A;
• cosec (90° – A) = sec A
• cos(90° – A) = sin A
• sec(90° – A) = cosec A
• tan(90° – A) = cot A
• cot(90° – A) = tan A
• sin²A + cos²A = 1
• sec²A – tan²A = 1
• cosec²A – cot²A = 1

Flow Chat:

Aryabhatta (476 – 550 A.D):

• The first use of the idea of ‘sine’ in the way we use it today was in the book Aryabhatiyam by Aryabhatta, in A.D. 500.
• Aryabhatta used the word ‘ardhajya1 for the half-chord, which was shortened to jya or jiva in due course.
• When the Aryabhatiyam was translated into Arabic, the word jiva was retained as it is. The word jiva was translated into sinus, which means curve, when the Arabic version was translated into Latin.
• Soon the word sinus, also used as sine, became common in mathematical texts throughout Europe. An English Professor of astronomy Edumund Gunter (1581¬1626), first used the abbreviated notation ‘sin’.

We are offering TS 10th Class Maths Notes Chapter 10 Mensuration to learn maths more effectively.

TS 10th Class Maths Notes Chapter 10 Mensuration

Cuboid :

l, b and h denote respectively the length, breadth and height of a cuboid then

• Lateral surface area = 2h(l + b)
• Total surface area = 2(lb + bh + hl)
• Volume = lbh
• Diagonal of the cuboid = \(\sqrt{l^2+b^2+h^2}\)

Cube :

If the length of each edge of cube is “a” units then

• Lateral surface area = 4a²
• Total surface area = 6a²
• Volume = a³
• Diagonal of the cube = √3 × a = a√3

Right Prism :

• Lateral surface area = Perimeter of base × height
• Total Surface area = Lateral Surface area + 2(Area of end Surface)
• Volume = Area of base × height

Right Circular Cylinder:

If r is the radius of the base and ‘h’ is the height, then

• Lateral surface area = 2πrh
• Total surface area = 2πr(h + r)
• Volume = πr²h

Right Pyramid :

• Lateral surface area = \(\frac{1}{2}\) × perimeter of base × slant height
• Total Surface area = Lateral surface area + area of base
• Volume = \(\frac{1}{3}\) × area of base × height

Right Circular Cone :

If ‘r’ is the radius of the base, ‘h’ is the height and is slant height, then

• Lateral surface area = πrl.
• Total Surface area = πr(l + r)
• Volume = \(\frac{1}{3}\)πr²h
• l² = h² + r²

Sphere :

If ‘r’ is radius of sphere, then

• Lateral surface area = 4πr²
• Total surface area = 4πr²
• Volume = \(\frac{4}{3}\) πr³

Hemisphere :

If Y is the radius of hemi-sphere, then

• Lateral surface area = 2πr²
• Total surface area = 3πr²
• Volume = \(\frac{4}{3}\)πr³

Right Circular Hollow Cylinder:

• Area of each end = π(R² – r²)
• Curved surface area of hollow Cylinder = External area + Internal area
  = 2πrh + 2πRh = 2πh(R + r)
• Total surface area = 2πRh + 2πrh + 2(πR² – πr²)
  = 2πh(R + r) + 2π(R + r)(R – r)
  = 2π(R + r) (R + h – r)
• Volume of the material = External volume – Internal volume
  = πR²h – πr²h = 7th(R² – r²)

Spherical Shell:

If R and r are the outer and inner radii of a spherical shell, then

• Outer surface area = 4πR²
• Volume of material = \(\frac{4}{3}\) π

→ The volume of the solid-formed by joining two basic solids is the sum of the volumes of the constituents.

→ In calculating the S.A of a combination of solids, we cannot add the surface area of the two constituents, because some part of the surface area disappears in the process of joining them.

Flow Chat:

Brahmagupta (598 – 668):

• Brahmagupta was born in the state of Rajasthan.
• He worked in the great astronomical centre of ancient India – Ujjain.
• He made significant contributions to Trigonometry.

Telangana SCERT TS 10th Class Physical Science Study Material Pdf 11th Lesson Principles of Metallurgy Textbook Questions and Answers.

TS 10th Class Physical Science 11th Lesson Questions and Answers Principles of Metallurgy

Improve Your Learning
I. Reflections on concepts

Question 1.
List three metals that are found In nature as Oxide ores.
Answer:
Zinc, Ferrous, Aluminium, and Magnesium are metals which are found in nature as oxide ores.
They are :

Question 2.
List three metals that are found in nature n uncombined form.
Answer:

1. Gold
2. Platinum
3. Silver
4. Copper

Question 3.
Write a note on dressing of ore in metallurgy.
Answer:

1. Dressing is the first step in extraction of metals.
2. Ores that are mined from earth are usually contaminated with impurities such as soil and sand etc.
3. Dressing means, simply getting rid of as much of the unwanted rocky material as possible before the ore is converted into the metal.
4. Physical methods are used to enrich the ore.
5. These methods adopted in dressing the ore depend upon difference between physical properties of ore and gangue.
6. The following physical methods involved in dressing are 1) Hand picking 2) Washing 3) Froth floatation 4) Magnetic separation.

Question 4.
How do metals occur in nature? Give examples to any two types of minerals.
Answer:
The earth’s crust is the major source of metals. Sea water also contains some soluble salts such as sodium chloride and magnesium chloride etc. Some metals like Gold (Au), Silver (Ag) etc., are available in nature in a free state (native) as they are least reactive.

Other metals mostly are found in nature in the combined form due to their reactivity. The elements or compounds of the metals which occur in nature ¡n the earth’s crust are called ‘minerals’. Minerals in oxide form: Bauxite, Zincite, Magnetite, etc.

Question 5.
What is the difference between roasting and calcination? Give one example for each.
Answer:

Question 6.
Draw the diagram showing i) Froth floatation ii) Magnetic separation.
Answer:
i) Froth floats tian

ii) Magnetic separation

Question 7.
Draw a neat diagram of the Reverberatory furnace and label it neatly.
Answer:

Question 8.
What is an ore? On what basis a mineral is chosen as an ore?
Answer:
Ore: A mineral from which a metal can be extracted economically and conveniently is called ‘ore’.
To choose a mineral as an ore the following are considered

• The percentage of the metal in that mineral.
• Whether metal can be profitably extracted from it or not.
• The convenience of extraction of metal.

Question 9.
Write the names of any two ores of iron.
Answer:

1. Haematite – Fe₂O₃
2. Magnetite – Fe₃O₄

Question 10.
How do metals occur In nature? Give examples of any two types of minerals.
Answer:
The earth’s crust is the major source of metals. Sea water also contains some soluble salts such as sodium chloride and magnesium chloride etc. Some metals like Gold (Au), Silver (Ag) etc., are available in nature in free state (native) as they are least reactive. Other metals mostly are found in nature in the combined form due to their reactivity.

The elements or compounds of the metals which occur in nature in the earth’s crust are called ‘minerals’.
Minerals in oxide form: Bauxite, Ziricite, Magnetite, etc.
Minerals in sulphide form: Copper iron pyrites, Gatena, etc.

Question 11.
Write short notes on froth floatation process.
Answer:
Froth Floatation process:

Froth Floatation process for the concentration of sulphide ores.

1. This method is mainly useful for sulphide ores which have no wetting property whereas impurities get wetted.
2. The ore with impurities is finely powdered and kept ¡n water taken in a floatation cell.
3. Air under pressure is blown to produce froth in water.
4. Froth so produced takes the ore particles to the surface whereas, impurities settle at the bottom.
5. Froth is separated and washed to get ore particles.

Question 12.
When do we use magnetic separation method for concentration of an ore? Explain with an example.
Answer:
Magnetic Separation Method:
If the ore contains impurities such that one, of them, is magnetic and the other is non – magnetic they are separated by magnetic separation method.
Eg: Magnetic ores like iron pyrites, (FeS) and magnetite (Fe₃O₄) are concentrated by this method. The crushed ore is allowed to pass through electromagnetic belts. The mineral particles are retained and gangue particles are thrown away as a separate heap.

Question 13.
Write short notes on each of the following:
(i) Roasting.
(ii) Calcination.
(iii) Smelting.
Answer:
(i) Roasting:

• Roasting is a pyrochemical process in which the ore is heated in the presence of oxygen or air below its melting point.
• The products obtained in the process are also produced in solid state.
• Generally, reverberatory furnace is used for roasting.
  Eg : 2ZnS + 3O₂ → 2ZnO + 2SO₂

(ii) Calcination:

• Calcination is a pyrochemical process in which the ore is heated in the absence of air.
• The ore gets generally decomposed n the process.
  Eg: MgCO₃ → MgO + CO₂

(iii) Smelting:

• Smelting is a pyrochemical process ¡n which the ore is mixed with flux and fuel and strongly heated.
• The heat is so strong that the ore is reduced to even metal and the metal is obtained in molten state.
• During smelting, the impurities (gangue) in the ore react with flux to form slag which is removed.
• The smelting is carried out n a specially built furnace known as blast furnace.

Question 14.
What is gangue and slag?
Answer:

• Gangue: The impurity present in the ore is called gangue.
• Slag: A flux is a chemical substance added to convert gangue into fusible mass. This fusible mass is called slag.
  Gangue + Flux Slag

Application of concepts

Question 1.
Magnesium is an active metal, if it occurs as a chloride in nature, which method of reduction is suitable for its extraction?
Answer:
Magnesium is an active metal. If it occurs as chloride in nature, the only method viable to extract magnesium ( any active metal) is electrolysis of fused Magnesium chloride. In electrolysis of fused Magnesium chloride, magnesium is deposited at cathode and chlorine gas is liberated at the anode.
MgCl₂ → Mg⁺² + 2Cl^–
At cathode, Mg⁺²+ 2e^– → Mg
At anode, 2Cl^– → Cl₂ + 2e^–

Question 2.
Mention two methods which produce very pure metals from impure metals.
Answer:
Electrolysis and reduction are the two methods which produce pure metals.

Question 3.
Which method do you suggest for extracting of high reactivity metals? Why?
Answer:
High reactivity metals like K. Na, Ca, Mg, etc., can be extracted by electrolysis.
Reasons:

1. Simple reduction methods like heating with C, CO, etc., to reduce the ores of these metals are not feasible.
2. The temperature required for the reduction is too high and more expensive.,
3. Hence electrolysis is the suggestable method to extract high reactive metals.

Question 4.
Explain Thermite process and mention its applications in our daily life.
Answer:
Thermite process

1. When highly reactive metals such as Na, Ca, Al are used as reducing agents they displace metals of lower reactivity from their compounds.
2. These displacement reactions are highly exothermic. The amount of heat evolved s so large that the metals produced will be in molten state.
3. The reaction of iron oxide (Fe₂O₃), with aluminium is used to join railings of railway tracks or cracked machine parts. This reaction is known as the thermite reaction.
   2Al + Fe₂O₃ → Al₂O₃ + 2Fe + Heat

Applications in daily life
1. To join railings of railway tracks.
2. Used to join cracked machine parts.

Question 5.
Where do we use handpicking and washing methods in our daily life? Give examples. How do you correlate these examples with enrichment of ore?
Answer:
We use hand picking in separating stones from rice and da I. We use washing methods to separate dust from rice, dal, vegetables, fruits etc.

Hand-picking: The colour and size of impurities is different from rice or dal. So we can easily separate them by hand-picking. In the same way if the ore particles and the impurities are n different sizes, colour etc., we can see this hand-picking method to separate ore from impurities.

Washing: Less-density particles like dust is separated from more density particles like rice, vegetables etc., by washing. In the same way ore particles are crushed and kept on a slopy surface. They are washed with a controlled flow of water. Less sensitive impurities are carried away by water flow, leaving the more sensitive ore particles behind.

Question 6.
What is activity series? How it helps in extraction of metals?
Answer:
Activity series: The arrangement of the metals in decreasing order of their reactivity is known as ‘activity series’.
Use of Activity series in extraction of metals
1. The method used for a particular metal for the reduction of its ore to the metal depends mainly on the position of the metal in the activity series.
Eg:
The metals at the top of the activity series (highly reactive) can be extracted by electrolysis.
The metals at the middle of the activity series can be extracted by

• reduction of metal oxide with carbon
• reduction of oxide ores with Co,
• self-reduction of sulphide ores
• reduction of ores with more reactive metals (thermite process).

3. The metals at the bottom of the activity series (less reactive) can be extracted by heating along, and displacement from their aqua solution.

Multiple choice questions

Question 1.
The impurity present in the ore is called as [ ]
(a) Ganguc
(b) fluid
(c) Slag
(d) Mineral
Answer:
(a) Ganguc

Question 2.
Which of the following is a carbonate ore? [ ]
(a) Magncsitc
(b) Bauxitc
(c) Gypsum
(d) tiaicna
Answer:
(a) Magncsitc

Question 3.
Which of the following is the corrcct formula of Gypsum [ ]
(a) CuSO₄. 2H₂O
(b) CaSO₄. 1/2H₂O
(c) CuSO₄. 5H₂O
(d) CaSO₄. 2H₂O
Answer:
(d) CaSO₄. 2H₂O

Question 4.
The oil used in the froth floatation process is [ ]
(a) kerosene oil
(b) pencil
(c) coconut oil
(d) olive coil.
Answer:
(b) pencil

Question 5.
Froth floatation is method used for the purification of …………………….. ore. [ ]
(a) sulphide
(b) oxide
(c) carbonate
(d) nitrate
Answer:
(a) sulphide

Question 6.
Galena is an ore of [ ]
(a) Zn
(b) Pb
(c) Hg
(d) Al
Answer:
(b) Pb

Question 7.
The metal that occurs in the native form is [ ]
(a) Pb
(b) Au
(c) Fc
(d) Hg
Answer:
(b) Au

Question 8.
The most abundant metal in th earth’s cruat is [ ]
(a) Silver
(b) Aluminium
(c) zinc
(d) iron
Answer:
(b) Aluminium

Question 9.
The reducing agent in thermite process is [ ]
(a) Al
(b) Mg
(c) Fe
(d) Si
Answer:
(a) Al

Question 10.
The purpose of smelting an ore is [ ]
(a) Oxidisc
(b) Reduce
(c) Neutndisc
(d) one of these
Answer:
(b) Reduce

Suggested Experiments

Question 1.
Suggest an experiment to prove that the presence of air and water are essential for corrosion. Explain the procedure.
Answer:
Corrosion: Corrosion is the deterioration of a metal, as a result of chemical reaction between it and the surrounding environment.

Experiment:
Aim: To prove that the presence of air and water are essential for corrosion. Materials required : 3 test tubes, 3 iron nails, oil, water, anhydrous calcium chloride, rubber corks.

Procedure:
1. Take three test tubes and place clean iron nails in each of them.
2. Label these tests tubes A, B and C. Pour some water in test tube A and cork it.
3. Pour boiled distilled water in test tube B, add about 1 ml of oil and cork it. The oil will float on water and prevent the air from dissolving in the water.
4. Put some anhydrous calcium chloride in test tube C and cork it. Anhydrous calcium chloride will absorb the moisture.
5. Leave these test tubes for a few days and then observe.

6. We will observe that ¡ron nails rust in test tube A, but they do not rust in test tubes B and C.
7. In the test tube A the nails are exposed to both air and water whereas in the test tube ‘B’ the nails are exposed to only water and in the test tube ‘C’ the nails are exposed to dry air.
8. This shows air and water are essential for corrosion.

Suggested Projects

Question 1.
Collect information about extraction of metals of low reactivity silver, platinum and gold and prepare a report.
Answer:
Extraction of Silver:

1. Silver occurs both in combined state as well as In free state. The important ores of silver are Argentite (or) Silver glance (Ag₂S) Pyrargyrite (or) Ruby silver 3 Ag₂S Sb₂S₃ silver copper glance (CuAg)₂S
2. Silver is extracted from the ore-Argentite (Ag₂S).
3. The process of extraction of silver is called cyanide process, as sodium cyanide solution is used.
4. The ore Is crushed, concentrated and then treated with sodium cyanide solution.
5. This reaction forms sodium argent cyanide [Na[Ag(CN)₂]]
   Ag₂S + 4 NaCN → 2Na[Ag(CN)₂] + Na₂S
6. This solution of sodium argent cyanide combines with zinc dust and forms tetra cyano zincate and precipitated silver. This precipitated silver is called spongy silver.
   Zn + 2Na[Ag(CN)₂] → Na₂[Zn(CN)₄)] + 2Ag
7. This spongy silver is fused with potassium nitrate to obtain pure silver. Then the silver obtained is purified by electrolytic process.

Extraction of platinum

• Platinum is rarely found on its own, but In combination with other base and precious metals.
• The extraction process of platinum is a complex process which includes milling the ore and smelting at high temperatures. This removes base metals notably sulphur and concentrates PGM (Platinum Group Metals) – Gold, Platinum and Palladium.
• The PGM matter is further processed by electrolysis to remove Nickel, Cobalt and Copper.
• The high-grade concentrate is treated by solvent extraction, distilling, and ion- exchange treatments to separate the PGMs Into its separated metals.

Extraction of Gold:

1. Gold is usually found alone or alloyed with mercury or silver.
2. In all methods of gold ore refining, the ore is usually washed and filtered at the mine, then sent to the mill. At the mill, the ore is ground into smaller particles with water, then ground again in a ball mill to further pulverize the ore.
3. Several processes can be used to separate the Gold from its ore. They are:

a) Cyanide process:

• The ground ore Is put In a tank containing a weak cyanide solution and zinc is added.
• The zinc causes a chemical reaction which separates the gold from the ore.
• The gold is then removed from the solution with a filter press.

b) Carbon-in-pulp method:

1. In this method, the ground ore is mixed with water before cyanide Is added. Then carbon is added to bond with the gold.
2. The carbon-gold particles are put into a caustic carbon solution, separating out the gold.

c) Heap leaching:

1. The ore is placed on open-air pads and cyanide is sprayed over It, taking several weeks to leach down to an imperious base.
2. The solution then pours off and pad into a pond and is pumped from there to a recovery plant, where the gold is recovered.
3. Heap-leaching helps recover gold from ore that would otherwise be to expensive to process.

TS 10th Class Physical Science Principles of Metallurgy Intext Questions

Page 237

Question 1.
Can you mention some articles that are made up of metals?
Answer:
Utensils in kitchen, window gnUs, pots, chairs, iron gates, bodies of motor cars, etc.

Question 2.
Do metals exist in nature in the same form as that we use ¡n our daily life?
Answer:
No, metals do not exist in nature ¡n the form same as that we use in our daily life.

Question 3.
Have you ever heard the words like ore, mineral and metallurgy?
Answer:
Yes.

Question 4.
Do you know how these metals are obtained?
Answer:
The metals are extracted from their ores mainly in three stages.

1. The concentration of ore.
2. Extraction of crude metal.
3. Refining of the metal.

Question 5.
How the metals are present In nature?
Answer:
The metals are present in nature In combined form as their compounds.

Page 239

Question 6.
What metals can we get from the ore mentioned in Table-1?
Answer:

Question 7.
Can you arrange these metals in the order of their reactivity.
Answer:
K>Na>Ca>Mg>Al >Zn>Fe>Pb>Cu>Ag>Au

Question 8.
What do you notice In table-2?
Answer:
I noticed that the ores of many metals are oxides and sulphides.

Question 9.
Can you think how do we get these metals from their ores?
Answer:
These metals are obtained from their ores by suitable metallurgical processes.

Question 10.
Does the reactivity of a metal and form of its ore (oxides, sulphides, chlorides, carbonates, sulphates) has any relation with process of extraction?
Answer:
Yes, highly reactive metals are obtained by electrolysis from their molten salts, moderately reactive metals are obtained by reducing with suitable reagents whereas least reactive metals are available in native form.

Question 11.
How are metals extracted from mineral ores?
Answer:
Metals are extracted from mineral ores In three steps.

1. Concentration of ore or Dressing.
2. Extraction of crude metal.
3. Refining of the metal.

Question 12.
What methods are to be used?
Answer:
Hand-picking, Washing, Froth floatation and Magnetic Separation methods are to be used.

Page 247

Question 13.
Do you know why corrosion occurs?
Answer:
Metals are stable in the form In which they are available in nature. So by means of corrosion, they change to the form as they occur n nature.

Question 14.
What does this tell us about the conditions under which iron articles rust?
Answer:
Corrosion of iron ( commonly known as rusting ) occurs in presence of moisture and air.

Page 250

Question 15.
What is the role of furnace in metallurgy?
Answer:
A furnace is used for heating the ores and crude metals to required temperatures in metallurgical operations.

Question 16.
How they bear large amounts of heat?
Answer:
The furnaces are lined inside with refractory materials and hence they can bear large amounts of heat.
The substances which are capable of withstanding very high temperatures without melting or becoming soft are called refractory materials.

Question 17.
Do all furnaces have same structure?
Answer:
No, all furnaces do not have same structure.

TS 10th Class Physical Science Principles of Metallurgy Activities

Activity 1

Question 1.
How do you classify ores based on their formula?
1) Look at the following ores.
2) Identify the metal present in each ore.

Now classify them as shown in the table.
Answer:
Classification of ores as oxides, sulphides, chlorides, carbonates, and sulphates is done as follows.

Activity 2

Question 2.
Show that both air and water are necessary for corrosion of iron.
Answer:

1. Take three test tubes and place clean iron nails in each of them.
2. Label these test tubes as A, B and C. Pour cork it.
3. Pour boiled distilled water in test tube. B Add about 1 ml of oil and cork it. The oil will float on water and prevent the air from dissolving in the water.
4. Put some anhydrous calcium chloride in test tube C and cork it. Anhydrous calcium chloride will absorb the moisture if any from the air. Leave these test tubes for a few days and then observe.

Observation: Iron nails rust in test tube A but they do not rust in test tubes B and C. In the test tube A the nails are exposed to both air and water. In the test tube B the nails are exposed to distilled water and the nails in test tube C are exposed to dry air only.

Inference: From this we can conclude that both air and water are necessary for corrosion of iron.

We are offering TS 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle to learn maths more effectively.

TS 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle

→ Secant: A line which intersects a circle in two distinct points is called a secant.

PAB is secant of the circle with centre ‘o’

→ Tangent: A tangent to a circle is a line that intersects the circle is exactly one point.

Tt is the tangent to the circle with centre ‘o’

• No tangent can be drawn to a circle from a point lying inside it.
• One and only one tangent can be drawn to a circle at a point on a circle.
• Two tangents can be drawn to a circle from a point lying outside it.
• The lengths of two tangents drawn from an external point to a circle are equal.
• A tangent to a circle is perpendicular to the radius drawn through the point of contact.
• A line drawn through the end point of a radius and perpendicular to it is a tangent to the circle.
• The common point of a tangent to a circle is called point of contact.
• The line containing the radius through the point of contact the normal to the circle at the point.

→ Sector: The portion of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.
OAPB is a sector of the circle with centre ‘O’
∠AOB is called the angle of the sector. OAPB is called the minor sector and OAQB is called the major sector.

Area of the sector = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × πr² where x° is the angle of the sector & ‘r’ is the radius.
Length of arc = \(\frac{\mathrm{x}^{\circ}}{360^{\circ}}\) × 2πr

→ Segment: The chord AB divides the circle with centre ‘O’ into two parts. APB is called the minor segment where as AQB is called the major segment.

Area of the segment: Area of the segment APB = Area of the sector OAPB – Area of OAB.
Area of the major sector OAQB = Area of the circle – Area of the minor sector OAPB
Area of major segment of a circle = Area of the corresponding sector – Area of the corresponding triangle.

→ The locus of points which are joined by a curve and are equidistant from a fixed point is called a circle. The fixed point here is called the centre of the circle.

(Or)
A simple closed curve consisting of all points in a plane which are equidistant from a fixed point is called a circle. The fixed point is its centre and the fixed distance is its radius.

→ The path followed by circular object is a straight line.

→ The line segment joining any two points on a circle is called a ‘chord’. The longest of all chords of a circle passes through the centre and is called a diameter.

\(\overline{\mathrm{AB}}\) is a chord and \(\overline{\mathrm{PQ}}\) is a diameter. (PO and OQ is the radius of the circle.
Diameter = 2 × radius
d = 2r
r = \(\frac{r}{2}\)

→ There are three different possibilities for a given line and a circle.

Case (i): The line PQ and the circle have no point in common (or) they do not touch each other.
Case (ii): The line PQ and the circle have two common points (or) a line which intersects a circle at two distinct points is called a “secant” of the circle.
The line PQ intersects the circle at two distinct points A and B. Here the line PQ is a “secant” of the circle.
Case (iii): The line PQ touches the circle at an unique point A(or) there is one and only one point common to both the line and circle.
Here \(\overleftrightarrow{\mathrm{PQ}}\) is called a tangent to the circle at ‘A’.

→ The word tangent is derived from the Latin word “TANGERE” which means “to touch” and was introduced by Danish mathematician “Thomas Fineke” in 1583.

→ There is only one tangent to the circle at one point.

→ The tangent at any point of a circle is perpendicular to the radius through the point of contact.

The radius OP is perpendicular to \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) at P. i.e., OP ⊥ AB.

→ Construction of a tangent to a circle :

• Draw a circle with centre ‘O’.
• Draw a perpendicular line to OP through ‘P’.
• Let it be \(\stackrel{\leftrightarrow}{\mathrm{XY}}\).
• XY is the required tangent to the given circle passing through P.

→ Let ‘O’ be the centre of the given circle and \(\overline{\mathrm{AP}}\) is a tangent through a Where OA is the radius, then the length of the tangent AP = \(\sqrt{O P^2-\mathrm{OA}^2}\)

→ Two tangents can be drawn to a circle from an external point.

Important Formula:

• Area of Sector = \(\frac{\mathrm{X}^{\circ}}{360^{\circ}}\) × πr²
• Length of arc = \(\frac{\mathrm{X}^{\circ}}{360^{\circ}}\) × 2πr
• A line which intersects a circle In two distinct points Is called a secant.
• A tangent to a circle is a line that Intersects the circle Is exactly one point.

Flow Chat:

Archimedes (287 – 212 B.C):

• “Archimedes of Syracuse” was a Greek mathematician, physicist and engineer.
• He is regarded as one of the leading scientists in classical antiquity.
• He made several discoveries in the fields of mathematics particularly in geometry.

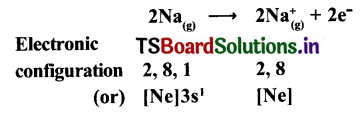
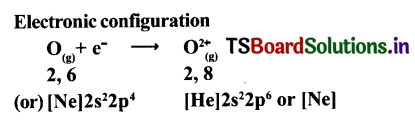
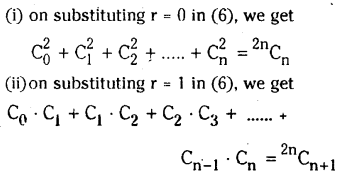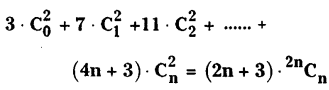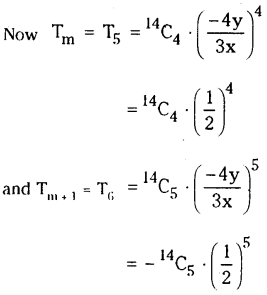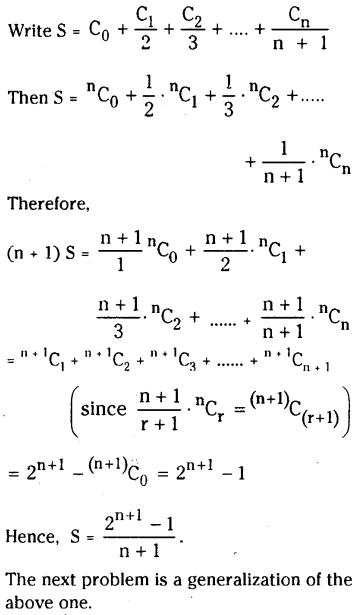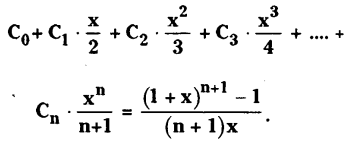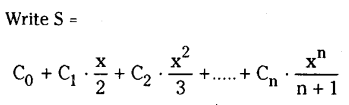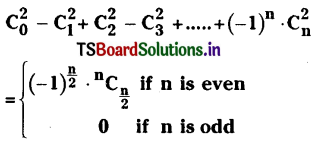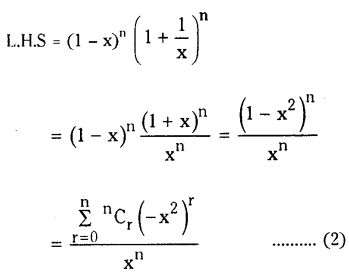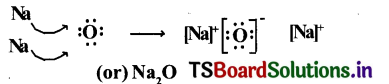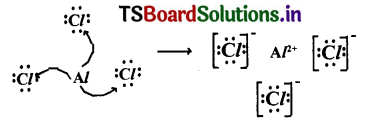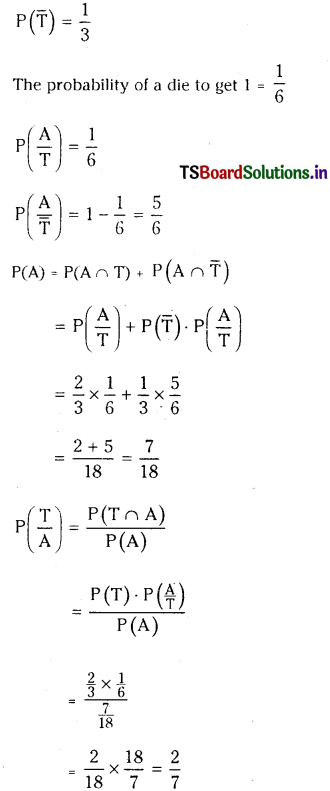Solving these TS 10th Class Maths Bits with Answers Chapter 8 Similar Triangles Bits for 10th Class will help students to build their problem-solving skills.

Similar Triangles Bits for 10th Class

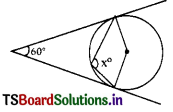
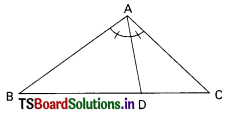
Question 1.
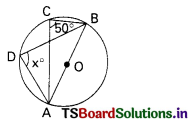
From the figure ∠DAC = ……………….

A) 35°
B) 55°
C) 45°
D) 60°
Answer:
A) 35°

Question 2.
The ratio of the corresponding sides of two similar triangles is 5 : 3 then the ratio of their areas
A) 5 : 3
B) 3 : 5
C) 6 : 10
D) 25 : 9
Answer:
D) 25 : 9

Question 3.
If ∆ABC ~ ∆DEF; BC = 4 cm, EF = 5 cm and ∆ABC = 80 cm² then ∆DEF = ………………….
A) 100 cm²
B) 150 cm²
C) 125 cm²
D) 225 cm²
Answer:
C) 125 cm²

Question 4.
In the figure DE // BC and AD : DB = 1 : 2 then ∆ADE : ∆ABC =
A) 1 : 4
B) 4 : 1
C) 1 : 9
D) 2 : 9
Answer:
C) 1 : 9

Question 5.
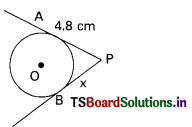
∆ABC ~ ∆PQR. M is the mid point of BC. N is the mid point of QR. If the area of ∆ABC = 100 cm² and area of ∆PQR = 144 cm2 and AM = 4 cm then PN = ………………… cm
A) 5 cm
B) 4.8 cm
C) 4 cm
D) 3.8 cm
Answer:
B) 4.8 cm

Question 6.
In ∆PQR, PQ = 6\(\sqrt{3}\) cm; PR = 12 cm, QR = 6 cm then ∠B = ………………..
A) 30°
B) 45°
C) 90°
D) 60°
Answer:
B) 45°

Question 7.
The lengths of diagonals of a rhombus are 24 cm and 32 cm then the perimeter of rhombus
A) 180°
B) 120°
C) 220°
D) 112°
Answer:
A) 180°

Question 8.
Which of the following does not belongs to side of right triangle ?
A) 9cm, 15cm, 12cm
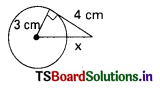
B) 9cm, 5cm, 7cm
C) 400mm, 300mm, 500mm
D) 2cm, \(\sqrt{5}\) cm, 1cm
Answer:
B) 9cm, 5cm, 7cm

Question 9.
In an isosceles ∆PQR, PR = QR and PQ² = 2PR² then ∠R = ……………….
A) 60°
B) 30°
C) 90°
D) 45°
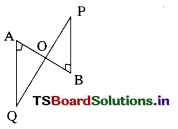
Answer:
C) 90°

Question 10.
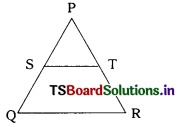
In ∆ABC the mid points are D, E and F of the sides AB, BC, CA then ∆DEF : ∆ABC
A) 1 : 1
B) 1 : 3
C) 1 : 2
D) 1 : 4
Answer:
D) 1 : 4

Question 11.
The diagonal of a square is 7\(\sqrt{2}\) cm then its area
A) 28 cm²
B) 14\(\sqrt{2}\) cm²
C) 21 cm²
D) 49 cm²
Answer:
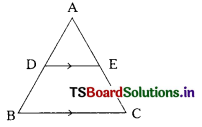
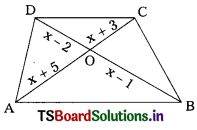
D) 49 cm²

Question 12.
In the figure AB = 2.5 cm, AC = 3.5 cm. If AD is the bisector of ∠BAC then BD : DC = …………..

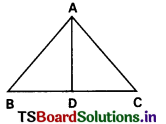
A) 5 : 3
B) 3 : 5
C) 5 : 7
D) 2 : 7
Answer:
C) 5 : 7

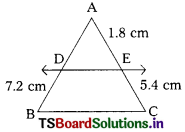
Question 13.
In the figure DE divides AB and AC in the ratio 1 : 3 If DE = 2.4 cm then BC = ………………

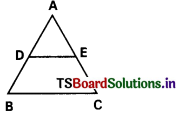
A) 4.8 cm
B) 7.2 cm
C) 9.6 cm
D) 12 cm
Answer:
B) 7.2 cm

Question 14.
The height of an equilateral triangle whose side is a unit
A) \(\frac{\mathrm{a}}{2}\)
B) \(\frac{\sqrt{3}}{2}\)a
C) \(\sqrt{3}\)a
D) \(\frac{\sqrt{3}}{4}\)a
Answer:
B) \(\frac{\sqrt{3}}{2}\)a

Question 15.
If ∆ABC ~ ∆XYZ, ∠C = 60° ∠B = 75° then ∠Z = ……………….
A) 90°
B) 75°
C) 45°
D) 60°
Answer:
D) 60°

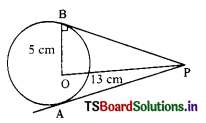
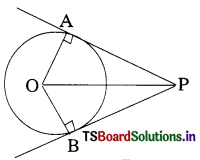
Question 16.
Maximum possible tangents that can drawn to a circle is ………. (A.P. Mar. ’15)
A) Infinity
B) 4
C) 100
D) 2
Answer:
A) Infinity

Question 17.
∆ABC ~ ∆DEF and areas of ∆ABC, ∆DEF are 64 cm² and 121 cm² then the ratio of corresponding sides. (A.P. Mar. ’15)
A) 11 : 8
B) 8 : 11
C) 3 : 11
D) 19 : 8
Answer:
B) 8 : 11

Question 18.
Area of a regular hexagon whose side is ‘a’ cm is ………………. (A.P. Mar. ’15)
A) 6 \(\left(\frac{\sqrt{3}}{4} a^2\right)\)
B) 6 \(\left(\frac{3}{4} a^2\right)\)
C) \(\sqrt{6}\left(\frac{3}{4} a^2\right)\)
D) 6\(\left(\frac{\sqrt{3}}{4} a^2\right)\)
Answer:
D) 6\(\left(\frac{\sqrt{3}}{4} a^2\right)\)

Question 19.
If a man walks 6 m to East and 8m to North. Now he is at a distance of ……………… from origin point. (A.P. Mar.’15 )
A) 10 m
B) 48 m
C) 14 m
D) 2 m
Answer:
A) 10 m

Question 20.
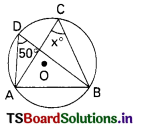
∠CAD in the given figure is …………………

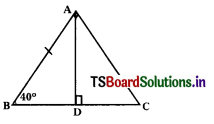
A) 50°
B) 60°
C) 40°
D) 90°
Answer:
A) 50°

Question 21.
Example for the sides of a Right angled triangle is …………….. (A.P. June ’15)
A) 5, 6, 9
B) 5, 12, 13
C) 5, 11, 12
D) 7, 8, 9
Answer:
B) 5, 12, 13

Question 22.
Height of an equilateral triangle whose side is ‘a’ cm is ……………. (A.P. Mar. ’16)
A) \(\frac{\sqrt{3}}{2}\)a
B) \(\frac{2}{\sqrt{3}}\)a²
C) \(\sqrt{\frac{3}{2}}\)a
D) \(\frac{\sqrt{3}}{2}\)a²
Answer:
A) \(\frac{\sqrt{3}}{2}\)a

Question 23.
∆ABC ~ ∆XYZ, ∠C = 60° ∠B = 70° then ∠ X = ……………… (A.P. Mar.’16)
A) ∠ X = 70°
B) ∠ X = 50°
C) ∠X = 60°
D) ∠X = 10°
Answer:
B) ∠ X = 50°

Question 24.
When we construct a triangle similar to a given triangle as per given scale factor, we construct on the basis of ………….. (T.S. Mar. ’15)
A) SSS similarity
B) AAA similarity
C) Basic proportionality theorem
D) A and C are correct
Answer:
C) Basic proportionality theorem

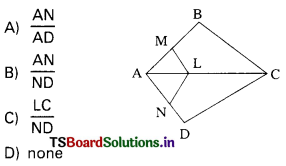
Question 25.
∆ABC ~ ∆DEF is given then which of the following is correct. (T.S. Mar. ’15)


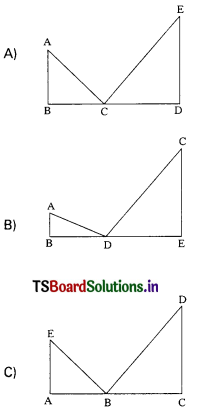
Answer:
(A)

Question 26.
In ∆ABC ∠C = 90°, BC = a, AB = c, AC = b and ‘p‘ is length of height drawn from ‘C’ to AB then ……… is correct. (T.S. Mar. ’15)
A) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) – \(\frac{1}{\mathrm{b}^2}\)
B) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{b}^2}\) – \(\frac{1}{\mathrm{a}^2}\)
C) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) + \(\frac{1}{\mathrm{b}^2}\)
D) \(\frac{2}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) + \(\frac{1}{\mathrm{b}^2}\)
Answer:
C) \(\frac{1}{\mathrm{p}^2}\) = \(\frac{1}{\mathrm{a}^2}\) + \(\frac{1}{\mathrm{b}^2}\)

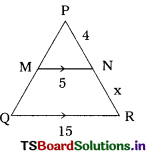
Question 27.
From the figure, x = …………………

A) 10
B) 15
C) 12
D) 25
Answer:
B) 15

Question 28.
In the given figure, DE // BC and AD : DB = 5 : 4, then \(\frac{\text { D DEF }}{\text { D CFB }}\) =

A) \(\frac{81}{25}\)
B) \(\frac{5}{9}\)
C) \(\frac{5}{4}\)
D) \(\frac{25}{81}\)
Answer:
D) \(\frac{25}{81}\)

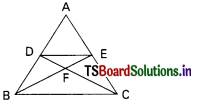
Question 29.
In the figure, ∆ ABC is an isosceles triangle right angled at B. Two equilateral triangles are constructed with sides AC and BC. Then ∆ BCD = …………

A) ∆ ACE
B) ∆ ABC
C) \(\frac{1}{2}\) (∆ ABC)
D) \(\frac{1}{2}\) (∆ ACE)
Answer:
D) \(\frac{1}{2}\) (∆ ACE)

Question 30.
In the figure ∆PQR and ∆SQR are two triangles on the same base QR. If PS intersects QR at ‘O’, then ∆PQR : ∆SQR = …………

A) PO : SO
B) PQ : QS
C) PR : SR
D) PQ : SR
Answer:
A) PO : SO

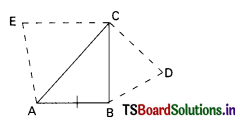
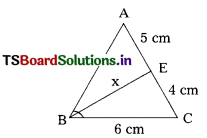
Question 31.
In the figure, ∠BAD = ∠CAD; AB = 3.4 cm, BD = 4 cm, BC = 10 cm, then AC = ……………

A) 5.1 cm
B) 3.4 cm
C) 6 cm
D) 5.3 cm
Answer:
A) 5.1 cm

Question 32.
All ……………… triangles similar.
A) equilateral
B) scalene
C) isosceles
D) none
Answer:
A) equilateral

Question 33.
Two polygons are similar if …………………
A) corresponding angles are equal
B) corresponding sides are equal
C) both A & B
D) none
Answer:
C) both A & B

Question 34.
The ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding ……………
A) sides
B) areas
C) angles
D) none
Answer:
A) sides

Question 35.
A perpendicular is drawn from the vertex of a right angle to the hypotenuse then the tri-angles on each side of the perpendicular are ……………..
A) similar
B) not similar
C) square
D) none
Answer:
A) similar

Question 36.
If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar. This property is …………………
A) SSS
B) ASA
C) AAA
D) SAS
Answer:
D) SAS

Question 37.
If the sides of two similar triangles are in the ratio 7 : 2 then the ratio of their areas is …………….
A) 9 : 2
B) 8 : 9
C) 4 : 49
D) 49 : 4
Answer:
D) 49 : 4

Question 38.
∆ABC ~ ∆PQR, ∠A = 32°, ∠R = 65° then ∠B = ………………
A) 64°
B) 73°
C) 83°
D) none
Answer:
C) 83°

Question 39.

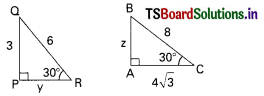
If ∆ABC ~ ∆PQR then y + z = ……………..
A) 1 + 3\(\sqrt{3}\)
B) 4 + 3\(\sqrt{3}\)
C) 3\(\sqrt{3}\) + 7
D) 9 + \(\sqrt{3}\)
Answer:
B) 4 + 3\(\sqrt{3}\)

Question 40.
In ∆LMN, ∠L = 60°, ZM = 50° and ∆LMN ~ ∆PQR then ∠R = ……………..
A) 70°
B) 80°
C) 90°
D) none
Answer:
A) 70°

Question 41.
The perimeter of ∆ABC ~ ∆LMN are 60 cm and 48 cm of LM = 8 cm then AB = ………………. cm.
A) 19
B) 11
C) 7
D) 10
Answer:
D) 10

Question 42.
In ∆ABC, BC² + AB² = AC² then ……………… is the right angle.
A) ∠B
B) ∠A
C) ∠C
D) none
Answer:
A) ∠B

Question 43.
The bisector of ∠A of ∆ABC intersects BC at D. If BD : DC = 4 : 7 and AC = 3.5. Then AB = ……………..
A) 2
B) 8
C) 10
D) 11
Answer:
A) 2

Question 44.
∆ABC ~ ∆PQR, ∠A = 50° then ∠Q + ∠R = ……………….
A) 120°
B) 110°
C) 130°
D) 180°
Answer:
C) 130°

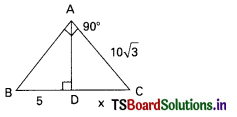
Question 45.
In the figure, CD = …………….. cm.

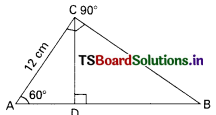
A) \(\sqrt{3}\)
B) 2\(\sqrt{3}\)
C) 3\(\sqrt{3}\)
D) 6\(\sqrt{3}\)
Answer:
D) 6\(\sqrt{3}\)

Question 46.
In the figure, AC = ……………. cm.

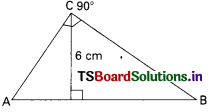
A) 19
B) 9
C) 12
D) 10
Answer:
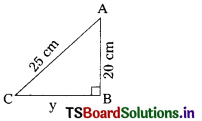
C) 12

Question 47.
The ratio of corresponding sides of two similar triangles is 3 : 2 then the ratio of their corresponding heights is …………….
A) 3 : 2
B) 2 : 3
C) 1 : 4
D) 1 : 7
Answer:
A) 3 : 2

Question 48.
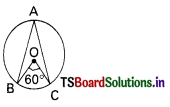
In the figure, ∠ABC = ………………..

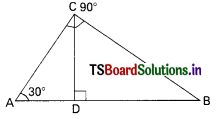
A) 30°
B) 70°
C) 50°
D) 60°
Answer:
D) 60°

Question 49.
In ∆ABC, XY || BC, AX : XB = 2 : 1 then ∆ AXY : ∆ABC = ………………
A) 9 : 4
B) 4 : 9
C) 1 : 9
D) 2 : 3
Answer:
B) 4 : 9

Question 50.
In a square, the diagonal is ………………. times of its side.
A) \(\sqrt{7}\)
B) \(\sqrt{3}\)
C) \(\sqrt{2}\)
D) 2
Answer:
C) \(\sqrt{2}\)

Question 51.
The side of an equilateral triangle is ‘a’ units. Its height is …………….. units.
A) \(\frac{\sqrt{3 a}}{2}\)
B) \(\frac{\sqrt{3}}{4}\)a
C) \(\frac{3}{a}\)
D) \(\frac{3}{2}\)
Answer:
A) \(\frac{\sqrt{3 a}}{2}\)

Question 52.
The ratio of the areas of two similar triangles is 1 : 4 then the ratio of their corresponding sides …………….
A) 9 : 1
B) 1 : 1
C) 2 : 1
D) 1 : 2
Answer:
D) 1 : 2

Question 53.
∆ABC ~ ∆PQR then AB : PQ = ……………….
A) AC : PR
B) AC : PQ
C) AB : PR
D) none
Answer:
A) AC : PR

Question 54.
∆ABC is an isosceles right triangle ∠C = 90° then AB² = ……………….
A) AB² + BC²
B) AC² + BC²
C) AC² + 2
D) none
Answer:
B) AC² + BC²

Question 55.
Each angle in an equilateral triangle is ……………….
A) 60°
B) 80°
C) 100°
D) 70°
Answer:
A) 60°

Question 56.
Each exterior angle of an equilateral triangle is …………….
A) 180°
B) 130°
C) 110°
D) 120°
Answer:
D) 120°

Question 57.
The longest side in a right triangle is ……………..
A) smaller
B) hypotenuse
C) adjacent
D) none
Answer:
B) hypotenuse

Question 58.
In the figure, ∆ABC, DE // BC and \(\frac{A D}{D B}\) = \(\frac{3}{5}\), AC = 5.6 then AE = …………….. cm.

A) 1.8
B) 3.5
C) 1.2
D) 2.1
Answer:
D) 2.1

Question 59.
From the figure, AD = ……………. cm.

A) 2.4
B) 4.2
C) 8.2
D) 9.2
Answer:
A) 2.4

Question 60.
In the figure, LM // CB and LN // CD then \(\frac{A M}{A B}\) = ……………….

Answer:
(A)

Question 61.
In a trapezium, diagonals divide each other ………………
A) proportionally
B) not proportional
C) congruent
D) none
Answer:
A) proportionally

Question 62.
In ∆ABC, AB = BC = AC then ∠A = ∠B = ∠C = …………..
A) 70°
B) 60°
C) 80°
D) 90°
Answer:
B) 60°

Question 63.
In the figure, two triangles are similar then x = ……………… cm.

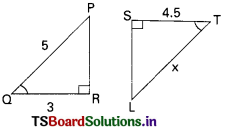
A) 9.3
B) 1.5
C) 7.5
D) 8.5
Answer:
C) 7.5

Question 64.
In the figure, x = …………… cm

A) 10
B) 12
C) 9
D) 8
Answer:
D) 8

Question 65.
In the figure, x = ……………. cm.

A) 12 cm
B) 8 cm
C) 3 cm
D) data is not sufficient
Answer:
D) data is not sufficient

Question 66.
∆ABC ~ ∆PQR, ∠A + ∠B = 100°, ∠R = ……………
A) 60°
B) 80°
C) 90°
D) 100°
Answer:
B) 80°

Question 67.
∆ABC ~ ∆DEF and their areas are respectively 64 cm² and 121 cm² if EF = 15.4 cm then BC = …………….. cm.
A) 10.2
B) 8.7
C) 11.2
D) 10.3
Answer:
C) 11.2

Question 68.
Which of the following are the sides of a right triangle ?
A) 10 cm, 8 cm, 6 cm
B) 12 cm, 1 cm, 9 cm
C) 3 cm, 5 cm, 12 cm
D) all
Answer:
A) 10 cm, 8 cm, 6 cm

Question 69.
From the figure y = …………….. cm.

A) 9
B) 10
C) 12
D) 15
Answer:
D) 15

Question 70.
The diagonal of a trapezium ABCD in which AB // CD intersect at ‘O’. If AB = 2CD then the ratio of areas of triangles AOB and COD is …………….
A) 14 : 1
B) 1 : 2
C) 1 : 9
D) none
Answer:
D) none

Question 71.
∆ABC ~ ∆DEF and 2AB = DE and BC = 8 cm then EF = ………………. cm.
A) 16
B) 19
C) 12
D) none
Answer:
A) 16

Question 72.
∆ABC ~ ∆DEF, BC = 4 cm, EF = 5 cm and area of ∆ABC = 80 cm² then area of ∆DEF = …………… cm².
A) 105
B) 165
C) 125
D) none
Answer:
C) 125

Question 73.
In the figure PQR, ∠QPR = 90°, PQ = 24 cm and QR = 26 cm and in ∆PKR, ∠PKR = 90° and KR = 8 cm then PK = ……………… cm.

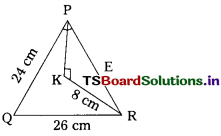
A) 10
B) 6
C) 19
D) 8
Answer:
B) 6

Question 74.
In the figure, QA ⊥ AB and PB ⊥ AB if AO = 20 cm, BO = 12 cm, PB = 18 cm then AQ = ……………. cm.

A) 70
B) 60
C) 40
D) 30
Answer:
D) 30

Question 75.
In the figure, ∠A = ∠B and AD = BE then …………

A) DE // AB
B) DE = AB
C) CD = EB
D) none
Answer:
A) DE // AB

Question 76.
In the figure, in ∆PQR, QR // ST, \(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{3}{5}\) and PR = 28 cm then PT = ……………. cm.

A) 6.5
B) 10.5
C) 8.1
D) 3.3
Answer:
B) 10.5

Question 77.
In an equilateral triangle ABC, AD ⊥ BC meeting BC in D then AD² = …………….
A) 3 BD²
B) BD²
C) AB²
D) none
Answer:
A) 3 BD²

Question 78.
In the figure, if AB // CD then x = …………….. cm.

A) 10
B) 12
C) 7
D) 9
Answer:
C) 7

Question 79.
If the diagonals in a quadrilateral divide each other proportionally then it is ………….
A) square
B) trapezium
C) triangle
D) none
Answer:
B) trapezium

Question 80.
In the figure, DE // AB and FE // DB then DC² …………….

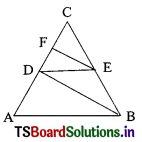
A) CF × AC
B) FE × AB
C) CF × FD
D) none
Answer:
A) CF × AC

Question 81.
D, E and F are the mid points of the sides BC, CA and AB respectively of ∆ABC then the ratio of the areas of ∆DEF and ABC = …………..
A) 1 : 9
B) 2 : 1
C) 1 : 2
D) 1 : 4
Answer:
D) 1 : 4

Question 82.
In the figure \(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{\mathrm{PT}}{\mathrm{TR}}\) and ∠PST = ∠PRQ then ∆PQR is ………………. triangle.
A) isosceles
B) equilateral
C) scalene
D) none
Answer:
A) isosceles

Question 83.
Side of a rhombus is 4 cm then its perimeter is ……………. cm
A) 22
B) 21
C) 16
D) 20
Answer:
C) 16

Question 84.
In the figure, x = ………………

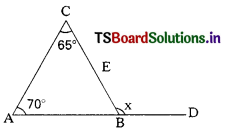
A) 130°
B) 135°
C) 45°
D) 15°
Answer:
B) 135°

Question 85.
Two sides of a right triangle are 3 cm and 4 cm then the third side is …………… cm.
A) 9
B) 6
C) 6.1
D) 5
Answer:
D) 5

Question 86.
∆ABC ~ ∆PQR, AB : PQ = 3 : 4 then ar ∆ ABC : ar ∆ PQR = ……………
A) 9 : 16
B) 9 : 1
C) 16 : 9
D) none
Answer:
A) 9 : 16

Question 87.
If 8² + 15² = k² then k = ………………
A) 16
B) 17
C) 19
D) 20
Answer:
B) 17

Question 88.
The angles of a triangle arc in the ratio 1 : 2 : 3 then the largest angle is ………………
A) 70°
B) 60°
C) 90°
D) 20°
Answer:
C) 90°

Question 89.
Straight angle means ………………..
A) 180°
B) 190°
C) 200°
D) 100°
Answer:
A) 180°

Question 90.
In the figure, PQ // MN, \(\frac{\mathrm{K P}}{\mathrm{P M}}\) = \(\frac{4}{13}\) and KN = 20.4 cm then KQ ……………… = cm.

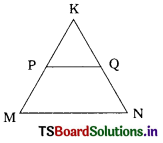
A) 6.3
B) 4.8
C) 1.8
D) 2.8
Answer:
B) 4.8

Question 91.
In the figure DE // BC if AD = x, AE = x + 2, DB = x – 2 and CE = x – 1 then x = ………………

A) 4
B) 5
C) 6
D) 7
Answer:
A) 4

Question 92.
∆ABC ~ ∆DEF if DE : AB = 2 : 3 and ar ∆DEF = 44 sq. units then ar ∆ABC = ……………. sq.units.
A) 90
B) 101
C) 99
D) 110
Answer:
C) 99

We are offering TS 10th Class Maths Notes Chapter 8 Similar Triangles to learn maths more effectively.

TS 10th Class Maths Notes Chapter 8 Similar Triangles

→ The geometrical figures which have the same shape but are not necessarily of the same size are called similar figures.

→ The heights and distances of distant objects can be found using the principles of similar figures.

→ Two polygons with same number of sides are said to be similar if their corresponding angles are equal and their corresponding sides are in proportion.

→ A polygon in which all sides and all its angles are equal is called a regular polygon.

→ The ratio of the corresponding sides is referred to as scale factor or representative factor.

→ All squares are similar.

→ All circles are similar.

→ All equilateral triangles are similar.

→ Two congruent figures are similar but two similar figures need not be congruent.

→ A square ABCD and a rectangle PQRS are of equal corresponding angles, but their corresponding sides are in proportion.
∴ The square ABCD and the rectangle PQRS are not similar.

→ The corresponding sides of a square ABCD and a rhombus PQRS are equal but their corresponding angles are not equal. So they are not similar.

→ If a line is draw parallel to one side of a triangle inter-secting the other two sides at two distinct points then the other two sides are divided in the same ratio.

In ΔABC; DE ∥ BC then \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
This is called Basic Proportionality theorem (or) Thale’s theorem.

→ If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
In ΔABC, a line intersecting AB in D and AC in E such that \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
Then l ∥ BC.
This is converse of Thale’s theorem.

→ Two triangles are similar, if
i) their corresponding angles are equal.
ii) their corresponding sides are in the same ratio.
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio or proportional and hence the two triangles are similar.

In ΔABC, ΔDEF
∠A = ∠D
∠B = ∠E
∠C = ∠F ⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
∴ ΔABC ~ ΔDEF (A . A. A)

→ If in two triangles, sides of one triangle are proportional to the sides of other triangle, then their corre-sponding angles are equal and hence the two triangles are similar.

In ΔABC, ΔDEF
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) ⇒ ∠A = ∠D
∠B = ∠E
∠C = ∠F
Hence, ΔABC ~ ΔDEF (S.S.S)

→ If two angles of a triangle are equal to two corresponding angles of another triangle then the two triangles are similar.

In ΔABC, ΔDEF
∠A = ∠D
∠B = ∠E
⇒ ∠C = ∠F (By Angle sum property)
∴ ΔABC ~ ΔDEF (A.A)

→ If one angle of a triangle is equal to one angle of other triangle and the sides including these angles are proportional, then the two triangles are similar.

In ΔABC, ΔDEF
∠A = ∠D
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
∴ ΔABC ~ ΔDEF (S.A.S)
The ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
\(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{DEF}}=\frac{\mathrm{AB}^2}{\mathrm{DE}^2}=\frac{\mathrm{BC}^2}{\mathrm{EF}^2}=\frac{\mathrm{AC}^2}{\mathrm{DF}^2}\)

→ If a perpendicular is drawn from the vertex, containing the right angle of a right triangle to the hypotenuse, then the triangles on each side of perpendicular are similar to one another and to the original triangle. Also the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.

In ΔABC, ∠B = 90°
BD ⊥ AC
Then ΔADB – ΔBDC ~ ΔABC
and BD² = AD. DC

→ Pythagoras theorem: In a right angled triangle the square of hypotenuse is equal to the sum of the squares of other two sides.

In ΔABC; ∠A = 90°; AB² + AC² = BC²

→ In a triangle, if square of one side is equal to sum of squares of the other two sides, then the angle opposite to the first side is right angle.

In ΔABC, AC² = AB² + BC² then ∠B = 90°
This is converse of Pythagoras theorem.

→ Baudhayan Theorem (about 800 BC) : The diagonal of a rect¬angle produces itself the same area as produced by its both sides.
(i.e., length and breadth)

In rectangle ABCD, area produced by the diagonal AC = AC . AC = AC², area produced by the length = AB . BA = AB², area produced by the breadth = BC. CB = BC²
Hence, AC² = AB² + BC²

→ A sentence which is either true or false but not both is called a simple statement.

→ A statement formed by combining two or more simple statements is called a compound statement.

→ A compound statement of the form “If… then…” is called a Conditional or Implication.

→ A statement obtained by modifying the given statement by ‘NOT’ is called its negation.

Important Formulas:

• Pythagoras Theorem AC² = AB² + BC²
• If ΔABC ~ ΔPQR then \(\frac{\operatorname{ar}(\mathrm{ABC})}{\operatorname{ar}(\mathrm{PQR})}=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^2=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^2=\left(\frac{\mathrm{CA}}{\mathrm{RP}}\right)^2\)

Flow Chat:

Pythagoras (570 – 495 B.C):

• Pythagoras was an Ionian Greek philosopher, mathematician and founder of the religious movement called Pythagoreanism.
• Pythagoras made influential contributions to philosophy and religious teaching in the late 6th century BC.
• He is often revered as a great mathematician, mystic and scientist, but he is best) known for the Pythagorean theorem which bears his name.