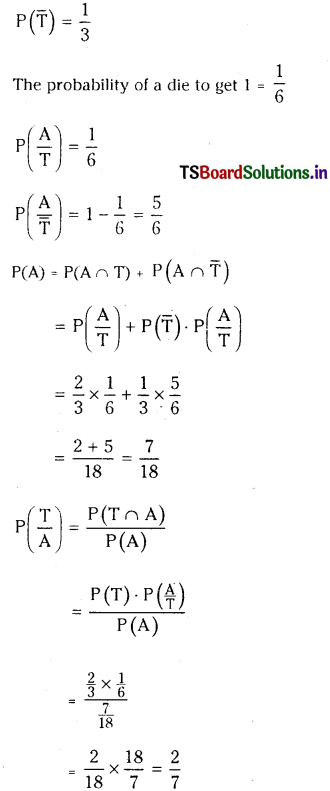TS Inter 2nd Year Maths 2A Solutions Chapter 9 Probability Ex 9(c)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 9 Probability Ex 9(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 9 Probability Ex 9(c)

I.
Question 1.
Three screws are drawn at random from a lot of 50 screws, 5 of which are defective. Find the probability of the event that all 3 screws are non-defective assuming that the drawing is
a) with replacement
b) without replacement
Solution:
Total number of screws = 50
Number of defective screws = 5
Number of non-defective screws = 45
∴ n (S) = ⁵⁰C₃
a) With replacement:
P(E) = \(\frac{45}{50} \times \frac{45}{50} \times \frac{45}{50}=\frac{9}{10} \times \frac{9}{10} \times \frac{9}{10}\)
= \(\left(\frac{9}{10}\right)^3\)

b) Without replacement:
P(E) = \(\frac{45}{50} \times \frac{44}{49} \times \frac{43}{48}=\frac{1419}{1960}\).

Question 2.
If A, B, C are three independent events of an experiment such that
p(A ∩ B ∩ C) = \(\frac{1}{4}\), P\(\left(A^c \cap B \cap C^c\right)\) = \(\frac{1}{8}\), P(C) = \(\frac{1}{4}\) then find P(A), P(B) and P(C).
Solution:

Question 3.
There are 3 black and 4 white balls in one bag, 4 black and 3 white balls In the second bag. A die is rolled and the first bag is selected if the die shows up 1 or 3, and the second bag for the rest Find the probability of drawing a black ball from the bag thus selected.
Solution:
Let E₁, E₂ be the events of selecting first and second bag respectively.
P(E1) = \(\frac{2}{6}\)
P(E2) = 1 – \(\frac{2}{6}\)
= \(\frac{4}{6}\)
Let B be the event of getting black ball from the selected bag.
\(P\left(\frac{B}{E_1}\right)=\frac{3}{7}\),
\(P\left(\frac{B}{E_2}\right)=\frac{4}{7}\)
∴ Required probability = P(E₁ ∩ B) + P(E₂ ∩ B)
= P(E₁) . \(P\left(\frac{B}{E_1}\right)\) + P(E₂). \(P\left(\frac{B}{E_2}\right)\)
= \(\frac{2}{6} \times \frac{3}{7}+\frac{4}{6} \times \frac{4}{7}\)
= \(\frac{6}{42}+\frac{16}{42}=\frac{22}{42}=\frac{11}{21}\)
Probability of drawing a black ball from the bag selected = \(\frac{11}{21}\).

Question 4.
A, B, C are aiming to shoot a balloon. A will succeed 4 times out of 5 attempts. The chance of B to shoot the balloon is 3 out of 4 and that of C is 2 out of 3. If the three aim the balloon simultaneously, then find the probability that atleasi two of them hit the balloon.
Solution:
Given that
P(A) = \(\frac{4}{5}\); P(B) = \(\frac{3}{4}\); P(C) = \(\frac{2}{3}\)
At least two of them will hit the balloon means if A, B hits the balloon then C will not hit or A, C hits the balloon then B will not hit or B, C hits the balloon then A will not hit or all the three will hit the balloon.
Required probability,

Question 5.
If A, B are two events, then show that P(A/B) P(B) + P(A/\(\mathbf{B}^c\)) P(\(\mathbf{B}^c\)) = P(A).
Solution:

Question 6.
A pair of dice are roiled. What is the probability that they sum to 7 given that neither dic shows a 2?
Solution:
Given that neither die shows a ‘2’, when the two dice are rolled, the number of sample points.
n(S) = 36 – 11 = 25
(Faces showing ‘2’ will be excluded)
If E is the event of not getting ‘2’ on both the dice and sum is 7, then
E = {( 1, 6), (3, 4), (4, 3), (6, 1)}
∴ n(E) = 4
∴ Required probability = \(\frac{4}{25}\).

Question 7.
A pair of dice are rolled. What is the probability that neither die shows a 2 gIven that they sum to 7?
Solution:
Since S consists of points whose sum of points on faces is 7.
S = {(1, 6) (2, 5), (3, 4), (4, 3),(5, 2), (6, 1)}
∴ n(S) = 6
Let E be the event of a die not showing ‘2’. then
E = { (1, 6), (3, 4), (4, 3), (6, 1)}
n(E) = 4
∴ Required probability = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}=\frac{4}{6}=\frac{2}{3}\).

Question 8.
If A, B are any two events in an experiment, and P (B) ≠ 1. Show that
P(A/\(\mathbf{B}^c\)) = \(\frac{P(A)-P(A \cap B)}{1-\mathbf{P}(\mathbf{B})}\)
Solution:
\(P\left(\frac{A}{B^{\prime}}\right)=\frac{P(A \cap \bar{B})}{P(\bar{B})}\)
= \(\frac{P(A)-P(A \cap B)}{1-P(B)}\)

Question 9.
An urn contains 12 red balls and 12 green balls. Suppose two balls are drawn one after another wlt.hout replacement Find the probability that the second ball drawn; is green, given that the first ball drawn is red.
Solution:
Let E₁ be the event of drawing a red ball
n (S) = Total number of balls = 24
∴ n(E₁) = ¹²C₁ = 12
∴ P(E) = \(\frac{\mathrm{n}\left(\mathrm{E}_1\right)}{\mathrm{n}(\mathrm{S})}=\frac{12}{24}=\frac{1}{2}\)
Now there are 23 balls remaining.
∴ n(S) = 23
Let \(\frac{E_2}{E_1}\) be the event of drawing a green ball in the second attempt.
∴ n(\(\frac{E_2}{E_1}\)) = ¹²C₁ = 12
∴ P(\(\frac{E_2}{E_1}\)) = \(\frac{12}{23}\)
P(E₁ ∩ E₂) = P(E₁) . P(\(\frac{E_2}{E_1}\))
= \(\frac{1}{2} \cdot \frac{12}{23}=\frac{6}{23}\)
Hence the probability that the second ball drawn is green, given that the first ball drawn is red is \(\frac{6}{23}\).

Question 10.
A single die is rolled twice in succession. What is the probability that the number on the second toss is greater than that on the first rolling?
Solution:
n(S) = 36
Let E be the event that the number on the second toss is greater than that on the first rolling when a single die is rolled twice in succession.
Then E = {(1, 2), ( 1, 3), ( 1, 4),(1, 5), (1, 6 ), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}
n(E) = 15
Hence the probability oF required event
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}=\frac{15}{36}\).

Question 11.
If one card is drawn at random from a pack of cards then show that the event of getting an ace and getting a heart are independent events.
Solution:
Let E₁ be the event of getting an ace and E₂ be the event of getting a heart.
P(E₁) = \(\frac{4}{52}\)
P(E₂) = \(\frac{13}{52}\)
P(E₁) . P(E₂) = \(\frac{4}{52} \times \frac{13}{52}=\frac{1}{52}\)
Common to E₁ and E₂ is an ace from hearts
∴ P(E₁ ∩ E₂) = \(\frac{1}{52}\)
∴ P(E₁ ∩ E₂) = P ( E₁) . P (E₂)
∴ E₁ and E₂ are independent events.

Question 12.
The probability that a boy A will get a scholarship is 0.9 and that another boy B will get is 0.8. What is the probability that atleast one of them will get the scholarship?
Solution:
Let E₁ be the event that A will get scholarship and E₂ be the event that B will get scholarship.
P(E₁) = 0.9;
P(E₂) = 0.8
Required probability
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
= P(E₁) + P(E₂) – P(E₁) . P(E₂)
= 0.9 + 0.8 – 0.72
= 1.7 – 0.72 = 0.98.

Question 13.
If A, B are two events with P(A ∪ B) = 0.65, P (A ∩ B) = 0.15, then find the value of P(\(A^{\mathrm{C}}\)) + P(\(B^{\mathrm{C}}\)).
Solution:
Given that P (A ∪ B) = 0.65;
P (A ∩ B ) = 0.15
From addition theorem on probabilities
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ P(A) + P(B) = P(A ∪ B) + P(A ∩ B)
= 0.65 + 0.15 = 0.8
∴ \(P(\bar{A})+P(\bar{B})\) = 1 – P(A) + 1 – P(B)
= 2 – [P(A) + P(B)]
= 2 – 0.8 = 1.2.

Question 14.
If A, B, C are independent events then show that A B and C are also independent events.
Solution:
P[(A ∪ B) ∩ C] = P(A ∩ C) ∪ (B ∩ C)]
= P(A ∩ C) + P(B ∩ C) – P[(A ∩ C) ∪ (B ∩ C)]
= P(A ∩ C) + P(B ∩ C) – P(A ∩ B ∩ C)
= P(A) . P(C) + P(B) . P(C) – P(A)P(B)P(C)
(∵ A, B, C are independent events)
= [P (A) + P ( B ) – P (A) . P (B)] P( C)
= [P(A) P(B) – P(A ∩ B) ] . P(C)
= P(A ∪ B) . P(C)
= (A ∪ B ) and C are independent events.

Question 15.
A, B are two independent events such that, the probability of both the events to occur is \(\frac{1}{6}\) and the probability of both the events do not occur \(\frac{1}{3}\). Find P(A).
Solution:
Given P(A ∩ B) = \(\frac{1}{6}\) …………..(1)
\(\mathrm{P}(\overline{\mathrm{A}} \cap \overline{\mathrm{B}})=\frac{1}{3}\) ………….(2)
∴ \(\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\overline{\mathrm{B}})=\frac{1}{3}\)
⇒ [1 – P(A)] [1 – P(B)] = \(\frac{1}{3}\)
⇒ 1 – P(A) – P(B) + P(A) . P(B) = \(\frac{1}{3}\)
⇒ 1 – [P(A) + P(B)] + P(A ∩ B) = \(\frac{1}{3}\)
⇒ 1 – [P(A) + P(B)] + \(\frac{1}{6}\) = \(\frac{1}{3}\)
⇒ P(A) + P(B) = \(\frac{5}{6}\)
From (1) P(A) . P(B) = \(\frac{1}{6}\)
P(B) = \(\frac{1}{6 \mathrm{P}(\mathrm{A})}\)
Substituting this in (3)
P(A) + \(\frac{1}{6 \mathrm{P}(\mathrm{A})}\) = \(\frac{5}{6}\)
⇒ 6[P(A)]² + 1 = 5P(A)
⇒ 6[P(A)]² – 5P(A) + 1 = 0
⇒ [3P(A) – 1] [2P(A) – 1] = 0
⇒ P(A) = \(\frac{1}{3}\) or P(A) = \(\frac{1}{2}\).

Question 16.
A fair die is rolled. Consider the events A = {1, 3, 5}, B = {2, 3) and C = {2, 3, 4, 5}.
Find
i) P (A ∩ B), P (A ∪ B)
ii) P(A/B), P(J3/A)
iii) P(A/C), P(C/A)
iv) P(B/C), P(C/B)
Solution:
n(S) = 6
P(A) = \(\frac{3}{6}=\frac{1}{2}\);
P(B) = \(\frac{2}{6}=\frac{1}{3}\) and
P(C) = \(\frac{4}{6}=\frac{2}{3}\)

i) A ∩ B = {3}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{1}{6}\)
A ∪ B = {1, 2, 3, 4, 5}
n(A ∪ B) = 4,
∴ P(A ∪ B) = \(\frac{4}{6}=\frac{2}{3}\)

ii)

iii)

iv)

Question 17.
If A, B, C are three events in a random experiment, prove the following
i) P(A/A) = 1
ii) P(Φ / A) = 0
iii) A ⊆ B ⇒ P(A/C) ≤ P(B/C)
iv) P(A – B) = P(A) – P(A ∩ B)
v) If A, B are mulnally exclusive and P(B) > 0 ihen P (A/B) = 0.
vi) If A, C are mutually exclusive then \(\mathbf{P}\left(\mathbf{A} / \mathbf{B}^{\mathrm{C}}\right)=\frac{\mathbf{P}(\mathbf{A})}{1-\mathbf{P}(\mathbf{B})}\) where P(B) ≠ 1
vii) If A and B are mutually exclusive and P (A ∪ B) ≠ 0 then
P(A/A ∪ B) = \(\frac{\mathbf{P}(\mathbf{A})}{\mathbf{P}(\mathbf{A})+\mathbf{P}(\mathbf{B})}\)
Solution:
i) A ∩ A is the common sample points of A and A is A.
\(P\left(\frac{A}{A}\right)=\frac{P(A \cap A)}{P(A)}=\frac{P(A)}{P(A)}\)
= 1 = R.H.S.

ii) \(P\left(\frac{\phi}{A}\right)=\frac{P(\phi \cap A)}{P(A)}\)
= \(\frac{\mathrm{P}(\phi)}{\mathrm{P}(\mathrm{A})}=\frac{\theta}{\mathrm{P}(\mathrm{A})}\)
= 0 (∵ P(Φ) = 0)

iii) A ⊆ B
⇒ A ∩ C ≤ B ∩ C
⇒ P(A ∩ C) ≤ P(B ∩ C)
\(P\left(\frac{A}{C}\right)=\frac{P(A \cap C)}{P(C)} \leq \frac{P(B \cap C)}{P(C)} \leq P\left(\frac{B}{C}\right)\)
∴ \(\mathrm{P}\left(\frac{\mathrm{A}}{\mathrm{C}}\right) \leq \mathrm{P}\left(\frac{\mathrm{B}}{\mathrm{C}}\right)\)

iv) P(A – B) P(A ∩ \(\))
= P(A ∩ (S – B))
= P[(A ∩ S) – (A ∩ R)]
= P(A) – P(A ∩ B)

v) Given A, B are mutually exclusive.
⇒ A ∩ B = Φ
⇒ P(A ∩ B) = P(Φ) = 0
∴ \(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}=\frac{0}{P(B)}\) = 0
(∵ P(B) > 0).

vi) Given A, B are mutually exclusive.

vii) Given A, B are mutually exclusive.

Question 18.
Suppose that a coin is tossed three times. Let event A be “getting three heads” and B be the event of “getting a head on the first toss”. Show that A and B are dependent events.
Solution:
When a coin is tossed 3 times,
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT)
⇒ n(S) = 6, n(A) = 1,
P(A) = \(\frac{1}{6}\)
When event B occurred, the possibilities are HHH, FIHT, HTI-I, HTT in which HHH is favourable for the event \(\frac{A}{B}\).
P(\(\frac{A}{B}\)) = \(\frac{1}{4}\)
Hence P(A) ≠ P(\(\frac{A}{B}\))
∴ A, B are dependent events.

Question 19.
Suppose that an unbiased pair of dice is rolled. Let A denote the event that the same number shows on each die. Let B denote the event that the sum is greater than 7. Find
(i) P(\(\frac{A}{B}\))
(ii) P(\(\frac{B}{A}\))
Solution:
n(S) = 36
Let A be the event of getting the same number on two dice.
n(A) = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} = 6
P(A) = \(\frac{6}{36}\)
Let B be the event at getting the sum greater then 7.
n(B) = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2), (3, 6), (4, 5), (5, 4), (6, 3), (4, 6), (5, 5), (6, 4), (5, 6), (6, 5), (6, 6)} = 15
P(B) = \(\frac{15}{36}\)
n(A ∩ B) = {(4, 4), (5, 5), (6, 6)} = 3
P(A ∩ B) = \(\frac{3}{36}\)

i) \(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}\)
= \(\frac{\frac{3}{36}}{\frac{15}{36}}=\frac{3}{15}=\frac{1}{5}\)

ii) \(P\left(\frac{B}{A}\right)=\frac{P(B \cap A)}{P(A)}\)
= \(\frac{\frac{3}{36}}{\frac{1}{6}}=\frac{3}{6}=\frac{1}{2}\).

Question 20.
Prove that A and B are independent events if and only if \(P\left(\frac{A}{B}\right)=\mathbf{P}\left(\frac{A}{B^C}\right)\).
Solution:
Let A and B are independent.

∴ L.H.S = R.H.S.

II.
Question 1.
Suppose A and B are independent events with P(A)= 0.6, P (B)= 0.7 thencompute
i) P(A ∩ B)
ii) P(A ∪ B)
iii) P(B/A)
iv) \(\mathbf{P}\left(\mathbf{A}^{\mathrm{C}} \cap \mathbf{B}^{\mathrm{C}}\right)\).
Solution:
i) Given P(A) = 0.6, P(B) = 0.7
and A, B are independent events.
i) P(A ∩ B) = P(A) . P(B)
= 0.6 × 0.7 = 0.42.

ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.7 – 0.42
= 1.3 – 0.42 = 0.88.

iii) \(P\left(\frac{B}{A}\right)=\frac{P(B \cap A)}{P(A)}=\frac{0.42}{0.6}\) = 0.7

iv) \(P(\overline{\mathrm{A}} \cap \overline{\mathrm{B}})=\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\overline{\mathrm{B}})\)
= [ 1 – P(A)] [1 – P(B)]
= ( 1 – 0.6) ( 1 – 0.7)
= (0.4) (0.3) = 0.12.

Question 2.
The probability that Australia wins a match against India in a ciickel gaine is given to be if India and Australia play 3 matches, what is the probability that
i) Australia will loose all the three matches?
ii) Australia will win atleast one match?
Solution:
Let E₁, E₂, E₃ be the events that Australia wins a cricket match against India in the 1st, 2nd and 3rd matches respectively.
P(E₁) = P(E₂) = P(E₃) =
\(\mathrm{P}\left(\overline{\mathrm{E}}_1\right)=\mathrm{P}\left(\overline{\mathrm{E}}_2\right)=\mathrm{P}\left(\overline{\mathrm{E}}_3\right)\)
= 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\).

i) Australia will loose all the three matches is \(\mathrm{P}\left(\overline{\mathrm{E}}_1 \cap \overline{\mathrm{E}}_2 \cap \overline{\mathrm{E}}_3\right)\)
= \(P\left(\bar{E}_1\right) P\left(\overline{\mathrm{E}}_2\right) P\left(\overline{\mathrm{E}}_3\right)\)
= \(\frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3}=\frac{8}{27}\).

ii) Australia will win atleast one match is P(E₁ ∪ E₂ ∪ E₃)
= 1 – P\(\left(\overline{\mathrm{E}}_1 \cap \overline{\mathrm{E}}_2 \cap \overline{\mathrm{E}}_3\right)\)
= 1 – \(\frac{8}{27}\) = \(\frac{19}{27}[latex].

Question 3.
Three boxes numbered I, II, III contain the balls as Follows:

	White	Black	Red
I	1	2	3
II	2	1	1
II	4	5	3

 

One box is randomly selected and a ball is drawn from it. If the ball is red, then find the probability that it is from box II.
Solution:
Let E₁, E₂, E₃ be the events of selecting 1st, 2nd and 3rd boxes.
P(E₁) = P(E₂) = P(E₃) = [latex]\frac{1}{3}\)
Let us denote the event of drawing a red ball by R.

∴ The probability for the ball to he red that it is from box II is \(\frac{1}{4}\).

Question 4.
A person secures a job in a construction company in which the probability that the workers go ou strike is 0.65 and the probability that the construction job will be completed on time if there is no strike is 0.80. If the probability that the construction job will be completedon tinte even if there is a strike is 0.32, determine the probability that the construction job will be completed on time.
Solution:
Given that the probability that the workers go on strike = 0.65
∴ P(S) = 0.65
P\((\overline{\mathrm{S}})\) = 1 – P(S)
= 1 – 0.65 = 0.35.
The probability that the construction job will be completed on time, if there is no strike = 0.80.
\(\mathrm{P}\left(\frac{A}{\overline{\mathrm{S}}}\right)\) = 0.80
The probability that the onstruction job will be completed on time even if there is a strike = 0.32
P\(\left(\frac{A}{S}\right)\) = 0.32
∴ P(A) = P(A ∩ S) + P(A ∩ \(\overline{\mathrm{S}}\))
= P(S) . P\(\left(\frac{A}{S}\right)\) + P\((\overline{\mathrm{S}})\) . \(\mathrm{P}\left(\frac{A}{\overline{\mathrm{S}}}\right)\)
= 0.65 × 0.32 + 0.35 × 0.80 = 0.488.

Question 5.
For any two events A, B show that P(A ∩ B) – P(A) P(B) = \(P\left(A^C\right) P(B)-P\left(A^C \cap B\right)\)
= \(\mathbf{P}(\mathbf{A}) \mathbf{P}\left(\mathbf{B}^{\mathrm{C}}\right)-\mathbf{P}\left(\mathbf{A} \cap \mathbf{B}^{\mathrm{C}}\right)\)
Solution:
\(P\left(A^C\right) P(B)-P\left(A^C \cap B\right)\)
= [1 – P(A)] P(B) – P[(S – A) ∩ B]
= P(B) – P(A P(B) – P [B – (A ∩ B)]
= P(B) – P(A) P(B) – P(B) + P(A ∩ B)
= P(A ∩ B) – P(A)P(B) ……………………(1)
\(\mathbf{P}(\mathbf{A}) \mathbf{P}\left(\mathbf{B}^{\mathrm{C}}\right)-\mathbf{P}\left(\mathbf{A} \cap \mathbf{B}^{\mathrm{C}}\right)\)
= P(A)[1 – P(B)] – P(A ∩ (S – B))
= P(A) – P(A) P(B) – P[A – (A ∩ B)]
= P(A) – P(A) P(B) – P(A) + P(A ∩ B)
= P(A ∩ B) – P(A) P(B) ………….(2)
From (1) and (2) we get
P(A ∩ B) – P(A) P(B) = \(P\left(A^C\right) P(B)-P\left(A^C \cap B\right)\)
= \(\mathbf{P}(\mathbf{A}) \mathbf{P}\left(\mathbf{B}^{\mathrm{C}}\right)-\mathbf{P}\left(\mathbf{A} \cap \mathbf{B}^{\mathrm{C}}\right)\).

III.
Question 1.
Three urns have the following composition of balls.
Urn I: 1 white, 2 black
Urn II: 2 white 1 black
(ini III: 2 white, 2 black
One of the urns is selected at random and a ball is drawn. It turns out to he while. Find the probability that it came from uni III.
Solution:
Let E₁, E₂, E₃ be the events of selecting Urns B₁, B₂, B₃ respectively.
Then P(E₁) = P( E₂) = P(E₃) = \(\frac{1}{3}\)
Let W denote the event of white ball chosen from the Urn III.
Then we have to find P\(\left(\frac{E_3}{\mathrm{~W}}\right)\)
Now
\(P\left(\frac{\mathrm{W}}{\mathrm{E}_1}\right)=\frac{1}{3}, \mathrm{P}\left(\frac{\mathrm{W}}{\mathrm{E}_2}\right)=\frac{2}{3}, \mathrm{P}\left(\frac{\mathrm{W}}{\mathrm{E}_3}\right)=\frac{2}{4}\)
∴ Probability for the ball to be white selected from Urn III by Bayes theorem is

Question 2.
In a shooting lest the probability of A, B, C hitting the targets are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\) and respectively. If all of them fire at the same target, find the probability that (i) only one of them hits the target (ii) atleast one of them bits the target.
Solution:
Given P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{3}\) and P(C) = \(\frac{3}{4}\)
i) The probability that only one of them hits the target

Question 3.
In a certain college, 25% of the boys and 10% of the girls are studying mathematics. The girls constItute 60% of student strength. If a student selected at random is found studying mathematics, find the probability that the student is a girl.
Solution:
Given girls constitute 60% of student strength, we have 40% students are boys probability of an event being girl.

Question 4.
A person is known to speak truth 2 out of 3 times. He throws a die and reports that it is 1. Find the probability that it is actually 1.
Solution:
Given that the probability of a person to speak truth = \(\frac{2}{3}\)
P(T) = \(\frac{2}{3}\)