TS Inter 2nd Year Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(a)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(a)

I.
Question 1.
A p.d.f of a discrete random variable h zero except at the point to x = 0, 1, 2. At these points it has the value P(0) = 3c³ P(1)= 4c – 10c², P(2)= 5c – 1 for same c > 0. Find the value of c.
Solution:
Given P(0) = 3c³,
P(1) = 4c – 10c²,
P(2) = 5c – 1
we have \(\sum_{i=0,1,2}\) P(i) = 1
⇒ P(0) + P(1) + P(2) = 1
⇒ 3c³ + 4c – 10c² + 5c – 1 = 1
⇒ 3c³ – 10c² + 9c – 2 = 0
c = 1 satisfy the equation by inspection and for c = 1, we have
P(0) = 3,
P(1) = 4 – 10 = 6,
P(2) = 4
Hence c = 1 does not satisfy 0 ≤ P (E) ≤ 1.
So we try for other solutions by synthetic division method.

∴ 3c² – 7c + 2 = 0
⇒ 3c² – Gc – c . 2 0
⇒ 3c (c – 2) – 1 (c – 2 )= 0
(3c – 1) (c – 2 ) = 0
c – 2 = 0
⇒ c = 2 is not admissible;
∴ c = \(\frac{1}{3}\) suit the solutions P (0), P (1) and P (2)
∴ c = \(\frac{1}{3}\).

Question 2.
Find the constant c, so that F(x)= c\(\frac{2}{3}\), x = 1, 2, 3, …………… is the p.d.f. of a discrete random variable X.
Solution:
Since F (x) is the p.d.f. oF discrete random variable x.
we have \(\sum_{x=1}^{\infty}\) F(x) = 1

Question 3.

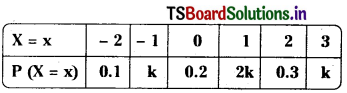
is the probability distribution of a random variable X. Find the value of k and the variance of X.
Solution:
Sum of the probability = 1
⇒ 0.1 + k + 0.2 + 2k + 0.3 + k = 1
⇒ 4k + 0.6 = 1
⇒ 4k = 0.4
⇒ k = 0.1

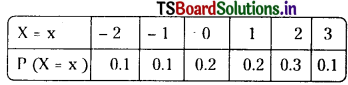
Mean = Σx_i P (X = x_i)
= (- 2 ) × 0.1 + (- 1 ) × 0.1 + 0 × 0.2 + 1 × 0.2 + 2 × 0.3 + 3 × 0.1 = 0.8
Variance σ² = Σx² P (X = x ) – μ²
= ( – 2 )² × 0.1 + ( – 1)² × 0.1 + 0² × 0.2 + 1² × 0.2 + 2² × 0.3 + 3² × 0.1 – ( 0.8 )² = 2.16.

Question 4.

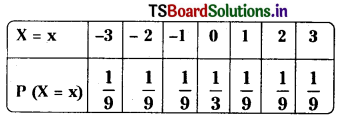
is the probability distribution of a random variable X. Find the value of k and the variance of X.
Solution:

Question 5.
A random variable X has the following probability distribution.

Find i) k ii) the mean and iii) P(0 < X < 5).
Solution:
Sum of the probability = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k²+ 10k – k – 1 = 0
⇒ 10k(k + 1) -1 (k + 1) = 0
⇒ (10k – 1) (k + 1) = 0
⇒ k = \(\frac{1}{10}\); (k = – 1 is not admissible since probability is non-negative).

II.
Question 1.
The range of a random variable X Is (0, 1, 2). Given that P (X = 0) = 3c³,
P (X = 1) = 4c – 10c², P (X = 2) = 5c – 1.
Find (i) the value of c
ii) P(X < 1), P (1 < X ≤ 2) and P (0 < X ≤ 3).
Solution:
i) Sum of the probabilities = 1
⇒ P( X = 0) + P (X = 1) + P (X = 2) = 1
⇒ 3c³ + 4c – 10c² + 5c – 1 = 1
⇒ 3c³ – 10c² + 9c – 2 = 0
⇒ (3c – 1) (c – 1) (c – 2) = 0
⇒ c = \(\frac{1}{3}\) [∵ c ≠ 1, 2].

ii) P(X < 1) = P(X = 0)
= 3c³
= 3 × (\(\frac{1}{27}\)) = \(\frac{1}{9}\)

P(1 < X ≤ 2) = P(X = 2)
= 5c – 1
= 5(\(\frac{1}{27}\)) – 1
= \(\frac{2}{3}\).

P(0 < X ≤ 3) = P(X = 1) + P(X = 2)
= 4c – 10c² + 5c – 1
= – 10c² + 9c – 1
= \(-\frac{10}{9}+\frac{9}{3}-1=\frac{8}{9}\).

Question 2.
The range of a random variable X is {1, 2, 3, …………} and P (X = k) = \(\frac{c^{\mathbf{k}}}{\mathbf{k} !}\). Find the value of c and P (0 < X < 3).
Solution:
∵ Σ P(X = k) = 1