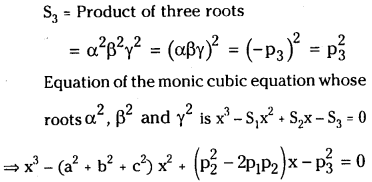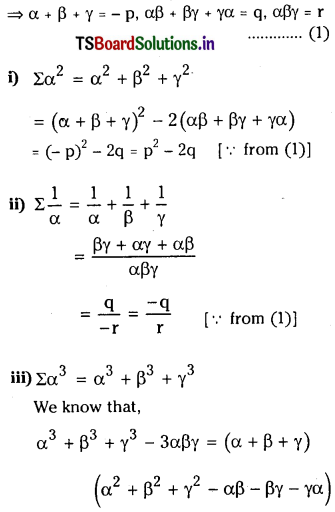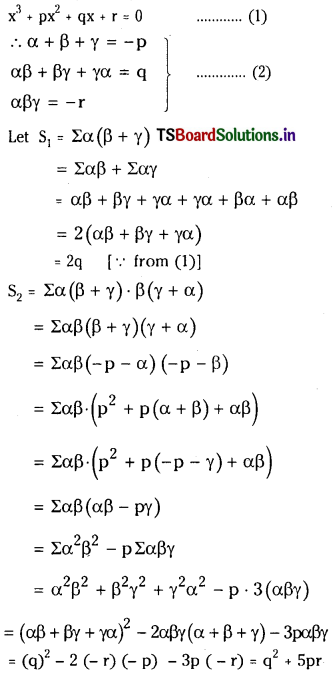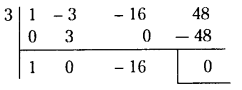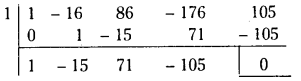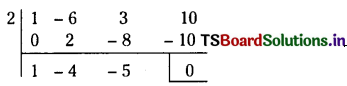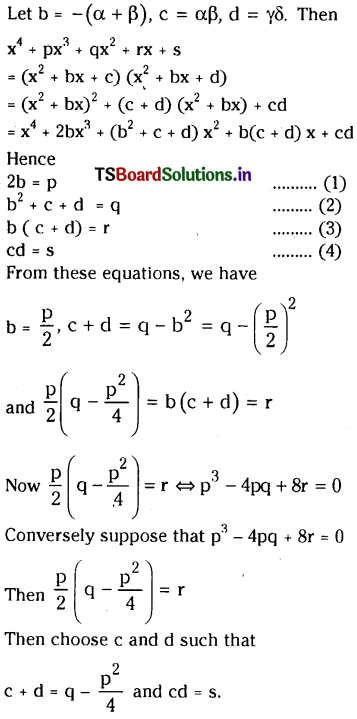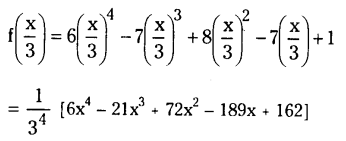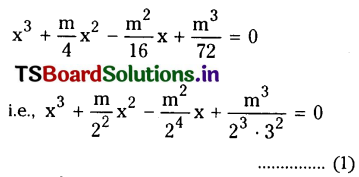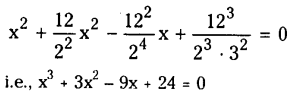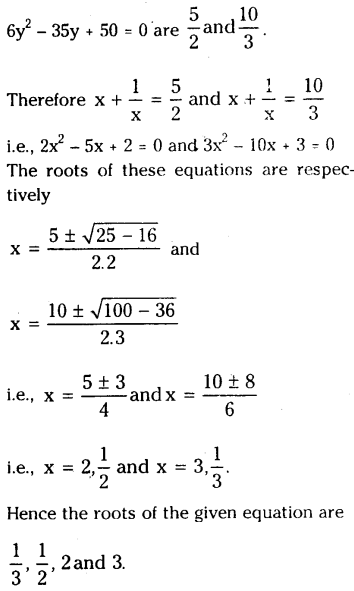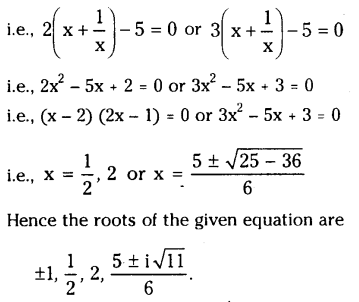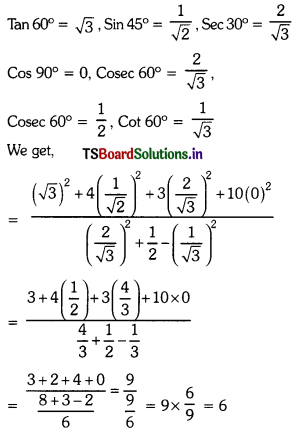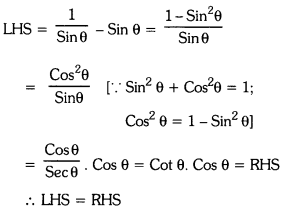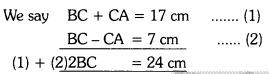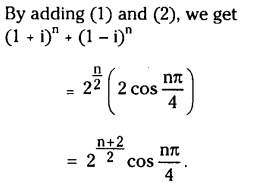Students must practice this TS Intermediate Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(b) to find a better approach to solving the problems.
TS Inter 2nd Year Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(b)
I.
Question 1.
In the experiment of tossing a coin n times, If the variable X denotes the number of heads and P (X = 4), P (X = 5), p (X = 6) are in arithmetic progression then find n.
Solution:
X follows binomial distribution with p = \(\frac{1}{2}\), q = \(\frac{1}{2}\)
P (X = 4), P (X = 5), P (X = 6) are in A.P.
∴ 2P (X = 5) = P (X = 4) + P (X = 6)

⇒ n2 – 21n + 98 = 0
⇒ (n – 7) (n – 14) = 0
⇒ n = 7 or 14.
![]()
Question 2.
Find the minimum number of times a fair coin must be tossed so that the probability of getting atleast one head is 0.8.
Solution:
When a coin is tossed we have p = \(\frac{1}{2}\), q = \(\frac{1}{2}\)
P(X = x) = nCx pxqn-x
P(X = 0) = nC0 p0qn-0
Given probability 0f getting atleast one head is atleast 0.8
P(X ≥ 1 ) ≥ 0.8
⇒ 1 – P (X = 0) ≥ 0.8
⇒ 1 – \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) ≥ 0.8
⇒ – \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) ≥ – 0.2
⇒ \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) < (0.2). Which is true for n = 3.
Question 3.
The probability of a bomb hitting a bridge is 1/2 and three direct hits (not necessarily consecutive) are needed to destroy it. Find the mmiinuni number of bombs required so that the probability of bridge being destroyed is greater than 0.9.
Solution:
Given probability of a bomb hitting a bridge is \(\frac{1}{2}\).
∴ p = \(\frac{1}{2}\);
q + p = 1 ⇒ q = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Let X represents the minimum number of bombs to be dropped so that the bridge can be destroyed. Given that P (X ≥ 3) > 0.9
⇒ 1 – P(X < 3) > 0.9
⇒ 1 – [ P(X = 0) + P(X = 1) + P (X = 2)] > 0.9
⇒ 1 – [\({ }^n \mathrm{C}_0\left(\frac{1}{2}\right)^{\mathrm{n}}+{ }^{\mathrm{n}} \mathrm{C}_1\left(\frac{1}{2}\right)^{\mathrm{n}-1}\left(\frac{1}{2}\right)\) + \({ }^{\mathrm{n}} C_2\left(\frac{1}{2}\right)^{\mathrm{n}-2}\left(\frac{1}{2}\right)^2\)] > 0.9

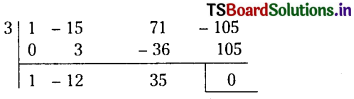
By substituting the values for ‘n’ we see that n = 9, 10, 11. satisfies the above in equation.
∴ The minimum number of bombs to be dropped so that the bridge Is to be destroyed is n = 9.
![]()
Question 4.
If the difference between the mean and the variance of a binomial variate is 5/9 then find the probability for the event of 2 successes when the experiment is conducted 5 times.
Solution:
Given n = 5 and
given that mean – variance of a Binomial variate is \(\frac{5}{9}\).
∴ np – npq = \(\frac{5}{9}\)
np(1 – q) = \(\frac{5}{9}\)
⇒ npq = \(\frac{5}{9}\)
⇒ 5p (1 – q) = \(\frac{5}{9}\)
⇒ 5p (p) = \(\frac{5}{9}\)
⇒ p2 = \(\frac{5}{9}\)
⇒ p = \(\frac{1}{3}\)
∴ q = \(\frac{2}{3}\)
∴ P(X = 2) = 5C2 \(\left(\frac{1}{3}\right)^2\left(\frac{2}{3}\right)^{5-2}\)
= 10 × \(\frac{1}{9} \times \frac{8}{27}=\frac{80}{243}\)
Question 5.
One in 9 ships is likely to be wrecked, when they are set on sail. When 6 ships set on sail, find the probability for
i) Atleast one will arrive safely
ii) Exactly three will arrive safely.
Solution:
Let q = Probability of one in 9 ships to be wrecked = \(\frac{1}{9}\)
p = 1 – q
= 1 – \(\frac{1}{9}\) = \(\frac{8}{9}\)
Here n = 6.
i) Probability ¡or atleast one will arrive safely
P (X ≥ 1) = 1 – P(X = 0)
= 1 – \({ }^6 C_0\left(\frac{8}{9}\right)^0\left(\frac{1}{9}\right)^{6-0}\)
= 1 – \(\frac{1}{9^6}\)
ii) Exactly, three will arrive safely
P (X = 3) = 6C3 \(\left(\frac{8}{9}\right)^3\left(\frac{1}{9}\right)^{6-3}\)
= \({ }^6 C_3 \frac{8^3}{9^3} \frac{1}{9^3}={ }^6 C_3 \frac{8^3}{9^6}\)
= \(20\left(\frac{8^3}{9^6}\right)\).
![]()
Question 6.
If the mean and variance of a binomial variate X are 2.4 and 1.44 respectively, find P (1 < X ≤ 4).
Solution:
Mean = np = 2.4;
Variance = npq = 1.44
∴ \(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{1.44}{2.4}\) = 0.6
⇒ q = 0.6
and p = 1 – 0.6 = 0.4
∴ np = 2.4
⇒ n (0.4) = 2.4
⇒ n = 6
∴ P(1 < X ≤ 4) = P (X = 2) + P(X = 3) + P (X = 4)

Question 7.
If is given that 10% of the electric bulbs manufactured by a company are defective. In a sample of 20 bulbs, find the probability that more than 2 are defective.
Solution:
Probability for an electric bulb to be defective, p = \(\frac{10}{100}\) = 0.1
∴ Probability for a non defective bulb
q = 1 – p = 1 – 0.1 = 0.9
Probability to have more than 2 are defectives
⇒ P(X > 2) = 1 – P(X ≤ 2)
1 – [P (X = 0) + P(X = 1) + P(X = 2)]
We have
P(X = x) = nCx pxqn-x

![]()
Question 8.
On an average, rain falls on 12 days in every 30 days, find the probability that, rain will fall on just 3 days of a given week.
Solution:
Given the probability for the day to be rainy = \(\frac{12}{30}=\frac{2}{5}\)
∴ p = \(\frac{2}{5}\) and
q = 1 – p
= 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Also, n = 7
∴ Probability for the rain to fall on just 3 days of a given week
P(X = 3) = 7C3 \(\left(\frac{2}{5}\right)^3\left(\frac{3}{5}\right)^{7-3}\)
= 7C3 \(\left(\frac{2}{5}\right)^3\left(\frac{3}{5}\right)^4\)
= \(\frac{35 \times 2^3 \times 3^4}{5^7}\)
Question 9.
For a binomial distribution with mean 6 and variance 2, find the first two terms of the distribution.
Solution:
Given mean = np = 6
and variance = npq = 2
∴ q = \(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{2}{6}=\frac{1}{3}\)
∴ p = 1 – q
= 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
∴ np = 6
⇒ \(\frac{2 n}{3}\) = 6
⇒ n = 9
We have P (X = x)
= nCx px qn-x
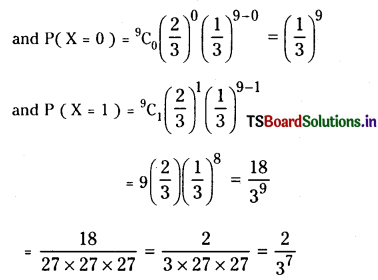
![]()
Question 10.
In a city 10 accidents take place in a span of 50 days. Assuming that the number of accidents follows the Poisson distribution, find the probability that there will be 3 or more accidents in a day.
Solution:
Here λ = \(\frac{10}{50}=\frac{1}{5}\)
∴ The probability that there will be 3 or more accidents in a day using Poisson variate.
P (X = x) = \(\frac{c^{-\lambda} \lambda^x}{x !}\)
P (X ≥ 3) = 1 – [P (X = 0) + P(X = 1) + P(X = 2)]

![]()
II.
Question 1.
Five coins are tossed 320 times. Find the frequencies of the distribution of the number of heads and tabulate the result.
Solution:
When a coin is tossed we have p = \(\frac{1}{2}\) and q = \(\frac{1}{2}\).
Here n = 5;
The frequencies of distribution of the number of heads is given using binomial distribution given by
fx = N. nCx px qn-x,
x = 0,1, 2, 3, 4, 5, (Number of heads)
when x = 0

![]()
Question 2.
Find the probability of guessing atleast 6 out of 10 of answers in
(i) True or false type examination
(ii) Multiple choice with 4 possible answers.
Solution:
i) Probability of guessing atleast 6 out of 10 answers in
(i) True or false type examination is
P(X ≥ 6) = P(X = 6) P(X = 7) + P (X = 8) + P (X = 9)
Here P (X = x) = nCx px qn-x and
probability for an answer to be true or false,
p = \(\frac{1}{2}\), q = \(\frac{1}{2}\), n = 10
p – q = n = 10

ii) Probability for a question to guess in multiple choice type with 4 answers is
p = \(\frac{1}{4}\), q = \(\frac{3}{4}\)
∴ P(X ≥ 6) = P(X = 6) + P(X = 7) + P(X = 8) + P (X = 9) + P(X = 10)
where P (X = x) = nCx px qn-x
= 10Cx \(\left(\frac{1}{4}\right)^x\left(\frac{3}{4}\right)^{10-x}\)

In the above two cases (i) and (ii).
i) Probability to guess 6 out of 10 questions in true or false examination is = 10C6 \(\left(\frac{1}{2}\right)^{10}\)
ii) Probability to guess 6 out of 10 questions in Multiple choice type with 4 answers = 10C6 . \(\frac{3^4}{4^{10}}\).
![]()
Question 3.
The number of persons joining a cinema ticket counter in a minute has poisson distribution with parameter 6. Find the probability that
(i) no one joins the queue in a particular minute
(ii) two or more persons join in the queue in a minute.
Solution:
Given λ = 6, and poisson distribution function is given by
P (X = x) = \(\frac{\lambda^x e^{-\lambda}}{x !}\), x = 0, 1, 2, 3, ………..
i) Probability that no one joins the queue in a particular minute is
P (X = 0) = \(\frac{\lambda^0 \mathrm{e}^{-6}}{0 !}\) = e-6.
ii) Probability for two or more persons join in the queue in a minute is
P (X ≥ 2) = 1 – [P (X = 0) + P (X = 1)]
= 1 – \(\left[\mathrm{e}^{-6}+\frac{\lambda \mathrm{e}^{-\lambda}}{1 !}\right]\)
= 1 – e-6 – 6 e-6.