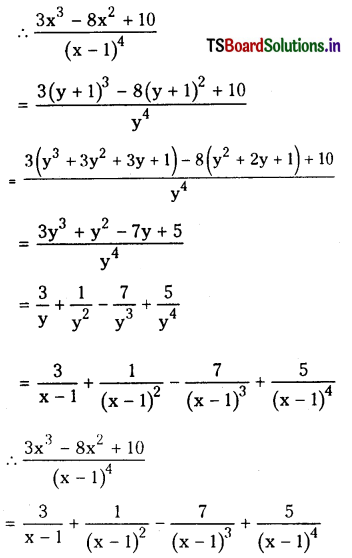TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(a)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(a)

Resolve the following fractions into partial fractions.

I.
Question 1.
\(\frac{2 x+3}{(x+1)(x-3)}\)
Solution:
Let \(\frac{2 x+3}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}\)
⇒ A (x – 3) + B (x + 1) = 2x – 3 …………..(1)
Substituting x = 3 in (1),
weget 4B = 9 .
⇒ B = \(\frac{9}{4}\)
Substituting x = – 1 in (1),
we get – 4A = 1
⇒ A = \(\frac{-1}{4}\)
∴ \(\frac{2 x+3}{(x+1)(x-3)}=\frac{9}{4(x-3)}-\frac{1}{4(x+1)}\).

Question 2.
\(\frac{5 x+6}{(2+x)(1-x)}\)
Solution:
Let \(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\)
⇒ A (1 – x) + B (2 + x) = 5x + 6 ……………..(1)
Substituting x = 1 in (I),
weget 3B = 11
⇒ B = \(\frac{11}{3}\)
Substituting x = – 2 in (1),
we get 3A = – 4
⇒ A = \(\frac{-4}{3}\)
∴ \(\frac{5 x+6}{(2+x)(1-x)}=\frac{11}{3(1-x)}-\frac{4}{3(2+x)}\).

II.
Question 1.
\(\frac{3 x+7}{x^2-3 x+2}\)
Solution:
We know that
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-2)(x-1)}\)
Let \(\frac{3 x+7}{(x-2)(x-1)}=\frac{A}{x-2}+\frac{B}{x-1}\)
⇒ A (x – 1) + B(x – 2) = 3x + 7 …………..(1)
SubstitutIng x = 2 in (1)
we get A = 13
Substituting x = 1 in (1)
we get – B = 10 i.e., B = – 10
∴ \(\frac{3 x+7}{x^2-3 x+2}=\frac{13}{x-2}-\frac{10}{x-1}\)

Question 2.
\(\frac{x+4}{\left(x^2-4\right)(x+1)}\)
Solution:
We know that
\(\frac{x+4}{\left(x^2-4\right)(x+1)}=\frac{x+4}{(x-2)(x+2)(x+1)}\)
Let \(\frac{x+4}{(x-2)(x+2)(x+1)}\) = \(\frac{A}{x-2}+\frac{B}{x+2}+\frac{C}{x+1}\)
A (x + 2) (x + 1) + B (x – 2) (x + 1) + C (x – 2) (x + 2) = x + 4 …………..(1)
Substituting x = 2 in (1), we have
12A = 6
A = \(\frac{1}{2}\)
Substituting x = – 2 in (1), we have
4B = 2
⇒ B = \(\frac{1}{2}\)
Substituting x = – 1 in (1), we have
– 3C = 3
⇒ C = – 1
∴ \(\frac{x+4}{\left(x^2-4\right)(x+1)}\) = \(\frac{1}{2(x-2)}+\frac{1}{2(x+2)}-\frac{1}{x+1}\)

Question 3.
\(\frac{2 x^2+2 x+1}{x^3+x^2}\)
Solution:
We know that
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}\)
Let \(\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
⇒ Ax (x + 1) + B (x + 1) + Cx2 = 2x + 2x + 1
Substituting x = 0 in (1), we have B = 1
Substituting x = – 1 in (1), we have C = 1
Equating coefficient of x² on both sides in (1), we have
A + C = 2
⇒ A = 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\).

Question 4.
\(\frac{2 x+3}{(x-1)^3}\)
Solution:
Let \(\frac{2 x+3}{(x-1)^3}\) = \(\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{(x-1)^3}\)
⇒ A(x – 1)² + B(x – 1) + C = 2x + 3 ……………..(1)
Substituting x = 1 in (1).
we get C = 5
Equating coefficient of x² on both sides in (1)
We get A = 0
Equating coefficient of x on both sides in (1)
We get – 2A + B = 2
⇒ B = 2.

Alternate method:
Let x – 1 = y

Question 5.
\(\frac{x^2-2 x+6}{(x-2)^3}\)
Solution:
Let x – 2 = y

III.
Question 1.
\(\frac{x^2-x+1}{(x+1)(x-1)^2}\)
Solution:
Let \(\frac{x^2-x+1}{(x+1)(x-1)^2}\) = \(\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\)
A (x – 1)² + B (x + 1) (x – 1) + C (x + 1) = x² – x + 1 ………..(1)
Substituting x = 1 in (1), we get
2C = 1
⇒ C = \(\frac{1}{2}\)
Substituting x = – 1 in (1), we get
4A = 3
⇒ A = \(\frac{3}{4}\)
Equating coefficient of x² on both sides in (1)
We get A + B = 1
\(\frac{3}{4}\) + B = 1
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}\) = \(\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\)

Question 2.
\(\frac{9}{(x-1)(x+2)^2}\)
Solution:
Let \(\frac{9}{(x-1)(x+2)^2}\) = \(\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\)
⇒ A (x + 2)² + B (x – 1) (x + 2) + C (x – 1) = 9 …………….(1)
Substituting x = 1 in (1), we get
9A = 9
⇒ A = 1
Substituting x = – 2 in (1), we get
– 3C = 9
⇒ C = – 3
Equating coefficient of x² on both sides in (1),
we get A + B = 0
⇒ B = – 1
∴ \(\frac{9}{(x-1)(x+2)^2}\) = \(\frac{1}{x-1}-\frac{1}{(x+2)}-\frac{3}{(x+2)^2}\).

Question 3.
\(\frac{1}{(1-2 x)^2(1-3 x)}\)
Solution:
Let \(\frac{1}{(1-2 x)^2(1-3 x)}\) = \(\frac{A}{(1-3 x)}+\frac{B}{(1-2 x)}+\frac{C}{(1-2 x)^2}\)
⇒ A (1 – 2x)² + B (1 – 3x) (1 – 2x) + C (1 – 3x) = 1 …………..(1)
Substituting x = \(\frac{1}{2}\) in (1),
we get \(\frac{-C}{2}\) = 1
⇒ C = – 2
Substituting x = \(\frac{1}{3}\) in (1),
we get \(\frac{\mathrm{A}}{9}\) = 1
⇒ A = 9
Substituting x = 0 in (1),
We get A + B + C = 1
⇒ 9 + B – 2 = 1
⇒ B = – 6
∴ \(\frac{1}{(1-2 x)^2(1-3 x)}\) = \(\frac{9}{1-3 x}-\frac{6}{1-2 x}-\frac{2}{(1-2 x)^2}\)

Question 4.
\(\frac{1}{x^3(x+a)}\)
Sol.
Let \(\frac{1}{x^3(x+a)}=\frac{A}{x+a}+\frac{B}{x}+\frac{C}{x^2}+\frac{D}{x^3}\)
⇒ Ax³ + Bx² (x + a) + Cx (x + a) + D (x + a) = 1 …………(1)
Substituting x = – a in (1),
we get – a³A = 1
⇒ A = \(\frac{-1}{a^3}\)
Equating coefficient of x³ on both sides,
we get A + B = 0
⇒ B = \(\frac{-1}{a^3}\)
Substituting x = 0 in (1),
we get aD = 1
Equating coefficient of x on both sides,
we get aC + D = 0
⇒ aC + \(\frac{1}{a}\) = 0
⇒ C = \(\frac{-1}{a^2}\)
∴ \(\frac{1}{x^3(x+a)}\) = \(\frac{-1}{a^3(x+a)}+\frac{1}{a^3 x}-\frac{1}{a^2 x^2}+\frac{1}{a x^3}\).

Question 5.
\(\frac{x^2+5 x+7}{(x-3)^3}\)
Solution:
Let x – 3 = y

Question 6.
\(\frac{3 x^3-8 x^2+10}{(x-1)^4}\)
Solution:
Let x – 1 = y