TS 10th Class Maths Important Questions Chapter 12 Applications of Trigonometry

These TS 10th Class Maths Chapter Wise Important Questions Chapter 12 Applications of Trigonometry given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 12 Applications of Trigonometry

Previous Exams Questions

Question 1.
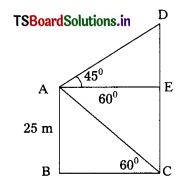
A person from the top of a building of height 25 m has observed another building top and bottom at an angle of elevation 45° and at an angle of depression 60° respectively. Draw a diagram for this data. (T.S. Mar. ’15)
Solution:

Question 2.
A ladder of 3.9 m length is laid against a wall. The distance between the foot of the wall and the ladder is 1.5 m. Find the height at which the ladder touches the wall. (T.S. Mar. ’15)
Solution:

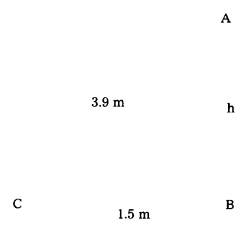
h² = (3.9)² – (1.5)²
= (3.9 + 1.5) (3.9 – 1.5)
= 5. 4 × 2.4
= (0.6 × 9) × (0.6 × 4)
= (0.6)² × 6²
∴ h = 6 × 0.6 = 3.6 m

Question 3.
An observer flying in an aeroplane at an altitude of 900 m observes two ships in front of him, which are in the same direction at an angles of depression of 60° and 30° respectively. Find the distance between the two ships. (T.S. Mar. ’15)
Solution:

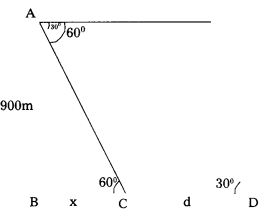
In ∆ABC
Tan 60 = \(\frac{900}{\mathrm{x}}\)
\(\sqrt{3}\) = \(\frac{900}{\mathrm{x}}\)
⇒ x = \(\frac{900}{\sqrt{3}}\) = 300\(\sqrt{3}\)
In ∆ ABD
Tan 30 = \(\frac{900}{\mathrm{x+d}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{900}{300 \sqrt{3}+d}\)
d = 600\(\sqrt{3}\) m

Question 4.
If the angle of elevation of sun increases from ‘O’ to 90 then the length of shadow of a tower decreases. Is this true ? Justify your answer. (T.S. Mar. ’16)
Solution:
Yes, this statement is true.
We observe this in day to day life.

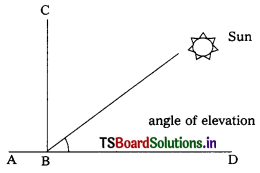
AD – ground
BC – tower
AB – shadow

Question 5.
A boat has to cross a river. It crosses river by making an angle of 60° with bank, due to the stream of river it travels a distance of 450 m to reach another side of river. Draw a diagram to this data. (T.S. Mar. ’15)
Solution:

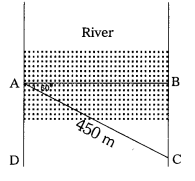
AB – width of river
AD, BC are river banks
AC – The distance travelled in river = 450 m
A – initial point, C – terminal point

Question 6.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road, the angles of elevation of top of the poles are 60° and 30°. Find the height of poles, (T.S. Mar. ’16)
Solution:
As shown in the figure

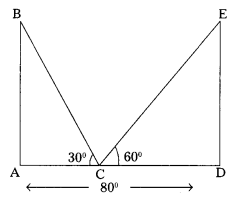
AD = width of road = 80 m.
AB, DE are two poles
AB = DE (∵ they have equal heights)
‘C’ is a point on road.
∠ACB = 30°, ∠DCE = 60°
Then in ∆ ACB
tan C = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ tan 30 = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ AC = AB\({\sqrt{3}}\) ……………….. (1)
In ∆ CDE
tan C = \(\frac{\mathrm{DE}}{\mathrm{CD}}\)
⇒ tan 60 = \(\frac{\mathrm{DE}}{\mathrm{CD}}\)
\({\sqrt{3}}\) = \(\frac{\mathrm{DE}}{\mathrm{CD}}\)
⇒ CD = \(\frac{\mathrm{DE}}{\sqrt{3}}\) ……………… (2)
but AC + CD = AD
⇒ AB\({\sqrt{3}}\) + \(\frac{\mathrm{DE}}{\sqrt{3}}\) = 80
But DE = AB
⇒ AB\({\sqrt{3}}\) + \(\frac{\mathrm{AB}}{\sqrt{3}}\) = 80
⇒ \(\frac{3 \mathrm{AB}+\mathrm{AB}}{\sqrt{3}}\) = 80
⇒ 4AB = 80\({\sqrt{3}}\)
⇒ AB = \(\frac{80 \sqrt{3}}{4}\) = 20 \({\sqrt{3}}\) m.
So height of the pole = 20 m.

Additional Questions

Question 1.
The angle of elevation of the top of a Tree from the foot of building is 60° and the angle of elevation of the top of the building from the foot of the tree is 30° what is the ratio of heights of tree and building.
Solution:

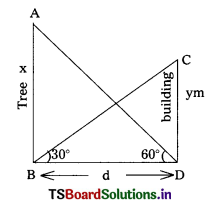
Let the height of the tree = x m = AB
Let the height of the building = y m = CD
distance between the tree and building = d = BD
Angle of elevation of the top of the tree = 60°
From the figure tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\) = \(\frac{\mathrm{x}}{\mathrm{d}}\)
\(\sqrt{3}\) = \(\frac{\mathrm{x}}{\mathrm{d}}\)
d = \(\frac{\mathrm{x}}{\sqrt{3}}\) ……………. (1)
∴ tan 30° = \(\frac{\mathrm{CD}}{\mathrm{BD}}\) = \(\frac{\mathrm{y}}{\mathrm{d}}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{y}}{\mathrm{d}}\)
d = y\(\sqrt{3}\) ………………. (2)
\(\frac{\mathrm{x}}{\sqrt{3}}\) = y\(\sqrt{3}\)
\(\frac{\mathrm{x}}{\mathrm{y}}\) = \(\sqrt{3}\) × \(\sqrt{3}\)
\(\frac{\mathrm{x}}{\mathrm{y}}\) = \(\frac{3}{1}\)
x : y = 3 : 1
Hence, the ratio of the heights of the tree and building = 3 : 1.

Question 2.
The angle of the top of a pillar from two points are at a distance of 7m and 12m Find the height of the pillar from the base of the pillar and in the same straight line with it are complementary.
Solution:

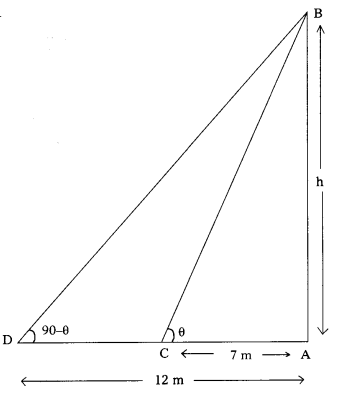
From the figure,
Let AB be a height of the pillar = h m
Let the two points on the ground be ’c and d’ such that they make a distance 7 m and 12 m
From foot of the pillar
AC = 7m ; AD = 12m
Angles of elevation are ∠ACB = 0 ;
∠ADB = (90 – θ)
In the right angled ∆ABC, we have
tan θ = \(\frac{\mathrm{AB}}{\mathrm{AD}}\)
tan θ = \(\frac{\mathrm{h}}{7}\) …………… (1)
From.the right angled ∆ABC we have
tan (90 – θ) = \(\frac{\mathrm{AB}}{\mathrm{AD}}\)
cot θ = \(\frac{\mathrm{h}}{12}\)
\(\frac{1}{\tan \theta}\) = \(\frac{\mathrm{h}}{12}\)
tan θ = \(\frac{12}{\mathrm{~h}}\) …………….. (2)
From (1) and (2)
\(\frac{\mathrm{h}}{12}\) = \(\frac{12}{\mathrm{~h}}\)
h² = 84
h = \(\sqrt{4 \times 21}\)
h = 2 \(\sqrt{21}\) m
∴ The height of the pillar = h = 2 \(\sqrt{21}\)

Question 3.
A wire of length 25m had been tied with electric pole at an angle of elevation 30° with the ground. Because it was covering a long distance, it was cut and tied at an angle of elevation 60° with the ground how much length of the wire was cut.
Solution:

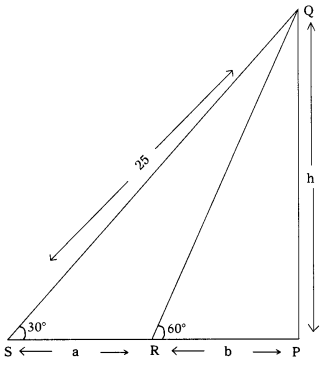
In the figure
Let PQ be a height of the electric pole = h m
given QS be the actual length of the wire = 25 m
let Q is length of the wire was cut S, R are the first and second points of observations.
Let PS = a + b ; PR = b
Angles of elevations are ∠PSQ = 30°
∠PRQ = 60°
From ∆PSQ
sin 30° = \(\frac{\mathrm{PQ}}{\mathrm{QS}}\)
\(\frac{1}{2}\) = \(\frac{\mathrm{PQ}}{\mathrm{QS}}\)
2 PQ = 25
PQ = 12.5
From ∆PRQ
tan 60° = \(\frac{\mathrm{PQ}}{\mathrm{QS}}\)
\(\sqrt{3}\) = \(\frac{12.5}{\mathrm{b}}\)
PR = b = \(\frac{12.5}{\sqrt{3}}\)
∆PQR, From
cos 60° = \(\frac{\mathrm{PR}}{\mathrm{QR}}\)
\(\frac{1}{2}\) = \(\frac{\frac{12.5}{\sqrt{3}}}{\mathrm{QR}}\)
\(\frac{1}{2}\) = \(\frac{12.5}{\sqrt{3 \mathrm{QR}}}\)
QR = \(\frac{25}{\sqrt{3}}\)
∴ Length of the wire was cut = \(\frac{25}{\sqrt{3}}\)

Question 4.
Two boys are on opposite sides of a tower 200m height. They measure the angle of elevation of the top of the tower as 45°, 60° respectively. Find the distance through which the boys are separated.
Solution:

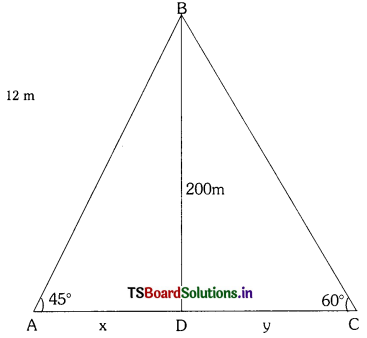
Given height of Tower = 200 m
We say ‘x’ is the distance between 1^st person and base of the tower and ‘y’ is the distance between 2^nd person and base of the tower.
From ∆ ABD
Tan 45° = \(\frac{\mathrm{BD}}{\mathrm{AD}}\)
1 = \(\frac{200}{\mathrm{x}}\)
x = 200m
From ∆ BDC
Tan 60° = \(\frac{\mathrm{BD}}{\mathrm{DC}}\)

Question 5.
The tower height is l5mts and length of shadow is 15 \(\sqrt{3}\) m what is the angle of elevation of the sun.
Solution:

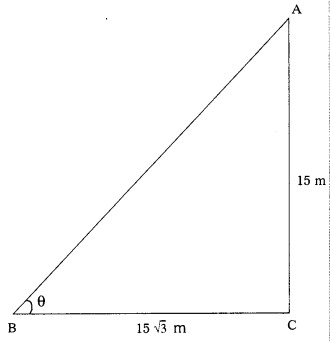
Let AC be the height of the tower = 15 m
Length of shadow = 15\(\sqrt{3}\) m
Let angle of elevation be θ.
From ∆ ABC Tan θ = \(\frac{\mathrm{AC}}{\mathrm{BC}}\) = \(\frac{15}{15 \sqrt{3}}\)
Tan θ = \(\frac{1}{\sqrt{3}}\)
Tan θ = Tan 30°
θ = 30°
∴ the angle of elevation of the sun θ = 30°