TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(d)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(d)

Question 1.
Find the coefficietil of x³ in the power series expansion of \(\frac{5 x+6}{(x+2)(1-x)}\) specifying the region in which the expansion is valid.
Solution:
Given rational fraction \(\frac{5 x+6}{(x+2)(1-x)}\)
Let \(\frac{5 x+6}{(x+2)(1-x)}\) = \(\frac{A}{x+2}+\frac{B}{1-x}\)
⇒ A (1 – x) + B (x + 2) = 5x + 6 …………..(1)
Substituting x = 1 in (1), we get
3B = 11
⇒ B = \(\frac{11}{3}\)
Substituting x = – 2 in (1), we get
3A = – 4
⇒ A = \(\frac{-4}{3}\)

Question 2.
Find the coefficient of x⁴ in the power series expansion of \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}\) specifying the Interval in which the expansion is valid.
Solution:
Let \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}=\frac{A}{x-3}+\frac{B x+C}{x^2+2}\)
⇒ A (x² + 2) + (Bx + C) (x – 3) = 3x² + 2x ……………(1)
Substituting x = 3 ¡n (1), we get
11A = 33
⇒ A = 3
Equating coefficient of x² on both sides in (1), we get
A + B = 3
⇒ 3 + B = 3
⇒ B = 0
Substituting x = 0 in (1), we get
2A – 3C = 0
⇒ 3C = 2A
⇒ C = 2

The above expansions are valid for |x| < √2.

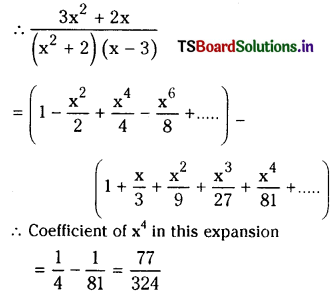
Question 3.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x-4}{x^2-5 x+6}\) specifying the region in which the expansion is valid.
Solution:
We know that
\(\frac{x-4}{\left(x^2-5 x+6\right)}=\frac{x-4}{(x-2)(x-3)}\)
Let \(\frac{x-4}{x^2-5 x+6}=\frac{A}{(x-2)}+\frac{B}{(x-3)}\)
⇒ A(x – 3) + B(x – 2) = x – 4 …………(1)
Substituting x = 3 in (1), we get B = – 1
substituting x = 2 in (1), we get A = 2

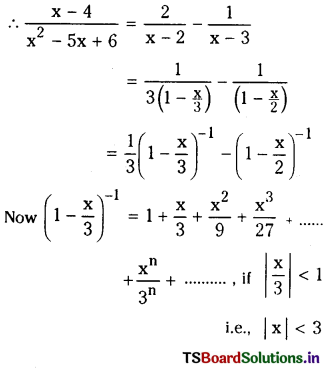
Question 4.
Find the coefficient of xⁿ in the power series expansion of \(\frac{3 x}{(x-1)(x-2)^2}\)
Solution:
Let \(\frac{3 x}{(x-1)(x-2)^2}\) = \(\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{(x-2)^2}\)
A (x – 2)² + B (x – 1) (x – 2) + C (x – 1) = 3x
Substituting x = 1 in (1), we get A = 3
Substituting x = 2 in (2), we get C = 6
Equating coefficient of x² in (1) we get
A + B = 0
⇒ B = – A
⇒ B = – 3
∴ \(\frac{3 x}{(x-1)(x-2)^2}\) = \(\frac{3}{x-1}-\frac{3}{x-2}+\frac{6}{(x-2)^2}\)
= – 3 (1 – x)^-1 + \(\frac{3}{2}\left(1-\frac{x}{2}\right)^{-1}+\frac{3}{2}\left(1-\frac{x}{2}\right)^{-2}\)
Now
(1 – x)^-1 = 1 + x + x² + …………. + xⁿ + ……….., if |x| < 1