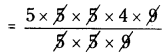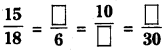Mahesh

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 13 Practical Geometry Ex 13.3 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 13 Practical Geometry Exercise 13.3

Question 1.
Draw a line segment PQ = 5.8 cm and construct its perpendicular bisector using ruler and compasses.
Answer:

Steps of construction:

1. Draw a line segment \(\overline{\mathrm{PQ}}\) = 5.8 cm.
2. Take P as centre and radius more than half of PQ draw two arcs above and below the line segment \(\overline{\mathrm{PQ}}\).
3. Take Q as centre and with the same radius, draw two more arcs intersecting the previous arcs at A and B.
4. Join A and B. This line intersects PQ at O.
5. AB is the required perpendicular bisector of the line PQ.

Question 2.
Ravi made a line segment of length 8.6 Find the length of AC and BC.
Answer:

Steps of construction :

1. Draw a line segment AB = 8.6 cm.
2. Take A as centre and radius more
   than half of the length AB, draw two arcs above and below the line segment AB. ,
3. Take B as cfentre and with the same radius, draw two more arcs intersecting the previous- arcs at P and Q.
4. Join PQ. This line intersects AB at C.
5. Measure AC and BC. On measuring, it is noticed that AC = BC = 4.3 cm.

Question 3.
Using ruler and compasses, draw AB = 6.4 cm. Find its mid point.
Answer:
We can find the mid point of the line segment AB = 6.4 cm by drawing its perpendicular bisector.

Steps of construction:

1.  Draw a line segment AB = 6.4 cm.
2. Take A as centre and radius more than half of the length AB draw two arcs above and below the line segment AB.
3. Take B as centre and with the same radius draw two more arcs intersecting the previous arcs at M and N.
4. Join MN. This line intersects AB at O. ‘O’ is the mid point of AB.

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 13 Practical Geometry Ex 13.2 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 13 Practical Geometry Exercise 13.2

Question 1.
Construct a circle with centre M and radius 4 cm.
Answer:

Steps of construction:

1. Open the compasses for 4 cm radius.
2. Mark a point with a sharp pencil. This is the centre. Mark it as ‘O’.
3. Place the pointer of the compasses firmly at ‘O’.
4. Without moving its metal point, now slowly rotate the pencil till it comes back to the starting point.

Question 2.
Construct a circle with centre X and diameter 10 cm.
Answer:
Diameter of the required circle = 10 cm
Radius of the circle = \(\frac{10}{2}\) = 5 cm

Steps of construction:

1. Open the compasses for 5 cm radius.
2. Mark ’a point with a sharp pencil. This is the centre. Mark it as ‘X’. ‘
3. Place the pointer of the compasses firmly at X.
4. Without moving its metal point, now slowly rotate the pencil till it comes back to the starting point.

Question 3.
Draw four circles of radii 2 cm, 3 cm, 4 cm and 5 cm with the same centre P.
Answer:

Steps of construction:

1. Mark a point with sharp pencil. This is the centre mark it as ‘P’.
2. Place the pointer of the compasses firmly at P.
3. Without moving its metal point, slowly rotate the pencil till it comes back to the, starting point.
4. With ‘P’ as centre and radii 3, 4 and 5 cm, repeat the procedure given in the steps 2 and 3.
5. Now we have four circles with radii 2 cm, 3 cm, 4 cm and 5 cm having centre ‘P’. These circles are called concentric circles.

Question 4.
Draw any circle and mark three points A, B and C such that
(i) A Is on the circle.
(ii) B is in the interior of the circle.
(iii) C is in the exterior of the circle.
Answer:
‘O’ is the centre of the circle.
(i) A is on the circle.
(ii) B is in the interior of the circle.
(iii) C is in the exterior of the circle.

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 13 Practical Geometry Ex 13.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 13 Practical Geometry Exercise 13.1

Question 1.
Construct a line segment of length 6.9 cm using a ruler and compasses.
Answer:

Steps of construction:

1. Draw a line l. Mark a point A on the line l.
2. Place the metal pointer of the compasses on the zero mark of the ruler. Open the compasses so that pencil point touches 6.9 cm mark on the ruler.
3. Place the pointer on A on the line l and draw an arc to cut the line. Mark the point where the arc cuts the line as B.
4. On the line l, we got the line segment AB of required length.

Question 2.
Construct a line segment of length 4.3 cm using the ruler.
Answer:

Steps of construction:

1. Place the ruler on paper and hold it firmly. Mark a point with a sharp edged pencil against 0 cm mark of the ruler. Name the point as A.
2. Mark another point against 3 small divisions just after the 4 cm mark. Name this point as B.
3. Join points A and B along the edge of the ruler.
4. AB is the required line segment of length 4.3 cm.

Question 3.
Construct a line segment MN of length 6 cm. Mark any point O on it. Measure MO, ON and MN. What do you observe ?
Answer:

Steps of construction :

1. Draw a line l. Mark a point M on the line l.
2. Place the metal pointer of the compasses on the zero mark of the ruler. Open it to
   place the pencil point upto the 6 cm mark.
3. Taking caution that the opening of the compasses has not changed, place the pointer on M and swing an arc to cut / at N.
4. MN is a line segment of required length.
5. Mark any point ‘O’ on MN.
6. Measure the length of MO and ON. It is found that MO = 3.8 cm and ON = 2.2 cm MO + ON = 3.8 +2.2 = 6 cm
   It is noticed that \(\overline{\mathrm{MO}}+\overline{\mathrm{ON}}\) = \(\overline{\mathrm{MN}}\)

Question 4.
Draw a line segment \(\overline{\mathbf{A B}}\) of length 12 cm. Mark a point C on the line segment \(\overline{\mathbf{A B}}\), such that \(\overline{\mathbf{A C}}\) = 5.6 cm. What should be the length of \(\overline{\mathbf{C B}}\)? Measure the length of \(\overline{\mathbf{C B}}\).
Answer:

Steps of construction:

1. Draw a line l. Mark a point A on the line l.
2. Place the metal pointer of the compasses on the zero mark of the ruler. Open it to place the pencil point upto the 12 cm mark.
3. Taking caution that the opening of the compasses has not changed, place the pointer on A and swing an arc to cut / at B.
4. \(\overline{\mathbf{A B}}\) is a line segment of required length.
5. Similarly mark the point C on l such that \(\overline{\mathbf{A C}}\) = 5.6 cm.
6. The length of \(\overline{\mathbf{C B}}\) should be 6.4 cm = (12 – 5.6) on measuring, the length of \(\overline{\mathbf{C B}}\) = 6.4 cm.

Question 5.
Given that AB = 12 cm

(i) From the figure measure the lengths of the following line segments.
(a) \(\overline{\mathrm{CD}}\)
(b) \(\overline{\mathrm{DB}}\)
(c) \(\overline{\mathrm{EA}}\)
(d) \(\overline{\mathrm{AD}}\)
Answer:
(a) \(\overline{\mathrm{CD}}\) = 2.8 cm
(b) \(\overline{\mathrm{DB}}\) = 4.3 cm
(c) \(\overline{\mathrm{EA}}\) = 17.3 cm
(d) \(\overline{\mathrm{AD}}\) = 16.3 cm

(ii) Verify \(\overline{\mathbf{A E}}-\overline{\mathbf{C E}}\) = \(\overline{\mathbf{A C}}\)
Answer:
\(\overline{\mathbf{A E}}-\overline{\mathbf{C E}}\) = 17.3 cm – 3.8 cm = 13.5 cm
\(\overline{\mathrm{BC}}\) = 1.5 cm
\(\overline{\mathrm{AC}}\) = \(\overline{\mathbf{A B}}+\overline{\mathbf{B C}}\)
= 12 cm + 1.5 cm
= 13.5 cm
∴ \(\overline{\mathrm{AE}}-\overline{\mathrm{CE}}\) = \(\overline{\mathrm{AC}}\)

Question 6.
\(\overline{\mathrm{AB}}\) = 3.8 cm. Construct \(\overline{\mathrm{MN}}\) by compasses such that the length of \(\overline{\mathrm{MN}}\) = 3AB’is thrice that of \(\overline{\mathrm{AB}}\). Verify this with the help of a ruler.
Answer:

Steps of construction:

1. Draw a line l. Mark a point M on it.
2. Place the compasses pointer on the zero mark of the ruler.-Open it to place the pencil upto the 3.8 cm mark.
3. Taking caution that the opening of the compasses has not changed, place the pointer on M and swing an arc to cut l at A.
4. \(\overline{\mathrm{MA}}\) is a line segment of 3.8 cm.
5. Similarly place the pointer on A and swing an arc to cut l at B such that MA = AB.
6. Again place the pointer on B and swing an arc to cut l at N such that AB = BN.
7. Now \(\overline{\mathrm{MN}}\) is a line segment of 11.4 cm.

Students can practice TS SCERT Class 6 Maths Solutions Chapter 11 Ratio and Proportion Ex 11.4 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 11 Ratio and Proportion Exercise 11.4

Question 1.
If three apples cost ₹ 45, how much would five apples cost ₹ *
Answer:
Cost of 3 apples = ₹ 45
Cost of each apple = ₹45 ÷ 3
= ₹ 15
∴ Cost of 5 apples = ₹ 15 × 5
= ₹ 75

Question 2.
Laxmi bought 7 books for a total of ₹ 56. How much would she pay for just 3 books ?
Answer:
Cost of 7 books = ₹ 56
Cost of one book = ₹ 56 ÷ 7 = ₹ 8
∴ Cost of 3 books = ₹ 8 × 3 = ₹ 24

Question 3.
Reena wants to prepare vegetable pulao, she needs 300 grams of rice, if she has to feed 4 people. How much of rice is needed if the same pulao is prepared for 7 people ?
Answer:
Quantity of rice required for the preparation of vegetable pulao for 4 people is 300 grams.
Quantity of rice needed to prepare pulao for 1 person = \(\frac{300}{4}\) = 75 grams
Quantity of rice needed to prepare pulao for 7 people = 75 × 7 grams = 525 grams

Question 4.
The cost of 16 chairs is ₹ 3600. Find the number of chairs that can be purchased for ₹ 4500.
Answer:
Cost of 16 chairs = ₹ 3600
Cost of one chair = \(\frac{3600}{16}\) = ₹ 225
Number of chairs that can purchased for ₹ 4500 = \(\frac{4500}{225}\)

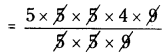
Question 5.
A train moving at a constant speed covers a distance of 90 km in 2 hours. Find the time taken by the train to cover a distance of 540 km at the same speed.
Answer:
Time taken by the train to cover a distance of 90 km in 2 hours.
It covers 45 km in = \(\left(=\frac{90}{2}\right)\) 1 hour.
Time taken by the train to cover 540 km 540
= – \(\frac{540}{45}\) hours
= 12 hours

Question 6.
The income of Kumar for 3 months is ₹ 15,000. If his monthly income remains the same then,
(i) How much will he earn in 5 months ?
(ii) In how many months will he earn ₹ 95,000 ?
Answer:
The income of Kumar for 3 months is ₹ 15,000.
The income of Kumar for 1 month is = ₹ \(\frac{15,000}{3}\) = ₹ 5,000
Kumar earns ₹ 5000 in one month.

(i) The income of Kumar for 5 months = ₹ 5000 × 5 = ₹ 25,000

(ii) The time needed to earn ₹ 95,000
= \(\frac{95,000}{5,000}\) = 19 months
∴ In 1 year and 7 months, he will earn ₹ 95,000.

Question 7.
If the cost of 7 meters of cloth is ₹ 294, find the cost of 5 m of cloth.
Answer:
Cost of 7 meters of cloth = ₹ 294
Cost of 1 meter of cloth = ₹ \(\frac{294}{7}\) = ₹ 42
The cost of 5 meters of cloth = ₹ 42 × 5 = ₹ 210

Question 8.
A farmer has sheep and cows in the ratio 8:3.
(i) How many sheep has the farmer, if he has 180 cows ?
(ii) Find the ratio of the number of sheep to the total number of animals the farmer has.
(iii) Find the ratio of the total number of animals with the farmer to the number of cows with him.
Answer:
The ratio of sheep and cows is 8 : 3.
(i) Total number of parts = 8 + 3 = 11
Value of 3 parts = 180
Value of 1 part = \(\frac{180}{3}\) = 60
The number of sheep that the farmer has = 60 × 8 = 480
Total number of animals that the farmer has = 180 + 480 = 660

(ii) The ratio of the number of sheep to that of total animals = 480 : 660
= 8 : 11

(iii) The ratio of the number of animals to that of cows = 660 : 180 = 11:3

Question 9.
Are 3, 5, 15, 9 in proportion ? If we change their order, can we think of proportional pairs ? Write as many proportionality statements as you can for the above example ?
Answer:
3, 5, 15, 9 are the given numbers.
Ratio of 3 to 5 = 3 : 5
Ratio of 15 to 9 = 15 : 9 (i.e) 5 : 3
Since 3 : 5 5 : 3
3, 5, 15, 9 are not in proportion. .
We can think of proportional pairs if the order is changed.
3, 9, 5, 15 are in proportion.
5, 3, 15, 9 are in proportion.
3, 5, 9,15 are in proportion.
9, 3, 15, 5 are also in proportion.

Question 10.
The temperature has dropped by 15 degree Celsius in the last 30 days. If the rate of temperature drop remains the same, how much more will the temperature drop in the next 10 days ?
Answer:
In 30 days the temperature dropped by 15°, Celsius
In 1 day the temperature dropped by 150 \(\frac{15^{\circ}}{30}\) Celsius
In 10 days the temperature will drop 15 by \(\frac{15}{30}\) × 10 = 5° Celsius

Question 11.
Fill in the following blanks.

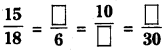
Answer:

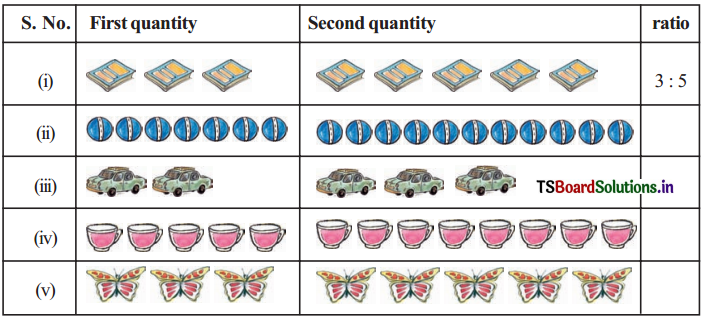
Question 12.
(i) Ratio of breadth and length of a hall is 2:5. Complete the following table that shows some possible breadths and lengths of the hall.

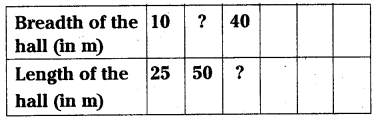
Add 3 more of your choice.
(ii) Find the ratio of length to breadth of your classroom.
Answer:
(i) Ratio of breadth and length of a hall is 2 :5.

(ii) Length of our classroom = 5 m
Breadth of our classroom = 4 m
The ratio of length to breadth of our classroom = 5m : 4m = 5 : 4

Question 13.
Geetha earns ₹ 12,000 a month, out of which she saves ₹ 3,000. Find the ratio of her
(i) Expenditure to savings
(ii) Savings to her income
(iii) Expenditure to her income
Answer:
Earning of Geetha = ₹ 12,000 per month
Geetha’s saving = ₹ 3,000
Geetha’s expenditure
= ₹ 12,000 – ₹ 3000 = ₹ 9,000
(i) The ratio of Geetha’s expenditure to savings is 9000 : 3000 = 3:1
(ii) The ratio of Geetha’s savings to her income is 3000 :12000 = 1:4
(iii) The ratio of Geetha’s expenditure to her income is 9000 : 12000 = 3:4

Question 14.
There are 45 persons working in an office. The number of females is 25 and the remaining are males. Find the ratio of .
(i) The number of females to number of males.
(ii) The number of males to the number of females.
Answer:
The number of persons in the office . =45
The number of females = 25
The number of males = 45 – 25 = 20
(i) The ratio of the number of females to the number of males = 25 : 20 = 5 : 4
(ii) The ratio of number of males to the number of females = 20 : 25 = 4 : 5

Question 15.
A bag of sweets contain yellow and green sweets. For every 2 yellow sweets, there are 6 green sweets. Complete this table based on the above information.

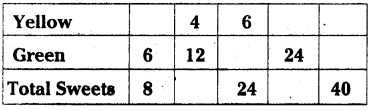
Answer the following questions.
(i) What is the ratio of green to yellow sweets ?
(ii) If you have 8 yellow sweets, how many green sweets will you have ?
(iii) If there are 32 sweets in the medium sized bag. How many will be yellow ?
(iv) In the super fat size bag there are 40 sweets. How many will be green ?
(v) In a bag if there are 16 yellow sweets. How many total sweets are in the bag?
Answer:

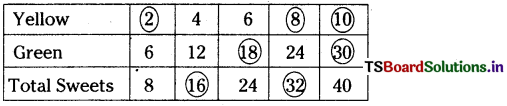
(i) The ratio of green to yellow sweets is 6 : 2 (i.e.,) 3:1
(ii) For 2 yellow sweets, there are 6 green sweets. For 8 yellow sweets, there are \(\frac{6}{2}\) × 8 = 24
(iii) In a bag of 32 sweets, the number of yellow sweets = \(\frac{2}{8}\) × 32 = 8
(iv) In a bag of 40 sweets, the number of green sweets = \(\frac{6}{8}\) × 40 = 30
(v) For 16 yellow sweets, total sweets in the bag = \(\frac{8}{2}\) × 16 = 64

Question 16.
In a school survey it was found that for every 4 girls there were 5 boys. Fill In the following table.

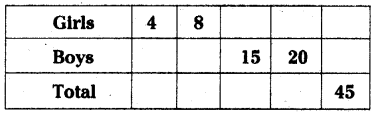
Now answer these questions:
(i) What Is the ratio of girls to boys ?
(ii) In a class of 27 children, how many would be girls ?
(iii) There are 54 children In a class. How many are boys ?
(iv) If 20 girls join in a year. How many boys would join ?
Answer:
For every 4 girls, there were 5 boys.

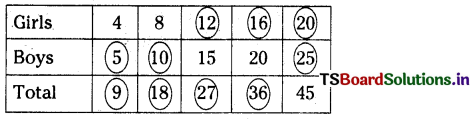
(i) The ratio of girls to boys is 4 : 5
(ii) The number of girls in a class of 27 children is \(\frac{4}{9}\) × 27 = 12
(iii) The number of boys in a class of 54 students is \(\frac{5}{9}\) × 54 = 30
(iv) If 20 girls join in a year, the number of boys that would join is \(\frac{5}{4}\) × 20 = 25

Students can practice TS SCERT Class 6 Maths Solutions Chapter 11 Ratio and Proportion Ex 11.3 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 11 Ratio and Proportion Exercise 11.3

Question 1.
A bag of 25 marbles is shared between Rahul and Kiran in the ratio 2:3.
(i) How many marbles does Kiran receive?
(ii) How many marbles does Rahul receive?
Answer:
Ratio of Rahuls marbles to Kiran’s marbles is 2 : 3.
Total parts = 2 + 3 = 5
Total number of marbles = 25
(i) Kirans share of marbles = \(\frac{25 \times 3}{5}\) = 15
(ii) Rahuls share of marbles = \(\frac{25 \times 2}{5}\) = 10

Question 2.
A point X on AB = 14 cm divides it in the ratio 3 : 4. Find the length of AX and XB.
Answer:

Length of line segment AB = 14 cm.
Ratio of line segments \(\overline{\mathrm{AX}}\) and \(\overline{\mathrm{XB}}\) is 3:4
Total parts = 3 + 4 = 7
Length of 7 parts = 14 cm
Length of each part = \(\frac{14}{7}\) = 2 cm
Length of the line segment \(\overline{\mathrm{AX}}\) = 3 × 2 = 6 cm
Length of the line segment \(\overline{\mathrm{XB}}\) = 4 × 2 = 8 cm

Question 3.
Geetha and Laxmi won ₹ 1,050 in a game. They agreed to share the amount in the ratio of 3 : 4. How much does each person receive ?
Answer:
Amount won in the game and shared between Geetha and Laxmi is Rs. 1,050.
Ratio of Geetha’s amount to Laxmi’s amount is 3 : 4.
Total number of parts = 3 + 4 = 7
Value of 7 parts = 1,050
Therefore, value of each part = \(\frac{1050}{7}\) = 150
Geetha’s share = Rs. 150 × 3
Laxmi’s share = Rs. 150 × 4

Question 4.
Divide ₹ 3600 between Satya and Vishnu in the ratio 3:5.
Answer:
Amount that is divided between Satya and Vishnu = ₹ 3,600
Ratio of Satya’s amount to Vishnu’s amount is 3 : 5
Total parts =3 + 5 = 8
Value of 8 parts = ₹ 3,600
Value of each part = ₹ \(\frac{3600}{8}\) = Rs. 450
Satya’s share = ₹ 450 × 3 = ₹ 1350
Vishnu’s share = ₹ 450 × 5 = ₹ 2250

Question 5.
Two numbers are in the ratio 5 : 6. If the sum of the numbers is 132, find the two numbers.
Answer:
Sum of the two numbers = 132
Ratio of two numbers is 5 : 6.
Total parts = 5 + 6 = 11
Value of 11 parts = 132
∴ Value of each part = \(\frac{132}{11}\) = 12
The first number = 12 × 5 = 60
The second number = 12 × 6 = 72
The two numbers are 60 and 72

Question 6.
Estimate the ratio in which X divides AB and then check your estimation by measuring it.

Answer:
The ratio of \(\overline{\mathrm{AX}}\) to \(\overline{\mathrm{XB}}\) is 1 : 1
Verification : \(\overline{\mathrm{AX}}\) = 3.65 ; \(\overline{\mathrm{XB}}\) = 3.65

Question 7.
The income and savings of an employee are in the ratio 11: 2. If his expenditure is ₹ 5346. Then find his income and savings.
Answer:
The ratio of the income and savings of an employee is 11 : 2.
If income is 11 parts, savings 2 parts, then the expenditure will be equal to 9(= 11-2) parts.
Value of 9 parts = ₹ 5346
∴ Value of each part = \(\frac{5346}{9}\) = ₹594
Employee’s income = ₹ 594 × 11 = ₹ 6534
Employee’s savings = ₹ 594 × 2 = ₹ 1188

Students can practice TS SCERT Class 6 Maths Solutions Chapter 11 Ratio and Proportion Ex 11.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 11 Ratio and Proportion Exercise 11.1

Question 1.
Complete the following table.

Answer:

Question 2.
Compare:

(i) Number of blue coloured squares is ………………. times the number of blue red colour squares.
Answer:
Red coloured squares are 4 and blue coloured squares are 6.
So, blue coloured squares is \(\frac{3}{2}\) times the number of red colour squares.

(ii) Number of red coloured squares is ………………… times of the number of blue red coloured squares.
Answer:
\(\frac{2}{3}\)

(iii) Find the ratio of number of blue squares to the number of red squares.
Answer:
6 : 4 (or) 3 : 2

Question 3.
Solve the following.
(i) A milk man adds 250 ml of water to 1 litre of milk. Find the ratio of water to milk.
Answer:
Quantity of water = 250 ml
Quantity of milk = 1 litre = 1000 ml (∵ 1 litre = 1000 ml)
∴ Ratio of water to milk = 250 : 1000 = 1:4

(ii) Satya’s mother bought 4 kg pulses and 50g chilli powder. Find the ratio of weights of chilli powder to pulses. What is the ratio of weights of the pulses to chilli powder ?
Answer:
Weight of pulses = 4 kg
= 4 × 1000 gms (∵ 1 kg = 1000 grams)
= 4000 gms
Weight of chilli powder = 50 gms
Ratio of weights of chilli powder to pulses = 50 : 4000 = 1 : 80
Ratio of weights of the pulses to chilli powder = 4000 : 50 = 80 : 1

(iii) Rani takes 30 minutes to reach school from home. Ismail takes √2 an hour to cover the same distance. Find the ratio of time taken by Rani to the time taken by Ismail.
Answer:
Time taken by Rani to reach school from home = 30 minutes
Time taken by Ismail to cover the same distance = ½ hour = 30 minutes (∵ 1 hour = 60 minutes)
Ratio of time taken by Rani to the time taken by Ismail = 30 : 30 = 1 : 1

Students can practice 10th Class Maths Solutions Telangana Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Exercise 4.1

Question 1.
By comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\), \(\frac{c_1}{c_2}\) find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or coincident.
a) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
b) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
c) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solution:
a) The given pair of linear equations are
5x – 4y + 8 = 0 ———- (1)
7x + 6y – 9 = 0 —— (2)
Comparing equations (1) and (2) with standard pair of linear equations (i.e.,)
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂= 0, we get
a₁ = 5; b₁ = -4; c₁ = 8
a₂ = 7; b₂ = 6; c₂ = -9
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{5}{7}\); \(\frac{b_1}{b_2}\) = \(\frac{-4}{6}\); \(\frac{c_1}{c_2}\) = \(\frac{8}{-9}\)
Since, \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\), the pair of linear equations will represent intersecting lines.

b) The given pair of linear equations are
9x + 3y + 12 = 0 —- (1)
18x + 6y + 24 = 0 —- (2)
Here, a₁ = 6; b₁ = 3; c₁ = 12
a₂ = 18; b₂ = 6; c₂ = 24
\(\frac{a_1}{a_2}\) = \(\frac{9}{18}\) = \(\frac{1}{2}\) ;
\(\frac{b_1}{b_2}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{12}{24}\) = \(\frac{1}{2}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) = \(\frac{1}{2}\), The pair of linear equations will represent coincident lines.

c) The given pair of linear equations are
6x – 3y + 10 = 0
2x – y + 9 = 0
Here,
a₁ = 6; b₁ = -3; c₁ = 10
a₂ = 2; b₂ = -1; c₂ = 9
\(\frac{a_1}{a_2}\) = \(\frac{6}{2}\) = \(\frac{3}{1}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-3}{-1}\) = \(\frac{3}{1}\);
\(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{10}{9}\)
Since \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\), the pair of linear equations will represent parallel lines.

Question 2.
Check whether the following equations are consistent or inconsistent. Solve them graphically.
a) 3x + 2y = 5; 2x – 3y = 7
b) 2x – 3y = 8; 4x – 6y = 9
c) \(\frac{3}{2}\)x + – y = 7; 9x – 10y = 14
d) 5x – 3y = 11; -10x + 6y = -22
e) \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
f) x + y = 5; 2x + 2y = 10
g) x – y = 8; 3x – 3y = 16
h) 2x + y – 6 = 0; 4x – 2y – 4 = 0
i) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
Solution:
a) 3x + 2y – 5 = 0
2x – 3y – 7 = 0
Here
a₁ = 3; b₁ = 2; c₁ = -5
a₂ = 2; b₂ = -3; c₂ = -7
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{3}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{2}{-3}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-5}{-7}\) = \(\frac{5}{7}\)
⇒ \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given equations are consistent.
They intersect at one point. There is an unique solution.
The given equations are 3x + 2y = 5 and 2x – 3y = 7
3x + 2y = 5 —– (1)
⇒ 2y = 5 – 3x
⇒ y = \(\frac{5-3 x}{2}\)

2x – 3y = 7 —- (2)
⇒ 3y = 2x – 7
⇒ y = \(\frac{2 x-7}{3}\)

Scale :
X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

The given lines intersect at one point. The solution is (2,-1).
x = \(\frac{29}{13}\) ; y = \(\frac{-11}{13}\)

b) 2x – 3y = 8
4x – 6y = 9
Solution:
2x – 3y – 8 = 0
4x – 6y – 9 = 0
Here,
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{-3}{-6}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-8}{-9}\) = \(\frac{8}{9}\)
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations are inconsistent.
They are parallel lines. There is no solution.
The given equations are 2x – 3y = 8 and
4x — 6y = 9
2x – 3y = 8 —– (1)
⇒ 3y = 2x – 8
⇒ y = \(\frac{2 x-8}{3}\)

4x – 6y = 9
⇒ 6y = 4x – 9
⇒ y = \(\frac{4 x-9}{6}\)

The given lines parallel to each other.
There is no solution.

Scale: X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 0.5 cm

c) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
9x – 10y = 14
Solution:
\(\frac{3 x}{2}\) + \(\frac{5 y}{3}\) = 7
\(\frac{6(3 x)}{2}\) + \(\frac{6(5 y)}{3}\) = 7 × 6
(Multiplying each term by 6, we get)
⇒ 9x + 10y = 42
⇒ 9x + 10y – 42 = 0 —- (1)
⇒ 9x – 10y – 14 = 0 —- (2)
Here, a₁ = 9; b₁ = 10; c₁ = -42
a₂ = 9; b₂ = -10; c₂ = -14

∴ The given equations are consistent.
They intersect at one point. There is an unique solution.
The given equations are \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 and 9x – 10y = 14
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 —– (1)
⇒ 9x + 10y = 42 ⇒ 10y = 42 – 9x
⇒ y = \(\frac{42-9 x}{10}\)

9x – 10y = 14
⇒ 10y = 9x – 14
y = \(\frac{9 x-14}{10}\)

The given lines intersect at one point.
x = \(\frac{28}{9}\) and y = \(\frac{7}{5}\)

Scale : X-axis: 1 unit = 1 cm
Y-axis: 1 unit = 0.5 cm

d) 5x – 3y = 11
-10x + 6y = -22
Solution:
5x – 3y – 11 = 0
-10x + 6y + 22 = 0
Here, a₁ = 5; b₁ = -3; c₁ = -11
a₂ = -10: b₂ = 6; c₂ = 22
\(\frac{a_1}{a_2}\) = \(\frac{5}{-10}\) = \(\frac{-1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-3}{6}\) = \(\frac{-1}{2}\);
\(\frac{c_1}{c_2}\) = \(\frac{-11}{22}\) = \(\frac{-1}{2}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.
The given equations are 5x – 3y = 11 and -10x + 6y = -22
5x – 3y = 11 —– (1)
⇒ 3y = 5x – 11
⇒ y = \(\frac{5 x-11}{3}\)

⇒ 10x + 6y = -22 —– (2)
⇒ 6y = 10x – 22
⇒ y = \(\frac{10 x-22}{6}\)

The given lines are coincident.
There are infinitely many solutions.

Scale: X – axis: 1 cm = 1 unit
Y – axis: 1 cm = 1 unit

e) \(\frac{4}{3}\)x + 2y = 8
2x + 3y = 12
Solution:
4x + 6y = 24
Multiplying each term by (3), we get
⇒ 4x + 6y – 24 = 0 —— (1)
2x + 3y – 12 = 0 ——- (2)
a₁ = 4; b₁ = 6; c₁ = -24
a₂ = 2; b₂ = 3; c₂ = -12
Here,
\(\frac{a_1}{a_2}\) = \(\frac{4}{2}\) = 2; \(\frac{b_1}{b_2}\) = \(\frac{6}{3}\) = 2 ; \(\frac{c_1}{c_2}\) = \(\frac{-24}{-12}\) = 2
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent.
There are infinitely many solutions.
The given equations are \(\frac{4}{3}\)x + 2y = 8 and 2x + 3y = 12
\(\frac{4}{3}\)x + 2y = 8 —– (1)
⇒ 4x + 6y = 24
⇒ 6y = 24 – 4x
⇒ y = \(\frac{24-4 x}{6}\)

2x + 3y = 12 —– (2)
⇒ 3y = 12 – 2x
⇒ y = \(\frac{12-2 x}{3}\)


The given lines are coincident.
There are infinitely many solutions.

f) x + y = 5 (A.P. Jun.15)
2x + 2y = 10
Solution:
x + y – 5 = 0
2x + 2y – 10 = 0
Here, a₁ = 1; b₁ = 1; c₁ = -5
a₂ = 2; b₂ = 2; c₂ = -1O
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{1}{2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-5}{-10}\) = \(\frac{1}{2}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
∴ The given equations are dependent and consistent. There are infinitely many solutions.
The given equations are x + y = 5 and 2x + 2y = 10
x + y = 5 —— (1)
⇒ y = 5 – x

2x + 2y = 10 —– (2)
⇒ 2y = 10 – 2x
⇒ y = \(\frac{10-2 \mathrm{x}}{2}\)

The given lines are coincident.
There are infinitely many solutions.

g) x – y = 8
3x – 3y = 16
Solution:
x – y – 8 = 0
3x – 3y – 16 = 0
Here, a₁ = 1; b₁ = -1; c₁ = -8
a₂ = 3; b₂ = -3; c₂ = -16
⇒ \(\frac{a_1}{a_2}\) = \(\frac{1}{3}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-1}{-3}\) = \(\frac{1}{3}\);
\(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{-8}{-16}\) = \(\frac{1}{2}\)
⇒ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
The given equations are inconsistent.
They are parallel lines. There is no
solution.
The given equations are x – y = 8 and 3x – 3y = 16
x – y = 8 —– (1)
⇒ y = x – 8

3x – 3y = 16 —- (2)
⇒ 3y = 3x – 16
⇒ y = \(\frac{3 x-16}{3}\)

The given lines are parallel to each other. There is no solution.

Scale: X – axis : 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

h) 2x + y – 6 = 0
4x – 2y – 4 = 0
Solution:
2x + y – 6 = 0
4x – 2y – 4 = 0
Here, a₁ = 2; b₁ = 1; c₁ = -6
a₂ = 4; b₂ = -2; c₂ = -4
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{b_1}{b_2}\) = \(\frac{1}{-2}\) ; \(\frac{c_1}{c_2}\) = \(\frac{-6}{-4}\) = \(\frac{3}{2}\)
⇒ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given equations are consistent.
They intersect at one point. There is a unique solution.
The given equations are 2x + y – 6 = 0 and 4x – 2y – 4 = 0
2x + y – 6 = 0 —– (1)
⇒ y = 6 – 2x

4x – 2y – 4 = 0 —– (2)
⇒ 2y = 4x – 4
⇒ y = \(\frac{4 x-4}{2}\)

Scale: X-axis : 1 unit = 1 cm
Y-axis : 1 unit = 1 cm

The given lines intersect at one point (2, 2).
The solution is x = 2 and y = 2.

i) 2x – 2y – 2 = 0
4x – 4y – 5 = 0
Solution:
2x – 2y – 2 = 0
4x – 4y – 5 = 0
Here, a₁ = 2; b₁ = -2; c₁ = -2
a₂ = 4; b₂ = -4; c₂ = -5
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{-2}{-4}\) = \(\frac{1}{2}\)
\(\frac{\mathrm{c}_1}{\mathrm{~c}_2}\) = \(\frac{-2}{-5}\) = \(\frac{2}{5}\)
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ The given equations are consistent.
They are parallel lines. There is no solution.
The given equations are 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0
2x – 2y – 2 = 0 —– (1)
⇒ 2y = 2x – 2
⇒ y = \(\frac{2 x-2}{2}\)

4x – 4y – 5 = 0 —– (2)
⇒ 4y = \(\frac{4 x-5}{4}\)
⇒ y = \(\frac{4 x-5}{4}\)

The given lines are parallel to each other.
There is no solution.

Scale: X – axis: 1 unit = 1 cm
Y – axis: 1 unit = 1 cm

Question 3.
Neha went to a ‘sale’ to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered “The number of skirts are two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number of pants purchased”. Help her friend to find how many pants and skirts Neha bought.
Solution:
Let the number of pants Neha bought be x.
Let the number of skirts Neha bought be y.
By problem,
y = 2x – 2
⇒ 2x – y = 2 —— (1)
y = 4x – 4
⇒ 4x – y = 4 —– (2)

Substitute x = 1 in (1) or (2), we get
⇒ 2(1) – y = 2
⇒ 2 – y = 2
⇒ -y = 2 – 2 = 0
∴ y = o
Number of pants purchased = 1
∴ Number of skirts purchased = 0

Question 4.
10 students of Class-X took part in a mathematics quiz. If the number of girls is 4 more than the number of boys then, find the number of boys and the number of girls who took part in the quiz.
Solution:
Number of boys who took part in the quiz = x
Number of girls who took part in the quiz = y
It is given that 10 students took part in the quiz.
∴ x + y = 10 ——— (1)
Since the number of girls is 4 more than the number of boys, we have
y = x + 4
⇒ -x + y = 4 —– (2)
Adding (1) and (2)

Substitute y = 7 in equation (1), we get
x + 7 = 10
x = 10 – 7 = 3
Therefore, Number of boys who took part in the quiz = 3
Number of girls who took part in the quiz = 7

Question 5.
5 pencils and 7 pens together cost ₹ 50 whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
Let the cost of one pencil = ₹ x
Cost of one pen = ₹ y
Total cost of 5 pencils and 7 pens = 5x + 7y
Total cost of 7 pencils and 5 pens = 7x + 5y
By problem, 5x + 7y = 50 —- (1)
7x + 5y = 46 —– (2)
We equate the coefficients of ‘x’ in (1) and (2).

Substitute y = 5 in equation (1), we get
5x + (7 × 5) = 50
5x + 35 = 50
5x = 50 – 35 =15
∴ x = \(\frac{15}{5}\) = 3
Therefore, cost of one pencil = ₹ 3
Cost of one pen = ₹ 5

Question 6.
Half of the perimeter of a rectangular garden, whose length is 4m more than its width is 36m. Find the dimensions of the garden.
Solution:
Let the length of the garden be x metres.
Let the breadth of the garden be y metres.
Perimeter of the garden = 2(x + y) metres.
Half of the perimeter of the garden =
\(\frac{2(x+y)}{2}\) = x + y
By problem, x + y = 36 —— (1)
It is given that the length is 4 metres more than its width.
(i.e.,) x = y + 4
⇒ x – y = 4 —– (2)
Solving (1) and (2)

Substitute, x = 20 in equation (1),
20 + y = 36
⇒ y = 36 – 20 = 16
Therefore, length of the garden = 20 metres
Breadth of the garden =16 metres

Question 7.
We have a linear equation 2x + 3y – 8 = 0. Write another linear equation in two variables such that the geometrical representation of the pair is formed intersecting lines. Now, write two more linear equations so that one forms a pair of parallel lines and the second forms coincident line with the given equation.
Solution:
The given linear equation is 2x + 3y – 8 = 0.

1. The required linear equation in two variables such that it is formed an intersecting line with the given one, is 6x – 5y – 10 = 0.
2. The linear equation in two variables (i.e.,) 4x + 6y – 10 = 0 forms a parallel line with the given one.
3. The linear equation in two variables (i.e.,) 6x + 9y – 24 = 0 forms a coincident line with the given one.

Question 8.
The area of a rectangle gets reduced by 80 sq units if its length is reduced by 5 units and breadth is increased by 2 units. If we increase the length by 10 units and decrease the breadth by 5 units, the area will increase by 50 sq units. Find the length and breadth of the rectangle.
Solution:
Let the length of the rectangle be x units and the breadth be y units.
Then the area of the rectangle = length × breadth = x × y = xy
If the length is reduced by 5 units and breadth is increased by 2 units, then its area is reduced by 80 sq. units.
∴ (x – 5) (y + 2) = xy – 80
⇒ xy + 2x – 5y – 10 = xy – 80
⇒ 2x – 5y = -70 —– (1)
When the length is increased by 10 units and breadth is decreased by 5 units, the area is increased by 50 sq. units.
∴ (x + 10) (y – 5) = xy + 50
⇒ xy – 5x + 10y – 50 = xy + 50
⇒ -5x + 10 y = 100 —– (2)
Equation (1) × 2
Solving (1) and (2), we get
4x – 10y = -140
-5x + 10y = 100 Adding
-x = -40
∴ x = 40
Substitute x = 40 in (2), we get
⇒ (-5 × 40) + 10y = 100
⇒ – 200 + 10y = 100
⇒ 10y = 100 + 200 = 300
∴ y = \(\frac{300}{10}\) = 30
Length of the rectangle = 40 units
Breadth of the rectangle = 30 units

Question 9.
In class X, if three students sit on each bench, one student will be left. If four students sit on each bench, one bench will be left. Find the number of students and the number of benches in that class.
Solution:
Let the number of students in class X be x.
Let the number of benches in that class be y.
If three students sit on each bench, one student will be left.
∴ 3y = x – 1
⇒ x – 3y = 1 —- (1)
If four students sit on each bench, one bench will be left.
∴ 4(y – 1) = x
⇒ 4y – 4 = x
⇒ x – 4y = -4 —– (2)
Solving (1) and (2), we get

Substitute y = 5 in (1), we get
x – (3 × 5) = 1
⇒ x – 15 = 1
∴ x = 1 + 15 = 16
∴ Number of students in class X = 16
Number of benches in that class = 5
Form a pair of linear equations for each of the following problems and find their solution.

Students can practice TS SCERT Class 6 Maths Solutions Chapter 11 Ratio and Proportion Ex 11.2 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 11 Ratio and Proportion Exercise 11.2

Question 1.
Among the following, which ratios are in the simplest form ? If not, convert them into the simplest form.
(i) 2 : 3
(ii) 16 : 20
(iii) 5 : 6
(iv) 20 : 60
(v) 8 : 15
(vi) 19 : 2
Answer:
Simplest form:
(i) 2 : 3,
(iii) 5 : 6,
(v) 8 : 15,
(vi) 19 : 2

Convert form:
(ii) \(\frac{16}{4}: \frac{20}{4}\) (i.e) 4 : 5
(iv) \(\frac{20}{20}: \frac{60}{20}\) (i.e) 1 : 3

Question 2.
A bag contains 20 kg of rice and another bag contains 60 kg of wheat. Find the ratio of the amount of rice to that of wheat. What is the ratio of rice to the total weight ?
Sol.
Quantity of rice = 20 kg
Quantity of wheat = 60 kg
Ratio of the amount of rice to that of wheat
= 20 : 60
= 1 : 3
Total weight of bag containing rice and wheat = 20 + 60 = 80 kg
Ratio of rice to the total weight
= 20 : 80
= 1 : 4

Question 3.
There are 32 students in a class out of which 12 are girls. Find :
(i) The ratio of number of boys to number of girls.
Answer:
Total number of students in the class = 32
Number of girls in the class = 12
Number of boys in the class
= 32 – 12 = 20
The ratio of number of boys to number of girls = 20 : 12
= \(\frac{20}{4}: \frac{12}{4}\) = 5 : 3

(ii) The ratio of number of boys to total number of students.
Answer:
The ratio of number of boys to total number of students = 20 : 32
= \(\frac{20}{4}: \frac{32}{4}\) = 5 : 8

(iii) The ratio of number of girls to total number of students.
Answer:
The ratio of number of girls to total number of students = 12:32
= \(\frac{12}{4}: \frac{32}{4}\) = 3 : 8

Question 4.
Draw a four sided closed figure and divide it into some number of equal parts. Shade the figure with any colour so that the ratio of shaded parts to unshaded parts 1 : 3. Draw two more different figures and do the same.
Answer:

Number of shaded parts = 3
Number of unshaded parts = 9
Ratio of shaded parts to unshaded parts = 3 : 9 = \(\frac{3}{3}: \frac{9}{3}\) = 1:3
Number of shaded parts = 2
Number of unshaded parts = 6

Ratio of shaded parts to unshaded parts = 2 : 6 = \(\frac{2}{2}: \frac{6}{2}\) = 1 : 3
Number of shaded parts = 4
Number of unshaded parts = 12
Ratio of shaded parts to un shaded parts = 4 : 12
= \(\frac{4}{4}: \frac{12}{4}\) = 1 : 3

Question 5.
Imran bought 2 litres of oil and Vijay bought 500 ml of oil. Find the ratio of quantities of oil bought by Imran to oil bought by Vijay.
Answer:
Quantity of oil bought by Imran
= 2 litres = 2 × 1000 ml = 2000 ml
Quantity of oil bought by Vijay = 500 ml
The ratio of quantities of oil bought by Imran to oil bought by Vijay
= 2000 : 500
= \(\frac{2000}{500}: \frac{500}{500}\) = 4 : 1

Question 6.
Weight of Abraham is 20 kg and his father’s weight is 60 kg. Find the ratio of weight of Abraham and his father. Express it in the simplest form.
Answer:
Weight of Abraham = 20 kg
Weight of Abraham’s father = 60 kg
Ratio of weight of Abraham and his father = 20 : 60
= \(\frac{20}{20}: \frac{60}{20}\) = 1 : 3
∴ The simplest form is 1:3.

Question 7.
Ramu spent \(\frac{2}{5}\) th of his money on a story book. Find the ratio of money spent to the money with him at the beginning.
Answer:
Let the money with Ramu be Rs. 1.
Then money spent by Ramu on a story book = Rs. 1 × \(\frac{2}{5}\) = Rs. \(\frac{2}{5}\)
The ratio of money spent to the money with him at the beginning = \(\frac{2}{5}\) : 1
= \(\frac{2}{5}\) × 5 : 1 × 5 = 2 : 5

Students can practice TS SCERT Class 6 Maths Solutions Chapter 9 Introduction to Algebra Ex 9.3 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 9 Introduction to Algebra Exercise 9.3

Question 1.
State which of the following are equations.
(i) x – 3 = 7
(ii) l + 5 > 9
(iii) p – 4 < 10
(iv) 5 + m = – 6
(v) 2s – 2 = 12
(vi) 3x + 5 > 13
(vii) 3x < 15
(viii) 2x – 5 = 3
(ix) 7y + 1 < 22
(x) – 3z + 6 = 12
(xi) 2x – 3y = 3
(xii) z = 4
Answer:
The following are the equations.
(i) x- 3 = 7
(iv) 5 + m = – 6
(v) 2s – 2 = 12
(viii) 2x – 5 = 3
(x) – 3z + 6 = 12
(xi) 2x – 3y = 3
(xii) z = 4

Question 2.
Write LHS and RHS of the following equations.
(i) x – 5 = 6
(ii) 4y = 12
(iii) 2z + 3 = 7
(iv) 3p = 24
(v) 4 = x – 2
(vi) 2a – 3 = – 5
Answer:
The value of expression to the left of the sign ‘=’ is called Left Hand Side (LHS) and that of expression to the right of the sign ‘=’ is called Right Hand Side
(RHS)
(i) x – 5 (LHS) 6(RHS)
(ii) 4y (LHS) 12 (RHS)
(iii) 2z + 3 (LHS) 7 (RHS)
(iv) 3p (LHS) 24 (RHS)
(v) 4 (LHS) x – 2 (RHS)
(vi) 2a – 3 (LHS) -5 (RHS)

Question 3.
Solve the following equations by Trial & Error method.
(i) x + 3 = 5
Answer:

We find that for x = 2, both LHS and RHS are equal. Therefore x = 2 is the solution of the equation.

(ii) y – 2 = 7
Answer:

We find that for y = 9, both LHS and RHS are equal. Therefore y = 9 is the solution of the equation.

(iii) a – 2 = 6
Answer:

We find that for a = 8, both LHS and RHS are equal. Therefore a = 8 is the solution of the equation.

(iv) 5y = 15
Answer:

We find that for y = 3, both LHS and RHS are equal. Therefore y = 3 is the solution of the equation.

(v) 6n = 30
Answer:

We find that for n = 5, both LHS and RHS are equal. Therefore n = 5 is the solution of the equation.

(vi) 3z = 27
Answer:

We find that for z = 9, both LHS and RHS are equal. Therefore z = 9 is the solution of the equation.

Students can practice TS SCERT Class 6 Maths Solutions Chapter 9 Introduction to Algebra Ex 9.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 9 Introduction to Algebra Exercise 9.1

Question 1.
Find the rule which gives the number of matchsticks required to make the following matchsticks patterns.
(i) A pattern of letter ‘T’
Answer:
The rule which gives the number of sticks required to make the pattern T is 2n.

(ii) A pattern of letter ‘E’
Answer:
The rule which gives the number of sticks required to make the pattern E is 5n.

(iii) A pattern of letter ‘Z’
Answer:
The rule which gives the number of sticks required to make the pattern Z is 3n.

Question 2.
Make a rule between the number of blades required and the number of fans (say n) in a hall ?

Answer:
The number of blades that a fan has = 3
Number of fans = n (say)
∴ The number of blades for ‘n’ fans = 3 × n = 3n
The required rule is 3n.

Question 3.
Find a rule for the following patterns between number of shapes formed and number of matchsticks required.
(a)

Answer:
The first shape has 2 matchsticks, the second shape 4 and the third shape 6.
∴ The required rule 2s.
(‘s’ stands for number of shapes.)

(b)

Answer:
The first shape has 3 matchsticks, the second shape 6 and the third shape 9.
∴ The required rule is 3s.
(‘s’ stands for number of shapes.)

Question 4.
The cost of one pen is ₹ 7 then what is the rule for the cost of ‘n’ pens.
Answer:
Cost of one pen is Rs. 7.
Cost of ‘n’ pens = 7 × n = 7n
The rule for cost of n’ pens is 7n.

Question 5.
The cost of one bag is ₹ 90, what is the rule for the cost of ‘m’ bags ?
Answer:
The cost of one bag = Rs. 90.
Cost of ‘m’ bags = 90 × m = 90m
The rule for the cost of ‘m’ bags is 90m.

Question 6.
The rule for purchase of books is-that the cost of q books is ₹ 23; then find the price of one book ?
Answer:
Cost of ‘q’ books = Rs. 23
∴ Cost of one book = \(\frac{23}{q}\)
The rule for the price of one book is \(\frac{23}{q}\).

Question 7.
John says that he has two books less than Gayathri. Write the relationship using letter x.
Answer:
Let the number of books that Gayathri has be x.
Then the number of books that John has = (x – 2)
(∵ John says that he has two books less than Gayathri)
The required relationship is (x – 2).

Question 8.
Rekha has 3 books more than twice the books with Suresh. Write the relationship using letter y.
Answer:
Let the number of books with Suresh be ‘y’.
Twice the number of books with Suresh = 2 × y – 2y.
As per the problem, the number of ‘ books that Rekha has = (2y + 3)
The required relationship is 2y + 3.

Question 9.
A teacher distributes 6 pencils per student. Can you find how many pencils are needed for the given number of students (use V for the number of students).
Answer:
Let the number of students be ’z’.
The teacher gives 6 pencils to each student.
The number of pencils that are given to ‘z’ students = 6 × z = 6z
The rule that is required is 6z.

Question 10.
Complete each table to generate the given functional relationship.

Answer:

Question 11.
Observe the following pattern.

Count the number of line segments in each shape.
(i) How many line segments will the 9th shape contain ?
(ii) Write the rule for the above pattern.
Answer:
(i) Shape – 1 contains 3 line segments.
Shape – 2 contains 5 line segments.
Shape – 3 contains 7 line segments.
Shape – 4 contains 9 line segments.
Shape – 5 contains 11 line segments.
Shape – 6 contains 13 line segments.
Shape – 7 contains 15 line segments.
Shape – 8 contains 17 line segments.
Shape – 9 contains 19 line segments.
The number of line segments that 9 such shapes contains is 99.
(∵ 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19)

(ii) The rule for the above pattern is 3 + 2(n – 1).

Students can practice Telangana 6th Class Maths Textbook Solutions Chapter 5 Measures of Lines and Angles InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 5 Measures of Lines and Angles Exercise InText Questions

Think, Discuss and Write

Question 1.
How do we compare them ?
To compare them, we trace the line segments \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) on a tracing paper such that they are roughly aligned in the same direction. Do their end points coincide ?
Answer:
We can now say \(\overline{\mathrm{AB}}\) is longer than \(\overline{\mathrm{CD}}\). In the same way we can compare \(\overline{\mathrm{PQ}}\) with \(\overline{\mathrm{RS}}\). We can see \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{RS}}\) are of equal length.
(Or)
We can compare the lengths of \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{RS}}\) by a using a scale or a divider.
Now, we can say \(\overline{\mathrm{PQ}}\) > \(\overline{\mathrm{RS}}\)
∴ \(\overline{\mathrm{PQ}}\) = 3cm; \(\overline{\mathrm{RS}}\) = 25cm
∴ \(\overline{\mathrm{PQ}}\) > \(\overline{\mathrm{RS}}\)

Question 2.
What other errors can you find while measuring the length of line segment ?
For example, to find the length of a pencil, the eye Wrong Right Wrong should be correctly positioned as shown in the figure i.e., just vertically above the mark for both points. Other wise there may be an error due to angular viewing.

Answer:
(i) Eye error
(ii) Parallax error.

Try These

Question 1.
Take a post card and measure the length and breadth with ruler and divider. Do all post cards have the same dimensions ?
Answer:
By using ruler and a divider we can say that the dimensions of a post card are Length = 12 cm, Breadth = 7 cm
Same type of post cards are all having the same dimensions.

Question 2.
Select any three objects eraser, small pencil, etc. Trace their length on a paper. Measure the length of these line segments.
Answer:

The length of an eraser is 3 cm.
The length of a small pencil is 10 cms.

Try These

Question 1.
Use the right angle tester made of straw’s and identify the following angles.

Answer:
(i) Obtuse angle
(ii) Right angle
(iii) Acute angle
(iv) Obtuse angle

Question 2.
List out five daily life situations where you observe acute angles and obtuse angles
Answer:
Acute angles and obtuse angles are formed in following cases

1. The angle between the slant slopes of buffoon cap.
2. At the time of 2’o clock p.m. in a clock.
3. At the time of 10’o clock.
4. When the wrist is bonded.
5. When the knee is bonded.

Question 3.
Draw some angles of your choice. Test them by the “angle tester” and write which are acute and which are obtuse and which are right angles.
Answer:

Think, Discuss and Write

In the adjacent figure ∠AOB and ∠AOC are given. Which angle is clock-wise and which angle is anti clock-wise. Think and discuss with your friends.

Answer:
∠AOB is formed in a clock-wise direction.
∠AOC is formed in an anti clock-wise direction.

Try These

Question 1.
Which angle is greater ? Discuss with your friends.

Verify by measuring the angles using protractor. Is your estimation is correct ? Give reasons.
Answer:
The measure of ∠1 = 30° and that of ∠2 = 30°
∴ Both the angles ∠1 and ∠2 are of equal measure.

Question 2.
Which are acute angles ? Find and write their measures.

Answer:
(i) The measure of angle in figure (i) is 30°. So it is an acute angle,
(ii) The measure of angle in figure (ii) is 50°. So it is an acute angle.
(iii) The measure of angle in figure (iii) is 130°. It is not an acute angle. Because it is an obtuse angle.
(iv) The measure of angle in figure (iv) is 90°. So it is a right angle.
(v) The measure of angle in figure (v) is 80°. So it is an acute angle.

Question 3.
Which are obtuse angles?

Answer:
(i) The measure of angle in figure (i) is 110°. So it is an obtuse angle.
(ii) The measure of angle in figure (ii) is 90°. So it is a right angle.
(iii) The measure of angle in figure (iii) is 130°. So it is an obtuse angle.
(iv) The measure of angle in figure (iv) is 50°. So it is an acute angle.
(v) The measure of angle in figure (v) is 325°. So it is a reflex angle.

Question 4.
Draw any two acute and two obtuse angles of your choice.
Answer:
Acute angles:

AOB and POQ are acute angles.

Obtuse angles:

XOY and MON are obtuse angles.

Question 5.
Classify the following angles into acute, right, obtuse and straight angles.
40°, 140°, 90°, 210°, 44°, 215°, 345°, 125°
10°, 120°, 89°, 270°, 30°, 115°, 180°
Answer:
Acute angles : 40°, 44°, 10°, 89°, 30°
Right angle : 90°
Obtuse angles : 140°, 125°, 120°, 115°
Straight angle : 180°
Reflex angles : 210°, 215°, 345°, 270°

Think, Discuss and Write

Question 1.
If l ⊥ m, then can we say that m ⊥ l?
Answer:
If l ⊥ m then m ⊥ l.
Since both l, m are perpendicular to each other.

Question 2.
How many perpendicular lines can be drawn to a given line ?
Answer:
We can draw only one line which is perpendicular to the given line.

Question 3.
Which letters in English alphabet possess perpendicularity ?
Answer:
L, T possess the perpendicularity.

Try These

Question 1.
Draw two lines on a paper as shown in the figure.
Do they intersect each other ?
Can you call them parallel lines ? Give reason.

Answer:
The above lines are not intersecting. If, they are extended on either sides they will intersect at a point. They are called intersecting lines i.e., they are not parallel lines.

Question 2.
Make a pair of parallel lines. What is the angle formed between them ? Think, discuss with your friends and teacher.
Answer:
The angle between the parallel lines is 0° (zero). Since they do not intersect.