TS 6th Class Maths Solutions Chapter 13 Practical Geometry Ex 13.1

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 13 Practical Geometry Ex 13.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 13 Practical Geometry Exercise 13.1

Question 1.
Construct a line segment of length 6.9 cm using a ruler and compasses.
Answer:

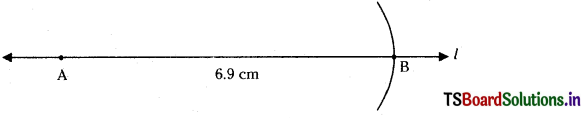
Steps of construction:

1. Draw a line l. Mark a point A on the line l.
2. Place the metal pointer of the compasses on the zero mark of the ruler. Open the compasses so that pencil point touches 6.9 cm mark on the ruler.
3. Place the pointer on A on the line l and draw an arc to cut the line. Mark the point where the arc cuts the line as B.
4. On the line l, we got the line segment AB of required length.

Question 2.
Construct a line segment of length 4.3 cm using the ruler.
Answer:

Steps of construction:

1. Place the ruler on paper and hold it firmly. Mark a point with a sharp edged pencil against 0 cm mark of the ruler. Name the point as A.
2. Mark another point against 3 small divisions just after the 4 cm mark. Name this point as B.
3. Join points A and B along the edge of the ruler.
4. AB is the required line segment of length 4.3 cm.

Question 3.
Construct a line segment MN of length 6 cm. Mark any point O on it. Measure MO, ON and MN. What do you observe ?
Answer:

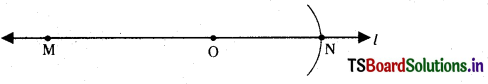
Steps of construction :

1. Draw a line l. Mark a point M on the line l.
2. Place the metal pointer of the compasses on the zero mark of the ruler. Open it to
   place the pencil point upto the 6 cm mark.
3. Taking caution that the opening of the compasses has not changed, place the pointer on M and swing an arc to cut / at N.
4. MN is a line segment of required length.
5. Mark any point ‘O’ on MN.
6. Measure the length of MO and ON. It is found that MO = 3.8 cm and ON = 2.2 cm MO + ON = 3.8 +2.2 = 6 cm
   It is noticed that \(\overline{\mathrm{MO}}+\overline{\mathrm{ON}}\) = \(\overline{\mathrm{MN}}\)

Question 4.
Draw a line segment \(\overline{\mathbf{A B}}\) of length 12 cm. Mark a point C on the line segment \(\overline{\mathbf{A B}}\), such that \(\overline{\mathbf{A C}}\) = 5.6 cm. What should be the length of \(\overline{\mathbf{C B}}\)? Measure the length of \(\overline{\mathbf{C B}}\).
Answer:

Steps of construction:

1. Draw a line l. Mark a point A on the line l.
2. Place the metal pointer of the compasses on the zero mark of the ruler. Open it to place the pencil point upto the 12 cm mark.
3. Taking caution that the opening of the compasses has not changed, place the pointer on A and swing an arc to cut / at B.
4. \(\overline{\mathbf{A B}}\) is a line segment of required length.
5. Similarly mark the point C on l such that \(\overline{\mathbf{A C}}\) = 5.6 cm.
6. The length of \(\overline{\mathbf{C B}}\) should be 6.4 cm = (12 – 5.6) on measuring, the length of \(\overline{\mathbf{C B}}\) = 6.4 cm.

Question 5.
Given that AB = 12 cm

(i) From the figure measure the lengths of the following line segments.
(a) \(\overline{\mathrm{CD}}\)
(b) \(\overline{\mathrm{DB}}\)
(c) \(\overline{\mathrm{EA}}\)
(d) \(\overline{\mathrm{AD}}\)
Answer:
(a) \(\overline{\mathrm{CD}}\) = 2.8 cm
(b) \(\overline{\mathrm{DB}}\) = 4.3 cm
(c) \(\overline{\mathrm{EA}}\) = 17.3 cm
(d) \(\overline{\mathrm{AD}}\) = 16.3 cm

(ii) Verify \(\overline{\mathbf{A E}}-\overline{\mathbf{C E}}\) = \(\overline{\mathbf{A C}}\)
Answer:
\(\overline{\mathbf{A E}}-\overline{\mathbf{C E}}\) = 17.3 cm – 3.8 cm = 13.5 cm
\(\overline{\mathrm{BC}}\) = 1.5 cm
\(\overline{\mathrm{AC}}\) = \(\overline{\mathbf{A B}}+\overline{\mathbf{B C}}\)
= 12 cm + 1.5 cm
= 13.5 cm
∴ \(\overline{\mathrm{AE}}-\overline{\mathrm{CE}}\) = \(\overline{\mathrm{AC}}\)

Question 6.
\(\overline{\mathrm{AB}}\) = 3.8 cm. Construct \(\overline{\mathrm{MN}}\) by compasses such that the length of \(\overline{\mathrm{MN}}\) = 3AB’is thrice that of \(\overline{\mathrm{AB}}\). Verify this with the help of a ruler.
Answer:

Steps of construction:

1. Draw a line l. Mark a point M on it.
2. Place the compasses pointer on the zero mark of the ruler.-Open it to place the pencil upto the 3.8 cm mark.
3. Taking caution that the opening of the compasses has not changed, place the pointer on M and swing an arc to cut l at A.
4. \(\overline{\mathrm{MA}}\) is a line segment of 3.8 cm.
5. Similarly place the pointer on A and swing an arc to cut l at B such that MA = AB.
6. Again place the pointer on B and swing an arc to cut l at N such that AB = BN.
7. Now \(\overline{\mathrm{MN}}\) is a line segment of 11.4 cm.