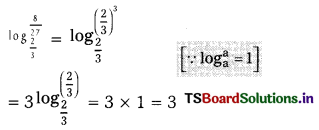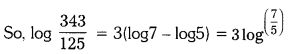Students can practice TS 10th Class Maths Solutions Chapter 1 Real Numbers InText Questions to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 1 Real Numbers InText Questions
Do This
Question 1.
Find ‘q’ and ‘r’ for the following pairs of positive integers ‘a’ and ‘b’, satisfied a = bq + r
i) a = 13, b = 3
Solution:
a = 13, b = 3
a = bq + r
13 = 3(4) + 1 Here q = 4; r = 1
13 = 13
ii) a = 8, b = 80
Solution:
a = 8, b = 80
a = bq + r Here q = \(\frac{1}{10}\) and r = 0
8 = 80\(\left(\frac{1}{10}\right)\) + 0, 8 = 8

iii) a = 125; b = 5
Solution:
a = 125; b = 5
a = bq + r
q = 25, r = 0
125 = 5(25) + 0
125 = 125
iv) a = 132; b = 11
Solution:
a = 132; b = 11
a = bq + r
q = 12, r = 0
132 = 11(12) + 0
132 = 132
Question 2.
Find the HCF of the following by using Euclid division lemma (Page No. 4)
i) 50 and 70
ii) 96 and 72
iii) 300 and 550
iv) 1860 and 2615
Euclid Division Lemma
a = bq + r, q > 0 and 0 ≤ r < b
Solution:
i) 50 and 70 When 70 is divided by 50, the remainder is 20 to get 70 = 50 × 1 + 20
Now consider the division of 50, with the remainder 20 in the above and apply the division lemma to get 50 = 20 × 2 + 10
Now consider the division of 20, with the remainder 10 in apply the division lemma to get 20 = 10 × 2 + 0
The remainder = 0, when we cannot proceed further.
We conclude that the HCF of 50 and 70 is the divisor at this stage, i.e., 10
∴ So, HCF of 50 and 70 is 10.
ii) 96 and 72 When 96 is divided by 72, the remainder is 24 to get 96 = 72 × 1 + 24
Now consider the division of 72, with the remainder 24 in the above and apply the division lemma to get, 72 = 24 x 3 + 0
The remainder = 0, when we cannot proceed further.
We conclude that the HCF of 96 and 72 is the divisor at this stage, i.e., 24 so, the HCF of 96 and 72 is 24
iii) 300 and 550 When 550 is divided by 300, the remainder is 250, to get 550 = 300 × 1 + 250
Now consider the division of 300 with the remainder 250, and apply the division lemma to get 300 = 250 × 1 + 50
Now consider the division of 250 with the remainder 50, and apply the division lemma to get 250 = 50 × 5 + 0. The remainder is zero, when we cannot proceed further. We conclude that the H.C.F of 300 and 550 is the divisor at this stage i.e., 50. So, the H.C.F of 300 and 550 is 50.
iv) 1860 and 2015 When 2015 is divided by 1860, the remainder is 155, to get 2015 = 1860 × 1 + 155
Now consider the division of 1860 with the remainder 155, and apply the division lemma to get 1860 = 155 × 12 + 0
The remainder is zero, then we cannot proceed further.
We conclude that the HCF of 1860 and 2015 is the divisor at this stage i.e., 155 So, the HCF of 1860 and 2015 is 155

Think – Discuss
Question 1.
From the above questions in do this what is the nature of q and r ? (Page No. 3)
Solution:
Given a = bq + r q > 0 and r ≤ 0 r < b r lies between 0 and b
Question 2.
Can you find the HCF of 1.2 and 0.12 ? Justify your answer. (Page No. 4)
Solution:
1.2 = \(\frac{12}{10}\) and 0.12 = \(\frac{12}{100}\)
When \(\frac{12}{10}\) is divided by \(\frac{12}{100}\), then the remainder is 0.
\(\frac{12}{10}\) = \(\frac{12}{100}\) × 10 + 0
∴ yes, we can find the HCF of 1.2 and 0.12 HCF (1.2, 0.12) = 10
Textual Examples
Question 1.
Show that every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer. (Page No. 5)
Solution:
Let a be any positive integer and b = 2. Then, by Euclid’s algorithm, a = 2q + r, for some integer q ≥ 0, and r = 0 or r = 1, because 0 ≤ r < 2. So, a = 2q or 2q + 1.
If a is of the form 2q, then a is an even integer. Also, a positive integer can be either even or odd. Therefore, any positive odd integer is of the form 2q + 1.
Question 2.
Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer. (Page No. 5)
Solution:
Let us start with taking a, where a is a positive odd integer. We apply the division algorithm with a and b = 4. Since 0 ≤ r < 4, the possible remainders are 0, 1, 2 and 3.
That is, a can be 4q, or 4q + 1, or 4q + 2, or 4q + 3, where q is the quotient. However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Therefore, any odd integer is of the form 4q + 1 or 4q + 3.
Think – Discuss
Question 1.
If r = 0, then what is the relationship between a, b and q in a = bq + r of Euclid division lemma? (Page No. 6)
Solution:
a = bq + 0 (∵ r = 0) ⇒ a = bq
Do This
Question 1.
Express 2310 as a product of prime factors. Also see how your friends have factorized the number. Have they done it like you ? Verify your final product with your friend’s result. Try this for 3 or 4 more numbers. What do you conclude ?
(Page No. 7)
Solution:
2310 = 2 × 1155
= 2 × 5 × (231)
= 2 × 5 × 3 × 77
= 2 × 5 × 3 × 7 × 11
= 2 × 3 × 5 × 7 × 11
Ramu, Kiran and Mohan are my friends. They factorized the number in the following way :
Ramu : 2310 = 231 × 10
= 3 × 77 × 2 × 5
= 3 × 7 × 11 × 2 × 5
Kiran : 2310 = 3 × 770
= 3 × 10 × 77
= 3 × 10 × 11 × 7
= 3 × 2 × 5 × 11 × 7
Mohan : 2310 = 7 × 330
= 7 × 3 × 110
= 7 × 3 × 11 × 10
= 7 × 3 × 11 × 2 × 5
No, but the prime factors are same.
The final product with your friends result is same.
Conclusion : The order in which the prime factors occur, the composite number is unique.

Question 2.
Find the HCF and LCM of the following given pairs of numbers by prime factorisation.
i) 120, 90
ii) 50, 60
iii) 37, 49 (Page No. 8)
H.C.F. : (Product of smallest power of each common prime factor of the numbers)
L.C.M. : (Product of greatest power of each prime factors of the numbers)
Solution:
i) 120, 90
120 = 2 × 2 × 2 × 3 × 5 = 23 × 31 × 51
90 = 2 × 3 × 3 × 5 = 21 × 32 × 51
HCF (120, 90) = 21 × 31 × 51 = 30
LCM (120, 90) = 23 × 32 × 51 = 360
ii) 50, 60
50 = 2 × 5 × 5 = 21 × 52
60 = 2 × 2 × 3 × 5 = 22 × 31 × 51
HCF (50, 60) = 21 × 51 = 10 (Product of smallest power of each common prime factors of the numbers)
LCM (50, 60) = 22 × 52 × 31 = 300 (Product of greatest power of each prime factors of the numbers)
iii) 37, 49
37 is a prime number and 49 is a composite number, so the HCF(37, 49) is 1 and LCM(37, 49) is 1813.
Textual Examples
Question 1.
Consider the numbers 4n, where n is a natural number. Check whether there is any value of n for which 4n ends with the digit zero. (Page No. 5)
Solution:
For the number 4n to end with digit zero for any natural number n, it should be divisible by 5. This means that the prime factorisation of 4n should contain the prime number 5. But it is not possible because 4n = (2)2n so 2 is the only prime in the factorization of 4n. Since 5 is not present in the prime factorization, so there is no natural number n for which 4n ends with the digit zero.
Question 2.
Find the HCF and LCM of 12 and 18 by the prime factorization method. (Page No. 7)
Solution:
We have 12 = 2 × 2 × 3 = 22 × 31
18 = 2 × 3 × 3 = 21 × 32
Note that HCF (12, 18) = 21 x 31 = 6
HCF : Product of the smallest power of each common prime factors in the numbers.
LCM (12, 18) = 22 × 32 = 36 = Product of the greatest power of each prime factors in the numbers.
Try This
Question 1.
Show that 3n × 4m cannot end with the digit 0 or 5 for any natural numbers ‘n’ and ‘m’. (Page No. 8)
Solution:
Let the number 3n × 4m
= 3n × (22)m
= 3n × 22m
Number 3n × 22m to end with ‘0’ or ‘5’. It should be divisible by 2 and 5. This means that the prime factorization of 3n × 4m should contain prime numbers. But it is not possible because 3n × 4m = 3n × 22m
So 2 or 3 are the only prime factors in its factorization. Since 5 is not present in the prime factorization 3n × 4m can not end with the digits 0 or 5.
Try This
Question 1.
Show that 3n × 4m cannot end with the digit 0 or 5 for any natural numbers ‘n’ and’m’. (Page No. 8)
Solution:
Let the number 3n × 4m = 3n × (22)m
= 3n × 22m
Number 3n × 22m to end with ‘0’ or ‘5’. It should be divisible by 2 and 5. This means that the prime factorization of 3n × 4m should contain prime numbers. But it is not possible because 3n × 4m = 3n × 22m
So 2 or 3 are the only prime factors in its factorization. Since 5 is not present in the prime factorization 3n × 4m can not end with the digits 0 or 5.
Do This
Question 1.
Write the following terminating decimals in the form of \(\frac{\mathbf{p}}{\mathbf{q}}\). q ≠ 0 and p, q are co-primes.
i)15.265
ii) 0.1255
iii) 0.4
iv) 23.34
v) 1215.8
What can you conclude about the denominators through this process? (Page No. 6)
Solution:
i) 15.265 = \(\frac{15265}{10^3}\) = \(\frac{152625}{2^3 \times 5^3}\) = \(\frac{3053}{2^3 \times 5^2}\) = \(\frac{3053}{200}\)
ii) 0.1255 = \(\frac{1255}{10^4}\) = \(\frac{1255}{2^4 \times 5^4}\) = \(\frac{3053}{200}\)

iii) 0.4 = \(\frac{4}{10}\) = \(\frac{2}{5}\)
iv) 23.34 = \(\frac{2334}{10^2}\) = \(\frac{2334}{2^2 \times 5^2}\) = \(\frac{1167}{50}\)
v) 1215.8 = \(\frac{12158}{10}\) = \(\frac{12158}{2 \times 5}\) = \(\frac{6079}{5}\)
We can conclude that the denominator in the problems have only power of 2 or power of 5 or both.
Question 2.
Write the following rational numbers in the form of \(\frac{\mathbf{p}}{\mathbf{q}}\), where q is of the form 2n5m where n, m are non-negative integers and these write the negative Integers and then write the numbers in their decimal form.
i) \(\frac{3}{4}\)
ii) \(\frac{7}{5}\)
iii) \(\frac{51}{64}\)
iv) \(\frac{14}{25}\)
v) \(\frac{80}{100}\)
Solution:
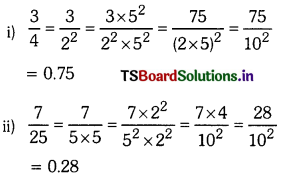
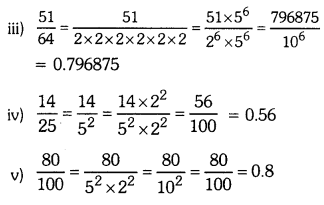
Question 3.
Write the following rational numbers as decimals and find out the block of digits, repeating ¡n the quotient.
i) \(\frac{1}{3}\)
ii) \(\frac{2}{7}\)
iii) \(\frac{5}{11}\)
iv) \(\frac{10}{13}\) (Page No. 11)
Solution:
i) \(\frac{1}{3}\) = 0.33333 …….

The block of digits repeating in the quotient is only 3.
ii) \(\frac{2}{7}\) = 0.285714285714 ……

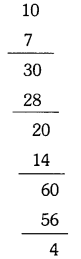
The block of digits repeating in the quotient is only 285714.
iii) \(\frac{5}{11}\) = 0.454545…..

The block of digits repeating in the quotient is only 45.

iv) \(\frac{10}{13}\) = 0.769230769230 …..
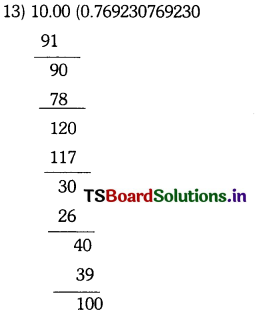
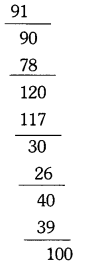
The block of digits repeating in the quotient is only 769230.
Textual Examples
Question 1.
Using the above theorems, without actual division, state whether the following rational numbers are terminating or non-terminating, repeating decimals.
i) \(\frac{16}{125}\)
ii) \(\frac{25}{32}\)
iii) \(\frac{100}{81}\)
iv) \(\frac{41}{75}\)
Solution:
\(\frac{16}{125}\) = \(\frac{16}{555}\) = \(\frac{16}{5^3}\)
is terminating decimal.
ii) \(\frac{25}{32}\) = \(\frac{25}{2 \times 2 \times 2 \times 2 \times 2}\) = \(\frac{25}{2^5}\)
is terminating decimal.
iii) \(\frac{100}{81}\) = \(\frac{100}{3 \times 3 \times 3 \times 3}\) = \(\frac{10}{3^4}\)
is non-terminating, repeating decimal.
iv) \(\frac{41}{75}\) = \(\frac{41}{3 \times 5 \times 5}\) = \(\frac{41}{3 \times 5^2}\)
is non-terminating, repeating decimal.
Question 2.
Write the decimal expansion of the following rational numbers without actual division.
i) \(\frac{35}{40}\)
ii) \(\frac{21}{25}\)
iii) \(\frac{7}{8}\)
Solution:
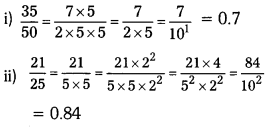
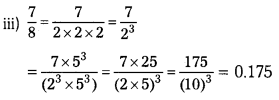
Do This
Question 1.
Verify the statement proved above for p = 2, p = 5 and for a2 = 1, 4, 9, 25, 36, 49, 64 and 81. (Page No. 14)
Solution:
The statement proved already is as follow.
Let p be a prime number.
If p divides a2 where ‘a’ is a positive integer then ‘p’ divides ‘a’ when p = 2 if 2 divides a (= 4, 36, 64) then p divide ‘a’ (= 2, 6, 8)
In other cases when a2 = 1, 9, 25, 49 and 81 the statement is not correct.
When p = 5 if 5 divide a2 then p divide ‘a’
In other cases i.e., when a2(= 1, 4, 9, 16, 36, 49, 64, 81). the statement is not correct.
Textual Examples
Question 1.
Prove that \(\sqrt{2}\) is irrational. (Page No. 14)
Solution:
Since we are using proof by contradiction, let us assume the contrary, i.e., \(\sqrt{2}\) is rational.
If it is rational, then there must exist two integers r and s (s ≠ 0) such that
\(\sqrt{2}\) = \(\frac{\mathrm{r}}{\mathrm{s}}\)
Suppose r and s have a common factor other than 1. Then, we divide by the common factor to get \(\sqrt{2}\) = \(\frac{a}{b}\)’ w^ere a and b are co-primes.
So, b\(\sqrt{2}\) = a
On squaring both sides and rearranging, we get 2b2 = a2. Therefore, 2 divides a2.
Now, by statement 1, it follows that if 2 divides a2 it also divides a.
So, we can write a = 2c for some integer c. Substituting for a, we get 2b2 = 4c2, that is, b2 = 2c2.
This means that 2 divides b2, and so 2 divides b (again using statement 1 with p = 2).
Therefore, both a and b have 2 as a common factor.
But this contradicts the fact that a and b are co-prime and have no common factors other than 1.
This contradiction has arisen because of our assumption that \(\sqrt{2}\) is rational. So, we conclude that \(\sqrt{2}\) is irrational.

Question 2.
Show that 5 – \(\sqrt{3}\) is irrational. (Page No. 14)
Solution:
Let us assume, to the contrary, that 5 – \(\sqrt{3}\) is rational.
That is, we can find co-primes a and b (b ≠ 0)
such that 5 – \(\sqrt{3}\) = \(\frac{\mathrm{a}}{\mathrm{b}}\)
Therefore, 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) = \(\sqrt{3}\)
Rearranging this equation,
we get \(\sqrt{3}\) = 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) = \(\frac{5 b-a}{b}\)
Since a and b are integers, we get 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) is rational so \(\sqrt{3}\) is rational.
But this contradicts the fact that \(\sqrt{3}\) is irrational.
This contradiction has arisen because of our incorrect assumption that
5 – \(\sqrt{3}\) is rational.
So, we conclude that 5 – \(\sqrt{3}\) is irrational.
Question 3.
Show that 3\(\sqrt{2}\) is irrational.(Page No. 15)
Solution:
Let us assume, the contrary, that 3\(\sqrt{2}\) is rational.
i.e., we can find co-primes a and b (b ≠ 0) such that 3\(\sqrt{2}\) = \(\frac{\mathrm{a}}{\mathrm{b}}\)
Rearranging, we get \(\sqrt{2}\) = \(\frac{a}{3 b}\)
Since 3, a and b are integers, \(\frac{a}{3 b}\) is rational, and so \(\sqrt{2}\) is rational.
But this contradicts the fact that \(\sqrt{2}\) is irrational.
So, we conclude that 3\(\sqrt{2}\) is irrational.
Question 4.
Prove that \(\sqrt{2}\) + \(\sqrt{3}\) is irrational. (Page No. 15)
Solution:
Let us suppose that \(\sqrt{2}\) + \(\sqrt{3}\) is rational.
Let \(\sqrt{2}\) + \(\sqrt{3}\) = \(\frac{a}{b}\), where a, b are integers and
b ≠ 0.
Therefore, \(\sqrt{2}\) = \(\frac{a}{b}\) – \(\sqrt{3}\)
Squaring on both sides, we get
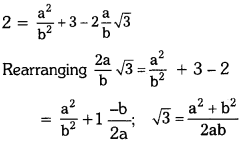
∴ Since a, b are intetgers, \(\frac{a^2+b^2}{2 a b}\) is rational, and so, \(\sqrt{3}\) is rational.
This contradicts the fact that \(\sqrt{3}\) is irrational.
∴ Hence, \(\sqrt{2}\) + \(\sqrt{3}\) is irrational
Think – Discuss
Question 1.
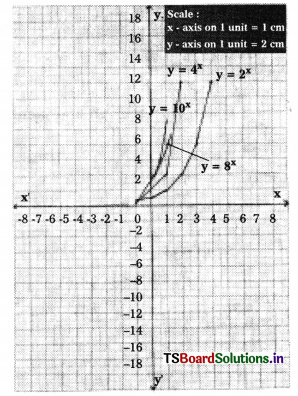
Draw the graphs of y = 2x; y = 4x; y = 8x and y = 10x in a single graph and mention your observation. (Page No. 17)
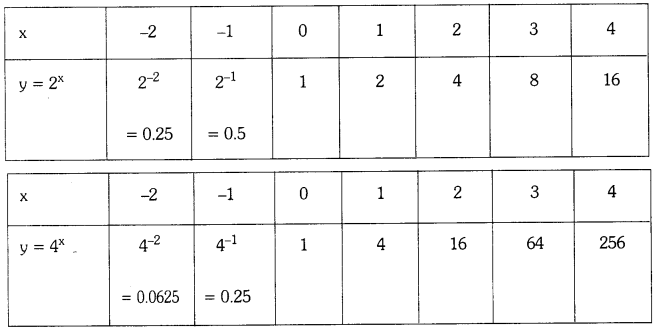
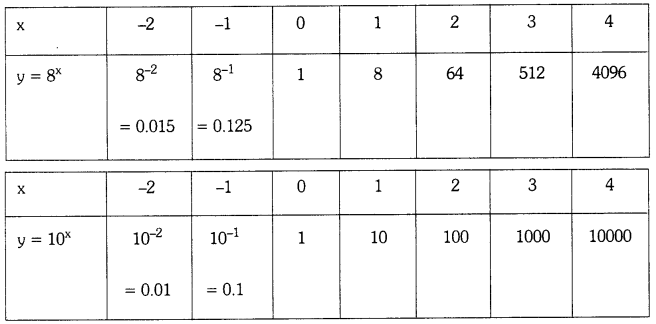
Observations:
1. The curve never cuts the X – axis.
2. The value of y is same x = 0.
i.e., y = 2x = 4x = 8 = 1ox = 1 where x = 0.
3. The value of y gets very close to zero for the values of x.
4. All curves meet Y-axis at the same point when x = 0.
Solution:
Question 2.
Write the nature of y, a and x in y = a,sup>x. Can you determine the value of x ford given y justify your answer. (Page No. 17)
Solution:
y = ax means, the relative change is not same for all real values of x.
We are unable to determine the value of x for a given value of y in y = ax.
For example y = 3 in y = 7x
What should be the power to which 7 must be raised to get 3.
Question 3.
From the graph y = 2x, y = 4x, y = 8x and y = 10x you have drawn earlier have you noticed the value log 1 (any base) (Page No. 18)
Solution:
Yes, log 1 to any base is zero.

Question 4.
You know that 21 = 2, 41 = 4, 81 = 8 and 101 = 10. What do you notice about the values of \(\log _2^2\), \(\log _4^4\), \(\log _8^8\) and \(\log _10^10\)?
What can you generalise from this? (Page No. 18)
Solution:
We know that 21 = 2, 41 = 4, 81 = 8 and 101 = 10.
\(\log _2^2\) = 1, \(\log _4^4\) = 1, \(\log _8^8\) = 1 and \(\log _10^10\) = 1
∴ We generalise from this, a = N then the \(\log _a^a\) = 1
Question 5.
Does \(\log _0^10\) exist?
Solution:
No, \(\log _0^10\) does not exist.
ax ≠ 0, a, x ∈ N
Question 6.
We know that, if 7 = 2x then x = \(\log _2 7\). Then what is the value of \(2^{\log _2^7}\) = ? Justify your answer. Generalise the above by taking same more examples for \(a^{\log _a^N}\). (Page No. 23)
Solution:
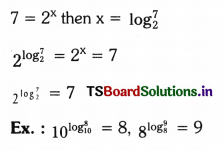
Do THIS
Question 1.
Write the powers to which the bases to be raised in the following:
i) 7 = 2x
ii) 10 = 5b
iii) \(\frac{1}{81}\) = 3c
iv) 100 = 10z
v) \(\frac{1}{257}\) = 4a.
Solution:
i) 7 = 2x
We cannot determined the power of x.
ii) 10 = 5b
2 × 5 = 5b
We can not determined the power of b.

iii) \(\frac{1}{81}\) = 3c
(81)-1 = 3c
(34)-1 = 3c
(3)-4 = 3c
∴ C = -4
iv) 100 = 10z
102 = 10z
∴ z = 2
v) \(\frac{1}{257}\) = 4a
We cannot determine the power of a.
Question 2.
Express the logarithms of the following Into sum of the logarithms:
i) 35 × 46
ii) 235 × 437
iii) 2437 × 3568 (Page No. 19)
Solution:
i) 35 × 46
log xy = log x + log y
∴ log10 35 × 46 = log10 35 + log10 46
ii) 235 × 437
log10 35 × 437 = log10 235 + log10 437
[∵ log xy = log x + log y]
iii) 2437 × 3568
log10 2437 × 3568 = log10 2437 + log10 3568
[∵ log xy = log x + log y]
Question 3.
Express the logarithms of the following into difference of the logarithms
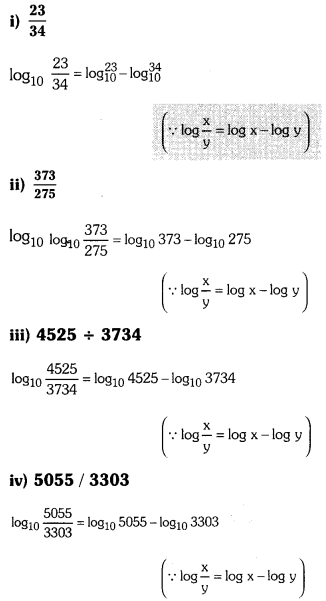
i) \(\frac{23}{34}\)
ii) \(\frac{373}{275}\)
iii) 4525 ÷ 3734
iv) 5055/3303
Solution:
Question 4.
By using the formula \(\log _a^{x^n}\) = \(n \log _a^{\mathbf{x}}\) convert the following
i) \(\log _2^{7^{25}}\)
ii) \(\log _5^{8^{50}}\)
iii) \(\log 5^{23}\)
iv) log1024 (Page No. 21)
Solution:
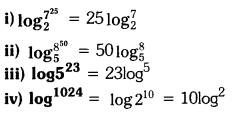
TRY THIS
Question 1.
Write the following relation in exponential form and find the values of respective variables. (Page No. 18)
i) \(\log _2^{32}\) = x
ii) \(\log _5^{625}\) = y
iii) \(\log _{10}^{10000}\) = z
iv) \(\log _7\left(\frac{1}{343}\right)\) = -a
Solution:

Question 2.
i) Find the value of \(\log _2^{32}\) (Page No. 21)
log xm = m log x and \(\log _a^a\) = 1
Solution:
= \(\log _2^{2^5}\) = \(5 \log _2^2\) = 5 × 1 = 5
ii) Find the value of \(\log _c^{\sqrt{c}}\) (Page No. 21)
Solution:
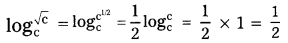
iii) Find the value of \(\log _{10}^{0.001}\) (Page No. 21)
Solution:
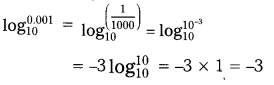
iv) Find the value of 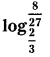 (Page No. 21)
(Page No. 21)
Solution:
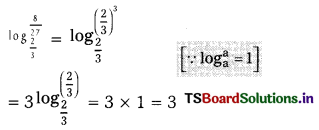
Textual Examples
Question 1.
Expand log \(\frac{343}{125}\).
Solution:
As you know, loga \(\frac{x}{y}\) = logax – logay
So, log \(\frac{343}{125}\) = log343 – log125
= log73 – log53
∴ Since, logaxm = m logax
= 3log7 – 3log5
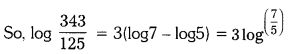

Question 2.
Write 2log3 + 3log5 – 5log2 as a single logarithm.
Solution:
2log3 + 3log5 – 5log2
= log32 + log53 – log25
(Since in m logax=logaxm)
= log9 + log125 – log32
= log (9 × 125) – log32
(Since logax + logay = logaxy)
= log1125 – log32
= logl \(\frac{1125}{32}\) (Since logax – logay = \(\log _a \frac{x}{y}\))
Question 3.
Solve 3x = 5x-2 (Page No. 22)
Solution:
Taking log on both the sides
x log10 3 = (x – 2) log10 5
x log10 3 = x log10 5 – 2 log10 5
x log10 5 – 2 log10 5 = x log10 3
x(log10 5 – log10 3) = 2 log10 5
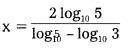
Question 4.
Find x if 2 log 5 + \(\frac{1}{2}\) log 9 – log 3 = log x. (Page No. 22)
Solution:
log x = 21og 5 + \(\frac{1}{2}\) log 9 – log 3
= log 52 + log \(9^{\frac{1}{2}}\) – log 3
= log 25 + log \(\sqrt{9}\) – log 3
= log 25 + log 3 – log 3
log x = log 25
∴ x = 25
![]()

![]()



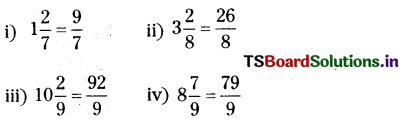



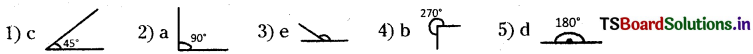




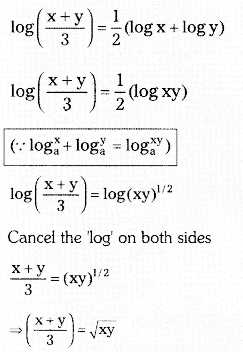
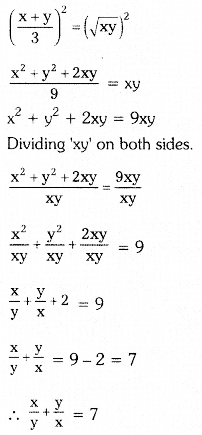
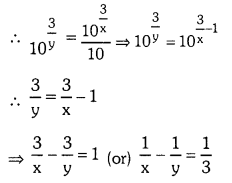









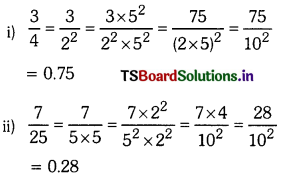
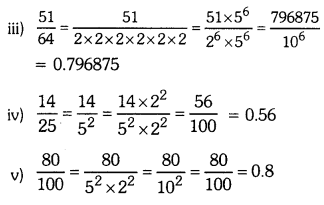





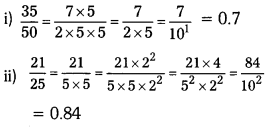
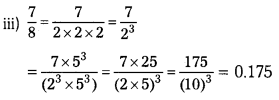
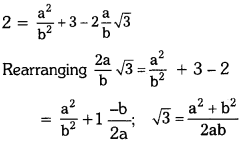



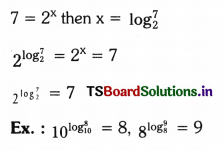

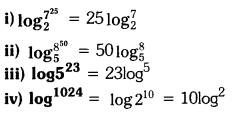

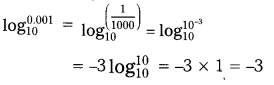
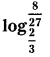 (Page No. 21)
(Page No. 21)