TS Inter 1st Year

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Differentiation Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Differentiation Important Questions Very Short Answer Type

Question 1.
Find the derivative of f(x) = e^x (x² + 1). [May ’02]
Solution:
Given f(x) = e^x (x² + 1)
Let y = e^x (x² + 1)
Differentiating with respect to x on both sides

Question 2.
If f(x) = x² . 2^x . log x (x > 0), find f'(x). [May ’10]
Solution:
Given f(x) = x² . 2^x . log x
Let y = x² . 2^x . log x
Differentiating with respect to x on both sides

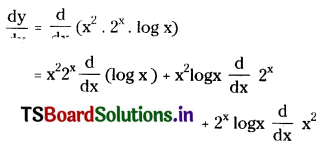
Question 3.
If f(x) = \(7^{x^3+3 x}\) (x > 0), then find f'(x). [Mar. ’17 (TS); May ’05]
Solution:

Question 4.
If y = e^2x log(3x + 4) then find \(\frac{d y}{d x}\). [May ’13; Mar. ’13 (Old)]
Solution:
Given, f(x) = e^2x log(3x + 4)
Let y = e^2x log(3x + 4)
Differentiating on both sides with respect to x
\(\frac{d y}{d x}=\frac{d}{d x}\left[e^{2 x} \log (3 x+4)\right]\)

Question 5.
If y = \(\frac{\mathbf{a x}+\mathbf{b}}{\mathbf{c x}+\mathbf{d}}\) then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\).
Solution:
Given, f(x) = \(\frac{\mathbf{a x}+\mathbf{b}}{\mathbf{c x}+\mathbf{d}}\)
Let y = \(\frac{\mathbf{a x}+\mathbf{b}}{\mathbf{c x}+\mathbf{d}}\)
Differentiating on both sides with respect to x

Question 6.
If f(x) = \(\mathbf{a}^{\mathbf{x}} \cdot \mathrm{e}^{\mathbf{x}^2}\), then find f'(x). [May ’08; B.P.]
Solution:
Given, f(x) = \(\mathbf{a}^{\mathbf{x}} \cdot \mathrm{e}^{\mathbf{x}^2}\)
Let y = \(\mathbf{a}^{\mathbf{x}} \cdot \mathrm{e}^{\mathbf{x}^2}\)
Differentiating on both sides with respect to x

Question 7.
If f(x) = log(sec x + tan x), find f'(x). [Mar. ’14; May ’11]
Solution:
Given, f(x) = log(sec x + tan x)
Differentiating on both sides with respect to x

Question 8.
If f(x) = 1 + x + x² + ……….. + x¹⁰⁰, then find f'(1). [Mar. ’19 (TS); May ’14]
Solution:
Given f(x) = 1 + x + x² + ……… + x¹⁰⁰
Differentiating on both sides with respect to ‘x’.

Question 9.
If y = \(\sin ^{-1} \sqrt{x}\), find \(\frac{d \mathbf{y}}{d x}\). [Mar. ’13]
Solution:
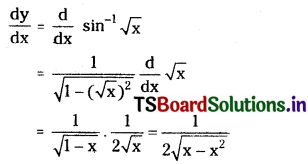
Given, y = \(\sin ^{-1} \sqrt{x}\)
Differentiating on both sides with respect to x

Question 10.
If y = sec(√tan x), find \(\frac{d \mathbf{y}}{d x}\). [May ’07]
Solution:
Given, y = sec(√tan x)
Differentiating on both sides with respect to x

Question 11.
If y = log(cosh 2x), find \(\frac{d \mathbf{y}}{d x}\). [Mar. ’12]
Solution:
Given y = log(cosh 2x)
Differentiating on both sides with respect to x

Question 12.
If y = log(sin(log x)), find \(\frac{\mathrm{dy}}{\mathrm{dx}}\).
Solution:
Given, y = log(sin(log x))
Differentiating on both sides with respect to ‘x’.

Question 13.
If y = \(\left(\cot ^{-1} x^3\right)^2\), find \(\frac{\mathrm{dy}}{\mathrm{dx}}\). [May ’13, ’09; Mar. ’18 (TS)]
Solution:
Given y = \(\left(\cot ^{-1} x^3\right)^2\)
Differentiating on both sides with respect to ‘x’.

Question 14.
Find the derivative of log(tan 5x). [Mar. ’08]
Solution:
Given, y = log(tan 5x)
Differentiating on both sides with respect to ‘x’.

Question 15.
Find the derivative of \(\sinh ^{-1}\left(\frac{3 x}{4}\right)\). [May ’13 (Old)]
Solution:
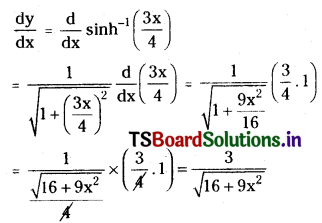
Let y = \(\sinh ^{-1}\left(\frac{3 x}{4}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 16.
Find the derivative of \(\log \left(\frac{x^2+x+2}{x^2-x+2}\right)\). [May ’06]
Solution:
Let y = \(\log \left(\frac{x^2+x+2}{x^2-x+2}\right)\)
Differentiating on both sides with respect to ‘x’.
\(\frac{d y}{d x}=\frac{d}{d x} \log \left(\frac{x^2+x+2}{x^2-x+2}\right)\)

Question 17.
Find the derivative of \(\log \left[\sin ^{-1}\left(e^x\right)\right]\). [Mar. ’10]
Solution:
Let y = \(\log \left[\sin ^{-1}\left(e^x\right)\right]\)
Differentiating on both sides with respect to ‘x’.

Question 18.
Find the derivation of x = tan(e^-y) with respect to x. [Mar. ’17 (TS), ’05; May ’03]
Solution:
Given, x = tan(e^-y)
⇒ tan^-1x = e^-y
Differentiating on both sides with respect to ‘x’.

Question 19.
Find the derivative of cos[log(cot x)]. [Mar. ’13 (old)]
Solution:
Let y = cos[log(cot x)]
Differentiating on both sides with respect to ‘x’.

Question 20.
If y = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’15 (AP), ’04; May ’98, ’92]
Solution:

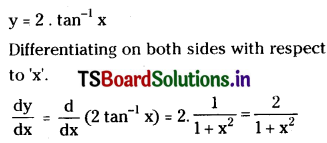
Question 21.
If y = x^x (x > 0), find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’11; May ’97, ’96]
Solution:
Given, y = x^x
Taking logarithms on both sides,
log y = log x^x
log y = x log x
Differentiating on both sides with respect to ‘x’.

Question 22.
If x = a cos³t, y = a sin³t, find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’16 (AP), ’12, ’07, ’02; May ’12, ’11]
Solution:

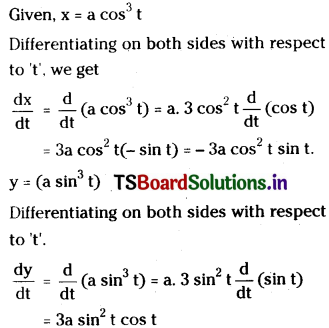
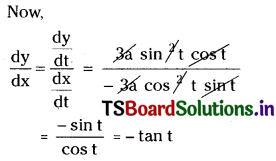
Question 23.
If x³ + y³ – 3axy = 0, find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’00]
Solution:
Given, x³ + y³ – 3axy = 0
Differentiating on both sides with respect to ‘x’.

Question 24.
Find the derivative of sin^-1(3x – 4x³) with respect to ‘x’. [Mar. ’16 (TS), May ’11, ’97]
Solution:
Let y = sin^-1(3x – 4x³)
Put x = sin θ
⇒ θ = sin^-1x
Now, y = sin^-1(3 sin θ – 4 sin³θ)
= sin^-1(sin 3θ)
= 3θ
y = 3 sin^-1x
Differentiating on both sides with respect to ‘x’.
\(\frac{\mathrm{dy}}{\mathrm{dx}}=3 \frac{\mathrm{d}}{\mathrm{dx}} \sin ^1 \mathrm{x}\)
= \(3 \frac{1}{\sqrt{1-x^2}}\)
= \(\frac{3}{\sqrt{1-x^2}}\)

Question 25.
Find the derivative of \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\). [May ’15 (TS); Mar. ’15 (TS), ’12, ’98]
Solution:

Question 26.
Find the derivative of \(\tan ^{-1} \sqrt{\frac{1-\cos x}{1+\cos x}}\). [May ’13 (old); May ’02]
Solution:

Question 27.
Find the derivative of \(\sec ^{-1}\left(\frac{1}{2 x^2-1}\right)\). [Mar. ’17 (AP), ’13]
Solution:
Let y = \(\sec ^{-1}\left(\frac{1}{2 x^2-1}\right)\)

Question 28.
If x = 3 cos t – 2 cos³t, y = 3 sin t – 2 sin³t, then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\).
Solution:

Question 29.
Find the derivative of y = x^y. [Mar. ’04, ’00, ’99]
Solution:
Given, y = x^y
Taking logarithms on both sides, we get
log y = log x^y
⇒ log y = y log x
Differentiating on both sides with respect to ‘x’.
\(\frac{d}{d x}(\log y)=\frac{d}{d x}(y \log x)\)

Question 30.
Find the derivative of ex with respect to √x. [Mar. ’03]
Solution:
Given, f(x) = e^x, g(x) = √x
Let u = e^x
Differentiating on both sides with respect to ‘x’.
\(\frac{d u}{d x}=\frac{d}{d x} e^x=e^x\)
Let v = √x
Differentiating on both sides with respect to ‘x’.

Question 31.
If y = \(\frac{2 x+3}{4 x+5}\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [May ’15 (AP)]
Solution:

Question 32.
Find the derivative of y = \(\sqrt{2 x-3}+\sqrt{7-3 x}\). [Mar. ’15 (TS)]
Solution:
Given y = \(\sqrt{2 x-3}+\sqrt{7-3 x}\)

Question 33.
Find the derivative of 5 sin x + e^x log x. [Mar. ’17 (AP)]
Solution:
Let y = 5 sin x + e^x log x
Differentiating on both sides with respect to x

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(c)

I.
Question 1.
Find the ratios in which the following straight lines divide the line segment joining the given points. State whether the points lie on the same side or on either side of the straight line. (V.S.A.Q.)
(i) 3x – 4y = 7; ( 2, – 7 ) and ( – 1, 3 )
ii) 3x + 4y = 6; ( 2, – 1 ) and (1,1)
iii) 2x + 3y = 5; (0, 0) and (- 2,1) (Mar. ’14)
Answer:
(i) 3x – 4y = 7, (2, – 7 ) and (- 1, 3)
3x – 4y – 7 = 0
we have the formula for the ratio Ln -(axj + by! + c) l22 ” (ax2 + by2 + c)

Since L₁₁ and L₂₂ are of opposite signs, the given points lie on either side of the straight line.

(ii) 3x + 4y = 6; ( 2, -1 ) and ( 1, 1 )
Equation of the given line is 3x + 4y – 6 = 0

Since L₁₁ and L₂₂ are of opposite signs, the given points lie on either side of the straight line.

(iii) 2x + 3y = 5; ( 0, 0 ) and (- 2, 1 )

Since L₁₁ and L₂₂ are of same sign, the points lie on the same side of line.

Question 2.
Find the point of intersection of the following lines
(i) 4x + 8y – 1 = 0; 2x – y + 1 = 0
(ii) 7x + y + 3 = 0;x + y = 0 (VJS.A.Q.)
Answer:
(i) 4x + 8y – 1 = 0; 2x – y + 1 = 0
Point of intersection of above lines is obtained by solving the two equations (or) by the formula.

(ii) 7x + y + 3 = 0; x + y = 0
The point of intersection of the lines is obtained by solving the above equations.

Question 3.
Show that the straight lines
(a – b)x + (b – c)y = c – a,
(b – c)x + (c – a)y = a – b and
(c – a)x + (a – b)y = b – c are concurrent.
Answer:
Take given lines as
(a – b)x + (b – c)y = c – a ……………….. (1)
(b – c) x + (c – a) y = (a – b) ……………… (2)
(c – a) x + (a – b) y = (b – c) ……………. (3)
solving (1) and (2)

∴ Point of intersection of (1) and ( 2 ) is (-1, -1)
Substituting in equation (3) we get (c – a) (- 1) + ( a – b) (- 1) = – c + a – a + b = b – c
P (-1, -1) is a point on (3) and hence the given lines are concurrent.

Question 4.
Transform the following equations into the form L₁ + λL₂ = 0 and find the point of concurrency of the family of straight lines represented by the equation.
(i) (2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0
(ii) (k + 1)x + (k + 2)y + 5 = 0 (SA.Q.)
Answer:
(2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0
(2 + 5k ) x – 3 ( 1 + 2k ) y + (2 – k) = 0
⇒ (2x – 3y + 2 ) + k ( 5x – 6y – 1 ) = 0
This is of the form L₁ + λL₂ = 0
L₁ = 2x – 3y + 2 = 0
L₂ = 5x – 6y – 1 = 0
solving these equations

∴ The point of concurrency is P(5, 4)

(ii) (k + 1)x + (k + 2)y + 5 = 0
Answer/;
k (x + y) + (x + 2y + 5) = 0
⇒(x + 2y + 5) + k(x + y) = 0
This is of the form
∴ L₁ + λL₂ = 0
L₂ = x + y = 0 solving them

⇒ x = 5, y = -5
∴ point of concurrency = (5, -5)

Question 5.
Find the value of p, if the straight lines x + p = 0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent. (V.S.A.Q.)
Answer:
Equations of the given lines
x + p = 0 ………………….. (1)
y + 2 = 0 ………………….. (2)
3x + 2y + 5 = 0 ………………….. (3)
From (2) we have y = – 2
and from (3) 3x – 4 + 5 = 0 ⇒ x = – \(\frac{1}{3}\)
∴ From (1), p = – x = \(\frac{1}{3}\)

Question 6.
Find the area of the triangle formed by the following straight lines and the coordinate axes.
(i) x – 4y + 2 = 0
(ii) 3x – 4y + 12 = 0 (V.S.A.Q.)
Answer:
(i) x – 4y + 2 = 0
Equation of the line x – 4y + 2 = 0
⇒ x – 4y = – 2
⇒ \(\frac{x}{-2}+\frac{y}{\left(\frac{1}{2}\right)}\) = 1
∴ X – intercept = – 2, Y – intercept = \(\frac{1}{2}\)
∴ Area of ∆ OAB = \(\frac{1}{2}\) |ab|
= \(\frac{1}{2}\left|(-2)\left(\frac{1}{2}\right)\right|\) = \(\frac{1}{2}\)

(ii) 3x – 4y + 12 = 0
Equation of the given line is 3x – 4y + 12 = 0
⇒ 3x – 4y = – 12
⇒ \(\frac{3}{-12} x-\frac{4}{-12} y\) = 1
⇒ \(\frac{x}{-4}+\frac{y}{3}\) = 1
X-intercept = – 4, Y-intercept = 3
∴ Area of ∆ OAB = \(\frac{1}{2}\) |ab|
= \(\frac{1}{2}\) |(- 4) (3)| = 6 square units

II.
Question 1.
A straight line meets the coordinate axes at A and B. Find the equation of straight line, when
(i) \(\overline{\mathbf{A B}}\) is divided in the ratio 2 : 3 at (- 5, 2)
(ii) \(\overline{\mathbf{A B}}\) is divided in the ratio 1 : 2 at (- 5, 4)
(iii) (p, q) bisects \(\overline{\mathbf{A B}}\) (S.A.Q.)
Answer:
(i) \(\overline{\mathbf{A B}}\) is divided in the ratio 2 : 3 at (- 5, 2 )

Let OA = a and OB = b
∴ A = (a, 0) and B = (0, b)
M divides AB in the ratio 2 : 3

(ii) \(\overline{\mathbf{A B}}\) is divided in the ratio 1 : 2 at (- 5, 4)
Answer:
Let OA = a and OB = b
then A = (a, O) and B= (O, b)
P divides AB in the ratio 1 : 2

(iii) (p, q) bisects \(\overline{\mathbf{A B}}\)
Answer:
Let OA = a, and OB = b
Then A = (a, 0) and B = (0, b)

Question 2.
Find the equation of the straight line pass-ing through the points (-1, 2) and ( 5, -1) and also find the area of the triangle formed by it with the axes of coordinates. (S.A.Q.)
Answer:
Let A (- 1, 2) and B (5, – 1) are the given points. Equation of AB is
\(\frac{y-2}{2+1}=\frac{x+1}{-1-5}\) ⇒ \(\frac{y-2}{3}=\frac{x+1}{-6}\)
⇒ – 2(y – 2) = x + 1
⇒ x + 2y – 3 = 0
Area of the ∆^le formed by it with the axes of coordinate = \(\frac{1}{2} \frac{c^2}{|a \cdot b|}=\frac{1}{2} \frac{9}{|(1)(2)|}=\frac{9}{4}\) sq.units.

Question 3.
A triangle of area 24 sq. units is formed by a straight line and the coordinate axes is in the first quadrant. Find the equation of the straight line, if it passes through (3, 4). (S.A.Q.)
Answer:
Equation of line in the intercepts form is \(\frac{x}{a}+\frac{y}{b}\) = 1
If this passes through P(3, 4) then

⇒ a² = 12 (a – 3)
⇒ a² – 12a + 36 = 0
⇒ (a – 6)² = 0
⇒ a = 6
∴ b = \(\frac{4 a}{a-3}=\frac{24}{3}\) = 8
Equation of AB is \(\frac{x}{6}+\frac{y}{8}\) = 1
⇒ 4x + 3y = 24
⇒ 4x + 3y – 24 = 0

Question 4.
A straight line with slope 1 passes through Q (- 3, 5) and meets the straight line x + y – 6 = 0 at P. Find the distance PQ. (S.A.Q.)
Answer:

Given slope = 1, tan α = 1 = tan 45° ⇒ α = 45°
The line passes through Q (-3, 5)
Coordinates of P are
(x₁ + r cos α, y₁ + r sin α)
= (- 3 + r cos 45°, 5 + r sin 45°)
= (- 3 + \(\frac{\mathrm{r}}{\sqrt{2}}\), 5 + \(\frac{\mathrm{r}}{\sqrt{2}}\))
P is a point on x + y – 6 = 0
⇒ – 3 + \(\frac{\mathrm{r}}{\sqrt{2}}\) + 5 + \(\frac{\mathrm{r}}{\sqrt{2}}\) – 6 = 0
⇒\(\frac{2 r}{\sqrt{2}}\) = 4 r = 2√2
∴ PQ = 2√2

Question 5.
Find the set of values of ‘a’ if the points (1, 2) and (3, 4) lie to the same side of the straight line 3x – 5y + a = 0 (S.A.Q.)
Answer:
A (1, 2) and B (3, 4) are the given points
Equation of the given line is 3x – 5y + a = 0
L₁₁ = 3 (1) – 5 (2) + a = a – 7
L₂₂ = 3 (3) – 5 (4) + a = a – 11
a – 7 and a – 11 both must be positive or both negative
Case (i) : a – 7 > 0, a – 11 > 0
⇒ a > 7 and a > 11
∴ a > 7, 11 a ∈ (11, ∞)
Case (ii): a – 7 < 0, a – 11 < 0
⇒ a < 7 and a < 11
⇒ a ∈ (- ∞, 7)
∴ a ∈ (- ∞, 7) ∪ (11, ∞)

Question 6.
Show that the lines 2x + y – 3 = 0, 3x + 2y – 2 = 0 and 2x – 3y – 23 = 0 are concurrent and find the point of concurrency. (S.A.Q)
Answer:
Equations of the given lines are
2x + y – 3 = 0 ……………. (1)
3x + 2y – 2 = 0 ……………. (2)
2x – 3y – 23 = 0 ……………. (3)
Solving (1) and (2) we get the point of intersection of the lines.

⇒ x = 4, y = – 5
∴ Point of intersection of the lines (1) and (2) is (4,- 5)
Now from (3) 2x – 3y – 23
= 2 (4) – 3 (-5) – 23 = 8 + 15 – 23 = 0
∴ So the point lies on (3) and lines (1), (2), (3) are concurrent. The point of concurrence is (4, -5)

Question 7.
Find the value of p if the following lines are concurrent (SA.Q.) (May 2006)
(i) 3x + 4y = 5, 2x + 3y = 4 : px + 4y = 6
(ii) 4x – 3y – 7 = 0, 2x + py + 2 = 0, 6x + 5y – 1 = 0
Answer:
(i) 3x + 4y = 5, 2x + 3y = 4 : px + 4y = 6
Equations of lines are
3x + 4y – 5 = 0 and …………….. (1)
2x + 3y – 4 = 0 …………….. (2)
Point of intersection of (1) and (2) x y 1

⇒ x = – 1, y = 2 ;
Point of intersection is P (-1,2) given lines are concurrent and the point P (-1, 2) must lie on px + 4y – 6 = 0
⇒ – p + 8 – 6 = 0 ⇒ p = 2

(ii) 4x – 3y – 7 = 0, 2x + py + 2 = 0,6x + 5y – 1 = 0
Answer:
Equations of lines are
4x – 3y – 7 = 0 ……………. (1)
6x + 5y – 1 = 0 ……………. (2)
solving (1) and (2) we get

⇒ x = 1, y = – 1
∴ Point of intersection = ( 1, – 1)
Since the given lines are concurrent, consider 2x + py + 2 = 0
⇒ 2 (1) + p (-1) + 2 = 0 ⇒ p = 4

Question 8.
Determine whether or not the four straight lines with equations x + 2y – 3 = 0, 3x + 4y – 7 = 0, 2x + 3y – 4 = 0 and 4x + 5y – 6 = 0 are concurrent. (S.A.Q.)
Answer:
Equations of the given lines are
x + 2y – 3 = 0 ……………………. (1)
3x + 4y – 7 = 0 ……………………. (2)
2x + 3y – 4 = 0 ……………………. (3)
4x + 5y – 6 = 0 ……………………. (4)
Solving (1) and (2) we have

⇒ x = 1, y = 1
∴ Point of intersection = (1, 1)
2x + 3y – 4 = 2 (1) + 3 (1) – 4 = 1 ≠ 0
4x + 5y – 6 = 4 (1) + 5 (1) – 6 = 3 ≠ 0
∴ P (1, 1) is not a point on (3) and (4)
∴ The given lines are not concurrent.

Question 9.
If 3a + 2b + 4c = 0, then show that the equation ax + by + c = 0 represents a family of concurrent straight lines and find the point of concurrency. (S.A.Q.)
Answer:
Given condition is 3a + 2b + 4c = 0
⇒ c = – \(\left(\frac{3}{4}\right) a-\left(\frac{2}{4}\right) b\)
For all values of a, b the lines ax + by + c = 0 passes through ‘a’ the point \(\left(\frac{3}{4}, \frac{1}{2}\right)\) since

∴ The equation ax + by + c = 0 represents a family of concurrent lines
∴ Point of concurrence = \(\left(\frac{3}{4}, \frac{1}{2}\right)\)

Question 10.
If non-zero numbers a, b, care in harmonic progression, then show that the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) represents a family of concurrent lines and find the point of concurrency. (S.A.Q.)
Answer:
Given a, b, c are in harmonic progression, we have \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in arithmetic progression.

For all values of a, b, c the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) represents a family of concurrent lines.
∴ Point of concurrence = P (1, – 2)

III.
Question 1.
Find the point on the straight line 3x + y + 4 = 0 which is equidistant from the points (- 5, 6) and (3, 2). (March 2013) (S.A.Q)
Answer:

Let P (x₁, y₁) be any point on 3x + y + 4 = 0
∴ 3x₁ + y₁ + 4 = 0 ………………….. (1)
Given PA = PB ⇒ PA² = PB²
⇒(x₁ + 5)² + (y₁ – 6)²
= (x₁ – 3)² + (y₁ – 2 )²
⇒ x₁² + 10x₁] + 25 + y₁² – 12y₁ + 36
⇒ x₁² – 6x₁ + 9 + y₁² – 4y₁ + 4
⇒ 16x₁ – 8y₁ + 48 = 0
⇒ 2x₁ – y₁ + 6 = 0 …………………… (2)
Solving (1) and (2) 5x₁ + 10 = 0 ⇒ x₁ = – 2
From (1) ⇒ 3 (- 2) + y₁ + 4 = 0 ⇒ y₁ = 2
∴ Coordinates of P are (- 2, 2)

Question 2.
A straight line through P (3, 4) makes an angle of 60° with the positive direction of the X – axis. Find the coordinates of the points on that line which are 5 units away from P. (S.A.Q.)
Answer:
Equation of the straight line in symmetric form is \(\frac{x-x_1}{\cos \theta}=\frac{y-y_1}{\sin \theta}\) = r
∴ Coordinates of any point on the line
Q = (x₁ + r cos θ, yi + r sin θ)
Given (x₁, y₁) = (3, 4)
θ = 60° ⇒ cos θ = cos 60° = \(\frac{1}{2}\),
sin θ = sin 60° = \(\frac{\sqrt{3}}{2}\)

Case (i): r = 5 ; Co-ordinates of Q are

Case (ii): r = – 5; Co-ordinates of Q are

Question 3.
A straight line through Q(√3, 2) makes an angle \(\frac{\pi}{6}\) with the positive direction of the X- axis. If the straight line intersects the line √3x – 4y + 8 = 0 at P, find the distance PQ. (March 2004) (E.Q)
Answer:

Given that the straight line, PQ through Q makes an angle \(\frac{\pi}{6}\) with the positive direction of the X-axis.
∴ Slope of PQ = m = tan 30°= \(\frac{1}{\sqrt{3}}\)
PQ passes through Q (√3 , 2)
Equation of PQ is y – 2 = \(\frac{1}{\sqrt{3}}\)(x – √3 )
⇒ √3 y – 2√3 = x – √3
⇒ x – √3 = -√3 ……………… (1)
Equation of AB is √3x – 4y + 8 = 0 ………………… (2)
From (1) √3x – 3y = – 3 ……………. (3)
Solving (2) and (3) y = 5
From (1) x = √3y – √3 = 5√3 – √3 = 4√3
∴ Coordinates of P = (4√3, 5) and Coordinates of Q = (√3 , 2)
∴ PQ² = ( 4√3 – √3)² + ( 5 – 2)²
= (3√3)² + 3² = 27 + 9 = 36
∴ PQ = 6 units

Question 4.
Show that the origin is with in the triangle whose angular points are (2, 1 ) ( 3, – 2 ) and (-4,-1) (E.Q)
Answer:
Let P (2, 1), Q (3, -2) and R (-4, -1) be the regular points of a triangle PQR

Equation of QR is

∴ L₃ = 3x + y – 7 = 0 ………………… (3)
L₃ (- 4, – 1) = 3 (- 4) – 1 – 7 = – 20 < 0
L₃ (0, 0) = 3 (0) + 0 – 7 = – 7 < 0
Hence (-4, -1) , (0,0) lies on the same side of
PQ and (0, 0) lies to the left of PQ ………………… (4)
L₂ (3, -2) = 3 + 6 + 1 = 10 > 0
L₂ (0, 0) = 0 – 3 (0) + 1 = 1 > 0
So (0, 0) and (3, -2) lie on the same side of PR ………………… (5)
L₁ (2, 1) = 2 + 7(1) + 11 = 20 > 0
L₁ (0, 0) = 0 + 7 (0) + 11 = 11 > 0
So (0, 0) and (2, 1) lie on the same side of QR ……………………. (6)
From (4), (5) and (6) we have O(0, 0) lies downwards to PR, upward of QR, and to the left of PQ. Hence O(0, 0) will lie inside the ∆PQR.

Question 5.
A straight line through Q (2, 3) makes an angle \(\frac{3 \pi}{4}\) with the negative direction or X – axis. If the straight line intersects the line x + y – 7 = 0 at P, find the distance of PQ. (E.Q)
Answer:

The line PQ makes an angle \(\frac{3 \pi}{4}\) with the negative direction of X- axis ie., PQ makes an angle. π – \(\frac{3 \pi}{4}\) = \(\frac{\pi}{4}\) with the positive direction of X-axis.
Coordinates of Q are (2, 3)
Coordinates of P are (x₁ + r cos θ, y₁ + r sin θ)

Question 6.
Show that the straight lines x + y = 0, 3x + y – 4 = 0 and x + 3y – 4 = 0 form an isosceles triangle. (E.Q)
Answer:
Given lines are
x + y = 0 …………………. (1)
3x + y – 4 = 0 …………………… (2)
x + 3y – 4 = 0 ……………….. (3)
Solving (1) and (2)

⇒ x = 2, y = – 2
Point of intersection of (1) and (2) is (2, – 2)
Solving (2) and (3)
By solving the equations (2) and (3)

∴ Point of intersection of (2) and (3) is (1, 1) Solving equations (1) and (3)

⇒ x = – 2, y = 2
∴ Point of intersection of lines ( 1) and (3) = (-2, 2)
Let A = (2, -2), B = (1, 1), C = (-2, 2) be the vertices of the triangle ABC formed by the lines (1), (2) and (3), then
Then AB =

∴ AB = BC we can say that an isosceles triangle can be formed with the given lines.

Question 7.
Find the area of the triangle formed by the straight lines 2x-y-5 = 0, x – 5y + 11 = 0 and x + y – 1 = 0. (E.Q)
Answer:
Given lines are
2x – y – 5 = 0 ……………………. (1)
x – 5y + 11 = 0 (2)
x + y – 1 = 0 (3)
By solving the equations (1) and (2)

∴ Point of intersection of lines (1) and (2) is A (4, 3). Solving (2) & (3)

⇒ x = – 1, y = 2
∴ Point of intersection of the lines (2) and (3) is B (- 1, 2 ).
Solving (1) and (3)

⇒ x = 2; y = – 1
∴ Point of intersection of lines (1) and (3) is C(2, -1) Area of ∆ ABC

Telangana TSBIE TS Inter 1st Year Hindi Study Material Grammar लिंग एवं वचन Questions and Answers.

TS Inter 1st Year Hindi Grammar लिंग एवं वचन

संज्ञा के जिस रूप से जाना जाये कि अमुक व्यक्ति अथवा प्राणी या वस्तु की जाति (पुरुष या स्त्री) क्या है, उसे ‘लिंग’ कहते हैं। हिन्दी में दो ही लिंग हैं पुंलिंग और स्त्री लिंग ।

पुंलिंग : पुरुष जाति का बोध करानेवाले शब्द ‘पुंलिंग’ होते हैं ।
उदा : भाई, लड़का, घोड़ा, शेर आदि ।

स्त्रीलिंग: स्त्री जाति का बोध करानेवाले शब्द स्त्रीलिंग होते हैं ।
उदा : बेहन, लड़की, घोड़ी, शेरनी आदि ।

लिंग की पहचान :
1. प्राणिवाचक संज्ञाओं के लिंग की पहचान आसान है । क्यों कि प्रकृति ने ही पुरुष था स्त्री जाति के लिंग का निर्णय निश्चित रुप से कर दिया है। अतः इनका लिंग निर्णय इनके अर्थ के आधार पर होता है ।

पुरुष जाति के प्रणिवाचक शब्द (पुंलिंग) : पिता, भाई, बेटा, पुत्र, पुरुष, मर्द, नाना, दादा, साला, मामा, चाचा, देवर, लड़का, नर, बालक, नायक, राजा, गुरु, अभिनेता, माली, नेता, ससुर, पंडित, बनिया, धोबी, तेली, घोड़ा, बैल, कुत्ता, हाथी, बंदर बकरा, बाघ, शेर आदि ।

स्त्री जाति के प्राणिवाचक शब्द (स्त्री लिंग) : माता, बहन, बेटा, पुत्री, स्त्री, नारी, नानी, दादी, साली, मामी, चाची, भाभी, मौसी, रानी, विधवा, छात्रा, बहू, सास, वधू, युवती, महिला, दीदी, देवी, नायिका, गायिका, घोड़ी, बकरी, गाय, बिल्ली, मोरनी, बाघिन, मुर्गी, ऊँटनी, शेरनी आदि ।

ద్వంద్వ సమాసపు प्राणिवाचक शब्द पुंलिंग గా పరిగణింపబడతాయి.
उदा : नर – नारी, भाई – बहन, माँ – बाप, राजा – रानी, सीता – राम, राधा – कृष्ण आदि ।

2. अप्राणिवाचक संज्ञा శబ్దాల लिंग निर्णय కఠినమైన విషయం. వీనిలో. వస్తువుల పేర్లు भाव- विचार సంభందించిన संज्ञा శబ్దాలు వస్తాయి. వీని యొక్క, लिगं – विभाजन పూర్తిగా యాదృఛ్చికం, కేవలం ప్రయోగాన్ని బట్టే వీటి लिंग తెలుసుకోవలసి ఉంటుంది.
पुंलिंग
पानी, घर, कपड़ा, खिलौना,
खेल, मकान, काव्य, आम, फूल

स्त्रीलिंग
कविता, बात, तस्वीर, सड़क,
छाँछ, जेब, कलम, किताब, तलवार

डब्लू వస్తువుల పెద్ద – చిన్న ఆకారాన్ని బట్టి पुंलिंग లేక स्त्रीलिंग భేధం చూపించబడుతుంది.
उदा :
पुंलिंग – स्त्रीलिंग
पहाड़ – पहाड़ी
डिब्बा – डिबिया
कटोरा – कटोरी
खाट – खटिया

पुलिंग शब्दों को पहचानने के नियम :

1. సమయం, నెలలు, రోజులు మొదలైనవాటి పేర్లు पुलिंग శబ్దాలుగా పరిగణింప బడతాయి.
उदा : घंटा, मिनट, क्षण, चैत्र, वैशाख, जनवरी, मई, सोमवार, बुहस्पतिवार आदि ।

2. ‘पृथ्वी’ తప్ప ఇతర గ్రహాల పేర్లు पुंलिंग ।
उदा : सूर्य, चन्द्र, मंगल, ध्रुव आदि ।

3. దేశాల, పట్టణాల, సముద్రాల, పర్వతాల పేర్లు पुंलिंग
उदा : भारत, अमेरिका, हैदराबाद, मुंबई, अरबसागर, महासागर, हिमालय, विन्ध्याचल आदि ।

4. శరీరావయవాల పేర్లు पुंलिंग
उदा : सिर, हाथ, कान, पैर, नाक आदि,
अपवाद (Exception) : उँगली, आँख, जीभ, पीठ, हड्डी आदि ।

5. ధాన్యాలు మరియు చెట్ల పేర్లు पुंलिंग
उदा : नारियल, पीपल, गेहूँ, चावल आदि,
अपवाद (Exception) : इमली, बेल, लता, आदि ।

6. ద్రవ పదార్ధాలు పేర్లు पुंलिंग
उदा : पानी, शर्बत, तेल, घी, दही, आदि ।
अबवाद (Exception) : छाँछ, लस्सी आदि ।

7. లోహాల धातु రత్నాల పేర్లు पुंलिंग
उदा : लोहा, सोना, हीरा, मोती, नीलम आदि ।

8. ‘अ’, ‘आ’, ‘आव’, ‘पा’, ‘पन’ తో అంతమయ్యే హిందీ శబ్దాలు पुंलिंग
उदा : बल, धन, घड़ा, लोटा, बहाव, बुढ़ापा, बचपन आदि

9. అకారాంత तत्सम శబ్దాలు पुंलिंग
उदा : फूल, प्रचार, सुख, लेख, आम आदि ।

10. ‘त’, ‘इत’, ‘आर’, ‘आप’, ‘न’ ‘ తో అంతమయ్యే సంస్కృత శబ్దాలు पुंलिंग
उदा : गीत, गणित, आकार, परिताप, नयन आदि ।

स्त्रीलिंग शब्दों को पहचानने के नियम :

1. భాషల పేర్లు स्त्रीलिंग
उदा: तेलुगु, हिन्दी, संस्कृत, अंग्रेजी, उर्दु आदि ।

2. నదుల పేర్లు स्त्रीलिंग
उदा : यमुना, गंगा, गोदावरी, अलकनन्दा आदि ।

3. నక్షత్రాల పేర్లు स्त्रीलिंग
उदा : अश्विनी, भरणी, कृत्तिका आदि ।

4. తిధుల పేర్లు स्त्रीलिंग
उदा : पूर्णिमा, अमावास्या, दूज, तीज आदि ।

5. భోజన పదార్ధాల మరియు మసాలాల పేర్లు स्त्रीलिंग
उदा : पूरी, रोटी, खीर, इलायची, लौंग आद
अपवाद (Exception) : हलवा, लड्डू, भात, बादाम आदि (पुंलिंग) ।

6. ईकारांत మరియు ‘आई’ ‘ తో అంతమయ్యే హిందీ శబ్దాలు स्त्रीलिंग ।
उदा : लड़की, मिट्टी, टोपी, नदी, पढ़ाई, भलाई आदि,
अपवाद (Exception) : पानी, दही, मोती, ईसाई आदि (पुंलिंग)

7. आकारांत సంస్కృత శబ్దాలు स्त्रीलिंग
उदा : दशा, ममता, दया, करुणा, माया आदि ।
अपवाद (Exception): देवता ( पुंलिंग )

8. आकारांत ఉర్దూ संज्ञा శబ్దాలు स्त्रीलिंग
उदा : दवा, हवा, सजा, आदि ।

9. ‘ता’, ‘श’, ‘न्त’, ‘वट’, ‘आहट’ మొదలైన వాటితో అంతమయ్యే भाववाचक संज्ञा శబ్దాలు स्त्रीलिंग
उदा : मित्रता, मालिश, गढन्त, आहट, सजावट, घबराहट आदि ।

10. ‘त’ తో అంతమయ్యే संज्ञा శబ్దాలు स्त्रीलिंग
उदा : लात, रात, बात, ताकत, छत आदि ।
अपवाद (Exception): भात, खेत, सूत आदि (पुंलिंग)

लिंग परिवर्तन के नियम : హిందీలో ఎక్కువ శబ్దాలు पुंलिंग, కొద్దిపాటి మార్పు చేసి వాటిని स्त्रीलिंग గా చేయటం జరుగుతుంది.

1. ‘अ’ कारांत లేక ‘आ’ कारांत సంబంధ వాచక మరియు ప్రాణివాచక पुंलिंग सुंज्ञा శబ్దాల చివర ‘अ’ లేక ‘आ’ స్థానంలో ‘ई’ प्रत्यय చేర్చటం ద్వారా అవి स्त्रीलिंग గా మారతాయి.

उदा : पुंलिंग – स्त्रीलिंग
लड़का – लड़की
दास – दासी
पुत्र – पुत्री
नाना – नानी
बेटा – बेटी
मामा – मामी
बकरा – बकरी
कबूतर – कबूतरी
हीरण – हीरणी

2. వృత్తి పరమైన ( व्यावसायिक) पुंलिंग संज्ञा శబ్దాలకు ‘इन’ చేర్చటం ద్వారా అవి स्त्रीलिंग గా మారతాయి.
उदा :
पुंलिंग – स्त्रीलिंग
धोबी – धोबिन
सुनार – सुनारिन
कुम्हार – कुम्हारिन
माली – मालिन
तेली – तेलिन
लुहार – लुहारिन
जोगी – जोगिन

3. కొన్ని ప్రాణివాచక पुंलिंग శబ్దాల చివర ‘नी’ చేర్చటం ద్వారా అవి स्त्रीलिंग గా మారతాయి.
उदा: पुंलिंग – स्त्रीलिंग
मोर – मोरनी
शेर – शेरनी
हाथी – हाथिनी
ऊँट – ऊँटनी
रीछ – रीछनी

4. కొన్ని आदरसूचक पुंलिंग శబ్దాలకు ‘आइन’ చేర్చటం ద్వారా అవి स्त्रीलिंग గా మారతాయి.
उदा :
पुंलिंग – स्त्रीलिंग
ठाकुर – ठाकुराइन
पंडिन – पंडिताइन
चौधरी – चौधराइन

5. కొన్ని संबंधसूचक पुंलिंग శబ్దాలకు ‘आनी’ చేర్చటం ద్వారా అవి स्त्रीलिंग గా మారతాయి.
उदा :
पुंलिंग – स्त्रीलिंग
सेठ – सेठानी
जेठ – जेठानी
देवर – देवरानी
नौकर – नौकरानी

6. కొన్ని संस्कृत पुंलिंग శబ్దాలకు ‘आ’ చేర్చటం ద్వారా అవి स्त्रीलिंग గా మారతాయి.
उदा :
पुंलिंग – स्त्रीलिंग
छान – छात्रा
सुत – सुता
प्रिय – प्रिया
महोदय – महोदया
अध्यक्ष – अध्यक्षा
प्रियतम – प्रियतमा

7. ‘अक’ తో అంతమయ్యే पुंलिंग శబ్దాల చివర ‘अक’ ను इका గా మార్చటం ద్వారా అవి स्त्रीलिंग గా అవుతాయి.
उदा :
पुंलिंग – स्त्रीलिंग
लेखक – लेखिका
सेवक – सेविका
अध्यापक – अध्यापिका
पाठक – पाठिका
संपादक – संपादिका

8. ‘आन’ తో అంతమయ్యే पुंलिंग శబ్దాల చివర ‘आन’ ని ‘अति’ గా మార్చటం ద్వారా అవి स्त्रीलिंग గా అవుతాయి..
उदा :
पुंलिंग – स्त्रीलिंग
श्रीमान – श्रीमती
भगवान – भगवती
गुणवान – गुणवती
‘अपवाद (Exception) : विद्वान – विदुषी

9. కొన్ని पुंलिंग శబ్దాలు, स्त्रीलिंग కావటానికి ప్రత్యేకమైన నియమం ఏమీ ఉండదు. వీటి लिंग పూర్తిగా భిన్నంగా ఉంటుంది.
उदा :
पुंलिंग – स्त्रीलिंग
राजा – रानी
बैल – गाय
पिता – माता
भाई – बहन

10. కొన్ని శబ్దాల लिंग వ్యత్యాసం కనపర్చుకోవడం కోసం पुंलिंग అయితే దాని ముందు ‘नर’ అని, स्त्रीलिंग అయితే దాని ముందు ‘मादा’ అని చేర్చబడుతుంది.
उदा:
पुंलिंग – स्त्रीलिंग
नर कौआ – मादा कौआ
नर कोयल – मादा कोयल
नर चील – मादा चील

11. शब्दों के साथ प्रत्यय लगा कर लिंग परीवर्तन करना :

अभ्याश

रेखांकित शब्द का लिंग बदलकर वाक्य लिखिए:

प्रश्न 1.
लुहार लोहे के औजार बनाता है ।
उत्तर:
लुहारिन लोहे के औज़ार बनाती है ।

प्रश्न 2.
नानी घर आयी है ।
उत्तर:
नाना घर आया है ।

प्रश्न 3.
नौकर बाज़ार गया है ।
उत्तर:
नौकरानी बाजार गयी है ।

प्रश्न 4.
मौर सुंदर पक्षी है ।
उत्तर:
मोरनी सुंदर पक्षी है ।

प्रश्न 5.
छात्र पढ़ रहा है ।
उत्तर:
छात्रा पढ़ रही है ।

प्रश्न 6.
गाय खेत में है ।
उत्तर:
बैल खेत में है ।

प्रश्न 7.
शेर मांसाहारी जानवर है ।
उत्तर:
शेरनी मांसाहारी जानवर है।

प्रश्न 8.
पंडित पूजा कर रहा है ।
उत्तर:
पंडिताइन पूजा कर रही है।

प्रश्न 9.
माली बगीचे में बैठा है ।
उत्तर:
मालिन बगीचे में बैठी है ।

प्रश्न 10.
लेखक ने कहानी लिखी ।
उत्तर:
लेखका ने कहानी लिखी ।

प्रश्न 11.
सीता का देवर सुशील है ।
उत्तर:
सीता की देवरानी सुशील है ।

प्रश्न 12.
तपस्वी ने शाप दिया ।
उत्तर:
तपस्विनी ने शाप दिया ।

प्रश्न 13.
वह एक गुणवान छात्र है ।
उत्तर:
वह एक गुणवती छात्रा है ।

प्रश्न 14.
ताऊजी से मेरा बड़ा प्यार है ।
उत्तर:
ताईजी से मेरा बड़ा प्यार है ।

प्रश्न 15.
गायें बहुत सुंदर है ।
उत्तर:
बैल बहुत सुंदर हैं ।

वचन

शब्द के जिस रूप से यह प्रकट हो कि वह एक के लिए प्रयुक्त हुआ है या एक से अधिक केलिए प्रयुक्त हुआ है, उसे ‘वचन’ कहते हैं । हिन्दी में दो वचन हैं –

एकवचन : शब्द के जिस रूप से एक ही व्यक्ति या पदार्थ का बोध हो, उसे एकवचन कहते हैं ।
उदा : लड़का, किताब, कमरा, बहन, पंखा, कासी आदि ।

बहुवचन : शब्द के जिस रूप से एक से अधिक व्यक्तियों अथवा वस्तुओं का बोध हो, उसे बहुवचन कहते हैं ।
उदा : लड़के, किताबें, कमरे, बहनें, पंखे, कुर्सियाँ आदि । ‘वचन’ కారణంగా संज्ञा, सर्वनाम, विशेषण, क्रिया మొదలైన వాటి రూపాలు మారుతాయి.

पुंलिंग शब्दों के बहुवचन बनाने के नियम : హిందీలో అకారాంత पुंलिंग शब्द ఏకవచనం నుండి బహువచనంలోకి మార్చటానికి ‘ఆ’ కారాంతాన్ని ‘ఏ’ కారాంతం చెయ్యవలసి ఉంటుంది.
उदा :
एकवचन – बहुवचन
लड़का – लड़के
पहिया – पहिये
घोड़ा – घोड़े
कपड़ा – कपड़े
कमरा – कमरे
प्याला – प्याले
बेटा – बेटे
लोटा – लोटे
रास्ता – रास्ते
बच्चा – बच्चे

संबंधियों के लिए प्रयुक्त शब्द भी ‘आ’ कारांत को ‘ए’ कारांत कर देने से बहुवचन बनते हैं ।
उदा :
एकवचन – बहुवचन
पोता – पोते
बेटा – बेटे
भतीजा – भतीजे
साला – साले

‘అ’ కారాంత సంస్కృత శబ్దాలు बहुवचन లో మార్పు చెందవు
उदा :
एकवचन – बहुवचन
दाता – दाता
देवता – देवता
कतां – कतां
पिता – पिता
नेता – नेता
योद्धा – योद्धा

‘ఆ’ కారాంతం కాని ఇతర पुंलिंग బహువచనంలో మార్పు చెందవు.
उदा :
एकवचन – बहुवचन
घर – घर
गुरु – गुरु
ऋषि – ऋषि
पक्षी – पक्षी
चौबे – चौबे
आलू – आलू
(एक) घर – तीन घर
गुरु – चार गुरु
ऋषि – दो ऋषि
पक्षी – पाँच पक्षी
चौबे – चार चौबे
आलू – दस आलू

ఇలాంటి శబ్దాలకు वचन भेद ఖడె అవసరమైతే ఆ శబ్దానికి ముందు సంఖ్య చెప్పబడుతుంది. లేక ఆ శబ్దాలు మనుష్య సంబంధమైనవి అయితే ఈ క్రింది పదాలను వాటి తర్వాత చేర్చి बहुवचन గా మార్చవచ్చు.
उदा :
एकवचन – बहुवचन
साधु – साधु लोग
गुरु – गुरु जन
बन्धु – बन्धु वर्ग
गुरु – गुरु जन
पाठक – पाठक गण
सज्जन – सज्जन वृन्द

आकारांत स्त्रीलिंग शब्द :
एकवचन – बहुवचन
घटना – घटनाएँ
रेखा – रेखाएँ
योजना – योजनाएँ
सुचना – सुचनाएँ
माला – मालाएँ
घटना से – घटनाओं से
रेखा का – रेखाओं का
योजना में – योजनाओं में
सूचना में – सूचनाओं को
माला के लिए – मालाओं के लिए

इकारांत और ईकारांत स्त्रीलिंग शब्द :
एकवचन – बहुवचन
नदी – नदियों
जाति – जातियों
तिथि – तिथियों
रीति – रीतियाँ
नारी – नारीयाँ
नदी में – नदियों में
जाति से – जातियों से
तिथि का – तिथियों का
रीति को – रीतियों को
नारी के लिए – नारीयों के लिए

आदर सूचक : ఆదరాన్ని సూచించే సమయంలో एकवचन కూడా बहुवचन లో ప్రయోగించబడుతుంది
उदा :
1. पिताजी बाजार से तरकारी लाये ।
2. विनोबाजी बापूजी के परम भक्त थे ।
3. प्रधान मंत्री अभी – अभी पधारे हैं।
4. राम जी विभीषण से बोले ।

अभिमान या अधिकार सूचक : स्वाभिमाव లేక अधिकार ని సూచించేటప్పుడు संज्ञा లేక सर्वनाम బహువచనంలో ప్రయోగించ బడుతుంది.
उदा :
1. हम (ए. व ) कभी ऐसा नही करेंगे ।
2. हमें भी याद किया करें ।.
3. हम तुम्हारे बाप हैं, तुम मेरी बात मानो ।

అప్పుడప్పుడు जातिवाचक संज्ञा ఏకవచనంలో కూడా बहुवचन ని ధ్వనింపచేస్తుంది.
उदा :
1. यहाँ आम बहुत मिलता है। (‘आम’ एकवचन होकर भी बहुवचन का अर्थ देता है)
2. हाथी बहुत बुद्धिमान होता है । (‘हाथी’ बहुवचन का बोध कराता है)
కొన్ని स्त्रीलिंग శబ్దాలకు చివర ‘एँ’ గాని ‘यें’ గాని చెప్పి బహువచనంగా మార్చబడుతుంది. उकारांत శబ్దాల చివర ఉన్న ‘ऊ’ ని హ్రస్వంగా మార్చవలసి ఉంటుంది.
उदा :
एकवचन – बहुवचन
बहू – बहुएँ
लता – लताएँ
माता – माताएँ

विभक्ति सहित – विभक्ति रहित: ఈ దిగువ శబ్దాలు विभक्ति सहित గా ప్రయోగింపబడినా, ఏకవచనంలో వాటి రూపాలు ఎట్టి మార్పు చెందవు. కాని బహువచనంలో మాత్రం మార్పు చెందుతాయి.
उदा :
एकवचन (विभक्ति रहित) – बहुवचन (विभक्ति सहित)
नर – नर ने
कवि – कवि से
साधु – साधु को
हाथी – हाथी पर
डाकू – डाकू के लिए

एकवचन(विभक्ति रहित) – बहुवचन (विभक्ति सहित)
नर से – नरों से
कवि ने – कवियों ने
साधु को – साधुओं को
हाथी पर – हाथियों पर
डाकू का – डाकुओं का

विभक्ति रहित (अकारांत स्त्री लिंग) विभक्ति सहित :
एकवचन – बहुवचन
बात – बातें
रात – रातें
गाय – गायें
आँख – आँखे
बात का – बातों का
रात में – रातों में
गाय को – गायों को
आँख से – आँखो से

स्त्रीलिंग शब्दों के बहुवचन बनाने के नियम : అకారాంత स्त्री शब्द బహువచనంలోనికి మార్చటానికి ‘अ’ ని ‘एँ’ మార్చాలి.
उदा :
एकवचन – बहुवचन
बहन – बहनें
आँख – आँखें
रात – रातें
पुस्तक – पुस्तकें
चीज – चीजें

इकारांत और ईकारांत స్త్రీ లింగ ‘संज्ञा’ శబ్దాలలోని ‘ई’ ని హ్రస్వంగా మార్చి చివర ‘याँ’ చేర్చాలి.
उदा :
एकवचन – बहुवचन
रानी – रानियाँ
सखी – सखियाँ
टोपी – टोपियाँ
नदी – नदियाँ
कली – कलियाँ
नारी – नारियाँ
नाली – नालियाँ

‘या’ తో అంతమయ్యే संज्ञा शब्त యొక్క ‘या’ పై चंद्र बिन्दु చేర్చిగాని, శబ్దానికి ‘एँ’ జతపరిచి గాని దానిని బహువచనం చెయ్య బడుతుంది.
उदा :
एकवचव – बहुवचन
चिड़िया – चिड़ियाँ / चिड़ियाएँ
गुड़िया – गुड़ियाँ / गुड़ियाएँ
डिबिया – डिबियाँ / डिबियाएँ
बुढिया – बुढियाँ / बुढियाएँ
लुटिया – लुटियाँ / लुटियाएँ
खटिया – खटियाँ / खटियाएँ

ఎన్నో जातिवाचक संज्ञा శబ్దాలు అప్పుడప్పుడు ఏకవచనంలోకి बहुवचन ని ధ్వనింపజేస్తాయి.
उदा :
1. मेरे पिताजी के पास लाख रुपया है ।
2. मुम्बई का केला बहुत प्रसिद्ध है ।
పై వాక్యాల్లో ‘रुपया’, ‘केला’ శబ్దాలు ఏకవచనమై ఉండి కూడా బహువచనపు అర్ధానిస్తాయి.

अभ्यास

खांकित शब्द का वचन बदलकर वाक्य लिखिए :

प्रश्न 1.
लड़का खलता है ।
उत्तर:
लड़के खेलते हैं ।

प्रश्न 2.
दर्जी कपड़े सीता है ।
उत्तर:
दर्जी कपड़ा सीता है ।

प्रश्न 3.
मेरे पास घड़ा है ।
उत्तर:
मेरे पास घड़े हैं ।

प्रश्न 4.
वह रुपये लाया ।
उत्तर:
वह रुपया लाया ।

प्रश्न 5.
मै केला खाता हूँ ।
उत्तर:
मै केले खाता हूँ ।

प्रश्न 6.
उसके घर के पास आम का पेड़ है ।
उत्तर:
उसके घर के पास आम के पेड़ है ।

प्रश्न 7.
यह राजु का घर है ।
उत्तर:
ये राजु के घर हैं ।

प्रश्न 8.
बिल्ली दूध पीती है ।
उत्तर:
बिल्लियाँ दूध पीती हैं ।

प्रश्न 9.
वह पुस्तक पढ़ता है ।
उत्तर:
वह पुस्तकें पढता है ।

प्रश्न 10.
जड़ मजबूत है ।
उत्तर:
जड़ मजबूत हैं ।

प्रश्न 11.
बिटिया रोने लगी ।
उत्तर:
बिटियाँ रोने लगी ।

प्रश्न 12.
गरम पूडी खाओ ।
उत्तर:
गरम पूड़ियाँ खाओ ।

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(d)

I. Find the angle between the following straight lines. (V.S.A.Q.)

Question 1.
y = 4 – 2x, y = 3x + 7
Answer:
y = 4 – 2x ⇒ 2x + y – 4 = 0 and
3x – y + 7 = 0 are equations of given lines
If θ is the angle between the lines

Question 2.
3x + 5y = 7, 2x – y + 4 = 0 (V.S.A.Q)
Answer:

Question 3.
y = – √3 x + 5, y = \(\frac{1}{\sqrt{3}}\)x – \(\frac{2}{\sqrt{3}}\) (V .S.A.Q.)
Answer:
m₁ = -√3 and m₂ = \(\frac{1}{\sqrt{3}}\) = from the given lines. Since m₁m₂ = – 1, the lines are perpendicular ⇒ θ = \(\frac{\pi}{2}\)

Question 4.
ax + by = a + b, a(x – y) + b(x + y) = 2b (V.S.A.Q)
Answer:
ax + by = a + b, (a + b)x + (- a + b)y = 2b

Find the length of the perpendicular drawn from the given point given against the following straight lines.

Question 5.
5x – 2y + 4 = 0; ( – 2, – 3 ) … (V.S.A.Q.)
Answer:
Length of the perpendicular from the point (-2, -3) to the line 5x – 2y + 4 = 0 is by the formula

Question 6.
3x – 4y + 10 = 0 ……………… (3, 4) (V.S.A.Q)
Answer:
Length of the perpendicular

Question 7.
x – 3y – 4 = 0 ……………… ( 0, 0 ) (V.S.A.Q.)
Answer:
Length of the perpendicular
= \(\left|\frac{0-3(0)-4}{\sqrt{1+9}}\right|\) = \(\frac{4}{\sqrt{10}}\)

Find the distance between the following parallel lines. (V.S.A.Q.)

Question 8.
3x – 4y = 12, 3x – 4y = 7
Answer:
Given equations of lines are
3x – 4y = 12, 3x – 4y = 7
So by the formula distance between two parallel lines = \(\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}\) = \(\frac{|-12+7|}{\sqrt{9+16}}\) = 1

Question 9.
5x – 3y – 4 = 0, 10x – 6y – 9 = 0 (May 2012)
Answer:
Equations of the lines can be taken as
10x – 6y – 8 = 0
10x – 6y – 9 = 0
∴ Distance between two parallel lines
= \(\frac{|-8+9|}{\sqrt{100+36}}\) = \(\frac{1}{2 \sqrt{34}} \)

Question 10.
Find the equation of the straight line parallel to the line 2x + 3y + 7 = 0 and passing through the point (5, 4). (March 2013) (V.S.A.Q.)
Answer:
Equation of the given line is
2x + 3y + 7 = 0 …………………. ( 1 )
We suppose the equation of line parallel to line (1) is 2x + 3y + k = 0 …………………. ( 2 )
Since the required line passes through (5, 4)
we have 2(5) + 3(4) + k = 0 ⇒ k + 22 = 0 ⇒ k = -22
∴ From (2) the equation of the required line is 2x + 3y – 22 = 0

Question 11.
Find the equation of the straight line perpendicular to the line 5x – 3y + 1 = 0 and passing through the point ( 4, – 3). (V.S.A.Q.)
Answer:
Equation of the given line is
5x – 3y – 1 = 0 ……… (1)
The equation of the line perpendicular to (1) is of the form 3x + 5y + k = 0 ……… (2)
If (2) passes through (4, -3) then
3(4) + 5 (- 3) + k = 0
⇒ 12 – 15 + k = 0
⇒k = 3
∴ From (2) the equation of the required line is 3x + 5y + 3 = 0

Question 12.
Find the value of k if the straight lines 6x – 10y + 3 = 0 and kx – 5y + 8 = 0 are parallel.
Answer:
Equations of the given lines are (V.S.A.Q.)
6x – 10y + 3 = 0
kx – 5y + 8 = 0
These lines are parallel, so a₁ b₂ = a₂ b₁
⇒ – 30 = – 10 k
⇒ k = 3

Question 13.
Find the value of p if the straight lines 3x + 7y – 1 = 0 and 7x – py + 3 = 0 are mutually perpendicular. (V.S.A.Q.)
Answer:
Equations of the given lines are
3x + 7y – 1 = 0
7x – py + 3 = 0
These lines are perpendicular
⇒ a₁ a₂ + b₁ b₂ = 0
⇒ 3(7) + 7(- p) = 0
⇒ 21 – 7p = 0 ⇒ p = 3

Question 14.
Find the value of k, if the straight lines y – 3kx + 4 = 0 and (2k – 1)x – (8k – 1) y – 6 = 0 are perpendicular. (V.S.A.Q.)
Answer:
Equations of the given lines are
y – 3kx + 4 = 0 and
(2k – 1)x – ( 8k – 1 )y – 6 = 0
The lines are perpendicular
⇒ a₁ a₂ + b₁ b₂ = 0
⇒ – 3k (2k – 1) – 1 (8k – 1) = 0
⇒ – 6k² + 3k – 8k + 1 = 0
⇒ 6k² + 5k – 1 = 0
⇒ (k + 1) (6k – 1) = 0
⇒ k = – 1 (or) k = 1/6.

Question 15.
(- 4, 5) is a vertex of a square and one of W its diagonals is 7x – y + 8 = 0. Find the equation of the other diagonal. (S.A.Q.)
Answer:

ABCD is a square. Equation of the diagonal is AC given by 7x – y + 8 = 0
The other diagonal BD is perpendicular to AC.
Equation of BD is x + 7y + k = 0. BD passes through D(- 4, 5). Hence – 4 + 7(5) + k = 0
⇒ k = – 31
∴ Equation of the other diagonal BD is x + 7y – 31 = 0

II.
Question 1.
Find the equations of the straight lines passing through (1, 3) and (i) parallel to (ii) perpendicular to the line passing through the points (3, – 5 ) and ( – 6, 1 )
Answer:

(i) Q(3, – 5) and R(-6, 1) are the given points
Slope of QR = \(\frac{-5-1}{3+6}=\frac{-6}{9}\) = \(\frac{-2}{3}\)
∴ Slope of the line passing through P, parallel to QR is -2/3
∴ Equation of the line is y – 3 = –\(\frac{2}{3}\) (x – 1)
⇒ 3y – 9 = -2x + 2
⇒ 2x + 3y – 11 = 0

(ii) Slope of the line perpendicular to the line QR is 3/2.
∴ Equation of the line passing through P(1, 3) and perpendicular to QR is
y – 3 = 3/2 (x – 1)
⇒ 2y – 6 = 3x – 3
⇒ 3x – 2y + 3 = 0

Question 2.
The line \(\frac{x}{a}-\frac{y}{b}\) = 1 meets the X – axis at P.
Find the equation of the line perpendicular to this line at P. (S.A.Q.)
Answer:

Equation of PQ is \(\frac{x}{a}-\frac{y}{b}\) = 1
Equation of X-axis is y = 0 ∴ x = a
∴ Coordinates of P = (a, 0)
Line PA is perpendicular to PQ
∴ Equation of PA is \(\frac{x}{b}+\frac{y}{a}\) = k
The line PA is passing through (a, 0) hence
\(\frac{a}{b}+\frac{0}{a}\) = k ⇒ k = \(\frac{a}{b}\)
∴ Equation of the line perpendicular to the line PQ at P is \(\frac{x}{b}+\frac{y}{a}=\frac{a}{b}\)

Question 3.
Find the equation of the line perpendicular to the line 3x + 4y + 6 = 0 and making an intercept – 4 on the X-axis. (S.A.Q.)
Answer:
Equation of the given line is
3x + 4y + 6 = 0 ……………. (1)
Equation of the line perpendicular to (1) is 4x – 3y + k = 0
⇒ 4x – 3y = – k

Since the line makes X-intercept – 4 on the X-axis we have – \(\frac{k}{4}\) = – 4 ⇒ k = 16
∴ Equation of the required line is 4x – 3y + 16 = 0

Question 4.
A (- 1, 1), B ( 5, 3 ) are opposite vertices of a square in the XY-planfe. Find the equation of the other diagonal (not passing through A, B ) of the square. (S.A.Q.)
Answer:

A (- 1, 1), B (5, 3) are opposite vertices of the square.
Slope of AB = \(\frac{3-1}{5+1}=\frac{2}{6}=\frac{1}{3}\)
∴ Slope of CD = – 3
O is the point of intersection of the diagonals
∴ Coordinates of O are
\(\left(\frac{-1+5}{2}, \frac{1+3}{2}\right)\) = (2, 2)
CD passes through 0 (2, 2)
∴ Equation of CD is y – 2 = – 3 (x – 2)
⇒ 3x + y- 8 = 0

Question 5.
Find the foot of the perpendicular drawn from (4, 1) upon the straight line 3x – 4y + 12 = 0. (S.A.Q.)
Answer:
Given equation of the straight line is
3x-4y + 12 = 0 ………………… ( 1 )
Equation of the line perpendicular to (1) is
4x + 3y + k = 0 ……………….. ( 2 )
This line passes through (4, 1) that
4(4) + 3(1) + k = 0 ⇒ k = – 19
∴ Equation of line (2) is 4x + 3y – 19 = 0 …. ( 3 )
Solving (1) and (2) we get the coordinates of the foot of the perpendicular

Question 6.
Find the foot of the perpendicular drawn from (3, 0) upon the straight line 5x + 12y – 41 = 0. (S.A.Q.)
Answer:
Equation of the given line is 5x + 12y – 41 = 0
If (x₂, y₂) is the foot of the perpendicular from (x₁, y₁) on the line ax + by + c = 0 then

Question 7.
x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining the points A, B. If A = (- 1, – 3 ), find the coordinates of B. (S.A.Q)
Answer:

Let (x, y) be the coordinates of B which is the image of A(-1, -3).
Equation of line AB is of the form 3x + y + k = 0
This passes through A(- 1, -3) then
3(- 1) – 3 + k = 0 ⇒ k = 6
∴ Equation of the line AB is
3x + y + 6 = 0 …………………. (1)
Equation of the given line is
x – 3y – 5 = 0 ………………… (2)
Solving (1) and (2) we get the coordinates of E

Alter: If (x₂, y₂) is the image of (x₁, y₁) with respect to the line ax + by + c = 0 then

Question 8.
Find the image of the point (1, 2) in the straight line 3x + 4y – 1 = 0. (S.A.Q.)
Answer:
If (x₂, y₂) is the image of (x₁, y₁) with respect to the line ax + by + c = 0 then

Question 9.
Show that the distance of the point (6, – 2) from the line 4x + 3y = 12 is half the distance of the point (3, 4) from the line 4x – 3y = 12. (S.A.Q.)
Answer:
Distance of the point P(x₁, y₁) to the line ax + by + c = 0 is \(\left|\frac{a x_1+b y_1+c}{\sqrt{a^2+b^2}}\right|\)
Distance of the point (6, -2) from the line 4x + 3y = 12 is
\(\left|\frac{24-6-12}{\sqrt{4^2+3^2}}\right|=\left|\frac{6}{5}\right|\)
Distance of the point (3, 4) from the line 4x – 3y = 12 is
\(\left|\frac{12-12-12}{\sqrt{4^2+(-3)^2}}\right|=\frac{12}{5}\)
Hence, distance of the point (6, – 2) from the line 4x + 3y = 12 is one half of the distance of the point (3, 4) from the line 4x – 3y = 12

Question 10.
Find the locus of the foot of the perpendicular hum the origin to available straight line which always passes through a fixed point (a, b). (S.A.Q.)
Answer:
m is the slope of the line AB passing through a fixed point A(a, b).
Then the equation of AB is y – b = m (x – a)
⇒ mx – y + (b – ma) = 0 ……………. (1)
Let the locus of the foot of the perpendicular from origin to a variable straight line.
Then equation of the line perpendicular to AB is passing through the origin is
my + x = 0 …………………… (2)
Solving (1) and (2)

⇒ – x² – y² + by + xa = 0
⇒ x² + y² – ax – by = 0
∴ Locus of (x, y) is x² + y² – ax – by = 0

III.
Question 1.
Show that the lines x – 7y – 22 = 0, 3x + 4y + 9 = 0 and 7x + y – 54 = 0 form a right angled isosceles triangle. (S.A.Q.)
Answer:
Given lines are
x – 7y – 22 = 0 …………….. (1)
3x + 4y + 9 = 0 …………… (2)
7x + y – 54 = 0 …………….. (3)
Let the angle between lines (1) and (2) be A

Let the angle between the lines (2) and (3) be B then
tan B = \(\left|\frac{3(1)-7(4)}{3(7)+4(1)}\right|=\left|\frac{-25}{25}\right|\) = 1 = tan 45°
⇒ B = 45°
Let the angle between (1) and (3) be C
Since A + B + C = 180°
we have C = 180 – (A + B) = 180 – 45 – 45 = 90°
Lines (1), (2) and (3) form a right angled isosceles triangle.

Question 2.
Find the equation of straight lines passing through the point (- 3, 2) and making an angle of 45° with the straight line 3x – y + 4 = 0 (S.A.Q)
Answer:
Given (x₁, y₁) = (- 3, 2)
and given line is 3x – y + 4 = 0 ………………… (1)

Case (i): m = – 2
Equation of line PR is y – 2 = – 2(x + 3)
⇒ 2x + y + 4 = 0

Case (ii): m = \(\frac{1}{2}\)
Equation of the line PR is
y – 2 = \(\frac{1}{2}\) (x + 3)
⇒ 2y – 4 = x + 3 ⇒ x – 2y + 7 = 0

Question 3.
Find the angles of the triangle whose sides are x + y – 4 = 0, 2x + y – 6 = 0 and 5x + 3y – 15 = 0 (S.A.Q.)
Answer:
Let the equations of sides AB, BC and CA of the triangle ABC be x + y – 4 = 0,
2x + y – 6 = 0 and 5x + 3y – 15 = 0

Question 4.
Prove that the feet of the perpendiculars from the origin on the lines x + y = 4, x + 5y = 26 and 15x – 27y = 424 are collinear. (E.Q.)
Answer:
Given the lines
x + y – 4 = 0 ………………… ( 1 )
x + 5y – 26 = 0 ………………. ( 2 )
15x – 27y – 424 = 0 ……………….. (3)
Let P (x₂, y2₂) be the foot of the perpendicular of (x₁, y₁) = (0, 0) on (1)
⇒ \(\frac{x_2-0}{1}=\frac{y_2-0}{1}\) = \(\frac{-(0+0-4)}{1+1}=\frac{4}{2}\) = 2
∴ x₂ = 2, y₂ = 2 ∴ P = (2, 2)
Let Q (x₃, y₃) be the foot of the perpendicular of (x₁, y₁) = (0, 0) on (2)
\(\frac{x_3-0}{1}=\frac{y_3-0}{5}\) = \(\frac{-(0+0-26)}{1+25}\) = \(\frac{26}{26}\) = 1
∴ x₃ = 1, y₃ = 5 ⇒ Q = (1, 5)
Let R (x₄, y₄) be the foot of the perpendicular of (x₁, y₁) = (0, 0) on (3)

∴ Foot of the perpendicular of origin on the lines lies on a straight line.

Question 5.
Find the equations of straight lines passing through the point of intersection of the lines 3x + 2y + 4 = 0, 2x + 5y = 1 and whose distance from ( 2, – 1) is 2. (E.Q.)
Answer:
Equation of the lines passing through the point of intersection of the line
L₁ = 3x + 2y + 4 = 0,
L₂ = 2x + 5y – 1 = 0 is of the form
L₁ + λL₂ = 0
⇒ (3x + 2y + 4) + λ(2x + 5y – 1) = 0
⇒ (3 + 2λ)x + (2 + 5λ)y + (4 – λ) = 0 …………… (1)
Given that the distance from (2, -1) to (1) is 2

⇒ (- λ + 4)² = 9 + 4λ² + 12λ + 4 + 25λ² + 20λ
⇒ 28λ² + 40λ – 3 = 0
⇒ 28λ² – 2λ + 42λ – 3 = 0
⇒ (2λ + 3) (14λ – 1) = 0
⇒ λ = \(\frac{1}{14}\), λ = \(\frac{-3}{2}\)
From (1)
If λ = \(\frac{1}{14}\) then
(3x + 2y + 4) + \(\frac{1}{14}\)(2x + 5y – 1) = 0
⇒ 44x + 33y + 55 = 0
⇒ 4x + 3y + 5 = 0 , -3
If λ = \(\frac{-3}{2}\) then
(3x + 2y + 4) – \(\frac{3}{2}\)(2x + 5y – 1) = 0
⇒ 6x + 4y + 8 – 6x – 15y + 3 = 0
⇒ – 11y + 11 = 0 ⇒ y – 1 = 0 are the required equations of lines.

Question 6.
Each side of a square is of length 4 units. The centre of the square is ( 3, 7) and one of its diagonals is parallel to y = x. Find the coordinates of its vertices. (S.A.Q.)
Answer:
Let ABCD be a square. Point of D intersection of diagonals is the centre P(3, 7).
Draw PN ⊥ AB.
Then N is the mid point of AB
∴ AN = NB = PN = 2

Since a diagonal is parallel to y = x its sides are parallel to the coordinate axes AB = BC = CD = DA = 4 Centre of the square P = (3, 7) and one diagonal is parallel to y = x ⇒ x – y = 0 ……. (1)
⇒ AB, CD lines are parallel to X-axis and remaining two sides BC, AD are parallel to Y-axis. Vertices of the square ABCD are
A = (x₁, y₁), B = (x₁ + 4, y₁) ;
C = (x₁ + 4, y₁ + 4), D = (x₁, y₁ + 4)
Centre of ABCD is (3, 7) and point of intersection of diagonals is (3, 7)
∴ \(\left(\frac{x_1+x_1+4}{2}, \frac{y_1+y_1+4}{2}\right)\) = (3, 7)
⇒ \(\left(\frac{2 \mathrm{x}_1+4}{2}, \frac{2 \mathrm{y}_1+4}{2}\right)\) = (3, 7)
⇒ x₁ + 2 = 3, y₁ + 2 = 7
⇒ x₁ = 1 and y₁ = 5
∴ Coordinates of vertices are
A = (1, 5), B = (1 + 4, 5) = (5, 5)
C = (1 + 4, 5 + 4) = (5, 9)
and D = (1, 5 + 4) = (1, 9)

Question 7.
If ab > 0, find the area of the rhombus enclosed by the four straight lines
ax ± by ± c = 0 (S.A.Q)
Answer:

Equation of AB is ax + by + c = 0 …………………. (1)
Equation of CD is ax + by – c = 0 …………………. (2)
Equation of BC is ax – by + c = 0 ……………………. (3)
Equation of AD is ax – by – c = 0 ………………………. (4)
Solving (1) and (3) Coordinates of B are \(\left(\frac{-c}{a}, 0\right)\)
Solving (1) and (4) Coordinates of A are \(\left(0, \frac{-c}{b}\right)\)
Solving (2) and (3) Coordinates of C are \(\left(0, \frac{\mathrm{c}}{\mathrm{b}}\right)\)
Solving (2) and (4) Coordinates of D are \(\left(\frac{\mathrm{c}}{\mathrm{a}}, 0\right)\)
Area of Rhombus

Question 8.
Find the area of the parallelogram whose sides are 3x + 4y + 5 = 0, 3x + 4y – 2 = 0, 2x + 3y + 1 = 0 and 2x + 3y – 7 = 0. (S.A.Q.)
Answer:
Given sides are
3x + 4y + 5 = 0 …………….. (1)
3x + 4y – 2 = 0 ……………… (2)
2x + 3y + 1 = 0 …………….. (3)
2x + 3y – 7 = 0 ……………. (4)
Area of parallelogram formed by (1), (2), (3). (4)

Question 9.
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4= 0 and 3x + 4y – 5 = 0 wants to reach the path Whose equation is 6x – 7y + 8 = 0 in the least lime. Find the equation of the path that he should follow. (S.A.Q)
Answer:

By Solving 2x – 3y + 4 = 0 and
3x + 4y – 5 = 0 we get

Question 10.
A ray of light passing through the point (1, 2) reflects on the X – axis at a point A and the reflected ray passes through the point (5, 3). Find the coordinates of A. (S.A.Q.)
Answer:

Let m be the slope then the equation of the line passing through (1, 2) is y – 2 = m (x – 1)
⇒ m = \(\frac{y-2}{x-1}\)
Let – m be the slope of the reflected ray then the equation of the line passing through (5, 3) is y – 3 = – m (x – 5)
⇒ m = \(\frac{y-3}{5-x}\)
∴ \(\frac{y-2}{x-1}=\frac{y-3}{5-x}\) ∴ Since A lies on X-axis
then y = 0 ∴ \(\frac{-2}{x-1}=\frac{-3}{5-x}\)
⇒ 2(5 – x) = 3(x – 1)
⇒ 5x = 13 ⇒ x = \(\frac{13}{5}\)
∴ A = (\(\frac{13}{5}\), 0)