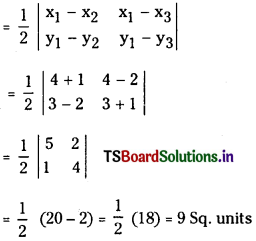TS Inter 1st Year Maths 1B Solutions Chapter 3 Straight Lines Ex 3(c)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(c)

I.
Question 1.
Find the ratios in which the following straight lines divide the line segment joining the given points. State whether the points lie on the same side or on either side of the straight line. (V.S.A.Q.)
(i) 3x – 4y = 7; ( 2, – 7 ) and ( – 1, 3 )
ii) 3x + 4y = 6; ( 2, – 1 ) and (1,1)
iii) 2x + 3y = 5; (0, 0) and (- 2,1) (Mar. ’14)
Answer:
(i) 3x – 4y = 7, (2, – 7 ) and (- 1, 3)
3x – 4y – 7 = 0
we have the formula for the ratio Ln -(axj + by! + c) l22 ” (ax2 + by2 + c)

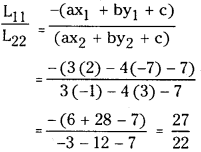
Since L₁₁ and L₂₂ are of opposite signs, the given points lie on either side of the straight line.

(ii) 3x + 4y = 6; ( 2, -1 ) and ( 1, 1 )
Equation of the given line is 3x + 4y – 6 = 0

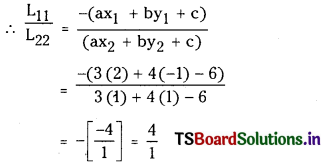
Since L₁₁ and L₂₂ are of opposite signs, the given points lie on either side of the straight line.

(iii) 2x + 3y = 5; ( 0, 0 ) and (- 2, 1 )

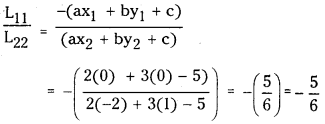
Since L₁₁ and L₂₂ are of same sign, the points lie on the same side of line.

Question 2.
Find the point of intersection of the following lines
(i) 4x + 8y – 1 = 0; 2x – y + 1 = 0
(ii) 7x + y + 3 = 0;x + y = 0 (VJS.A.Q.)
Answer:
(i) 4x + 8y – 1 = 0; 2x – y + 1 = 0
Point of intersection of above lines is obtained by solving the two equations (or) by the formula.

(ii) 7x + y + 3 = 0; x + y = 0
The point of intersection of the lines is obtained by solving the above equations.

Question 3.
Show that the straight lines
(a – b)x + (b – c)y = c – a,
(b – c)x + (c – a)y = a – b and
(c – a)x + (a – b)y = b – c are concurrent.
Answer:
Take given lines as
(a – b)x + (b – c)y = c – a ……………….. (1)
(b – c) x + (c – a) y = (a – b) ……………… (2)
(c – a) x + (a – b) y = (b – c) ……………. (3)
solving (1) and (2)

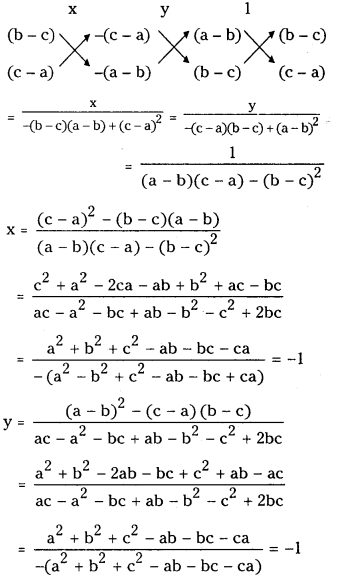
∴ Point of intersection of (1) and ( 2 ) is (-1, -1)
Substituting in equation (3) we get (c – a) (- 1) + ( a – b) (- 1) = – c + a – a + b = b – c
P (-1, -1) is a point on (3) and hence the given lines are concurrent.

Question 4.
Transform the following equations into the form L₁ + λL₂ = 0 and find the point of concurrency of the family of straight lines represented by the equation.
(i) (2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0
(ii) (k + 1)x + (k + 2)y + 5 = 0 (SA.Q.)
Answer:
(2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0
(2 + 5k ) x – 3 ( 1 + 2k ) y + (2 – k) = 0
⇒ (2x – 3y + 2 ) + k ( 5x – 6y – 1 ) = 0
This is of the form L₁ + λL₂ = 0
L₁ = 2x – 3y + 2 = 0
L₂ = 5x – 6y – 1 = 0
solving these equations

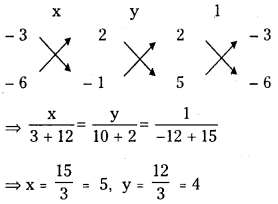
∴ The point of concurrency is P(5, 4)

(ii) (k + 1)x + (k + 2)y + 5 = 0
Answer/;
k (x + y) + (x + 2y + 5) = 0
⇒(x + 2y + 5) + k(x + y) = 0
This is of the form
∴ L₁ + λL₂ = 0
L₂ = x + y = 0 solving them

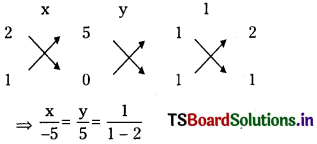
⇒ x = 5, y = -5
∴ point of concurrency = (5, -5)

Question 5.
Find the value of p, if the straight lines x + p = 0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent. (V.S.A.Q.)
Answer:
Equations of the given lines
x + p = 0 ………………….. (1)
y + 2 = 0 ………………….. (2)
3x + 2y + 5 = 0 ………………….. (3)
From (2) we have y = – 2
and from (3) 3x – 4 + 5 = 0 ⇒ x = – \(\frac{1}{3}\)
∴ From (1), p = – x = \(\frac{1}{3}\)

Question 6.
Find the area of the triangle formed by the following straight lines and the coordinate axes.
(i) x – 4y + 2 = 0
(ii) 3x – 4y + 12 = 0 (V.S.A.Q.)
Answer:
(i) x – 4y + 2 = 0
Equation of the line x – 4y + 2 = 0
⇒ x – 4y = – 2
⇒ \(\frac{x}{-2}+\frac{y}{\left(\frac{1}{2}\right)}\) = 1
∴ X – intercept = – 2, Y – intercept = \(\frac{1}{2}\)
∴ Area of ∆ OAB = \(\frac{1}{2}\) |ab|
= \(\frac{1}{2}\left|(-2)\left(\frac{1}{2}\right)\right|\) = \(\frac{1}{2}\)

(ii) 3x – 4y + 12 = 0
Equation of the given line is 3x – 4y + 12 = 0
⇒ 3x – 4y = – 12
⇒ \(\frac{3}{-12} x-\frac{4}{-12} y\) = 1
⇒ \(\frac{x}{-4}+\frac{y}{3}\) = 1
X-intercept = – 4, Y-intercept = 3
∴ Area of ∆ OAB = \(\frac{1}{2}\) |ab|
= \(\frac{1}{2}\) |(- 4) (3)| = 6 square units

II.
Question 1.
A straight line meets the coordinate axes at A and B. Find the equation of straight line, when
(i) \(\overline{\mathbf{A B}}\) is divided in the ratio 2 : 3 at (- 5, 2)
(ii) \(\overline{\mathbf{A B}}\) is divided in the ratio 1 : 2 at (- 5, 4)
(iii) (p, q) bisects \(\overline{\mathbf{A B}}\) (S.A.Q.)
Answer:
(i) \(\overline{\mathbf{A B}}\) is divided in the ratio 2 : 3 at (- 5, 2 )

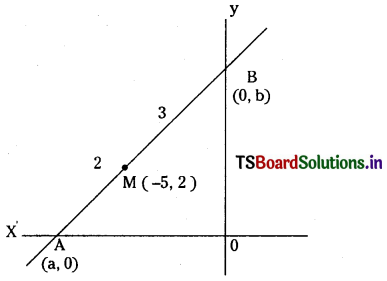
Let OA = a and OB = b
∴ A = (a, 0) and B = (0, b)
M divides AB in the ratio 2 : 3

(ii) \(\overline{\mathbf{A B}}\) is divided in the ratio 1 : 2 at (- 5, 4)
Answer:
Let OA = a and OB = b
then A = (a, O) and B= (O, b)
P divides AB in the ratio 1 : 2

(iii) (p, q) bisects \(\overline{\mathbf{A B}}\)
Answer:
Let OA = a, and OB = b
Then A = (a, 0) and B = (0, b)

Question 2.
Find the equation of the straight line pass-ing through the points (-1, 2) and ( 5, -1) and also find the area of the triangle formed by it with the axes of coordinates. (S.A.Q.)
Answer:
Let A (- 1, 2) and B (5, – 1) are the given points. Equation of AB is
\(\frac{y-2}{2+1}=\frac{x+1}{-1-5}\) ⇒ \(\frac{y-2}{3}=\frac{x+1}{-6}\)
⇒ – 2(y – 2) = x + 1
⇒ x + 2y – 3 = 0
Area of the ∆^le formed by it with the axes of coordinate = \(\frac{1}{2} \frac{c^2}{|a \cdot b|}=\frac{1}{2} \frac{9}{|(1)(2)|}=\frac{9}{4}\) sq.units.

Question 3.
A triangle of area 24 sq. units is formed by a straight line and the coordinate axes is in the first quadrant. Find the equation of the straight line, if it passes through (3, 4). (S.A.Q.)
Answer:
Equation of line in the intercepts form is \(\frac{x}{a}+\frac{y}{b}\) = 1
If this passes through P(3, 4) then

⇒ a² = 12 (a – 3)
⇒ a² – 12a + 36 = 0
⇒ (a – 6)² = 0
⇒ a = 6
∴ b = \(\frac{4 a}{a-3}=\frac{24}{3}\) = 8
Equation of AB is \(\frac{x}{6}+\frac{y}{8}\) = 1
⇒ 4x + 3y = 24
⇒ 4x + 3y – 24 = 0

Question 4.
A straight line with slope 1 passes through Q (- 3, 5) and meets the straight line x + y – 6 = 0 at P. Find the distance PQ. (S.A.Q.)
Answer:

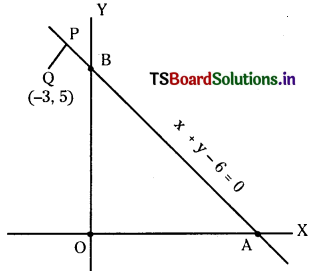
Given slope = 1, tan α = 1 = tan 45° ⇒ α = 45°
The line passes through Q (-3, 5)
Coordinates of P are
(x₁ + r cos α, y₁ + r sin α)
= (- 3 + r cos 45°, 5 + r sin 45°)
= (- 3 + \(\frac{\mathrm{r}}{\sqrt{2}}\), 5 + \(\frac{\mathrm{r}}{\sqrt{2}}\))
P is a point on x + y – 6 = 0
⇒ – 3 + \(\frac{\mathrm{r}}{\sqrt{2}}\) + 5 + \(\frac{\mathrm{r}}{\sqrt{2}}\) – 6 = 0
⇒\(\frac{2 r}{\sqrt{2}}\) = 4 r = 2√2
∴ PQ = 2√2

Question 5.
Find the set of values of ‘a’ if the points (1, 2) and (3, 4) lie to the same side of the straight line 3x – 5y + a = 0 (S.A.Q.)
Answer:
A (1, 2) and B (3, 4) are the given points
Equation of the given line is 3x – 5y + a = 0
L₁₁ = 3 (1) – 5 (2) + a = a – 7
L₂₂ = 3 (3) – 5 (4) + a = a – 11
a – 7 and a – 11 both must be positive or both negative
Case (i) : a – 7 > 0, a – 11 > 0
⇒ a > 7 and a > 11
∴ a > 7, 11 a ∈ (11, ∞)
Case (ii): a – 7 < 0, a – 11 < 0
⇒ a < 7 and a < 11
⇒ a ∈ (- ∞, 7)
∴ a ∈ (- ∞, 7) ∪ (11, ∞)

Question 6.
Show that the lines 2x + y – 3 = 0, 3x + 2y – 2 = 0 and 2x – 3y – 23 = 0 are concurrent and find the point of concurrency. (S.A.Q)
Answer:
Equations of the given lines are
2x + y – 3 = 0 ……………. (1)
3x + 2y – 2 = 0 ……………. (2)
2x – 3y – 23 = 0 ……………. (3)
Solving (1) and (2) we get the point of intersection of the lines.

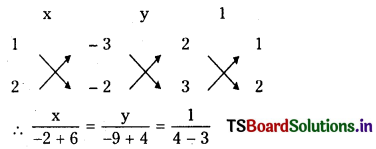
⇒ x = 4, y = – 5
∴ Point of intersection of the lines (1) and (2) is (4,- 5)
Now from (3) 2x – 3y – 23
= 2 (4) – 3 (-5) – 23 = 8 + 15 – 23 = 0
∴ So the point lies on (3) and lines (1), (2), (3) are concurrent. The point of concurrence is (4, -5)

Question 7.
Find the value of p if the following lines are concurrent (SA.Q.) (May 2006)
(i) 3x + 4y = 5, 2x + 3y = 4 : px + 4y = 6
(ii) 4x – 3y – 7 = 0, 2x + py + 2 = 0, 6x + 5y – 1 = 0
Answer:
(i) 3x + 4y = 5, 2x + 3y = 4 : px + 4y = 6
Equations of lines are
3x + 4y – 5 = 0 and …………….. (1)
2x + 3y – 4 = 0 …………….. (2)
Point of intersection of (1) and (2) x y 1

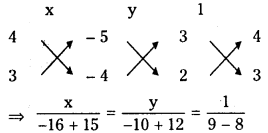
⇒ x = – 1, y = 2 ;
Point of intersection is P (-1,2) given lines are concurrent and the point P (-1, 2) must lie on px + 4y – 6 = 0
⇒ – p + 8 – 6 = 0 ⇒ p = 2

(ii) 4x – 3y – 7 = 0, 2x + py + 2 = 0,6x + 5y – 1 = 0
Answer:
Equations of lines are
4x – 3y – 7 = 0 ……………. (1)
6x + 5y – 1 = 0 ……………. (2)
solving (1) and (2) we get

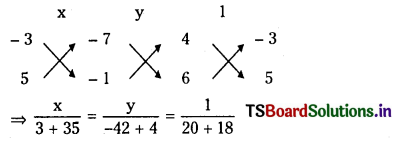
⇒ x = 1, y = – 1
∴ Point of intersection = ( 1, – 1)
Since the given lines are concurrent, consider 2x + py + 2 = 0
⇒ 2 (1) + p (-1) + 2 = 0 ⇒ p = 4

Question 8.
Determine whether or not the four straight lines with equations x + 2y – 3 = 0, 3x + 4y – 7 = 0, 2x + 3y – 4 = 0 and 4x + 5y – 6 = 0 are concurrent. (S.A.Q.)
Answer:
Equations of the given lines are
x + 2y – 3 = 0 ……………………. (1)
3x + 4y – 7 = 0 ……………………. (2)
2x + 3y – 4 = 0 ……………………. (3)
4x + 5y – 6 = 0 ……………………. (4)
Solving (1) and (2) we have

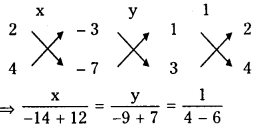
⇒ x = 1, y = 1
∴ Point of intersection = (1, 1)
2x + 3y – 4 = 2 (1) + 3 (1) – 4 = 1 ≠ 0
4x + 5y – 6 = 4 (1) + 5 (1) – 6 = 3 ≠ 0
∴ P (1, 1) is not a point on (3) and (4)
∴ The given lines are not concurrent.

Question 9.
If 3a + 2b + 4c = 0, then show that the equation ax + by + c = 0 represents a family of concurrent straight lines and find the point of concurrency. (S.A.Q.)
Answer:
Given condition is 3a + 2b + 4c = 0
⇒ c = – \(\left(\frac{3}{4}\right) a-\left(\frac{2}{4}\right) b\)
For all values of a, b the lines ax + by + c = 0 passes through ‘a’ the point \(\left(\frac{3}{4}, \frac{1}{2}\right)\) since

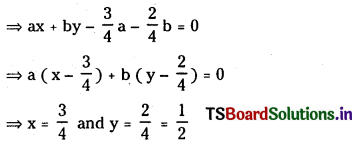
∴ The equation ax + by + c = 0 represents a family of concurrent lines
∴ Point of concurrence = \(\left(\frac{3}{4}, \frac{1}{2}\right)\)

Question 10.
If non-zero numbers a, b, care in harmonic progression, then show that the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) represents a family of concurrent lines and find the point of concurrency. (S.A.Q.)
Answer:
Given a, b, c are in harmonic progression, we have \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in arithmetic progression.

For all values of a, b, c the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) represents a family of concurrent lines.
∴ Point of concurrence = P (1, – 2)

III.
Question 1.
Find the point on the straight line 3x + y + 4 = 0 which is equidistant from the points (- 5, 6) and (3, 2). (March 2013) (S.A.Q)
Answer:

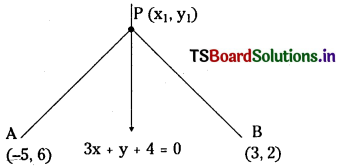
Let P (x₁, y₁) be any point on 3x + y + 4 = 0
∴ 3x₁ + y₁ + 4 = 0 ………………….. (1)
Given PA = PB ⇒ PA² = PB²
⇒(x₁ + 5)² + (y₁ – 6)²
= (x₁ – 3)² + (y₁ – 2 )²
⇒ x₁² + 10x₁] + 25 + y₁² – 12y₁ + 36
⇒ x₁² – 6x₁ + 9 + y₁² – 4y₁ + 4
⇒ 16x₁ – 8y₁ + 48 = 0
⇒ 2x₁ – y₁ + 6 = 0 …………………… (2)
Solving (1) and (2) 5x₁ + 10 = 0 ⇒ x₁ = – 2
From (1) ⇒ 3 (- 2) + y₁ + 4 = 0 ⇒ y₁ = 2
∴ Coordinates of P are (- 2, 2)

Question 2.
A straight line through P (3, 4) makes an angle of 60° with the positive direction of the X – axis. Find the coordinates of the points on that line which are 5 units away from P. (S.A.Q.)
Answer:
Equation of the straight line in symmetric form is \(\frac{x-x_1}{\cos \theta}=\frac{y-y_1}{\sin \theta}\) = r
∴ Coordinates of any point on the line
Q = (x₁ + r cos θ, yi + r sin θ)
Given (x₁, y₁) = (3, 4)
θ = 60° ⇒ cos θ = cos 60° = \(\frac{1}{2}\),
sin θ = sin 60° = \(\frac{\sqrt{3}}{2}\)

Case (i): r = 5 ; Co-ordinates of Q are

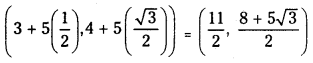
Case (ii): r = – 5; Co-ordinates of Q are

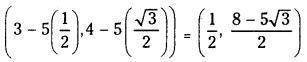
Question 3.
A straight line through Q(√3, 2) makes an angle \(\frac{\pi}{6}\) with the positive direction of the X- axis. If the straight line intersects the line √3x – 4y + 8 = 0 at P, find the distance PQ. (March 2004) (E.Q)
Answer:

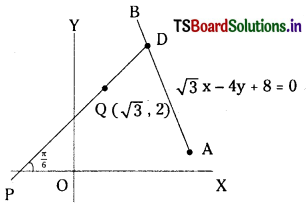
Given that the straight line, PQ through Q makes an angle \(\frac{\pi}{6}\) with the positive direction of the X-axis.
∴ Slope of PQ = m = tan 30°= \(\frac{1}{\sqrt{3}}\)
PQ passes through Q (√3 , 2)
Equation of PQ is y – 2 = \(\frac{1}{\sqrt{3}}\)(x – √3 )
⇒ √3 y – 2√3 = x – √3
⇒ x – √3 = -√3 ……………… (1)
Equation of AB is √3x – 4y + 8 = 0 ………………… (2)
From (1) √3x – 3y = – 3 ……………. (3)
Solving (2) and (3) y = 5
From (1) x = √3y – √3 = 5√3 – √3 = 4√3
∴ Coordinates of P = (4√3, 5) and Coordinates of Q = (√3 , 2)
∴ PQ² = ( 4√3 – √3)² + ( 5 – 2)²
= (3√3)² + 3² = 27 + 9 = 36
∴ PQ = 6 units

Question 4.
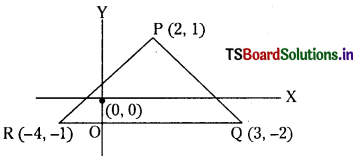
Show that the origin is with in the triangle whose angular points are (2, 1 ) ( 3, – 2 ) and (-4,-1) (E.Q)
Answer:
Let P (2, 1), Q (3, -2) and R (-4, -1) be the regular points of a triangle PQR

Equation of QR is

∴ L₃ = 3x + y – 7 = 0 ………………… (3)
L₃ (- 4, – 1) = 3 (- 4) – 1 – 7 = – 20 < 0
L₃ (0, 0) = 3 (0) + 0 – 7 = – 7 < 0
Hence (-4, -1) , (0,0) lies on the same side of
PQ and (0, 0) lies to the left of PQ ………………… (4)
L₂ (3, -2) = 3 + 6 + 1 = 10 > 0
L₂ (0, 0) = 0 – 3 (0) + 1 = 1 > 0
So (0, 0) and (3, -2) lie on the same side of PR ………………… (5)
L₁ (2, 1) = 2 + 7(1) + 11 = 20 > 0
L₁ (0, 0) = 0 + 7 (0) + 11 = 11 > 0
So (0, 0) and (2, 1) lie on the same side of QR ……………………. (6)
From (4), (5) and (6) we have O(0, 0) lies downwards to PR, upward of QR, and to the left of PQ. Hence O(0, 0) will lie inside the ∆PQR.

Question 5.
A straight line through Q (2, 3) makes an angle \(\frac{3 \pi}{4}\) with the negative direction or X – axis. If the straight line intersects the line x + y – 7 = 0 at P, find the distance of PQ. (E.Q)
Answer:

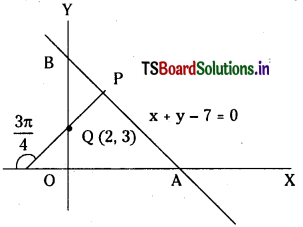
The line PQ makes an angle \(\frac{3 \pi}{4}\) with the negative direction of X- axis ie., PQ makes an angle. π – \(\frac{3 \pi}{4}\) = \(\frac{\pi}{4}\) with the positive direction of X-axis.
Coordinates of Q are (2, 3)
Coordinates of P are (x₁ + r cos θ, y₁ + r sin θ)

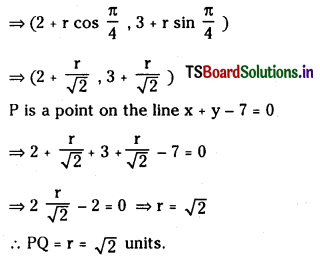
Question 6.
Show that the straight lines x + y = 0, 3x + y – 4 = 0 and x + 3y – 4 = 0 form an isosceles triangle. (E.Q)
Answer:
Given lines are
x + y = 0 …………………. (1)
3x + y – 4 = 0 …………………… (2)
x + 3y – 4 = 0 ……………….. (3)
Solving (1) and (2)

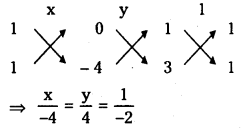
⇒ x = 2, y = – 2
Point of intersection of (1) and (2) is (2, – 2)
Solving (2) and (3)
By solving the equations (2) and (3)

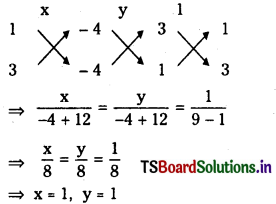
∴ Point of intersection of (2) and (3) is (1, 1) Solving equations (1) and (3)

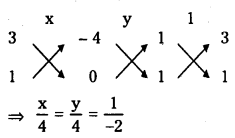
⇒ x = – 2, y = 2
∴ Point of intersection of lines ( 1) and (3) = (-2, 2)
Let A = (2, -2), B = (1, 1), C = (-2, 2) be the vertices of the triangle ABC formed by the lines (1), (2) and (3), then
Then AB =

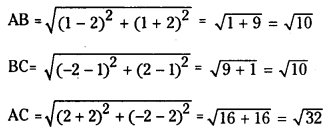
∴ AB = BC we can say that an isosceles triangle can be formed with the given lines.

Question 7.
Find the area of the triangle formed by the straight lines 2x-y-5 = 0, x – 5y + 11 = 0 and x + y – 1 = 0. (E.Q)
Answer:
Given lines are
2x – y – 5 = 0 ……………………. (1)
x – 5y + 11 = 0 (2)
x + y – 1 = 0 (3)
By solving the equations (1) and (2)

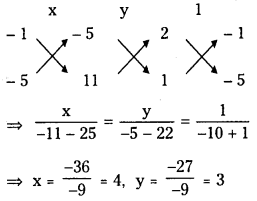
∴ Point of intersection of lines (1) and (2) is A (4, 3). Solving (2) & (3)

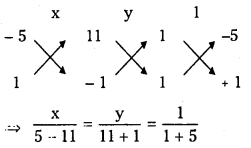
⇒ x = – 1, y = 2
∴ Point of intersection of the lines (2) and (3) is B (- 1, 2 ).
Solving (1) and (3)

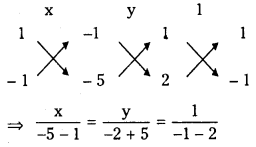
⇒ x = 2; y = – 1
∴ Point of intersection of lines (1) and (3) is C(2, -1) Area of ∆ ABC