TS Inter 1st Year Maths 1B Solutions Chapter 3 Straight Lines Ex 3(d)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(d)

I. Find the angle between the following straight lines. (V.S.A.Q.)

Question 1.
y = 4 – 2x, y = 3x + 7
Answer:
y = 4 – 2x ⇒ 2x + y – 4 = 0 and
3x – y + 7 = 0 are equations of given lines
If θ is the angle between the lines

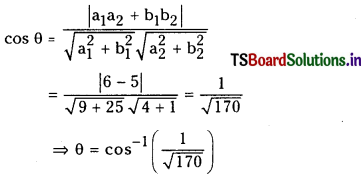
Question 2.
3x + 5y = 7, 2x – y + 4 = 0 (V.S.A.Q)
Answer:

Question 3.
y = – √3 x + 5, y = \(\frac{1}{\sqrt{3}}\)x – \(\frac{2}{\sqrt{3}}\) (V .S.A.Q.)
Answer:
m₁ = -√3 and m₂ = \(\frac{1}{\sqrt{3}}\) = from the given lines. Since m₁m₂ = – 1, the lines are perpendicular ⇒ θ = \(\frac{\pi}{2}\)

Question 4.
ax + by = a + b, a(x – y) + b(x + y) = 2b (V.S.A.Q)
Answer:
ax + by = a + b, (a + b)x + (- a + b)y = 2b

Find the length of the perpendicular drawn from the given point given against the following straight lines.

Question 5.
5x – 2y + 4 = 0; ( – 2, – 3 ) … (V.S.A.Q.)
Answer:
Length of the perpendicular from the point (-2, -3) to the line 5x – 2y + 4 = 0 is by the formula

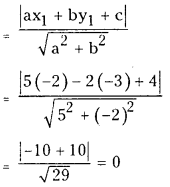
Question 6.
3x – 4y + 10 = 0 ……………… (3, 4) (V.S.A.Q)
Answer:
Length of the perpendicular

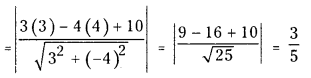
Question 7.
x – 3y – 4 = 0 ……………… ( 0, 0 ) (V.S.A.Q.)
Answer:
Length of the perpendicular
= \(\left|\frac{0-3(0)-4}{\sqrt{1+9}}\right|\) = \(\frac{4}{\sqrt{10}}\)

Find the distance between the following parallel lines. (V.S.A.Q.)

Question 8.
3x – 4y = 12, 3x – 4y = 7
Answer:
Given equations of lines are
3x – 4y = 12, 3x – 4y = 7
So by the formula distance between two parallel lines = \(\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}\) = \(\frac{|-12+7|}{\sqrt{9+16}}\) = 1

Question 9.
5x – 3y – 4 = 0, 10x – 6y – 9 = 0 (May 2012)
Answer:
Equations of the lines can be taken as
10x – 6y – 8 = 0
10x – 6y – 9 = 0
∴ Distance between two parallel lines
= \(\frac{|-8+9|}{\sqrt{100+36}}\) = \(\frac{1}{2 \sqrt{34}} \)

Question 10.
Find the equation of the straight line parallel to the line 2x + 3y + 7 = 0 and passing through the point (5, 4). (March 2013) (V.S.A.Q.)
Answer:
Equation of the given line is
2x + 3y + 7 = 0 …………………. ( 1 )
We suppose the equation of line parallel to line (1) is 2x + 3y + k = 0 …………………. ( 2 )
Since the required line passes through (5, 4)
we have 2(5) + 3(4) + k = 0 ⇒ k + 22 = 0 ⇒ k = -22
∴ From (2) the equation of the required line is 2x + 3y – 22 = 0

Question 11.
Find the equation of the straight line perpendicular to the line 5x – 3y + 1 = 0 and passing through the point ( 4, – 3). (V.S.A.Q.)
Answer:
Equation of the given line is
5x – 3y – 1 = 0 ……… (1)
The equation of the line perpendicular to (1) is of the form 3x + 5y + k = 0 ……… (2)
If (2) passes through (4, -3) then
3(4) + 5 (- 3) + k = 0
⇒ 12 – 15 + k = 0
⇒k = 3
∴ From (2) the equation of the required line is 3x + 5y + 3 = 0

Question 12.
Find the value of k if the straight lines 6x – 10y + 3 = 0 and kx – 5y + 8 = 0 are parallel.
Answer:
Equations of the given lines are (V.S.A.Q.)
6x – 10y + 3 = 0
kx – 5y + 8 = 0
These lines are parallel, so a₁ b₂ = a₂ b₁
⇒ – 30 = – 10 k
⇒ k = 3

Question 13.
Find the value of p if the straight lines 3x + 7y – 1 = 0 and 7x – py + 3 = 0 are mutually perpendicular. (V.S.A.Q.)
Answer:
Equations of the given lines are
3x + 7y – 1 = 0
7x – py + 3 = 0
These lines are perpendicular
⇒ a₁ a₂ + b₁ b₂ = 0
⇒ 3(7) + 7(- p) = 0
⇒ 21 – 7p = 0 ⇒ p = 3

Question 14.
Find the value of k, if the straight lines y – 3kx + 4 = 0 and (2k – 1)x – (8k – 1) y – 6 = 0 are perpendicular. (V.S.A.Q.)
Answer:
Equations of the given lines are
y – 3kx + 4 = 0 and
(2k – 1)x – ( 8k – 1 )y – 6 = 0
The lines are perpendicular
⇒ a₁ a₂ + b₁ b₂ = 0
⇒ – 3k (2k – 1) – 1 (8k – 1) = 0
⇒ – 6k² + 3k – 8k + 1 = 0
⇒ 6k² + 5k – 1 = 0
⇒ (k + 1) (6k – 1) = 0
⇒ k = – 1 (or) k = 1/6.

Question 15.
(- 4, 5) is a vertex of a square and one of W its diagonals is 7x – y + 8 = 0. Find the equation of the other diagonal. (S.A.Q.)
Answer:

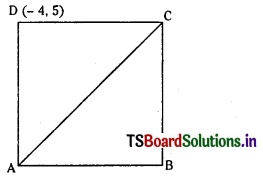
ABCD is a square. Equation of the diagonal is AC given by 7x – y + 8 = 0
The other diagonal BD is perpendicular to AC.
Equation of BD is x + 7y + k = 0. BD passes through D(- 4, 5). Hence – 4 + 7(5) + k = 0
⇒ k = – 31
∴ Equation of the other diagonal BD is x + 7y – 31 = 0

II.
Question 1.
Find the equations of the straight lines passing through (1, 3) and (i) parallel to (ii) perpendicular to the line passing through the points (3, – 5 ) and ( – 6, 1 )
Answer:

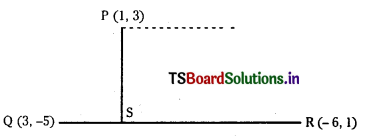
(i) Q(3, – 5) and R(-6, 1) are the given points
Slope of QR = \(\frac{-5-1}{3+6}=\frac{-6}{9}\) = \(\frac{-2}{3}\)
∴ Slope of the line passing through P, parallel to QR is -2/3
∴ Equation of the line is y – 3 = –\(\frac{2}{3}\) (x – 1)
⇒ 3y – 9 = -2x + 2
⇒ 2x + 3y – 11 = 0

(ii) Slope of the line perpendicular to the line QR is 3/2.
∴ Equation of the line passing through P(1, 3) and perpendicular to QR is
y – 3 = 3/2 (x – 1)
⇒ 2y – 6 = 3x – 3
⇒ 3x – 2y + 3 = 0

Question 2.
The line \(\frac{x}{a}-\frac{y}{b}\) = 1 meets the X – axis at P.
Find the equation of the line perpendicular to this line at P. (S.A.Q.)
Answer:

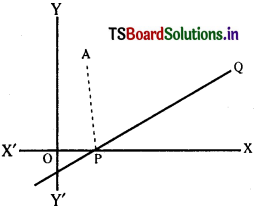
Equation of PQ is \(\frac{x}{a}-\frac{y}{b}\) = 1
Equation of X-axis is y = 0 ∴ x = a
∴ Coordinates of P = (a, 0)
Line PA is perpendicular to PQ
∴ Equation of PA is \(\frac{x}{b}+\frac{y}{a}\) = k
The line PA is passing through (a, 0) hence
\(\frac{a}{b}+\frac{0}{a}\) = k ⇒ k = \(\frac{a}{b}\)
∴ Equation of the line perpendicular to the line PQ at P is \(\frac{x}{b}+\frac{y}{a}=\frac{a}{b}\)

Question 3.
Find the equation of the line perpendicular to the line 3x + 4y + 6 = 0 and making an intercept – 4 on the X-axis. (S.A.Q.)
Answer:
Equation of the given line is
3x + 4y + 6 = 0 ……………. (1)
Equation of the line perpendicular to (1) is 4x – 3y + k = 0
⇒ 4x – 3y = – k

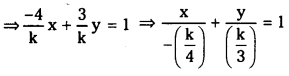
Since the line makes X-intercept – 4 on the X-axis we have – \(\frac{k}{4}\) = – 4 ⇒ k = 16
∴ Equation of the required line is 4x – 3y + 16 = 0

Question 4.
A (- 1, 1), B ( 5, 3 ) are opposite vertices of a square in the XY-planfe. Find the equation of the other diagonal (not passing through A, B ) of the square. (S.A.Q.)
Answer:

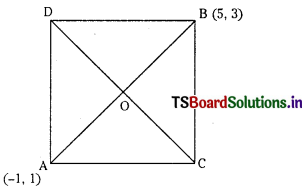
A (- 1, 1), B (5, 3) are opposite vertices of the square.
Slope of AB = \(\frac{3-1}{5+1}=\frac{2}{6}=\frac{1}{3}\)
∴ Slope of CD = – 3
O is the point of intersection of the diagonals
∴ Coordinates of O are
\(\left(\frac{-1+5}{2}, \frac{1+3}{2}\right)\) = (2, 2)
CD passes through 0 (2, 2)
∴ Equation of CD is y – 2 = – 3 (x – 2)
⇒ 3x + y- 8 = 0

Question 5.
Find the foot of the perpendicular drawn from (4, 1) upon the straight line 3x – 4y + 12 = 0. (S.A.Q.)
Answer:
Given equation of the straight line is
3x-4y + 12 = 0 ………………… ( 1 )
Equation of the line perpendicular to (1) is
4x + 3y + k = 0 ……………….. ( 2 )
This line passes through (4, 1) that
4(4) + 3(1) + k = 0 ⇒ k = – 19
∴ Equation of line (2) is 4x + 3y – 19 = 0 …. ( 3 )
Solving (1) and (2) we get the coordinates of the foot of the perpendicular

Question 6.
Find the foot of the perpendicular drawn from (3, 0) upon the straight line 5x + 12y – 41 = 0. (S.A.Q.)
Answer:
Equation of the given line is 5x + 12y – 41 = 0
If (x₂, y₂) is the foot of the perpendicular from (x₁, y₁) on the line ax + by + c = 0 then

Question 7.
x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining the points A, B. If A = (- 1, – 3 ), find the coordinates of B. (S.A.Q)
Answer:

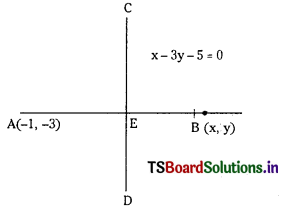
Let (x, y) be the coordinates of B which is the image of A(-1, -3).
Equation of line AB is of the form 3x + y + k = 0
This passes through A(- 1, -3) then
3(- 1) – 3 + k = 0 ⇒ k = 6
∴ Equation of the line AB is
3x + y + 6 = 0 …………………. (1)
Equation of the given line is
x – 3y – 5 = 0 ………………… (2)
Solving (1) and (2) we get the coordinates of E

Alter: If (x₂, y₂) is the image of (x₁, y₁) with respect to the line ax + by + c = 0 then

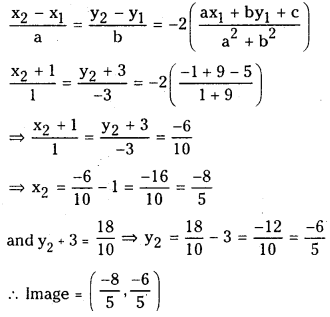
Question 8.
Find the image of the point (1, 2) in the straight line 3x + 4y – 1 = 0. (S.A.Q.)
Answer:
If (x₂, y₂) is the image of (x₁, y₁) with respect to the line ax + by + c = 0 then

Question 9.
Show that the distance of the point (6, – 2) from the line 4x + 3y = 12 is half the distance of the point (3, 4) from the line 4x – 3y = 12. (S.A.Q.)
Answer:
Distance of the point P(x₁, y₁) to the line ax + by + c = 0 is \(\left|\frac{a x_1+b y_1+c}{\sqrt{a^2+b^2}}\right|\)
Distance of the point (6, -2) from the line 4x + 3y = 12 is
\(\left|\frac{24-6-12}{\sqrt{4^2+3^2}}\right|=\left|\frac{6}{5}\right|\)
Distance of the point (3, 4) from the line 4x – 3y = 12 is
\(\left|\frac{12-12-12}{\sqrt{4^2+(-3)^2}}\right|=\frac{12}{5}\)
Hence, distance of the point (6, – 2) from the line 4x + 3y = 12 is one half of the distance of the point (3, 4) from the line 4x – 3y = 12

Question 10.
Find the locus of the foot of the perpendicular hum the origin to available straight line which always passes through a fixed point (a, b). (S.A.Q.)
Answer:
m is the slope of the line AB passing through a fixed point A(a, b).
Then the equation of AB is y – b = m (x – a)
⇒ mx – y + (b – ma) = 0 ……………. (1)
Let the locus of the foot of the perpendicular from origin to a variable straight line.
Then equation of the line perpendicular to AB is passing through the origin is
my + x = 0 …………………… (2)
Solving (1) and (2)

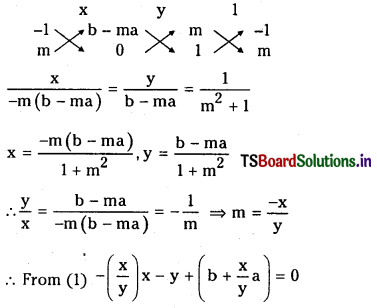
⇒ – x² – y² + by + xa = 0
⇒ x² + y² – ax – by = 0
∴ Locus of (x, y) is x² + y² – ax – by = 0

III.
Question 1.
Show that the lines x – 7y – 22 = 0, 3x + 4y + 9 = 0 and 7x + y – 54 = 0 form a right angled isosceles triangle. (S.A.Q.)
Answer:
Given lines are
x – 7y – 22 = 0 …………….. (1)
3x + 4y + 9 = 0 …………… (2)
7x + y – 54 = 0 …………….. (3)
Let the angle between lines (1) and (2) be A

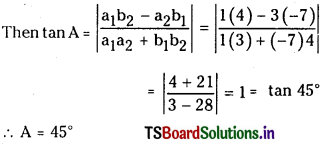
Let the angle between the lines (2) and (3) be B then
tan B = \(\left|\frac{3(1)-7(4)}{3(7)+4(1)}\right|=\left|\frac{-25}{25}\right|\) = 1 = tan 45°
⇒ B = 45°
Let the angle between (1) and (3) be C
Since A + B + C = 180°
we have C = 180 – (A + B) = 180 – 45 – 45 = 90°
Lines (1), (2) and (3) form a right angled isosceles triangle.

Question 2.
Find the equation of straight lines passing through the point (- 3, 2) and making an angle of 45° with the straight line 3x – y + 4 = 0 (S.A.Q)
Answer:
Given (x₁, y₁) = (- 3, 2)
and given line is 3x – y + 4 = 0 ………………… (1)

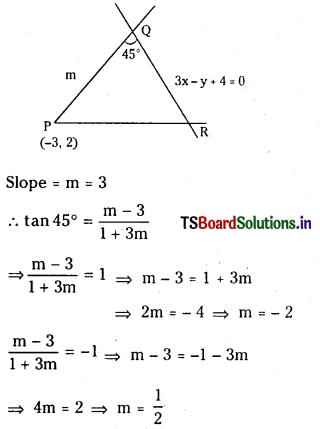
Case (i): m = – 2
Equation of line PR is y – 2 = – 2(x + 3)
⇒ 2x + y + 4 = 0

Case (ii): m = \(\frac{1}{2}\)
Equation of the line PR is
y – 2 = \(\frac{1}{2}\) (x + 3)
⇒ 2y – 4 = x + 3 ⇒ x – 2y + 7 = 0

Question 3.
Find the angles of the triangle whose sides are x + y – 4 = 0, 2x + y – 6 = 0 and 5x + 3y – 15 = 0 (S.A.Q.)
Answer:
Let the equations of sides AB, BC and CA of the triangle ABC be x + y – 4 = 0,
2x + y – 6 = 0 and 5x + 3y – 15 = 0

Question 4.
Prove that the feet of the perpendiculars from the origin on the lines x + y = 4, x + 5y = 26 and 15x – 27y = 424 are collinear. (E.Q.)
Answer:
Given the lines
x + y – 4 = 0 ………………… ( 1 )
x + 5y – 26 = 0 ………………. ( 2 )
15x – 27y – 424 = 0 ……………….. (3)
Let P (x₂, y2₂) be the foot of the perpendicular of (x₁, y₁) = (0, 0) on (1)
⇒ \(\frac{x_2-0}{1}=\frac{y_2-0}{1}\) = \(\frac{-(0+0-4)}{1+1}=\frac{4}{2}\) = 2
∴ x₂ = 2, y₂ = 2 ∴ P = (2, 2)
Let Q (x₃, y₃) be the foot of the perpendicular of (x₁, y₁) = (0, 0) on (2)
\(\frac{x_3-0}{1}=\frac{y_3-0}{5}\) = \(\frac{-(0+0-26)}{1+25}\) = \(\frac{26}{26}\) = 1
∴ x₃ = 1, y₃ = 5 ⇒ Q = (1, 5)
Let R (x₄, y₄) be the foot of the perpendicular of (x₁, y₁) = (0, 0) on (3)

∴ Foot of the perpendicular of origin on the lines lies on a straight line.

Question 5.
Find the equations of straight lines passing through the point of intersection of the lines 3x + 2y + 4 = 0, 2x + 5y = 1 and whose distance from ( 2, – 1) is 2. (E.Q.)
Answer:
Equation of the lines passing through the point of intersection of the line
L₁ = 3x + 2y + 4 = 0,
L₂ = 2x + 5y – 1 = 0 is of the form
L₁ + λL₂ = 0
⇒ (3x + 2y + 4) + λ(2x + 5y – 1) = 0
⇒ (3 + 2λ)x + (2 + 5λ)y + (4 – λ) = 0 …………… (1)
Given that the distance from (2, -1) to (1) is 2

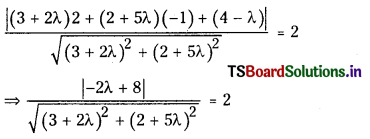
⇒ (- λ + 4)² = 9 + 4λ² + 12λ + 4 + 25λ² + 20λ
⇒ 28λ² + 40λ – 3 = 0
⇒ 28λ² – 2λ + 42λ – 3 = 0
⇒ (2λ + 3) (14λ – 1) = 0
⇒ λ = \(\frac{1}{14}\), λ = \(\frac{-3}{2}\)
From (1)
If λ = \(\frac{1}{14}\) then
(3x + 2y + 4) + \(\frac{1}{14}\)(2x + 5y – 1) = 0
⇒ 44x + 33y + 55 = 0
⇒ 4x + 3y + 5 = 0 , -3
If λ = \(\frac{-3}{2}\) then
(3x + 2y + 4) – \(\frac{3}{2}\)(2x + 5y – 1) = 0
⇒ 6x + 4y + 8 – 6x – 15y + 3 = 0
⇒ – 11y + 11 = 0 ⇒ y – 1 = 0 are the required equations of lines.

Question 6.
Each side of a square is of length 4 units. The centre of the square is ( 3, 7) and one of its diagonals is parallel to y = x. Find the coordinates of its vertices. (S.A.Q.)
Answer:
Let ABCD be a square. Point of D intersection of diagonals is the centre P(3, 7).
Draw PN ⊥ AB.
Then N is the mid point of AB
∴ AN = NB = PN = 2

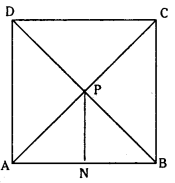
Since a diagonal is parallel to y = x its sides are parallel to the coordinate axes AB = BC = CD = DA = 4 Centre of the square P = (3, 7) and one diagonal is parallel to y = x ⇒ x – y = 0 ……. (1)
⇒ AB, CD lines are parallel to X-axis and remaining two sides BC, AD are parallel to Y-axis. Vertices of the square ABCD are
A = (x₁, y₁), B = (x₁ + 4, y₁) ;
C = (x₁ + 4, y₁ + 4), D = (x₁, y₁ + 4)
Centre of ABCD is (3, 7) and point of intersection of diagonals is (3, 7)
∴ \(\left(\frac{x_1+x_1+4}{2}, \frac{y_1+y_1+4}{2}\right)\) = (3, 7)
⇒ \(\left(\frac{2 \mathrm{x}_1+4}{2}, \frac{2 \mathrm{y}_1+4}{2}\right)\) = (3, 7)
⇒ x₁ + 2 = 3, y₁ + 2 = 7
⇒ x₁ = 1 and y₁ = 5
∴ Coordinates of vertices are
A = (1, 5), B = (1 + 4, 5) = (5, 5)
C = (1 + 4, 5 + 4) = (5, 9)
and D = (1, 5 + 4) = (1, 9)

Question 7.
If ab > 0, find the area of the rhombus enclosed by the four straight lines
ax ± by ± c = 0 (S.A.Q)
Answer:

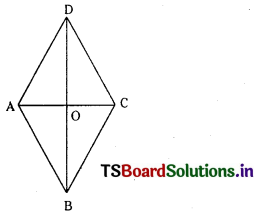
Equation of AB is ax + by + c = 0 …………………. (1)
Equation of CD is ax + by – c = 0 …………………. (2)
Equation of BC is ax – by + c = 0 ……………………. (3)
Equation of AD is ax – by – c = 0 ………………………. (4)
Solving (1) and (3) Coordinates of B are \(\left(\frac{-c}{a}, 0\right)\)
Solving (1) and (4) Coordinates of A are \(\left(0, \frac{-c}{b}\right)\)
Solving (2) and (3) Coordinates of C are \(\left(0, \frac{\mathrm{c}}{\mathrm{b}}\right)\)
Solving (2) and (4) Coordinates of D are \(\left(\frac{\mathrm{c}}{\mathrm{a}}, 0\right)\)
Area of Rhombus

Question 8.
Find the area of the parallelogram whose sides are 3x + 4y + 5 = 0, 3x + 4y – 2 = 0, 2x + 3y + 1 = 0 and 2x + 3y – 7 = 0. (S.A.Q.)
Answer:
Given sides are
3x + 4y + 5 = 0 …………….. (1)
3x + 4y – 2 = 0 ……………… (2)
2x + 3y + 1 = 0 …………….. (3)
2x + 3y – 7 = 0 ……………. (4)
Area of parallelogram formed by (1), (2), (3). (4)

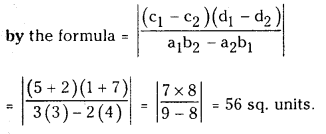
Question 9.
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4= 0 and 3x + 4y – 5 = 0 wants to reach the path Whose equation is 6x – 7y + 8 = 0 in the least lime. Find the equation of the path that he should follow. (S.A.Q)
Answer:

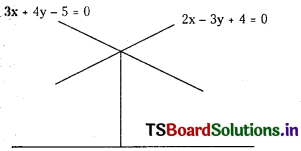
By Solving 2x – 3y + 4 = 0 and
3x + 4y – 5 = 0 we get

Question 10.
A ray of light passing through the point (1, 2) reflects on the X – axis at a point A and the reflected ray passes through the point (5, 3). Find the coordinates of A. (S.A.Q.)
Answer:

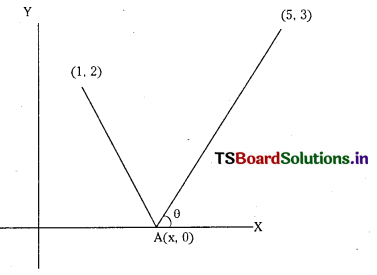
Let m be the slope then the equation of the line passing through (1, 2) is y – 2 = m (x – 1)
⇒ m = \(\frac{y-2}{x-1}\)
Let – m be the slope of the reflected ray then the equation of the line passing through (5, 3) is y – 3 = – m (x – 5)
⇒ m = \(\frac{y-3}{5-x}\)
∴ \(\frac{y-2}{x-1}=\frac{y-3}{5-x}\) ∴ Since A lies on X-axis
then y = 0 ∴ \(\frac{-2}{x-1}=\frac{-3}{5-x}\)
⇒ 2(5 – x) = 3(x – 1)
⇒ 5x = 13 ⇒ x = \(\frac{13}{5}\)
∴ A = (\(\frac{13}{5}\), 0)