Students must practice these Maths 1B Important Questions TS Inter First Year Maths 1B Straight Lines Important Questions Short Answer Type to help strengthen their preparations for exams.
TS Inter First Year Maths 1B Straight Lines Important Questions Short Answer Type
Question 1.
Transform the equation \(\frac{x}{a}+\frac{y}{b}=1\) into the normal form when a > 0 and b > 0. If the perpendicular distance of the straight line from the origin is p, deduce that \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\). [May ’08, ’04, ’02, ’97, ’95, ’90; Mar. ’07, ’02, ’00]
Solution:

Question 2.
Find the points on the line 3x – 4y – 1 = 0 which are at a distance of 5 units from the point (3, 2). [Mar. ’16 (AP); ’15 (AP); B.P.]
Solution:
Let the given point A(x1, y1) = (3, 2)
Given the equation of the straight line is 3x – 4y – 1 = 0
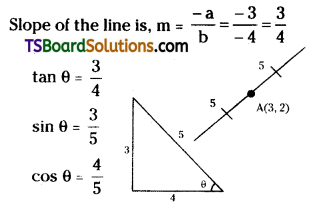
Distance |r| = 5
Required points = (x1 + |r| cos θ, y1 + |r| sin θ)
= (x1 ± r cos θ, y1 + r sin θ)
= (3 ± 5 . \(\frac{4}{5}\), 2 ± 5 . \(\frac{3}{5}\))
= (3 ± 4, 2 ± 3)
= (3 + 4, 2 + 3); (3 – 4, 2 – 3)
= (7, 5), (-1, 1)
![]()
Question 3.
Find the value of k, if the lines 2x – 3y + k = 0, 3x – 4y – 13 = 0 and 8x – 11y – 33 = 0 are concurrent. [May ’07, ’95; Mar. ’05, ’80; Mar. ’18 (TS)]
Solution:
Given, the equations of the straight lines are,
2x – 3y + k = 0 ……..(1)
3x – 4y – 13 = 0 ……..(2)
8x – 11y – 33 = 0 ………(3)
Solving (2) & (3)
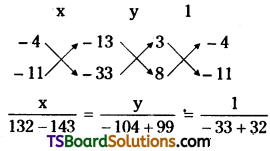

∴ The point of intersection (11, 5) lies on (1)
2x – 3y + k = 0
⇒ 2(11) – 3(5) + k = 0
⇒ 22 – 15 + k = 0
⇒ 7 + k = 0
⇒ k = -7
Question 4.
If the straight lines ax + by + c = 0, bx + cy + a = 0 and cx + ay + b = 0 are concurrent, then prove that a3 + b3 + c3 = 3abc. [Mar. ’19 (AP); Mar. ’08; May. ’00]
Solution:
Given, the equations of the straight lines are,
ax + by + c = 0 ……(1)
bx + cy + a = 0 ………(2)
cx + ay + b = 0 ……..(3)
Solving (2) & (3)
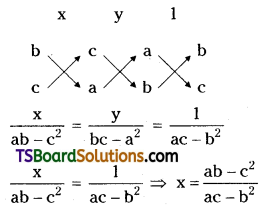
\(\frac{y}{b c-a^2}=\frac{1}{a c-b^2}\) ⇒ y = \(\frac{b c-a^2}{a c-b^2}\)
∴ Point of intersection of the straight lines (1) & (2) is \(\left(\frac{a b-c^2}{a c-b^2}, \frac{b c-a^2}{a c-b^2}\right)\)
Since the given lines are concurrent, then the point of intersection lies on line (3)
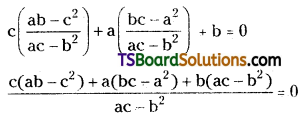
⇒ c(ab – c2) + a(bc – a2) + b(ac – b2) = 0
⇒ abc – c3 + abc – a3 + abc – b3 = 0
⇒ 3abc – a3 – b3 – c3 = 0
⇒ a3 + b3 + c3 = 3abc
Question 5.
A variable straight line drawn through the point of intersection of the straight lines \(\frac{x}{a}+\frac{y}{b}=1\) and \(\frac{x}{a}+\frac{y}{b}=1\) meets the coordinate axes at A and B. Show that the locus of the midpoint of \(\overline{\mathbf{A B}}\) is 2(a + b) xy = ab(x + y). [May ’05]
Solution:
Given equations of the straight lines are,
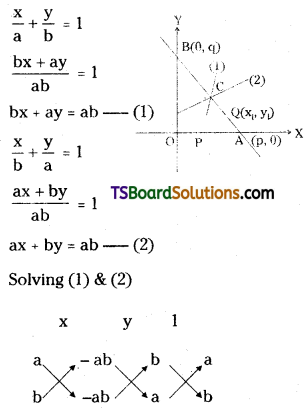
The point of intersection of lines (1) & (2) is
C = \(\left(\frac{a b}{a+b}, \frac{a b}{a+b}\right)\)
The equation of the straight line \(\overline{\mathbf{A B}}\) is the intercept from \(\frac{x}{p}+\frac{y}{q}=1\) ……(3)
The straight line (3) meets the X-axis at A(p, 0), Y-axis at B(0, q).
Let Q(x1, y1) be any point on the locus.
Since Q(x1, y1) is the midpoint of \(\overline{\mathbf{A B}}\)
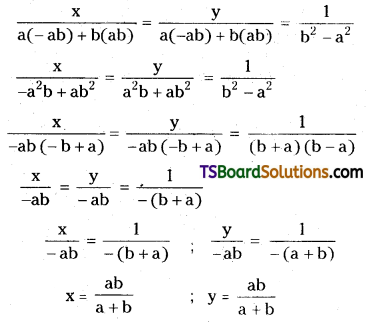
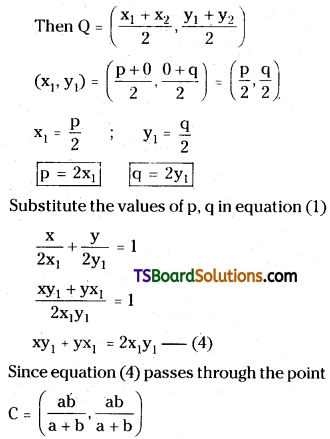
then, \(y_1\left(\frac{a b}{a+b}\right)+\left(\frac{a b}{a+b}\right) x_1=2 x_1 y_1\)
\(\frac{a b y_1+a b x_1}{a+b}=2 x_1 y_1\)
ab(x1 + y1) = (a + b) 2x1y1
∴ The locus of the midpoint ‘Q’ of AB is 2(a + b) xy = ab(x + y)
![]()
Question 6.
A straight line meets the coordinate axes in A and B. Find the equation of the straight line when (p, q) bisects \(\overline{\mathbf{A B}}\). [May ’90]
Solution:
The equation of the straight line in the intercept form is \(\frac{x}{a}+\frac{y}{b}=1\) …….(1)
The straight line (1) meets the X-axis at A(a, 0), Y-axis at B(0, b).
Now, C(p, q) bisects \(\overline{\mathbf{A B}}\), then C is the midpoint of \(\overline{\mathbf{A B}}\).
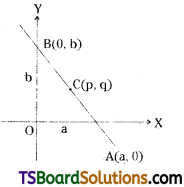
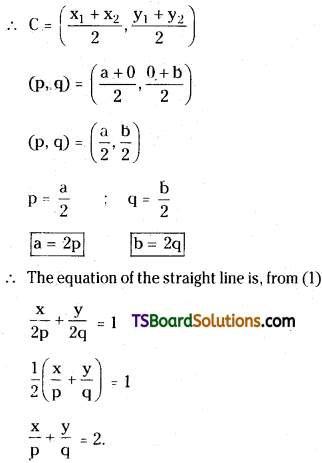
Question 7.
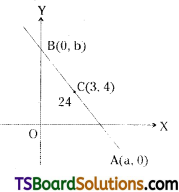
A triangle of area 24 sq. units is formed by a straight line and the coordinate axes in the first quadrant, find the equation of the straight line if it passes through (3, 4). [May ’07]
Solution:
Equation of the straight line in the intercept form is \(\frac{x}{a}+\frac{y}{b}=1\) …….(1)
Since equation (1) passes through the point (3, 4) then,
\(\frac{3}{a}+\frac{4}{b}=1\)
\(\frac{3 b+4 a}{a b}\) = 1
3b + 4a = ab
4a = ab – 3b
4a = b(a – 3)
b = \(\frac{4 a}{a-3}\) ……(2)
Given that, area of ΔOAB = 24 sq.units
\(\frac{1}{2}\)ab = 24
ab = 48
\(a\left(\frac{4 a}{a-3}\right)=48\)
a2 = 12(a – 3)
a = 12a – 36
a2 – 12a + 36 = 0
(a – 6)2 = 0
a = 6
from (2), b = \(\frac{4(6)}{6-3}\) = 8
The equation of the straight line is, from (1)
\(\frac{x}{6}+\frac{y}{8}\) = 1
\(\frac{4 x+3 y}{24}\) = 1
4x + 3y = 24
Question 8.
If 3a + 2b + 4c = 0, then show that the equation ax + by + c = 0, represents a family of concurrent straight lines and find the point of concurrency. [May ’10]
Solution:
Given that,
3a + 2b + 4c = 0
4c = -3a – 2b
c = \(\frac{-3 a-2 b}{4}\)
Now, ax + by + c = 0
ax + by + \(\left(\frac{-3 a-2 b}{4}\right)\) = 0
\(\frac{4 a x+4 b y-3 a-2 b}{4}\) = 0
4ax + 4by – 3a – 2b = 0
a(4x – 3) + b(4y – 2) = 0
(4x – 3) + \(\frac{b}{a}\) (4y – 2) = 0
This is of the form L1 + λL2 = 0
Here, ax + by + c = 0, represents a set of lines passing through the point of intersection of the lines
L1 = 4x – 3 = 0 …….(1)
L2 = 4y – 2 = 0 ………(2)
Solving (1) & (2)
From (1), 4x – 3 = 0
4x = 3
x = \(\frac{3}{4}\)
from (2), 4y – 2 = 0
4y = 2
y = \(\frac{1}{2}\)
∴ The point of concurrence = \(\left(\frac{3}{4}, \frac{1}{2}\right)\)
∴ ax + by + c = 0 represents a set of concurrent lines.
The point of concurrence = \(\left(\frac{3}{4}, \frac{1}{2}\right)\)
![]()
Question 9.
Find the point on the straight line 3x + y + 4 = 0, which is equidistant from the points (-5, 6) and (3, 2). [Mar. ’13; Nov. ’98]
Solution:
Given, equation of the straight line is 3x + y + 4 = 0 …….(1)
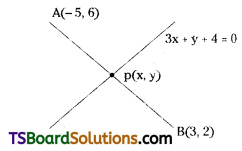
Let the given points are A(-5, 6) & B(3, 2)
Let P(x, y) be a point on the straight line 3x + y + 4 = 0,
Given that, PA = PB
\(\sqrt{(x+5)^2+(y-6)^2}=\sqrt{(x-3)^2+(y-2)^2}\)
Squaring on both sides
(x + 5)2 + (y – 6)2 = (x – 3)2 + (y – 2)2
x2 + 25 + 10x + y2 + 36 – 12y = x2 + 9 – 6x + y2 – 4y + 4
10x – 12y + 61 = -6x – 4y + 13
16x – 8y + 48 = 0
2x – y + 6 = 0 ………(2)
Solving (1) & (2)

Question 10.
A straight line through Q(√3, 2) makes an angle \(\frac{\pi}{6}\) with the positive direction of the X-axis. If the straight line intersects the line √3x – 4y + 8 = 0 at P, find the distance PQ. [Mar. ’19 (TS); Mar. ’04]
Solution:
Given equation of the straight line is √3x – 4y + 8 = 0 ……..(1)
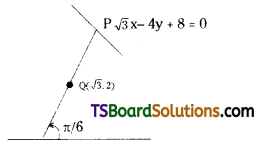
Given point Q(x1, y1) = (√3, 2)
Inclination of a straight line, θ = \(\frac{\pi}{6}\) = 30°
Slope of a straight line, m = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ The equation of the straight line \(\overline{\mathrm{PQ}}\) having slope \(\frac{1}{\sqrt{3}}\) and passing through the
point Q(√3, 2) is, y – y1 = m(x – x1)
y – 2 = \(\frac{1}{\sqrt{3}}\) (x – √3)
√3y – 2√3 = x – √3
x – √3y + √3 = 0 …….(2)
Solving (1) & (2)

Question 11.
The line \(\frac{x}{a}-\frac{y}{b}=1\) meets the X-axis at P. Find the equation of the line perpendicular to the line at P. [May ’03]
Solution:
Given, the equation of the straight line is \(\frac{x}{a}-\frac{y}{b}=1\) …..(1)
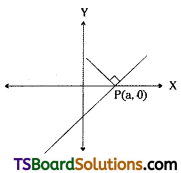
Since line (1) meets the X-axis at P.
Then y-coordinate = 0
\(\frac{x}{a}-\frac{0}{b}=1\)
x = a
∴ The coordinates of P = (a, 0)
The slope of the line (1) is m = \(\frac{\frac{-1}{a}}{\frac{-1}{b}}=\frac{b}{a}\)
Slope of the perpendicular line = \(\frac{-1}{b/a}=\frac{-a}{b}\)
∴ The equation of the line passing through P(a, 0) and having slope \(\frac{-a}{b}\) is,
y – y1 = \(\frac{-1}{m}\) (x – x1)
y – 0 = \(\frac{-a}{b}\) (x – a)
y = \(\frac{-a}{b}\) (x – a)
by = -ax + a2
ax + by – a2 = 0
which is the required equation of a straight line.
Question 12.
Find the equation of the line perpendicular to the line 3x + 4y + 6 = 0 and make an intercept -4 on the X-axis. [Mar. ’10]
Solution:
Given, equation of the straight line is 3x + 4y + 6 = 0 …….(1)
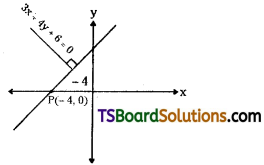
Slope of the line (1) is m = \(\frac{-3}{4}\)
Slope of the perpendicular line = \(\frac{-1}{m}=\frac{-1}{\left(\frac{-3}{4}\right)}=\frac{4}{3}\)
Given that, the required a straight line making an intercept -4 on X-axis. Then P = (-4, 0).
Equation of the straight line passing through P(-4, 0) and having slope \(\frac{4}{3}\) is
(y – y1) = \(\frac{-1}{m}\) (x – x1)
y – 0 = \(\frac{4}{3}\) (x + 4)
3y = 4x + 16
4x – 3y + 16 = 0
![]()
Question 13.
Find the equation of the straight line making non-zero equal intercepts on the coordinate axes and passing through the point of intersection of the lines 2x – 5y + 1 = 0 and x – 3y – 4 = 0. [Mar. ’06, ’00]
Solution:
Given the equation of the lines are
2x – 5y + 1 = 0 …….(1)
x – 3y – 4 = 0 …….(2)
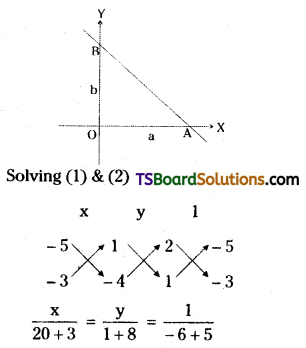
\(\frac{x}{23}=\frac{y}{9}=\frac{1}{-1}\)
\(\frac{x}{23}\) = -1; \(\frac{y}{9}\) = -1
x = -23; y = -9
∴ Point of intersection of lines (1) & (2) is, P = (-23, -9)
The equation of the straight line in the intercept form is, \(\frac{x}{a}+\frac{y}{b}=1\) = 1 ……..(3)
The straight line (3) makes equal intercepts on the coordinate axes
from (3),
\(\frac{x}{a}+\frac{y}{a}\)
x + y = a ……..(4)
Since equation (4) passes through the point P(-23, -9) then,
-23 – 9 = a
a = -32
∴ The equation of the straight line is x + y = -32
x + y + 32 = 0
Question 14.
Find the length of the perpendicular drawn from the point of intersection of the lines 3x + 2y + 4 = 0 and 2x + 5y – 1 = 0 to the straight line 7x + 24y – 15 = 0. [May ’01; Mar. ’91]
Solution:
Given, the equation of the straight lines are
3x + 2y + 4 = 0 ……(1)
2x + 5y – 1 = 0 ……..(2)
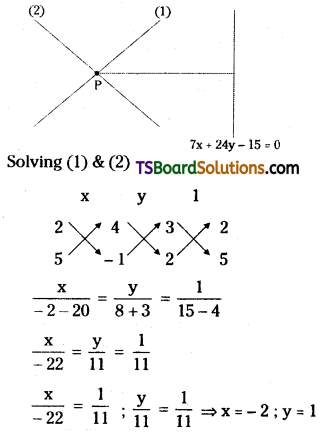
∴ The point of intersection of lines (1) & (2) is, P = (-2, 1)
Given the equation of the straight line is 7x + 24y – 15 = 0
Comparing with ax + by + c = 0 then a = 7, b = 24, c = -15
Point of intersection P(x1, y1) = (-2, 1)
The perpendicular distance from P(-2, 1) to the straight line
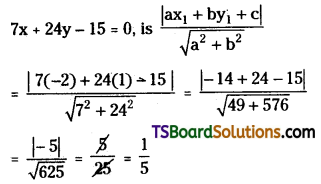
Question 15.
If θ is the angle between the lines \(\frac{x}{a}+\frac{y}{b}=1\) and \(\frac{x}{b}+\frac{y}{a}=1\), find the value of sin θ, where a > b. [May ’09]
Solution:
Given, the equation of the straight lines are
\(\frac{x}{a}+\frac{y}{b}=1\)
\(\frac{b x+a y}{a b}\) = 1
bx + ay = ab
bx + ay – ab = 0 ……..(1)
\(\frac{x}{b}+\frac{y}{a}=1\)
ax + by = ab
ax + by – ab = 0 ………(2)
Comparing (1) with a1x + b1y + c1 = 0, we get
a1 = b, b1 = a, c1 = -ab
Comparing (2) with a2x + b2y + c2 = 0, we get
a2 = a, b2 = b, c2 = -ab
If ‘θ’ is the angle between lines (1) & (2) then,

![]()
Question 16.
Find the equations of the straight lines passing through (1, 3) and (i) parallel to (ii) perpendicular to the line passing through the points (3, -5) and (-6, 1). [May ’15 (AP)]
Solution:
The slope of the line passing through the points (3, -5) and (-6, 1) is
m = \(\frac{y_2-y_1}{x_2-x_1}=\frac{1+5}{-6-3}=\frac{-6}{9}=\frac{-2}{3}\)
(i) Equation of the line passing through (1, 3) and parallel to the line passing through the points (3, -5) and (-6, 1) is y – y1 = m(x – x1)
⇒ y – 3 = \(\frac{-2}{3}\) (x – 1)
⇒ 3y – 9 = -2x + 2
⇒ 2x + 3y – 11 = 0
(ii) Equation of the line passing through (1, 3) and perpendicular to the line passing through the points (3, -5) and (-6, 1) is y – y1 = \(\frac{-1}{m}\) (x – x1)
⇒ y – 3 = \(\frac{1}{2}\) (x – 1)
⇒ 2y – 6 = 3x – 3
⇒ 3x – 2y + 3 = 0