TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Optional Exercise

Students can practice TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Optional Exercise

Question 1.
Some points are plotted on a plane. Each point is joined with all remaining points by line segments. Find the number of points if the number of line segments are 10.
Solution:
Number of distinct line segments that can be formed out of n-points = \(\frac{\mathrm{n}(\mathrm{n}-1)}{2}\)
Given : No. of line segments \(\frac{\mathrm{n}(\mathrm{n}-1)}{2}\) = 10
⇒ n² – n = 20
⇒ n² – n – 20 = 0
⇒ n² – 5n + 4n – 20 = 0
⇒ n(n- 5) + 4(n – 5) = 0
⇒ (n – 5) (n + 4) = 0
⇒ n – 5 = 0 (or) n + 4 = 0
⇒ n = 5 (or) – 4
∴ n = 5 [n – can’t be negative]

Question 2.
A two digit number is such that the product of the digits is 8. When 18 is added to the number, they interchange their places. Determine the number.
Solution:
Let the digit in the units place = x
Let the digit in the tens place = y
∴ The number = 10y + x
By interchanging the digits the number becomes 10x + y
By problem (10x + y) – (10y + x) = 18
⇒ 9x + 9y = 18
⇒ 9(x – y) = 18
⇒ x – y = \(\frac{18}{9}\) = 2
⇒ y = x – 2
(i.e.) digit in the tens place = x – 2
digit in the units place = x
Product of the digits = (x – 2) x
By problem x² – 2x = 8
x² – 2x – 8 = 0
⇒ x² – 4x + 2x – 8 = 0
⇒ x(x – 4) + 2(x – 4) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x – 4 = 0 (or) x + 2 = 0
⇒ x = 4 (or) x = -2
x = 4 [ ∵ x can’t be negative]
∴ The number is 24.

Question 3.
A piece of wire 8m in length, cut into two pieces and each piece is bent into a square. Where should the cut in the wire be made if the sum of the areas of these squares is to be 2 m² ?
[Hint: x + y = 8, (\(\frac{x}{4}\))² + (\(\frac{y}{4}\))² = 2
⇒ (\(\frac{x}{4}\))² + \(\left(\frac{8-x}{4}\right)\) = 2
Solution:
Let the length of the first piece = x m
Then length of the second piece = (8 – x) m
∴ Side of the 1^st square = \(\frac{x}{4}\) m and
Side of the second square = \(\frac{8-x}{4}\) m
Sum of the areas = 2 m²
\(\left(\frac{x}{4}\right)^2\) + \(\left(\frac{8-x}{4}\right)^2\) = 2
⇒ x² + 64 + x² – 16x = 16 × 2 = 32
⇒ 2x² – 16x + 64 = 32
⇒ 2x² – 16x + 32 = 0
⇒ 2(x² – 8x + 16) = 0
⇒ x² – 4x – 4x + 16 = 0
⇒ x(x – 4) – 4(x – 4) = 0
⇒ (x – 4) (x – 4) = 0
∴ x = 4
The cut should be made at the centre making two equal pieces of length 4m, 4m.

Question 4.
Vinay and Praveen working together can paint the exterior of a house in 6 days. Vinay by himself can complete the job in 5 days less than Praveen. How long will it take Vinay to complete the job by himself ?
Solution:
Let the time taken by Vinay to complete the job = x days
Then the time taken by Praveen to complete the job = x + 5 days
Both worked for 6 days to complete a job.
∴ Total work done by them is
\(\frac{6}{x}\) + \(\frac{6}{x+5}\) = 1
⇒ 6(2x + 5) = x² + 5x
⇒ x² – 7x – 30 = 0
⇒ x² – 10x + 3x – 30 = 0
⇒ x(x – 10) + 3(x – 10) = 0
⇒ x – 10 = 0 (or) x + 3 = 0
⇒ x = 10(or) x = -3
x = 10 (∵ x can’t be negative)
∴ Time taken by Vinay = x = 10 days
Time taken by Praveen = x + 5 = 15 days.

Question 5.
Show that the sum of roots of a quadratic equation is \(\frac{-\mathbf{b}}{\mathbf{a}}\).
Solution:
Let the Q.E. = ax² + bx + c = 0 (a ≠ 0)
⇒ ax² + bx = -c
⇒ x² + \(\frac{\mathrm{b}}{\mathrm{a}}\)x = \(\frac{-\mathrm{c}}{\mathrm{a}}\)
⇒ x² + 2.\(x \cdot \frac{b}{2 a}\) = \(-\frac{c}{a}\)

sum of the roots

∴ Sum of roots of a Q.E. is \(\frac{-b}{a}\)

Question 6.
Show that the product of the roots of a Q.E is \(\frac{\mathbf{c}}{\mathrm{a}}\).
Solution:
Let the Q.E. = ax² + bx + c = 0(a ≠ 0)
⇒ ax² + bx = -c


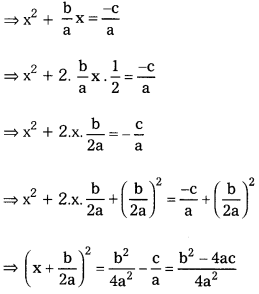
Product of the roots

Question 7.
The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2\(\frac{16}{21}\), find the fraction.
Solution:
Let the numerator = x
then denominator = 2x + 1
Then the fraction = \(\frac{x}{2 x+1}\)
Its reciprocal = \(\frac{2 x+1}{x}\)

⇒ 105x² + 84x + 21 = 116x² + 58x
⇒ 11x² – 26x – 21 = 0
⇒ 11x² – 33x + 7x – 21 = 0
⇒ 11x (x – 3) + 7(x – 3) = 0
⇒ (x – 3)(11x + 7) = 0
⇒ x – 3 = 0 (or) 11x + 3 = 0
⇒ x = 3 (or) \(\frac{-3}{11}\)
∴x = 3
Numerator = 3;
Denominator = 2 × 3 + 1 = 7
Fraction = \(\frac{3}{7}\)