TS Inter 1st Year Maths 1A Hyperbolic Functions Important Questions

Students must practice these TS Inter 1st Year Maths 1A Important Questions Chapter 9 Hyperbolic Functions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Hyperbolic Functions Important Questions

I.

Question 1.
Show that \(t \tanh ^{-1}\left(\frac{1}{2}\right)=\frac{1}{2} \log _e^3\)
Solution:

Question 2.
If cosh \(x=\frac{5}{2}\) find the values of
(i) cosh (2x)
(ii) sinh (2x)
Solution:

Question 3.
Prove that for any x ∈ R sinh (3x) =3 sinh (3x) + 3sinh x +4sin³h³ x.
Solution:
LHS : sinh(3x) = sinh (2x + x)
= sinh (2x) cosh x + cosh (2x) sinh x
= (2sinh x cosh x) cosh x + (1 + 2sinh² x) slnh x
= 2 sinh x cosh² x + sinh x + 2sinh³ x
= 2sinh x (1 + sinh² x) + sinh x + 2sinh³ x
= 3sinh x + 4sinh³ x = R.H.S.

Question 4.
Prove that for any x∈R
\(\tanh 3 x=\frac{3 \tanh x+\tanh ^3 x}{1+3 \tanh ^2 x}\)
Solution:

Question 5.
If cosh x = secθ then prove that \(\tanh ^2\left(\frac{x}{2}\right)=\tan ^2\left(\frac{\theta}{2}\right)\)
Solution:

Question 6.
sinhx = 5 then show that \(x=\log _e(5+\sqrt{26})\)
Solution:

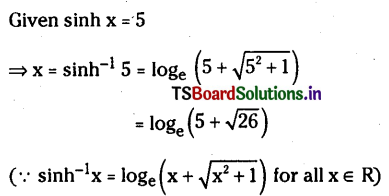
II.

Question 1.
\(\theta \in\left(-\frac{\pi}{4}, \frac{\pi}{4}\right)\) and \(x=\log _{\mathrm{e}}\left(\cot \left(\frac{\pi}{4}+\theta\right)\right)\) that prove that
(i) cosh x = sec2θ
(ii) sin hx= – tan2θ.
Solution:

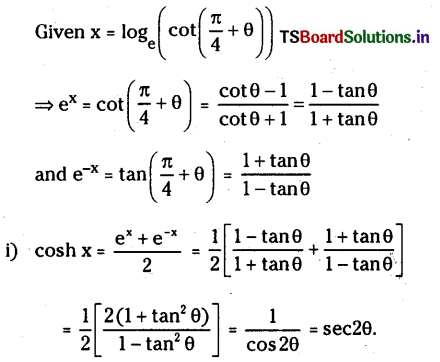
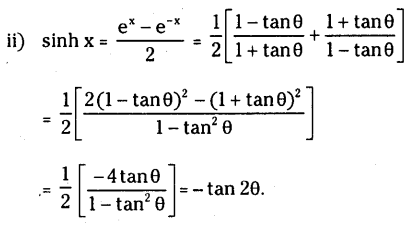
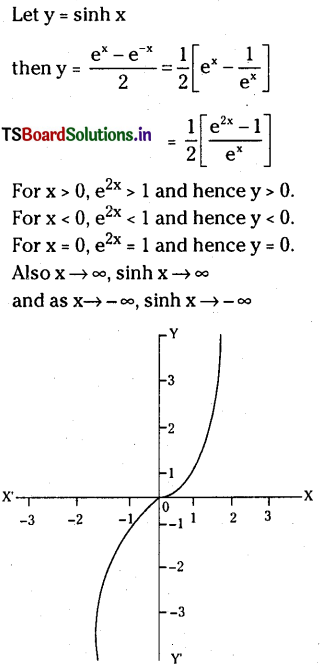
Question 2.
Draw the graph of y = sinh x.
Solution:

Question 3.
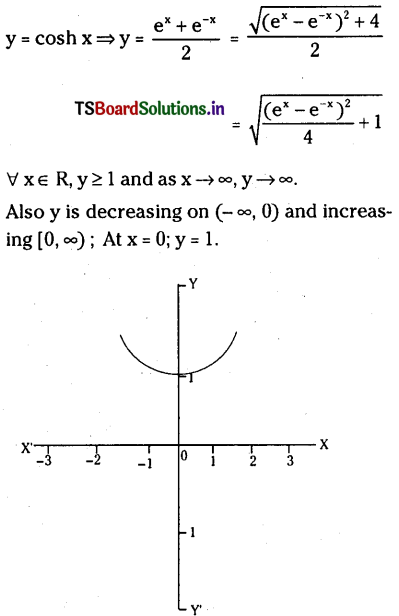
Draw the graph of y = cosh x.
Solution: