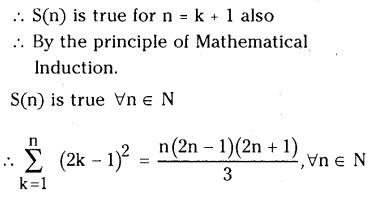Telangana TSBIE TS Inter 2nd Year English Study Material Revision Test-II Exercise Questions and Answers.
TS Inter 2nd Year English Study Material Revision Test-II
Time: 1 1/2 Hrs
Marks : 50
Section – A
Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]
a) Undoubtedly women in ancient India enjoyed a much higher status than their descendants in the eighteenth and nineteenth centuries.
Answer:
The given lines occur in the informative essay “The Awakening of Women”. This article was composed by a committed writer K.M. Phanikkar. The article deals with the status of women over various periods. Every statement is backed with supporting details.
The essay focuses mainly on the impact the Gandhian Movement had on the progress of women. Yet, the writer states how women’s status was in the past. Women ancient India had a respectable position. It is only in the eighteenth and nineteenth centuries that women’s condition touched a pathetic low. The given lines highlight the fact that writer is balanced but not biased.

b) It was a matter of surprise to the outside world that independence of India should have appointed women to the highest posts so freely, as members of the Cabinet,
Answer:
The given lines occur in the informative essay “The Awakening of Women”. This article was composed by a committed writer, K.M. Phanikkar. The article deals with the status of women’s over various periods. Every statement is backed with supporting details. The position of women started to improve with their active participation in the Gandhian Movement, showed constant progress in all fields.
In pre-independent India, legislation was made in favour of their rights. After India became independent, women were appointed in both key government and administrative posts. This surprised the world. People outside India thought that India was very conservative regarding women’s position. Thus the lines play an important role in clearing certain prejudices.
Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]
a) He rests at case beneath some pleasant weed.
Answer:
Introduction:
The above line is taken from the sonnet “On the Grasshopper and Cricket” written by John Keats. He denoted his life to the perfection of poverty.
Context and Meaning:
Here the poet expresses his feelings, regarding natures song. The Grasshopper and the Cricket are used as symbols. Seasons may come and go. But Nature never fails to inspire us with its songs. When birds, stop singing in extreme heat, during the summer. The earth is filled with songs of a grasshopper. We can hear the voice of the grasshopper who runs from hedge to hedge. He keeps singing tiredlessly and when he gets tired with fun, he goes under some pleasant weed to take rest.
Critical Comment:
The poet sends the message that nature is beautiful all the line, irrespective of the season.

b) And seems to one in drowsiness half lost, The Grasshopper’s among some grassy hills.
Answer:
Introduction:
These are the conducting lines of the poem “On the Grasshopper and Cricket?? written by John Keats, a Romantic poet. He devoted his life to the perfection of poetry.
Context and Meaning:
John Keats celebrates the music of the Earth. He finds beauty in hot summer as well as in the cold winter. Here, the grasshopper is symbol of hot summer and cricket is symbol of cold winter. During the winter season in the frosty evening, the birds stop singing songs. At that time the cricket begins to sing. He spreads the warmth ofjoy everywhere. The people who are half sleep feel that it is the grasshopper song which is coming from the grassy hills. Thus, he depicts the beauty of Nature.
Critical Comment:
The poet sends the message that nature is beautiful all the time, irrespective of the season. In a similar way, we should be joyful in our life and be happy in all situations.
Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]
a) But when the movement was actually started, women were everywhere at the forefront. Elaborate.
Answer:
The essay “The Awakening of Women” traces the evolution women’s progress in India over ages. K.M. Panikkar, a multifaceted genius, discusses the theme at length. Facts have been presented in a systematic order. Supporting details have been provided, Gandhiji understood the power of women. He believed that women could be an inexhaustible source of power.
He gave a call to them to participate in his movement. But, he had certain doubts about their readiness. His doubts were proved to be baseless. Women were very active in every area. They picketed liquor shops. They boycotted foreign goods. They took part in civil disobedience. Nowhere were women inferior to men. It was in fact the other way round.

b) Name some legislative reforms mentioned in the essay The Awakening of Women that seek to establish the equality of women.
Answer:
“The Awakening of Women” traces the evolution women’s progress in India over ages. K.M. Panikkar, a multifaceted genius, discusses the theme at length. Facts have been presented in a systematic order. Supporting details have been provided. Women’s active part in the struggle for freedom initiated a positive change in their status.
Even before India attained independence, laws were enacted and enforced in their favour. And that process continued after independence. Rights to property, to freedom of marriage, to education and employment, raising the age of marriage and the prevention of the dedication of women to temple services were some major legislative reforms.
Question 4.
Answer ANYONE of the following questions in about 100 words [1 × 4 = 4]
a) What is the theme of the poem On the Grasshopper and Cricket?
Answer:
The poem “On the Grasshoppers and Cricket’ is written by John Keats, an English Romantic poet. He has devoted his life to the perfection of poetry. In this poem, John Keats depicts the beauty of Nature. He says that the poetry of earth as symbols to praise Nature is never ending beauty. Seasons may come and go but Nature never fails to inspire us with its songs.
When birds stop singing in extreme heat, the earth is filled with the songs of a grasshopper. He sings endlessly, but when tired rests under some pleasant weed. During winter birds stop singing. There is a deathly silence. Frost spreads its blanket over Nature. Regardless, a shrill second cOmes from beneath stones and it is the cricket singing. Its song restores warmth. Thus, the small creatures prove to the world that the poetry of earth never ceases.

b) Discuss the common features between the grasshopper and cricket.
Answer:
The poem “ On the Grasshopper and Cricket” is written by John Keats. He is an English Romantic poet. He has developed his life to the perfections of poetry. In this poem, he depicts the beauty of nature. He says that the poetry of earth never ceases. He uses the Grasshopper and the Cricket as symbol to praise nature’s never ending beauty.
Seasons may come and go. But, nature never fails to inspire us with its songs. Therefore both the grasshopper and the cricket are the representative voices of nature’s music or poetry. Both offer a soothing effect to the extremities of climate. The grasshoppers song balances the extreme heat during the summer by providing music that is comforting and pleasing the cricket does the same during winter.
Question 5.
Answer ANYONE of the following questions in about 100 words. [1 × 4 = 4]
a) “Love, sacrifice and generosity are the essential elements for happy living”. Explain the statement with reference to the story A Gift for Christmas.
Answer:
A Gift for Christmas” is a well-known short story by O. Henry. The original name of the author is William Sydney Porter. This story was first published in 1905. A Gift for Christmas” is a Christmas story, and it functions as a parable about both the nature of love and the true meaning of generosity. Della’s earnest desire to buy a meaningful Christmas gift for Jim drives the plot of the story, and Jim’s reciprocity of that sentiment is shown when he presents Della with the tortoise-shell combs. Both Jim and Della give selflessly, without expectation of reciprocity. Their sole motivation is to make the other person happy. This, combined with the personal meaning imbued in each of the gifts, conveys the story’s moral that true generosity is both selfless and thoughtful.

b) Sketch the character of Jim.
Answer:
A Gift for Christmas” is a well-known short story by O. Henry. The original name of the author is William Sydney Porter. This story was first published in1905. Jim is a thin man of twenty two. He does not have enough income to support his wife. He bears the burden of fulfilling everyday demands of his wife. He is a very punctual person that why he constantly looks at his watch.
Section – B
Question 6.
Read the following passage and answer ANV FIVE questions given below: [5 × 1 = 5]
Della’s white fingers quickly opened the package. And then at first a scream of joy followed by a quick feminine change to tears. For, there lay The Combs — the set of combs, side and back, that Della had seen in a Broadway window and liked so much. They were beautiful combs, so expensive and they were hers now. But alas, the hair in which she was to wear them was sold and gone! She took them up lovingly, smiled through her tears and said, ‘My hair grows so fast, Jim!’
i) Who gave the package to Delia?
Answer:
to sharpen it
ii) What was Della’s reaction at first?
Answer:
We become better persons
iii) How did her joy change?
Answer:
No
iv) What did Della find in the package?
Answer:
the graphite inside
v) Where had she seen the combs earlier?
Answer:
because every action leaves a mark

vi) The combs were inexpensive. Write true or false.
Answer:
True
vii) Write the antonym of the word happy from the passage.
Answer:
exterior
viii) Write he synonym of the word shout from the passage.
an:
sorrows
Question 7.
Study the following advertisement and answer ANY FIVE questions that follow. [5 × 1 = 5]

i) Expand SHIP.
Answer:
Swach Hyderabad Internship Programme
ii) What are the eligibility criteria for participating in the programme?
Answer:
Social responsibility, passion, above 18years of age.
iii) Can very young boys and girls participate in this programme?
Answer:
no
iv) State any two themes of the internship programme.
Answer:
Lake cleanup, plantation
v) Registration is both online and offline. Write true or false.
Answer:
false

vi) When is the programme scheduled to begin?
Answer:
21st January 2022
vii) The number of hours of-the schedule is ___________ . (Fill in the blank.)
Answer:
20
viii) Write the word used in the ad to mean ‘a short term training period for practical experience’.
Answer:
Internship
Question 8.
Study the bar graph below and answer ANT FIVE questions given after it. [5 × 1 = 5]
i) What does the bar graph present?
Answer:
Sales of ice-creams of different flavours
ii) Ice cream of which flavour do people like the most in shop A?
Answer:
Ice-cream of mango flavours
iii) How many ice creams of almond flavour are sold in shop B?
Answer:
65

iv) Find the total number of ice creams of chocolate flavour sold in shop A and shop B.
Answer:
165
v) 30 ice creams of coconut flavour are sold in ___________. (Fill in the blank.)
Answer:
shop B
vi) Ice cream of which flavour do people like more in shop B, Chocolate or Vanilla?
Answer:
Chocolate
vii) How many ice creams of mango flavour are sold in shop A?
Answer:
100
viii) How many ice cream flavours are shown in the graph?
Answer:
5
Section – C
Question 9.
Rewrite the following passage using FIVE punctuation marks wherever necessary- [5 × 1 = 5]
The brahmo samaj led the movement for emancipation the ancient rules of purdah were broken and brahmo women moved freely in society: but this was. but a false dawn as it was far in advance of popular opinion.
Answer:
The Brahmo Samaj led the movement for emancipation. The ancient rules of purdah were broken and Brahmo women moved freely in society: but this was but a false dawn as it was far in advance of popular opinion.

Question 10.
Match the following words in Column ‘A’ with their definitions in Column ‘B’. [5 × 1 = 5]
Column A —– Column B
i) amphibious ( ) a) lasting for a very short time
ii) antidote ( ) b) designed to cause death
iii) ephemeral ( ) c) living on land as well as in water
iv) lethal ( ) d) someone who has a lot of experience in a field
v) veteran ( ) e) a substance that can act against the effect of poison
Answer:
i) c
ii) e
iii) a
iv) b
v) d

![]()