TS Inter 1st Year Maths 1A Mathematical Induction Important Questions

Students must practice these TS Inter 1st Year Maths 1A Important Questions Chapter 2 Mathematical Induction to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Mathematical Induction Important Questions

Question 1.
By using mathematical induction show that ∀ n ∈ N
\(\frac{1}{1 \cdot 4}+\frac{1}{4 \cdot 7}+\frac{1}{7 \cdot 10}+\) ………….. upto n terms \(=\frac{n}{3 n+1}\)
Solution:
1, 4, 7. are in A.P whose n^th term is 1 (n – 1) 3 = 3n – 2
and 4, 7, lo are in A.P. whose n^th term is 4 (n – 1) 3 = 3n + 1
∴ The n^th term of the given series


Hence S(k + 1) is true ∀ n ∈ N = k + 1
∴ By the principle of MathematicaL
Induction, S(n) is true ∀ n ∈ N

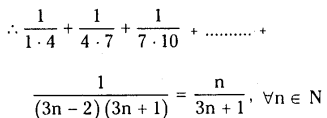
Question 2.
Use mathematical induction to prove the statement 2 + 3 . 2 + 4 . 2² + upto n terms = n 2ⁿ∀n∈N
Solution :

∴ S(n) is true for n = k + 1 also
∴ By the principle of Mathematical Induction.
S(n) is true for all n ∈ N.
∴ 2+3 . 2 + 4 . 2²+ ………………….. + (n+1) 2^n-1
= n . 2ⁿ ∀ n ∈ N

Question 3.
If x and y are natural numbers and x ≠ y using mathematical induction show that xⁿ-yⁿ is divisible by x – y, ∀n∈N
Solution:
Let S(n) be the statement
”xⁿ-yⁿ is divisible by (x – y)”
For n = 1, x¹ – y¹ is divisible by x’ – y’
We have S(1) is true for n = 1
Assume S(n) is true for n = k
Then x^k – y^k is divisible by (x-y)
Then (x^k – y^k) = (x – y) p where p ∈ Z …………………. (1)
We have prove that the statement S(n) is true for n = k + 1 also

Question 4.
Show that 49ⁿ + 16n – 1 is divisible by 64 for all positive integers ‘n’.
Solution:
Let S(n) be the statement.
49ⁿ + 16n – 1 is divisible by 64.
Since 49¹ + 16 (1) – 1 = 64 is divisible by 64.
The statement S(n) is true for n = 1.
Suppose the statement is true for S = k then
49^k + 16k – 1 = 64t for t ∈ N
We have to prove that S(n) is true for
n = k + 1 also
We have to prove that S(n) is true for
n = k + 1 also
Consider 49^k+1. + 16 (k + 1) – 1
49^k . 49 + 16k+ 16 – 1
=(64t – 16k+ 1)49 + 16k + 15
= (49) 64t + 16k (1 – 49) + 64
= 64 [49t – 12k + 1] and 49t – 12k + 1 is an integer.
∴ 49^k+1 + 16 (k + 1) – 1 is divisible by 64
∴ The statement is true for n = k + 1.
∴ By the principle of mathematical induction S(n) is true ∀ n ∈ N
∴ 49ⁿ + 16n – 1 is divisible by 64, ∀ n∈ N

Question 5.
Use mathematical induction to prove the statement
\(1^3+2^3+3^3+\ldots \ldots+n^3=\frac{n^2(n+1)^2}{4}, \forall n \in N\)
Solution:
Let S(n) be the statement
\(1^3+2^3+3^3+\ldots +n^3=\frac{n^2(n+1)^2}{4}\)

∴ Statement is true for n = k + 1 also
∴ By the principle of Mathematical Induction, S(n) is true ∀ n ∈ N

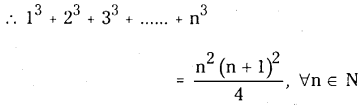
Question 6.
Use mathematical induction to prove the statement.
\(\sum_{k=1}^n(2 k-1)^2=\frac{n(2 n-1)(2 n+1)}{3}, \forall n \in N\)
Solution:
Let S(n) be the statement

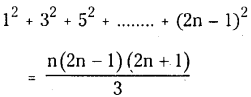
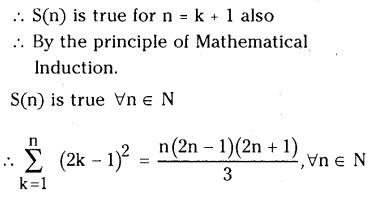
Question 7.
Use mathematical induction to prove that
2n – 3 ≤ 2^n-2  ∀ n ≥ 5, n ∈ N
Solution:
Let S(n) be the statement
2n – 3 ≤ 2^n-2  ∀ n ≥ 5, n ∈ N
∴ Since 2(5) – 3 ≤ 2^5-2

∴ The statement S(n) is true for
n k + 1, k ≥ 5
∴ By the principle of mathematical induction S(n) is true for all n ≥ 5, n ∈ N.

Question 8.
Use mathematical induction to prove that
(1 + x)ⁿ > 1 + nx for n ≥ 2, x > – 1, x ≠ 0.
Solution:
Let S(n) be the statement
(1+ x)ⁿ > 1 + nx for n ≥ 2, x > – 1, x ≠ 0.
The basis of induction is 2
and x ≠ 0, x > – 1 ⇒ x+1>0
For n = 2,
(1 + x)² = 1 + 2x + x² > 1 + 2x; the statement
S(n) is true for n = 2
Assume that the statement is true for n = k, k ≥ 2

∴ By the principle of mathematical induction the statement S(n) is true for all n≥2.
∴ (1 + x)ⁿ > 1 + nx, ∀ n ≥ 2, X > 1, X ≠ 0

Question 9.
Using mathematical induction show that x^m + y^m is divisible by x + y, if in is an odd natural number and x, y are natural numbers.
Solution:
Since m is an odd natural number
Let m = 2n – 1 where n is a non negative integer
Let S(n) be the statement

Now px² – (x y) y^2k+1 + is an integer
∴ x^2k+3 + y^2k+3 is divisible by (x + y)
∴ The statement is true for n = k + 1.
∴ By the principle of mathematical induction S(n) is true ∀n.
∴ x²ⁿ⁺¹ + y^{2n -1} is divisible by (X y) for all non negative integers.
∴ x^m + y^m is divisible by (x + y) if n is an odd natural number.

Question 10.
Use mathematical induction to prove that 2.4⁽²ⁿ⁺¹⁾ + 3⁽³ⁿ⁺¹⁾ + is divisible by 11, ∀ n ∈ N.
Solution:
Let S(n) be the statement
2.4⁽²ⁿ⁺¹⁾ + 3⁽³ⁿ⁺¹⁾ is divisible by 11
For n = 1
S(I) is 2.4³ + 3⁴ = 128 + 81 = 209 is divisible by 11.
∴ S(n) is true is for n = I
Suppose S(n) is true for n = k then
2.4⁽²ⁿ⁺¹⁾ + 3⁽³ⁿ⁺¹⁾ is divisible by 11