Srinivas

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 13 Probability InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 13 Probability InText Questions

Do This

(a) Outcomes of which of the following experiments cure equally likely. (AS₃)(Page No. 307)

Question 1.
Getting a digit 1, 2, 3, 4, 5 or 6 when a die is rolled.
Solution:
Equally likely

Question 2.
Selecting a different colour ball from a bag of 5 red balls, 4 blue balls and 1 black ball.
Note : Picking two different colour balls, i.e., Picking a red, a blue (or) black ball from a ………
Solution:
Not equally likely

Question 3.
Winning in a game of carrom.
Solution:
Not equally likely

Question 4.
Units place of a two digit number selected may be 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9.
Solution:
equally likely

Question 5.
Selecting a different colour ball from a bag of 10 red balls, 10 blue balls and 10 black balls.
Solution:
equally likely

Question 6.
Raining on a particular day of July.
Solution:
equally likely

(b) Are the outcomes of every experiment equally likely ?
Solution:
Outcomes of all experiments need not necessarily be equally likely.

(c) Give examples of 5 experiments that have equally likely outcomes and five more examples that do not have equally likely outcomes.
Solution:
Equally likely events :
a) Getting an even or odd number when a die is rolled.
b) Getting tail or head when a coin is tossed.
c) Getting an even (or) odd number when a card is drawn at random from a pack of cards numbered from 1 to 10.
d) Picking a green or black ball from a bag containing 8 green balls and 8 black balls.
e) Selecting a boy or girl from a class of 20 boys and 20 girls.
f) Selecting a red or black card from a deck of cards.

Events which are not equally likely :
a) Getting a prime (or) composite number when a die is thrown.
b) Getting an even or odd number when a card is drawn at random from a pack of cards numbered from 1 to 5.
c) Getting a number which is a multiple of 3 (or) not a multiple of 3 from numbers 1, 2, …….., 10.
d) Getting a number less than 5 or greater than 5.
e) Drawing a white ball or green ball from a bag containing 5 green balls and 8 white balls.

Think of 5 situations with equally likely events and find the sample space.
a) Tossing a coin : Getting a tail or head when a coin is tossed.
Sample space = {T, H}
b) Getting an even (or) odd number when a die is rolled.
Sample space = {1, 2, 3, 4, 5, 6}
c) Winning a game of shuttle Sample space = {win, loss}
d) Picking a black (or) blue ball from a bag containing 3 blue balls and 3 black balls = {blue, black}
e) Drawing a red coloured card or black coloured card from a deck of cards = {black, red}

d) Is getting a head complementary to getting a tail ? Give reasons.
Solution:
Number outcomes favourable to head = 1
Probability of getting a head = \(\frac{1}{2}\) [P(E)]
Number of outcomes not favourable to head = 1
Probability of not getting a head = \(\frac{1}{2}\) (P (\(\overline{\mathrm{E}}\)))
Now P(E) + P(\(\overline{\mathrm{E}}\)) = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
∴ Getting a head is complementary to getting a tail.

e) In case of a die is getting a 1 complementary to events getting 2, 3, 4, 5, 6 ? Give reasons for your answer.
Solution:
Yes, complementary events
∴ Probability of getting a 1 = \(\frac{1}{6}\) [P(E)]
Probability of getting 2, 3, 4, 5, 6
= P (\(\overline{\mathrm{E}}\)) = \(\frac{5}{6}\)
p(E) + P(\(\overline{\mathrm{E}}\)) = \(\frac{1}{6}\) + \(\frac{5}{6}\) = \(\frac{6}{6}\) = 1

f) Write of five new pair of events that are complementary.
Solution:
a) When a die is thrown, getting an even number is complementary to getting an odd number.
b) Drawing a red card from a deck of cards is complementary to getting a black card.
c) Getting an even number is complementary to getting an odd number from numbers 1, 2, ……….., 8.
d) Getting a Sunday is complementary to getting any day other than Sunday in a week.
e) Winning a running race is complementary to loosing it.

Try This

Question 1.
A child has a die whose six faces show the letters A, B, C, D, E and F. The die is thrown once. What is the probability of getting (i) A ? (ii) D ? (AS₄)(Page No. 312)
Solution:
Total number of outcomes [A, B, C, D, E and F] = 6
i) Number of favourable outcomes to A = 1
Probability of getting A = P(A)

= \(\frac{1}{6}\)

ii) Number of outcomes favourable to D = 1
Probability of getting D
= P(D)

= \(\frac{1}{6}\)

Question 2.
Which of the following cannot be the probability of an event ? (AS₃)(Page No. 312)
a) 2.3
b) – 1.5
c) 15%
d) 0.7
Solution:
a) 2.3 – Not possible
b) -1.5 – Not possible
c) 15% – May be the probability
d) 0.7 – May be the probability

Question 3.
You have a single deck of well shuffled cards. Then,
i) What is the probability that the card drawn will be a queen ? (AS₄)(Page No. 313)
Solution:
Number of all possible outcomes
= 4 × 13 = 1 × 52 = 52
Number of outcomes favourable to Queen
= 4[♥Q ♥Q ♥Q ♥Q]
Probability P(E)
= \(\frac{\text { No. of favourable outcomes }}{\text { Total no.of outcomes }}\)
= \(\frac{4}{52}\)
= \(\frac{1}{13}\)

ii) What is the probability that it is a face card ? (Page No. 314)
Solution:
Face cards are J, Q, K.
∴ Number of outcomes favourable to face cards = 4 × 3 = 12
No. of all possible outcomes = 52
P(E) = \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\)
= \(\frac{12}{52}\) = \(\frac{3}{13}\)

iii) What is the probability that it is a spade ? (Page No. 314)
Solution:
Number of spade cards = 13
Total number of cards = 52
Probability = \(\frac{\text { Number of outcomes favourable to spade }}{\text { Number of all outcomes }}\)
= \(\frac{13}{52}\) = \(\frac{1}{4}\)

iv) What is the probability that is the face cards of spades ? (Page No. 314)
Solution:
Number of outcomes favourable to face cards of spades = (K, Q, J) = 3
Number of all outcomes = 52 3
∴ P(E) = \(\frac{3}{52}\)

v) What is the probability it is not a face card ? (Page No. 314)
Solution:
Probability of a face card = \(\frac{12}{52}\)
∴ Probability that the card is not a face card
= 1 – \(\frac{12}{52}\) [P (\(\overline{\mathrm{E}}\)) = 1 – P(E)]
= \(\frac{52-12}{52}\)
= \(\frac{40}{52}\) = \(\frac{10}{13}\)

(Or)

Number of favourable outcomes = 4 × 10 = 40
Number of all outcomes = 52
∴ Probability = \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\)
= \(\frac{40}{52}\) = \(\frac{10}{13}\)

Think – Discuss

Question 1.
Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of any game ? (Page No. 312)
Solution:
Probability of getting a head is \(\frac{1}{2}\) and a tail is
\(\frac{1}{2}\) = 1
Hence, tossing a coin is a fair way.

Question 2.
Can \(\frac{7}{2}\) be the probability of an event ? Explain. (AS₃) (Page No. 312)
Solution:
\(\frac{7}{2}\) can’t be the probability of any event. Since probability of any event should lie between 0 and 1.

Question 3.
Which of the following arguments are correct and which are not correct ? Given reasons. (Page No. 312)

i) If two coins are tossed simultaneously, there are three possible outcomes – two heads, two tails (or) one of each. Therefore, for each. If these outcomes, the probability is \(\frac{1}{3}\)
Solution:
False
Reason :
All possible outcomes are 4. They are HH, HT, TH, TT
Thus, probability of two heads = \(\frac{1}{4}\)
Probability of two tails = \(\frac{1}{4}\)
Probability of one each = \(\frac{2}{4}\) = \(\frac{1}{2}\)

ii) If a die is thrown, there are two possible outcomes – an odd number (or) an even number. Therefore, the probability of getting an odd number is \(\frac{1}{2}\).
Solution:
True
Reason :
All possible outcomes = (1, 2, 3, 4, 5, 6) = 6
Outcomes favourable to an odd number = (1, 3, 5) = 3
Outcomes favourable to an even number = (2, 4, 6) = 3
∴ Probability (odd number)
= \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 13 Probability Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 13 Probability Optional Exercise

Question 1.
Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
(i) the same day ?
(ii) consecutive days ?
(iii) different days ?
Solution:
i) Shyam and Ekta can visit the shop in the following combination :


Number of Total outcomes
= 5 × 5 = 5² = 25 (also from the above table)
Number of favourable outcomes to that of visiting on the same day
(Tu, Tu), (W, W), (Th, Th), (I; F), (S, S) = 5
∴ Probability that visiting the shop on the same day
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{5}{25}\) = \(\frac{1}{5}\)

ii) Number of outcomes favourable to consecutive days
(Tu, W), (W, Th), (Th, F), (F, S) (W, Tu), (Th, W), (F, Th), (S, F) = 8
∴ Probability of visiting the shop on consecutive days = \(\frac{8}{25}\)

iii) If P(E) is the probability of visiting the shop on the same day, then P(\(\overline{\mathrm{E}}\)) is the probability of visiting the shop not on the same day. i.e., P(\(\overline{\mathrm{E}}\)) is the probability of visiting the shop on different days such that P(E) + P(\(\overline{\mathrm{E}}\)) =1
P(\(\overline{\mathrm{E}}\)) = 1 – P(E) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)

Question 2.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Solution:
Number of red balls in the bag = 5
As the probability of blue balls is double the probability of red balls, we have that number of blue balls is double the number of red balls.
∴ Blue balls = 5 × 2 = 10.

!! Let the number of blue balls = x
Number of red balls = 5
Total no. of balls = x + 5
Total outcomes in drawing a ball at random = x + 5
Number of outcomes favourable to red ball = 5
∴ P(R) = \(\frac{5}{x+5}\)
from the problem.
P(B) = 2 × \(\frac{5}{x+5}\) = \(\frac{10}{x+5}\)
Also, \(\frac{5}{x+5}\) + \(\frac{10}{x+5}\) = 1
[∵ P(\(\overline{\mathrm{E}}\)) + P(E) = 1]
⇒ \(\frac{5+10}{x+5}\) = 1
⇒ \(\frac{15}{x+5}\) = 1 ⇒ x + 5 = 15
⇒ x = 15 – 5 = 10

Question 3.
A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball ? If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
Solution:
Number of black balls = x
Total number of balls in the box = 12
Probability of drawing a black ball
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{x}{12}\) ……………. (1)
When 6 more black balls are placed in the box, number of favourable outcomes to black ball becomes = x + 6.
Total number of balls in the box becomes = 12 + 6 = 18.
Now the probability of drawing a black ball becomes = \(\frac{x+6}{18}\) …………… (2)
By problem,
\(\frac{x+6}{18}\) = 2 . \(\frac{x}{12}\)
⇒ \(\frac{x+6}{18}\) = \(\frac{x}{6}\)
⇒ 6(x + 6) = 18(x)
⇒ 6x + 36 = 18x ⇒ 18x – 6x = 36
⇒ 12x = 36 ⇒ x = \(\frac{36}{12}\) = 3
Check:
Equation (1) ⇒ \(\frac{x}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Equation (2) ⇒ \(\frac{x+6}{18}\) = \(\frac{3+6}{18}\)
= \(\frac{9}{18}\) = \(\frac{1}{2}\)
Equation (1) × 2 = \(\frac{1}{2}\) 2 = \(\frac{1}{2}\) and hence proved.

Question 4.
A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is 2 green is \(\frac{2}{3}\). Find the number of blue marbles 3 in the jar.
Solution:
Total number of marbles in the jar = 24
Let the number of green marbles = x
Then number of blue marbles = 24 – x.
Probability of drawing a green marbles
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{x}{24}\)
By Problem, \(\frac{x}{24}\) = \(\frac{2}{3}\)
⇒ 3 × x = 24 × 2
x = \(\frac{24 \times 2}{3}\) = 16
∴ Number of green marbles = 6
Number of blue marbles = 24 – 16 = 8

!! P(G) = \(\frac{2}{3}\)
P(G) + P(B) = 1
∴ P(B) = 1 – P(G) = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)
Number of blue marbles in the jar
= \(\frac{1}{3}\) × 24 = 8.

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 13 Probability Ex 13.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 13 Probability Exercise 13.2

Question 1.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball selected is (i) red ? (ii) not red ? (AS₁)
Solution:
i) Total number of balls in the bag = 3 red + 5 black = 8 balls
Number of total outcomes when a ball is selected at random = 3 + 5 = 8
Now, number of favourable outcomes of red ball = 3
∴ Probability of getting a red ball
P(E) = \(\frac{\text { No. of favourable outcome }}{\text { No. of total outcomes }}\)
= \(\frac{3}{8}\)

ii) If P(\(\overline{\mathrm{E}}\)) is the probability of selecting no red balls, then
P(E) + P(\(\overline{\mathrm{E}}\)) = 1
P(\(\overline{\mathrm{E}}\)) = 1 – P(E) = 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)

Question 2.
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red ? (ii) white ? (iii) not green ? (AS₁)
Solution:
There are 5 red marbles, 8 white marbles and 4 green marbles in a bag.
∴ Total number of marbles in the bag = 5 + 8 + 4= 17
∴ Number of all possible outcomes = 17
i) Let E be the event that the marble taken out will be red.
Total number of red marbles in the bag = 5
∴ Number of outcomes favourable to E = 5
P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{5}{17}\)

ii) Let E be the event that the marble taken out will be white.
Total number of white marbles in the bag = 8
∴ Number of outcomes favourable to E = 8
P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{8}{17}\)

iii) Let E be the event that the marble taken out will be green.
Total number of green marbles in the bag = 4
∴ Number of outcomes favourable to E = 4
P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{4}{17}\)
∴ Probability that the marble taken out will not be green.
= 1 – P (Probability that the marble taken out will be green)
= 1 – P(E) = 1 – \(\frac{4}{17}\) = \(\frac{13}{17}\)

Question 3.
A Kiddy bank contains hundred 50p coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin (i) will be a 50p coin ? (ii) will not be a ₹ 5 coin ? (AS₁)
Solution:
i) Number of 50p coins = 100
Number of ₹ 1 coins = 50
Number of ₹ 2 coins = 20
Number of ₹ 5 coins = 10
∴ Total number of coins
= 100 + 50 + 20 + 10 = 180
Number of total outcomes for a coin to fall down = 180
Number of outcomes favourable to 50p coins to fall down = 100
∴ Probability of a 50p coin to fall down No. of favourable outcomes
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{100}{180}\) = \(\frac{5}{9}\)

ii) Let P(E) be the probability for a ₹ 5 coin to fall down.
= \(\frac{1}{2}\) (P(\(\overline{\mathrm{E}}\))) = \(\frac{1}{2}\) (P(\(\overline{\mathrm{E}}\)))
No. of outcomes favourable to ₹ 5 coin = 10
∴ Probability for a ₹ 5 coin to fall down
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{10}{180}\) = \(\frac{1}{18}\)
Then P(\(\overline{\mathrm{E}}\)) is the probability of a coin which fall down is not a ₹ 5 coin.
Again P(E) + P(\(\overline{\mathrm{E}}\)) = 1
∴ P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{1}{18}\)
= \(\frac{17}{18}\)

Question 4.
Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (See figure). What is the probability that the fish taken out is a male fish ? (AS₄)

Solution:
Number of male fish in the acquarium = 5
Number of female fish in the acquarium = 8
Total number of fish in the acquarium = 5 + 8 = 13
∴ Number of all possible outcomes = 13
Let E be the event that the fish taken out is a male fish.
Number of outcomes favourable to E = 5
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{5}{13}\)

Question 5.
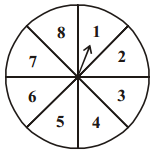
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See figure) and these are equally likely outcomes. What is the probability that it will point at

i) 8?
ii) an odd number ?
iii) a number greater than 2 ?
iv) a number less than 9 ?
Solution:
i) The figure shows the numbers from 1 to 8.
Let E be the event that the arrow comes to rest pointing at 8.
Number of outcomes favourable to E = 1
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{1}{8}\)

ii) The odd numbers shown in the figure are 1, 3, 5 and 7 = 4.
Let E be the event that the arrow will point an odd number.
Number of outcomes favourable to E = 4
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{4}{8}\) = \(\frac{1}{2}\)

iii) The numbers which are greater than 2 as per the figure given are 3, 4, 5, 6, 7 and 8 = 6
Let E be the event that the arrow will point a number greater than 2.
Number of outcomes favourable to E = 6
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{6}{8}\) = \(\frac{3}{4}\)

iv) The numbers less than 9 are 1, 2, 3. 4, 5, 6, 7,8
Let E be the event that the arrow will point a number less than 9.
Number of outcomes favourable to E = 8
Number of all possible outcomes = 8
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{8}{8}\) = 1

Question 6.
One card is selected from a well-shuffled deck of 52 cards. Find the probability of getting
i) a king of red colour
ii) a face card
iii) a red face card
iv) the jack of hearts
v) a spade
vi) the queen of diamonds.
Solution:
Total number of cards = 52
∴ Number of all possible outcomes in selecting a card at random = 52
i) Number of out comes favourable to the kings of red colour = 2(♥k, ♥k)
∴ Probability of getting the king of red colour
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{2}{52}\) = \(\frac{1}{26}\)

ii) Number of face cards in a deck of cards = 4 × 3 = 12(K, Q, J)
No. of outcomes favourable to select face card = 12
∴ Probability of getting a face card
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{12}{52}\) = \(\frac{3}{13}\)

iii) Number of red face cards = 2 × 3 = 6
∴ No. of outcomes favourable to select a red face card = 6
∴ Probability of getting a red face card
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{6}{52}\) = \(\frac{3}{26}\)

iv) No. of outcomes favourable to the jack of hearts = 1
∴ Probability of getting the jack of hearts.
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{1}{52}\)

v) No. of spade cards = 13
∴ No. of outcomes favourable to ‘a spade card’ = 13
∴ Probability of getting a spade card
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{13}{52}\) = \(\frac{1}{4}\)

vi) No. of outcomes favourable to the queen of diamonds = 1
∴ Probability of getting the queen of diamonds
= \(\frac{\text { No. of favourable outcomes }}{\text { No. of total outcomes }}\)
= \(\frac{1}{52}\)

Question 7.
Five cards-the ten, jack, queen, king and ace of diamonds, are well shuffled with their face downwards. One card is selected at random.
i) What is the probability that the card is the queen ?
ii) If the queen is selected and put aside (without replacement), what is the probability that the second card selected is
(a) an ace ? (b) a queen ?
Solution:
Total number of cards = 5
Well – Shuffled with their face downwards.
i) Let E be the event that the card is the queen. Therefore, the number of outcomes favourable to E = 1
So, P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{1}{5}\)

ii) If the queen is selected & put a side then the number of remaining cards is 4 (i.e.,) (5 – 1 = 4)
∴ No. of all possible outcomes = 4

a) Let E be the event that the second card picked up is an ace.
Then, the number of outcomes favourable toE = 1
So. P(E)
= \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{1}{4}\)

b) Let E be the event that the second card selected is a queen.
Then, the number of outcomes favourable to E is 0 (∵ there is no queen)
So, P(E)
= \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{0}{4}\) = 0

Question 8.
12 defective pens are accidentally mixed 10. with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Number of defective pens = 12
Number of good pens = 132
∴ Total number of pens = Number of defective pens + number of good pens
= 12 + 132 = 144
Let E be the event that the pen taken out is a good one,
Then, the number of outcomes favourable to
E = 132
So, P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{132}{144}\) = \(\frac{11}{12}\)

Question 9.
A lot of 20 bulbs contain 4 defective ones. One bulb is selected at random from the lot. What is the probability that this bulb is defective ? Suppose the bulb selected in previous case is not defective and is not replaced. Now one bulb is selected at random from the rest. What is the probability that this bulb is not defective ? (AS₁, AS₄)
Solution:
Total number of bulbs = 20
∴ No. of all possible outcomes = 20
i) Let E be the event that the bulbs drawn at random from the lot is defective.
Then, the number of outcomes favourable to E = 4
∴ P(E) = \(\frac{\text { Number of outcomes favourable to E}}{\text { Number of all possible outcomes }}\)
= \(\frac{4}{20}\) = \(\frac{1}{5}\)

ii) As one bulb is selected at random from the rest,
Total number of bulbs = 20 – 1 = 19
Number of defective bulbs = 4
Let E be the event that the bulb selected is not defective.
Then, the number of outcomes favourable to E is 15 since, now there are 19 – 4 = 15 bulbs which are not defective.
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{15}{19}\)

Question 10.
A box contains 90 discs which are numbered from 1 to 90. If one disc is selected at random from the box, find the probability that it bears (i) a two-digit number (ii) a perfect square number (iii) a number divisible by 5. (AS₁)
Solution:
Number of discs in the box = 90
∴ Number of all possible outcomes = 90
i) Let E be the event that the disc bears a two-digit number.
One digit numbers are 1, 2, 3, 4, 5, 6, 7, 8 and 9. These are 9 in numbers.
Then, the number of outcomes favourable to E = 90 – 9 = 81
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{81}{90}\) = \(\frac{9}{10}\)

ii) Let E be the event that the disc bears a perfect square number.
The perfect square numbers from 1 to 90 are 1, 4, 9, 16, 25, 36, 49, 64, 81. These are 9.
Then, the number of outcomes favourable to E = 9
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{9}{90}\) = \(\frac{1}{10}\)

iii) Let E be the event that the disc bears a number divisible by 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90. These are 18.
Then, the number of outcomes favourable to E = 18
∴ P(E) = \(\frac{\text { No. of outcomes favourable to E}}{\text { No. of all possible outcomes }}\)
= \(\frac{18}{90}\) = \(\frac{1}{5}\)

Question 11.
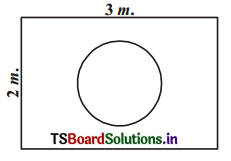
Suppose you drop a die at random on the rectangular region shown in figure. What is the probability that it will land inside the circle with diameter 1m ? (AS₄)

Solution:
Length of the rectangular region = 3 m
Breadth of the rectangular region = 2m
Area of the rectangular region =
Length × Breadth = 3 × 2 = 6m²
Diameter of the circle = 1 m
∴ Radius of the circle = \(\frac{1}{2}\) m
∴ Area of the circle = πr²
= \(\frac{22}{7}\) \(\frac{1}{2}\) \(\frac{1}{2}\) = \(\frac{11}{14}\) m²
∴ Probability that the dice will land inside the circle
= \(\frac{\frac{11}{14}}{6}\)
= \(\frac{11}{14}\) \(\frac{1}{6}\) = \(\frac{11}{84}\)

Question 12.
A lot consists of 144 ball pens of which 20 are defective and the others are good. The shopkeeper draws one pen at random and gives it to Sudha. What is the probability that
(i) She will buy it ?
(ii) She will not buy it ? (AS₄)
Solution:
Total number of ball pens = 144
i) ∴ Number of all possible outcomes = 144
Number of defective ball pens = 20
∴ Number of good ball pens
= 144 – 20 = 124
∴ Probability that Sudha will buy it
= \(\frac{124}{144}\) = \(\frac{31}{36}\)

ii) Probability that Sudha will not buy it = 1 – (Probability that Sudha will buy it)
= 1 – \(\frac{31}{36}\) = \(\frac{5}{36}\)

Question 13.
Two dice are rolled simultaneously and counts are added (i) complete the table given below :

i) A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of
them has a probability \(\frac{1}{11}\). Do you agree with this argument ? Justify your answer. (AS₃)
Solution:
When two dice are rolled simultaneously there are 36 possible out comes. So n(s) = 36.
i) Let E₃ denotes that event that the sum on two dice is 3 the outcomes favourable to the event E₃ = (1, 2), (2, 1)
No. of favourable out comes n(E₃) = 2
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_3\right)}{\mathrm{n}(\mathrm{S})}=\frac{2}{36}=\frac{1}{18}\)

ii) Let E₄ denotes the event that the sum on two dice is 4 the outcomes favourable to the event E₄ = (1,3), (2, 2), (3, 1).
No. of favourable outcomes n(E₄) = 3
probability = \(\frac{\mathrm{n}\left(\mathrm{E}_4\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{36}\) = \(\frac{1}{12}\)

iii) Let E₅ denotes the event that the sum on two dice is 5 the outcomes favourable to the event E₅ = (1, 4), (2, 3), (3, 2), (4, 1)
No. of favourable outcomes n(E₅) = 4
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_5\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{36}\) = \(\frac{1}{9}\)

iv) Let E₆ denotes the event that the sum on two dice is 6 the outcomes favourable to the event E6 = (1, 5), (2, 4), (3, 3), (4, 2), (5, 1)
No. of favourable outcomes n(E₆) = 5
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_6\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{5}{36}\)

v) Let E₇ denotes the event that the sum on two dice is 7 the outcomes favourable to the event E₇ = (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
No. of favourable outcomes n(E₇) = 6
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_7\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{6}{36}\) = \(\frac{1}{6}\)

vi) Let E₈ denotes the event that the sum on two dice is 8
probability = \(\frac{\mathrm{n}\left(\mathrm{E}_8\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{5}{36}\)

vii) Let E₉ denotes the event that the sum on two dice is 9 the outcomes favourable to the event E₉ = (3, 6), (4, 5), (5, 4), (6, 3), (7,2), (8,1)
No. of favourable outcomes n (E₉) = 8
probability = \(\frac{\mathrm{n}\left(\mathrm{E}_9\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{36}\) = \(\frac{1}{9}\)

viii) Let E₁₀ denotes the event that the sum on two dice is 10 the outcomes favourable to the event E₁₀ = (1, 9), (2, 8), (3, 7), (4, 6), (5, 5), (6. 4), (7, 3), (8, 2), (9, 1).
No. of favourable outcomes n(E₁₀) = 3
Probability = \(\frac{\mathrm{n}\left(\mathrm{E}_10\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{36}\) = \(\frac{1}{12}\)

ix) Let E₁₁ denotes the event that the sum on two dice is 11 the outcomes favourable to the event E₁₁ = (5, 6), (6, 5)

Question 14.
A game consists of tossing a one rupee coin 3 times and recording its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution:
Let H : Head, T : Tail
When we toss a one rupee coin 3 times,
S = {H, T} × (H, T} × {H, T} where ‘S’ denotes the cartesian product.
So, n(S) = 2 × 2 × 2 = 8
Let E be the event that Hanif will win the game
i.e., either three heads or three tails will come.
So, E = {(H, H, H), (T, T, T)}
n(E) = 2
So, probability that Hanif will win the game,
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{8}\) = \(\frac{1}{4}\)
So. probability that Hanif will lose the game,
P(\(\overline{\mathrm{E}}\)) = 1 – P(E) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

Question 15.
A dice is thrown twice. What is the probability that (i) 5 will not come up either time ? (ii) 5 will come up at least once ? [Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment.]
Solution:
When a dice is thrown twice.
S = {1, 2, 3, 4, 5, 6} × (1, 2, 3, 4, 5, 6}
So, n (S) = 6 × 6 = 36
Let E denote the event that 5 will come up at least once.
Then, E = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}.
∴ n(E) = 11
i) Probability that 5 will not come up either time = P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\)
= 1 – \(\frac{11}{36}\)
= \(\frac{25}{36}\)

ii) Probability that 5 will come up at least once,
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{11}{36}\)

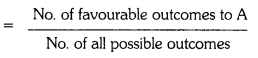
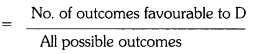
Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 12 Applications of Trigonometry Ex 12.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Exercise 12.1

Question 1.
A tower stands vertically on the ground. From a point which is 15 meter away from the foot of the tower, the angle of elevation of the top of the tower is 45°. What is the height of the tower ? (AS₄)
Solution:

In ∆ ABC, ∠B = 90°
AB represents the height of the tower and ∠ACB = 45°
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
1 = \(\frac{\mathrm{AB}}{15}\)
⇒ AB = 15 meters.
Therefore, the height of the tower = 15 meters.

Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground by making 30° angle with the ground. The distance between the foot of the tree and the top of the tree on the ground is 6 m. Find the height of the tree before falling. (AS₄) (A.P. Mar. ’16)
Solution:
Let AB represents the height of the tree

AC represents the broken part.
AC = CD (∵ the broken part touches the ground)
Let BC = x meters, the height of the tree after it is broken
In ∆CBD, ∠B = 90° and ∠BDC = 30°
tan 30° = \(\frac{\mathrm{BC}}{\mathrm{BD}}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{x}{6}\)
⇒ \({\sqrt{3}}\) x = 6
⇒ x = \(\frac{6}{\sqrt{3}}\) (∵ \(\frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{6 \sqrt{3}}{3}=2 \sqrt{3}\))
⇒ x = \(2 \sqrt{3}\)
sin 30° = \(\frac{\mathrm{BC}}{\mathrm{BD}}\)
\(\frac{1}{2}\) = \(\frac{2 \sqrt{3}}{C D}\)
⇒ CD = 2 × 2\({\sqrt{3}}\) = 4\({\sqrt{3}}\)
∴ The height of the tree before falling down
= AB
= AC + CB
= 4\({\sqrt{3}}\) + 2\({\sqrt{3}}\) (∵ AC = CD = 4\({\sqrt{3}}\))
= 6\({\sqrt{3}}\) m

Question 3.
A contractor wants to set up a slide for the children to play in the park. He wants to set it up at the height of 2m and by making an angle of 30° with the ground. What should be the length of the slide ? (AS₄)
Solution:
In the triangle ABC, ∠B = 90°
Let AC represents the length of the side
AB = 2 m
sin 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{1}{2}\) = \(\frac{2}{\mathrm{AC}}\)
⇒ Ac = 4

Hence, length of the side = 4m

Question 4.
Length of the shadow of a 15 meter high pole is 5\({\sqrt{3}}\) m at 7 o’ clock in the morning. Then, what is the angle of elevation of the sun rays with the ground at the time ? (A.P. Mar.’15) (AS₄)
Solution:
In ∆ABC, ∠B = 90°
AB represents the height of the pole.
AB = 15m
Let BC represents its shadow at 7 o’ clock in the morning.
BC = 5\({\sqrt{3}}\) m
Let the angle of elevation of the sun rays with the ground be ‘θ’.
Now, tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
= \(\frac{15}{5 \sqrt{3}}\)
= \(\frac{3}{\sqrt{3}}\)

We know that tan 60° = \({\sqrt{3}}\)
∴ θ = 60°
Hence, the angle of elevation of the sun rays with the ground at the time = 60°.

Question 5.
You want to erect a pole of height 10 m with the support of three ropes. Each rope has to make an angle 30° with the pole. What should be the length of the rope ? (AS₄)
Solution:
In the figure,

Let AB be the height of the pole = 10 m
Let AC be the length of the rope
Angle of elevation is 30°
From right angled ∆ ABC
cos 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{10}{\mathrm{AC}}\)
⇒ AC = \(\frac{2 \times 10}{\sqrt{3}}\)
⇒ AC = \(\frac{20}{1.732}\) (∵ \({\sqrt{3}}\) = 1.732)
⇒ AC = 11.547 cm
Hence, the length of the rope is 11.547 m

Question 6.
Suppose you are shooting an arrow from the top of a building at a height of 6 m to a target on the ground at an angle of depression of 60°. What is the distance be-tween you and the object ? (AS₄) (A.P. Mar.15)
Solution:

In figure,
Let BC be the height of a building = 6 m
‘C’ be the point of the observation and A’ be the target on the ground.
Angle of depression is ∠CAB = 60°
Let AC be the distance between me and the object
From the right angled ∆ABC,
sin 60° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{6}{\mathrm{AB}}\)
⇒ AB = \(\frac{6 \times 2}{\sqrt{3}}=\frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{12 \sqrt{3}}{3}\) = 4\({\sqrt{3}}\) m
Hence, the distance between me and the object is 4\({\sqrt{3}}\) m.

Question 7.
An electrician wants to repair an electric connection on a pole of height 9 m. He needs to reach 1.8 m below the top of the pole to do repair work. What should be the length of the ladder which he should use, when he climbs it at an angle of 60° with the ground ? What will be the distance between foot of the ladder and foot of the pole ? (AS₄)
Solution:
In the figure,
Let AB be the height of a pole is 9 m
AC be the actual required height of the pole is 7.2 m
Angle of elevation is ∠CDA = 60°.
CD be the length of the ladder.
AD be the distance between foot of the ladder and foot of the pole.
From the right angled ∆ADC,
tan 60° = \(\frac{\mathrm{AC}}{\mathrm{AD}}\)
⇒ \({\sqrt{3}}\) = \(\frac{7.2}{\mathrm{AD}}\)

⇒ AD = \(\frac{7.2}{\sqrt{3}}=\frac{7.2}{1.732}\)
⇒ AD = 4.15692 m
Again, from the ∆ADC,
sin 60° = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{7.2}{\mathrm{CD}}\)
⇒ CD = \(\frac{7.2 \times 2}{\sqrt{3}}\)
⇒ CD = \(\frac{7.2 \times 2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
CD = \(\frac{7.2 \times 2 \times \sqrt{3}}{3}\)
CD = 2.4 × 2 × \({\sqrt{3}}\)
CD = 4.8 × \({\sqrt{3}}\)
CD = 8.3138 m
Hence, the distance between foot of the ladder and foot of the pole is 4.15692 m and the length of the ladder is 8.3138 m.

Question 8.
A boat has to cross a river. It crosses the river by making an angle of 60° with the bank of the river due to the stream of the river and travels a distance of 600 m to reach the another side of the river. What is the width of the river ? (AS₄)
Solution:

In the figure,
Let A’ be the required point to reach the bank of the river.
Let ‘C’ be the present position of the boat (or) observation point.
AC be the distance travelled by the boat is 600 m
Angle of elevation is ∠ACB = 60°
AB be the actual width of the river
From the right angled ∆ABC,
sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{\mathrm{AB}}{600}\)
⇒ AB = 600 × \(\frac{\sqrt{3}}{2}\)
⇒ AB = 300\({\sqrt{3}}\) m
⇒ Hence, the width of the river is 300\({\sqrt{3}}\) m

Question 9.
An observer of height 1.8m is 13.2m away from a palm tree. The angle of elevation of the top of the tree from his eyes is 45°. What is the height of palm tree ? (AS₄)
Solution:
AB represents the height of the observer.
CD denotes the height of the palm tree.
AB = 1.8 m; BC = 13.2 m AE = 13.2 m (∵ ABCE is a rectangle so, opposite sides of BC and AE are equal)
(AB and EC are also opposite sides of the rectangle ABCE)
∴ AB = EC
In ∆AED, ∠E = 90°
tan 45° = \(\frac{\mathrm{DE}}{\mathrm{AE}}\)
1 = \(\frac{\mathrm{DE}}{13.2}\)
⇒ DE = 13.2 m

Therefore, the height of the palm tree CD
= DE + EC
= 13.2 + 1.8
= 15 meters.

Question 10.
In the adjacent figure
In ∆ABC, AC = 6 cm, AB = 5 cm and ∠BAC = 30°. Find the area of the triangle. (AS₄)
Solution:
In ∆ ABC,
AB = 5 cm, AC = 6 cm
∠BAC = 30°
Draw BD ⊥ AC

In ∆ ABD, ∠ADB = 90°
sin 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
\(\frac{1}{2}\) = \(\frac{\mathrm{BD}}{5}\)
⇒ 2 × BD = 5
BD = \(\frac{5}{2}\) = 2.5 cm
Hence, area of the triangle ABC
= \(\frac{1}{2}\) × Base × Altitude
= \(\frac{1}{2}\) × AC × BD
= \(\frac{1}{2}\) × 6 × 2.5
= 3 × 2.5 = 7.5 cm²

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 14 Understanding 3D and 2D Shapes Ex 14.2 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 14 Understanding 3D and 2D Shapes Exercise 14.2

Question 1.
Examine whether the following are polygons if not why ?

Answer:
i) Figure is kept open. So it is not a polygon.
ii) Figure is a closed one made up of 4 line segments. So it is a polygon.
iii) Figure is a circle. It is curved. It is not made up of line segments. So it is not a polygon.

Question 2.
Count the number of sides of the polygons given below and name them.

Answer:
Figure (i) has 5 sides. It is called a pentagon.
Figure (ii) has 8 sides. It is called an octagon.
Figure (iii) has 6 sides. It is called a hexagon.
Figure (iv) has 3 sides. It is called a triangle.

Question 3.
Identify the regular polygons among the figures given below :

Answer:
Figure (i) is a square. Its sides and angles are all equal. So it is a regular polygon.
Figure (iv) is a regular hexagon. It has equal sides and its angles are equal.
Figure (vi) is an equilateral triangle. Its sides are equal. Its angles are equal.

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 14 Understanding 3D and 2D Shapes Ex 14.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 14 Understanding 3D and 2D Shapes Exercise 14.1

Question 1.
A triangular pyramid has a triangle at its base. It is also known as a tetrahedron. Find the number of

i) No. of Faces :
ii) No. of Edges :
iii) No. of Vertices :
Answer:
A triangular pyramid (tetrahedron) has
i) No. of Faces : 4
ii) No. of Edges : 6
iii) No. of Vertices : 4

Question 2.
A square pyramid has a square at its base. Find the number of

i) No. of Faces :
ii) No. of Edges :
iii) No. of Vertices :
Answer:
A square pyramid has
i) No. of Faces 5
ii) No. of Edges : 8
iii) No. of Vertices : 5

Question 3.
Fill the table.

Answer:

Question 4.
A triapgular prism is often in the shape of a kaleidoscope. It has triangular faces.

i) No. of triangular Faces :
ii) No. of rectangular Faces :
iii) No. of Edges :
iv) No. of Vertices :
Answer:
i) No. of triangular Faces : 2
ii) No. of rectangular Faces : 3
iii) No. of Edges : 9
iv) No. of Vertices : 6

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 12 Symmetry InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 12 Symmetry InText Questions

Do This

Question 1.
Match each letter with its mirror image. The dotted line with every letter shows in the mirror.

Can you think of more such alphabets and words which will remain the same in their mirror image ?
Answer:

Yes. They are 0, X,H, I, which are same as mirror images.

Try This

Question 1.
Place a mirror along the dotted lines and draw their mirror images.

Do you observe any change ? Are angles in the images equal to the angles in the given figures ?
Answer:
We can observe the angles formed in the original figures and its mirror images are same.

Do This

Question 1.
In the figures given below find which are symmetric figures.

Can we find line of symmetry for every figure ?
Answer:
(i), (ii) figures are symmetric figures.
(iii) & (iv) are not symmetric figures.

Try This

Write the letters of English alphabet A to Z and find out which have
i) Vertical lines of symmetry
ii) Horizontal lines of symmetry
iii) No lines of symmetry
Answer:
i) Vertical lines of symmetry :

ii) Horizontal lines of symmetric

iii) No lines of symmetric

Try These

Question 1.
Draw any five objects which have a line of symmetry.
Answer:
The following figure having the line of symmetry.

Question 2.
Draw any five objects which are not symmetric.
Answer:

Think, Discuss And Write

Question 1.
If the paper is folded four times how many lines of symmetry can be formed with paper cutting ?
Answer:
If a paper is folded 4 times then 8 symmetric lines are formed.

Question 2.
To cut four similar figures side by side by folding the paper, how many folds are needed ?
Answer:
Two paper foldings are to be needed to form 4 similar figures.

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 13 Practical Geometry InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 13 Practical Geometry InText Questions

Try These

Question 1.
Construct two circles with same radii in such a way that

i) the circles intersect at two points.
ii) touch each other at one point only.
Answer:
i) Circles intersect at two points :
ii) Touch each other at one point only :

Think, Discuss And Write

Question 1.
How would you check whether It Is perpendicular or not ? Note that it passes through P as required.
Answer:

The perpendicularity can be measured by protractor.
So, the perpendicular line always passes through P’.

Do This

Question 1.
Measure the lengths of \(\overline{\mathrm{A P}}\) and \(\overline{\mathrm{B P}}\) in both the constructions. Are they equal?
Answer:

\(\overline{\mathrm{A P}}\) = 1.7 cm
\(\overline{\mathrm{B P}}\) = 1.7 cm
yes. They are equal

Think, Discuss And Write

Question 1.
In the construction of perpendicular bisector in step 2. What would happen if we take the length of radius to be smaller than half the length of \(\overline{\mathrm{A B}}\)?
Answer:
Explanation:
1) Construct a line segment \(\overline{\mathrm{A B}}\) with a suitable radius.
2) To construct a perpendicular line to the given line, take the radius more than half of a given line segment \(\overline{\mathrm{A B}}\).
3) With the centres A, B draw two arcs as mentioned above.
4) The two arcs are intersected at a point. Name it P, Q.
5) Join these two points by a straight line. Name it as l. ∴ l ⊥ \(\overline{\mathrm{A B}}\).

If we does not taken the radius half of the given line segment, then the perpendicular bisector doesn’t formed. Since the arcs doesn’t interest each other.

Do This

Question 1.
Construct angles of 180°, 240°, 300°.
Answer:

Question 2.
Construct an angle of 45° by using compasses.
Answer:
Steps of construction:

1) Construct \(\overline{\mathrm{OA}}\) line segment with suitable radius.
2) Draw an arc on \(\overline{\mathrm{OA}}\) from the centre ‘O’, its cuts \(\overline{\mathrm{OA}}\) at ‘C’.
3) Draw two arcs with the centres O, C with equal radii the two arcs meet at ‘D’.
4) Draw another two arcs with the centres D, C they meet at point E. Join O, E.
5) With the centres D, G draw another two arcs, they meet at point F. Join O, F.
∴ ∠AOB = 45°
So we get the required angle.

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 14 Understanding 3D and 2D Shapes InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 14 Understanding 3D and 2D Shapes InText Questions

Try These

Question 1.
(i) What is the shape of the face of a cube ?
(ii) What is the shape of the face of a cuboid ?
Answer:
i) Square shape.
ii) Rectangular shape.

Question 2.
Ramesh has collected some boxes in his room. Pictures of these are given here. How many are cubes and how many are cuboids?

Answer:
Number of cubes = 3
Number of cuboids = 4

Question 3.
Ajith has made a cuboid by arranging cubes of 2 cms each. What is the length, breadth and height of the cuboid so formed ?

Answer:
Length of the first cuboid = 2 + 2 = 4 cm
breadth = 2 cm height = 2cm
Length of the second cuboid =2 + 2 + 2 = 6 cm
breadth = 2 cm height = 2 cm

Think, Discuss And Write

Question 1.
What is the difference between a cylinder and a cone with respect to the number of faces, vertices and edges? Discuss with your friends.
Answer:

Do This

Question 1.
Fill the table accordingly :

The cylinder, the cone and the sphere have no straight edges. What is the base of a cone ? Is it a circle ? The cylinder has two bases. What shape is the base ? Of course, a sphere has no face ! Think about it.
Answer:

The base of a cone is circle.
The shape of the base of a cylinder is circle.

Do This

Question 1.
Draw ten polygons with different shapes in your notebook.
Answer:

Question 2.
Use match-sticks or broom-sticks and form closed figures using :
i) Six sticks
ii) Five sticks
iii) Four sticks
iv) Three sticks
v) Two sticks
In which case was it not possible to form a polygon ? Why ?
Answer:

Observation : In the fifth case it is not possible to form a polygon.
Conclusion : We find that we could not form a polygon using two sticks.
Reason : A polygon must have at least three sides.

Try This

Question 1.
Find out the differences :

Measure the lengths of the sides and angles of (i) and (ii). What did you find ?
Answer:
i) Length of sides
AB = 3.2 cm
BC = 1. 2 cm
CD = 2 cm
ED – 2 6 cm
AE = 1. 6 cm
angles ∠A = 125°
∠B = 70°
∠C = 160°
∠D = 105°
∠E = 80°
∴ sides and angles are not equal.
The given figure is an irregular polygon (pentagon).
∴ Sides, angles are not equal.

ii) In the given figure AB = BC = CD = DE
= AE = 1.9 cm
Each angle = 108°
angles ∠A = ∠B = ∠C = ∠D = ∠E = 108°
∴ Sides, angles are equal.
The given figure is a regular pentagon.

Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 12 Symmetry Ex 12.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 12 Symmetry Exercise 12.1

Question 1.
Check whether the given figures are symmetric or not ? Draw the line of symmetry as well.

Answer:

The dotted lines represents a line of symmetry.

Question 2.
Draw a line of symmetry for each of the figures, wherever possible.

Answer:

Question 3.
In the figure, l is the line of symmetry.
Complete the diagram to make it symmetric.

Answer:

Question 4.
Complete the figures such that the dotted line is the line of symmetry.

Answer:

Students can practice Telangana 6th Class Maths Textbook Solutions Chapter 7 Fractions and Decimals InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 7 Fractions and Decimals InText Questions

Try These

Question 1.
How will you represent the following pictorially ?
(i) \(\frac{3}{4}\)
Answer:
\(\frac{3}{4}\)

(ii) \(\frac{2}{8}\)
Answer:
\(\frac{2}{8}\)

(iii) \(\frac{1}{3}\)
Answer:
\(\frac{1}{3}\)

(iv) \(\frac{5}{8}\)
Answer:
\(\frac{5}{8}\)

Question 2.
Write the fraction representing the shaded portion.

Answer:
(i) \(\frac{1}{3}\)
(ii) \(\frac{1}{4}\)
(iii) \(\frac{2}{6}\)

Do This

Question 1.
Write 5 proper fractions and draw them pictorially.
Answer:

Question 2.
Rani says that shaded portion in the given figure represents \(\frac{1}{4}\). Do you agree with her? Give reason to support your answer.

Answer:
Yes. The reason is out of fourportions only one portion is shaded.

Do This

Question 1.
Write improper fractions represented by the following pictures.

Answer:

Answer:

Answer:

Question 2.
Represent the following fractions pictorially :
\(\frac{7}{4}, \frac{5}{3}, \frac{7}{6}\)
Answer:

Do This

Question 1.
Write the following as mixed fractions
\(\frac{7}{2}, \frac{8}{5}, \frac{9}{4}, \frac{13}{5}, \frac{17}{3}\)
Answer:

Try These

Question 1.
Write the numerator and denominators of the following fractional numbers:
\(\frac{1}{3}, \frac{2}{5}, \frac{7}{2}, \frac{19}{3}, \frac{7}{29}, \frac{11}{13}, \frac{1}{7}, \frac{8}{3}\)
Answer:

Question 2.
Sort the following fractions into the category of proper and improper fractions. Also write improper fraction as mixed fractions:
\(\frac{1}{3}, \frac{2}{5}, \frac{7}{2}, \frac{19}{3}, \frac{7}{29}, \frac{11}{13}, \frac{1}{7}, \frac{8}{3}\)
Answer:
Improper fractions:

Proper fractions:
\(\frac{1}{3}, \frac{2}{7}, \frac{3}{5}, \frac{1}{9}\)

Do This

Question 1.
Show that following on number lines.
(i) \(\frac{7}{6}\)
Answer:

(ii) \(\frac{5}{2}\)
Answer:

(iii) \(\frac{7}{5}\)
Answer:

(iv) \(\frac{9}{6}\)
Answer:

Question 2.
Consider the following numbers. Which of these would lie on the number line
i) before 1
Answer:
Fractions before 1 are \(\frac{1}{3}, \frac{7}{9}, \frac{6}{11}\)

ii) between 1 and 2
Answer:
Fractions between 1 and 2 are \(\frac{7}{5}, \frac{9}{5}\)

Try These

Question 1.
Write 5 fractional numbers that are in the standard form.
Answer:
Standard form of 5 fractional numbers
= \(\frac{1}{2}, \frac{2}{3}, \frac{4}{5}, \frac{5}{6}, \frac{8}{9}\)

Question 2.
Write 5 fractional numbers that are not in standard form.
Answer:
\(\frac{10}{6}, \frac{144}{100}, \frac{51}{17}, \frac{48}{16}, \frac{36}{44}\)

Question 3.
Convert the following fractions into their standard form.
i) \(\frac{7}{28}\)
ii) \(\frac{15}{90}\)
iii) \(\frac{11}{33}\)
iv) \(\frac{39}{13}\)
Answer:

Think, Discuss And Write

Question 1.
Rafi says “there can be no equivalent fractions that are also like fractions”. Do you agree with him ? Explain your answer and justify.
Answer:
Equivalent fractions = \(\frac{1}{2}, \frac{2}{4}, \frac{8}{16}, \frac{32}{64}\)
Like fraction = \(\frac{3}{2}, \frac{5}{2}, \frac{7}{2}, \frac{8}{2}, \frac{9}{2}\)
Equivalent fractions are like fractions also. So, I agree with him.

Do This

Question 1.
Identify the biggest and the smallest in these group of fractional numbers.
(i) \(\frac{1}{7}, \frac{3}{7}, \frac{2}{7}, \frac{5}{7}\)
Answer:
Biggest fraction = \(\frac{5}{7}\)
Smallest fraction = \(\frac{1}{7}\)

(ii) \(\frac{1}{9}, \frac{13}{9}, \frac{11}{9}, \frac{5}{9}\)
Answer:
Biggest fraction = \(\frac{13}{9}\)
Smallest fraction = \(\frac{1}{9}\)

(iii) \(\frac{1}{3}, \frac{5}{3}, \frac{17}{3}, \frac{9}{3}\)
Answer:
Biggest fraction = \(\frac{17}{3}\)
Smallest fraction = \(\frac{1}{3}\)

Question 2.
Which of these is the smaller fraction ?
(i) \(\frac{2}{5}, \frac{3}{7}\)
Answer:

(ii) \(\frac{7}{8}, \frac{5}{4}\)
Answer:

(iii) \(\frac{3}{11}, \frac{1}{2}\)
Answer:

(iv) \(\frac{5}{6}, \frac{2}{3}\)
Answer:

Question 3.
Write the following fractional number in ascending order.
(i) \(\frac{1}{7}, \frac{13}{7}, \frac{11}{7}, \frac{5}{7}, \frac{15}{7}\)
Answer:
Ascending order:
\(\frac{1}{7}<\frac{5}{7}<\frac{11}{7}<\frac{13}{7}<\frac{15}{7}\)

(ii) \(\frac{2}{3}, \frac{5}{6}, \frac{3}{9}, \frac{24}{18}\)
Answer:

(iii) \(\frac{2}{3}, \frac{1}{2}, \frac{5}{6}, \frac{7}{12}\)
Answer:

(iv) \(\frac{1}{5}, \frac{1}{2}, \frac{1}{8}, \frac{1}{3}, \frac{1}{12}\)
Answer:

Do this

Question 1.
Write the following in descending order.
i) \(\frac{1}{9}, \frac{13}{9}, \frac{11}{9}, \frac{15}{9}, \frac{3}{9}\)
Answer:

ii) \(\frac{1}{6}, \frac{2}{3}, \frac{3}{9}, \frac{5}{6}\)
Answer:

iii) \(\frac{1}{5}, \frac{9}{5}, \frac{3}{5}, \frac{6}{5}\)
Answer:
Descending Order = \(\frac{9}{5}>\frac{6}{5}>\frac{3}{5}>\frac{1}{5}\)

iv) \(\frac{1}{4}, \frac{1}{2}, \frac{1}{8}, \frac{3}{4}\)
Answer:
Descending Order = \(\frac{3}{4}>\frac{1}{2}>\frac{1}{4}>\frac{1}{8}\)

Question 8.
Simplify:
(i) \(\frac{1}{18}+\frac{1}{18}\)
Answer:
\(\frac{1}{18}+\frac{1}{18}=\frac{1+1}{18}=\frac{2}{18}=\frac{1}{9}\)

(ii) \(\frac{8}{15}+\frac{3}{15}\)
Answer:
\(\frac{8}{15}+\frac{3}{15}=\frac{8+3}{15}=\frac{11}{15}\)

(iii) \(\frac{7}{7}-\frac{5}{7}\)
Answer:
\(\frac{7}{7}-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7}\)

(iv) \(\frac{1}{22}+\frac{21}{22}\)
Answer:
\(\frac{1}{22}+\frac{21}{22}=\frac{1+21}{22}=\frac{22}{22}\) = 1

(v) \(\frac{12}{15}-\frac{7}{15}\)
Answer:
\(\frac{12}{15}-\frac{7}{15}=\frac{12-7}{15}=\frac{5}{15}=\frac{1}{3}\)

(vi) \(\frac{5}{8}+\frac{3}{8}\)
Answer:
\(\frac{5}{8}+\frac{3}{8}=\frac{5+3}{8}=\frac{8}{8}\) = 1

(vii) 1 – \(\frac{2}{3}\left(1=\frac{3}{3}\right)\)
Answer:
1 – \(\frac{5}{8}+\frac{3}{8}=\frac{5+3}{8}=\frac{8}{8}\) [∵ 1 = \(\frac{3}{3}\)]

(viii) \(\frac{1}{4}+\frac{0}{4}\)
Answer:
\(\frac{1}{4}+\frac{0}{4}=\frac{1+0}{4}=\frac{1}{4}\)

(ix) 3 – \(\frac{12}{5}\)
Answer:
3 – \(\frac{12}{5}=\frac{3 \times 5}{1 \times 5}-\frac{12}{5}=\frac{15}{5}-\frac{12}{5}=\frac{15-12}{5}=\frac{3}{5}\)

Question 9.
Fill in the missing fractions.
i) \(\frac{7}{10}\) – ___ = \(\frac{3}{10}\)
Answer:

ii) __ – \(\frac{3}{21}=\frac{5}{21}\)
Answer:

iii) ___ – \(\frac{3}{3}=\frac{3}{6}\)
Answer:

iv) ___ – \(\frac{5}{27}=\frac{12}{27}\)
Answer:

Question 10.
Narendra painted \(\frac{2}{3}\) area of the wall in his room. His brother Ritesh helped and painted \(\frac{1}{3}\) area of the wall. How much did they paint together ?
Answer:
Area of the wall painted by Narendra = \(\frac{2}{3}\)
Area of the wall painted by Ritesh = \(\frac{1}{3}\)
Area of the wall painted by both
Narendra and Ritesh = \(\frac{2}{3}+\frac{1}{3}\)
= \(\frac{2+1}{3}=\frac{3}{3}\) = 1
Narendra and his brother Ritesh painted the complete wall.

Question 11.
Neha was given \(\frac{5}{7}\) of a basket of bananas. What fraction of bananas was left in the basket?
Answer:
The part of a basket of bananas given to Neha = \(\frac{5}{7}\)
The part of bananas left in the basket
= 1 – \(\frac{5}{7}=\frac{1 \times 7}{1 \times 7}-\frac{5}{7}=\frac{7}{7}-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7}\)

Question 12.
A piece of rod \(\frac{7}{8}\) metre long is broken into two pieces. One piece was \(\frac{1}{4}\) metre long. How long is the other piece?
Answer:
Length of a piece of rod = \(\frac{7}{8}\) metre
Length of one broken piece of rod = \(\frac{1}{4}\) metre.
Length of the other piece = \(\frac{7}{8}-\frac{1}{4}\)
= \(\frac{7}{8}-\frac{1 \times 2}{4 \times 2}=\frac{7}{8}-\frac{2}{8}=\frac{7-2}{8}=\frac{5}{8}\)m
∴ \(\frac{5}{8}\)m long is the other piece.

Question 13.
Renu takes 2\(\frac{1}{5}\) minutes to walk 5 around the school ground. Snigdha takes \(\frac{7}{4}\) minutes to do the same. Who takes less time and by what fraction?
Answer:
Time taken by Renu to walk around the school ground = 2\(\frac{1}{5}\) minutes
= \(\frac{11}{5}\) minutes
Time taken by Snigdha to walk around the school ground = \(\frac{7}{4}\) minutes
To find the person who takes less time to do the same, we write the fractions \(\frac{11}{5}\) and \(\frac{7}{4}\) having the same denominators.
\(\frac{11}{5} \times \frac{4}{4}=\frac{44}{20} ; \frac{7}{4} \times \frac{5}{5}=\frac{35}{20}\)
We know that \(\frac{35}{20}<\frac{44}{20}\)
Therefore, Snigdha takes \(\frac{9}{20}\) minutes less time to walk around the school ground.
(∵ \(\frac{44}{20}-\frac{35}{20}=\frac{44-35}{20}=\frac{9}{20}\))

Try These

Question 1.
(i) Write fractions for the following decimal and also find how many tenth parts are there in each :
0.4, 0.2, 0.8, 1.6, 5.4, 555.3, 0.9
Answer:
0.4 = \(\frac{4}{10}\)
0.2 = \(\frac{2}{10}\)
0.8 = \(\frac{8}{10}\)
4 tenth parts 2 tenth parts 8 tenth parts

1.6 = 1\(\frac{6}{10}\) = 1 + \(\frac{6}{10}\) 6 tenth parts
5.4 = 5\(\frac{4}{10}\) = 5 + \(\frac{4}{10}\) 4 tenth parts
555.3 = 553 + \(\frac{3}{10}\) = 3 tenth parts
0.9 = \(\frac{9}{10}\) = 9 tenth parts

(ii) Complete the following table.

Answer:

(iii) Complete the following table.

Answer:

(iv) Measure the length of these line segments and fill it in the table given below.

Answer:

Do This

Question 1.
Fill in the blanks.
(i) 325 paise = _________ rupees _________ paise = ₹ _________
(ii) 570 paise = _________ rupees _________ paise = ₹ _________
(iii) 2050 paise = _________ rupees _________ paise = ₹ _________
Answer:
(i) 325 paise = 3 rupees 25 paise = ₹ 3.25
(ii) 570 paise = 5 rupees 70 paise = ₹ 5.70
(iii) 2050 paise = 20 rupees 50 paise = ₹ 20.50

Do This

Question 1.
Find: i) 0.39 + 0.26
ii) 0.8 + 0.07
iii) 1.45 + 1.90
iv) 3.44 + 1.58
Answer: