Students can practice Telangana SCERT Class 6 Maths Solutions Chapter 13 Practical Geometry InText Questions to get the best methods of solving problems.
TS 6th Class Maths Solutions Chapter 13 Practical Geometry InText Questions
Try These
Question 1.
Construct two circles with same radii in such a way that

i) the circles intersect at two points.
ii) touch each other at one point only.
Answer:
i) Circles intersect at two points :
ii) Touch each other at one point only :
Think, Discuss And Write
Question 1.
How would you check whether It Is perpendicular or not ? Note that it passes through P as required.
Answer:
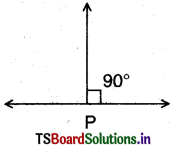
The perpendicularity can be measured by protractor.
So, the perpendicular line always passes through P’.
Do This
Question 1.
Measure the lengths of \(\overline{\mathrm{A P}}\) and \(\overline{\mathrm{B P}}\) in both the constructions. Are they equal?
Answer:
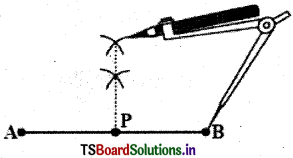
\(\overline{\mathrm{A P}}\) = 1.7 cm
\(\overline{\mathrm{B P}}\) = 1.7 cm
yes. They are equal
![]()
Think, Discuss And Write
Question 1.
In the construction of perpendicular bisector in step 2. What would happen if we take the length of radius to be smaller than half the length of \(\overline{\mathrm{A B}}\)?
Answer:
Explanation:
1) Construct a line segment \(\overline{\mathrm{A B}}\) with a suitable radius.
2) To construct a perpendicular line to the given line, take the radius more than half of a given line segment \(\overline{\mathrm{A B}}\).
3) With the centres A, B draw two arcs as mentioned above.
4) The two arcs are intersected at a point. Name it P, Q.
5) Join these two points by a straight line. Name it as l. ∴ l ⊥ \(\overline{\mathrm{A B}}\).
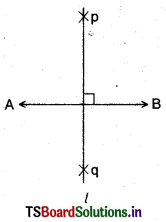
If we does not taken the radius half of the given line segment, then the perpendicular bisector doesn’t formed. Since the arcs doesn’t interest each other.
Do This
Question 1.
Construct angles of 180°, 240°, 300°.
Answer:
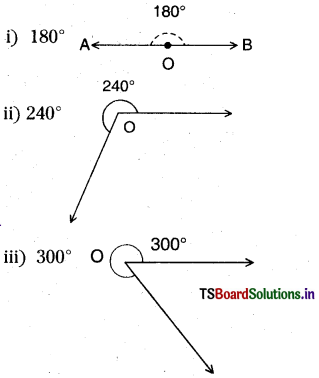
![]()
Question 2.
Construct an angle of 45° by using compasses.
Answer:
Steps of construction:
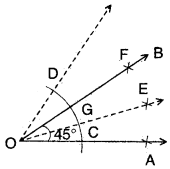
1) Construct \(\overline{\mathrm{OA}}\) line segment with suitable radius.
2) Draw an arc on \(\overline{\mathrm{OA}}\) from the centre ‘O’, its cuts \(\overline{\mathrm{OA}}\) at ‘C’.
3) Draw two arcs with the centres O, C with equal radii the two arcs meet at ‘D’.
4) Draw another two arcs with the centres D, C they meet at point E. Join O, E.
5) With the centres D, G draw another two arcs, they meet at point F. Join O, F.
∴ ∠AOB = 45°
So we get the required angle.