TS Inter 2nd Year Maths 2B Ellipse Important Questions

Students must practice these TS Inter 2nd Year Maths 2B Important Questions Chapter 4 Ellipse to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2B Ellipse Important Questions

Very Short Answer Type Questions

Question 1.
If the length of the latus rectum is equal to half of its minor axis of an ellipse in the standard form, then find the eccentricity of the ellipse.
Solution:
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) + 1(a > b) be the ellipse in its standard form.
Given that the length of the latus rectum = \(\frac{1}{2}\) (minor axis)

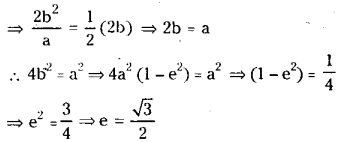
Question 2.
The orbit of the Earth is an ellipse with eccentricity with the \(\frac{1}{60}\) Sun at one of its foci, the major axis being approximately 186 x 10⁶ miles in length. Find the shortest and longest distance of the Earth from the Sun.
Solution:
Let the earths orbit be an ellipse given by
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) + 1(a > b)
Since the major axis is 186 x 10⁶ miles
we have 2a = 186 x 10⁶ ⇒ a = 93 x 10⁶ miles
If e is the eccentricity of ellipse then e = \(\frac{1}{60}\)
The longest and shortest distances of the earth from the sun are respectively a + ae and a – ae.
Here the longest distance of earth from the sun = a +ae \(\left(1+\frac{1}{60}\right)\)
= 9445 x 10⁴ miles and shortest distance of earth from the sun = a – ae
= 93 x 10⁴  \(\left(1-\frac{1}{60}\right)\)
= 9145 x 10⁴  miles

Short Answer Type Questions

Question 1.
Find the eccentricity, coordinates of foci, length of latus rectum and equations of directrices of the following ellipse
9x² + 16y²– 36x + 32y – 92 = 0
Solution:
Given equation of ellipse is
9x² + 16y²– 36x + 32y – 92 = 0
which can be written as

(ii) 3x+ y² – 6x -2y -5 = 0
Solution:
Given equation can be written as
3x² – 6x + y² – 2y = 5
⇒ 3(x²– 2x) + (y²– 2y) = 5
⇒ 3(x² -2x + 1)+(y²-2y+1) = 5 + 4
⇒ 3(x – 1)² + (y – 1)² = 9
⇒ \(\frac{(x-1)^2}{3}+\frac{(y-1)^2}{9}=1\)
which is of the form
\(\frac{(\mathrm{x}-\mathrm{h})^2}{\mathrm{a}^2}+\frac{(\mathrm{y}-\mathrm{k})^2}{\mathrm{~b}^2}=1\)
which a² = 3 and b² = 9 and a < b.
Also (h, k) = (1, 1); eccentrIcity

Question 2.
Find the equation of the ellipse referred to its major and minor axes as the coordinate axes X, Y – respectively with latus rectum of length 4 and distance between foci \(4 \sqrt{2}\).
Solution:
Let the equation of ellipse be

Question 3.
C is the centre, A A’ and B B’ are major and minor axis of ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).If
PN is the ordinate of a point P on the ellipse then show that \(\frac{(\mathrm{PN})^2}{(\mathrm{AN})(\mathrm{AN})}+\frac{(\mathrm{BC})^2}{(\mathrm{CA})^2} \)
Solution:
Let P(θ) = (a cos θ, b sin θ) be any point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

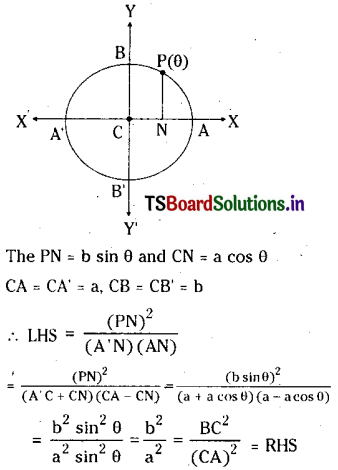
Question 4.
S and T are the foci of an ellipse and B is one end of the minor axis. If STB is an equilateral triangle, then find the
eccentricity of the ellipse.
Solution:
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 :(a>b) be an ellipse whose foci are S and T. B is the end of minor axis such that STB is an equilateral triangle.
than SB = ST = SB. Also S = (ae, 0).
T = (- ae. 0) and B = (0, b).

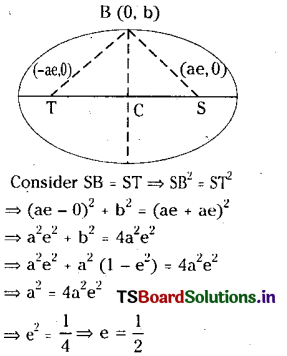
Question 5.
Show that among the points on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1,(a>b) ;(-a, 0) is the farthest point and (a, 0) is the nearest point form the focus (ae, 0).
Solution:
Let P(x, y) be any point on the ellipse so that < x < a and S = (ae, 0) is the focus. Since (x. y) is on the ellipse.

Maximum value of SP is a + ae when P(-a.0)
and Minimum value of SP is a – ae when P (a. 0).
The nearest point is (a, 0) and the farthest point is (-a, 0).

Question 6.
Find the equation of tangent and normal to the ellipse 9x² + 16y² = 144 at the end of latus rectum in the first quadrant.
Solution:
Given equation of ellipse is 9x² + 16y² = 144

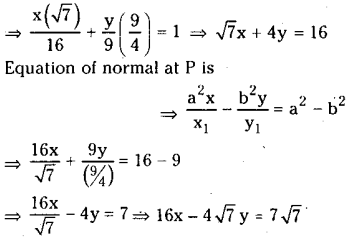
Question 7.
If a tangent to the ellipse = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b)\) meets its major axis and minor axis at M and N respectively then prove that \(\frac{a^2}{(\mathrm{CM})^2}+\frac{b^2}{(\mathrm{CN})^2}=1\) where C is the centre of the ellipse.
Solution:

Question 8.
Find the condition for the line,
(i) lx + my + n = 0 to be a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
(ii) lx + my + n = 0 to be a normal to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Solution:
Let lx + my + n = 0 be a tangent at
P (θ) (a cos θ . b sin θ) on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

(ii) Let lx + myn = 0 be a normal to the ………………  (2)
Ellipse at the point P (θ). Then equation of normal at ‘θ’ is

Question 9.
If PN is the ordinate of a point P on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and the tangent at P
meets the x-axis at T then show that (CN) (CT) = a² where C is the centre of ellipse.
Solution:
Let P (θ) = P (a cos θ, b sin θ) be a point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) .
Then the equation of the tangent at p (θ) is.

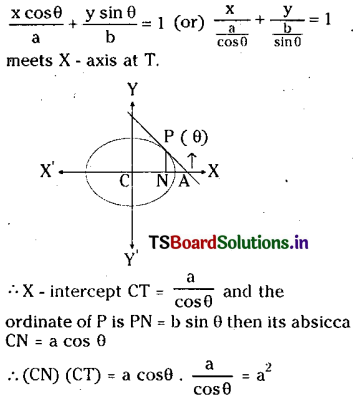
Question 10.
Show that the points of intersection of the perpendicular tangents to any ellipse lie on the circle.
Solution:
Let the equation of ellispe be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a>b)
Any tangent to the above ellipse is of the form y = mx ± \(\pm \sqrt{a^2 m^2+b^2}\)
Let the perpendicular tangents intersect at

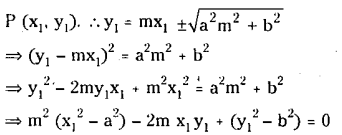
This being a quadratic is ‘rn has two roots m₁ and m₂ which corresponds to the slopes of tangents drawn from P to ellipse then

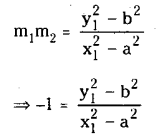
(∵ Product of slopes = – 1 for perpendicular tangents)
⇒ x₁²+y₁² = a² +b²
∴ Locus of (x₁, y₁) is x² + y² = a²+ b² which is a circle.

Long Answer Type Questions

Question 1.
If θ₁, θ₂ are the eccentric angles of the extremeties of a focal chord (other than the verticles) of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a> b) and e is its eccentricity. Then show that

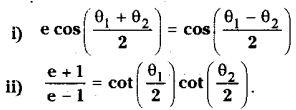
Solution:

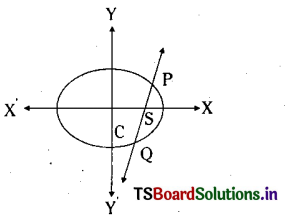
Let P(θ₁), Q(θ₂) be the two extremeties of a focal chord of the ellipse
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b)\)
∴ P = (acos θ₁, b sin θ₁),(θ₁ ≠ 0)
Q = (a cos θ₂, b sin θ₂), (θ₂ ≠ π)
and focus S = (ae, 0). Now PQ is a focal chord and hence P, S. Q are collinear.
∴ Slope of \(\overline{\mathrm{PS}}\) = slope of \(\overline{\mathrm{SQ}}\)
\(\frac{b \sin \theta_1}{a\left(\cos \theta_1-\mathrm{e}\right)}=\frac{\mathrm{b} \sin \theta_2}{\mathrm{a}\left(\cos \theta_2-\mathrm{e}\right)}\)

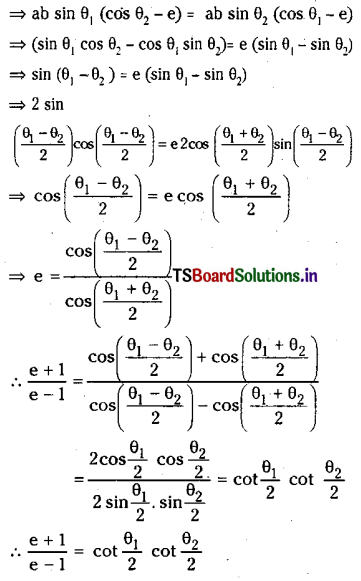
Question 2.
If the normal at one end of a latus rectum of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) passes through one end of the minor axis, then show that e⁴ + e² = 1 (e is the eccentricity of the ellipse)
Solution:
Let L be the one end of the latus rectum of \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). Then the coordinates of
\(L=\left(a e, \frac{b^2}{a}\right)\)
∴Equation of normal at L is

Question 3.
If a circle is concentric with the ellipse, find the inclination of their common tangent to the major axis of the ellipse.
Solution:
Let the circle x² + y² = r² and the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) with a> b.
The major axis of ellipse is X – axis.
If r< b <a, then the circle lies completely in the ellipse making no common tangents.
If b < a < r (ellipse lies completely in circle) no common tangent is passive.

Case (i) : If b <r <a

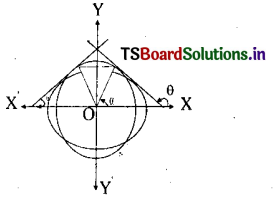
Let one of the common tangent make angle θ with positive X- axis and suppose the equation of tangent to the circle be x Cos α + y sin α = r where a is the angle made by the radius of circle with positive X – axis.
∴ \(\theta=\frac{\pi}{2}+\alpha \text { (or) } \theta=\alpha-\frac{\pi}{2}\)
Since x cos α + y sina r touches the ellipse also, we have a² cos²a + b² sin² = r²

Case (ii): When r = a the circle touches the ellipse at the ends of major axis of the ellipse so that the common tangents are x = ± a and θ = \(\frac{\pi}{2}\)

Case (iii): When r = b, the circle touches the ellipse at the ends of minor axis of ellipse so that common tangents
y = ± b making θ = 0.