Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 8 Limits and Continuity Ex 8(b) to find a better approach to solving the problems.
TS Inter 1st Year Maths 1B Limits and Continuity 8(b)
Find the right and left hand limits of the functions in 1, 2, 3 of I and 1, 2 of II at the point ‘a’ mentioned against them. Hence, check whether the functions have limits at those a’s.
I.
Question 1.
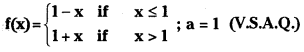
Answer:

![]()
Question 2.
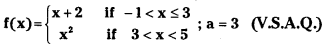
Answer:

Question 3.
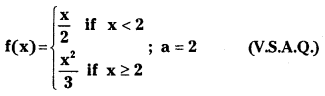
Answer:
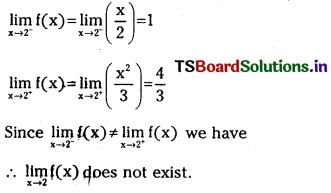
II.
Question 1.
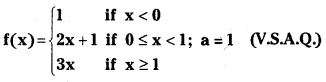
Answer:
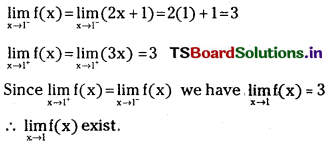
Question 2.
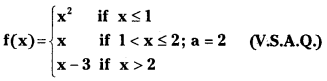
Answer:
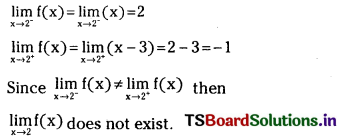
![]()
Question 3.
Show that \(\lim _{x \rightarrow 2^{-}} \frac{|x-2|}{x-2}\) = – 1 (V.S.A.Q.)
Answer:
We have x → 2– means x < 2
When x < 2, |x – 2| = – (x – 2)
![]()
Question 4.
Show that \(\lim _{x \rightarrow 0^{+}}\left(\frac{2|x|}{x}+x+1\right)\) = 3 (V.S.A.Q.)
Answer:
As x → 0+ means x > 0 and |x| = x if x > 0

Question 5.
Compute \(\lim _{x \rightarrow 2^{+}}\) and \(\lim _{x \rightarrow 2^{-}}\) ([x] + x) (S.A.Q.)
Answer:
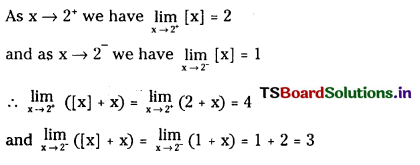
Question 6.
Show that \(\lim _{x \rightarrow 0^{-}}\) x3 cos \(\left(\frac{3}{x}\right)\) = 0 (V.S.A.Q.)
Answer:
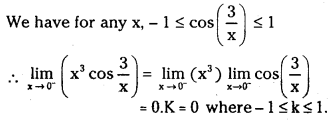
III.
Question 1.
Find \(\lim _{x \rightarrow 0}\) f(x) where (V.S.A.Q.)
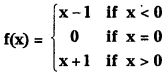
Answer:
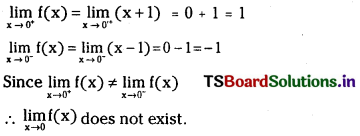
![]()
Question 2
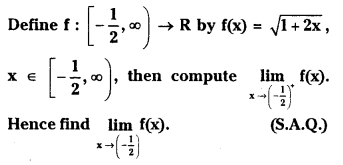
Answer:
