TS Inter 1st Year Maths 1A Solutions Chapter 2 Mathematical Induction Ex 2(a)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 2 Mathematical Induction Ex 2(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Mathematical Induction Solutions Exercise 2(a)

Using Mathematical Induction prove each of the following statement for all n ∈ N.

Question 1.
1² + 2² + 3² + …………. + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Answer:
Let S(n) be the given statement
1² + 2² + 3² + …………. + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Since 1² = \(\frac{1(1+1)(2+1)}{6}\)
⇒ 1 = 1; the statement is true for n = 1
Suppose the statement is true for n = k then
(1² + 2² + 3² + ………….. + k²) + \(\frac{k(k+1)(2 k+1)}{6}\)
We have to prove that the statement is true for n = k + 1 also then
(1² + 2² + 3² + …………… + k²) + (k + 1)²

∴ The statement is true for n = k + 1 also.
∴ By the principle of Finite Mathematical Induction S(n) is true for all n ∈ N.
i.e., 1² + 2² + 3² + ……….. + n² = \(\frac{\mathrm{n}(\mathrm{n}+1)(2 \mathrm{n}+1)}{6}\), ∀ n ∈ N

Question 2.
2.3 + 3.4 + 4.5 + ………………. upto n terms = \(\frac{n\left(n^2+6 n+11\right)}{3}\) (March 13, May 06)
Answer:
Let S(n) be the statement.
The n^th term of 2.3 + 3.4 + 4.5 + …………… is (n + 1) (n + 2)
∴ 2 . 3 + 3 . 4 + 4 . 5 + …………….. + (n + 1) (n + 2)
= \(\frac{n\left(n^2+6 n+11\right)}{3}\)
Now S(1) = 2 . 3 = \(\frac{1\left(1^2+6+11\right)}{3}\) = 6
∴ The statement is true for n = 1.
Suppose that the statement is true for n = k, then 2.3 + 3.4 + 4.5 + …………….. + (k + 1) (k + 2)
= \(\frac{k\left(k^2+6 k+11\right)}{3}\)
Adding (k + 1) th term of L.H.S both sides
S(k + 1) = 2.3 + 3.4 + 4.5 + ……………. + k (k + 1) (k + 2) + (k + 2) (k + 3)

∴ S(k + 1) = \(\frac{1}{3}\) (k + 1) [k² + 2k + 1 + 6 (k + 1) + 11]
= \(\frac{1}{3}\) (k + 1) [(k + 1)² + 6(k + 1) + 11]
∴ The statement is true for n = k + 1
So by the principle of Finite Mathematical Induction S(n) is true ∀ n ∈ N
∴ 2 . 3 + 3 . 4 + 4 . 5 + ……………. + (n + 1) (n + 2) = \(\frac{n\left(n^2+6 n+11\right)}{3}\)

Question 3.
\(\frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}\) + ……………. + \(\frac{1}{(2 n-1)(2 n+1)}\) = \(\frac{n}{2 n+1}\) (May 2014)
Answer:
Let S_n be the statement
\(\frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}\) + ……………. + \(\frac{1}{(2 n-1)(2 n+1)}\)
Then S(1) = \(\frac{1}{1 \cdot 3}=\frac{1}{2(1)+1}=\frac{1}{3}\)
∴ S(1) is true.
Suppose the statement is true for n = k, then
S(K) = \(\frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}+\ldots .+\frac{1}{(2 k-1)(2 k+1)}\) = \(\frac{\mathbf{k}}{2 \mathbf{k}+1}\)
We have to show that the statement is true for n = k + 1 also,

The statement S(n) is true for n = k + 1
∴ By the principle of Mathematical Induction S(n) is true for all n ∈ N.
∴ \(\frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}\) + ……………. + \(\frac{1}{(2 n-1)(2 n+1)}\) = \(\frac{n}{2 n+1}\)

Question 4.
4³ + 8³ + 12³ + ………… + upto n terms = 16n² (n + 1)²
Answer:
4, 8, 12, are in A.P. and nth term of A.P. is = a + (n – 1) d
= 4 + (n – 1) 4 = 4n
Let S(n) be the statement
4³ + 8³ + 12³ + ……………… + (4n)³ = 16n² (n + 1)²
Let n = 1, then
S(1) = 4³ = 16 (1 + 1)² = 64
∴ The statement is true for n = 1 also.
Suppose the statement is true for n = k then
4³ + 8³ + 12³+ ……………… + (4k)³ = 16k² (k + 1)²
We have to prove that the result is true for n = k + 1 also. Adding (k + 1) th term
= [4 (k + 1)]³ = [4k + 4]³ both sides
4³ + 8³ + 12³ + ……………….. + (4k)³ + (4k + 4)³
= 16k³ (k + 1)² + [4 (k + 1)]³
= 16 (k + 1)2 [k² + 4k + 4]
= 16 (k + 1)² (k + 2)²
= 16 (k + 1)² [(k + 1) + 1]²
Hence the result is true for n = k + 1.
∴ By the principle of Mathematical Induction S(n) is true ∀ n ∈ N.
∴ 4³ + 8³ + 12³ + ……………….. + (4n)³ = 16n² (n + 1)²

Question 5.
a + (a + d) + (a + 2d) + ……………… upto n terms = \(\frac{n}{2}\) [2a + (n – 1) d]
Answer:
Let S(n) be the statement
a + (a + d) + (a + 2d) + + [a + (n – 1) d] = \(\frac{n}{2}\) [2a + (n – 1) d]
Now S(1) is a = \(\frac{1}{2}\) [2a + 0 (d)] = a
∴ S(1) is true.
Assume that the statement is true for n = k
∴ S(k) = a + (a + d) + (a + 2d) + ……………….. + [a + (k – 1) d]
= \(\frac{k}{2}\) [2a + (k – 1) d]
We have to prove that the statement is true for n = k + 1 also.
Adding a + kd both sides
a + (a + d) + ……………. + [a + (k – 1) d] + [a + kd]

∴ The statement is true for n = k + 1 also
∴ By the principle of Mathematical Induction.
S(n) is true for all n ∈ N
∴ a + (a + d) + (a + 2d) + + [a + (n – 1) d] = \(\frac{n}{2}\) [2a + (n -1) d]

Question 6.
a + ar + ar² + ………………… + n terms = \(\frac{a\left(r^n-1\right)}{r-1}\), r ≠ 1 (March 2011)
Answer:
Let S(n) be the statement
a + ar + ar² + ………….. + ar^{n – 1} = \(\frac{\left(\mathrm{r}^{\mathrm{n}}-1\right)}{\mathrm{r}-1}\), r ≠ 1
Then S(1) = a = \(\frac{a\left(r^1-1\right)}{r-1}\) = a
∴ The result is true for n = 1
Suppose the statement is true for n = k then
a + ar + ar² + …………… + ar = \(\frac{a\left(r^k-1\right)}{r-1}\), r ≠ 1
We have to prove that the result is true for n = k + 1 also.
Adding ar^k both sides
(a + ar + ar² + ………….. + ar^{k – 1} + ar^k)

∴ The statement is true for n = k + 1 also
∴ By the principle of Mathematical Induction p(n) is true for all n ∈ N
a + ar + ar² + ………………… + n terms = \(\frac{a\left(r^n-1\right)}{r-1}\), r ≠ 1

Question 7.
2 + 7 + 12 + ………. + (5n – 3) = \(\frac{n(5 n-1)}{2}\)
Answer:
Let S(n) be the statement
2 + 7 + 12 + ………. + (5n – 3) = \(\frac{n(5 n-1)}{2}\) = \(\frac{1(5-1)}{2}\) = 2,
Since S(1) = 2,
S(1) is true.
Suppose the statement is true for n k then
(2 + 7 + 12 + ………….. + (5k – 3) = \(\frac{k(5 k-1)}{2}\)
We have to show that S(n) is true for n = k + 1 also.
Adding (k + 1)th term 5 (k + 1) – 3 = 5k + 2 both sides
[2 + 7 + 12 + ……. + 5k – 3)] + (5k + 2)

∴ S(n) is true for n = k + 1 also
∴ By the principal of Mathematical Induction
S(n) is true ∀ n ∈ N
∴ 2 + 7 + 12 + …………… + (5n – 3) = \(\frac{n(5 n-1)}{2}\).

Question 8.
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \ldots \ldots\left(1+\frac{2 n+1}{n^2}\right)\) = (n + 1)² (March 2015-A.P)
Answer:
Let S_n be the statement

∴ S(n) is true for n = 1
Suppose S_n is true for n = k then
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \ldots\left(1+\frac{2 \mathrm{k}+1}{\mathrm{k}^2}\right)\)
= (k + 1)² ………………. (1)
We have to prove that the statement is true for n = k + 1 also
(k + 1) th term is

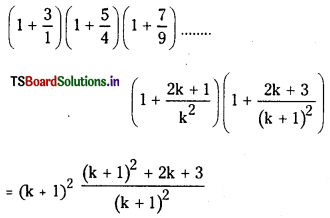
= k² + 4k + 4
= (k + 2)²
∴ S(n) is true for n = k + 1 also
∴ By the principal of Mathematical Induction S(n) is true for ∀ n ∈ N

Question 9.
(2n + 1) < (n + 3)²
Answer:
Let S(n) be the statement
When n = 1, then 9 < 16
∴ S(n) is true for n = 1
Suppose S(n) is true for n = k
then(2k + 7) < (k + 3)² …………….. (1)
We have to prove that the result is true for n = k + 1
i.e., 2(k + 1) + 7 < (k + 4)²
∴ 2 (k + 1) + 7 = 2k + 2 + 7 = (2k + 7) + 2 < (k + 3)² + 2 (From (1))
= k² + 6k + 9 + 2
= k² + 6k + 11 < (k² + 6k + 11) + (2k + 5)
= k² + 8k + 16
= (k + 4)²
∴ S(n) is true for n = k + 1 also
By principle of Mathematical Induction
S(n) is true ∀ n ∈ N

Question 10.
1² + 2² + ……………. + n² > \(\frac{n^3}{3}\)
Answer:
Let S(n) be the statement
When n = 1, then 1 > \(\frac{1}{3}\)
∴ S(n) is true for n = 1
Assume S(n) to be true for n = k then
1² + 2² + ……………. + k² > \(\frac{k^3}{3}\)
We have to prove that the result is true for n = k + 1 also.

∴ S(n) is true for n = k + 1 also
∴ By principle of Mathematical Induction.
S(n) is true ∀ n ∈ N

Question 11.
4ⁿ – 3n – 1 is divisible by 9
Answer:
Let S(n) be the statement,
4ⁿ – 3n – 1 is divisible by 9
For n = 1, 4 – 3 – 1 = 0 is divisible by 9
∴ Statement S(n) is true for n = 1.
Suppose the statement S(n) is true for n = k
Then 4^k – 3k – 1 is divisible by 9.
∴ 4^k – 3k – 1 = 9t for t ∈ N ……………. (1)
We have to show that statement is true for n = k + 1 also.
From (1), 4^k = 9t + 3k + 1
∴ 4^{k + 1} – 3 (k + 1) – 1 = 4 . 4^k – 3 (k + 1) – 1
= 4 (9t + 3k + 1) – 3k – 3 – 1
= 4 (9t) + 9k
= 9 (4t + k) divisible by 9
(∵ 4t + k is an integer)
Hence, S(n) is true for n = k + 1 also.
∴ 4^{k + 1} – 3 (k + 1) – 1 is divisible by 9
∴ The statement is true for n = k + 1
∴ By the principle of Mathematical Induction.
S(n) is true for all n e K
∴ 4n – 3n – 1 is divisible by 9

Question 12.
3.5^{2n + 1} + 2^{3n + 1} is divisible by 17 (May 2012, 2008)
Answer:
Let S_n be the statement
3.5^{2n + 1} + 2^{3n + 1} is divisible by 17
S(1) is 3 . 5^{2(1) + 1} + 2^{3 (1) + 1}
= 3 . 5³ + 2⁴ = 3 (125) + 16
= 375 + 16 = 391 is divisible by 17
Hence, S(n) is true for n = 1.
Suppose that the statement is true for n = k, then
3.5^{2k + 1} + 2^{3k + 1} is divisible by 17 and
3.52^{k + 1} + 2^{3k + 1} = 17t for t ∈ N
then we have to show that the result is true for n = k + 1 also
Consider 3.5^{2(k + 1)} + 1 + 2^{3(k + 1)} + 1
= 3.5^{2k + 1} . 5² + 2^{3(k + 1)} . 2
= (17t – 2^{3k + 1}) 5² + 2^{3k + 3} . 2
= 17t (25) – 2^3k (50) + 2^3k (16)
= 17 t (25) + 2^3k (16 – 50)
= 17 t (25) – 34 2^3k
= 17 [25t – 2^{3k + 1}
25t – 2^{3k + 1} is an integer.
∴ 3.5^{2(k + 1) + 1} + 2^{3 (k + 1) + 1} is divisible by 17.
∴ The statement S(n) is true for n = k + 1 also.
∴ By the principle of Mathematical induction S(n) is true for ∀n ∈ N
∴ 3.5^{2n + 1} + 2^{3n + 1} is divisible by 17

Question 13.
1.2.3 + 2.3.4 + 3.4.5 + ……………. upto n terms = \(\frac{n(n+1)(n+2)(n+3)}{4}\). (March 2015-T.S) (Mar. 08)
Answer:
The n^th term of the given series is n (n + 1) (n + 2) and let S_n be the statement.
1.2.3 + 2.3.4 + 3.4.5 + ……………. + n (n + 1) (n + 2)
= \(\frac{n(n+1)(n+2)(n+3)}{4}\)
For n = 1
S(1) = 1.2.3 = 6
= \(\frac{1(1+1)(1+2)(1+3)}{4}\)
= \(\frac{2(3)(4)}{4}\) = 6
∴ S(n) is true for n = 1
Let S(n) is true for n = k then
1.2.3 + 2.3.4 + 3.4.5 + ……………. + k (k + 1) (k + 2)
= \(\frac{\mathrm{k}(\mathrm{k}+1)(\mathrm{k}+2)(\mathrm{k}+3)}{4}\) …………….. (1)
We have to prove that the result is true for n = k + 1 also.
Adding (k + 1) th term, (k + 1) (k + 2) (k + 3) both sides we get
1.2.3 + 2.3.4 + 3.4.5 + ……………. + k(k + 1)(k + 2) + (k + 1) (k + 2) (k + 3)

∴ S(n) is true for n = k + 1 also.
Hence by the principle of Mathematical Induction.
S(n) is true for ∀n ∈ N
∴ 1.2.3 + 2.3.4 + 3.4.5 + ……………. + n (n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)

Question 14.
\(\frac{1^3}{1}+\frac{1^3+2^3}{1+3}+\frac{1^3+2^3+3^3}{1+3+5}\) + ……………… upto n terms = \(\frac{n}{24}\) (2n² + 9n + 13). (Mar. 14, 04, 05)
Answer:
The n^th term of the given series is

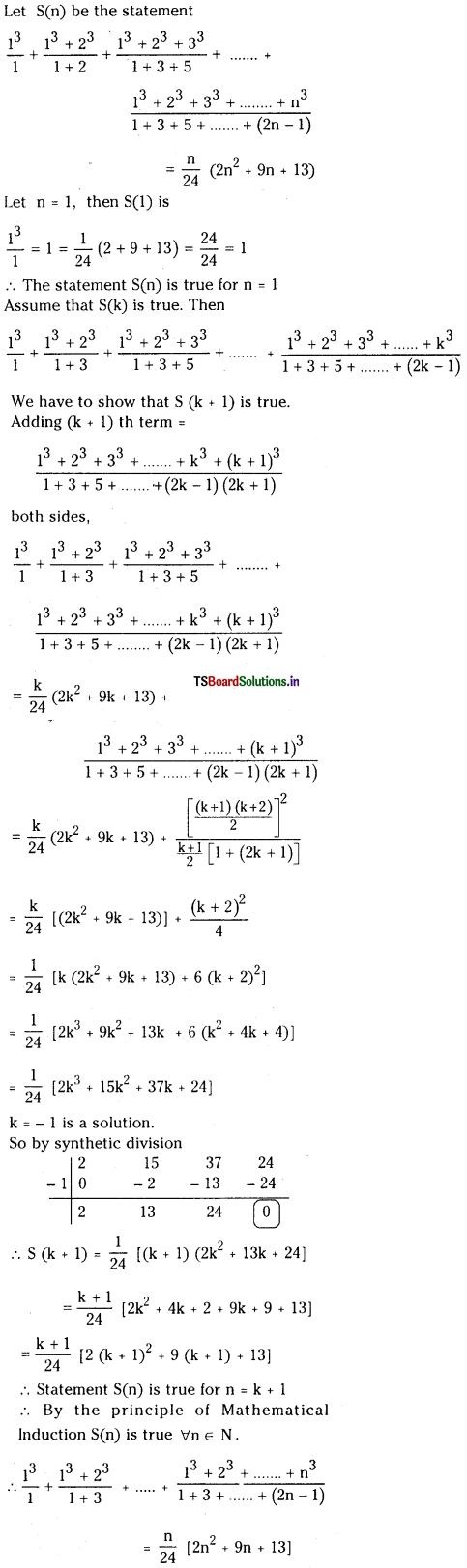
Question 15.
1² + (1² + 2²) + (1² + 2² + 3²) + ……………. upto n terms = \(\frac{n(n+1)^2(n+2)}{12}\). (March 2012)
Answer:
Let S(n) be the statement and
nth term of series is 1² + 2² + 3² + ……………… + n²
∴ S(n) = 1² + (1² + 2²) + (1² + 2² + 3²) + ……… + (1² + 2² + 3² + ………………. + n²)

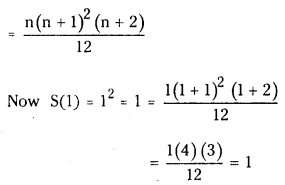
∴ S(n) is true for n = 1.
Suppose S(n) is true for n = k then
1² + (1² + 2²) + (1² + 2² + 3²) + ……… + (1² + 2² + 3² + ………………. + k²) = \(\frac{k(k+1)^2(k+2)}{12}\)
Now we have to prove that S(k + 1) is true.
So 1² + (1² + 2²) + (1² + 2² + 3²) + ……… + (1² + 2² + 3² + ………………. + k²) + (1² + 2² + 3² + ……………. + k² + (k + 1)²

∴ The statement S(n) hold for n = k + 1 also
∴ By the principle of Mathematical Induction S(n)is true ∀n ∈ N.
∴ 1² + (1² + 2²) + (1² + 2² + 3²) + (1² + 2² + 3² + …………… + n²) = \(\frac{\mathrm{n}(\mathrm{n}+1)^2(\mathrm{n}+2)}{12}\)